2018,1,5 二次函数

专题01二次函数（2个知识点3大题型1个易错点）【目录】【学习目标】1.理解二次函数的概念，能将二次函数化为一般形式2.能根据概念判断函数是不是二次函数3.了解实际问题中存在的二次函数关系及对其自变量的要求。

【知识导图】【倍速学习四种方法】【方法一】脉络梳理法知识点1．二次函数的定义1.二次函数的定义：一般地，形如y＝ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c是常数项．y═ax2+bx+c（a、b、c是常数，a≠0）也叫做二次函数的一般形式．判断函数是否是二次函数，首先是要看它的右边是否为整式，若是整式且仍能化简的要先将其化简，然后再根据二次函数的定义作出判断，要抓住二次项系数不为0这个关键条件．2.二次函数的取值范围：一般情况下，二次函数中自变量的取值范围是全体实数，对实际问题，自变量的取值范围还需使实际问题有意义．要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a 的绝对值越大，抛物线的开口越小.例1．（2022秋•霍邱县期中）下列函数表达式中，一定为二次函数的是（ ）A．y＝2x+2B．s＝3t2﹣1C．y＝ax2+bx+c D．知识点2．根据实际问题列二次函数关系式根据实际问题确定二次函数关系式关键是读懂题意，建立二次函数的数学模型来解决问题．需要注意的是实例中的函数图象要根据自变量的取值范围来确定．①描点猜想问题需要动手操作，这类问题需要真正的去描点，观察图象后再判断是二次函数还是其他函数，再利用待定系数法求解相关的问题．②函数与几何知识的综合问题，有些是以函数知识为背景考查几何相关知识，关键是掌握数与形的转化；有些题目是以几何知识为背景，从几何图形中建立函数关系，关键是运用几何知识建立量与量的等式．例2．（2022秋•无为市月考）据安徽省统计局公布的数据，初步核算2021年安徽省生产总值为42959.2亿元，若设2023年安徽省生产总值为y亿元，平均年增长的百分率为x，则y关于x的函数表达式是（ ）A．y＝42959.2（1+2x）B．y＝42959.2（1﹣x）2C．y＝42959.2x2D．y＝42959.2（1+x）2【方法二】实例探索法题型一：根据二次函数的定义求参数的值例3．（2022秋•淮北月考）如果函数y＝（m﹣2）是二次函数，则m的值为　﹣3　．例4．（2022秋•定远县期中）已知函数y＝﹣（m+2）x m2﹣2（m为常数），求当m为何值时：（1）y是x的一次函数？（2）y是x的二次函数？并求出此时纵坐标为﹣8的点的坐标．题型二：根据实际问题列二次函数的表达式例5．（2022•大观区校级开学）某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为40米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米，围成的苗圃面积为y平方米，则y关于x的函数关系式为（ ）A．y＝x（40﹣x）B．y＝x（18﹣x）C．y＝x（40﹣2x）D．y＝2x（40﹣2x）例6．（2022秋•杜集区校级月考）进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为（ ）A．y＝2a（x﹣1）B．y＝2a（1﹣x）C．y＝a（1﹣x2）D．y＝a（1﹣x）2例7．（2022秋•琅琊区校级月考）n个球队参加篮球比赛，每两队之间进行一场比赛，比赛的场次数m与球队数n（n≥2）之间的函数关系是 ．题型三：根据动态问题列二次函数的表达式例8．（2022秋·黑龙江齐齐哈尔·九年级校考阶段练习）如图，在Rt△ABC中，∠B＝90°，AC＝30cm，∠A ＝60°，动点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时动点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts，过点D作DF⊥BC于点F，连接EF．(1)若四边形AEFD为菱形，则t值为多少？(2)在点D、E的运动过程中，设四边形ADFE的面积为y，请求出y与t的函数关系式？【方法三】差异对比法易错点1根据二次函数的定义求字母参数的值式，容易忽略二次函数系数不为0这个条件而导致错误例9．（2022秋•蜀山区校级月考）若y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，则a的值是（ ）A．1B．﹣5C．﹣1D．﹣5或﹣1易错总结：求二次函数中字母参数的值，要根据二次函数定义，在保证二次函数中含自变量的代数式是整式的前提下，还必须满足自变量的最高次数是2和二次项系数不为0的条件。

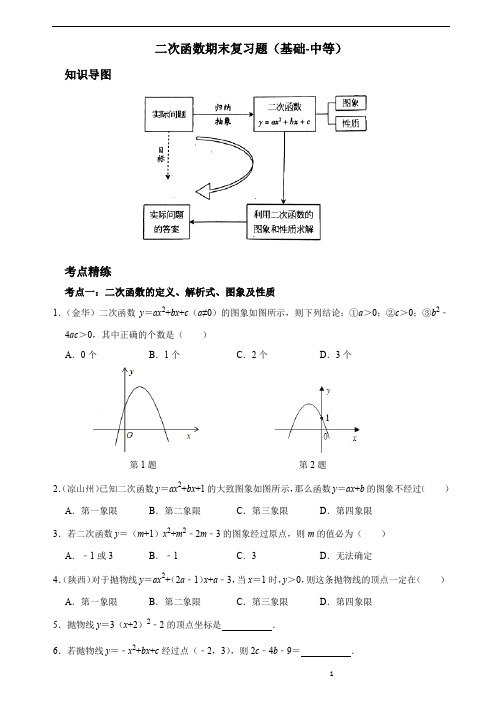
二次函数期末复习题（基础-中等）知识导图考点精练考点一：二次函数的定义、解析式、图象及性质1．（金华）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论：①a＞0；②c＞0；③b2﹣4ac＞0，其中正确的个数是（）A．0个B．1个C．2个D．3个第1题第2题2．（凉山州）已知二次函数y＝ax2+bx+1的大致图象如图所示，那么函数y＝ax+b的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限3．若二次函数y＝（m+1）x2+m2﹣2m﹣3的图象经过原点，则m的值必为（）A．﹣1或3B．﹣1C．3D．无法确定4．（陕西）对于抛物线y＝ax2+（2a﹣1）x+a﹣3，当x＝1时，y＞0，则这条抛物线的顶点一定在（）A．第一象限B．第二象限C．第三象限D．第四象限5．抛物线y＝3（x+2）2﹣2的顶点坐标是．6．若抛物线y＝﹣x2+bx+c经过点（﹣2，3），则2c﹣4b﹣9＝．7．（辽阳）如图，抛物线y＝x2﹣2x﹣3与y轴交于点C，点D的坐标为（0，﹣1），在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，则点P的横坐标为．考点二：二次函数的图象变换1．把抛物线y＝﹣2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（）A．y＝﹣2（x+1）2+1B．y＝﹣2（x﹣1）2+1C．y＝﹣2（x﹣1）2﹣1D．y＝﹣2（x+1）2﹣12．（山西）将抛物线y＝x2﹣4x﹣4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为（）A．y＝（x+1）2﹣13B．y＝（x﹣5）2﹣3C．y＝（x﹣5）2﹣13D．y＝（x+1）2﹣33．（山西）抛物线y＝﹣2x2﹣4x﹣5经过平移得到y＝﹣2x2，平移方法是（）A．向左平移1个单位，再向下平移3个单位B．向左平移1个单位，再向上平移3个单位C．向右平移1个单位，再向下平移3个单位D．向右平移1个单位，再向上平移3个单位4．如果将抛物线y＝x2﹣2x﹣1向上平移，使它经过点A（0，3），那么所得新抛物线的表达式是．5．（宁波）如图抛物线y＝ax2﹣5ax+4a与x轴相交于点A、B，且过点C（5，4）．（1）求a的值和该抛物线顶点P的坐标．（2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．考点三：用待定系数法求二次函数解析式1．（宁波）已知抛物线y＝ax2+bx+c与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．（1）求抛物线的解析式和顶点坐标；（2）请你写出一种平移的方法，使平移后抛物线的顶点落在直线y＝﹣x上，并写出平移后抛物线的解析式．2．（牡丹江）如图，抛物线y＝﹣x2+bx+c交x轴于A，B两点，交y轴于点C，对称轴是直线x＝﹣3，B（﹣1，0），F（0，1），请解答下列问题：（1）求抛物线的解析式；（2）写出抛物线顶点E的坐标，并判断AC与EF的位置关系．考点四：二次函数与一元二次方程、一元二次不等式的关系1．抛物线y＝x2﹣2x﹣3与x轴的交点个数是（）A．0个B．1个C．2个D．3个2．（随州）对于二次函数y＝x2﹣2mx﹣3，下列结论错误的是（）A．它的图象与x轴有两个交点B．方程x2﹣2mx＝3的两根之积为﹣3C．它的图象的对称轴在y轴的右侧D．x＜m时，y随x的增大而减小3．（2018•莱芜）函数y＝ax2+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）A．x＜﹣4或x＞2B．﹣4＜x＜2C．x＜0或x＞2D．0＜x＜24．如图，抛物线y＝ax2+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b2﹣4ac＝0；②a+b+c＞0；③2a﹣b＝0；④c﹣a＝3；⑤（a+c）2＞b2 。

专题02 二次函数章末重难点题型【举一反三】【考点1 二次函数的概念】二次函数的定义：一般地，形如y ＝ax 2+bx +c （a 、b 、c 是常数，a ≠0）的函数，叫做二次函数．其中x 、y 是变量，a 、b 、c 是常量，a 是二次项系数，b 是一次项系数，c 是常数项．y ═ax 2+bx +c （a 、b 、c 是常数，a ≠0）也叫做二次函数的一般形式．【例1】（2019秋•泰兴市校级月考）下列函数关系式中，y 是x 的二次函数是( )A ．2y ax bx c =++B ．21y x x =-C ．2325y x x ++D ．2(32)(43)12y x x x =+--【思路点拨】根据二次函数的定义，可得答案．【答案】解：A 、a ＝0时，不是二次函数，故A 错误；B 、不是二次函数，故B 错误；C 、是二次函数，故C 正确；D 、不含二次项，不是二次函数，故D 错误；故选：C ．【方法总结】本题考查了二次函数的定义，利用了二次函数的定义，二次函数：y ＝ax 2+bx +c （a ≠0）是二次函数．【变式1-1】（2019秋•文水县期中）已知函数：①2y ax =；②23(1)2y x =-+；③22(3)2y x x =+-；④21y x x =+．其中，二次函数的个数为( ) A ．1个 B ．2个 C ．3个 D ．4个【思路点拨】根据形如y ＝ax 2+bx +c （a ≠0）的函数为二次函数即可得到结论．【答案】解：根据定义②y ＝3（x ﹣1）2+2；③y ＝（x +3）2﹣2x 2是二次函数故选：B ．【方法总结】本题考查二次函数的定义，解题的关键正确理解二次函数的定义，本题属于基础题型．【变式1-2】（2019秋•苍溪县期中）已知函数||(2)1m y m x mx =-+-，其图象是抛物线， 则m 的取值是( )A ．2m =B ．2m =-C ．2m =±D ．0m ≠【思路点拨】根据二次函数最高次数是二次，二次项的系数不等于零，可得方程，根据解方程，可得答案．【答案】解：∵函数y ＝（m ﹣2）x |m |+mx ﹣1，其图象是抛物线，∴|m |＝2且m ﹣2≠0，解得m ＝﹣2．故选：B ．【方法总结】本题考查了二次函数的定义，利用了二次函数的定义：形如y ＝ax 2+bx +c （a ≠0）是二次函数，注意二次项的系数不等于零是解题关键．【变式1-3】（2019秋•南康区期中）若22(2)32my m x x -=-+-是二次函数，则m 等于( ) A ．2- B ．2 C ．2±D ．不能确定 【思路点拨】根据二次函数的定义求解即可．【答案】解：由题意，得m 2﹣2＝2，且m ﹣2≠0，解得m ＝﹣2，故选：A ．【考点2 二次函数与一次函数图象】【例2】（2019秋•花都区期中）在同一直角坐标系中2y ax b =+与(0,0)y ax b a b =+≠≠图象大致为( )A ．B ．C ．D ．【思路点拨】本题由一次函数y ＝ax +b 图象得到字母系数的正负，再与二次函数y ＝ax 2+b 的图象相比较看是否一致．【答案】解：A 、由抛物线可知，a ＜0，b ＜0，由直线可知，a ＜0，b ＜0，故本选项正确；B 、由抛物线可知，a ＜0，b ＞0，由直线可知，a ＞0，b ＞0，故本选项错误；C 、由抛物线可知，a ＞0，b ＜0，由直线可知，a ＞0，b ＞0，故本选项错误；D 、由抛物线可知，a ＞0，b ＞0，由直线可知，a ＜0，b ＞0，故本选项错误．故选：A ．【方法总结】本题考查了一次函数和二次函数的图象．解答该题时，一定要熟记一次函数、二次函数的图象的性质．【变式2-1】（2018秋•厦门期中）在同一平面直角坐标系中，函数2y ax bx =+与y bx a =-+的图象可能是()A ．B ．C ．D ．【思路点拨】首先根据图形中给出的一次函数图象确定a 、b 的符号，进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意，根据选项逐一讨论解析，即可解决问题．【答案】解：A 、对于直线y ＝﹣bx +a 来说，由图象可以判断，a ＞0，b ＜0；而对于抛物线y ＝ax 2+bx 来说，对称轴x ＝﹣＞0，在y 轴的右侧，符合题意，图形正确．B 、对于直线y ＝﹣bx +a 来说，由图象可以判断，a ＜0，b ＞0；而对于抛物线y ＝ax 2+bx 来说，图象应开口向下，故不合题意，图形错误．C 、对于直线y ＝﹣bx +a 来说，由图象可以判断，a ＜0，b ＜0；而对于抛物线y ＝ax 2+bx 来说，对称轴＝﹣＜0，应位于y 轴的左侧，故不合题意，图形错误，D 、对于直线y ＝﹣bx +a 来说，由图象可以判断，a ＞0，b ＜0；而对于抛物线y ＝ax 2+bx 来说，图象应开口向下，故不合题意，图形错误．故选：A ．【方法总结】此主要考查了一次函数、二次函数图象的性质及其应用问题；解题的方法是首先根据其中一次函数图象确定a 、b 的符号，进而判断另一个函数的图象是否符合题意；解题的关键是灵活运用一次函数、二次函数图象的性质来分析、判断、解答．【变式2-2】（2019秋•沂水县期中）在同一直角坐标系中，一次函数y ax c =+和二次函数2()y a x c =+的图象大致为( )A ．B ．C ．D ．【思路点拨】本题形数结合，一次函数y ＝ax +b ，可判断a 、c 的符号；根据二次函数y ＝a （x +c ）2的图象位置，可得a ，c ．经历：图象位置﹣系数符号﹣图象位置．【答案】解：A 、函数y ＝ax +c 中，a ＞0，c ＞0，y ＝a （x +c ）2中，a ＜0，c ＜0，故A 错误；B 、函数y ＝ax +c 中，a ＜0，c ＞0，y ＝a （x +c ）2中，a ＞0，c ＞0，故B 正确；C 、函数y ＝ax +c 中，a ＞0，c ＜0，y ＝a （x +c ）2中，a ＞0，c ＞0，故C 错误；D 、函数y ＝ax +c 中，a ＜0，c ＞0，y ＝a （x +c ）2中，a ＞0，c ＜0，故D 错误．故选：B ．【方法总结】此题考查二次函数图象，利用一次函数，二次函数系数及常数项与图象位置之间关系是解题关键．【变式2-3】（2016秋•工业园区期中）如图，一次函数y x =与二次函数2y ax bx c =++图象相交于A 、B两点，则函数2(1)y ax b x c =+-+的图象可能是( )A ．B ．C ．D ．【思路点拨】由直线y ＝x 与抛物线y ＝ax 2+bx +c 有两个交点，且两交点的横坐标均为负数可知：方程ax 2+bx +c ＝x ，即ax 2+（b ﹣1）x +c ＝0有两个同为异号的实数根，根据二次函数的图象与一元二次方程的根之间的关系即可得．【答案】解：由图象知直线y ＝x 与抛物线y ＝ax 2+bx +c 有两个交点，且两交点的横坐标均为负数， ∴方程ax 2+bx +c ＝x ，即ax 2+（b ﹣1）x +c ＝0有两个同为异号的实数根，∴函数y ＝ax 2+（b ﹣1）x +c 的图象与x 轴的负半轴有两个交点，故选：B ．【方法总结】本题主要考查二次函数的图象与一元二次方程的根之间的关系，由题目已知图象得出方程ax 2+bx +c ＝x ，即ax 2+（b ﹣1）x +c ＝0有两个同为异号的实数根是解题的关键．【考点3 二次函数的增减性】【例3】（2018春•利津县期末）设1(2,)A y -，2(1,)B y ，3(2,)C y 是抛物线2(1)y x k =-++上的三点，则1y ，2y ，3y 的大小关系为( )A ．123y y y >>B ．132y y y >>C ．231y y y >>D ．312y y y >>【思路点拨】由二次函数解析式可知抛物线开口向下，且对称轴为x ＝﹣1．根据图象上的点的横坐标距离对称轴的远近来判断纵坐标的大小．【答案】解：∵二次函数线y ＝﹣（x +1）2+k ，∴该二次函数的抛物线开口向下，且对称轴为：x ＝﹣1．∵A （﹣2，y 1），B （1，y 2），C （2，y 3）是抛物线y ＝﹣（x +1）2+k 上的三点，而三点横坐标离对称轴x ＝3的距离按由近到远为：（﹣2，y 1）、（1，y 2）、（2，y 3），∴y 1＞y 2＞y 3故选：A ．【方法总结】本题考查了函数图象上的点的坐标与函数解析式的关系，同时考查了函数的对称性及增减性．【变式3-1】（2019秋•宣威市校级月考）已知二次函数21572y x x =--+，若自变量x 分别取1x ，2x ，3x ，且1230x x x <<<，则对应的函数值1y ，2y ，3y 的大小关系正确的是( )A ．123y y y >>B ．123y y y <<C ．231y y y >>D ．231y y y <<【思路点拨】先根据抛物线的性质得到抛物线对称轴，则x ＞﹣时，y 随x 的增大而减小，于是由0＜x 1＜x 2＜x 3即可得到y 1，y 2，y 3的大小关系．【答案】解：抛物线的对称轴为直线x ＝﹣＝﹣，而抛物线开口向下，所以当x ＞﹣时，y 随x 的增大而减小，所以当0＜x 1＜x 2＜x 3时，y 1＞y 2＞y 3．故选：A ． 【方法总结】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．【变式3-2】（2018秋•建昌县期中）已知抛物线2(0)y ax bx c a =++<过(3,0)A -，(1,0)B ，1(5,)C y -，2(2,)D y -四点，则1y 与2y 的大小关系是( )A ．12y y >B ．12y y =C ．12y y <D ．不能确定【思路点拨】根据A （﹣3，0）、B （1，0）两点可确定抛物线的对称轴，再根据开口方向，C 、D 两点与对称轴的远近，判断y 1与y 2的大小关系．【答案】解：∵抛物线过A （﹣3，0）、B （1，0）两点，∴抛物线的对称轴为x ＝＝﹣1，∵a ＜0，抛物线开口向下，离对称轴越远，函数值越小，比较可知C 点离对称轴远，对应的纵坐标值小，即y 1＜y 2．故选：C ．【方法总结】此题主要考查了二次函数图象上点的坐标特征，比较抛物线上两点纵坐标的大小，关键是确定对称轴，开口方向，两点与对称轴的远近．【变式3-3】（2018•南海区期中）已知二次函数2y ax bx c =++中，其函数y 与自变量x 之间的部分对应值如下表所示： x ⋯0 1 2 3 ⋯ y⋯ 5 2 1 2 ⋯ 点1(A x ，1)y 、2(B x ，2)y 在函数的图象上，则当101x <<，223x <<时，1y 与2y 的大小关系正确的是()A ．y 1≥y 2B ．y 1＞y 2C ．y 1＜y 2D ．y 1≤y 2【思路点拨】根据题意知图象过（0，5）（1，2）（2，1），代入得到方程组，求出方程组的解即可得到抛物线的解析式，化成顶点式得到抛物线的对称轴，根据对称性得到A 的对称点，利用增减性即可得出答案．【答案】解：根据题意知图象过（0，5）（1，2）（2，1）， 代入得：且，解得：a ＝1，b ＝﹣4，c ＝5，∴抛物线的解析式是y ＝x 2﹣4x +5＝（x ﹣2）2+1，∴抛物线的对称轴是直线x ＝2，∵0＜x 1＜1，2＜x 2＜3，0＜x 1＜1关于对称轴的对称点在3和4之间，当x ＞2时，y 随x 的增大而增大，∴y 1＞y 2，故选：B ．【方法总结】本题主要考查对二次函数图象上点的坐标特征，解二元一次方程组，用待定系数法求二次函数的解析式等知识点的理解和掌握，能根据二次函数的对称性判断两点的纵坐标的大小是解此题的关键．【考点4 二次函数图象的平移】【例4】（2018秋•花都区期中）抛物线22y x =-经过平移得到22(1)3y x =--+，平移方法是( )A ．向左平移1个单位，再向下平移3个单位B ．向左平移1个单位，再向上平移3个单位C ．向右平移1个单位，再向下平移3个单位D ．向右平移1个单位，再向上平移3个单位【思路点拨】由抛物线y ＝﹣2x 2得到顶点坐标为（0，0），而平移后抛物线y ＝﹣2（x ﹣1）2+3的顶点坐标为（1，3），根据顶点坐标的变化寻找平移方法．【答案】解：∵抛物线y ＝﹣2x 2得到顶点坐标为（0，0），而平移后抛物线y ＝﹣2（x ﹣1）2+3的顶点坐标为（1，3），∴平移方法为向右平移1个单位，再向上平移3个单位．故选：D ．【方法总结】本题考查了抛物线的平移规律．关键是确定平移前后抛物线的顶点坐标，寻找平移规律．【变式4-1】（2019•天津校级期中）已知抛物线243y x x =-+与x 轴相交于点A ，B （点A 在点B 左侧），顶点为M ．平移该抛物线，使点M 平移后的对应点M '落在x 轴上，点B 平移后的对应点B '落在y 轴上，则平移后的抛物线解析式为( )A ．221y x x =++B ．221y x x =+-C ．221y x x =-+D ．221y x x =--【思路点拨】直接利用抛物线与坐标轴交点求法结合顶点坐标求法分别得出A ，B ，M 点坐标，进而得出平移方向和距离，即可得出平移后解析式．【答案】解：当y ＝0，则0＝x 2﹣4x +3，（x ﹣1）（x ﹣3）＝0，解得：x 1＝1，x 2＝3，∴A （1，0），B （3，0），y ＝x 2﹣4x +3＝（x ﹣2）2﹣1，∴M 点坐标为：（2，﹣1），∵平移该抛物线，使点M 平移后的对应点M '落在x 轴上，点B 平移后的对应点B '落在y 轴上，∴抛物线向上平移一个单位长度，再向左平移3个单位长度即可，∴平移后的解析式为：y ＝（x +1）2＝x 2+2x +1．故选：A ．【方法总结】此题主要考查了抛物线与坐标轴交点求法以及二次函数的平移，正确得出平移方向和距离是解题关键．【变式4-2】（2018秋•鼓楼区校级期中）在平面直角坐标系中，如果抛物线22y x =不动，而把x 轴、y 轴分别向下、向右平移2个单位长度，那么在新坐标系下抛物线的解析式为( )A ．22(2)2y x =-+B ．22(2)2y x =+-C ．22(2)2y x =--D ．22(2)2y x =++【思路点拨】根据平移确定出抛物线的顶点在新坐标系中的坐标，然后利用顶点式解析式写出即可．【答案】解：抛物线y ＝2x 2的顶点坐标为（0，0），∵把x 轴、y 轴分别向下、向右平移2个单位，∴在新坐标系中抛物线的顶点坐标为（﹣2，﹣2），∴抛物线的解析式为y ＝2（x +2）2﹣2．故选：D ．【方法总结】本题考查了二次函数图象与几何变换，利用顶点的变化确定函数解析式的变化更简便易懂．【变式4-3】（2018秋•襄州区期中）将二次函数2y x bx c =++的图象先向左平移3个单位长度，再向上平移2个单位长度得到二次函数221y x x =-+的图象，用b ，c 的值分别是( )A ．14b =，8c =-B ．2b =-，4c =C ．8b =-，14c =D ．4b =，2c =-【思路点拨】把二次函数y ＝x 2﹣2x +1的图象先向右平移3个单位长度，再向下平移2个单位长度得到y ＝x 2+bx +c 的图象．【答案】解：∵y ＝x 2﹣2x +1＝（x ﹣1）2，∴二次函数y ＝x 2﹣2x +1的图象的顶点坐标为（1，0），把点（1，0）先向右平移3个单位长度，再向下平移2个单位长度所得对应点的坐标为（4，﹣2）， ∴原抛物线解析式为y ＝（x ﹣4）2﹣2，即y ＝x 2﹣8x +14，即b ＝﹣8，c ＝14．故选：C ．【方法总结】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a 不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．【考点5 二次函数的图象与a ，b ，c 的关系】【例5】（2018秋•渝中区校级期中）已知二次函数的图象如下所示，下列5个结论：①0abc >；②0b a c -->；③42a c b +>-；④30a c +>；⑤()(1a b m am b m +>+≠的实数），其中正确的结论有( )A ．①②③B ．②③④C ．②③⑤D ．③④⑤【思路点拨】由抛物线对称轴的位置判断ab 的符号，由抛物线与y 轴的交点判断c 的符号，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【答案】解：①∵对称轴在y 轴的右侧，∴ab ＜0，由图象可知：c＞0，∴abc＜0，故①不正确；②当x＝﹣1时，y＝a﹣b+c＜0，∴b﹣a﹣c＞0，故②正确；③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，∴4a+c＞﹣2b，故③正确；④∵x＝﹣＝1，∴b＝﹣2a，∵a﹣b+c＜0，∴a+2a+c＜0，3a+c＜0，故④不正确；⑤当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m时，y＝am2+bm+c，所以a+b+c＞am2+bm+c（m≠1），故a+b＞am2+bm，即a+b＞m（am+b），故⑤正确．故②③⑤正确，故选：C．【方法总结】本题主要考查了图象与二次函数系数之间的关系，二次函数y＝ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定，熟练掌握二次函数的性质是关键．【变式5-1】（2018秋•苍溪县期中）二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac ﹣b2＜0；②3b+2c＜0；③m（am+b）+b≤a；④（a+c）2＜b2；其中正确结论的个数有（）个．A ．1B ．2C ．3D ．4【思路点拨】利用二次函数图象的相关知识与函数系数的联系，需要根据图形，逐一判断．【答案】解：∵抛物线和x 轴有两个交点，∴b 2﹣4ac ＞0，∴4ac ﹣b 2＜0，∴①正确；∵把x ＝1代入抛物线得：y ＝a +b +c ＜0，∴2a +2b +2c ＜0， ∵﹣＝﹣1，∴b ＝2a ，∴3b +2c ＜0，∴②正确；∵抛物线的对称轴是直线x ＝﹣1，∴y ＝a ﹣b +c 的值最大，即把x ＝m 代入得：y ＝am 2+bm +c ≤a ﹣b +c ，∴am 2+bm +b ≤a ，即m （am +b ）+b ≤a ，∴③正确；∵a +b +c ＜0，a ﹣b +c ＞0，∴（a +c +b ）（a +c ﹣b ）＜0，则（a +c ）2﹣b 2＜0，即（a +c ）2＜b 2，故④正确；故选：D ．【方法总结】此题主要考查了二次函数图象与系数的关系，在解题时要注意二次函数的系数与其图象的形状，对称轴，特殊点的关系，也要掌握在图象上表示一元二次方程ax 2+bx +c ＝0的解的方法，同时注意特殊点的运用．【变式5-2】（2018秋•江岸区期中）已知二次函数2(0)y ax bx c a =++≠，过(1，1)(2y ，2)y ．①若10y >时，则0a b c ++>②若a b =时，则12y y <③若10y <，20y >，且0a b +<，则0a >④若21b a =-，3c a =-，且10y >，则抛物线的顶点一定在第三象限上述四个判断正确的有( )个．A ．1B ．2C ．3D ．4【思路点拨】①若y 1＞0时，当x ＝1时，y 1＝a +b +c ，此时，确定不了y 的值，∴a +b +c ＞0，正确； ②若a ＝b 时，即函数的对称轴是x ＝﹣，分两种情况，a ＝b ＞0，则y 2＞y 1，否则，故y 1＜y 2，故错误； ③若y 1＜0，y 2＞0，即：a +b +c ＜0，4a +2b +c ＞0，而a +b ＜0，即：﹣2a ＜0，a ＞0，正确；④若b ＝2a ﹣1，c ＝a ﹣3，且y 1＞0，即：a +b +c ＞0，把b 、c 的值代入上式得：a ＞1，则b ＞1，c ＞﹣2，代入顶点坐标即可求解，正确．【答案】解：①若y 1＞0时，当x ＝1时，y 1＝a +b +c ＞0此时，正确；②若a ＝b 时，即函数的对称轴是x ＝﹣，也确定不了y 1、y 2的大小，故y 1＜y 2，错误；③若y 1＜0，y 2＞0，即：a +b +c ＜0，4a +2b +c ＞0，解得：﹣3a ﹣b ＜0，而a +b ＜0，即：﹣2a ＜0，∴a ＞0，正确；④若b ＝2a ﹣1，c ＝a ﹣3，且y 1＞0，即：a +b +c ＞0，把b 、c 的值代入上式得：a ＞1，则b ＞1，c ＞﹣2，顶点的x 坐标＝﹣＜0，顶点的y 坐标＝＝﹣2﹣＜0，故顶点一定在第三象限，正确；故选：C ．【方法总结】本题考查的是二次函数图象与系数的关系，涉及到函数基本性质、解不等式等相关知识，难度较大．【变式5-3】（2019•凉山州）二次函数2y ax bx c =++的部分图象如图所示，有以下结论：①30a b -=；②240b ac ->；③520a b c -+>；④430b c +>，其中错误结论的个数是( )A．1 B．2 C．3 D．4【思路点拨】①对称轴为x＝﹣，得b＝3a；②函数图象与x轴有两个不同的交点，得△＝b2﹣4ac＞0；③当x＝﹣1时，a﹣b+c＞0，当x＝﹣3时，9a﹣3b+c＞0，得5a﹣2b+c＞0；④由对称性可知x＝1时对应的y值与x＝﹣4时对应的y值相等，当x＝1时a+b+c＜0，4b+3c＝3b+b+3c ＝3b+3a+3c＝3（a+b+c）＜0；【答案】解：由图象可知a＜0，c＞0，对称轴为x＝﹣，∴x＝﹣＝﹣，∴b＝3a，①正确；∵函数图象与x轴有两个不同的交点，∴△＝b2﹣4ac＞0，②正确；当x＝﹣1时，a﹣b+c＞0，当x＝﹣3时，9a﹣3b+c＞0，∴10a﹣4b+2c＞0，∴5a﹣2b+c＞0，③正确；由对称性可知x＝1时对应的y值与x＝﹣4时对应的y值相等，∴当x＝1时a+b+c＜0，∵b＝3a，∴4b+3c＝3b+b+3c＝3b+3a+3c＝3（a+b+c）＜0，∴4b+3c＜0，④错误；故选：A ．【方法总结】本题考查二次函数的图象及性质；熟练掌握从函数图象获取信息，将信息与函数解析式相结合解题是关键．【考点6 二次函数与一元二次方程之间的关系】【例6】（2019春•天心区校级期中）函数2y ax bx c =++的图象如图所示，那么关于一元二次方程220ax bx c ++-=的根的情况是( )A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根【思路点拨】由图可知ax 2+bx +c ﹣2＝0的根的情况即图中图象和x 轴交点的横坐标，为两个不相等的正数．【答案】解：∵函数的顶点的纵坐标为3，∴直线y ＝3与函数图象只有一个交点，∴y ＝ax 2+bx +c ﹣2，相当于函数y ＝ax 2+bx +c 的图象向下平移2个单位，∴方程ax 2+bx +c ﹣2＝0的根为两个不相等的实数根．故选：A ．【方法总结】本题考查了二次函数与一元二次方程的知识，关键是通过看图象直线y ＝3与抛物线的交点个数．【变式6-1】（2019春•安吉县期中）如图，抛物线2y x mx =-+的对称轴为直线2x =，若关于x 的一元二次方程20(x mx t t +-=为实数）在13x <<的范围内有解，则t 的取值范围是( )A ．﹣5＜t ≤4B ．3＜t ≤4C ．﹣5＜t ＜3D ．t ＞﹣5【思路点拨】先利用抛物线的对称轴方程求出m 得到抛物线解析式为y ＝﹣x 2+4x ，配方得到抛物线的顶点坐标为（2，4），再计算出当x ＝1或3时，y ＝3，结合函数图象，利用抛物线y ＝﹣x 2+4x 与直线y ＝t 在1＜x ＜3的范围内有公共点可确定t 的范围．【答案】解：∵抛物线y ＝﹣x 2+mx 的对称轴为直线x ＝2， ∴﹣＝2，解得m ＝4，∴抛物线解析式为y ＝﹣x 2+4x ，抛物线的顶点坐标为（2，4），当x ＝1时，y ＝﹣x 2+4x ＝3；当x ＝3时，y ＝﹣x 2+4x ＝3，∵关于x 的一元二次方程x 2+mx ﹣t ＝0（t 为实数）在1＜x ＜3的范围内有解，∴抛物线y ＝﹣x 2+4x 与直线y ＝t 在1＜x ＜3的范围内有公共点，∴3＜t ≤4．故选：B ．【方法总结】本题考查了抛物线与x 轴的交点：把求二次函数y ＝ax 2+bx +c （a ，b ，c 是常数，a ≠0）与x 轴的交点坐标问题转化为解关于x 的一元二次方程．也考查了二次函数的性质．【变式6-2】（2018秋•福清市期中）函数21y x x =+-中x 与y 的对应关系如下表所示，方程210x x +-=两实数根中有一个正根1x ，下列对1x 的估值正确的是( ) x ⋯0.5 0.55 0.6 0.65 0.7 0.75 ⋯ y ⋯ 0.25- 0.1475- 0.04- 0.0725 0.19 0.3125 ⋯A ．10.50.55x <<B ．10.550.6x <<C ．10.60.65x <<D ．10.650.7x << 【思路点拨】利用x ＝0.6时，y ＝x 2+x ﹣1＝﹣0.04；x ＝0.65时，y ＝x 2+x ﹣1＝0.0725，从而可判断当0.6＜x ＜0.65时，y ＝x 2+x ﹣1的值能等于0，从而得到方程x 2+x ﹣1＝0一个正根x 1的范围．【答案】解：∵x ＝0.6时，y ＝x 2+x ﹣1＝﹣0.04；x ＝0.65时，y ＝x 2+x ﹣1＝0.0725，∴当0.6＜x ＜0.65时，y ＝x 2+x ﹣1的值能等于0，∴方程x 2+x ﹣1＝0两实数根中有一个正根x 1，则0.6＜x 1＜0.65．故选：C ．【方法总结】本题考查了抛物线与x 轴的交点：把求二次函数y ＝ax 2+bx +c （a ，b ，c 是常数，a ≠0）与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标．【变式6-3】（2019秋•萧山区期中）已知关于x 的方程2()()0x m x n +--=，存在a ，b 是方程2()()0x m x n +--=的两个根，则实数m ，n ，a ，b 的大小关系可能是( )A ．m a b n <<<B ．m a n b <<<C ．a m b n <<<D ．a m n b <<<【思路点拨】令抛物线解析式中y ＝0，得到方程的解为a ，b ，即为抛物线与x 轴交点的横坐标为a ，b ，再由抛物线开口向上得到a ＜x ＜b 时y 小于0，得到x ＝m 与n 时函数值大于0，即可确定出m ，n ，a ，b 的大小关系．【答案】解：令函数y ＝2+（x ﹣m ）（x ﹣n ）＝x 2﹣（m +n ）x +mn +2，∴抛物线开口向上，令y ＝0，根据题意得到方程（x ﹣m ）（x ﹣n ）＝﹣2的两个根为a ，b ，∵当x ＝m 或n 时，y ＝2＞0，∴实数m ，n ，a ，b 的大小关系为m ＜a ＜b ＜n ．故选：A ．【方法总结】本题考查了一元二次方程的根与系数之间的关系，难度较大，熟练掌握抛物线的性质是解本题的关键．【考点7 二次函数解析式】【例7】经过(4,0)A ，(2,0)B -，(0,3)C 三点的抛物线解析式是 ．【思路点拨】根据A 与B 坐标特点设出抛物线解析式为y ＝a （x ﹣2）（x ﹣4），把C 坐标代入求出a 的值，即可确定出解析式．【答案】解：根据题意设抛物线解析式为y ＝a （x +2）（x ﹣4），把C （0，3）代入得：﹣8a ＝3，即a ＝﹣，则抛物线解析式为y ＝﹣（x +2）（x ﹣4）＝﹣x 2+x +3，故答案为y ＝﹣x 2+x +3．【方法总结】此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．【变式7-1】若二次函数2y ax bx c =++的x 与y 的部分对应值如下表： x 7- 6- 5- 4-3- 2- y 27- 13- 3- 3 53 则二次函数的解析式为 ．【思路点拨】取三组对应值（﹣4，3）、（﹣3，5）、（﹣2，3）代入y＝ax2+bx+c得到关于a、b、c 的方程组，然后解方程组求出a、b、c的值，从而得到抛物线解析式．【答案】解：把（﹣4，3）、（﹣3，5）、（﹣2，3）代入y＝ax2+bx+c得，解得．所以抛物线解析式为y＝﹣2x2﹣12x﹣13．故答案为y＝﹣2x2﹣12x﹣13．【方法总结】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．【变式7-2】（2019秋•荣成市期中）二次函数在32x=时，有最小值14-，且函数的图象经过点(0,2)，则此函数的解析式为．【思路点拨】由条件可知其顶点坐标为（，），可设顶点式，再把点（0，2）代入可求得函数的解析式．【答案】解：∵二次函数在x＝时，有最小值，∴抛物线的顶点是（，），∴设此函数的解析式为y＝a（x﹣）2﹣，∵函数图象经过点（0，2），∴2＝a（0﹣）2﹣，解得a＝1，∴此函数的解析式为y＝（x﹣）2﹣，即y＝x2﹣3x+2．故答案为y＝x2﹣3x+2．【方法总结】本题主要考查了用待定系数法求二次函数解析式，在已知抛物线顶点坐标的情况下，通常用顶点式设二次函数的解析式．【变式7-3】（2013秋•潜山县校级月考）抛物线2y ax bx c =++与x 轴两个交点为(1,0)-，(3,0)，其形状与抛物线22y x =相同，则抛物线解析式为 ． 【思路点拨】根据抛物线形状相同则a 的值相同，再将（﹣1，0），（3，0）代入抛物线求出b ，c 的值即可．【答案】解：∵抛物线y ＝ax 2+bx +c 与x 轴两个交点为（﹣1，0），（3，0），其形状与抛物线y ＝2x 2相同，∴或，∴解得：或，∴抛物线解析式为：y ＝2x 2﹣4x ﹣6或y ＝﹣2x 2+4x +6．故答案为：y ＝2x 2﹣4x ﹣6或y ＝﹣2x 2+4x +6．【方法总结】此题主要考查了待定系数法求二次函数解析式，得出a 的值是解题关键．【考点8 二次函数的应用—销售问题】【例8】（2018秋•鼓楼区校级期中）某公司投资销售一种进价为每件15元的护眼台灯．销售过程中发现，每月销售量y （件)与销售单价x （元)之间的关系可近似的看作一次函数：20800y x =-+，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．（1）设该公司每月获得利润为w （元)，求每月获得利润w （元)与销售单价x （元)之间的函数关系式，并确定自变量x 的取值范围．（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？【思路点拨】（1）由题意得，每月销售量与销售单价之间的关系可近似看作一次函数，利润＝（定价﹣进价）×销售量，从而列出关系式；（2）首先确定二次函数的对称轴，然后根据其增减性确定最大利润即可；【答案】解：（1）由题意，得：w ＝（x ﹣15）•y ＝（x ﹣15）•（﹣20x +800）＝﹣20x 2+1100x ﹣12000， 即w ＝﹣20x 2+1100x ﹣12000（15≤x ≤24）；（2）对于函数w ＝﹣20x 2+1100x ﹣12000（15≤x ≤24）的图象的对称轴是直线x ＝27.5又∵a ＝﹣20＜0，抛物线开口向下．∴当15≤x≤24时，W随着x的增大而增大，∴当x＝24时，W＝2880，答：当销售单价定为24元时，每月可获得最大利润，最大利润是2880元．【方法总结】此题考查二次函数的性质及其应用，还考查抛物线的基本性质，另外将实际问题转化为求函数最值问题，从而来解决实际问题．【变式8-1】（2019春•宿豫区期中）某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场采取了降价措施．假设在一定范围内，衬衫的单价每降1元，商场平均每天可多售出2件，设衬衫的单价降x元，每天获利y元．（1）如果商场里这批衬衫的库存只有44件，那么衬衫的单价应降多少元，才能使得这批衬衫一天内售完，且获利最大，最大利润是多少？（2）如果商场销售这批衬衫要保证每天盈利不少于1200元，那么衬衫的单价应降多少元？【思路点拨】（1）列出y＝44（40﹣x）＝﹣44x+1760，根据一次函数的性质求解；（2）根据题意列出y＝（20+2x）（40﹣x）＝﹣2（x﹣15）2+1250，结合二次函数的性质求解；【答案】解：（1）y＝44（40﹣x）＝﹣44x+1760，∵20+2x≥44，∴x≥12，∵y随x的增大而减小，∴当x＝12时，获利最大值1232；答：如果商场里这批衬衫的库存只有44件，那么衬衫的单价应12元，才能使得这批衬衫一天内售完，且获利最大1232元；（2）y＝（20+2x）（40﹣x）＝﹣2（x﹣15）2+1250，当y＝1200时，1200＝﹣2（x﹣15）2+1250，∴x＝10或x＝20，∵当x＜15时，y随x的增大而增大，当x＞15时，y随x的增大而减小，当10≤x≤20时，y≥1200，答：如果商场销售这批衬衫要保证每天盈利不少于1200元，那么衬衫的单价应降不少于10元且不超过20元；【方法总结】本题考查一次函数和二次函数的性质；能够从情境中列出函数关系式，借助函数的性质解决实际问题；【变式8-2】（2019春•安吉县期中）为建设美丽家园，某社区将辖区内的一块面积为21000m 的空地进行绿化，一部分种草，剩余部分栽花，设种草部分的面积为2()x m ，种草所需费用1y （元)与2()x m 的函数关系图象如图所示，栽花所需费用2y （元)与2()x m 的函数关系式为220.012030000(01000)y x x x =--+．（1）求1y （元)与2()x m 的函数关系式；（2）设这块21000m 空地的绿化总费用为W （元)，请利用W 与x 的函数关系式，求绿化总费用W 的最大值．【思路点拨】（1）根据函数图象利用待定系数法即可求得y 1（元）与x （m 2）的函数关系式（2）总费用为W ＝y 1+y 2，列出函数关系式即可求解【答案】解：（1）依题意当0≤x ≤600时，y 1＝k 1x ，将点（600，18000）代入得18000＝600k 1，解得k 1＝30 ∴y 1＝30x当600＜x ≤1000时，y 1＝k 2x +b ，将点（600，18000），（1000，26000）代入得 ，解得∴y 1＝20x +600综上，y 1（元）与x （m 2）的函数关系式为：（2）总费用为：W ＝y 1+y 2∴W ＝ 整理得故绿化总费用W的最大值为32500元【方法总结】本题主要考查二次函数在生活中的实际应用．根据函数解析式即可求最大值，但要注意自变量的取值范围．【变式8-3】（2019秋•沂源县期末）某公司生产的某种商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件)与时间t（天)的关系如下表：时间t（天) 1 3 5 10 36 ⋯94 90 86 76 24 ⋯日销售量m（件)未来40天内，前20天每天的价格y1（元/件）与时间t（天）的函数关系式为y1＝t+25（1≤t≤20且t 为整数），后20天每天的价格y2（元/件）与时间t（天）的函数关系式为y2＝﹣t+40（21≤t≤40且t为整数）．下面我们就来研究销售这种商品的有关问题：（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m（件)与t（天)之间的表达式；（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？【思路点拨】（1）从表格可看出每天比前一天少销售2件，所以判断为一次函数关系式；（2）日利润＝日销售量×每件利润，据此分别表示前20天和后20天的日利润，根据函数性质求最大值后比较得结论．【答案】解：（1）经分析知：m与t成一次函数关系．设m＝kt+b（k≠0），将t＝1，m＝94，t＝3，m＝90代入，解得，∴m＝﹣2t+96；（2）前20天日销售利润为P1元，后20天日销售利润为P2元，则P1＝（﹣2t+96）（t+25﹣20）＝﹣（t﹣14）2+578，∴当t＝14时，P1有最大值，为578元．。

第6讲二次函数与一元二次方程知识定位讲解用时：3分钟A、适用范围：人教版初三，基础一般B、知识点概述：本讲义主要用于人教版初三新课，本节课我们主要学习二次函数与一元二次方程之间的联系，能够根据二次函数与x轴的交点坐标联系相应方程的解的情况，此外了解二次函数与不等式之间的关系，能够根据图象写出相应不等式的解集等，本节课的难点是二次函数与方程、不等式之间的联系考查，希望同学们能够认真学习。

知识梳理讲解用时：10分钟二次函数与一元二次方程之间的关联求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标。

（1）二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系：①①=b2﹣4ac决定抛物线与x轴的交点个数；①①=b2﹣4ac＞0时，抛物线与x轴有2个交点；①①=b2﹣4ac=0时，抛物线与x轴有1个交点；①①=b2﹣4ac＜0时，抛物线与x轴没有交点．（2）二次函数的交点式：y=a（x﹣x1）（x﹣x2）（a，b，c是常数，a≠0），可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0），相应一元二次方程的根就是x1和x2.课堂精讲精练【例题1】在平面直角坐标系xOy中，二次函数y=x2+x+1的图象如图所示，则方程x2+ x+1=0的根的情况是（）。

A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．无法判断【答案】B【解析】此题主要考查了抛物线与x轴的交点，二次函数y=x2+x+1的图象如图所示，图象与x轴有两个交点，则方程x2+x+1=0的根的情况是：有两个不相等的实数根，故选：B．讲解用时：3分钟解题思路：直接利用二次函数图象得出方程x2+x+1=0的根的情况，即抛物线与x轴的交点情况，进而得出答案。

教学建议：利用数形结合分析。

第13讲二次函数的图像与性质知识点一：二次函数的概念及解析式关键点拨与对应举例1.一次函数的定义形如y＝ax2＋bx＋c (a，b，c是常数，a≠0)的函数，叫做二次函数.例：如果函数y=(a－1)x2是二次函数，那么a的取值范围是a≠0.【例题1】（2018•奉贤区一模）下列函数中是二次函数的是（）A．y=2（x﹣1）B．y=（x﹣1）2﹣x2C．y=a（x﹣1）2D．y=2x2﹣1【例题2】函数的图象是抛物线，则m=．知识点二：二次函数的图象与性质3.二次函数的图象和性质图象（1）比较二次函数函数值大小的方法：①直接代入求值法；②性质法：当自变量在对称轴同侧时，根据函数的性质判断；当自变量在对称轴异侧时，可先利用函数的对称性转化到同侧，再利用性质比较；④图象法：画出草图，描点后比较函数值大小.失分点警示（2）在自变量限定范围求二次函数的最值时，首先考虑对称轴是否在取值范围内，而不能盲目根据公式求解.例：当0≤x≤5时，抛物线y=x2+2x+7的最小值为.开口向上向下对称轴x＝2ba-顶点坐标24,24b ac ba a⎛⎫--⎪⎝⎭增减性当x>2ba-时，y随x的增大而增大；当x＜2ba-时，y随x的增大而减小.当x>2ba-时，y随x的增大而减小；当x＜2ba-时，y随x的增大而增大.最值x=2ba-，y最小＝244ac ba-.x=2ba-，y最大＝244ac ba-.考点1 ：二次函数的图像（1）二次函数y=ax2（a≠0）的图象的画法：①列表：先取原点（0，0）然后以原点为中心对称地选取x值求出函数值，列表．②描点：在平面直角坐标系中描出表中的各点．③连线：用平滑的曲线按顺序连接各点．④在画抛物线时，取的点越密集，描出的图象就越精确，但取点多计算量就大，故一般在顶点的两侧各取三四个点即可．连线成图象时，要按自变量从小到大（或从大到小）的顺序用平滑的曲线连接起来．画抛物线y=ax2（a≠0）的图象时，还可以根据它的对称性，先用描点法描出抛物线的一侧，再利用对称性画另一侧．xyy=ax2+bx+c(a＞0)Oxyy=ax2+bx+c(a＜0)O【例题剖析】二次函数的图像基本判断【例题1】（2017•河南模拟）二次函数y=﹣x2+bx+c的图象如图所示，则一次函数y=bx+c的图象不经过第（）象限．A.一B．二C．三D．四【例题2】（2016秋•慈溪市期末）二次函数y=﹣x2﹣2x+3的图象大致是（）A．B．C．D．【例题3】（2016秋•路北区期末）抛物线y=x2，y=﹣3x2，y=﹣x2，y=2x2的图象开口最大的是（）A．y=x2B．y=﹣3x2C．y=﹣x2D．y=2x2【例题4】（2017秋•诸暨市校级期中）函数y=x2+1与y=x2+2的图象的不同之处是（）A．对称轴B．开口方向C．顶点D．形状【例题剖析】二次函数与一次函数的综合图像判断【模型A】【例题1】（2017秋•肇源县期末）一次函数y=ax+b（a≠0）与二次函数y=ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．【例题2】在同一坐标系中，一次函数y=ax+b与二次函数y=ax2+b的大致图象为（）A．B．C．D．【模型B】【例题1】已知函数y=ax2+bx+c的图象如图所示，则函数y=ax+b的图象是（）A B C D【例题2】（2017•曲江区校级三模）已知二次函数y=a（x﹣1）2+c的图象如图，则一次函数y=ax+c的大致图象可能是（）A．B．C．D．【例题3】（2017秋•颍州区期中）一次函数y=ax+b（a≠0，b≠0）的图象如图所示，则二次函数y=bx2+a的大致图象是（）A．B．C．D．【模型C】【例题1】当ab＞0时，y=ax2与y=ax+b的图象大致是（）A．B．C．D．【例题2】（2017•广阳区二模）当ab＜0时，y=ax2与y=ax+b的图象大致是（）A．B．C．D．【例题3】（2016•重庆校级二模）已知正比例函数y=x与二次函数y=ax2+bx+c 的图象如图所示，则二次函数y=ax2+（b﹣1）x+c的图象可能是（）A．B．C．D．【例题4】（2016秋•宁海县期中）已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，当x=2时，y的值为．考点2 ：二次函数的性质二次函数y=ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x=﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y=ax2+bx+c（a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x=﹣时，y取得最大值，即顶点是抛物线的最高点．③抛物线y=ax2+bx+c（a≠0）的图象可由抛物线y=ax2的图象向右或向左（右）平移|﹣|个单位，再向上或向下平移||个单位得到的．【例题剖析】二次函数的对称轴【例题1】（2017秋•遵义期末）如图，若抛物线y=ax2+bx+c上的P（3，0），Q两点关于它的对称轴x=1对称，则Q点的坐标为（）A．（﹣4，0）B．（﹣3，0）C．（﹣2，0）D．（﹣1，0）【例题2】（2017•武侯区模拟）二次函数y=2x2+4x﹣3的图象的对称轴为（）A．直线x=2B．直线x=4C．直线x=﹣3D．直线x=﹣1【例题3】（2017秋•潮南区期末）抛物线y=（x+1）2+2的对称轴为，顶点坐标是．【例题剖析】二次函数的顶点【例题1】抛物线y=2x2﹣4的顶点在（）A．x轴上B．y轴上C．第三象限D．第四象限【例题2】（2018•崇明县一模）抛物线y=2（x+3）2﹣4的顶点坐标是（）A．（3，4）B．（3，﹣4）C．（﹣3，4）D．（﹣3，﹣4）【例题3】（2017•凉山州二模）若k为任意实数，则抛物线y=﹣2（x﹣k）2+k 的顶点在（）A．直线y=x上B．直线y=﹣x上C．x轴上D．y轴上【例题4】如果二次函数y=x2﹣8x+m﹣1的顶点在x轴上，那么m=．【例题5】已知二次函数y=ax2﹣2x﹣2（a≠0）图象的顶点为（1，﹣3），则a 的值为（）A．﹣2B．﹣1C．2D．1【例题6】（2017•宁波）抛物线y=x2﹣2x+m2+2（m是常数）的顶点在（）A．第一象限B．第二象限C．第三象限D．第四象限【例题剖析】二次函数的增减性【例题1】二次函数y=x2﹣（12﹣k）x+12，当x＞1时，y随着x的增大而增大，当x＜1时，y随着x的增大而减小，则k的值应取（）A．12B．11C．10D．9【例题2】（2016秋•文安县期末）在二次函数y=﹣x2+2x+1的图象中，若y随x的增大而增大，则x的取值范围是（）A．x＞1B．x＜1C．x＞﹣1D．x＜﹣1【例题3】已知二次函数y=﹣3（x﹣h）2+5，当x＞﹣2时，y随x的增大而减小，则有（）A．h≥﹣2B．h≤﹣2C．h＞﹣2D．h＜﹣2【例题剖析】二次函数的性质的综合【例题1】（2017•陕西）已知抛物线y=x2﹣2mx﹣4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）A．（1，﹣5）B．（3，﹣13）C．（2，﹣8）D．（4，﹣20）【例题2】（2017•南雄市模拟）对于二次函数y=2（x﹣1）2﹣8，下列说法正确的是（）A．图象的开口向下B．当x=﹣1时，取得最小值为y=﹣8C．当x＜1时，y随x的增大而减小D．图象的对称轴是直线x=﹣1【例题3】关于二次函数y=2x2+3，下列说法中正确的是（）A．它的开口方向是向下B．当x＜﹣1时，y随x的增大而减小C．它的顶点坐标是（2，3）D．当x=0时，y有最大值是3【例题4】对于抛物线y=﹣（x+1）2+3，下列结论：①抛物线的开口向下；②对称轴为直线x=1；③顶点坐标为（﹣1，3）；④x＞1时，y随x的增大而减小，其中正确结论的个数为（）A．1B．2C．3D．4【练习1】（2017•大石桥市校级一模）已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（）x…﹣2012…y…7﹣1﹣2﹣1…A．抛物线开口向下B．抛物线的对称轴是y轴C．x＜1时，y随x的增大而减小D．抛物线与y轴交于正半轴【练习2】（2016秋•杭州期末）对于二次函数y=﹣（x﹣4）2+5的图象，有下列说法：①其图象开口向上；②对称轴是直线x=4；③顶点坐标是（﹣4，5）；④与y轴的交点坐标是（0，3），其中正确的有（）A．1个B．2个C．3个D．4个【练习3】（2017秋•天津月考）已知二次函数y=（x﹣）2+1，下列说法：①其图象的开口向下；②其图象的对称轴为直线x=﹣；③其图象顶点坐标为（，﹣1）；④当x＜时，y随x的增大而减小．则其中说法正确的有（）A．1个B．2个C．3个D．4个系数a、b、c a决定抛物线的开口方向及开口大小当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下.某些特殊形式代数式的符号：①a±b+c即为x=±1时，y的值；②4a±2b+c即为x=±2时，y的值.③2a+b的符号，需判断对称轴－b/2a与1的大小.若对称轴在直线x=1的左边，则－b/2a＞1，再根据a的符号即可得出结果.④2a－b的符号，需判断对称轴与－1的大小.a、b决定对称轴（x=－b/2a）的位置当a，b同号，－b/2a＜0，对称轴在y轴左边；当b＝0时，－b/2a=0，对称轴为y轴；当a，b异号，－b/2a＞0，对称轴在y轴右边．c决定抛物线与y轴的交点的位置当c＞0时，抛物线与y轴的交点在正半轴上；当c＝0时，抛物线经过原点；当c＜0时，抛物线与y轴的交点在负半轴上.b2－4ac决定抛物线与x轴的交点个数b2－4ac＞0时，抛物线与x轴有2个交点;b2－4ac＝0时，抛物线与x轴有1个交点;b2－4ac＜0时，抛物线与x轴没有交点知识点四：二次函数与一元二次方程以及不等式5.二次函数与一元二次方程二次函数y=ax2＋bx＋c(a≠0)的图象与x轴交点的横坐标是一元二次方程ax2+bx+c=0的根.当Δ＝b2－4ac＞0，两个不相等的实数根；当Δ＝b2－4ac＝0，两个相等的实数根；当Δ＝b2－4ac＜0，无实根例：已经二次函数y=x2－3x+m(m为常数)的图象与x轴的一个交点为（1,0），则关于x的一元二次方程x2－3x+m=0的两个实数根为2,1.6.二次函数与不等式抛物线y= ax2＋bx＋c＝0在x轴上方的部分点的纵坐标都为正，所对应的x的所有值就是不等式ax2＋bx＋c＞0的解集；在x轴下方的部分点的纵坐标均为负，所对应的x的值就是不等式ax2＋bx＋c＜0的解集.【例题1】二次函数y=ax2+bx+c（a≠0）的图象如图所示，对于下列结论：①a ＜0；②b＜0；③c＞0；④2a+b=0；⑤a﹣b+c＜0，其中正确的个数是（）A．4个B．3个C．2个D．1个【例题2】（2017秋•遵义期末）如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，给出下列结论：①b2=4ac，②abc＜0；③a＞c；④4a﹣2b+c＜0，其中正确的个数有（）A．1个B．2个C．3个D．4个【例题3】（2017秋•定边县期末）二次函数y=ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④当x＜时，y随x的增大而减小；⑤a+b+c＞0．其中正确的有（）A．5个B．4个C．3个D．2个【例题4】（2017•黔东南州）如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，给出下列结论：①b2=4ac；②abc＞0；③a＞c；④4a﹣2b+c＞0，其中正确的个数有（）A．1个B．2个C．3个D．4个【例题5】（2017•资阳）如图，抛物线y=ax2+bx+c（a≠0）的顶点和该抛物线与y轴的交点在一次函数y=kx+1（k≠0）的图象上，它的对称轴是x=1，有下列四个结论：①abc＜0，②a＜﹣，③a=﹣k，④当0＜x＜1时，ax+b＞k，其中正确结论的个数是（）A．4B．3C．2D．1【例题6】（2017•黔南州）二次函数y=ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④其顶点坐标为（，﹣2）；⑤当x＜时，y随x的增大而减小；⑥a+b+c＞0正确的有（）A．3个B．4个C．5个D．6个【练习1】（2017•济南）二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣2，0），（x0，0），1＜x0＜2，与y轴的负半轴相交，且交点在（0，﹣2）的上方，下列结论：①b＞0；②2a＜b；③2a﹣b﹣1＜0；④2a+c＜0．其中正确结论的个数是（）A．1B．2C．3D．4【练习2】（2017•遵义）如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示．则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（）A．①③B．②③C．②④D．②③④【练习3】（2017•烟台）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，下列结论：①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0．其中正确的是（）A．①④B．②④C．①②③D．①②③④【练习4】（2017•南充）二次函数y=ax2+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（）A．4ac＜b2B．abc＜0C．b+c＞3a D．a＜b【练习5】（2017•安顺）二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m ≠﹣1），其中结论正确的个数是（）A．1B．2C．3D．4考点3 ：二次函数图像上的点的坐标特征二次函数y=ax2+bx+c（a≠0）的图象是抛物线，顶点坐标是（﹣，）．①抛物线是关于对称轴x=﹣成轴对称，所以抛物线上的点关于对称轴对称，且都满足函数函数关系式．顶点是抛物线的最高点或最低点．②抛物线与y轴交点的纵坐标是函数解析中的c值．③抛物线与x轴的两个交点关于对称轴对称，设两个交点分别是（x1，0），（x2，0），则其对称轴为x=．【例题剖析】二次函数的坐标点特征【例题1】抛物线y=2（x+1）2﹣2与y轴的交点的坐标是（）A．（0，﹣2）B．（﹣2，0）C．（0，﹣1）D．（0，0）【例题2】若抛物线y=ax2（a≠0）过点（﹣1，3），则a等于（）A．3B．﹣3C．﹣D．【例题3】抛物线y=﹣2（x﹣1）2﹣3与y轴的交点坐标为（）A．（0，3）B．（0，﹣5）C．（1，﹣3）D．（﹣1，﹣3）【例题4】抛物线y=ax2+bx﹣3经过点（2，4），则代数式8a+4b+1的值为（）A．3B．9C．15D．﹣15【例题剖析】二次函数的坐标特征应用【例题1】已知A（﹣1，y1）、B（2，y2）、C（﹣3，y3）在函数y=﹣5（x+1）2+3的图象上，则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y3＜y1D．y3＜y2＜y1【例题2】（2017秋•余姚市期末）已知：点（﹣1，y1），（0，y2），（4，y3）都在抛物线y=ax2﹣2ax+5（a＞0）上，则y1，y2，y3的大小关系是（）A．y1＞y2＞y3B．y3＞y1＞y2C．y2＞y1＞y3D．y2＞y3＞y1【例题3】设点A（﹣1，y1）、B（1，y2）、C（2，y3）是抛物线y=﹣2（x﹣1）2+m上的三点，则y1、y2、y3的大小关系正确的是（）A．y2＞y3＞y1B．y1＞y2＞y3C．y3＞y2＞y1D．y1＞y3＞y2【例题4】（2017•连云港）已知抛物线y=ax2（a＞0）过A（﹣2，y1）、B（1，y2）两点，则下列关系式一定正确的是（）A．y1＞0＞y2B．y2＞0＞y1C．y1＞y2＞0D．y2＞y1＞0【例题5】（2017•姑苏区校级二模）若点A（﹣4，y1），B（﹣1，y2），C（1，y3）在抛物线y=﹣（x+2）2﹣1上，则（）A．y1＜y3＜y2 B．y2＜y1＜y3C．y3＜y2＜y1D．y3＜y1＜y22.解析式（1）三种解析式：①一般式：y=ax2+bx+c①顶点式：y=a(x－h)2+k(a≠0)，其中二次函数的顶点坐标是（h,k）;①交点式：y=a(x－x1)(x－x2),其中x1,x2为抛物线与x轴交点的横坐标.（2）待定系数法：巧设二次函数的解析式；根据已知条件，得到关于待定系数的方程（组）；解方程（组），求出待定系数的值，从而求出函数的解析式.若已知条件是图象上的三个点或三对对应函数值，可设一般式；若已知顶点坐标或对称轴方程与最值，可设顶点式；若已知抛物线与x轴的两个交点坐标，可设交点式.【例题1】（2018•静安区一模）已知：二次函数图象的顶点坐标是（3，5），且抛物线经过点A（1，3）．（1）求此抛物线的表达式；（2）如果点A关于该抛物线对称轴的对称点是B点，且抛物线与y轴的交点是C点，求△ABC的面积．【例题2】（2017秋•荔湾区期末）已知抛物线y=x2+mx+n的图象经过点（﹣3，0），点（1，0）（1）求抛物线解析式；（2）求抛物线的对称轴和顶点坐标．【例题3】已知二次函数y=（m﹣2）x2+（m+3）x+m+2的图象过点（0，5）．（1）求m的值，并写出二次函数的解析式；（2）求出二次函数图象的顶点坐标和对称轴．【例题4】已知抛物线y=﹣x2+bx+c经过点A（3，0），B（﹣1，0）．（1）求抛物线的解析式；（2）求抛物线的顶点坐标．【例题5】已知抛物线y=x2﹣bx+2经过点A（﹣2，8）．（1）求此抛物线的函数解析式，并写出此抛物线的对称轴．（2）判断点B（﹣1，﹣4）是否在此抛物线上．知识点三 ：二次函数的平移4.平移与解析式的关系注意：二次函数的平移实质是顶点坐标的平移，因此只要找出原函数顶点的平移方式即可确定平移后的函数解析式失分点警示：抛物线平移规律是“上加下减，左加右减”,左右平移易弄反.例：将抛物线y =x 2沿x 轴向右平移2个单位后所得抛物线的解析式是y =（x －2）2．【例题1】 将抛物线y=（x +m ）2向右平移2个单位后，对称轴是y 轴，那么m的值是 ．【例题2】 抛物线y=2x 2+4向左平移2个单位长度，得到新抛物线的表达式为 ．【例题3】 把抛物线y=3x 2先向上平移2个单位，再向右平移3个单位，所得抛物线的解析式是 ．【例题4】 如果将抛物线y=x 2﹣2x ﹣1向上平移，使它经过点A （0，3），那么所得新抛物线的表达式是 ．平移|k |个单位平移|h |个单位向上(k ＞0)或向下(k ＜0)向左(h ＜0)或向右(h ＞0)y =a (x －h )2＋k 的图象y =a (x －h )2的图象y =ax 2的图象第13讲二次函数的应用知识点一：二次函数的应用关键点拨实物抛物线一般步骤若题目中未给出坐标系，则需要建立坐标系求解，建立的原则：①所建立的坐标系要使求出的二次函数表达式比较简单；①使已知点所在的位置适当（如在x轴，y轴、原点、抛物线上等），方便求二次函数丶表达式和之后的计算求解.①据题意，结合函数图象求出函数解析式；①确定自变量的取值范围；①根据图象，结合所求解析式解决问题.实际问题中求最值①分析问题中的数量关系，列出函数关系式；②研究自变量的取值范围；③确定所得的函数；① 检验x的值是否在自变量的取值范围内，并求相关的值；⑤解决提出的实际问题.解决最值应用题要注意两点：①设未知数，在“当某某为何值时，什么最大（最小）”的设问中，“某某”要设为自变量，“什么”要设为函数；①求解最值时，一定要考虑顶点（横、纵坐标）的取值是否在自变量的取值范围内.结合几何图形①根据几何图形的性质，探求图形中的关系式；②根据几何图形的关系式确定二次函数解析式；③利用配方法等确定二次函数的最值，解决问题由于面积等于两条边的乘积，所以几何问题的面积的最值问题通常会通过二次函数来解决.同样需注意自变量的取值范围.。

2017-2021年广东中考数学真题分类汇编之二次函数一．选择题（共8小题）1．（2018•深圳）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．abc＞0B．2a+b＜0C．3a+c＜0D．ax2+bx+c﹣3＝0有两个不相等的实数根2．（2021•深圳）二次函数y＝ax2+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）A．B．C．D．3．（2020•广东）如图，抛物线y＝ax2+bx+c的对称轴是直线x＝1，下列结论：①abc＞0；②b2﹣4ac＞0；③8a+c＜0；④5a+b+2c＞0，正确的有（）A．4个B．3个C．2个D．1个4．（2020•深圳）二次函数y＝ax2+bx+c（a≠0）的顶点坐标为（﹣1，n），其部分图象如图所示．以下结论错误的是（）A．abc＞0B．4ac﹣b2＜0C．3a+c＞0D．关于x的方程ax2+bx+c＝n+1无实数根5．（2020•广东）把函数y＝（x﹣1）2+2图象向右平移1个单位长度，平移后图象的函数解析式为（）A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2+3 6．（2021•广州）抛物线y＝ax2+bx+c经过点（﹣1，0）、（3，0），且与y轴交于点（0，﹣5），则当x＝2时，y的值为（）A．﹣5B．﹣3C．﹣1D．5 7．（2021•广东）我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a，b，c，记p ＝，则其面积S＝．这个公式也被称为海伦﹣秦九韶公式．若p＝5，c＝4，则此三角形面积的最大值为（）A．B．4C．2D．5 8．（2021•广东）设O为坐标原点，点A、B为抛物线y＝x2上的两个动点，且OA⊥OB．连接点A、B，过O作OC⊥AB于点C，则点C到y轴距离的最大值（）A．B．C．D．1二．填空题（共4小题）9．（2018•广州）已知二次函数y＝x2，当x＞0时，y随x的增大而（填“增大”或“减小”）．10．（2017•广州）当x＝时，二次函数y＝x2﹣2x+6有最小值．11．（2021•广东）把抛物线y＝2x2+1向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为．12．（2020•广州）对某条线段的长度进行了3次测量，得到3个结果（单位：mm）9.9，10.1，10.0，若用a作为这条线段长度的近似值，当a＝mm时，（a﹣9.9）2+（a﹣10.1）2+（a﹣10.0）2最小．对另一条线段的长度进行了n次测量，得到n个结果（单位：mm）x1，x2，…，x n，若用x作为这条线段长度的近似值，当x＝mm时，（x﹣x1）2+（x﹣x2）2+…+（x﹣x n）2最小．三．解答题（共8小题）13．（2021•深圳）某科技公司销售高新科技产品，该产品成本为8万元，销售单价x（万元）与销售量y（件）的关系如表所示：x（万元）10121416y（件）40302010（1）求y与x的函数关系式；（2）当销售单价为多少时，有最大利润，最大利润为多少？14．（2021•广东）端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同．在销售中，该商家发现猪肉粽每盒售价50元时，每天可售出100盒；每盒售价提高1元时，每天少售出2盒．（1）求猪肉粽和豆沙粽每盒的进价；（2）设猪肉粽每盒售价x元（50≤x≤65），y表示该商家每天销售猪肉粽的利润（单位：元），求y关于x的函数解析式并求最大利润．15．（2018•广东）如图，已知顶点为C（0，﹣3）的抛物线y＝ax2+b（a≠0）与x轴交于A，B两点，直线y＝x+m过顶点C和点B．（1）求m的值；（2）求函数y＝ax2+b（a≠0）的解析式；（3）抛物线上是否存在点M，使得∠MCB＝15°？若存在，求出点M的坐标；若不存在，请说明理由．16．（2017•广州）已知抛物线y1＝﹣x2+mx+n，直线y2＝kx+b，y1的对称轴与y2交于点A （﹣1，5），点A与y1的顶点B的距离是4．（1）求y1的解析式；（2）若y2随着x的增大而增大，且y1与y2都经过x轴上的同一点，求y2的解析式．17．（2017•深圳）如图，抛物线y＝ax2+bx+2经过点A（﹣1，0），B（4，0），交y轴于点C；（1）求抛物线的解析式（用一般式表示）；（2）点D为y轴右侧抛物线上一点，是否存在点D使S△ABC＝S△ABD？若存在请直接给出点D坐标；若不存在请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．18．（2021•广州）已知抛物线y＝x2﹣（m+1）x+2m+3．（1）当m＝0时，请判断点（2，4）是否在该抛物线上；（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；（3）已知点E（﹣1，﹣1）、F（3，7），若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．19．（2020•广东）如图，抛物线y＝x2+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO＝3AO＝3，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC＝CD．（1）求b，c的值；（2）求直线BD的函数解析式；（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ 相似时，请直接写出所有满足条件的点Q的坐标．20．（2018•广州）已知抛物线y＝x2+mx﹣2m﹣4（m＞0）．（1）证明：该抛物线与x轴总有两个不同的交点；（2）设该抛物线与x轴的两个交点分别为A，B（点A在点B的右侧），与y轴交于点C，A，B，C三点都在⊙P上．①试判断：不论m取任何正数，⊙P是否经过y轴上某个定点？若是，求出该定点的坐标；若不是，说明理由；②若点C关于直线x＝﹣的对称点为点E，点D（0，1），连接BE，BD，DE，△BDE的周长记为l，⊙P的半径记为r，求的值．2017-2021年广东中考数学真题分类汇编之二次函数参考答案与试题解析一．选择题（共8小题）1．（2018•深圳）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．abc＞0B．2a+b＜0C．3a+c＜0D．ax2+bx+c﹣3＝0有两个不相等的实数根【考点】二次函数图象与系数的关系；抛物线与x轴的交点．【专题】函数及其图象．【分析】根据抛物线开口方向得a＜0，由抛物线对称轴为直线x＝﹣，得到b＞0，由抛物线与y轴的交点位置得到c＞0，进而解答即可．【解答】解：∵抛物线开口方向得a＜0，由抛物线对称轴为直线x＝﹣，得到b＞0，由抛物线与y轴的交点位置得到c＞0，A、abc＜0，错误；B、2a+b＝0，不是2a+b＜0，错误；C、当x＝﹣1时，y＝a﹣b+c＜0，∴3a+c＝a﹣b+c＜0，所以C正确；D、由图可知，抛物线y＝ax2+bx+c与直线y＝3有一个交点，可得：ax2+bx+c﹣3＝0，此方程有一个实数根，错误；故选：C．【点评】本题考查了二次函数图象与系数的关系：二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下；一次项系数b和二次项系数a共同决定对称轴的位置，当a与b同号时（即ab＞0），对称轴在y轴左侧；当a与b异号时（即ab＜0），对称轴在y轴右侧；常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定，Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x 轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．2．（2021•深圳）二次函数y＝ax2+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）A．B．C．D．【考点】二次函数的图象；一次函数的图象．【专题】二次函数图象及其性质；几何直观．【分析】由二次函数y＝ax2+bx+c的图象得到字母系数的正负以及对称轴，与一次函数y ＝2ax+b的图象得到的字母系数的正负以及与x轴的交点相比较看是否一致．【解答】解：A、由抛物线可知，a＞0，b＜0，c＝1，对称轴为直线x＝﹣，由直线可知，a＞0，b＜0，直线经过点（﹣，0），故本选项符合题意；B、由抛物线可知，对称轴为直线x＝﹣，直线不经过点（﹣，0），故本选项不符合题意；C、由抛物线可知，对称轴为直线x＝﹣，直线不经过点（﹣，0），故本选项不符合题意；D、由抛物线可知，对称轴为直线x＝﹣，直线不经过点（﹣，0），故本选项不符合题意；故选：A．【点评】本题考查二次函数和一次函数的图象，解题的关键是明确一次函数和二次函数性质．3．（2020•广东）如图，抛物线y＝ax2+bx+c的对称轴是直线x＝1，下列结论：①abc＞0；②b2﹣4ac＞0；③8a+c＜0；④5a+b+2c＞0，正确的有（）A．4个B．3个C．2个D．1个【考点】二次函数图象与系数的关系；抛物线与x轴的交点．【专题】二次函数图象及其性质；推理能力．【分析】根据抛物线的开口方向、对称轴、与坐标轴的交点判定系数符号及运用一些特殊点解答问题．【解答】解：由抛物线的开口向下可得：a＜0，根据抛物线的对称轴在y轴右边可得：a，b异号，所以b＞0，根据抛物线与y轴的交点在正半轴可得：c＞0，∴abc＜0，故①错误；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故②正确；∵直线x＝1是抛物线y＝ax2+bx+c（a≠0）的对称轴，所以﹣＝1，可得b＝﹣2a，由图象可知，当x＝﹣2时，y＜0，即4a﹣2b+c＜0，∴4a﹣2×（﹣2a）+c＜0，即8a+c＜0，故③正确；由图象可知，当x＝2时，y＝4a+2b+c＞0；当x＝﹣1时，y＝a﹣b+c＞0，两式相加得，5a+b+2c＞0，故④正确；∴结论正确的是②③④3个，故选：B．【点评】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线上的点的坐标满足抛物线的解析式．4．（2020•深圳）二次函数y＝ax2+bx+c（a≠0）的顶点坐标为（﹣1，n），其部分图象如图所示．以下结论错误的是（）A．abc＞0B．4ac﹣b2＜0C．3a+c＞0D．关于x的方程ax2+bx+c＝n+1无实数根【考点】二次函数图象与系数的关系；抛物线与x轴的交点；根的判别式．【专题】二次函数图象及其性质；推理能力．【分析】根据抛物线开口方向，对称轴的位置以及与y轴的交点可以对A进行判断；根据抛物线与x轴的交点情况可对B进行判断；x＝1时，y＜0，可对C进行判断；根据抛物线y＝ax2+bx+c与直线y＝n+1无交点，可对D进行判断．【解答】解：A．∵抛物线开口向下，∴a＜0，∵对称轴为直线x＝﹣＝﹣1，∴b＝2a＜0，∵抛物线与y轴交于正半轴，∴c＞0，∴abc＞0，故A正确；B．∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即4ac﹣b2＜0，故B正确；C．∵抛物线的对称轴为直线x＝﹣1，抛物线与x轴的一个交点在（﹣3，0）和（﹣2，0）之间，∴抛物线与x轴的另一个交点在（0，0）和（1，0）之间，∴x＝1时，y＜0，即a+b+c＜0，∵b＝2a，∴3a+c＜0，故C错误；D．∵抛物线开口向下，顶点为（﹣1，n），∴函数有最大值n，∴抛物线y＝ax2+bx+c与直线y＝n+1无交点，∴一元二次方程ax2+bx+c＝n+1无实数根，故D正确．故选：C．【点评】本题考查了抛物线与x轴的交点：把求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质．5．（2020•广东）把函数y＝（x﹣1）2+2图象向右平移1个单位长度，平移后图象的函数解析式为（）A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2+3【考点】二次函数图象与几何变换．【专题】二次函数图象及其性质；推理能力．【分析】先求出y＝（x﹣1）2+2的顶点坐标，再根据向右平移横坐标加，求出平移后的二次函数图象顶点坐标，然后利用顶点式解析式写出即可．【解答】解：二次函数y＝（x﹣1）2+2的图象的顶点坐标为（1，2），∴向右平移1个单位长度后的函数图象的顶点坐标为（2，2），∴所得的图象解析式为y＝（x﹣2）2+2．故选：C．【点评】本题主要考查的是函数图象的平移，求出平移后的函数图象的顶点坐标直接代入函数解析式求得平移后的函数解析式．6．（2021•广州）抛物线y＝ax2+bx+c经过点（﹣1，0）、（3，0），且与y轴交于点（0，﹣5），则当x＝2时，y的值为（）A．﹣5B．﹣3C．﹣1D．5【考点】二次函数的性质；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；几何直观．【分析】根据抛物线与x轴两交点，及与y轴交点可画出大致图象，根据抛物线的对称性可求y＝﹣5．【解答】解：如图∵抛物线y＝ax2+bx+c经过点（﹣1，0）、（3，0），且与y轴交于点（0，﹣5），∴可画出上图，∵抛物线对称轴x＝＝1，∴点（0，﹣5）的对称点是（2，﹣5），∴当x＝2时，y的值为﹣5．故选：A．【点评】本题考查了抛物线的图象与性质、二次函数图象上点的坐标特征等知识，画出图象利用对称性是解题的关键．7．（2021•广东）我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a，b，c，记p ＝，则其面积S＝．这个公式也被称为海伦﹣秦九韶公式．若p＝5，c＝4，则此三角形面积的最大值为（）A．B．4C．2D．5【考点】二次函数的最值；代数式求值．【专题】二次根式；运算能力．【分析】根据公式算出a+b的值，代入公式即可求出解．【解答】解：∵p＝，p＝5，c＝4，∴5＝，∴a+b＝6，∴a＝6﹣b，∴S＝＝＝＝＝＝＝，当b＝3时，S有最大值为＝2．故选：C．【点评】本题考查二次根式的应用，解答本题的关键是明确题意，表示出相应的三角形的面积．8．（2021•广东）设O为坐标原点，点A、B为抛物线y＝x2上的两个动点，且OA⊥OB．连接点A、B，过O作OC⊥AB于点C，则点C到y轴距离的最大值（）A．B．C．D．1【考点】二次函数的最值；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；圆的有关概念及性质；图形的相似；推理能力；应用意识．【分析】分别作AE、BF垂直于x轴于点E、F，设OE＝a，OF＝b，由抛物线解析式可得AE＝a2，BF＝b2，作AH⊥BH于H，交y轴于点G，连接AB交y轴于点D，设点D（0，m），易证△ADG∽△ABH，所以，即．可得m＝ab．再证明△AEO∽△OFB，所以，即，可得ab＝1．即得点D为定点，坐标为（0，1），得DO＝1．进而可推出点C是在以DO为直径的圆上运动，则当点C到y轴距离为此圆的直径的一半，即时最大．【解答】解：如图，分别作AE、BF垂直于x轴于点E、F，设OE＝a，OF＝b，由抛物线解析式为y＝x2，则AE＝a2，BF＝b2，作AH⊥BF于H，交y轴于点G，连接AB交y轴于点D，设点D（0，m），∵DG∥BH，∴△ADG∽△ABH，∴，即．化简得：m＝ab．∵∠AOB＝90°，∴∠AOE+∠BOF＝90°，又∠AOE+∠EAO＝90°，∴∠BOF＝∠EAO，又∠AEO＝∠BFO＝90°，∴△AEO∽△OFB．∴，即，化简得ab＝1．则m＝ab＝1，说明直线AB过定点D，D点坐标为（0，1）．∵∠DCO＝90°，DO＝1，∴点C是在以DO为直径的圆上运动，∴当点C到y轴距离为＝时，点C到y轴的距离最大．故选：A．【点评】本题考查了二次函数结合动点问题背景下的最值求法，涉及相似三角形，圆周角定理，此题难度较大，关键是要找出点D为定点，确定出点C的轨迹为一段优弧，再求最值．二．填空题（共4小题）9．（2018•广州）已知二次函数y＝x2，当x＞0时，y随x的增大而增大（填“增大”或“减小”）．【考点】二次函数的性质．【专题】常规题型．【分析】根据二次函数的二次项系数a以及对称轴即可判断出函数的增减性．【解答】解：∵二次函数y＝x2，开口向上，对称轴为y轴，∴当x＞0时，y随x的增大而增大．故答案为：增大．【点评】本题主要考查了二次函数的性质，解答本题的关键是求出二次函数的对称轴为y 轴，开口向上，此题难度不大．10．（2017•广州）当x＝1时，二次函数y＝x2﹣2x+6有最小值5．【考点】二次函数的最值．【专题】推理填空题．【分析】把x2﹣2x+6化成（x﹣1）2+5，即可求出二次函数y＝x2﹣2x+6的最小值是多少．【解答】解：∵y＝x2﹣2x+6＝（x﹣1）2+5，∴当x＝1时，二次函数y＝x2﹣2x+6有最小值5．故答案为：1、5．【点评】此题主要考查了二次函数的最值，要熟练掌握，确定一个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．11．（2021•广东）把抛物线y＝2x2+1向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为y＝2x2+4x．【考点】二次函数图象与几何变换．【专题】二次函数图象及其性质；应用意识．【分析】可根据二次函数图象左加右减，上加下减的平移规律进行解答．【解答】解：把抛物线y＝2x2+1向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为：y＝2（x+1）2+1﹣3，即y＝2x2+4x故答案为y＝2x2+4x．【点评】本题考查的是函数图象的平移，用平移规律“左加右减，上加下减”直接代入函数解析式求得平移后的函数解析式．12．（2020•广州）对某条线段的长度进行了3次测量，得到3个结果（单位：mm）9.9，10.1，10.0，若用a作为这条线段长度的近似值，当a＝10.0mm时，（a﹣9.9）2+（a﹣10.1）2+（a﹣10.0）2最小．对另一条线段的长度进行了n次测量，得到n个结果（单位：mm）x1，x2，…，x n，若用x作为这条线段长度的近似值，当x＝mm时，（x﹣x1）2+（x﹣x2）2+…+（x﹣x n）2最小．【考点】二次函数的应用．【专题】二次函数图象及其性质；应用意识．【分析】构建二次函数，利用二次函数的性质即可解决问题．【解答】解：设y＝（a﹣9.9）2+（a﹣10.1）2+（a﹣10.0）2＝3a2﹣60.0a+300.02，∵a＝3＞0，∴当x＝﹣＝10.0时，y有最小值，设w＝（x﹣x1）2+（x﹣x2）2+…+（x﹣x n）2＝nx2﹣2（x1+x2+…+x n）x+（x12+x22+…+x n2），∵n＞0，∴当x＝﹣＝时，w有最小值．故答案为10.0，．【点评】本题考查二次函数的性质，解题的关键是学会构建二次函数解决最值问题．三．解答题（共8小题）13．（2021•深圳）某科技公司销售高新科技产品，该产品成本为8万元，销售单价x（万元）与销售量y（件）的关系如表所示：x（万元）10121416y（件）40302010（1）求y与x的函数关系式；（2）当销售单价为多少时，有最大利润，最大利润为多少？【考点】二次函数的应用．【专题】二次函数的应用；应用意识．【分析】（1）通过表格数据可以判断y与x之间的函数关系式为一次函数关系，设出函数解析式用待定系数法求函数解析式即可；（2）根据销售利润等于单件的利润与销售件数的乘积列出函数关系式，根据二次函数的性质求最值即可．【解答】解：（1）由表格中数据可知，y与x之间的函数关系式为一次函数关系，设y＝kx+b（k≠0），则，解得：，∴y与x的函数关系式y＝﹣5x+90；（2）设该产品的销售利润为w，由题意得：w＝y（x﹣8）＝（﹣5x+90）（x﹣8）＝﹣5x2+130x﹣720＝﹣5（x﹣13）2+125，∵﹣5＜0，∴当x＝13时，w最大，最大值为125（万元），答：当销售单价为13万元时，有最大利润，最大利润为125万元．【点评】本题考查一次函数的性质及待定系数法求函数解析式，关键是根据销售利润等于单件的利润与销售件数的乘积，列出函数关系式．14．（2021•广东）端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同．在销售中，该商家发现猪肉粽每盒售价50元时，每天可售出100盒；每盒售价提高1元时，每天少售出2盒．（1）求猪肉粽和豆沙粽每盒的进价；（2）设猪肉粽每盒售价x元（50≤x≤65），y表示该商家每天销售猪肉粽的利润（单位：元），求y关于x的函数解析式并求最大利润．【考点】二次函数的应用；分式方程的应用．【专题】二次函数的应用；应用意识．【分析】（1）设猪肉粽每盒进价a元，则豆沙粽每盒进价（a﹣10）元，根据商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同列出方程，解方程即可；（2）由题意得，当x＝50时，每天可售出100盒，当猪肉粽每盒售价x元（50≤x≤65）时，每天可售[100﹣2（x﹣50）]盒，列出每天销售猪肉粽的利润y与猪肉粽每盒售价x 元的函数关系式，根据二次函数的性质及x的取值范围求利润的最大值．【解答】解：（1）设猪肉粽每盒进价a元，则豆沙粽每盒进价（a﹣10）元，则，解得：a＝40，经检验a＝40是方程的解，∴猪肉粽每盒进价40元，豆沙粽每盒进价30元，（2）由题意得，当x＝50时，每天可售出100盒，当猪肉粽每盒售价x元（50≤x≤65）时，每天可售[100﹣2（x﹣50）]盒，∴y＝x[100﹣2（x﹣50）]﹣40×[100﹣2（x﹣50）]＝﹣2x2+280x﹣8000，配方，得：y＝﹣2（x﹣70）2+1800，∵x＜70时，y随x的增大而增大，∴当x＝65时，y取最大值，最大值为：﹣2×（65﹣70）2+1800＝1750（元）．答：y关于x的函数解析式为y＝﹣2x2+280x﹣8000（50≤x≤65），且最大利润为1750元．【点评】本题考查了二次函数的应用以及分式方程的解法，关键是根据题意列出每天销售猪肉粽的利润y与猪肉粽每盒售价x元的函数关系式．15．（2018•广东）如图，已知顶点为C（0，﹣3）的抛物线y＝ax2+b（a≠0）与x轴交于A，B两点，直线y＝x+m过顶点C和点B．（1）求m的值；（2）求函数y＝ax2+b（a≠0）的解析式；（3）抛物线上是否存在点M，使得∠MCB＝15°？若存在，求出点M的坐标；若不存在，请说明理由．【考点】二次函数综合题．【专题】函数及其图象．【分析】（1）把C（0，﹣3）代入直线y＝x+m中解答即可；（2）把y＝0代入直线解析式得出点B的坐标，再利用待定系数法确定函数关系式即可；（3）分M在BC上方和下方两种情况进行解答即可．【解答】解：（1）将（0，﹣3）代入y＝x+m，可得：m＝﹣3；（2）将y＝0代入y＝x﹣3得：x＝3，所以点B的坐标为（3，0），将（0，﹣3）、（3，0）代入y＝ax2+b中，可得：，解得：，所以二次函数的解析式为：y＝x2﹣3；（3）存在，分以下两种情况：①若M在B上方，设MC交x轴于点D，则∠ODC＝45°+15°＝60°，∴OD＝OC•tan30°＝，设DC为y＝kx﹣3，代入（，0），可得：k＝，联立两个方程可得：，解得：，所以M1（3，6）；②若M在B下方，设MC交x轴于点E，则∠OEC＝45°﹣15°＝30°，∴∠OCE＝60°，∴OE＝OC•tan60°＝3，设EC为y＝kx﹣3，代入（3，0）可得：k＝，联立两个方程可得：，解得：，所以M2（，﹣2），综上所述M的坐标为（3，6）或（，﹣2）．【点评】此题主要考查了二次函数的综合题，需要掌握待定系数法求二次函数解析式，待定系数法求一次函数解析式等知识是解题关键．16．（2017•广州）已知抛物线y1＝﹣x2+mx+n，直线y2＝kx+b，y1的对称轴与y2交于点A （﹣1，5），点A与y1的顶点B的距离是4．（1）求y1的解析式；（2）若y2随着x的增大而增大，且y1与y2都经过x轴上的同一点，求y2的解析式．【考点】待定系数法求二次函数解析式；一次函数的性质；待定系数法求一次函数解析式；二次函数的性质．【分析】（1）根据题意求得顶点B的坐标，然后根据顶点公式即可求得m、n，从而求得y1的解析式；（2）分两种情况讨论：当y1的解析式为y1＝﹣x2﹣2x时，抛物线与x轴的交点（0，0）或（﹣2，0），y2经过（﹣2，0）和A，符合题意；当y1＝﹣x2﹣2x+8时，解﹣x2﹣2x+8＝0求得抛物线与x轴的交点坐标，然后根据A的坐标和y2随着x的增大而增大，求得y1与y2都经过x轴上的同一点（﹣4，0），然后根据待定系数法求得即可．【解答】解：（1）∵抛物线y1＝﹣x2+mx+n，直线y2＝kx+b，y1的对称轴与y2交于点A （﹣1，5），点A与y1的顶点B的距离是4．∴B（﹣1，1）或（﹣1，9），∴﹣＝﹣1，＝1或9，解得m＝﹣2，n＝0或8，∴y1的解析式为y1＝﹣x2﹣2x或y1＝﹣x2﹣2x+8；（2）①当y1的解析式为y1＝﹣x2﹣2x时，抛物线与x轴交点是（0，0）和（﹣2，0），∵y1的对称轴与y2交于点A（﹣1，5），∴y1与y2都经过x轴上的同一点（﹣2，0），把（﹣1，5），（﹣2，0）代入得，解得，∴y2＝5x+10．②当y1＝﹣x2﹣2x+8时，解﹣x2﹣2x+8＝0得x＝﹣4或2，∵y2随着x的增大而增大，且过点A（﹣1，5），∴y1与y2都经过x轴上的同一点（﹣4，0），把（﹣1，5），（﹣4，0）代入得，解得；∴y2＝x+．【点评】本题考查了一次函数的性质，二次函数的性质，待定系数法求一次函数和二次函数的解析式，根据题意求得顶点坐标是解题的关键．17．（2017•深圳）如图，抛物线y＝ax2+bx+2经过点A（﹣1，0），B（4，0），交y轴于点C；（1）求抛物线的解析式（用一般式表示）；（2）点D为y轴右侧抛物线上一点，是否存在点D使S△ABC＝S△ABD？若存在请直接给出点D坐标；若不存在请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．【考点】二次函数综合题．【分析】（1）由A、B的坐标，利用待定系数法可求得抛物线解析式；（2）由条件可求得点D到x轴的距离，即可求得D点的纵坐标，代入抛物线解析式可求得D点坐标；（3）由条件可证得BC⊥AC，设直线AC和BE交于点F，过F作FM⊥x轴于点M，则可得BF＝BC，利用平行线分线段成比例可求得F点的坐标，利用待定系数法可求得直线BE解析式，联立直线BE和抛物线解析式可求得E点坐标，则可求得BE的长．【解答】解：（1）∵抛物线y＝ax2+bx+2经过点A（﹣1，0），B（4，0），∴，解得，∴抛物线解析式为y＝﹣x2+x+2；（2）由题意可知C（0，2），A（﹣1，0），B（4，0），∴AB＝5，OC＝2，∴S△ABC＝AB•OC＝×5×2＝5，∵S△ABC＝S△ABD，∴S△ABD＝×5＝，设D（x，y），∴AB•|y|＝×5|y|＝，解得|y|＝3，当y＝3时，由﹣x2+x+2＝3，解得x＝1或x＝2，此时D点坐标为（1，3）或（2，3）；当y＝﹣3时，由﹣x2+x+2＝﹣3，解得x＝﹣2（舍去）或x＝5，此时D点坐标为（5，﹣3）；综上可知存在满足条件的点D，其坐标为（1，3）或（2，3）或（5，﹣3）；（3）∵AO＝1，OC＝2，OB＝4，AB＝5，∴AC＝＝，BC＝＝2，∴AC2+BC2＝AB2，∴△ABC为直角三角形，即BC⊥AC，如图，设直线AC与直线BE交于点F，过F作FM⊥x轴于点M，由题意可知∠FBC＝45°，∴∠CFB＝45°，∴CF＝BC＝2，∴＝，即＝，解得OM＝2，＝，即＝，解得FM＝6，∴F（2，6），且B（4，0），设直线BE解析式为y＝kx+m，则可得，解得，∴直线BE解析式为y＝﹣3x+12，联立直线BE和抛物线解析式可得，解得或，∴E（5，﹣3），∴BE＝＝．【点评】本题为二次函数的综合应用，涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中求得D点的纵坐标是解题的关键，在（3）中由条件求得直线BE的解析式是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，有一定的难度．18．（2021•广州）已知抛物线y＝x2﹣（m+1）x+2m+3．（1）当m＝0时，请判断点（2，4）是否在该抛物线上；（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；（3）已知点E（﹣1，﹣1）、F（3，7），若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．【考点】二次函数综合题．【专题】综合题；函数思想；待定系数法；函数的综合应用；运算能力；应用意识．【分析】（1）当m＝0时，抛物线为y＝x2﹣x+3，将x＝2代入得y＝5，故点（2，4）不在抛物线上；（2）抛物线y＝x2﹣（m+1）x+2m+3的顶点为（，），而＝﹣（m﹣3）2+5，即得m＝3时，纵坐标最大，此时顶点移动到了最高处，顶点坐标为：（2，5）；（3）求出直线EF的解析式为y＝2x+1，由得直线y＝2x+1与抛物线y＝x2﹣（m+1）x+2m+3的交点为：（2，5）和（m+1，2m+3），因（2，5）在线段EF上，由已知可得（m+1，2m+3）不在线段EF上，即是m+1＜﹣1或m+1＞3，或（2，5）与（m+1，2m+3）重合，可得抛物线顶点横坐标x顶点＝＜﹣或x顶点＝＞或x顶点＝1．【解答】解：（1）当m＝0时，抛物线为y＝x2﹣x+3，将x＝2代入得y＝4﹣2+3＝5，∴点（2，4）不在抛物线上；（2）抛物线y＝x2﹣（m+1）x+2m+3的顶点为（，），化简得（，），顶点移动到最高处，即是顶点纵坐标最大，而＝﹣（m﹣3）2+5，∴m＝3时，纵坐标最大，即是顶点移动到了最高处，此时顶点坐标为：（2，5）；（3）设直线EF解析式为y＝kx+b，将E（﹣1，﹣1）、F（3，7）代入得：，解得，∴直线EF的解析式为y＝2x+1，由得：或，∴直线y＝2x+1与抛物线y＝x2﹣（m+1）x+2m+3的交点为：（2，5）和（m+1，2m+3），而（2，5）在线段EF上，∴若该抛物线与线段EF只有一个交点，则（m+1，2m+3）不在线段EF上，或（2，5）与（m+1，2m+3）重合，∴m+1＜﹣1或m+1＞3或m+1＝2（此时2m+3＝5），∴此时抛物线顶点横坐标x顶点＝＜﹣或x顶点＝＞或x顶点＝＝＝1．【点评】本题考查二次函数的综合应用，涉及图象上点坐标特征，顶点坐标，抛物线与线段交点等知识，解题的关键是用m的代数式表示抛物线与直线交点的坐标．19．（2020•广东）如图，抛物线y＝x2+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO＝3AO＝3，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC＝CD．（1）求b，c的值；（2）求直线BD的函数解析式；（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ 相似时，请直接写出所有满足条件的点Q的坐标．【考点】二次函数综合题．【专题】二次函数图象及其性质；等腰三角形与直角三角形；图形的相似；推理能力；应用意识．【分析】（1）先求出点A，点B坐标，代入交点式，可求抛物线解析式，即可求解；（2）过点D作DE⊥AB于E，由平行线分线段成比例可求OE＝，可求点D坐标，利用待定系数法可求解析式；（3）利用两点距离公式可求AD，AB，BD的长，利用锐角三角函数和直角三角形的性质可求∠ABD＝30°，∠ADB＝45°，分∠ABP＝30°或∠ABP＝45°两种情况讨论，利用相似三角形的性质可求解．【解答】解：（1）∵BO＝3AO＝3，∴点B（3，0），点A（﹣1，0），∴抛物线解析式为：y＝（x+1）（x﹣3）＝x2﹣x﹣，∴b＝﹣，c＝﹣；（2）如图1，过点D作DE⊥AB于E，。

课时作业(九)[第二章 2 第1课时 二次函数y ＝±x 2的图象与性质]一、选择题1．下列关于二次函数y ＝x 2的图象的说法：①是一条抛物线；②开口向上；③是轴对称图形；④过点(0，0)；⑤它的顶点是原点，且是抛物线的最高点；⑥y 的值随x 值的增大而增大．其中正确的有()A ．3个B ．4个C ．5个D ．6个2．下列函数中，当x >0时，y 的值随x 值的增大而减小的是( )A ．y ＝x 2B ．y ＝x －1C ．y ＝34xD ．y ＝1x3．下列关于抛物线y ＝x 2和y ＝－x 2的异同点说法错误的是( )A ．抛物线y ＝x 2和y ＝－x 2有共同的顶点和对称轴B ．在同一直角坐标系中，抛物线y ＝x 2和y ＝－x 2既关于x 轴对称，又关于原点对称C ．抛物线y ＝x 2和y ＝－x 2的开口方向相反D ．点A (－3，9)既在抛物线y ＝x 2上，也在抛物线y ＝－x 2上4．二次函数y ＝x 2与一次函数y ＝－x －1在同一直角坐标系中的图象大致为( )图K －9－15．已知a ＜－1，点(a －1，y 1)，(a ，y 2)，(a ＋1，y 3)都在函数y ＝x 2的图象上，则( ) 链接听课例2归纳总结A ．y 1＜y 2＜y 3B ．y 1＜y 3＜y 2C ．y 3＜y 2＜y 1D ．y 2＜y 1＜y 3 二、填空题6．函数y ＝x 2的图象的顶点坐标为________，若点(a ，4)在该函数图象上，则a 的值是________．7．如图K －9－2，A ，B 分别为抛物线y ＝x 2上的两点，且线段AB ⊥y 轴，若AB ＝6，则直线AB 的表达式为________．图K －9－28．如图K －9－3，边长为2的正方形ABCD 的中心在直角坐标系的原点O 处，AD ∥x 轴，以O 为顶点且过A ，D 两点的抛物线与以O 为顶点且过B ，C 两点的抛物线将正方形分割成几部分，则图中阴影部分的面积是________．图K－9－3三、解答题9．已知抛物线y＝－x2与直线y＝3x＋m都经过点(2，n)．(1)画出y＝－x2的图象，并求出m，n的值；(2)抛物线y＝－x2与直线y＝3x＋m是否存在另一个交点？若存在，请求出这个点的坐标．规律探究如图K－9－4，点A1，A2，A3，…，A n在抛物线y＝x2上，点B0，B1，B2，B3，…，B n在y轴上，若△A1B0B1，△A2B1B2，…，△A n B n－1B n都为等腰直角三角形(点B0在坐标原点处)，则△A2018B2017B2018的腰长等于________．图K－9－4详解详析【课时作业】 [课堂达标]1．[解析] B ①②③④正确． 2．[答案] D3．[解析] D 点A (－3，9)在抛物线y ＝x 2上，但不在抛物线y ＝－x 2上．故选D.4．[解析] D y ＝x 2中a ＝1＞0，图象开口向上，在第一、二象限；y ＝－x －1中，k ＝－1＜0，图象经过第二、四象限，b ＝－1＜0，图象与y 轴交于负半轴，所以直线经过第二、三、四象限．故选D.5．[答案] C6．[答案] (0，0) ±2[解析] 若点(a ，4)在函数y ＝x 2的图象上，则a 2＝4，a ＝±2. 7．[答案] y ＝9[解析] ∵线段AB ⊥y 轴，且AB ＝6，∴由抛物线的对称性可知，点B 的横坐标为3.当x ＝3时，y ＝x 2＝32＝9，∴直线AB 的表达式为y ＝9.8．[答案] 2[解析] 根据图示及抛物线、正方形的性质，得S 阴影＝12S 正方形＝12×2×2＝2.9．解：(1)图略．把点(2，n )代入y ＝－x 2中，得n ＝－22，∴n ＝－4.把点(2，－4)代入y ＝3x ＋m 中，得－4＝3×2＋m ，∴m ＝－10.(2)由题意，得⎩⎪⎨⎪⎧y ＝3x －10，y ＝－x 2， 解得⎩⎪⎨⎪⎧x ＝2，y ＝－4或⎩⎪⎨⎪⎧x ＝－5，y ＝－25.∴抛物线y ＝－x 2与直线y ＝3x ＋m 存在另一个交点，其坐标为(－5，－25)．[点评] 判断两个函数图象的交点个数就是看这两个函数表达式所组成的方程组的解的个数．[素养提升][答案] 2018 2[解析] 作A 1C ⊥y 轴，A 2E ⊥y 轴，A 1D ⊥x 轴，A 2F ⊥x 轴，垂足分别为C ，E ，D ，F .∵△A 1B 0B 1，△A 2B 1B 2都是等腰直角三角形，∴B 1C ＝B 0C ＝DB 0＝A 1D ，B 2E ＝B 1E ，设A 1(a ，a )．将点A 1的坐标代入表达式y ＝x 2，得a ＝a 2，解得a ＝0(不符合题意，舍去)或a ＝1.由勾股定理，得A1B0＝ 2.则B1B0＝2.过点B1作B1N⊥A2F于点N，设点A2(x2，y2)，可得A2N＝y2－2，B1N＝x2＝y2－2，又点A2在抛物线上，∴y2＝x22，即x2＋2＝x22，解得x2＝2或x2＝－1(不合题意，舍去)，则A2B1＝2 2，同理可得：A3B2＝3 2，A4B3＝4 2，…，∴A2018B2017＝2018 2，∴△A2018B2017B2018的腰长为2018 2.。

二次函数y＝ax2＋bx＋c的系数a，b，c与图象的关系►类型之一二次函数的图象与系数a，b，c的关系1．2017·成都在平面直角坐标系xOy中，二次函数y＝ax2＋bx＋c的图象如图2－ZT －1所示，下列说法正确的是( )A．abc＜0，b2－4ac＞0 B．abc＞0，b2－4ac＞0C．abc＜0，b2－4ac＜0 D．abc＞0，b2－4ac＜02－ZT－12－ZT－22．2017·广安如图2－ZT－2所示，抛物线y＝ax2＋bx＋c的顶点为B(－1，3)，与x 轴的交点A在点(－3，0)和(－2，0)之间，以下结论：①b2－4ac＝0；②a＋b＋c>0；③2a －b＝0；④c－a＝3.其中正确的结论有( )A．1个B．2个C．3个D．4个3．2017·绍兴模拟如图2－ZT－3，二次函数y＝ax2＋bx＋c(a≠0)的图象经过点(－1，2)，且与x轴交点的横坐标分别为x1，x2，其中－2＜x1＜－1，0＜x2＜1，下列结论：①4a－2b＋c＜0；②2a－b＜0；③a＋c＜1；④b2＋8a＞4ac.其中正确的结论有( )A．1个B．2个C．3个D．4个2－ZT－32－ZT－44．如图2－ZT－4，抛物线y＝ax2＋bx＋c(a≠0)过点(－1，0)和点(0，－3)，且顶点在第四象限，设P＝a＋b＋c，则P的取值范围是( )A．－3＜P＜－1B．－6＜P＜0C．－3＜P＜0D．－6＜P＜－35．如图2－ZT－5，已知二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴交于点A(－1，0)，与y轴的交点B在点(0，－2)和(0，－1)之间(不包括这两点)，对称轴为直线x＝1.下列结论：①abc＞0；②4a＋2b＋c＞0；③4ac－b2＜8a；④13＜a＜23；⑤b＞c.其中含所有正确结论的选项是( )A．①③B．①③④C．②④⑤D．①③④⑤2－ZT－52－ZT－66．2017·株洲如图2－ZT－6，二次函数y＝ax2＋bx＋c图象的对称轴在y轴的右侧，其图象与x轴交于点A(－1，0)，点C(x2，0)，且与y轴交于点B(0，－2)，小强得到以下结论：①0＜a ＜2；②－1＜b ＜0；③c＝－1；④当|a|＝|b|时，x 2＞5－1.其中正确结论的序号是________．7．如图2－ZT －7所示，二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交于B ，C 两点，与y 轴交于点A.(1)根据图象确定a ，b ，c 的符号；(2)如果OC ＝OA ＝13OB ，BC ＝4，求这个二次函数的表达式．图2－ZT －7► 类型之二 二次函数与其他函数的图象的综合8．在反比例函数y ＝m x中，当x ＞0时，y 随x 的增大而增大，则二次函数y ＝mx 2＋mx 的图象大致是图2－ZT －8中的( )图2－ZT －89．2017·安徽已知抛物线y ＝ax 2＋bx ＋c 与反比例函数y ＝b x的图象在第一象限有一个公共点，其横坐标为1，则一次函数y ＝bx ＋ac 的图象可能是( )图2－ZT －9图2－ZT －1010．二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图2－ZT －10，则反比例函数y ＝－a x与一次函数y ＝bx －c 在同一直角坐标系内的图象大致是( )图2－ZT －11►类型之三 二次函数的图象与方程(不等式)的关系图2－ZT －1211．已知二次函数y ＝ax 2＋bx ＋c (a ≠0)的顶点坐标为(－1，－3.2)及部分图象如图2－ZT －12所示，由图象可知关于x 的一元二次方程ax 2＋bx ＋c ＝0的两个根分别是x 1＝1.3和x 2＝( )A ．－1.3B ．－2.3C ．－0.3D ．－3.312．2017·杭州设直线x ＝1是函数y ＝ax 2＋bx ＋c (a ，b ，c 是实数，且a ＜0)的图象的对称轴，则下列说法正确的是( )A ．若m ＞1，则(m －1)a ＋b ＞0B ．若m ＞1，则(m －1)a ＋b ＜0C ．若m ＜1，则(m －1)a ＋b ＞0D ．若m ＜1，则(m －1)a ＋b ＜013．如果二次函数y ＝ax 2＋bx ＋c 的图象与x 轴有两个公共点，那么一元二次方程ax2＋bx ＋c ＝0有两个不相等的实数根．请根据你对这句话的理解，解决下面问题：若m ，n (m <n )是关于x 的方程2－(x －a )(x －b )＝0的两根，且a <b ，则a ，b ，m ，n 的大小关系是( )A ．m <a <b <nB ．a <m <n <bC ．a <m <b <nD ．m <a <n <b图2－ZT －1314．二次函数y ＝ax 2＋bx ＋c (a ≠0)和正比例函数y ＝23x 的图象如图2－ZT －13所示，则方程ax 2＋(b －23)x ＋c ＝0(a ≠0)的两根之和( )A ．大于0B ．等于0C ．小于0D ．不能确定15．2017·常州已知二次函数y ＝ax 2＋bx －3中自变量x 的部分取值和对应的函数值y 如下表：则在实数范围内能使得y －5>0成立的x 的取值范围是________．16．如图2－ZT －14，已知二次函数y 1＝－x 2＋134x ＋c 的图象与x 轴的一个交点为A (4，0)，与y 轴的交点为B ，过A ，B 两点的直线为y 2＝kx ＋b .(1)求二次函数的表达式及点B 的坐标；(2)由图象写出满足y1<y2的自变量x的取值范围．图2－ZT－14详解详析1．B [解析] 由二次函数y＝ax2＋bx＋c的图象开口向上，得a＞0，与y轴交点在y轴的负半轴上，得c<0，对称轴在y轴的右侧，得－b2a>0，所以b<0，所以abc＞0；图象与x轴有两个交点，则b2－4ac>0.综上，故选B.2．B [解析] 由图象可知，抛物线与x轴有两个交点，∴b2－4ac＞0，故结论①不正确；∵抛物线的对称轴为直线x＝－1，与x轴的一个交点A在点(－3，0)和(－2，0)之间，∴抛物线与x轴的另一个交点在点(0，0)和(1，0)之间，∴当x＝1时，y＜0，∴a＋b＋c＜0，故结论②不正确；∵抛物线的对称轴为直线x＝－b2a＝－1，∴2a＝b，即2a－b＝0，故结论③正确；∵抛物线y＝ax2＋bx＋c的顶点为B(－1，3)，∴a－b＋c＝3.∵抛物线的对称轴为直线x＝－1，∴2a＝b，∴a－2a＋c＝3，即c－a＝3，故结论④正确．综上所述，正确的结论有2个．故选B.3．D [解析]①由函数的图象可得：当x＝－2时，y＜0，即y＝4a－2b＋c＜0，故①正确；②由函数的图象可知：抛物线开口向下，则a＜0；抛物线的对称轴为直线x＝－b2a＞－1，得出2a－b＜0，故②正确；③已知抛物线经过点(－1，2)，即a－b＋c＝2(1)，由图象知：当x＝1时，y＜0，即a ＋b＋c＜0(2)，联立(1)(2)，得a＋c＜1，故③正确；④因为抛物线的对称轴在直线x＝1右侧，所以抛物线的顶点纵坐标应该大于2，即4ac－b24a＞2，因为a＜0，所以4ac－b2＜8a，即b2＋8a＞4ac，故④正确．故选D.4．B [解析]∵抛物线y＝ax2＋bx＋c(c≠0)过点(－1，0)和点(0，－3)，∴0＝a－b＋c，－3＝c，∴b＝a－3.∵当x＝1时，y＝ax2＋bx＋c＝a＋b＋c，∴P＝a＋b＋c＝a＋a－3－3＝2a－6.∵顶点在第四象限，a＞0，∴b＝a－3＜0，∴a＜3，∴0＜a ＜3， ∴－6＜2a －6＜0， 即－6＜P ＜0. 故选B.5．D [解析]∵函数图象开口方向向上， ∴a ＞0.∵对称轴在原点右侧，∴ab 异号，即b <0. ∵抛物线与y 轴的交点在y 轴负半轴上， ∴c ＜0，∴abc ＞0，故①正确；∵图象与x 轴交于点A (－1，0)，对称轴为直线x ＝1， ∴图象与x 轴的另一个交点为(3，0)，∴当x ＝2时，y ＜0，即4a ＋2b ＋c ＜0，故②错误； ∵图象与x 轴交于点A (－1，0)，∴当x ＝－1时，y ＝(－1)2a ＋(－1)b ＋c ＝0， ∴a －b ＋c ＝0， 即a ＝b －c ，c ＝b －a . ∵对称轴为直线x ＝1，∴－b2a＝1，即b ＝－2a ， ∴c ＝b －a ＝(－2a )－a ＝－3a ，∴4ac －b 2＝4·a ·(－3a )－(－2a )2＝－16a 2＜0. ∵8a ＞0，∴4ac －b 2＜8a ，故③正确；∵图象与y 轴的交点B 在点(0，－2)和(0，－1)之间，∴－2＜c ＜－1， ∴－2＜－3a ＜－1，∴13<a <23，故④正确；∵a ＞0，∴b －c ＞0，即b ＞c ，故⑤正确．6．①④ [解析] 由图象可知抛物线开口向上，则a ＞0，由抛物线经过点A (－1，0)，B (0，－2)，对称轴在y 轴的右侧可得⎩⎪⎨⎪⎧a －b ＋c ＝0，c ＝－2，－b 2a >0，可得a －b ＝2，b ＜0.故a ＝2＋b ＜2，综合可知0＜a ＜2；由a －b ＝2可得a ＝b ＋2，将其代入0＜a ＜2中得0＜b ＋2＜2，可得－2＜b ＜0；当|a |＝|b |时，因为a ＞0，b ＜0，故有a ＝－b .又a －b ＝2，可得a ＝1，b ＝－1.故原函数为y ＝x 2－x －2，当y ＝0时，有x 2－x －2＝0，解得x 1＝－1，x 2＝2，在这里，x 2＝2＞5－1.故答案为①④. 7．解：(1)∵抛物线开口向上，∴a >0. 又∵对称轴x ＝－b2a <0，∴a ，b 同号，即b >0. ∵抛物线与y 轴交于负半轴， ∴c <0.综上所述，a >0，b >0，c <0. (2)∵OC ＝OA ＝13OB ，BC ＝4，∴点A 的坐标为(0，－1)，点B 的坐标为(－3，0)，点C 的坐标为(1，0)． 把A ，B ，C 三点的坐标分别代入二次函数y ＝ax 2＋bx ＋c 中，可得⎩⎪⎨⎪⎧－1＝c ，0＝9a －3b ＋c ，0＝a ＋b ＋c ，解得⎩⎪⎨⎪⎧a ＝13，b ＝23，c ＝－1.∴这个二次函数的表达式是y ＝13x 2＋23x －1.8．A9．B [解析] 由公共点的横坐标为1，且在反比例函数y ＝b x的图象上，当x ＝1时，y ＝b ，即公共点坐标为(1，b )，又点(1，b )在抛物线y ＝ax 2＋bx ＋c 上，得a ＋b ＋c ＝b ，a ＋c ＝0，再由a ≠0知ac ＜0，故一次函数y ＝bx ＋ac 的图象与y 轴的交点在负半轴上，由反比例函数y ＝b x的图象的一支在第一象限，知b ＞0，故一次函数y ＝bx ＋ac 的图象满足y 随x 的增大而增大，选项B 符合条件．故选B.10．C [解析] 观察二次函数图象可知：开口向上，a ＞0；对称轴在y 轴右侧，即－b2a ＞0，∴b ＜0；二次函数图象与y 轴的交点在y 轴的正半轴上，∴c ＞0.∵反比例函数中k ＝－a ＜0，∴反比例函数图象在第二、四象限内； ∵一次函数y ＝bx －c 中，b ＜0，－c ＜0， ∴一次函数图象经过第二、三、四象限．11．D [解析] 关于x 的一元二次方程ax 2＋bx ＋c ＝0的一个根是x 1＝1.3，即二次函数y ＝ax 2＋bx ＋c 的图象与x 轴的一个交点的坐标是(1.3，0)．又知抛物线的对称轴是直线x ＝－1，由抛物线是轴对称图形，可得图象与x 轴的另一个交点的坐标是(－3.3，0)，∴方程ax 2＋bx ＋c ＝0的另一个根是x 2＝－3.3.故选D.12．C [解析]∵直线x ＝1是函数y ＝ax 2＋bx ＋c (a ，b ，c 是实数，且a ＜0)的图象的对称轴，∴x ＝－b2a ＝1，即2a ＋b ＝0.∵a ＜0，∴2a ＜0，∴b ＞0.当m ＜1时，(m －1)a >0，即(m －1)a ＋b ＞0.故选C.13．A14．A [解析] 设方程ax 2＋(b －23)x ＋c ＝0的两根分别为x 1，x 2，则x 1＋x 2＝－b －23a，由函数图象易得a >0，b <0，因此－b －23a>0，即x 1＋x 2>0.15．x <－2或x >411 [解析] 由表中自变量与函数值的对应关系可以知道，二次函数y ＝ax 2＋bx －3的图象的顶点坐标为(1，－4)，抛物线开口向上，当x ＝4时，y ＝5，∴使y －5>0成立的x 的取值范围是x <－2或x >4.16．解：(1)将A (4，0)代入y 1＝－x 2＋134x ＋c ，得0＝－42＋134×4＋c ，解得c ＝3，∴二次函数的表达式为y 1＝－x 2＋134x ＋3.∵当x ＝0时，y 1＝3，∴点B 的坐标为(0，3)．(2)由图象知满足y 1<y 2的自变量x 的取值范围是x <0或x >4.。