选修2—1 第二章 §2.4.1抛物线及其标准方程
- 格式:doc
- 大小:213.94 KB
- 文档页数:3


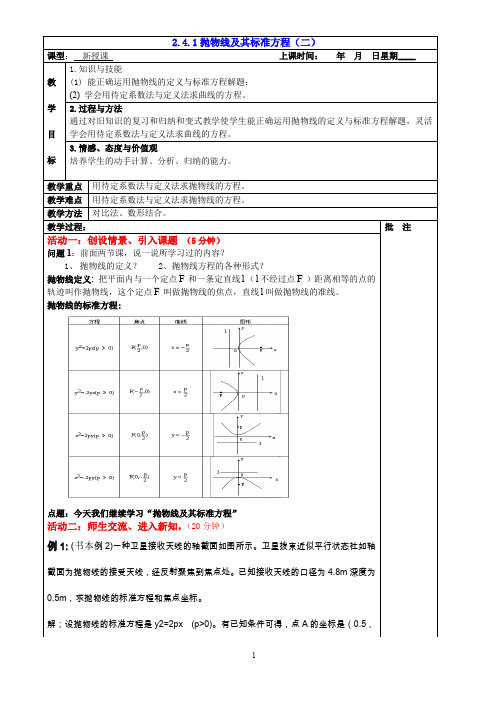



§2.4抛物线2.4.1抛物线及其标准方程学习目标 1.掌握抛物线的定义及其焦点、准线的概念.2.会求简单的抛物线方程.知识点一抛物线的定义1.定义:平面内与一定点F和一条定直线l(不经过点F)距离相等的点的轨迹.2.焦点:定点F.3.准线:定直线l.知识点二抛物线的标准方程图形标准方程焦点坐标准线方程y2=2px(p>0) ⎝⎛⎭⎫p2,0x=-p2y2=-2px(p>0) ⎝⎛⎭⎫-p2,0x=p2x2=2py(p>0) ⎝⎛⎭⎫0,p2y=-p2x2=-2py(p>0) ⎝⎛⎭⎫0,-p2y=p21.抛物线的方程都是二次函数.()2.抛物线的焦点到准线的距离是p.()3.抛物线的开口方向由一次项确定.()题型一求抛物线的标准方程例1分别求符合下列条件的抛物线的标准方程.(1)经过点(-3,-1);(2)焦点为直线3x-4y-12=0与坐标轴的交点.反思感悟用待定系数法求抛物线标准方程的步骤注意:当抛物线的类型没有确定时,可设方程为y2=mx(m≠0)或x2=ny(n≠0),这样可以减少讨论情况的个数.跟踪训练1 根据下列条件分别求出抛物线的标准方程: (1)准线方程为y =23;(2)焦点在y 轴上,焦点到准线的距离为5.题型二 抛物线定义的应用命题角度1 利用抛物线定义求轨迹(方程)例2 已知动圆M 与直线y =2相切,且与定圆C :x 2+(y +3)2=1外切,求动圆圆心M 的轨迹方程.反思感悟解决轨迹为抛物线问题的方法抛物线的轨迹问题,既可以用轨迹法直接求解,也可以先将条件转化,再利用抛物线的定义求解.后者的关键是找到满足动点到定点的距离等于到定直线的距离且定点不在定直线上的条件,有时需要依据已知条件进行转化才能得到满足抛物线定义的条件.跟踪训练2 已知动圆M 经过点A (3,0),且与直线l :x =-3相切,求动圆圆心M 的轨迹方程.命题角度2利用抛物线定义求最值例3如图,已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|P A|+|PF|的最小值,并求此时P点坐标.引申探究若将本例中的点A(3,2)改为点(0,2),求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.反思感悟抛物线的定义在解题中的作用,就是灵活地对抛物线上的点到焦点的距离与到准线的距离进行转化,另外要注意平面几何知识的应用,如两点之间线段最短,三角形中三边间的不等关系,点与直线上点的连线垂线段最短等.跟踪训练3已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和y轴的距离之和的最小值是() A. 3 B. 5 C.2 D.5-1抛物线的实际应用问题典例 河上有一抛物线形拱桥,当水面距拱桥顶5 m 时,水面宽为8 m ,一小船宽4 m ,高2 m ,载货后船露出水面上的部分高0.75 m ,问:水面上涨到与抛物线形拱桥拱顶相距多少m 时,小船开始不能通航?[素养评析] 首先确定与实际问题相匹配的数学模型.此问题中拱桥是抛物线型,故利用抛物线的有关知识解决此问题,操作步骤为:(1)建系:建立适当的坐标系. (2)假设:设出合适的抛物线标准方程. (3)计算:通过计算求出抛物线的标准方程. (4)求解:求出需要求出的量.(5)还原:还原到实际问题中,从而解决实际问题.1.若动点P 到定点F (-4,0)的距离与到直线x =4的距离相等,则P 点的轨迹是( )A .抛物线B .线段C .直线D .射线2.已知抛物线y =2px 2过点(1,4),则抛物线的焦点坐标为( )A .(1,0) B.⎝⎛⎭⎫116,0 C.⎝⎛⎭⎫0,116 D .(0,1)3.一动圆过点(0,1)且与定直线l 相切,圆心在抛物线x 2=4y 上,则l 的方程为( )A .x =1B .x =116C .y =-1D .y =-1164.若抛物线y 2=2px 的焦点坐标为(1,0),则p =________,准线方程为________.5.抛物线y 2=-2px (p >0)上有一点M 的横坐标为-9,它到焦点的距离为10,求此抛物线方程和M 点的坐标.1.利用抛物线定义可以把抛物线上的点到焦点的距离转化为到准线的距离,这一相互转化关系能给解题带来很大的方便,要注意运用定义解题.2.在求抛物线的标准方程时,由于其标准方程有四种形式,易于混淆,解题时一定要做到数形结合,按照“定形(抛物线焦点位置)→定量(参数p 的值)”的程序求解.一、选择题1.抛物线y =2x 2的焦点到准线的距离是( )A .2B .1 C.14 D.122.若动点P 与定点F (1,1)和直线l :3x +y -4=0的距离相等,则动点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .直线3.已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线焦点坐标为( )A .(-1,0)B .(1,0)C .(0,-1)D .(0,1)4.经过点P (4,-2)的抛物线的标准方程为( )A .y 2=x 或x 2=-8yB .y 2=x 或y 2=8xC .y 2=-8xD .x 2=-8y5.已知抛物线C :y 2=x 的焦点为F ,A (x 0,y 0)是C 上一点,|AF |=54x 0,则x 0等于( )A .4B .2C .1D .86.设圆C 与圆x 2+(y -3)2=1外切,与直线y =0相切,则C 的圆心轨迹为( )A .抛物线B .双曲线C .椭圆D .圆7.已知抛物线y 2=4x 上一点P 到焦点F 的距离为5,则△PFO 的面积为( ) A .1 B .2 C .3 D .48.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是( )A .2B .3 C.115 D.3716二、填空题9.已知双曲线x 2m -y 2=1的右焦点恰好是抛物线y 2=8x 的焦点,则m =________.10.若抛物线y 2=4x 上的点M 到焦点的距离为10,则M 到y 轴的距离是________.11.一抛物线形拱桥,当桥顶离水面2米时,水面宽4米,若水面下降2米,则水面宽为________米.三、解答题12.根据下列条件分别求抛物线的标准方程. (1)抛物线的焦点是双曲线16x 2-9y 2=144的左顶点;(2)抛物线的焦点F 在x 轴上,直线y =-3与抛物线交于点A ,|AF |=5.13.已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A的坐标是(8,7),则|P A|+|PQ|的最小值为()A.7 B.8 C.9 D.1014.平面上动点P到定点F(1,0)的距离比点P到y轴的距离大1,求动点P的轨迹方程.。
§2.4.1 抛物线及其标准方程(选修2-1)华中科技大学附属中学夏云晶教学目标:1.理解抛物线的定义,掌握抛物线的四种标准方程及其对应的图形、焦点和准线。
2.使学生进一步熟练掌握解析几何的基本思想方法,培养学生观察、联想、类比、猜测、归纳等合情推理的方法,提高学生抽象、概括、分析、综合的能力。
3.通过学生参与标准方程的推导,培养学生的自主探索精神和创新意识,培养学生运用数形结合的数学思想理解有关问题。
教学重点:抛物线的定义及标准方程教学难点:抛物线的标准方程的推导教学过程:一、创设情境引入新知大家初中学习过二次函数,知道函数y = -x2的图像是一条一一抛物线。
到4底什么是抛物线呢?抛物线上的点具有怎样的性质呢?我们知道,椭圆、双曲线和抛物线都是圆锥曲线。
椭圆上的点满足到一个定点F和一条定直线/的距离的比为定值,且定值小于1。
双曲线上的点到一个定点F和一条定直线/的距离的比为定值,且定值大于1。
(几何画板作图并演示动画)问题1:大家猜测下抛物线上的点具有怎样的性质呢?观察1:现在已知定点F (0, 1),定直线= -1, F^/o在图像上任取一点P,连接PF,并作PQ丄儿请观察,当P点在抛物线上运动时,它到定点F的距离与到定直线l:y = -\的距离之间有何关系?(几何画板演示动画)抛物线y = L x2可以看成是平面内与定点F (0, 1)和定直线/:y = -l的距' 4 ~离相等的点的轨迹。
其实我们可以验证所有抛物线上的点都具有到一个定点和一条定直线的距离相等这一性质。
反过来,具有这一性质的点的轨迹是不是抛物线呢?观察2:在平面内任取定点F和定直线几在/上取一点N,连接FN。
作FN的中垂线,过N作/的垂线,与NF的中垂线交于点M,连接MF。
由刚才的作图过程,点M满足到点F的距离和到直线/的距离相等。
让M点运动起来,它的轨迹是什么?(几何画板演示动画)二、探索研究构建方程问题2:通过刚才的讨论,你能给抛物线下一个定义吗?1.观察归纳抛物线的定义定义:平面内与一个定点F和一条定直线/的距离相等的点的轨迹叫做抛物线。
高二数学 选修2—1 第二章 §2.4.1抛物线及其标准方程(2014/12/8)班级 姓名问题:到定点距离与到定直线距离之比是定值e 的点的轨迹,当0<e<1时是 ,当e>1时是 .此时自然想到,当e=1时轨迹是什么?二、新课导学:1.定义:平面内与一个定点F 和一条定直线l 的距离 的点的轨迹叫做抛物线.点F 叫做抛物线的 ;直线l 叫做抛物线的 . 2.定点F 到定直线l 的距离为 . 3.建立适当的坐标系,得到抛物线的四种标准形式:抛物线220y x =的焦点坐标是 ,准线方程是 ;抛物线21x y =-的焦点坐标是 ,准线方程是 .例1、(1)已知抛物线的标准方程是26y x =,求它的焦点坐标和准线方程; (2)已知抛物线的焦点是(0,2)F -,求它的标准方程.变式1:根据下列条件写出抛物线的标准方程:⑴焦点坐标是(0,4); ⑵准线方程是14x =-; ⑶焦点到准线的距离是2.变式2: 求下列抛物线的焦点坐标和准线方程.(1)x y 122= (2)212x y =例2、一种卫星接收天线的轴截面如图所示,卫星波束呈近似平行状态的射入轴截面为抛物线的接收天线,经反射聚集到焦点处,已知接收天线的口径为4.8m ,深度为0.5m ,试建立适当的坐标系,求抛物线的标准方程和焦点坐标.例3、已知动点),(y x M 的坐标满足2)2(22+=+-x y x ,则动点M 的轨迹是( ) A.抛物线 B.双曲线 C.椭圆 D.以上均不对变式3:已知动点),(y x M 的坐标满足1243)2()1(522++=-+-y x y x ,则动点M 的轨迹是( ) A. 直线 B.双曲线 C.椭圆 D.抛物线练习:(1)抛物线22y px = (0)p >上一点M 到焦点距离是a ()2pa >,则点M 到准线的距离是 , 点M 的横坐标是 .(2)抛物线x y 122=上与焦点的距离等于9的点的坐标是 .三、总结提升 ※ 学习小结1.抛物线的定义;2.抛物线的标准方程、几何图形.一、基础训练题1.抛物线y 2=-8x 的焦点坐标是 ( ).A .(2,0)B .(-2,0)C .(4,0)D .(-4,0) 2.若抛物线y 2=8x 上一点P 到其焦点的距离为10,则点P 的坐标为( ).A .(8,8)B .(8,-8)C .(8,±8)D .(-8,±8) 3.以双曲线x 216-y 29=1的右顶点为焦点的抛物线的标准方程为( ).A .y 2=16xB .y 2=-16xC .y 2=8xD .y 2=-8x 4.动点到点(3,0)的距离比它到直线x =-2的距离大1,则动点的轨迹是( ).A .椭圆B .双曲线C .双曲线的一支D .抛物线 5.抛物线y =ax 2的准线方程是y =1,则a 的值为( )A.14 B .-14C .4D .-4 6.设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是________. 7.若直线ax -y +1=0经过抛物线y 2=4x 的焦点,则实数a =________. 8.根据下列条件写出抛物线的标准方程:(1)准线方程是y =3; (2)过点P (-22,4); (3)焦点到准线的距离为 2.9.已知动圆M 经过点A (3,0),且与直线l :x =-3相切,求动圆圆心M 的轨迹方程.10.若抛物线y 2=-2px (p >0)上有一点M ,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M 点的坐标.二、提高训练题11.若抛物线y 2=x 上一点P 到其准线的距离等于它到顶点的距离,则点P 的坐标为( )A.⎝⎛⎭⎫14,±24B.⎝⎛⎭⎫18,±24C.⎝⎛⎭⎫14,24D.⎝⎛⎭⎫18,2412.抛物线的焦点F 在x 轴上,直线y =-3与抛物线交于点A ,|AF |=5,求抛物线的标准方程.13.(创新拓展)设F (1,0),点M 在x 轴上,点P 在y 轴上,且(1)当点P 在y 轴上运动时,求点N 的轨迹C 的方程;(2)设A (x 1,y 1),B (x 2,y 2),D (x 3,y 3)是曲线C 上除去原点外的不同三点,且成等差数列,当线段AD 的垂直平分线与x 轴交于点E (3,0)时,求点B 的坐标.选修2—1 第二章 §2.4.1抛物线及其标准方程参考答案1、解析 依题意,抛物线开口向左,焦点在x 轴的负半轴上,由2p =8得p2=2,故焦点坐标为(-2,0). 答案 B2、解析 设P (x P ,y P ),∵点P 到焦点的距离等于它到准线x =-2的距离,∴x P =8,y P =±8. 答案 C3、解析 由双曲线方程x 216-y 29=1,可知其焦点在x 轴上,由a 2=16,得a =4,∴该双曲线右顶点的坐标是(4,0),∴抛物线的焦点为F (4,0).设抛物线的标准方程为y 2= 2px (p >0),则由p2=4,得p =8,故所求抛物线的标准方程为y 2=16x .答案 A4、解析 已知条件可等价于“动点到点(3,0)的距离等于它到直线x =-3的距离”,由抛 物线的定义可判断,动点的轨迹为抛物线,故选D. 答案 D5、解析:抛物线方程为x 2=1a y ,其准线方程为y =-14a ,∴-14a =1,∴a =-14.答案 B 6、解析 由抛物线的方程得p 2=42=2,再根据抛物线的定义,可知所求距离为4+2=6.答案 67、解析 抛物线y 2=4x 的焦点为(1,0),代入ax -y +1=0,解得a =-1. 答案 -18、解 (1)由准线方程为y =3知抛物线的焦点在y 轴负半轴上,且p2=3,则p =6,故所求抛物线的标准方程为x 2=-12y .(2)∵点P (-22,4)在第二象限,∴设所求抛物线的标准方程为y 2=-2px (p >0)或x 2=2py (p >0),将点P (-22,4)代入y 2=-2px ,得p =22;代入x 2=2py ,得p =1. ∴所求抛物线的标准方程为y 2=-42x 或x 2=2y .(3)由焦点到准线的距离为2,得p =2,故所求抛物线的标准方程为y 2=22x ,y 2= -22x ,x 2=22y 或x 2=-22y . 9、解 法一 设动点M (x ,y ),设⊙M 与直线l :x =-3的切点为N ,则|MA |=|MN |, 即动点M 到定点A 和定直线l :x =-3的距离相等,所以点M 的轨迹是抛物线,且以A (3,0)为焦点,以直线l :x =-3为准线,∴p2=3,∴p =6. ∴圆心M 的轨迹方程是y 2=12x .法二 设动点M (x ,y ),则点M 的轨迹是集合P ={M ||MA |=|MN |}, 即(x -3)2+y 2=|x +3|,化简,得y 2=12x . ∴圆心M 的轨迹方程为y 2=12x .10、解:由抛物线定义,设焦点F ⎝⎛⎭⎫-p2,0, 则准线为x =p2,过M 作准线的垂线,垂足为N ,则|MN |=|MF |=10,即p2-(-9)=10,∴p =2. 故抛物线方程为y 2=-4x . 将M (-9,y ),代入抛物线方程得y =±6. ∴M (-9,6)或M (-9,-6).11、解析:由抛物线定义可得,P 到顶点的距离等于它到抛物线焦点的距离,即P 点的横坐标为0+p 22=18. 故P 点的坐标为⎝⎛⎭⎫18,±24.答案 B12、解:设所求焦点在x 轴上的抛物线的方程为y 2=2px (p ≠0),A (m ,-3),由抛物线定义得5=|AF |=⎪⎪⎪⎪m +p2. 又(-3)2=2pm , ∴p =±1或p =±9,故所求抛物线方程为y 2=±2x 或y 2=±18x .13、解 (1)设N (x ,y ),由得点P 为线段MN 的中点,∴P (0,y2),M (-x ,0),∴=(-x ,-y2),=(1,-y2).由=-x +y 24=0,得y 2=4x .即点N 的轨迹方程为y 2=4x .(2)由抛物线的定义,知|AF |=x 1+1,|BF |=x 2+1,|DF |=x 3+1, ∵成等差数列,∴2x 2+2=x 1+1+x 3+1,即x 2=x 1+x 32.∵线段AD 的中点为(x 1+x 32,y 1+y 32),且线段AD 的垂直平分线与x 轴交于点E (3,0),∴线段AD 的垂直平分线的斜率为k =y 1+y 32-0x 1+x 32-3.又k AD =y 3-y 1x 3-x 1,∴y 3-y 1x 3-x 1·y 1+y 3x 1+x 3-6=-1,即4x 3-4x 1(x 32-x 12)-6(x 3-x 1)=-1.∵x 1≠x 3,∴x 1+x 3=2,又x 2=x 1+x 32,∴x 2=1.∵点B 在抛物线上,∴B (1,2)或(1,-2).。