《类比推理》参考教案1

幼儿园小班类比推理教案一、教学目标•培养幼儿的类比推理能力。

•提升幼儿的观察能力和逻辑思维能力。

•培养幼儿的创造力和问题解决能力。

二、教学内容1.类比推理的基本概念•通过示例引入类比推理的概念，让幼儿理解类比推理是一种通过相似性和关系来推断和判断的思维方式。

2.类比推理的分类•比例类比：学会根据物体的比例关系进行类比推理。

•特征类比：学会根据物体的共同特征进行类比推理。

•逻辑类比：学会根据逻辑关系进行类比推理。

3.类比推理的实践应用•利用不同的类比推理方法解决问题。

•进行小组活动，让幼儿合作进行类比推理的实践应用。

三、教学步骤1.引入类比推理的基本概念•引导幼儿观察一些物体，并提问：“你们有没有发现这些物体之间有什么相似性或者关系？”•通过幼儿的回答，引导他们理解类比推理的概念。

2.学习不同类型的类比推理•分别介绍比例类比、特征类比和逻辑类比的概念，并给出相应的示例。

•通过示例让幼儿理解不同类型的类比推理方法。

3.实践类比推理•准备一些具有类比关系的物体或图形。

•让幼儿观察这些物体或图形，并根据不同的类比推理方法，进行类比推理，找出规律或解决问题。

4.小组活动•将幼儿分为小组，每个小组给出一个类比推理问题。

•让幼儿在小组内合作讨论，并通过类比推理找出问题的答案。

•对每个小组进行评价和讨论，鼓励幼儿分享和交流类比推理的思路和方法。

四、教学评估1.观察幼儿在学习过程中的参与度和表现情况。

2.针对小组活动中的表现和解题能力进行评价。

3.收集幼儿的作品和解题思路，对幼儿的类比推理能力进行综合评估。

五、教学资源•物品：具有类比关系的物体或图形。

•白板、马克笔等教学用具。

六、教学延伸活动•给幼儿布置类比推理的作业，鼓励他们继续通过类比推理解决问题。

•在日常生活中引导幼儿观察周围事物，并进行类比推理讨论。

•组织小型类比推理竞赛，激发幼儿参与和学习的兴趣。

七、教学反思通过本节课的教学，我发现幼儿在类比推理方面具有一定的天赋和潜力。

教学目标：1. 让学生了解类比推理的概念和特点，提高类比推理能力。

2. 培养学生观察、分析、归纳和总结的能力。

3. 增强学生的逻辑思维能力和创新意识。

教学重难点：1. 理解类比推理的概念和特点。

2. 培养学生的类比推理能力。

教学方法：1. 讲授法：讲解类比推理的基本概念和特点。

2. 讨论法：引导学生讨论和总结类比推理的技巧和方法。

3. 案例分析法：通过案例分析，让学生更好地理解类比推理的应用。

教学过程：一、导入1. 教师简要介绍类比推理的概念和特点，激发学生的学习兴趣。

2. 提问：什么是类比推理？类比推理有什么特点？二、讲授新课1. 讲解类比推理的定义、基本形式和特点。

2. 举例说明类比推理在实际生活中的应用。

3. 分析类比推理的技巧和方法。

三、讨论与总结1. 教师提出问题，引导学生讨论类比推理的技巧和方法。

2. 学生分享自己的观点和经验，互相学习。

3. 教师总结讨论结果，强调类比推理的重要性。

四、案例分析1. 教师提供几个类比推理的案例，让学生分析并找出其中的规律。

2. 学生分组讨论，分析案例中的类比推理过程。

3. 各组汇报讨论结果，教师点评并总结。

五、巩固练习1. 教师布置几道类比推理的练习题，让学生巩固所学知识。

2. 学生独立完成练习，教师巡视指导。

3. 学生互相检查答案，共同讨论解题思路。

六、总结与反思1. 教师总结本节课的重点内容，强调类比推理的重要性。

2. 学生反思自己在类比推理方面的不足，提出改进措施。

3. 教师鼓励学生在日常生活中多运用类比推理，提高自己的思维能力。

教学反思：1. 本节课是否达到了教学目标？2. 学生对类比推理的理解程度如何？3. 教学过程中是否充分发挥了学生的主体作用？4. 教学方法是否合理，是否激发了学生的学习兴趣？5. 如何改进教学方法，提高教学效果？教学评价：1. 学生对类比推理的理解和掌握程度。

2. 学生在课堂上的参与度和积极性。

3. 学生类比推理能力的提高情况。

类比推理及其方法教案一、引言类比推理是一种常见且有用的推理方法，它通过将不同领域或事物之间的相似性和共同特点进行比较和推断，以帮助我们理解和解决问题。

本教案将介绍类比推理的基本概念、方法和应用，并为学生提供相关练习和案例分析，以提高他们运用类比推理解决问题的能力。

二、概述类比推理1. 理解类比推理的概念类比推理是一种基于相似性的推理方法。

它基于一个基本的前提，即两个或更多事物之间存在某种相似性或共同特点，通过将这些相似性和共同特点进行比较，以推断出它们可能具有相似的性质、特征或关系。

类比推理可以在不同领域和学科中应用，例如生物学、数学、物理学等。

2. 认识类比推理的重要性类比推理在日常生活和学习中具有重要的作用。

通过类比推理，我们可以将已知的知识、经验和解决方法应用到新的情境中，从而更好地理解和解决问题。

类比推理有助于培养学生的比较和归纳能力，提高他们的问题解决和创新思维能力。

三、类比推理的方法1. 根据共同特征进行类比推理类比推理的基本方法是找出两个或更多事物之间的共同特征，并将这些特征作为判断和推断的依据。

通过找到共同特征，我们可以认为这些事物在某些方面是相似的，从而推断出它们可能具有相似的性质、特征或关系。

2. 使用类比推理图示辅助推理类比推理图示是辅助进行类比推理的有效工具。

通过绘制类比推理图示，我们可以将两个或更多事物的共同特征以图形化的方式表示出来，从而更直观地进行推理和分析。

类比推理图示可以是思维导图、Venn图、流程图等形式。

四、类比推理的应用案例1. 科学领域中的类比推理在科学研究中，类比推理经常被用于推断和预测。

例如，基于地球上的生命形式，科学家通过类比推理认为在其他星球上可能存在着类似的生命形式。

类比推理还可以帮助科学家发现新的规律和关系，推动科学研究的进展。

2. 数学问题中的类比推理在解决数学问题时，类比推理可以帮助我们发现问题的模式和规律。

例如，当我们遇到一个数列问题时，可以通过观察和比较不同项之间的关系和特征，运用类比推理发现数列的递推公式，从而解决问题。

类比推理讲义（一）一、题型综述:类比推理是先给出一组或多组相关的词，然后要求你在备选答案中找出一组与之在逻辑关系上最为贴近、匹配的词：二、解题思路：事物间都存在逻辑关系，对事物间逻辑关系的抽象比较就是类比。

正确的解题思路是，准确判断题干给定的一组或多组相关词（概念）间的逻辑关系，然后，选择与之逻辑关系相同或相近的备选项作为答案。

三、类比推理导图:四、三种题型1）基本型：双词类比一一A；B解析要求：先给出一组相关的词，然后要求你在备选答案中找出一组与之在逻辑关系上最为贴近、匹配的词：例题：动物:牛A.汽车:轿车B.足球:球类C.公务员:教师D.松树:菊花这类题型，涉及到的横向逻辑往往比较单一联考题型：1.谎言：欺骗（）一一【2016联考85】A谣言：抱怨B谗言：无知C佯言：委婉D诤言：劝诫2.商品：琳琅满目（）一一【2016联考88】A商场：熙熙攘攘B公司：运筹帷幄C教学：紧张有序D家庭：相亲相爱3 .菜刀：食物A.子弹：枪支 8.毛巾：身体C.铅笔：书籍D.窗帘：窗户4 .学生证：学生A.驾驶证：开车B.学位证：学校C.结婚证：夫妻D.身份证：护照5 .白驹过隙：度日如年A .潜移默化：耳提面命B .浮光掠影：鞭辟入里C .阳春白雪：曲高和寡D .字斟句酌：咬文嚼字这类成语和古诗俗语题等多考察，褒贬、近反义词以及句子结构的逻 辑关系，要重点关注。

2、基本进阶型：三词类比一-A ； B ： C相关题型1 .蜡烛：电灯A.椅子：写字台C.拖把：吸尘器2 .富裕：扶贫A.干燥：抽湿B.茶杯：饮水机 D.电视：计算机 8.蒙昧：教育解析要求：在备选项中选择一组概念，这组概念相互之间的逻辑关系与题干相同或相似。

这类题，因为比双词多了一词，因此逻辑相关性更加严密和复杂，因此考点多为逻辑本身。

我们需要寻找AB、AC、BC、AB和C、BC和A 等等之间的关联性。

因此多利用造句法解题会使问题简单化。

例题：火车:汽车:交通工具A.公路:铁路:山路B.泰山:太行山:山脉C.公园:大厦:城市D.蔬菜:粮食:庄稼联考题型1.沟通：手机：金属（）一一【2016联考861A招聘：面试：简介B卫星：科技：科学家C物流：运输：公路D露营：帐篷：帆布2.出行：雾霾；口罩（）一一【2016联考891A休息：沙发：电视B超车：公路：路标C勘探：野外：地图D娱乐：海滨：游泳3.麻雀：动物：生物链（）一一【2016联考90】A豆浆：早餐：豆制品B开水：纸杯：便利品C发卡：首饰：妆扮品D钢笔：电脑：办公品4.水：森林：煤炭（）一一【2016联考91】A氮：蛋白质：智力B闪电：雨：打伞C雪：丰年：喜悦D表扬：自信：乐观相关题型1.站台：码头：停机坪 A .现金：支票：银行卡 C .夕卜套：婚纱：羽绒服2.研究生：硕士：博士 A.青少年：少年：青年 C.建筑：平房：高楼 3.行驶：违章：罚款 A.学习：成绩：奖励 C.竞争：优势：成功 4.春雨：杏花：江南 A.夏荷：烈日：江北 C.秋霜：枯草：塞外3）填空型（）对于B相当于C 对于（）解析要求：在备选项中选择一对概念，按照先后顺序分别填入括号， 使题干中前组合与后组合的逻辑关系相同或相似。

否正确仍然需要验证.
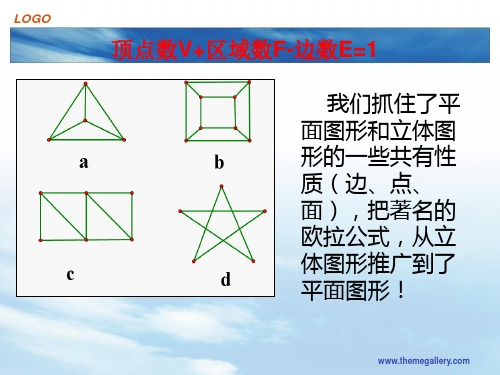
小结2：练习3由一个平面几何的结论推理出许多立体几何结论.
平面几何和立体几何两者在逻辑体系结构、构成问题的基本元素、研究对象和方法等方面都有非常相似的地方.从维度升高的
角度来看，他们的基本元素之间能有如下的对应关系
平面空间
点线
直线平面
平面图形立体图形
问题4：圆可类比为球，正方形呢？长方形呢？平行四边形呢？三角形呢？？
可类比可类比
小结：可类比得两类事物必有相类似的构成，对构成的理解不同，同一个图形可以有不同的类比对象.自然可能会有不同的推理结论.。

高中数学类比推理教案
教学目标：通过本课程学习，学生能够掌握类比推理的基本概念和方法，能够熟练运用类比推理解决实际问题。

教学重点：类比推理的基本概念和方法。

教学难点：灵活运用类比推理解决实际问题。

教学准备：
1. 教材：高中数学教材。

2. 教具：黑板、彩色粉笔、教案、习题册。

3. 教学内容：类比推理的概念和方法。

教学过程：
一、导入（5分钟）
教师通过举一个生活中的例子，引入类比推理的概念，让学生了解类比推理在日常生活中的重要性。

二、讲解（15分钟）
1. 教师向学生介绍类比推理的定义和基本概念。

2. 教师讲解类比推理的方法和步骤。

3. 教师通过实例详细讲解类比推理的过程和技巧。

三、练习（20分钟）
1. 学生通过课堂练习，独立完成类比推理的练习题。

2. 学生通过小组合作，讨论解答类比推理的难题。

四、总结（5分钟）
1. 教师对本节课的内容进行总结，并强调类比推理的重要性。

2. 学生积极参与讨论，对类比推理的方法和技巧进行总结。

五、作业布置（5分钟）
1. 布置课后作业，要求学生完成相关的习题。

2. 提醒学生认真复习类比推理的方法和技巧。

教学反思：
通过本节课的教学，学生能够掌握类比推理的基本概念和方法，能够灵活运用类比推理解决实际问题。

同时，学生能够培养逻辑思维能力，提高数学分析和推理能力。

课题：类比推理一.教学目标：1.知识与技能：了解类比推理的含义、特点，能利用类比进行简单的推理.2.过程与方法：通过生活和学习中的实例创设情境、进行探究，提高学生观察猜想、抽象概括能力，渗透类比的思想方法.3.情感、态度与价值观：体会类比推理在实际生活和数学发现中的作用，提高学习数学的兴趣，增强创新意识.二.教学重点：了解类比推理的含义，能利用类比进行简单的推理三.教学难点：能找到事物之间的共同或相似性质，不仅会在形式结构和叙述方式上进行类比，还需对推理过程和思维策略进行类比.四.教学方法：启发式教学五.教学过程：1.问题情境1.古代工匠鲁班类比带齿的草叶和蝗虫的牙齿,发明了锯．2.人们仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.3.苍蝇的眼睛是一种“复眼”，由3000多只小眼组成，人们模仿它制成了“蝇眼透镜”，一次就能照出千百张相同的相片。

设问：地球上存在生命，火星存在生命吗？2.讲授新课引例：“火星上是否有生命”圆的定义：平面内到一个定点的距离等于定长的点的集合.球的定义：到一个定点的距离等于定长的点的集合.圆←→球弦←→截面圆直径←→大圆▲类比推理的定义：这种由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理称为类比推理（简称类比）.简言之，类比推理是由特殊到特殊的推理.例1类比实数的加法和乘法，列出它们相似的运算性质.分析：实数的加法和乘法都是由两个数参与的运算，都满足一定的运算律，而且“0”和“1”分别在加法和乘法中占有特殊的地位.因此，我们可以从上述4个方面来类比这两种运算. 解：（1）两个实数经过加法运算或乘法运算后，所得的结果仍然是一个实数.（2）从运算律的角度考虑，加法和乘法都满足交换律和结合律，即a+b=b+a ab=ba（a+b ）+c=a+（b+c ） （ab ）c=a （bc ）（3）从逆运算的角度考虑，二者都有逆运算，加法的逆运算是减法，乘法的逆运算是除法，这就使得方程 a+x=0 ax=1（a ≠0）都有唯一解 x=-a x=1a（4）在加法中，任意实数与0相加都不改变大小；乘法中的1与加法中的0类似，即任意实数与1的积都等于原来的数.即 a+0=a a ⋅1=a▲类比推理的一搬步骤：（1）找出两类对象之间可以确切表述的相似特征；（2）用一类对象的已知特征去推测另一类对象的特征，从而得出一个猜想.探究二：你认为平面几何中的哪一类图形可以作为四面体的类比对象？相似性：（1）三角形是平面内由最少的线段所围成的最简单的封闭图形；四面体是空间中由最少的平面所围成的最简单的封闭图形.（2）三角形可以看做平面上一条线段所在直线外一点与这条线段两端点连线所形成的图形；四面体可以看做空间中一个三角形所在平面外一点与这个三角形三顶点连线所形成的图形 例2类比平面内直角三角形的勾股定理，试给出空间中四面体性质的猜想.解：如图所示，在Rt △ABC 中，∠C=90°.设a,b,c 分别表示三条边的长度，由勾股定理，得222.c a b =+于是，类比直角三角形的勾股定理，在四面体P-DEF 中，我们猜想2222123S S S S =++成立.注意：类比推理是由特殊到特殊的推理；以旧的知识为基础，推测新的结果，具有发现的功能；类比推理的结论不一定成立.4.归纳小结：(1)类比推理：特殊—→特殊(2)类比推理的一般步骤：①找出两类事物之间的相似性或者一致性。

教学目标：1. 让学生了解类比推理的概念，学会运用类比推理进行思考。

2. 培养学生的逻辑思维能力和创新能力。

3. 培养学生善于观察、分析、归纳的能力。

教学重点：1. 类比推理的概念2. 类比推理的方法教学难点：1. 如何运用类比推理进行思考2. 如何引导学生进行类比推理教学过程：一、导入1. 教师简要介绍类比推理的概念，引导学生了解类比推理的定义。

2. 教师提问：类比推理在生活中的应用有哪些？二、新课讲解1. 教师举例说明类比推理的方法，如：找出两个事物之间的相似点，通过相似点进行推理。

2. 教师引导学生分析例题，让学生学会运用类比推理进行思考。

三、课堂练习1. 教师出示练习题，让学生进行类比推理。

2. 教师讲解练习题的答案，并分析解题思路。

四、拓展延伸1. 教师引导学生思考：如何将类比推理应用于实际生活中？2. 学生分组讨论，分享自己的观点。

五、总结1. 教师总结本节课所学内容，强调类比推理的重要性。

2. 教师鼓励学生在日常生活中多运用类比推理，提高自己的思维能力。

教学反思：1. 本节课通过讲解类比推理的概念和方法，让学生了解了类比推理的基本知识。

2. 在课堂练习环节，学生能够运用所学知识进行类比推理，提高了自己的逻辑思维能力。

3. 在拓展延伸环节，学生积极参与讨论，分享了自己的观点，提高了自己的创新能力。

4. 在教学过程中，教师要注意引导学生积极参与，培养学生的自主学习能力。

教学评价：1. 学生能够理解类比推理的概念，并学会运用类比推理进行思考。

2. 学生在课堂练习中，能够独立完成类比推理题目，解题思路清晰。

3. 学生在拓展延伸环节，能够积极思考，分享自己的观点，提高了自己的创新能力。

类比推理及其方法教学设计一、引言类比推理是一种基于相似性的推理方法，通过将一个领域的问题映射到另一个已经熟悉的领域，从而解决问题或产生新的见解。

在认知科学和教育领域具有广泛的应用价值。

本文将介绍类比推理及其方法，并设计一份教学计划，以帮助学生掌握类比推理的技能和应用。

二、概念解释1. 类比推理：类比推理是一种通过找到问题与已知事物之间的相似之处来解决问题的方法。

它基于两个领域之间的相似性，将已知领域的知识应用到未知领域中。

2. 类比推理的作用：类比推理有助于问题解决、知识迁移、创造性思维等方面的发展。

通过类比推理，我们可以利用已有领域的知识和经验来解决新领域的问题，提升思维的灵活性和创造性。

三、类比推理的方法1. 表面类比法：表面类比法是最简单直接的方法，通过找到两个问题之间的表面相似之处来推断解决办法。

例如，解决一个物理问题时，可以找到一个相似的例子并应用相同的原理。

2. 结构类比法：结构类比法关注问题的结构和组织方式，而非表面的相似性。

通过找到两个问题之间的结构相似之处，可以将一个问题的解决方法应用到另一个问题中。

例如，解决一个工程问题时，可以找到类似结构的问题并将其解决方法应用于新问题。

3. 行为类比法：行为类比法是通过比较两个领域中的行为方式来解决问题。

通过创建一个类比模型，分析两个行为或过程的相似之处，可以从一个领域中的行为获得关于另一个领域的行为的见解。

四、类比推理的教学设计1. 目标设定：明确教学目标，例如学生能够理解类比推理的概念和作用，并能够灵活运用类比推理方法解决问题。

2. 教学原理：通过启发式教学方法，引发学生的兴趣和动机，帮助他们理解类比推理的原理和方法。

3. 教学步骤：a. 引入：通过实例引入，让学生从日常生活中找到类比推理的例子，激发学生的思考和讨论。

b. 概念解释：教师向学生解释类比推理的概念和作用，帮助他们理解这种推理方法的重要性。

c. 方法讲解：教师详细介绍表面类比法、结构类比法和行为类比法，并给出具体的例子进行解释。