2018中考数学压轴题复习 1.5 因动点产生的面积问题

专题10 动点产生的面积关系教学重难点1.体会点的运动过程，能从点的运动过程中抓住一些不变的量；2.能从点的运动过程中建立自变量与面积的关系式；3.让学生学会求一些基本图形的面积；4.体会压轴题的解题方法和思路。

【备注】：1.此部分知识点梳理，根据第1个图先让学生初步体会到压轴题中求图形面积的种类，可以看看每一类图形学生都是怎么求解的；2再根据第2个图引导学生总结求三角形面积的一般方法。

时间5分钟左右完成。

压轴题中求图形面积类型：三角形面积的一般求解方法：【备注】：1.以下每题教法建议，请老师根据学生实际情况参考；2.在讲解时：不宜采用灌输的方法，应采用启发、诱导的策略，并在读题时引导学生发现一些题目中的条件（相等的量、不变的量、隐藏的量等等），使学生在复杂的背景下自己发现、领悟题目的意思；3.可以根据各题的“参考教法”引导学生逐步解题，并采用讲练结合；注意边讲解边让学生计算，加强师生之间的互动性，让学生参与到例题的分析中来；4.例题讲解，可以根据“参考教法”中的问题引导学生分析题目，边讲边让学生书写，每个问题后面有答案提示；5.引导的技巧：直接提醒，问题式引导，类比式引导等等；6.部分例题可以先让学生自己试一试，之后再结合学生做的情况讲评；7.每个题目的讲解时间根据实际情况处理，建议每题7分钟，选讲例题在时间足够的情况下讲解。

例1（2020静安区建承中学一模）在平面直角坐标系xOy 中（如图），已知二次函数2y ax bx c =++（其中a 、b 、c 是常数，且a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ．（1）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果:3:2ABD BCD S S ∆∆=，求tan∠DBC 的值； （3）如果点E 在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．【整体分析】（1）直接利用待定系数法，把A 、B 、C 三点代入解析式，即可得到答案； （2）过点D 作DH ∠BC 于H ，在∠ABC 中，设AC 边上的高为h ，利用面积的比得到32AD DC =，然后求出DH 和BH ，即可得到答案；（3）延长AE 至x 轴，与x 轴交于点F ，先证明△OAB∠∠OFA ，求出点F 的坐标，然后求出直线AF 的方程，即可求出点E 的坐标. 【详解】解：（1）将A （0，-3）、B （1，0）、C （3，0）代入20y ax bx c a =++≠（）得，03,0934,300a b a b c =+-⎧⎪=+-⎨⎪-=++⎩解得143a b c =-⎧⎪=⎨⎪=-⎩，∴此抛物线的表达式是：243y x x =-+-．（2）过点D 作DH ⊥BC 于H ，在∠ABC中，设AC边上的高为h，则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==，又∠DH//y轴，∴25 CH DC DHOC AC OA===．∵OA=OC=3，则∠ACO=45°，∴△CDH为等腰直角三角形，∴26355 CH DH==⨯=．∴64255 BH BC CH=-=-=．∴tan∠DBC=32 DHBH=.（3）延长AE至x轴，与x轴交于点F，∠OA=OC=3，∴∠OAC=∠OCA=45°，∠∠OAB=∠OAC-∠BAC=45°-∠BAC，∠OFA=∠OCA-∠FAC=45°-∠FAC，∠∠BAC=∠FAC，∴∠OAB=∠OFA ． ∴△OAB∠∠OFA ， ∴13OB OA OA OF ==． ∴OF=9，即F （9，0）；设直线AF 的解析式为y=kx+b （k≠0），可得093k b b =+⎧⎨-=⎩ ，解得133k b ⎧=⎪⎨⎪=-⎩，∴直线AF 的解析式为：133y x =-， 将x=2代入直线AF 的解析式得：73y =-，∴E （2，73-）. 【点睛】本题考查了相似三角形的判定和性质，二次函数的性质，求二次函数的解析式，等腰直角三角形的判定和性质，求一次函数的解析式，解题的关键是掌握二次函数的图像和性质，以及正确作出辅助线构造相似三角形.例2..已知9023ABC AB BC AD BC P ∠===°，，，∥，为线段BD 上的动点，点Q 在射线AB 上，且满足PQ AD PC AB =（如图所示）。

§1．1 因动点产生的相似三角形问题
课前导学
相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．
判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．
如果已知∠A＝∠D，探求△ABC与△DEF相似，只要把夹∠A和∠D的两边表示出来，按
照对应边成比例，分AB DE
AC DF
和
AB DF
AC DE
两种情况列方程．
应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．
应用判定定理3解题不多见，根据三边对应成比例列连比式解方程（组）．
还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．
求线段的长，要用到两点间的距离公式，而这个公式容易记错．理解记忆比较好．
如图1，如果已知A、B两点的坐标，怎样求A、B两点间的距离呢？
我们以AB为斜边构造直角三角形，直角边与坐标轴平行，这样用勾股定理就可以求斜
边AB的长了．水平距离BC的长就是A、B两点间的水平距离，等于A、B两点的横坐标相减；竖直距离AC就是A、B两点间的竖直距离，等于A、B两点的纵坐标相减．
图1。

因动点产生的相似三角形问题例12018上海市宝山区嘉定区中考模拟第24题如图1，在平面直角坐标系中，双曲线（k≠0）与直线y＝x＋2都经过点A(2, m)．（1）求k与m 的值；（2）此双曲线又经过点B(n, 2)，过点B 的直线BC 与直线y＝x＋2平行交y轴于点C，联结AB、AC，求△AB C 的面积；（3）在（2）的条件下，设直线y＝x＋2与y轴交于点D，在射线C B 上有一点E，如果以点A、C、E 所组成的三角形与△AC D 相似，且相似比不为1，求点E 的坐标．图1例2 2017年武汉市中考第24题如图1，Rt△ABC中，∠ACB＝90°，AC＝6 cm，B C＝8 cm，动点P从点B出发，在BA边上以每秒5 cm 的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4 cm 的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接P Q．（1）若△BP Q与△ABC相似，求t的值；（2）如图2，连接A Q、CP，若AQ⊥CP，求t的值；（3）试证明：PQ的中点在△ABC的一条中位线上．图1 图2例 3 2017 年苏州市中考第 29 题1 4 1 b 如图 1，已知抛物线2 ( 1) （b 是实数且 b ＞2）与x 轴的正半轴分别交 b x y x 4 4于点 A 、B （点 A 位于点 B 是左侧），与 y 轴的正半轴交于点 C ．（1）点 B 的坐标为______，点 C 的坐标为__________（用含 b 的代数式表示）；（2）请你探索在第一象限内是否存在点 P ，使得四边形 PC O B 的面积等于 2b ，且△PB C 是以点 P 为直角顶点的等腰直角三角形？如果存在，求出点 P 的坐标；如果不存在，请说 明理由；（3）请你进一步探索在第一象限内是否存在点 Q ，使得△Q C O 、△Q O A 和△QAB 中 的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点 Q 的坐标； 如果不存在，请说明理由．图 1例42018年黄冈市中考模拟第25题如图1，已知抛物线的方程C1：(2)()(m＞0)与x轴交于点B、C，与y x x mmy轴交于点E，且点B在点C的左侧．（1）若抛物线C1 过点M(2, 2)，求实数m的值；（2）在（1）的条件下，求△BCE的面积；（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得B H＋E H最小，求出点H 的坐标；（4）在第四象限内，抛物线C1 上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．图1例52017年义乌市中考第24题如图1，已知梯形OAB C，抛物线分别过点O（0，0）、A（2，0）、B（6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M的坐标；（2）将图1中梯形OAB C的上下底边所在的直线O A、CB以相同的速度同时向上平移，分别交抛物线于点O、A、C、B，得到如图2的梯形O A B C．设梯形O A B C的面积111111111111为S，A、B的坐标分别为(x，y)、(x，y)．用含S的代数式表示x－x，并求出当S=36 11112221时点A的坐标；1（3）在图1中，设点D的坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段D M运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线P Q、直线AB、x轴围成的三角形与直线P Q、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．图1图2例62017年临沂市中考第26题如图1，抛物线经过点A(4，0)、B（1，0)、C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上的一个动点，过P作P M⊥x轴，垂足为M，是否存在点P，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC D的坐标．,图1因动点产生的相似三角形问题答案例12018上海市宝山区嘉定区中考模拟第24题如图1，在平面直角坐标系中，双曲线（k≠0）与直线y＝x＋2都经过点A(2, m)．（1）求k与m 的值；（2）此双曲线又经过点B(n, 2)，过点B 的直线BC 与直线y＝x＋2平行交y轴于点C，联结AB、AC，求△AB C 的面积；（3）在（2）的条件下，设直线y＝x＋2与y轴交于点D，在射线C B 上有一点E，如果以点A、C、E 所组成的三角形与△AC D 相似，且相似比不为1，求点E 的坐标．图1动感体验请打开几何画板文件名“15宝山嘉定24”，拖动点E 在射线CB 上运动，可以体验到，△ACE 与△AC D 相似，存在两种情况．思路点拨1．直线A D//BC，与坐标轴的夹角为45°．2．求△ABC 的面积，一般用割补法．3．讨论△ACE 与△AC D 相似，先寻找一组等角，再根据对应边成比例分两种情况列方程．满分解答（1）将点A(2, m)代入y＝x＋2，得m＝4．所以点A 的坐标为(2, 4)．k将点A(2, 4)代入y ，得k＝8．x8（2）将点B(n, 2)，代入y，得n＝4．x所以点B 的坐标为(4, 2)．设直线BC 为y＝x＋b，代入点B(4,2)，得b＝－2．所以点C 的坐标为(0,－2)．由A(2, 4)、B(4,2)、C (0,－2)，可知A、B 两点间的水平距离和竖直距离都是2，B、C 两点间的水平距离和竖直距离都是4．22，BC＝4 2，∠ABC＝90°．所以AB＝121所以S＝△ABC＝2242＝8．BA BC 2（3）由A(2, 4)、D(0, 2)、C(0,－2)，得A D＝2 2，AC＝210．由于∠DA C＋∠AC D＝45°，∠ACE＋∠AC D＝45°，所以∠DA C＝∠ACE．所以△ACE与△AC D相似，分两种情况：C E A D①如图3，当时，CE＝A D＝2 2．C A AC此时△AC D≌△CAE，相似比为1．C E A CC A A DC E210②如图4，当时，．解得CE＝10 2．此时C、E两点间的水2102 2平距离和竖直距离都是10，所以E(10, 8)．图3 图4考点伸展第（2）题我们在计算△AB C的面积时，恰好△ABC是直角三角形．一般情况下，在坐标平面内计算图形的面积，用割补法．如图5，作△AB C的外接矩形H C N M，M N//y轴．由S＝24，S＝6，S＝2，S＝8，得S＝8．△ABC矩形H C N M△A H C△A M B△BC N图5例22017年武汉市中考第24题如图1，Rt△ABC中，∠ACB＝90°，AC＝6 cm，B C＝8 cm，动点P从点B出发，在BA边上以每秒5 cm 的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4 cm 的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接P Q．（1）若△BP Q与△ABC相似，求t的值；（2）如图2，连接A Q、CP，若AQ⊥CP，求t的值；（3）试证明：PQ的中点在△ABC的一条中位线上．图1 图2动感体验请打开几何画板文件名“14武汉24”，拖动点P运动，可以体验到，若△BP Q可以两次成为直角三角形，与△AB C相似．当A Q⊥CP时，△AC Q∽△CD P．P Q的中点H在△ABC的中位线EF上．思路点拨1．△BP Q与△AB C有公共角，按照夹角相等，对应边成比例，分两种情况列方程．2．作P D⊥B C于D，动点P、Q的速度，暗含了B D＝C Q．3．P Q的中点H在哪条中位线上？画两个不同时刻P、Q、H的位置，一目了然．满分解答（1）Rt△ABC中，AC＝6，BC＝8，所以AB＝10．△BP Q与△AB C相似，存在两种情况：5t10BP BAB Q B C①如果，那么．解得t＝1．8 4t85t8 4t108 32BP BCB Q BA②如果，那么．解得．t41图3图4（2）作P D⊥B C，垂足为D．4在Rt△BP D中，BP＝5t，cosB＝，所以B D＝BPcosB＝4t，PD＝3t．5当A Q⊥CP时，△AC Q∽△C D P．684t，即4t7A C C DQ C P D所以．解得．t3t8图5图6（3）如图4，过P Q的中点H作BC的垂线，垂足为F，交AB于E．由于H是P Q的中点，HF//PD，所以F是Q D的中点．又因为B D＝C Q＝4t，所以BF＝C F．因此F是BC的中点，E是AB的中点．所以P Q的中点H在△AB C的中位线EF上．考点伸展本题情景下，如果以P Q为直径的⊙H与△AB C的边相切，求t的值．3241BP B CB Q BA如图7，当⊙H与AB相切时，QP⊥AB，就是如图8，当⊙H与BC相切时，P Q⊥BC，就是，．tBP BAB Q B C，t＝1．如图9，当⊙H与AC相切时，直径P D2Q D2t2t2(3)(88)，P Q半径等于FC＝4．所以(3)(88)8．t2t212873解得，或t＝0（如图10，但是与已知0＜t＜2矛盾）．t图7图8图9图10例 3 2017 年苏州市中考第 29 题如图 1，已知抛物线 y1 4x21( 4b1) xb （b 是实数且 b＞2）与x 轴的正半轴分别交 4于点 A、B（点 A 位于点 B 是左侧），与 y 轴的正半轴交于点 C．（1）点 B 的坐标为______，点 C 的坐标为__________（用含 b 的代数式表示）；（2）请你探索在第一象限内是否存在点 P，使得四边形 P C O B 的面积等于 2b，且△PB C是以点 P 为直角顶点的等腰直角三角形？如果存在，求出点 P 的坐标；如果不存在，请说明理由；（3）请你进一步探索在第一象限内是否存在点 Q ，使得△Q C O、△Q O A 和△ Q A B 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点 Q 的坐标；如果不存在，请说明理由．图1动感体验请打开几何画板文件名“12 苏州 29”，拖动点 B 在 x 轴的正半轴上运动，可以体验到， 点 P 到两坐标轴的距离相等，存在四边形P C O B 的面积等于 2b 的时刻．双击按钮“第（3） 题”，拖动点 B，可以体验到，存在∠O Q A＝∠B 的时刻，也存在∠O Q′A＝∠B 的时刻．思路点拨1．第（2）题中，等腰直角三角形 PB C 暗示了点 P 到两坐标轴的距离相等． 2．联结 O P，把四边形 P C O B 重新分割为两个等高的三角形，底边可以用含 b 的式子 表示． 3．第（3）题要探究三个三角形两两相似，第一直觉这三个三角形是直角三角形，点 Q 最大的可能在经过点 A 与 x 轴垂直的直线上．满分解答（1）B 的坐标为(b, 0)，点 C 的坐标为(0, b )． 4（2）如图 2，过点 P 作 P D⊥x 轴，PE⊥y 轴，垂足分别为 D、E，那么△P D B≌△PE C．因此 P D＝PE．设点 P 的坐标为(x,x)．如图 3，联结 OP．所以S四边形PCO＝SB △PC O＋S ＝△PB O1 2b 4x1 2bx5 ＝2b． 8 bx解得 x16 ．所以点 P 的坐标为(16 ,16 )．55511（3）由 y图21 x2 1 (b 1)x b444图3 1 (x 1)(x b)，得 A(1, 0)，OA＝1． 4①如图 4，以 O A 、O C 为邻边构造矩形 O A Q C，那么△O Q C≌△ Q O A． 当 B A Q A ，即Q A2 B A O A 时，△B Q A∽△ Q O A．QA OA所以( b)2 b 1．解得b 8 4 3 ．所以符合题意的点 Q 为(1,2 3 )． 4②如图 5，以 O C 为直径的圆与直线 x＝1 交于点 Q ，那么∠O Q C＝90°。

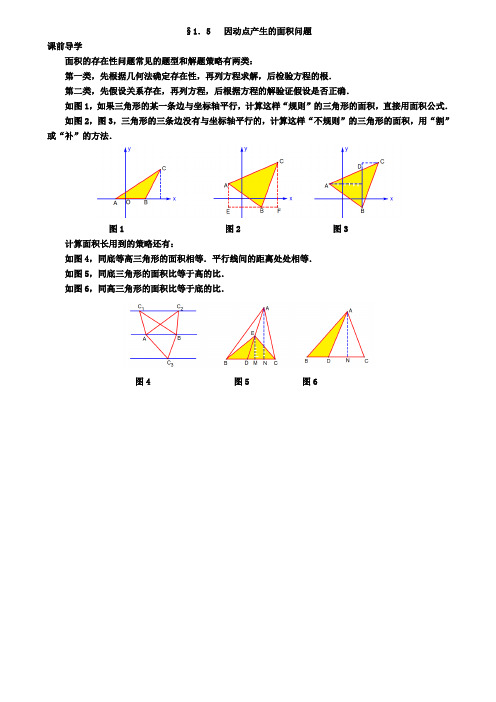
§1．5 因动点产生的面积问题课前导学面积的存在性问题常见的题型和解题策略有两类：第一类，先根据几何法确定存在性，再列方程求解，后检验方程的根．第二类，先假设关系存在，再列方程，后根据方程的解验证假设是否正确．如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．图1 图2 图3计算面积长用到的策略还有：如图4，同底等高三角形的面积相等．平行线间的距离处处相等．如图5，同底三角形的面积比等于高的比．如图6，同高三角形的面积比等于底的比．图4 图5 图6例 32 2019年湖南省常德市中考第25题如图1，已知二次函数的图象过点O(0,0)、A(4，0)、B(2,)，M 是OA 的中点． （1）求此二次函数的解析式；（2）设P 是抛物线上的一点，过P 作x 轴的平行线与抛物线交于另一点Q ，要使四边形PQAM 是菱形，求点P 的坐标；（3）将抛物线在x 轴下方的部分沿x 轴向上翻折，得曲线OB′A（B ′为B 关于x 轴的对称点），在原抛物线x 轴的上方部分取一点C ，连结CM ，CM 与翻折后的曲线OB′A 交于点D ，若△CDA 的面积是△MDA 面积的2倍，这样的点C 是否存在？若存在求出点C 的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14常德25”，拖动点P 在抛物线上运动，可以体验到，当四边形PQAM 是平行四边形时，也恰好是菱形．拖动点C 在抛物线上运动，还可以体验到，△MCA 与△MDA 是同底三角形，它们的面积比等于对应高的比． 思路点拨1．设交点式或顶点式求抛物线的解析式都比较简便． 2．先确定四边形PQAM 是平行四边形，再验证它是菱形．3．把△CDA 与△MDA 的面积比，转化为△MCA 与△MDA 的面积比，进而转化为点C 与点D 的纵坐标的比． 图文解析（1）因为抛物线与x 轴交于O(0,0)、A(4，0)两点，设y ＝ax(x －4)．代入点B(2,)，得4a =-．解得a ．所以(4)y x -． （2）如图2，由A(4，0)，M 是OA 的中点，可知OA ＝4，MA ＝2，M(2, 0)．如果四边形PQAM 是菱形，已知PQ//OA ，首先要满足PQ ＝2，再必须MP ＝2．因为抛物线的对称轴是直线x ＝2，P 、Q 关于x ＝2对称，所以点P 的横坐标为1，故点P 的坐标为(1,．由M(2, 0)、P (1,，可得MP ＝2．所以当点P 的坐标为(1,时，四边形PQAM 是菱形． （3）如图3，作CE ⊥x 轴于E ，作DF ⊥x 轴于F ． 我们把面积进行两次转换：如果△CDA 的面积是△MDA 面积的2倍，那么△MCA 的面积是△MDA 面积的3倍． 而△MCA 与△MDA 是同底三角形，所以高的比CE ∶DF ＝3∶1，即y C ∶y D ＝3∶1． 因此ME ∶MF ＝3∶1．设MF ＝m ，那么ME ＝3m ．原抛物线的解析式为(4)y x =-，所以翻折后的抛物线的解析式为(4)y x x =-．所以D (2,)(24))m m m +++-，C (233)(234))m m m +++-．根据y C ∶y D ＝3∶13)(234)3)(24)m m m m ⎡⎤++-=++-⎢⎥⎣⎦．整理，得3m2＝4．解得m=．所以232+=±m所以点C的坐标为(2+（如图3），或(2-（如图4）．图2 图3 图4 考点伸展第（1）题可以设抛物线的顶点式：由点O(0,0), A(4，0)，B(2,)的坐标，可知点B是抛物线的顶点．可设2=-O(0,0)，得a(2)y a x例 33 2019年湖南省永州市中考第25题如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴交于A(－1, 0)，B(4, 0)两点，与y 轴交于点C(0, 2)．点M(m, n)是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上．过点M 作x 轴的平行线交y 轴于点Q ，交抛物线于另一点E ，直线BM 交y 轴于点F ．（1）求抛物线的解析式，并写出其顶点坐标； （2）当S △MFQ ∶S △MEB ＝1∶3时，求点M 的坐标．图1动感体验请打开几何画板文件名“14永州25”，拖动点M 在抛物线左半侧上运动，观察面积比的度量值，可以体验到，存在两个时刻，△MEB 的面积等于△MFQ 面积的3倍． 思路点拨1．设交点式求抛物线的解析式比较简便．2．把△MFQ 和△MEB 的底边分别看作MQ 和ME ，分别求两个三角形高的比，底边的比（用含m 的式子表示），于是得到关于m 的方程．3．方程有两个解，慎重取舍．解压轴题时，时常有这种“一石二鸟”的现象，列一个方程，得到两个符合条件的解． 图文解析（1）因为抛物线与x 轴交于A(－1, 0)，B(4, 0)两点，设y ＝a(x ＋1)(x －4)． 代入点C(0, 2)，得2＝－4a ．解得12a =-．所以221131325(1)(4)2()222228y x x x x x =-+-=-++=--+．顶点坐标为325()28，．（2）如图2，已知M(m, n)，作MN ⊥x 轴于N ．由=FQ MNMQ BN，得=4FQ n m m -．所以=4mn FQ m -． 因为抛物线的对称轴是直线32x =，所以ME ＝32()322m m -=-．由于S △MFQ ＝12FQ MQ ⋅＝124mnm m⨯⨯-＝2124m n m ⨯-， S △MEB ＝12ME MN ⋅＝1(32)2m n -，所以当S △MFQ ∶S △MEB ＝1∶3时，24m nm-∶(32)m n -＝1∶3．整理，得m 2＋11m －12＝0．解得m ＝1，或m ＝－12．所以点M 的坐标为(1, 3)或(－12,－88)．图2考点伸展第（2）题S △MFQ ∶S △MEB ＝1∶3，何需点M 一定要在抛物线上？ 从上面的解题过程可以看到，△MFQ 与△MEB 的高的比=4FQ mMN m-与n 无关，两条底边的比=32MQ mME m-也与n 无关． 如图3，因此只要点E 与点M 关于直线x ＝32对称，点M 在直线的左侧，且点M 不在坐标轴上，就存在S △MFQ ∶S △MEB ＝1∶3，点M 的横坐标为1（如图3）或－12（如图4）．图3 图42019-2020学年数学中考模拟试卷一、选择题1．若关于的x 方程230x x a ++=有一个根为1-，则a 的值为（ ） A ．-4B ．-2C ．2D ．-42．下列运算正确的是（ ） A ．3a 3+a 3＝4a 6 B ．（a+b ）2＝a 2+b 2 C ．5a ﹣3a ＝2aD ．（﹣a ）2•a 3＝﹣a 63 ） A ．4B ．﹣4C ．2D ．±24．如图，四边形ABCD 内接于⊙O ，已知∠ADC=140°，则∠AOC 的大小是（ ）A.100B.80C.60D.4052的值在( ) A ．3和4之间B ．4和5之间C ．5和6之间D ．6和7之间6．如图，在矩形ABCD 中，120AOB ∠=︒，3AD =，则AC =（ ）A ．6B ．C ．5D ．7．下列计算正确（ ）A ．222a b a b +=+（） B ．235a a a ⋅=C ．822a a a ÷=D ．325a a a +=8．如图，为某校初三男子立定跳远成绩的统计图，从左到右各分数段的人数之比为1：2：5：6：4，第四组的频数是12，对于下面的四种说法 ①一共测试了36名男生的成绩．②立定跳远成绩的中位数分布在1.8～2.0组． ③立定跳远成绩的平均数不超过2.2．④如果立定跳远成绩1.85米以下（不含1.85）为不合格，那么不合格人数为6人． 正确的是（ ）A ．①③B ．①④C ．②③D ．②④9．文艺复兴时期，意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”，可看成圆与正方形的各边均相切，切点分别为,,,A B C D ，BD 所在圆的圆心为点A （或C ）. 若正方形的边长为2，则图中阴影部分的面积为（ ）AB ．2C ．1π-D ．42π-10．下列四个函数中，自变量的取值范围为x ≥1的是（ ）A ．y =B ．y =C ．y =D ．y =11．对于一组数据： 4, 3,6, 4, 8,下列说法错误的是（ ） A ．众数是4B ．平均数是5C ．众数等于中位数D ．中位数是512．已知AB ＝10，C 是射线AB 上一点，且AC ＝3BC ，则BC 的长为（ ）A.2.5B.103C.2.5或5D.103或5 二、填空题13．如图，在由边长都为1的小正方形组成的网格中，点A ，B ，C 均为格点，点P ，Q 分别为线段AB ，BC 上的动点，且满足AP BQ =．(1)线段AB 的长度等于__________；(2)当线段AQ CP +取得最小值时，请借助无刻度直尺在给定的网格中画出线段AQ 和CP ，并简要说明你是怎么画出点Q ，P 的：_______________________．14．据资料表明：中国已成为全球机器人第二大专利来源国和目标国.机器人几大关键技术领域包括：谐波减速器、RV减速器、电焊钳、3D视觉控制、焊缝跟踪、涂装轨迹规划等，其中涂装轨迹规划的来源国结构（仅计算了中、日、德、美）如图所示，在该扇形统计图中，美国所对应的扇形圆心角是__________度．15．计算432x x⋅的结果等于__________．16．如图，点A1、A2、A3…在直线y＝x上，点C1，C2，C3…在直线y＝2x上，以它们为顶点依次构造第一个正方形A1C1A2B1，第二个正方形A2C2A3B2…，若A2的横坐标是1，则B3的坐标是_____，第n个正方形的面积是_____．17．一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD 水平，BC与水平面的夹角为60°，其中AB=60cm，CD=40cm，BC=40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为____cm．18．在四边形ABCD中，向量、满足=-4，那么线段AB与CD的位置关系是_____．三、解答题19．先化简，再求值：22299(6)3a aaa a-+÷+-，其中a2﹣4a+3＝0．20．2﹣|1|﹣tan45°+（π﹣1978）0．21．如图,在小正方形的边长均为1的方格纸中点A、B、C均在格点上；(1)在图1中画出凸四边形ABCD,使四边形ABCD是轴对称图形,点D在格点上；(2)在图2中画出凸四边形ABCE,点E在格点上,∠AEC=90°,EC>EA，直接写出四边形ABCE的周长_____.22．如图，A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线相交于点D，E是BD的中点，延长AE与CB的延长线相交于点F．（1）求证：AF是⊙O的切线；（2）若BE＝5，BF＝12，求CD的长．23．为如图，已知女排球场的长度OD为18米，位于球场中线处的球网AB的高度2.24米，一队员站在点O处发球，排球从点O的正上方2米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点O的水平距离OE为6米时，到达最高点G，以O为原点建立如图所示的平面直角坐标系．（1）若排球运行的最大高度为2.8米，求排球飞行的高度p（单位：米）与水平距离x（单位：米）之间的函数关系式（不要求写自变量x的取值范围）；（2）在（1）的条件下，这次所发的球能够过网吗？如果能够过网，是否会出界？请说明理由；（3）若李明同学发球要想过网，又使排球不会出界（排球压线属于没出界）求二次函数中二次项系数的最大值．24．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C．（1）求抛物线y=ax 2+2x+c 的解析式:；（2）点D 为抛物线上对称轴右侧、x 轴上方一点，DE ⊥x 轴于点E ，DF ∥AC 交抛物线对称轴于点F ，求DE+DF 的最大值；（3）①在拋物线上是否存在点P ，使以点A ，P ，C 为顶点，AC 为直角边的三角形是直角三角形？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；②点Q 在抛物线对称轴上，其纵坐标为t ，请直接写出△ACQ 为锐角三角形时t 的取值范围．25．如图，在平面直角坐标系中，点O 为坐标原点，点()0,4A 与点B 关于x 轴对称，点(),0C m 为x 轴的正半轴上一动点.以AC 为边作等腰直角三角形ACD ，90ACD ∠=︒，点D 在第一象限内.连接BD ，交x 轴于点F .（Ⅰ）用含m 的式子表示点D 的坐标；（Ⅱ）在点C 运动的过程中，判断OF 的长是否发生变化？若不变求出其值，若变化请说明理由； （Ⅲ）过点C 作CG BD ⊥，垂足为点G ，请直接写出BF DF -与CG 之间的数量关系式.【参考答案】*** 一、选择题二、填空题13．取格点,,,D E F G ．连接,BD EF ，它们相交于点T ，连接,AT CG ，分别交,BC AB 于点,Q P ，则线段AQ 和CP 即为所求． 14．6 15．72x16．(4，2) 22n ﹣4． 17．18．平行 三、解答题 19．14. 【解析】 【分析】根据分式的运算法则即可求出答案． 【详解】 原式＝2(3)(3)(3)69a a aa a a a +-⋅-++＝23(3)a a a a +⋅+ ＝13a + ∵a 2﹣4a+3＝0，∴a 1＝1 a 2＝3（舍去） ∴原式＝14【点睛】本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．20．2020-【解析】 【分析】直接利用零指数幂的性质以及绝对值的性质和特殊角的三角函数值分别分析得出答案． 【详解】解：原式＝20191）﹣1+1＝2020 【点睛】此题主要考查了实数运算，正确化简各数是解题关键．21．（1）如图所示，见解析； （2）如图所示，周长为6+【分析】(1)根据轴对称的性质画出图形即可;(2)画出四边形 ABCDE,再求出其周长即可.【详解】（1）如图所示，（2）如图所示，四边形ABCE的周长为6【点睛】此题考查作图-轴对称变换，掌握作图法则是解题关键22．（1）见解析；（2）【解析】【分析】（1）利用直角三角形斜边中线的性质和等边对等角得到∠EAB＝∠EBA，结合⊙O的切线得出OA⊥AF，从而得出AF是⊙O的切线；（2）先根据勾股定理求得EF的长，再根据切线的性质得出EB＝EA＝5，即可求得AF的长，然后根据切割线定理求得FC，进而得出BC的长，根据E是BD的中点，得出BD的长，最后根据勾股定理即可求得CD 的长．【详解】解：（1）连接AB，OA，∵BC是⊙O的直径，∴∠BAC＝90°，∵DB是⊙O的切线，∴DB⊥BC，∴∠DBO＝90°，在RT△ABD中，E是斜边BD的中线，∴AE＝DE＝BE，∴∠EAB＝∠EBA，∵OA＝OB，∴∠OAB＝∠OBA，∴∠EAB+∠OAB＝∠EBA+∠OBA∴∠EAO＝∠DBO＝90°，∴AF是⊙O的切线；（2）∵在RT△BEF中，BE＝5，BF＝12，∴EF＝13，∵FA、DB是⊙O的切线，∴EA＝EB＝5，∴AF＝EF+EA＝13+5＝18，∵AF2＝FB•FC，∴FC＝22182712AFAB==∴BC＝FC﹣FB＝27﹣12＝15，∵E是BD的中点，∴BD＝2BE＝10，在RT△DBC中，CD==【点睛】本题考查了切线的判定和性质，直角三角形斜边中线的性质，等腰三角形的性质，勾股定理的应用等，正确的作出辅助线是解题的关键．23．（1）p＝145（x﹣6）2+2.8;（2）见解析;（3）154-.【解析】【分析】（1）利用抛物线的顶点坐标为（6，2.8），将点（0，2）代入解析式求出即可（2）利用当x＝9时，x＝18时，分别求出p值即可判断（3）设抛物线的解析式为：p＝a（x﹣6）2+h，将点C代入，此时抛物线的解析式为p＝a（x﹣6）2+2﹣36a，再根据x＝9时，p＞2.24，当x＝18时，p≤0，即可得a的范围，从而取得最大值．【详解】解：（1）由排球运行的最大高度为28米，则顶点的坐标点G为（6，2.8），则设抛物线的解析式为p＝a（x ﹣6）2+2.8∵点C坐标为（0，2），点C在抛物线上∴2＝a（0﹣6）2+2.8解得a＝﹣1 45∴p＝-145（x﹣6）2+2.8则排球飞行的高度p（单位：米）与水平距离x（单位：米）之间的函数关系式：p＝-145（x﹣6）2+2.8（2）当x＝9时，p＝-145（9﹣6）2+2.8＝2.6＞2.24当x＝18时，p＝-145（18﹣6）2+2.8＝﹣0.4＜0故这次发球可以过网且不出边界（3）设抛物线的解析式为：p＝a（x﹣6）2+h，将点C代入得：36a+h＝2，即h＝2﹣36a∴此时抛物线的解析式为p＝a（x﹣6）2+2﹣36a根据题意，不过边界时有：a（18﹣6）2+2﹣36a≤0，解得a≤-1 54要使网球过网：a（9﹣6）2+2﹣36a≥2.24，解得a≤2 225 -故李明同学发球要想过网，又使排球不会出界（排球压线属于没出界）二次函数中二次项系数的最大值为154【点睛】本题考查了二次函数的性质在实际生活中的应用．可根据二次函数的解析式的最值作为临界值来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．24．（1）y=﹣x2+2x+3；（2）DE+DF有最大值为132；（3）①存在，P的坐标为（73，209）或（103，139-）；②23-＜t＜83．【解析】【分析】（1）设抛物线解析式为y=a（x+1）（x﹣3），根据系数的关系，即可解答（2）先求出当x=0时，C的坐标，设直线AC的解析式为y=px+q，把A,C的坐标代入即可求出AC的解析式，过D作DG垂直抛物线对称轴于点G，设D（x，﹣x2+2x+3），得出DE+DF=﹣x2（x-1）=﹣x2+（），即可解答（3）①过点C作AC的垂线交抛物线于另一点P1，求出直线PC的解析式，再结合抛物线的解析式可求出P1，过点A作AC的垂线交抛物线于另一点P2，再利用A的坐标求出P2，即可解答②观察函数图象与△ACQ为锐角三角形时的情况，即可解答【详解】解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；（2）当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3，如答图1，过D作DG垂直抛物线对称轴于点G，设D（x，﹣x2+2x+3），∵DF∥AC，∴∠DFG=∠ACO，易知抛物线对称轴为x=1，∴DG=x-1，（x-1），∴DE+DF=﹣x2+2x+3+x-1）=﹣x2+（），∴当x=1，DE+DF有最大值为132；答图1 答图2（3）①存在；如答图2，过点C作AC的垂线交抛物线于另一点P1，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=13-x+m，把C（0，3）代入得m=3，∴直线P1C的解析式为y=13-x+3，解方程组223133y x xy x⎧=-++⎪⎨=-+⎪⎩，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P1点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P2，直线AP2的解析式可设为y=13-x+n，把A（﹣1，0）代入得n=13-，∴直线PC 的解析式为y=1133x --，解方程组2231133y x x y x ⎧=-++⎪⎨=--⎪⎩，解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩，则此时P 2点坐标为（103，139-），综上所述，符合条件的点P 的坐标为（73，209）或（103，139-）；②23-＜t ＜83．【点睛】此题考查二次函数综合题，解题关键在于把已知点代入解析式求值和作辅助线. 25．(1) G(4+m,m) (2) OF=4，OF 是不变化的 (3) BF DF -是CG 的两倍 【解析】 【分析】(1)过D 点作x 轴垂线，垂足为G 点，可知△CDG 相似△OAC ，即可求出D 点坐标.(2)利用B,D 两点的坐标给出直线BD 的解析式，然后令解析式的y=0，给出x 的值，如果x 含有参数，则OF 的长是变化的，若x 不含参数，则OF 的长无变化.(3)用含m 的式子表示出BF DF -和CG 的长，结果就出来了，其中BF DF -的长利用△DFG 相似△OBF 可求，CG 的长直接利用勾股定理可求. 【详解】解：(1) 过D 点作x 轴垂线，垂足为H 点， ∵90ACD ∠=︒， ∴=90ACO DCH ∠+∠︒ ∵=90ACO CAO ∠+∠︒, ∴CAO DCH ∠=∠ ，又∵90ACD CHD ∠=∠=︒,AC=CD, ∴在△OAC 和△CDH ，CAO DCHAOC CHD AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ACO CDH∴≌，∴CH=OA,DH=OC=m, ∴OH=4+m ， ∴D(4+m,m).(2)设BD 直线的解析式为：y=kx+b ， 将点B(0,-4)与点D(4+m,m)代入方程，()44+m b k b m =-⎧⎨+=⎩ ， 解得：11k b =⎧⎨=⎩，BD 的直线解析式为4y x =- ，当y=0时，x=4 ，OF=4，OF 是不变化的；(3)可知△DFH 相似△OBF ，∴::m 4DH OB DF BF ==：，由 B(0,-4)与点D(4+m,m)，可以知道)4m +,∴, DF= ，BF DF -m-4，CG === ∴BF DF -是CG 的两倍. 【点睛】本题是一道综合习题，第一问考查相似与坐标系中点的表示，第二问考查力一次函数，第三问考查力相似与勾股定理，本题第二问关键是给出直线BD 的解析式，第三问的关键是会表示两个线段的长2019-2020学年数学中考模拟试卷一、选择题1．一个数和它的倒数相等，则这个数是（）A．1 B．-1 C．±1D．±1和02．实数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（）A．a＞b B．a＝b＞0 C．ac＞0 D．|a|＞|c|3．二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示，则一次函数y=ax+b与反比例函数y=cx在同一平面直角坐标系中的图象可能是（）A． B．C．D．4．抛物线y＝x2向下平移一个单位，向左平移两个单位，得到的抛物线关系式为（）A．y＝x2+4x+3 B．y＝x2+2x﹣1 C．y＝x2+2x D．y＝x2﹣4x+35．下列运算正确的是（）A.a2×a3＝a6B.a2+a2＝2a4C.a8÷a4＝a4D.（a2）3＝a56．有一张矩形ABCD的纸片（AB＜BC），按如图所示的方式，在A，C两端截去两个矩形AEFG和CE′F′G′，且AE＝CE′，AG＝CG′，再分别过EF，FG，E′F′，F′G′四边的中点，沿平行于原矩形各边的方向剪裁，得到如图的阴影部分，分别记为L1，L2．若L1的周长是矩形ABCD的34，L2的周长是矩形ABCD的35，则AEAG的值为（）A．54B．85C．32D．20971，0( )AB ．﹣1C ．0D 8．某足球生产厂计划生产4800个足球，在生产完1200个后，采用了新技术，工作效率比原计划提高了20%，结果共用了21天完成全部任务．设原计划每天生产x 个足球，根据题意可列方程为（ ） A ．12004800(120%)x ++＝21 B ．120048001200(120%)x x-++＝21 C ．12004800120020%x x-+＝21 D ．480048001200(120%)x x-++＝21 9．如表是小明同学参加“一分钟汉字听写”训练近6次的成绩：则这组数据的平均数和中位数分别是（ ） A ．245个、244个 B ．244个、244个 C ．244个、241.5个D ．243个、244个10．如图，在▱ABCD 中，对角线AC ，BD 相交于点O ，AC=6，BD=10，则AD 的长度可以是（ ）A.2B.7C.8D.1011．一组数1，1，2，3，5，8，13是“斐波那契数列”的一部分，若去掉其中的两个数后这组数的中位数、众数保持不变，则去掉的两个数可能是（ ） A ．2，5B ．1，5C ．2，3D ．5，812．“定西市乒乓球夏令营”开始在学校报名了，已知甲、乙、丙三个夏令营组人数相等，且每组学生的平均年龄都是14岁，三个组学生年龄的方差分别是2S 甲=17，2S 乙=14.6，2S 丙=19，如果今年暑假你也准备报名参加夏令营活动，但喜欢和年龄相近的同伴相处，那么你应选择( ) A ．甲组 B ．乙组C ．丙组D ．采取抽签方式，随便选一个二、填空题13．如图，点A 是双曲线6y x=-在第二象限分支上的一个动点，连接AO 并延长交另一分支于点B ，以AB 为底作等腰ABC △，且120ACB ∠=︒，点C 在第一象限，随着点A 的运动点C 的位置也不断变化，但点C 始终在双曲线ky x=上运动，则k 的值为________.14．如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，已知CD ＝8，EB ＝2，则⊙O 的半径为_____．15．如图，在△ABO 中，∠ABO ＝90°，点A 的坐标为（3，4）．写出一个反比例函数y ＝kx（k≠0），使它的图象与△ABO 有两个不同的交点，这个函数的表达式为_____．16．如果点（m ，﹣2m ）在双曲线ky x=上，那么双曲线在_____象限． 17．如图，在△ABC 中，DE ∥BC ，AD ：DB=1：2，DE=2，则BC 的长是 ．18．《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三．问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱：若每人出7钱，还差3钱．则合伙人数为_____人；羊价为_____钱． 三、解答题19．如图，在ABC △中，AB AC =，以AB 为直径的⊙O 分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥，垂足为点H ，连接DE ，交AB 于点F .（1）求证：DH是⊙O的切线;=时，求AD的长(结果保留π)；②当sin B=求线段AF （2）若⊙O的半径为4，①当AE FE的长.20．如图，正方形网格中，△ABC为格点三角形（顶点都在格点上）（1）作出△ABC绕点A逆时针旋转90°后的△AB1C1；将△ABC向上平移3格，在向左平移4格得到△A2B2C2；（2）设小正方形的边长为1，求出△ABC旋转到△AB1C1的过程中AB所扫过的面积（结果保留π）21．已知：如图，在平行四边形中，点E在BC边上，连接AE．O为AE中点，连接BO并延长交AD于F．（1）求证：△AOF≌△BOE，（2）判断当AE平分∠BAD时，四边形ABEF是什么特殊四边形，并证明你的结论．22．如图，一种侧面形状为矩形的行李箱，箱盖打开后，盖子的一端靠在墙上，此时BC=10cm，箱底端点E与墙角G的距离为65cm，∠DCG=60°．（1）箱盖绕点A转过的角度为______，点B到墙面的距离为______cm；（2）求箱子的宽EF（结果保留整数，可用科学计算器）．=1.41=1.73）23．如图，某学校甲楼的高度AB是18.6m，在甲楼楼底A处测得乙楼楼顶D处的仰角为40，在甲楼楼顶B 处测得乙楼楼顶D 的仰角为19，求乙楼的高度DC 及甲乙两楼之间的距离AC （结果取整数）.参考数据：cos190.95≈，tan190.34≈，cos400.77≈，tan 400.84≈.24．先化简，再求值222221b a ab a b a b a 2ab b -⎛⎫-÷ ⎪---+⎝⎭，其中a=2sin45°，25．计算：11|2|3-⎛⎫-- ⎪⎝⎭．【参考答案】***一、选择题二、填空题13．214．515．答案不唯一，如：2y x =； 16．二．四；17．18．150三、解答题19．（1）见解析；（2）①AD 的长＝85π；②AF ＝43． 【解析】【分析】（1）根据同圆的半径相等和等边对等角证明：∠ODB ＝∠OBD ＝∠ACB ，则DH ⊥OD ，DH 是圆O 的切线；（2）①根据等腰三角形的性质的∠EAF ＝∠EAF ，设∠B ＝∠C ＝α，得到∠EAF ＝∠EFA ＝2α，根据三角形的内角和得到∠B ＝36°，求得∠AOD ＝72°，根据弧长公式即可得到结论；②连接AD ，根据圆周角定理得到∠ADB ＝∠ADC ＝90°，解直角三角形得到AD ＝性质得到AH ＝3，于是得到结论．【详解】（1）连接OD ，如图，∵OB ＝OD ，∴△ODB 是等腰三角形，∠OBD ＝∠ODB ①，在△ABC 中，∵AB ＝AC ，∴∠ABC ＝∠ACB ②，由①②得：∠ODB ＝∠OBD ＝∠ACB ，∴OD ∥AC ，∵DH ⊥AC ，∴DH ⊥OD ，∴DH 是圆O 的切线；（2）①∵AE ＝EF ，∴∠EAF ＝∠EAF ，设∠B ＝∠C ＝α，∴∠EAF ＝∠EFA ＝2α，∵∠E ＝∠B ＝α，∴α+2α+2α＝180°，∴α＝36°，∴∠B ＝36°，∴∠AOD ＝72°，∴AD 的长＝72481805ππ⋅⨯=； ②连接AD ，∵AB 为⊙O 的直径，∴∠ADB ＝∠ADC ＝90°，∵⊙O 的半径为4，∴AB ＝AC ＝8，∵sin 4B =，∴8AD =，∴AD ＝，∵AD⊥BC，DH⊥AC，∴△ADH∽△ACD，∴AH AD AD AC=，8=，∴AH＝3，∴CH＝5，∵∠B＝∠C，∠E＝∠B，∴∠E＝∠C，∴DE＝DC，∵DH⊥AC，∴EH＝CH＝5，∴AE＝2，∵OD∥AC，∴∠EAF＝∠FOD，∠E＝∠FDO，∴△AEF∽△ODF，∴AF AE OF OD=,∴2 44 AFAF=-，∴AF＝43．【点睛】本题考查了等腰三角形的性质和判定、切线的性质和判定、三角形相似的性质和判定、圆周角定理，正确的作出辅助线是解题的关键．20．（1）见解析；（2）254 Sπ=【解析】【分析】（1）根据旋转的性质及平移的性质画出△AB1C1，△A2B2C2即可．（2）利用扇形的面积公式计算即可．【详解】（1）△AB1C1，△A2B2C2如图所示．（2）2905253604S ππ==． 【点睛】本题考查作图-旋转变换，平移变换，扇形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21．（1）求证：见解析；（2）四边形ABEF 是菱形，见解析.【解析】【分析】(1)先利用平行四边形的性质得AD ∥BC ，则∠AFB ＝∠CBF ，然后根据“AAS”可判断△AOF ≌△BOE ；(2)利用△AOF ≌△BOE 得到FO ＝BO ，则可根据对角线互相平分可判定四边形ABEF 是平行四边形，根据AE 平分∠BAD ，得∠BAE ＝∠FAE ，又∠FAE ＝∠AEB ，得∠BAE ＝∠AEB ，AB ＝BE ，有一组对边相等的平行四边形是菱形，得四边形ABEF 是菱形．【详解】(1)∵O 为AE 中点，∴AO ＝EO ，∵四边形ABCD 为平行四边形，∴AD ∥BC ，∴∠AFB ＝∠CBF ，在△AOF 和△BOE 中AFO EBO AOF EOB AO EO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOF ≌△BOE ；(2)四边形ABEF 是菱形，理由如下：∵△AOF ≌△BOE ，∴FO ＝BO ，而AO ＝EO ，∴四边形ABEF 是平行四边形，∵AE 平分∠BAD ，∴∠BAE ＝∠FAE ，∵∠FAE ＝∠AEB ，∴∠BAE ＝∠AEB ，∴AB ＝BE ，∴四边形ABEF 是菱形．【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质，菱形的判定等，熟练掌握相关的性质与判定定理是解题的关键.22．（1）150°；5（2）32.4cm【解析】【分析】（1）如图，过点B 作BH ⊥CG 于H ，过点D 作CG 的垂线MN 交AF 于M ，交HG 于N ．利用矩形的性质、直角三角形的性质以及等角的余角相等得到∠MAD=30°，根据周角的定义易求箱盖绕点A 转过的角度；通过解直角△BHC 来求BH 的长度；（2）通过解直角△AMD 得到线段MD 的长度，则DN=65-EF-DM ，利用解直角△DCN 来求CD 的长度，即EF 的长度即可．【详解】（1）如图，过点B 作BH ⊥CG 于H ，过点D 作CG 的垂线MN 交AF 于M ，交HG 于N ．∵∠DCG=60°，∴∠CDN=30°．又∵四边形ABCD 是矩形，∴∠ADC=∠B CD=90°，∴∠MAD=∠CDN=30°（同角的余角相等），∴箱盖绕点A 转过的角度为：360°-90°-30°-90°=150°．在直角△BCH 中，∠BCH=30°，BC=10cm ，则BH=12BC=5cm ． 故答案是：150°；5；（2）在直角△AMD 中，AD=BC=10cm ，∠MAD=30°，则MD=AD•sin30°=12×10=5（cm ）． ∵∠CDN=30°，∴cos ∠CDN=cos30°=655DN EF DC EF --=，即655EF EF --= 解得EF=32.4．即箱子的宽EF 是32.4cm ．【点睛】本题考查了解直角三角形的应用．主要是余弦概念及运算，关键把实际问题转化为数学问题加以计算．23．乙楼的高度DC 约为31m ，甲乙两楼之间的距离AC 约为37m.【解析】【分析】过点B 作BE CD ⊥，垂足为点E ，从而判定四边形ABEC 是矩形，得到AB CE =，AC BE =设甲乙两楼之间的距离为x m,在直角三角形BDE 与直角三角形DAC 中，利用三角函数即可用x 表示出DE 与DC ，根据DC DE CE -=，列出方程解之即可．【详解】解：过点B 作BE CD ⊥，垂足为点E ，可知BAC ACE BEC 90∠∠∠===︒.∴四边形ACEB 是矩形.∴AB CE =，AC BE =.设甲乙两楼之间的距离为x m.则BE AC x ==，在Rt DBE 中，DBE 19∠=︒，DE tan DBE BE∠=. ∴DE BE tan DBE x tan19∠=⋅=⋅︒. 在Rt DAC 中，DAC 40∠=︒，DC tan DAC AC∠=. ∴DC AC tan DAC x tan DAC x tan40∠∠=⋅=⋅=⋅︒. ∵DC DE CE -=，∴x tan40x tan1918.6⋅︒-⋅︒=.∴0.84x 0.34x 18.6-≈.解得x 37.2≈.∴AC 37≈.DE x tan4037.2.8431=⋅︒≈⨯≈.答：乙楼的高度DC 约为31m ，甲乙两楼之间的距离AC 约为37m.【点睛】本题考查了解直角三角形的应用，解题的关键是从复杂的实际问题中整理出直角三角形并选择合适的边角关系列出方程．24．6【解析】【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a 与b 的值代入计算即可求出值．【详解】解：原式=()()a b b a b a b +-+-•()2(a b)a a b --=1a b +，当，．【点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．25．5【解析】【分析】原式利用算术平方根定义，负整数指数幂法则，以及绝对值的代数意义计算即可求出值．【详解】原式＝4+3﹣2＝5．【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．。

【类型综述】特殊四边形的几何动点问题，很多困难源于问题中的可动点，常见的动点四边形有平行四边形、矩形、菱形等问题，其中尤其是平行四边形的问题出现次数最多。

实际上，求解特殊四边形的动点问题，关键是利用图解法抓住它运动中的某一瞬间，寻找合理的代数关系式，确定运动变化过程中的数量关系、图形位置关系，分类画出符合条件的图形进行讨论，就能找到解决问题的途径，有效避免思维混乱。

【方法揭秘】我们先思考三个问题：1．已知A、B、C三点，以A、B、C、D为顶点的平行四边形有几个，怎么画？2．在坐标平面内，如何理解平行四边形ABCD的对边AB与DC平行且相等？3．在坐标平面内，如何理解平行四边形ABCD的对角线互相平分？图1 图2 图3如图1，过△ABC的每个顶点画对边的平行线，三条直线两两相交，产生三个点D．如图2，已知A(0, 3)，B(－2, 0)，C(3, 1)，如果四边形ABCD是平行四边形，怎样求点D的坐标呢？点B先向右平移2个单位，再向上平移3个单位与点A重合，因为BA与CD平行且相等，所以点C(3, 1) 先向右平移2个单位，再向上平移3个单位得到点D(5, 4)．如图3，如果平行四边形ABCD的对角线交于点G，那么过点G画任意一条直线（一般与坐标轴垂直），点A、C到这条直线的距离相等，点B、D到这条直线的距离相等．关系式x A＋x C＝x B＋x D和y A＋y C＝y B＋y D有时候用起来很方便．我们再来说说压轴题常常要用到的数形结合．如图4，点A是抛物线y＝－x2＋2x＋3在x轴上方的一个动点，AB⊥x轴于点B，线段AB交直线y＝x －1于点C，那么点A的坐标可以表示为(x,－x2＋2x＋3)，点C的坐标可以表示为(x, x－1)，线段AB的长可以用点A的纵坐标表示为AB＝y A＝－x2＋2x＋3，线段AC的长可以用A、C两点的纵坐标图4表示为AC＝y A－y C＝(－x2＋2x＋3)－(x－1)＝－x2＋x＋2．通俗地说，数形结合就是：点在图象上，可以用图象的解析式表示点的坐标，用点的坐标表示点到坐标轴的距离．【典例分析】例1 如图1，直线y＝－3x＋3与x轴、y轴分别交于点A、B，抛物线y＝a(x－2)2＋k经过A、B两点，并与x轴交于另一点C，其顶点为P．（1）求a，k的值；（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求点Q的坐标；（3）在抛物线及其对称轴上分别取点M、N，使以A、C、M、N为顶点的四边形为正方形，求此正方形的边长．】图1思路点拨1．第（2）题的等腰三角形只考虑QA＝QB的情形．2．第（3）题的正方形不可能AC为边，只存在AC为对角线的情形．满分解答图2 图3 图4考点伸展如果把第（3）题中的正方形改为平行四边形，那么符合条件的点M有几个？①如果AC为对角线，上面的正方形AMCN是符合条件的，M(2,－1)．②如图5，如果AC为边，那么MN//AC，MN＝AC＝2．所以点M的横坐标为4或0．此时点M的坐标为(4, 3)或(0, 3)．第（2）题如果没有限制等腰三角形ABQ的底边，那么符合条件的点Q有几个？①如图2，当QA＝QB时，Q(2, 2)．②如图6，当BQ＝BA B为圆心，BA为半径的圆与直线x＝2有两个交点．m=根据BQ2＝10，列方程22＋(m－3)2＝10，得3此时Q(2,3或(2,3．③如图7，当AQ＝AB时，以A为圆心，AB为半径的圆与直线x＝2有两个交点，但是点(2,－3)与A、B 三点共线，所以Q(2, 3)．图5 图6 图7例2如图1，在平面直角坐标系中，已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4)．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，沿线段AB向点B运动，同时动点Q从点C出发，沿线段CD向点D运动．点P、Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C、Q、E、H为顶点的四边形为菱形？请直接写出t的值．图1思路点拨1．把△ACG分割成以GE为公共底边的两个三角形，高的和等于AD．2．用含有t的式子把图形中能够表示的线段和点的坐标都表示出来．3．构造以C、Q、E、H为顶点的平行四边形，再用邻边相等列方程验证菱形是否存在．满分解答考点伸展第（3）题的解题思路是这样的：因为FE //QC ，FE ＝QC ，所以四边形FECQ 是平行四边形．再构造点F 关于PE 轴对称的点H ′，那么四边形EH ′CQ 也是平行四边形．再根据FQ ＝CQ 列关于t 的方程，检验四边形FECQ 是否为菱形，根据EQ ＝CQ 列关于t 的方程，检验四边形EH ′CQ 是否为菱形．1(1,4)2E t t +-，1(1,4)2F t +，(3,)Q t ，(3,0)C ． 如图2，当FQ ＝CQ 时，FQ 2＝CQ 2，因此2221(2)(4)2t t t -+-=．整理，得240800t t -+=．解得120t =-，220t =+如图3，当EQ ＝CQ 时，EQ 2＝CQ 2，因此2221(2)(42)2t t t -+-=． 整理，得213728000t t -+=．(1320)(40)0t t --=．所以12013t =，240t =（舍去）．图2 图3例3 如图1，抛物线经过A (1, 0)、B (5, 0)、C 10(0,)3三点．设点E (x , y )是抛物线上一动点，且在x 轴下方，四边形OEBF 是以OB 为对角线的平行四边形．（1）求抛物线的解析式；（2）当点E (x , y )运动时，试求平行四边形OEBF 的面积S 与x 之间的函数关系式，并求出面积S 的最大值；（3）是否存在这样的点E ，使平行四边形OEBF 为正方形？若存在，求点E 、F 的坐标；若不存在，请说明理由．思路点拨1．平行四边形OEBF 的面积等于△OEB 面积的2倍．2．第（3）题探究正方形OEBF ，先确定点E 在OB 的垂直平分线上，再验证EO ＝EB ．满分解答（1）因为抛物线与x 轴交于A (1, 0)、B (5, 0)两点，设y ＝a (x －1)(x －5)．代入点C 10(0,)3，得1053a =．解得23a =． 所以抛物线的解析式为22210(1)(5)4333y x x x x =--=-+．图2 图3考点伸展既然第（3）题正方形OEBF是存在的，命题人为什么不让探究矩形OEBF有几个呢？如图4，如果平行四边形OEBF为矩形，那么∠OEB＝90°．根据EH2＝HO·HB，列方程22(1)(5)(5)3x x x x⎡⎤---=-⎢⎥⎣⎦．或者由DE＝12OB＝52，根据DE2＝254，列方程225225()(1)(5)234x x x⎡⎤-+---=⎢⎥⎣⎦．这两个方程整理以后都是一元三次方程4x3－28x2＋53x－20＝0，这个方程对于初中毕业的水平是不好解的．事实上，这个方程可以因式分解，51(4)()()022x x x---=．如图3，x＝52；如图4，x＝4；如图5，x＝12，但此时点E在x轴上方了．这个方程我们也可以用待定系数法解：设方程的三个根是52、m、n，那么4x3－28x2＋53x－20＝54()()()2x x m x n---．根据恒等式对应项的系数相等，得方程组441028,1010453,1020.m nm n mnmn++=⎧⎪++=⎨⎪=⎩解得4,1.2mn=⎧⎪⎨=⎪⎩图4 图5例4如图1，在平面直角坐标系中，抛物线y＝ax2－2ax－3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线l：y＝kx＋b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD ＝4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）；（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为54，求a的值；（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．图1 备用图思路点拨1．过点E作x轴的垂线交AD于F，那么△AEF与△CEF是共底的两个三角形．2．以AD为分类标准讨论矩形，当AD为边时，AD与QP平行且相等，对角线AP＝QD；当AD为对角线时，AD与PQ互相平分且相等．满分解答（3）已知A(－1, 0)、D(4, 5a)，x P＝1，以AD为分类标准，分两种情况讨论：①如图2，如果AD为矩形的边，那么AD//QP，AD＝QP，对角线AP＝QD．由x D－x A＝x P－x Q，得x Q＝－4．当x＝－4时，y＝a(x＋1)(x－3)＝21a．所以Q(－4, 21a)．由y D－y A＝y P－y Q，得y P＝26a．所以P(1, 26a)．由AP2＝QD2，得22＋(26a)2＝82＋(16a)2．整理，得7a2＝1．所以a=P(1．②如图3，如果AD为矩形的对角线，那么AD与PQ互相平分且相等．由x D＋x A＝x P＋x Q，得x Q＝2．所以Q(2,－3a)．由y D＋y A＝y P＋y Q，得y P＝8a．所以P(1, 8a)．由AD2＝PQ2，得52＋(5a)2＝12＋(11a)2．整理，得4a2＝1．所以12a=-．此时P(14)-，．图1 图2 图3考点伸展第（3）题也可以这样解．设P(1,n)．①如图2，当AD时矩形的边时，∠QPD＝90°，所以AM DNMD NP=，即5553a na-=-．解得235ana+=．所以P235(1,)aa+．所以Q3(4,)a-．将Q3(4,)a-代入y＝a(x＋1)(x－3)，得321aa=．所以a=．②如图3，当AD为矩形的对角线时，先求得Q(2,－3a)．由∠AQD＝90°，得AG QKGQ KD=，即32335aa a-=--．解得12a=-．例5 如图1，已知抛物线C：y＝－x2＋bx＋c经过A(－3,0)和B(0, 3)两点．将这条抛物线的顶点记为M，它的对称轴与x轴的交点记为N．（1）求抛物线C的表达式；（2）求点M的坐标；（3）将抛物线C平移到抛物线C′，抛物线C′的顶点记为M′，它的对称轴与x轴的交点记为N′．如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？图1思路点拨1．抛物线在平移的过程中，M′N′与MN保持平行，当M′N′＝MN＝4时，以点M、N、M′、N′为顶点的四边形就是平行四边形．2．平行四边形的面积为16，底边MN＝4，那么高NN′＝4．3．M′N′＝4分两种情况：点M′在点N′的上方和下方．4．NN′＝4分两种情况：点N′在点N的右侧和左侧．满分解答图2 图3考点伸展本题的抛物线C 向右平移m 个单位，两条抛物线的交点为D ，那么△MM ′D 的面积S 关于m 有怎样的函数关系？如图4，△MM ′D 是等腰三角形，由M (－1,4)、M ′(－1＋m , 4)，可得点D 的横坐标为22m -． 将22m x -=代入y ＝－(x ＋1)2＋4，得244m y =-+．所以DH ＝244m -．所以S ＝2311(4)2248m m m m -=-．图4例6如图1，已知抛物线y ＝－x 2＋bx ＋c 经过A (0, 1)、B (4, 3)两点． （1）求抛物线的解析式； （2）求tan ∠ABO 的值；（3）过点B 作BC ⊥x 轴，垂足为C ，在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ，交抛物线于点M ，若四边形MNCB 为平行四边形，求点M 的坐标．图1思路点拨1．第（2）题求∠ABO 的正切值，要构造包含锐角∠ABO 的角直角三角形． 2．第（3）题解方程MN ＝y M －y N ＝BC ，并且检验x 的值是否在对称轴左侧．满分解答（1）将A (0, 1)、B (4, 3)分别代入y ＝－x 2＋bx ＋c ，得1,164 3.c b c =⎧⎨-++=⎩解得92b =，c ＝1． 所以抛物线的解析式是2912y x x =-++． （2）在Rt △BOC 中，OC ＝4，BC ＝3，所以OB ＝5． 如图2，过点A 作AH ⊥OB ，垂足为H ．在Rt △AOH 中，OA ＝1，4sin sin 5AOH OBC ∠=∠=，所以4sin 5AH OA AOH =⋅∠=． 图2 所以35OH =，225BH OB OH =-=．在Rt △ABH 中，4222tan 5511AH ABO BH ∠==÷=．图3 图4考点伸展第（3）题如果改为：点M 是抛物线上的一个点，直线MN 平行于y 轴交直线AB 于N ，如果M 、N 、B 、C 为顶点的四边形是平行四边形，求点M 的坐标．那么求点M 的坐标要考虑两种情况：MN ＝y M －y N 或MN ＝y N －y M ．由y N －y M ＝4x －x 2，解方程x 2－4x ＝3，得2x =5）．所以符合题意的点M 有4个：9(1,)2，11(3,)2，5(22，5(22+．图5例7将抛物线c1：2y=x轴翻折，得到抛物线c2，如图1所示．（1）请直接写出抛物线c2的表达式；（2）现将抛物线c1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x轴的交点从左到右依次为A、B；将抛物线c2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E．①当B、D是线段AE的三等分点时，求m的值；②在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．图1思路点拨1．把A、B、D、E、M、N六个点起始位置的坐标罗列出来，用m的式子把这六个点平移过程中的坐标罗列出来．2．B、D是线段AE的三等分点，分两种情况讨论，按照AB与AE的大小写出等量关系列关于m的方程．3．根据矩形的对角线相等列方程．满分解答①B、D是线段AE的三等分点，存在两种情况：情形一，如图2，B在D的左侧，此时123AB AE==，AE＝6．所以2(1＋m)＝6．解得m＝2．情形二，如图3，B在D的右侧，此时223AB AE==，AE＝3．所以2(1＋m)＝3．解得12m=．图2 图3 图4考点伸展第（2）题②，探求矩形ANEM，也可以用几何说理的方法：在等腰三角形ABM中，因为AB＝2，AB ABM是等边三角形．同理△DEN是等边三角形．当四边形ANEM是矩形时，B、D两点重合．因为起始位置时BD＝2，所以平移的距离m＝1．【变式训练】1.（2017四川省达州市）探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P 1（x 1，y 1），P 2（x 2，y 2），可通过构造直角三角形利用图1得到结论：12PP =他还利用图2证明了线段P 1P 2的中点P （x ，y ）P 的坐标公式：122x x x +=，122y y y +=．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M （2，﹣1），N （﹣3，5），则线段MN 长度为 ；②直接写出以点A （2，2），B （﹣2，0），C （3，﹣1），D 为顶点的平行四边形顶点D 的坐 标： ； 拓展：（3）如图3，点P （2，n ）在函数43y x =（x ≥0）的图象OL 与x 轴正半轴夹角的平分线上，请在OL 、x 轴上分别找出点E 、F ，使△PEF 的周长最小，简要叙述作图方法，并求出周长的最小值．【答案】（1）答案见解析；（23，3）或（7，1）或（﹣1，﹣3）；（3． 【解析】试题分析：（1）用P 1、P 2的坐标分别表示出OQ 和PQ 的长即可证得结论；试题解析：（1）∵P 1（x 1，y 1），P 2（x 2，y 2），∴Q 1Q 2=OQ 2﹣OQ 1=x 2﹣x 1，∴Q 1Q =212x x -，∴OQ =OQ 1+Q 1Q =x 1+212x x -=122x x + ，∵PQ 为梯形P 1Q 1Q 2P 2的中位线，∴PQ =11222PQ P Q + =122y y +，即 线段P 1P 2的中点P （x ，y ）P 的坐标公式为x =122x x +，y =122y y +；（2）①∵M （2，﹣1），N （﹣3，5），∴MN ；②∵A （2，2），B （﹣2，0），C （3，﹣1），∴当AB 为平行四边形的对角线时，其对称中心坐标为（0，1），设D （x ，y ），则x +3=0，y +（﹣1）=2，解得x =﹣3，y =3，∴此时D 点坐标为（﹣3，3），当AC 为对角线时，同理可求得D 点坐标为（7，1），当BC 为对角线时，同理可求得D 点坐标为（﹣1，﹣3），综上可知D 点坐标为（﹣3，3）或（7，1）或（﹣1，﹣3），故答案为：（﹣3，3）或（7，1）或（﹣1，﹣3）； （3）如图，设P 关于直线OL 的对称点为M ，关于x 轴的对称点为N ，连接PM 交直线OL 于点R ，连接PN 交x 轴于点S ，连接MN 交直线OL 于点E ，交x 轴于点F ，又对称性可知EP =EM ，FP =FN ，∴ PE +PF +EF =ME +EF +NF =MN ，∴此时△PEF 的周长即为MN 的长，为最小，设R （x ，43x ），由题意可知OR =OS =2，PR =PS =n =2，解得x =﹣65（舍去）或x =65，∴R （65，85），∴n =，解得n =1，∴P （2，1），∴N （2，﹣1），设M （x ，y ），则22x +=65，12y + =85，解得x =25，y =115，∴M （25，115），∴MN ，即△PEF 的周长的最小值．考点：1．一次函数综合题；2．阅读型；3．分类讨论；4．最值问题2.（2017湖北省襄阳市）如图，矩形OABC 的两边在坐标轴上，点A 的坐标为（10，0），抛物线24y ax bx =++过点B ，C 两点，且与x 轴的一个交点为D （﹣2，0），点P 是线段CB 上的动点，设CP =t （0＜t ＜10）． （1）请直接写出B 、C 两点的坐标及抛物线的解析式；（2）过点P 作PE ⊥BC ，交抛物线于点E ，连接BE ，当t 为何值时，∠PBE =∠OCD ？（3）点Q 是x 轴上的动点，过点P 作PM ∥BQ ，交CQ 于点M ，作PN ∥CQ ，交BQ 于点N ，当四边形PMQN 为正方形时，请求出t 的值．【答案】（1）B （10，4），C （0，4），215463y x x =-++；（2）3；（3）t 的值为103或203．试题解析：（1）在24y ax bx =++中，令x =0可得y =4，∴C （0，4），∵四边形OABC 为矩形，且A （10，0），∴B （10，4），把B 、D 坐标代入抛物线解析式可得：10010444240a b a b ++=⎧⎨-+=⎩，解得：1653a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线解析式为215463y x x =-++；考点：1．二次函数综合题；2．分类讨论；3．动点型；4．压轴题． 3.（2017山东省枣庄市）如图，抛物线212y x bx c =-++ 与x 轴交于点A 和点B ，与y 轴交于点C ，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E ，连接BD ．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA =∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN ∥x 轴与抛物线交于点N ，点P 在x 轴上，点Q 在坐标平面内，以线段MN 为对角线作正方形MPNQ ，请写出点Q 的坐标．【答案】（1）21262y x x =-++，D （2，8）；（2）（﹣1，72）或（﹣3，﹣92）；（3）（2，2-+或（2，2--试题解析：（1）把B 、C 两点坐标代入抛物线解析式可得：18606b c c -++=⎧⎨=⎩，解得：26b c =⎧⎨=⎩，∴抛物线解析式为21262y x x =-++ ，∵21262y x x =-++=21(2)82x --+，∴D （2，8）；（2）如图1，过F 作FG ⊥x 轴于点G ，设F （x ，21262x x -++），则FG =|21262x x -++|，∵∠FBA =∠BDE ，∠FGB =∠BED =90°，∴△FBG ∽△BDE ，∴FG BFBG DE=，∵B （6，0），D （2，8），∴E （2，0），BE =4，DE =8，OB =6，∴BG =6﹣x ，∴21264268x x x -++=-，当点F 在x 轴上方时，有21261262x x x -++=-，解得x =﹣1或x =6（舍去），此时F 点的坐标为（﹣1，72）；当点F 在x 轴下方时，有21261262x x x -++=--，解得x =﹣3或x =6（舍去），此时F 点的坐标为（﹣3，﹣92）； 综上可知F 点的坐标为（﹣1，72）或（﹣3，﹣92）；考点：1．二次函数综合题；2．分类讨论；3．动点型；4．压轴题．4. (2017湖北恩施第24题)如图12，已知抛物线2y ax c =+过点()2,2-，()4,5，过定点()0,2F 的直线:2l y kx =+与抛物线交于A ，B 两点，点B 在点A 的右侧，过点B 作x 轴的垂线，垂足为C .(1)求抛物线的解析式；(2)当点B 在抛物线上运动时，判断线段BF 与BC 的数量关系(>、<、=)，并证明你的判断； (3)P 为y 轴上一点，以,,,B C F P 为顶点的四边形是菱形，设点()0,P m ，求自然数m 的值；(4)若1k =，在直线l 下方的抛物线上是否存在点Q ，使得QBF △的面积最大，若存在，求出点Q 的坐标及QBF △的最大面积，若不存在，请说明理由.【答案】（1）y=14x 2+1；（2）BF=BC ，理由详见解析；（3）6；（4）当t=2时，S △QBF 有最大值，最大，此时Q 点坐标为（2，2）．试题解析：（1）把点（﹣2，2），（4，5）代入y=ax2+c得42165a ca c+=⎧⎨+=⎩，解得141ac⎧=⎪⎨⎪=⎩，所以抛物线解析式为y=14x2+1；（2）BF=BC．理由如下：设B（x，14x2+1），而F（0，2），∴BF2=x2+（14x2+1﹣2）2=x2+（14x2﹣1）2=（14x2+1）2，∴BF=14x2+1，∵BC⊥x轴，∴BC=14x2+1，∴BF=BC；（3）如图1，m为自然数，则点P在F点上方，∵以B、C、F、P为顶点的四边形是菱形，∴CB=CF=PF，而CB=FB，∴BC=CF=BF，∴△BCF为等边三角形，∴∠BCF=60°，∴∠OCF=30°，在Rt△OCF中，CF=2OF=4，∴PF=CF=4，∴P（0，6），即自然数m的值为6；考点：二次函数综合题.5.（2017山东临沂第26题）如图，抛物线23y ax bx =+-经过点()2,3A -，与x 轴负半轴交于点B ，与y 轴交于点C ，且3OC OB =.（1）求抛物线的解析式；（2）点D 在y 轴上，且BDO BAC ∠=∠，求点D 的坐标；（3）点M 在抛物线上，点N 在抛物线的对称轴上，是否存在以点A ，B ，M ，N 为顶点的四边形是平行四边形？若存在。

专题因动点产生的面积问题例 1 2012年菏泽市中考第21题如图1，在平面直角坐标系中放置一直角三角板，其顶点为A(0, 1)、B(2, 0)、O(0, 0)，将此三角板绕原点O逆时针旋转90°，得到三角形A′B′O．（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；（2）设点P是第一象限内抛物线上的一个动点，是否存在点P，使四边形PB′A′B的面积是△A′B′O面积的4倍？若存在，请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形PB′A′B是哪种形状的四边形？并写出它的两条性质．图1例 2 2012年河南省中考第23题如图1，在平面直角坐标系中，直线112y x=+与抛物线y＝ax2＋bx－3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a、b及sin∠ACP的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为9∶10？若存在，直接写出m的值；若不存在，请说明理由．图1、例 3 2011年南通市中考第28题如图1，直线l经过点A(1，0)，且与双曲线myx=(x＞0)交于点B(2，1)．过点(,1)P p p-(p＞1)作x轴的平行线分别交曲线myx=(x＞0)和myx=-(x＜0)于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．图1例4 2011年上海市松江区中考模拟第24题如图1，在平面直角坐标系xOy中，直角梯形OABC的顶点O为坐标原点，顶点A、C 分别在x轴、y轴的正半轴上，CB∥OA，OC＝4，BC＝3，OA＝5，点D在边OC上，CD ＝3，过点D作DB的垂线DE，交x轴于点E．（1）求点E的坐标；（2）二次函数y＝－x2＋bx＋c的图象经过点B和点E．①求二次函数的解析式和它的对称轴；②如果点M在它的对称轴上且位于x轴上方，满足S△CEM＝2S△ABM，求点M的坐标．图1。

备战2020中考数学之解密压轴解答题命题规律专题04 因动点产生的面积问题【类型综述】面积是平面几何中一个重要的概念，关联着平面图形中的重要元素边与角，由动点而生成的面积问题，是抛物线与直线形结合的觉形式，常见的面积问题有规则的图形的面积（如直角三角形、平行四边形、菱形、矩形的面积计算问题）以及不规则的图形的面积计算，解决不规则的图形的面积问题是中考压轴题常考的题型，此类问题计算量较大。

有时也要根据题目的动点问题产生解的不确定性或多样性。

解决这类问题常用到以下与面积相关的知识：图形的割补、等积变形、等比转化等数学方法. 面积的存在性问题常见的题型和解题策略有两类：一是先根据几何法确定存在性，再列方程求解，后检验方程的根．二是先假设关系存在，再列方程，后根据方程的解验证假设是否正确．【方法揭秘】解决动点产生的面积问题，常用到的知识和方法，如下：如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．图1 图2 图3计算面积长用到的策略还有：如图4，同底等高三角形的面积相等．平行线间的距离处处相等．如图5，同底三角形的面积比等于高的比．如图6，同高三角形的面积比等于底的比．图4 图5 图6【典例分析】【例1】如图，抛物线y＝ax2＋bx＋c（a≠0）与x轴交于A(－1, 0)，B(4, 0)两点，与y轴交于点C(0, 2)．点M(m, n)是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上．过点M作x轴的平行线交y轴于点Q，交抛物线于另一点E，直线BM交y轴于点F．（1）求抛物线的解析式，并写出其顶点坐标；（2）当S△MFQ∶S△MEB＝1∶3时，求点M的坐标．【例2】如图，在平面直角坐标系中，抛物线y=ax2+bx﹣3（a≠0）与x轴交于点A（﹣2，0）、B（4，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，当△PBQ 存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK：S△PBQ=5：2，求K点坐标．【例3】如图，在平面直角坐标系中，直线112y x=+与抛物线y＝ax2＋bx－3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a、b及sin∠ACP的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为9∶10？若存在，直接写出m的值；若不存在，请说明理由．【例4】如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动．过点P作PD⊥AC于点D（点P不与点A、B重合），作∠DPQ=60°，边PQ交射线DC于点Q．设点P的运动时间为t秒．（1）用含t的代数式表示线段DC的长；（2）当点Q与点C重合时，求t的值；（3）设△PDQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式；（4）当线段PQ的垂直平分线经过△ABC一边中点时，直接写出t的值．【例5】如图，直线l经过点A(1，0)，且与双曲线myx=(x＞0)交于点B(2，1)．过点(,1)P p p-(p＞1)作x轴的平行线分别交曲线myx=(x＞0)和myx=-(x＜0)于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．【例6】如图（1），在平面直角坐标系中，点A （0，﹣6），点B （6，0）．Rt △CDE 中，∠CDE=90°，CD=4，DE=43，直角边CD 在y 轴上，且点C 与点A 重合．Rt △CDE 沿y 轴正方向平行移动，当点C 运动到点O 时停止运动．解答下列问题：（1）如图（2），当Rt △CDE 运动到点D 与点O 重合时，设CE 交AB 于点M ，求∠BME 的度数． （2）如图（3），在Rt △CDE 的运动过程中，当CE 经过点B 时，求BC 的长．（3）在Rt △CDE 的运动过程中，设AC=h ，△OAB 与△CDE 的重叠部分的面积为S ，请写出S 与h 之间的函数关系式，并求出面积S 的最大值．【变式训练】1．如图，利用一个直角墙角修建一个梯形储料场ABCD ，其中∠C ＝120°．若新建墙BC 与CD 总长为12m ，则该梯形储料场ABCD 的最大面积是（ ）A ．18m 2B ．183m 2C ．243m 2D ．453m 2 2．如图，正方形ABCD 的边长为2cm ，动点P ，Q 同时从点A 出发，在正方形的边上，分别按A D C →→，A B C →→的方向，都以1/cm s 的速度运动，到达点C 运动终止，连接PQ ，设运动时间为x s ，APQ ∆的面积为2y cm ，则下列图象中能大致表示y 与x 的函数关系的是（ ）A ．B ．C ．D ．3．如图，已知直线334y x =-与x 轴、y 轴分别交于A 、B 两点，P 是以C （0，1）为圆心，1为半径的圆上一动点，连结PA 、PB ．则△PAB 面积的最大值是（ ）A ．8B ．12C ．212D ．1724．如图，在等腰直角三角形ABC 中，90ACB ∠=︒，8AB cm =，CH 是AB 边上的高，正方形DEFG 的边DE 在高CH 上，F ，G 两点分别在AC ，AH 上．将正方形DEFG 以每秒1cm 的速度沿射线DB 方向匀速运动，当点G 与点B 重合时停止运动．设运动时间为ts ，正方形DEFG 与BHC ∆重叠部分的面积为2Scm ，则能反映S 与t 的函数关系的图象（ ）A ．B ．C ．D ．5．如图，点A 是直线y=﹣x 上的动点，点B 是x 轴上的动点，若AB=2，则△AOB 面积的最大值为（ ）A．2B．+1C．-1D．26．如图，已知，以为圆心，长为半径作，是上一个动点，直线交轴于点，则面积的最大值是（）A．B．C．D．7．如图，在平面直角坐标系中，菱形OABC 的顶点A 在x 轴正半轴上，顶点C 的坐标为（4，3），D 是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD 面积的最大值为__________8．如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是______________．9．已知直角梯形OABC在如图所示的平面直角坐标系中，AB∥OC，AB=10，OC=22，BC=15，动点M从A点出发，以每秒一个单位长度的速度沿AB向点B运动，同时动点N从C点出发，以每秒2个单位长度的速度沿CO向O点运动。