什么是硬件乘法器(20210108120425)

MSP430程序库<十三>硬件乘法器使用硬件乘法器不占用CPU周期，有硬件实现，速度比软件实现的乘法速度快很多。

msp430f14x、msp430f16x中都含有硬件乘法器模块，方便用户需要速度的时候使用。

硬件介绍：在MSP430系列单片机中，硬件乘法器是外围模块，而不是CPU内核的一部分；所以它的活动与否与CPU的活动与否无关，它的寄存器和其他的外围寄存器一样通过CPU指令读写。

硬件乘法器模块支持一下功能：无符号乘法、有符号乘法、无符号乘加、有符号乘加；可以支持16*16 16*8 8*16 8*8bits的乘法。

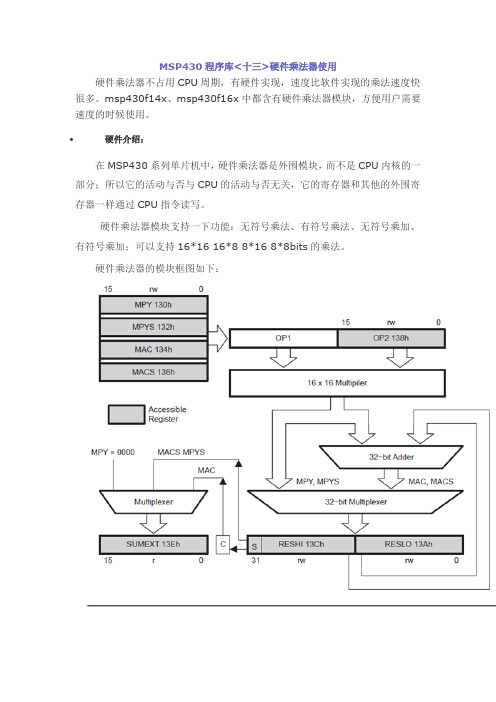
硬件乘法器的模块框图如下：硬件乘法器模块的四种操作类型(无符号乘法、有符号乘法、无符号乘加、有符号乘加)是由写入的第一个操作数的位置决定的。

这个模块有两个操作数寄存器：OP1和OP2、三个结果寄存器RESLO, RESHI, 和SUMEXT。

RESLO 寄存器存储结果的低字(低16位)；RESHI寄存器存储结果的高字(高16位)；SUMEXT寄存器存储结果的有关信息。

结果在3个时钟周期后即可完成；写入OP2后的下一条指令即可读取结果，有一种情况例外：用间接寻址方式访问结果。

用间接寻址方式访问结果时，读取结果之前需要有一条NOP指令。

操作数OP1有四个地址(MPY:0130h MPYS:0132h MAC:0134h MACS:0136h)，这四个寄存器用来选择乘法的操作模式。

写入第一个操作数寄存器决定用哪种操作：无符号用符号等，但是不启动相乘操作；写入第二个操作数寄存器启动相乘的操作。

计算完成后结果存入寄存器RESLO,RESHI, 和SUMEXT。

操作数1的四个地址对应的操作：四种操作模式下高位结果寄存器的内容如下：四种操作模式SUMEXT 寄存器的内容：连续乘法运算时，如果操作数1不需改变就可以运算，则可以不需要重新写入和以保存内容相同的数；但OP2必须重新写入以启动乘法运算。

模拟乘法器芯片乘法器芯片是一种电子设备，用于执行乘法运算。

它是计算机等电子设备中的重要组成部分，用于执行数字信号的乘法运算。

乘法器芯片的功能是将两个输入信号相乘，然后输出它们的乘积。

乘法器芯片通常由许多晶体管组成，可以进行高速且精确的乘法计算。

晶体管是一种半导体器件，可以控制电流的流动。

乘法器芯片利用晶体管的特性，通过将输入信号与适当的电路连接起来，可以在极短的时间内完成乘法运算。

乘法器芯片的输入包括两个数字信号，可以是二进制数、十进制数或其他进制数。

这些输入信号经过乘法器芯片的电路处理后，得到的输出信号就是它们的乘积。

乘法器芯片的输出信号通常以二进制数的形式表示。

乘法器芯片的工作原理是基于数学上的乘法算法。

例如，当输入信号是二进制数时，乘法器芯片将执行二进制乘法算法。

这个算法的基本原理是将每一位的乘积相加，并通过进位的方式保持结果的正确性。

乘法器芯片的速度通常非常快，可以在几纳秒的时间内完成乘法运算。

这使得乘法器芯片成为计算机等高性能设备中不可或缺的部分。

在现代计算机中，乘法器芯片通常与其他逻辑电路和存储器一起组成芯片集成电路（IC），用于执行复杂的计算任务。

乘法器芯片的应用非常广泛。

它被广泛用于计算机、通信设备、数字信号处理器、工业控制系统等领域。

在这些应用中，乘法器芯片可以快速、精确地执行大量的乘法运算，提高系统的计算性能。

虽然乘法器芯片在高性能计算设备中具有重要作用，但它并不是完美的。

乘法器芯片的主要限制是它需要消耗大量的能量和占用大量的空间。

此外，乘法器芯片也容易受到噪声和干扰的影响，可能导致计算错误。

为了解决这些问题，研究人员一直在努力开发新的乘法器芯片设计，以提高能效和稳定性。

总之，乘法器芯片是一种重要的电子设备，用于执行乘法运算。

它通过利用晶体管的特性和数学乘法算法，可以快速、精确地执行乘法运算。

乘法器芯片在计算机和其他高性能设备中被广泛应用，提高了系统的计算性能。

尽管乘法器芯片存在一些限制，但通过不断的研发和创新，相信它的性能将得到进一步提高。

计算机科学与工程学院课程设计报告题目全称：用硬件描述语言设计浮点乘法器（原码一位乘法）课程名称：计算机组成原理指导老师：职称：（注：学生姓名填写按学生对该课程设计的贡献及工作量由高到底排列，分数按排名依次递减。

序号排位为“1”的学生成绩最高，排位为“10”的学生成绩最低。

）指导老师评语：指导签字：摘要硬件乘法器，其基础就是加法器结构，它已经是现代计算机中必不可少的一部分。

其大致可分为定点乘法器和浮点乘法器。

其中浮点数的格式较定点数格式复杂，硬件实现的成本较高，完成一次浮点四则运算的时间也比定点运算要长。

但浮点数比定点数的表示范围更宽，有效精度更高，因此更适合科学与工程计算的需要。

但要求计算精度较高时，往往采用浮点运算。

浮点乘法器设计（原码一位乘法）模型就是基于“移位和相加”的算法，设浮点数A=2^AE·AM,B=2^BE·BM,则A×B=2^(AE+BE)·(AM×BM)，即阶码相加，尾数相乘。

其运算步骤可以简单的归为（1）检测能否简化操作，并置结果数符（2）阶码相加（3）尾数相乘（4）乘积规格化等。

本论文第一章讲述了该课程设计的研究背景及意义及其理论依据和实验基础、课题的难点、重点、核心问题及方向。

第二章重点讲述了原码一位乘法实现浮点乘法器设计的原理、操作流程及课程设计实验数据和结果关键词：浮点乘法器、原码一位乘法、阶码、尾数目录第1章课题背景 (3)1.1研究背景 (3)1.1.1国内外的研究现状 (3)1.1.2理论依据和实验基础 (4)1.2课题的难点、重点、核心问题及方向 (4)1.3研究目的和意义 (5)第2章课题的需求分析 (6)2.1 课题对应软硬件系统的性能 (6)2.2业务流程 (6)2.3其他需求 (7)第3章课题的设计与实现 (8)3.1课程设计的理论基础 (8)3.2开发工具简介 (8)3.2.1硬件部分 (8)3.2.2软件部分 (8)3.3课程设计的框架和流程图 (8)3.4课程设计的实现 (10)3.4.1创建工程 (10)3.4.2设计输入 (10)3.4.3约束（引脚绑定） (12)3.4.4综合 (12)3.4.5实现 (12)3.4.6 下载 (14)3. 4.7开始测试 (14)3.5结论 (16)第4章结束语 (17)第1章课题背景1.1研究背景1.1.1国内外的研究现状今日由于科技的突飞猛进，使得在一个小小的晶片上，能够容纳上百万的电晶体。

乘法器工作原理
乘法器是一种电子设备，用于实现两个数字（或模拟）信号的乘法运算。

其工作原理可以简单地描述如下：
1. 输入信号：乘法器通常有两个输入端，分别用于接收待相乘的数字信号A和B。

2. 位展开：乘法器将输入信号A和B进行位展开操作，即将
每一个输入位（或字节）进行分离和独立处理。

这可以通过触发器、逻辑门电路等实现。

3. 部分乘积计算：对每一对输入位进行乘法运算，并将结果存储在部分乘积寄存器中。

这可以通过加法器电路来实现，其中每一个乘积被加到累加器中。

4. 乘积累加：将所有的部分乘积相加得到最终的乘积结果。

这可以通过多级加法器电路来实现。

一般来说，乘法器采用树形结构或布斯-舍乘法算法（Booth's algorithm）来提高计算效率。

5. 结果输出：输出端给出乘法运算的结果。

根据需求，这个结果可以是数字信号，模拟电压或电流等形式。

乘法器的工作原理可以根据底层电路和算法的不同而有所变化。

现代的乘法器采用复杂的电路设计和优化算法，以实现更高的运算速度和精度。

四位硬件乘法器一、实验目的：1、学习移位相加时序式乘法器的设计方法2、学习层次化设计方法3、学习原理图调用VHDL模块方法4、熟悉EDA仿真分析方法二、实验原理：乘法器的原理是，乘法通过逐项移位相加原理来实现，从被乘数的最地位开始，若为1，则乘数左移后与上一次的和相加；若为0，左移后以全零相加，直至被乘数的最高位。

ARICTL是乘法运算控制电路，它的START信号的上升沿与高电平有两个功能，即16位寄存器清0和被乘数A向移位寄存器SREG加载；它的低电平则作为乘法使能信号CLK位乘法时钟信号，被乘数加载于4位右移寄存器SREG 后，在时钟同步下由低位至高位逐位移出，当其为1时，与门ANDARITH打开，4位乘数B在同一节拍进入4位加法器，与上一节拍锁存在16位锁存器REG的高4位进行相加，其和在下一时钟节拍的上升沿被锁进此锁存器；而当被乘数的移出位为0时，与门全0输出。

如此往复，直至4个时钟脉冲后，乘法运算过程中止，此时REG的输出值即最后乘积。

三、实验设备：计算机一台操作系统：WINDOWS XP软件：ispDesignEXPERT System四、实验步骤：1、4位右移寄存器SREGLIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY SREG ISPORT(EN:IN STD_LOGIC;CLK: IN STD_LOGIC;LOAD:IN STD_LOGIC;DIN: IN STD_LOGIC_VECTOR(3 DOWNTO 0);QB: OUT STD_LOGIC);END SREG;ARCHITECTURE ART1 OF SREG ISSIGNAL REG:STD_LOGIC_VECTOR(3 DOWNTO 0); BEGINPROCESS(CLK,LOAD)BEGINIF CLK'EVENT AND CLK='1'THENIF LOAD='1'THEN REG<=DIN;ELSEREG(2 DOWNTO 0)<=REG(3 DOWNTO 1);END IF;END IF;END PROCESS;QB<=REG(0);END ART1;2、4位加法器ADDERLIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL; ENTITY ADDER ISPORT(CIN:IN STD_LOGIC_VECTOR;B,A:IN STD_LOGIC_VECTOR(3 DOWNTO 0);S: OUT STD_LOGIC_VECTOR(4 DOWNTO 0);COUNT:OUT STD_LOGIC_VECTOR);END ADDER;ARCHITECTURE ART2 OF ADDER ISBEGINS<='0'&A+B;END ART2;3、选通与门模块ANDARITHLIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY ANDARITH ISPORT(ABIN:IN STD_LOGIC;DIN: IN STD_LOGIC_VECTOR(3 DOWNTO 0);DOUT:OUT STD_LOGIC_VECTOR(3 DOWNTO 0)); END ANDARITH;ARCHITECTURE ART3 OF ANDARITH ISBEGINPROCESS(ABIN,DIN)BEGINFOR I IN 0 TO 3 LOOPDOUT(I)<=DIN(I) AND ABIN;END LOOP;END PROCESS;END ART3;4、锁存器REGLIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY REG ISPORT(CLK,CLR,EN:IN STD_LOGIC;D: IN STD_LOGIC_VECTOR(4 DOWNTO 0);Q: OUT STD_LOGIC_VECTOR(7 DOWNTO 0)); END REG;ARCHITECTURE ART4 OF REG ISSIGNAL R8S:STD_LOGIC_VECTOR(7 DOWNTO 0);BEGINPROCESS(CLK,CLR)BEGINIF CLR='1'THEN R8S<=(OTHERS=>'0');ELSIF CLK'EVENT AND CLK='1'THENR8S(2 DOWNTO 0)<=R8S(3 DOWNTO 1);R8S(7 DOWNTO 3)<=D;END IF;END PROCESS;Q<=R8S;Q1<=R8S(7 DOWNTO 4);Q2<=R8S(3 DOWNTO 0);END ART4;5、运算控制器ARICTLLIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL; ENTITY ARICTL ISPORT(CLK: IN STD_LOGIC;START: IN STD_LOGIC;CLKOUT: OUT STD_LOGIC;RSTALL: OUT STD_LOGIC;ARIEND: OUT STD_LOGIC);END ENTITY ARICTL;ARCHITECTURE ART5 OF ARICTL ISSIGNAL CNT:STD_LOGIC_VECTOR(3 DOWNTO 0); BEGINRSTALL<=START;PROCESS(CLK,START) ISBEGINIF START='1'THEN CNT<="0000";ELSIF CLK'EVENT AND CLK='1'THENIF CNT<4 THENCNT<=CNT+1;END IF;END IF;END PROCESS;PROCESS(CLK,CNT,START) ISBEGINIF START='0'THENIF CNT<4 THENCLKOUT<=CLK;ARIEND<='0';ELSE CLKOUT<='0';ARIEND<='1';END IF;ELSE CLKOUT<=CLK;ARIEND<='0';END IF;END PROCESS;END ARCHITECTURE ART5;6、顶层原理图。

十六位硬件乘法器一、摘要1、设计要求：位宽十六，输入2个两位十进制相乘，能在数码管上显示积的信息！2、原理说明：十六位硬件乘法器可以分解为由2个8位2进制相乘得到，但要求输入十进制，故可用8421BCD码将2位十进制译成8位2进制即可，本次课设使用的是移位相加法来实现乘法！3、开发板使用说明：sw1到sw8开关是数据输入按键，即一次可同时输入八位数据，对于运算y=a*b,由于加入了辅助程序，总共要输入2次，每次输入的数据分别代表a转换为2进制的八位数，b转换成2进制的八位数，。

每按一次按键s3，即输入当前所设定的八位数据一次，,在数据输入完成后，按s2，进行运算，并由数码管输出用十进制表示的结果。

二、正文1、系统设计方案提出由于是2位的十进制，输入的数据不是很大，转换为二进制也是8位，故想到使用移位相加的方法来实现乘法的功能，同时移位相加是最节省资源的一种方法，其思路是乘法通过逐项移位相加来实现，根据乘数的每一位是否为1，若为1将被乘数移位相加，比较简单，适合本次课程设计。

2，电路划分，电路主要由3部分组成，第一部分是将输入的十进制译成2进制，第二部分是乘法器部分，第三部分是将得到的16位二进制结果译为十进制！第一部分LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY chengshu ISPORT (a: IN STD_LOGIC_VECTOR(3 DOWNTO 0);cq : OUT STD_LOGIC_VECTOR(7 DOWNTO 0) );END chengshu;ARCHITECTURE behav OF chengshu ISBEGINprocess(a)begincase a iswhen "0000" => cq<="00000000";when "0001" => cq<="00001010";when "0010" => cq<="00010100";when "0011" => cq<="00011110";when "0100" => cq<="00101000";when "0101" => cq<="00110010";when "0110" => cq<="00111100";when "0111" => cq<="01000110";when "1000" => cq<="01010000";when "1001" => cq<="01011010";when others =>null;end case ;end process;end ARCHITECTURE behav;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity add8 isport(a:in std_logic_vector(7 downto 0);b:in std_logic_vector(3 downto 0);qout:out std_logic_vector(7 downto 0));end add8;architecture ab of add8 issignal tmp1,tmp2,tmp:std_logic_vector(8 downto 0); begintmp1<='0'&a;tmp2<="00000"&b;tmp<=tmp1+tmp2;qout<=tmp(7 downto 0);end ab;第二部分：library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity cheng isport ( start : in std_logic;a : in std_logic_vector(7 downto 0);b : in std_logic_vector(7 downto 0);y : out std_logic_vector(15 downto 0)); end cheng;architecture behav of cheng issignal ql : std_logic_vector(7 downto 0);signal qz : std_logic_vector(7 downto 0);signal qy : std_logic_vector(15 downto 0);beginprocess(a,ql,qz,qy,b,start)variable q0 : std_logic_vector(15 downto 0); variable q1 : std_logic_vector(15 downto 0); variable q2 : std_logic_vector(15 downto 0); variable q3 : std_logic_vector(15 downto 0); variable q4 : std_logic_vector(15 downto 0); variable q5 : std_logic_vector(15 downto 0); variable q6 : std_logic_vector(15 downto 0); variable q7 : std_logic_vector(15 downto 0); variable q8 : std_logic_vector(15 downto 0); beginql<=a;qz<=b;q8:="0000000000000000";q7:="00000000"&ql;q0:="00000000"&ql;q7:=q7+q7;q1:=q7;q7:=q7+q7;q2:=q7;q7:=q7+q7;q3:=q7;q7:=q7+q7;q4:=q7;q7:=q7+q7;q5:=q7;q7:=q7+q7;q6:=q7;q7:=q7+q7;if start='1' thenif qz(0)='1' then q8:=q8+q0;end if;if qz(1)='1' then q8:=q8+q1;end if;if qz(2)='1' then q8:=q8+q2;end if;if qz(3)='1' then q8:=q8+q3;end if;if qz(4)='1' then q8:=q8+q4;end if;if qz(5)='1' then q8:=q8+q5;end if;if qz(6)='1' then q8:=q8+q6;end if;if qz(7)='1' then q8:=q8+q7;end if;end if;qy<=q8;end process;y<=qy;end behav;第三部分IBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian ISBEGINprocess(a)beginif a>8999 then cnt<=a-9000;qout<="1001";elsif a>7999 then cnt<=a-8000;qout<="1000";elsif a>6999 then cnt<=a-7000;qout<="0111";elsif a>5999 then cnt<=a-6000;qout<="0110";elsif a>4999 then cnt<=a-5000;qout<="0101";elsif a>3999 then cnt<=a-4000;qout<="0100";elsif a>2999 then cnt<=a-3000;qout<="0011";elsif a>1999 then cnt<=a-2000;qout<="0010";elsif a>999 then cnt<=a-1000;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian1 ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian1 ISBEGINprocess(a)beginif a>899 then cnt<=a-900;qout<="1001";elsif a>799 then cnt<=a-800;qout<="1000";elsif a>699 then cnt<=a-700;qout<="0111";elsif a>599 then cnt<=a-600;qout<="0110";elsif a>499 then cnt<=a-500;qout<="0101";elsif a>399 then cnt<=a-400;qout<="0100";elsif a>299 then cnt<=a-300;qout<="0011";elsif a>199 then cnt<=a-200;qout<="0010";elsif a>99 then cnt<=a-100;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian2 ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian2 ISBEGINprocess(a)beginif a>89 then cnt<=a-90;qout<="1001";elsif a>79 then cnt<=a-80;qout<="1000";elsif a>69 then cnt<=a-70;qout<="0111";elsif a>59 then cnt<=a-60;qout<="0110";elsif a>49 then cnt<=a-50;qout<="0101";elsif a>39 then cnt<=a-40;qout<="0100";elsif a>29 then cnt<=a-30;qout<="0011";elsif a>19 then cnt<=a-20;qout<="0010";elsif a>9 then cnt<=a-10;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;但是由于2个8位2进制在开发板上不好输入和最后的16位不好译成十进制，故加入几段辅助程序减少其输入次数！library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity test_in isport(test_in: in std_logic_vector(7 downto 0);test_out_ah: out std_logic_vector(3 downto 0);test_out_al: out std_logic_vector(3 downto 0);test_out_bh: out std_logic_vector(3 downto 0);test_out_bl: out std_logic_vector(3 downto 0);clk: in std_logic;led: out std_logic);end entity;architecture one of test_in issignal test_temp: std_logic_vector(7 downto 0);signal cnt: std_logic;begin--process(clk)--begin--if(clk'event and clk='1')then--led<='1';--else--led<='0';--end if;--end process;process(clk)beginif(clk'event and clk='0')thencnt<=not cnt;test_temp<=test_in;end if;end process;process(cnt)begin--if(clk'event and clk='0')thenif(cnt='1')thentest_out_ah<=test_temp(7 downto 4);test_out_al<=test_temp(3 downto 0);elsetest_out_bh<=test_temp(7 downto 4);test_out_bl<=test_temp(3 downto 0);end if;--end if;end process;end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity de_shake isport(key_in: in std_logic;key_out: out std_logic;clk_1_2hz: in std_logic);end entity;architecture one of de_shake issignal a,b,c: std_logic;beginprocess(clk_1_2hz)variable key_out_temp: std_logic;beginif(clk_1_2hz'event and clk_1_2hz='1')thena<= key_in;b<=a;c<=b;key_out_temp:=(a and b and c );end if;key_out<=key_out_temp;end process;end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity fre_deshake isport(clk_50m: in std_logic;clk_deshake: out std_logic;clk_50: out std_logic);end entity;architecture one of fre_deshake issignal clk_temp: std_logic_vector(20 downto 0); beginclk_50<=clk_50m;process(clk_50m)beginif(clk_50m'event and clk_50m='1')thenclk_temp<=clk_temp+1;end if;end process;clk_deshake<=clk_temp(20);--clk_deshake(1)<=clk_temp(20);end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity decode isport(clk_50M: in std_logic;input4: in std_logic_vector(3 downto 0);input3: in std_logic_vector(3 downto 0);input2: in std_logic_vector(3 downto 0);input1: in std_logic_vector(3 downto 0);output: out std_logic_vector(7 downto 0);address: out std_logic_vector(7 downto 0));end entity;architecture one of decode issignal div_clk: std_logic_vector(18 downto 0);signal mode: std_logic_vector(7 downto 0);signal data: std_logic_vector(3 downto 0);begindivclk:process(clk_50M)beginif(clk_50M'event and clk_50M='1')thendiv_clk<=div_clk+1;end if;end process;de_code_01: process(clk_50M,div_clk(18 downto 16))beginif(clk_50M'event and clk_50M='1')thencase div_clk(18 downto 16) iswhen "000"=>mode<="01111111";when "001"=>mode<="10111111";when "010"=>mode<="11011111";when "011"=>mode<="11101111";--when "100"=>--mode<="11110111";--when "101"=>--mode<="11111011";--when "110"=>--mode<="11111101";--when "111"=>--mode<="11111110";when others=>mode<="11111111";end case;end if;end process;de_code_02: process(mode)beginaddress <= mode;case mode iswhen "01111111"=>data<=input4;when "10111111"=>data<=input3;when "11011111"=>data<=input2;when "11101111"=>data<=input1;--when "11110111"=>--data<=input(15 downto 12);--when "11111011"=>--data<=input(11 downto 8);--when "11111101" =>--data<=input(7 downto 4);--when "11111110"=>--data<=input(3 downto 0);when others=>null;end case;end process;decode_03: process(data)begincase data iswhen "0000"=>output<="11000000";when "0001"=>output<="11111001";when"0010"=>output<="10100100";when"0011"=>output<="10110000";when"0100"=>output<="10011001";when"0101"=>output<="10010010";when"0110"=>output<="10000010";when"0111"=>output<="11111000";when"1000"=>output<="10000000";when"1001"=>output<="10010000";--when"1010"=>--output<="10001000";--when"1011"=>--output<="10000011";--when"1100"=>--output<="11000110";--when"1101"=>--output<="10100011";--when"1110"=>--output<="10000110";when others=>output<="10001110";end case;end process;end architecture;第二种方案（无硬件测试）library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity mult16_16 isport(clk: in std_logic;start: in std_logic;ina: in std_logic_vector(15 downto 0);inb: in std_logic_vector(15 downto 0);sout: out std_logic_vector(31 downto 0));end entity;architecture one of mult16_16 issignal cout1: std_logic_vector(19 downto 0);signal cout2: std_logic_vector(23 downto 0);signal cout3: std_logic_vector(27 downto 0);signal cout4: std_logic_vector(31 downto 0);signal a4b1: std_logic_vector(19 downto 0);signal a3b1: std_logic_vector(19 downto 0);signal a2b1: std_logic_vector(19 downto 0);signal a1b1: std_logic_vector(19 downto 0);signal a4b2: std_logic_vector(23 downto 0);signal a3b2: std_logic_vector(23 downto 0);signal a2b2: std_logic_vector(23 downto 0);signal a1b2: std_logic_vector(23 downto 0);signal a4b3: std_logic_vector(27 downto 0);signal a3b3: std_logic_vector(27 downto 0);signal a2b3: std_logic_vector(27 downto 0);signal a1b3: std_logic_vector(27 downto 0);signal a4b4: std_logic_vector(31 downto 0);signal a3b4: std_logic_vector(31 downto 0);signal a2b4: std_logic_vector(31 downto 0);signal a1b4: std_logic_vector(31 downto 0);beginprocess(clk)beginif(clk'event and clk='1')thena4b1<=((ina(15 downto 12)*inb(3 downto 0))&"000000000000");a3b1<=("0000"&(ina(11 downto 8)*inb(3 downto 0))&"00000000");a2b1<=("00000000"&(ina(7 downto 4)*inb(3 downto 0))&"0000");a1b1<=("000000000000"&(ina(3 downto 0)*inb(3 downto 0)));a4b2<=((ina(15 downto 12)*inb(7 downto 4))&"0000000000000000");a3b2<=("0000"&(ina(11 downto 8)*inb(7 downto 4))&"000000000000");a2b2<=("00000000"&(ina(7 downto 4)*inb(7 downto 4))&"00000000");a1b2<=("000000000000"&(ina(3 downto 0)*inb(7 downto 4))&"0000");a4b3<=((ina(15 downto 12)*inb(11 downto 8))&"00000000000000000000");a3b3<=("0000"&(ina(11 downto 8)*inb(11 downto 8))&"0000000000000000");a2b3<=("00000000"&(ina(7 downto 4)*inb(11 downto8))&"000000000000");a1b3<=("000000000000"&(ina(3 downto 0)*inb(11 downto 8))&"00000000");a4b4<=((ina(15 downto 12)*inb(15 downto 12))&"000000000000000000000000");a3b4<=("0000"&(ina(11 downto 8)*inb(15 downto 12))&"00000000000000000000");a2b4<=("00000000"&(ina(7 downto 4)*inb(15 downto 12))&"0000000000000000");a1b4<=("000000000000"&(ina(3 downto 0)*inb(15 downto 12))&"000000000000");end if;end process;process(clk)beginif(clk'event and clk='1')thencout1<=a4b1+a3b1+a2b1+a1b1;cout2<=a4b2+a3b2+a2b2+a1b2;cout3<=a4b3+a3b3+a2b3+a1b3;cout4<=a4b4+a3b4+a2b4+a1b4;end if;end process;process(clk,start)beginif(start='1')thensout<="00000000000000000000000000000000";elsesout<=("000000000000"&cout1)+("00000000"&cout2)+("0000"&cout3)+cout4;end if;end process;end architecture;仿真结果三，参考文献资料，EDA技术和VHDL，和同学一起讨论！四，仿真结果，随便输入几个数字后，进行仿真，结果正确，但只能用16进制看结果，因为是译成8421BCD码，是一位十进制数对应4位2进制，最终的结果范围是0~9801，需要16位2进制来对应！五，硬件测试在硬件上进行测试，结果正确！六，实验总结这次课设让我学会了很多东西，刚开始的时候对很多东西不是很理解，后来请教同学，查资料，虽然有些的程序不是自己写的，但跟同学讨论，请教，大概也懂得的那些程序是干什么用的，在最后测试的时候，在仿真阶段，刚开始一直仿真不对，以为是程序错误，但检验后程序并没有错误，由于是8421BCD码故应该用十六进制进行仿真。

乘法器原理乘法器原理是计算机科学中非常重要的原理，它是实现计算机高效计算的基础。

本文将详细介绍乘法器原理的相关知识，包括乘法器的基本概念、实现原理、应用场景等方面。

一、乘法器的基本概念乘法器是一种用于计算两个数的乘积的计算机硬件。

它是计算机中最常用的算术电路之一，可以用来进行乘法运算，是实现计算机高效计算的关键组件之一。

乘法器通常由多个门电路组成，其中最常用的是AND门、OR门和XOR门。

它的输入是两个二进制数，输出是它们的乘积。

乘法器的输出通常是一个二进制数，它的位数等于输入的两个二进制数的位数之和。

乘法器的输出可以通过一系列的加法器进行加法运算，从而得到最终的结果。

乘法器的性能取决于它的位宽、延迟和功耗等因素。

在实际应用中，乘法器的位宽通常是32位或64位，延迟时间通常在几个时钟周期内，功耗通常在几个瓦特以下。

二、乘法器的实现原理乘法器的实现原理可以分为两种，即基于布斯算法的乘法器和基于蒙哥马利算法的乘法器。

1、布斯算法乘法器布斯算法乘法器是一种基于移位和加法的乘法器。

它通过将一个数分解成多个部分，然后逐位进行计算，最后将它们相加得到最终结果。

布斯算法乘法器的核心是部分积的计算，它可以通过移位和相加操作来实现。

例如，假设要计算两个8位二进制数A和B的乘积，可以将A和B分别分解成4位二进制数A1、A0和B1、B0，然后按照如下方式计算部分积：P1 = A1 × B0P2 = A0 × B1P3 = A0 × B0P4 = A1 × B1最终的结果可以通过将这些部分积相加得到：P = P1 × 2^8 + P2 × 2^4 + P3 + P4 × 2^12布斯算法乘法器的主要优点是简单、易于实现，但它的缺点是速度较慢，需要多次移位和加法操作。

2、蒙哥马利算法乘法器蒙哥马利算法乘法器是一种基于模重复平方和模乘的算法。

它利用模运算的性质，将乘法转化为模运算和加法运算，从而减少了乘法器的复杂度和延迟时间。

mcu硬件乘除法
MCU（微控制器单元）的硬件乘除法指的是在微控制器中使用硬件电路来实现乘法和除法运算。

由于微控制器的处理能力有限，采用硬件乘除法可以提高运算速度和效率。

硬件乘法通常使用乘法器电路来实现。

乘法器电路可以将两个数相乘得到结果，并且在较短的时间内完成计算。

一些高性能的MCU甚至配备有专门的硬件乘法器单元，使得乘法运算更加高效。

硬件除法则是通过使用除法器电路实现的。

除法器电路能够将被除数与除数进行相除，并得到商和余数。

然而，硬件除法器通常较复杂，且在一些低端MCU中可能没有该功能，因此除法运算可能需要通过软件算法来实现。

需要注意的是，硬件乘除法的可用性和效率会根据不同的微控制器型号和硬件配置而有所不同。

在选择MCU时，需要根据具体的应用需求和算术运算的要求来确定是否需要硬件乘除法功能。

什么是硬件乘法器导读：我根据大家的需要整理了一份关于《什么是硬件乘法器》的内容，具体内容：硬件乘法器你听过吗?哈哈，我也是最近才听过这个词的。

下面将由我带大家一起来学习学习下吧，希望对大家有所收获!硬件乘法器，其基础就是加法器结构，它已经是现代计算机中必不...硬件乘法器你听过吗?哈哈，我也是最近才听过这个词的。

下面将由我带大家一起来学习学习下吧，希望对大家有所收获!硬件乘法器，其基础就是加法器结构，它已经是现代计算机中必不可少的一部分。

[1] 乘法器的模型就是基于"移位和相加"的算法。

在该算法中，乘法器中每一个比特位都会产生一个局部乘积。

第一个局部乘积由乘法器的LSB产生，第二个乘积由乘法器的第二位产生，以此类推。

如果相应的乘数比特位是1，那么局部乘积就是被乘数的值，如果相应的乘数比特位是0，那么局部乘积全为0。

每次局部乘积都向左移动一位。

乘法器可以用更普遍的方式来表示。

每个输入，局部乘积数，以及结果都被赋予了一个逻辑名称(如A1、A2、B1、B2)，而这些名称在电路原理图中就作为了信号名称。

在原理图的乘法例子中比较信号名称，就可以找到乘法电路的行为特性。

在乘法器电路中，乘数中的每一位都要和被乘数的每一位相与，并产生其相应的乘积位。

这些局部乘积要馈入到全加器的阵列中(合适的时候也可以用半加器)，同时加法器向左移位并表示出乘法结果。

最后得到的乘积项在CLA电路中相加。

注意，某些全加器电路会将信号带入到进位输入端(用于替代邻近位的进位)。

这就是一种全加器电路的应用;全加器将其输入端的任何三个比特相加。

随着乘数和被乘数位数的增加，乘法器电路中的加法器位树也要相应的增加。

通过研究CLA电路的特性，也可以在乘法器中开发出更快的加法阵列。

DSP中的专用硬件乘法器在DSPs中具有硬件连线逻辑的高速"与或"运算器(乘法器和累加器)，取两个操作数到乘法器中进行乘法运算，并将乘积累加到累加器中，这些操作都可以在单个周期内完成。