曲面体投影及曲面体上的点和线83页PPT

可见，则点A必在后半个圆柱面
上；A点在左半个圆柱面上，故a”
可见。
a
§4-1 曲面立体及表面上点的三视图
作图：
(1)过(a’ )作投影线，找到直
线与圆周的交点;
(2)根据投影规律求出a”。
三、回转体及其表面上的点和线
1、圆柱体
例2 已知圆柱面上线段的水平投影，求其余两面投影。
d' c' f'
a'
(b')
(3)在sm和s”m”上求得a和a”。
§4-1 曲面立体及表面上点的三视图
三、回转体及其表面上的点和线
2、圆锥体
锥体作辅助 线方法之二：
平切法
例4 已知圆锥面上的点A的水平投影，求其余两面投影。
s'
s”
分析：
PV m'
a'
A在圆锥面上，则过A必存在圆
(a”)
PW
锥面内的一个纬圆;A在前半个圆锥面 上，则a’ 可见；A点在右半个圆锥面
最后素线投影
X 前后分界线
Y 左右分界线
§4-1 曲面立体及表面上点的三视图
各面投影特点：
(1)圆锥面：一个 圆与两个等腰三角形；
(2)底面：一个圆 与两条直线。
一、曲面立体的三视图
3、圆球体
空间分析：
圆球面平行V面 的圆素线投影
前后分界线
Z
圆球面平行W面 的圆素线投影
三个圆都需要用 细点画线画出对
一、曲面立体的三视图
在工程上，回转体是应用广泛的曲面立体。常见的回转体 包括：
圆柱体
圆锥体
圆球体
圆环体
回转面——由母线绕固定轴线旋转得到的一类曲面 回转体——表面是回转面或回转面和平面的立体

线上，如图4-13(b)所示。因圆柱水平投影具有积聚性，
所以这三点的水平投影一定都在圆上，根据其位置判断
可见性即可，再根据三等关系即可求出侧面投影。
Page 22
单击此处编基辑母本版体标的题样投式影
曲面立体的投影
Page 23
作图步骤如下：点a′为可见点，根据点a′的位置分析，其侧面投影 位于前轮廓线素线上，可过点a′作水平线交前轮廓素线于一点(即a″点)， 根据三等关系可求出水平投影a。同理，c′点位于右轮廓素线上，根据 水平投影的积聚性，从c′点向圆柱水平投影作垂线交于一点即为c点， 根据三等关系可求出点c″的位置，其侧面投影为不可见点，需要用小 括号括起来。b′点位于后左平面上，根据水平投影的积聚性，从b′点向 圆柱水平投影作垂线交于一点即为b点，再根据三等关系可求出点b″的 位置。
单击此处编基辑母本版体标的题样投式影
曲面立体的投影
1.素线法 圆锥面由许多素线组成，圆锥面上任一点必在经过该点的素线 上，因此只要求出过该点素线的投影，即可求出该点的投影。 2.纬圆法 由回转面的形成可知，母线上任一点的运动轨迹为圆，且该圆 垂直于旋转轴线，这样的圆称为纬圆。圆锥体上任一点一定在与其 等高的纬圆上，因此可借助该点的纬圆求出该点的投影。
曲面立体的投影
2.投影分析 （1）俯视图。俯视图为一个圆，其投影的轮廓线是球的 最大水平面①的投影。球被分为上、下两部分，上部分可见， 下部分不可见。 （2）主视图。主视图为一个圆，其投影的轮廓线是球的 最大正平面②的投影。球被分为前、后两部分，前部分可见， 后部分不可见。 （3）左视图。左视图为一个圆，其投影的轮廓线是球的 最大侧平面③的投影。球被分为左、右两部分，左部分可见， 右部分不可见。
Page 29

精品课件
圆柱体的投影 ，如下图所示
精品课件
精品课件
4.2.2 圆锥体的投影
❖ 概念 圆锥是由圆锥面和底面围成。圆锥面是一条直线（ 母线）绕一条与其相交的直线（轴线）回转一周 所形成的曲面。
❖ 圆锥的投影如图4.2所示
精品课件
图4.2 圆锥体的投影
精品课件
精品课件
❖ 圆台轴线与水平投影面垂直。
精品课件
图4.1 正五棱锥的投影 精品课件
精品课件
4.1.3 棱台的投影 ❖ 棱台:用平行于棱锥底面的平面切割棱锥，
底面和截面之间的部分称为棱台。
精品课件
❖现以正四棱台为例进行分析，如下图 所示。
四棱台的投影 精品课件
❖ 平面体的投影，实质上就是其各个侧面的投 影，而各个侧面的投影实际上是用其各个侧 棱投影来表示，侧棱的投影又是其各顶点投 影的连线而成。
❖ 当底面为三角形、四边形、五 边形……时，所组成的棱柱分别 为三棱柱、四棱柱、五棱柱等 。见右图为三棱柱的示意图。
精品课件
现以下图所示正三棱柱为例分析棱柱投影特性
正三棱精品柱课的件 投影
精品课件
4.1.2 棱锥的投影 ❖ 棱锥是由一个多边形平面与多个有公共顶点的三角
形平面所围成的几何体。根据不同形状的底面，棱 锥有三棱锥、四棱锥和五棱锥等。现以正五棱锥为 例来进行分析，如图4.1所示
精品课件
平面体的投影特点
❖ 平面体的投影，实质上就是点、直线和平面投影的集合。 ❖ 投影图中的线条，可能是直线的投影，也可能是平面的积聚投影
。 ❖ 投影图中线段的交点，可能是点的投影，也可能是直线的积聚投
影。 ❖ 当向某投影面作投影时，凡看得见的直线用实线表示，看不见的

机械制图
MECHANICAL DRAWING
目录
CONTENTS
曲面立体的投影
曲面立体的投影
A
B
C
D
3
曲面立体的投影
回转体的侧面是光滑曲面，在向平行于轴线的投影面投射时，其上某条或某几 条素线会把回转面分为两半，是可见面和不可见面的分界线，称其为轮廓素线。
在平行于轴线的投影面上画回转体的投影时，对其回转表面只需画出其轮廓素 线的投影，同时用点画线画出轴线的投影。
9
曲面立体的投影
2 圆锥的投影
2) 圆锥表面上点的投影（辅助线法）
1′
1″
1
10
曲面立体的投影
2 圆锥的投影
2） 圆锥表面上点的投影（辅助圆法）
1′
1″
1
11
曲面立体的投影
3 圆球
1）圆球的投影 球的正面投影是球面上平行V 面的轮廓素线圆的投影。 球的水平投影是球面上平行H 面的轮廓素线圆的投影。 球的侧面投影是球面上平行W 面的轮廓素线圆的投影。
4
曲面立体的投影 1 圆柱的投影
5
圆柱面的水平投影积聚成一个圆。 圆柱正面投影中左、右两轮廓线是圆柱面上 最左、最右轮廓素线的投影。上面与下面两 直线段是圆柱上、下底面的正面投影。 圆柱侧面投影的两侧轮廓线是圆柱面上最前 和最后轮廓素线的投影。
曲面立体的投影 1 圆柱的投影
1). 圆柱的投影图
6
曲面立体的投影
1 圆柱的投影
b′
2). 圆柱表面上点的投影（特殊点）
a′
B A
7
a b
b″ a″
曲面立体的投影
1 圆柱的投影
（d′)
2)圆柱表面上点的投影（一般位置点） c′

1.3 圆台的投影
圆台可看作用平行于圆锥 底面的平面截切锥顶后得到的 形体，两个底面为相互平行的 圆。圆台三视图的作图方法和 步骤同圆锥。图5-13所示为圆 台的三视图。
圆台三面投影图的视图特 征为：两个视图为梯形线框， 第三视图为两个同心圆。

图5-13 圆台的三面投影图
1.4 圆球的投影
圆球由球面组成。圆球的三面投影图是三个全等的圆，其直径为球的 直径。这三个圆是球面上不同位置轮廓素线的投影。如图5-14所示，水平 投影表示球面上平行于水平面的最大轮廓素线圆①的投影，正面投影表示 球面上平行于正面的最大轮廓素线圆②的投影，侧面投影表示球面上平行 于侧面的最大轮廓素线圆③的投影。这些素线圆的其他投影均与相应的中 心线重合，不必画出。
1.2 圆锥的投影
2. 圆锥的作图步骤
圆锥的作图步骤如图5-12（b）所示，具体如下： （1）定中心线、轴线位置。 （2）画水平投影，作反映底面实形的圆。 （3）根据“长对正”和圆锥的高度画正面投影三角形线 框。 （4）根据“宽相等、高平齐”画侧面投影三角形线框。 （5）检查后加深。 圆锥三面投影图的视图特征为：两个视图为三角形线框， 第三视图为圆。
道路工程识图与绘图
道路工程识图与绘图
曲面体的投影
表面全由曲面或由曲面和平面共同围成的 形体为曲面体。常见曲面体有圆柱、圆锥、圆 球等。它们的曲表面均可看作是由一条动线绕 某固定轴线旋转而成的，这类曲面体又称回转 体，其曲表面称为回转面。动线称为母线，母 线在旋转过程中的任一具体位置称为曲面的素 线。曲面上有无数条素线。
曲面体的投影
图5-10所示为回转面的形成过程。图5-10（a）表示一条直 母线围绕与它平行的轴线旋转形成的圆柱面，图5-10（b）表示 一条直母线围绕与它相交的轴线旋转形成的圆锥面，图5-10（c） 表示一曲母线圆围绕其直径旋转而形成的球面。

求曲面体表面上点的投影:先分析这个空间点在曲面体的前、后、左、右、上、下哪半个部 分上，是可见的还是不可见的， 然后再展开找点的投影，方法有辅助素线法，辅助纬圆法，先作 出辅助素线或辅助纬圆的三个投影，再在辅助素线或纬圆上找点的投影。
工程上常见的零件形体多数具有立体被平面切割所形成 的截交线，或两立体相交而形成的相贯线、为了更好地正确、 快捷绘制好汽车零件、部件图; 有必要学习基本几何体的投 影画法，立体表面上点的投影作图、截交线和相贯线的画法。
学习目标
1 项目描述
1
(１)学习基本几何体的投影及立体表面上点、线的投影；
知识
2
13 知 识 准 备
三 圆球
圆球面可看作为由一条圆母线绕其直径回转而成，如常见的蓝球、足球、排球等。 １. 投影分析
圆球的三面投影都是圆，直径与球直径相等，如图 3-16所示。
13 知 识 准 备
三 圆球
主视图的投影是圆，它是圆球面前半部分与后半部分的分界线，而且在俯视图和左视图投 影都为中心线，前半部分可见，后半部分不可见。
如在图Ａ３４-1图1 幅所上示按：补１画∶三１视的图比，例并绘作制出支立架体零表 面件上平点面Ｍ轮、廓Ｎ图形的，另如两图个投１影￣。７ 所示。
图 3-11 补画三视图
2 任务目标
1 能画出曲面体的三面投影视图。 2 能作出曲面体表面上点的投影。
建议学时：2学时。
13 知 识 准 备
一 圆柱
常见的曲面立体是回转体，就是表面有回转曲面的立体。 曲面体常见的有圆柱、圆锥、圆 环和圆球。 曲面立体的投影，实质上是构成该体的所有表面的投影总和。
《汽车机械制图》
1 平面体投影及其表面上点投影作图 基曲面体投影及其表面上点投影作图 2 3 体立体表面交线绘制

【例4-6】 如下图所示，已知圆锥面上一点A的正面投影a′，求a、a″。
解：（1）分析
（2）作图
方法二：纬圆法。 【例4-7】 如下图所示，已知圆锥表面上一点A的投影a′，求a、a″。
解：（1）分析 （2）作图
2．圆锥表面上线的投影 作圆锥面上线段的投影的方法：是求出线段上的端点、轮廓线上的点、分界点 等特殊位置的点及适当数量的一般点，并依次连接各点的同面投影。 【例4-8】 如下图所示，已知圆锥表面上的线段AB的正面投影，求其另两面投影。
曲线 线、抛物线等）。 空间曲线：曲线上各点不在同一个平面内（如圆柱螺旋线等）。
（二）曲面
曲面可以看成是由直线或曲线在空间按一定规律运动而形成。
曲面
直线曲面：由直线运动而形成的曲面称为。 曲线曲面：由曲线运动而形成的曲面称为。
回转体是由一母线（直线或曲线）绕一固定轴线作回转运动形成的，因 此圆柱体、圆锥体、球体和环体都是回转体。
圆柱曲面是一条直线 围绕一条轴线始终保 持平行和等距旋转而 成。
母线
圆锥面是一条直线与轴线交于一点始终保持一定夹角旋转而成的。
母线
球面是由一个圆或圆弧线以直径为轴旋转而成。
（三）素线与轮廓线
形成曲面的母线，它们在曲面上的任何位置称为素线。 我们把确定曲面范围的外形线称为轮廓线（或转向轮廓线），轮廓 线也是可见与不可见的分界线。 当回转体的旋转轴在投影体系中摆放的位置合理时，轮廓线与素线重 合，这种素线称为轮廓素线。 在三面投影体系中，常用的四条轮廓素线分别为：形体最前边素线、 最后边素线、最左边素线和最右边素线。
第三章 曲面立体的投影
在建筑工程中，我们会接触到各种形状的建筑物（如：房屋、水塔） 及其构配件（如：基础、梁、柱等）的形状虽然复杂多样，但经过仔细 分析，不难看出它们一般都是由一些简单的几何体经过叠加、切割、或 相交等形式组合而成。

放置
将圆柱体立放在 三面投影体系中，使 上、下底面平行于 H 面，圆柱面垂直于 H 面。如图5-6a所示。 图5-6 圆柱体投影图的绘制
5.2 曲面体的投影
5.2.2 曲面体投影图的绘制
作图
先作H面投 影图，如图 5-6b 所示。
图5-6
圆柱体投影图的绘制
5.2 曲面体的投影
5.2.2 曲面体投影图的绘制
5.2 曲面体的投影
5.2.3 曲面体表面上的点和线的投影 例5-8 已知圆锥体 表面上点 A 的投影 a′ ， 求 作 点 A 的 其他两面投影。 采用素线法 ，作法如图 5-9 所 示。
图5-9 圆锥体表面上点的投影——素线法
5.2 曲面体的投影
5.2.3 曲面体表面上的点和线的投影 例5-8 采用纬圆法，作法如图5-10所示。
图5-10 圆锥体表面上点的投影——纬圆法
5.2.2 曲面体投影图的绘制 绘制曲面体的投影时，不但要作出曲面边 界线的投影，还要作出轮廓素线的投影。 轮廓素线就是曲面向某一方向投射时，其 可见部分与不可见部分的分界线。 对于不同方向的投影，曲面上的轮廓素线 是不同的。
5.2 曲面体的投影
5.2.2 曲面体投影图的绘制 例5-5 绘制圆柱体的投影图
圆柱体投影图的绘制
5.2 曲面体的投影
5.2.2 曲面体投影图的绘制 例5-6 绘制圆锥体的投影图
作图
作法如图5-7所示。
图5-7 圆锥体投影图的绘制
5.2 曲面体的投影
5.2.2 曲面体投影图的绘制
图5-7 圆锥体投影图的绘制
返回
5.2 曲面体的投影
5.2.3 曲面体表面上的点和线的投影 曲面体表面上点的投影作法：
中等职业教育德育课程国家规划新教材

1)、 圆球的投影
三个视图均为与圆球的直径相等的圆，它 们分别是圆球三个方向轮廓素线的投影。
2）圆球的投影特点
圆球的轮廓线的投影
3）圆球可见性的判别
4） 圆球表面上取点—维圆法
圆的半径？
例： 圆球面上特殊点的求法
a
( c )
b
(b)
a
c
(c) a
b
A为一般点； B、C为特殊点。
由两个底面 和六个侧棱面组
成。侧棱面与侧
棱面的交线叫侧
棱线，侧棱线相
互平行。
8
（1）六棱柱的投影视图
---无轴投影图
(2) 棱柱表面上取点
c c
a
( b )
(a) b
点的可见性 判别： 若点所 在的平面的 投影可见， 点的投影也 可见；若平 面的投影积 聚成直线， 点的投影也 可见。
二、平面立体
1 棱柱
2 棱锥
平面立体：是由若干个平面图形所围成的几 何体，如棱柱体、棱锥体等。
棱柱体
棱锥体
平面立体侧表面的交线称为棱线 若平面立体所有棱线互相平行，称为棱柱 若平面立体所有棱线交于一点，称为棱锥
平面立体的投影 是平面立体各表面投影的集合 ----由直线段组成的封闭图形。
棱柱
1. 六棱柱
b c a
10
2、三棱柱
(1)三棱柱投影 三棱柱的两 底面为水平面， 在俯视图中反映 实形。 其余三个侧 棱面都是铅垂面， 水平投影积聚， 与三角形的边重 合。
（2）三棱柱表面的点
由于三棱柱的表面都是平面，所以在三棱柱的表面上取 点与在平面上取点的方法相同。 m k m k 点的可见性判别： 若点所在的 平面的投影可见， 点的投影也可见； 若平面的投影积 聚成直线，点的 投影也可见。

返回
1、相贯线的性质
（1） 、一般情况下,相贯线为封闭的空间曲线。 （2）、相贯线是两立体表面的共有线，也是两立 体表面的分界线,相贯线上的点是两立体表面的共 有点。
相贯线
相贯线
相贯线
3、求解相贯线的关键
求出两曲面体表面的共有点，然后依次连线。
4、相贯线上共有点的基本求法
(1)、利用曲面的积聚投影法
截交线上的点是曲面上的素线与截平面的交点。
曲面体截交线的性质： 1、封闭的平面图形（曲、 直线围成）。 2、截交线为立体表面和截平面的共有线。 3、截交线上的点为立体表面和截平面的共有点。
求曲面体的截交线的方法： 找出立体表面和平面上的若干共有点，然后依 次连
线。
二、 平面与 圆柱相交
1 平面与圆柱相交所得截交线形状 2 圆柱截交线的求法 3 圆柱截交线例题
注意:所作的素线一
m``
定要过锥顶
S
(2) 纬圆法
由于母线上任一
点绕轴线旋转轨迹都
是垂直于轴线的圆,
K
图示圆锥轴线为铅垂
线,故过K点的纬圆为
M 水平圆,其水平投影
是圆。
例6-3 已知圆锥面上的折线SABC 的正面投影s`a`b`c`,求其它两面投影。
s`
解题分析
线段SA过锥顶,空间为 直线;线段AB为曲线;线段 BC平行底为一水平圆。如 立体图所示。
a b
(如点E)，求解方
法同点B。
d
e
c
5. 判别可见性，光滑连线。
解题分析
1 基本体及其投 影特性 2 点的位置及投 影特性 3 折线BCD空间 形状及投影特性
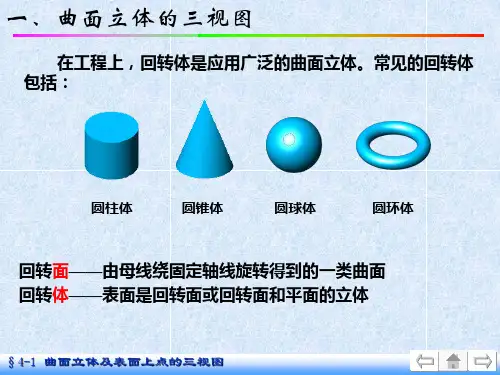
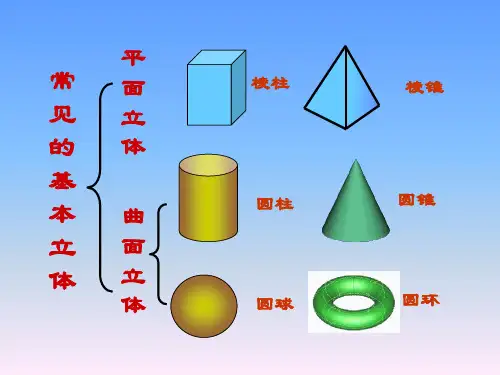
§6-2 平面与曲面立体相交
一 、 概述 二、 平面与 圆柱相交 三、平面与 圆锥相交 四、平面与 圆球相交 五、综合题