钢箱梁正交异性钢桥面板有效计算宽度分析研究

《正交异性钢桥面板焊缝力学行为研究》篇一一、引言随着现代交通建设的快速发展，桥梁工程作为重要的基础设施，其设计和建造技术不断进步。

正交异性钢桥面板因其良好的承载能力和较高的经济效益，在桥梁工程中得到了广泛应用。

然而，正交异性钢桥面板在制造和使用过程中，焊缝的质量对桥面结构的安全性和耐久性至关重要。

因此，本文着重研究正交异性钢桥面板焊缝的力学行为，为桥面结构的优化设计和维护提供理论支持。

二、研究背景及意义正交异性钢桥面板由钢板、加劲肋等组成，通过焊接等工艺连接成整体。

焊缝作为连接构件的纽带，其力学性能直接影响到整个桥面结构的安全性。

焊缝在承受荷载时，可能会出现裂纹、变形等力学行为，影响桥面的正常使用和安全。

因此，研究正交异性钢桥面板焊缝的力学行为，对于提高桥面结构的安全性和耐久性具有重要意义。

三、焊缝力学行为研究方法本文采用理论分析、数值模拟和试验研究相结合的方法，对正交异性钢桥面板焊缝的力学行为进行研究。

1. 理论分析：通过分析焊缝的构造特点、材料性能和受力状态，建立焊缝的力学模型，为后续的数值模拟和试验研究提供理论依据。

2. 数值模拟：利用有限元软件，对焊缝进行三维建模和网格划分，模拟焊缝在荷载作用下的应力、应变等力学行为，为试验研究提供参考。

3. 试验研究：通过制作正交异性钢桥面板试件，进行静载、动载等试验，观测焊缝的力学行为，验证理论分析和数值模拟结果的正确性。

四、焊缝力学行为分析1. 应力分布：焊缝在承受荷载时，会出现应力集中现象。

通过理论分析、数值模拟和试验研究，发现焊缝的应力分布与荷载大小、加载方式、焊缝类型等因素密切相关。

在设计和使用过程中，需根据实际情况合理布置焊缝，减小应力集中现象。

2. 变形行为：焊缝在承受荷载时，会发生弹性变形和塑性变形。

弹性变形在荷载消除后能恢复原状，而塑性变形则会导致桥面结构的永久性变形。

通过研究发现，通过优化焊缝结构和提高焊接质量，可以减小焊缝的变形行为。

《正交异性钢桥面板焊缝力学行为研究》篇一一、引言正交异性钢桥面板作为现代桥梁工程中的一种重要结构形式，其焊缝的力学行为研究对于保障桥梁的安全性和耐久性具有重要意义。

焊缝作为桥梁结构中的关键连接部分，其力学性能的优劣直接影响到整个桥梁的承载能力和使用寿命。

因此，对正交异性钢桥面板焊缝的力学行为进行研究，有助于提高桥梁工程的设计和施工水平，保障桥梁的安全运营。

二、焊缝力学行为的基本理论正交异性钢桥面板的焊缝力学行为涉及多个方面，包括焊缝的应力分布、变形行为、疲劳性能等。

首先，焊缝的应力分布是评估焊缝力学性能的重要指标，它受到焊接工艺、材料性能、荷载条件等多种因素的影响。

其次，焊缝的变形行为也是研究的重要方面，包括弹性变形和塑性变形等。

此外，焊缝的疲劳性能也是研究的重点，因为桥梁在长期使用过程中会受到反复的荷载作用，焊缝的疲劳性能直接影响到桥梁的使用寿命。

三、正交异性钢桥面板焊缝的类型与特点正交异性钢桥面板的焊缝主要包括角焊缝、斜焊缝和对接焊缝等类型。

不同类型的焊缝具有不同的力学特性，如角焊缝具有较高的抗拉强度和抗剪强度，但容易产生应力集中；斜焊缝则具有较好的抗弯性能和抗疲劳性能。

此外，正交异性钢桥面板的焊缝还具有复杂性、多样性和隐蔽性等特点，这增加了研究的难度。

四、正交异性钢桥面板焊缝的力学行为研究方法针对正交异性钢桥面板焊缝的力学行为研究，可以采用多种方法。

首先，可以通过理论分析方法，建立焊缝的力学模型，分析焊缝的应力分布和变形行为。

其次，可以采用数值模拟方法，利用有限元软件对焊缝进行模拟分析，以获得更准确的力学性能数据。

此外，还可以通过实验方法，对实际桥梁的焊缝进行测试和分析，以验证理论分析和数值模拟结果的准确性。

五、实验研究与结果分析为了深入了解正交异性钢桥面板焊缝的力学行为，我们进行了一系列的实验研究。

首先，我们制作了不同类型和尺寸的焊缝试件，并对其进行加载测试。

通过实验数据我们发现，焊缝的应力分布和变形行为受到多种因素的影响，如焊接工艺、材料性能、荷载条件等。

钢桁梁悬索桥正交异性钢桥面板受力分析摘要：本文对我国西南某山区大跨径钢桁梁悬索桥的正交异性钢桥面板进行了有限元仿真分析。

分析表明，目前主流的正交异性钢桥面板的构造和尺寸在车辆荷载的作用下能够满足强度和刚度的需求。

但对桥面铺装而言，尚可适当增加桥面系的刚度，以减小其在车辆荷载作用下的变形，从而提高的桥面铺装的耐久性。

本文的研究对今后类似桥面系的设计和改进有一定的参考意义。

关键字：悬索桥；钢桁梁；正交异性钢桥面板；车辆荷载引言随着桥梁跨径的增大，桥梁结构自身的重量（恒载）在结构承担的荷载中所占比重显著增大。

大跨径悬索桥的设计中，在保证安全、适用和耐久的前提下，减轻结构自重成为最为重要的工作之一。

悬索桥中，主梁及其桥面系贡献了相当大一部分的结构自重，桥梁工程师们因此致力于减小主梁及其桥面系的重量。

在目前的建设条件下，采用钢加劲梁是减小结构自重最有效的方法。

而桥面结构的自重往往在钢桥的总设计恒载中占有很大的比重，减轻桥面结构重量对于减轻钢桥恒载、提高跨越能力和经济效益有很大的意义。

在大跨度桥梁中通常采用钢桥面等轻型桥面系结构[1]，其中正交异性钢桥面板是目前受力性能最优、运用最广泛的钢桥面系。

由于正交异性钢桥面板的材料用量较少，其刚度较混凝土桥面系和钢混叠合桥面系更低，其强度、刚度和疲劳问题[2]在设计中必须予以足够的重视。

本文以我国西南地区某山区大跨径悬索桥为工程背景，对架设于钢桁梁上的正交异性钢桥面板进行了力学分析，重点对自重、沥青混凝土铺装和车辆荷载作用下的桥面钢板、纵梁、横隔板、U肋、扁钢等的应力和变形进行了有限元仿真计算分析。

1工程概况本文的研究内容基于实际工程——我国西南地区一座大跨度单跨悬索桥。

该桥主桥为主跨1200m的单跨简支钢桁架加劲梁悬索桥，主缆计算跨径为325m+1200m+205m，矢跨比为1:9.5，主塔采用门式钢筋混凝土结构。

该桥主梁为钢桁加劲梁、正交异性钢桥面板，采用板桁分离式的结构。

限元分析是很方便的∞“］。由简化的空间杆系结构 计算得到的位移可直接作为原结构的位移，对非桥 面系杆件，如斜杆、竖杆和上平联等可直接利用其内 力和截面特性计算应力；而对于桥面系杆件的应力， 由于“剪力滞后”的影响，原结构的桥面系杆件钢桥 面板应力的分布与简化的空间杆系结构的分布有所 不同，必须通过考虑桥面系杆件钢桥面板的有效宽 度的方法，来求原结构中桥面系杆件的最大应力。
３８
万方数据
桥面板有纵、横梁支承方式，也有不设纵梁，而采用 多横梁或密布横梁的支承方式。国内在建的很多高 速铁路钢桁梁桥都将采用正交异性整体钢桥面系， 如武广铁路客运专线新广州站东平水道桥，主桥为 （９９＋２４２＋９９）ｍ三跨连续钢桁（拱）桥，京沪高速铁 路南京大胜关长江大桥，主桥为（１０８＋１９２＋３３６＋ ３３６＋１９２＋１０８）ｍ六跨连续钢桁（拱）桥。
ｈ一１ ４．５（６／ｚ）２］６
ｏ．０２＜∥ｚ＜ｏ．３０
【Ｏ．１５Ｚ
６／ｚ≥０．３０
（１ｂ）
式中：６为主梁腹板间距的一半或悬臂板宽度；Ｚ为
等效跨径（图４）。
卜
主粱腹板巾心线
注：Ｌｉ、Ｌ２、Ｌ３为跨径；ｃＬｌ、ｃＬ２、Ｃｂ、ｃｓｌ、ｃｓ２、ｃＬ为有效宽度；ｆ为等效跨径。
图４ 主梁等效跨径及有效宽度沿桥跨的变化
度。其中Ａ。为主梁腹板间距一半的有效宽度；Ａ：为 侧伸出部分的有效宽度；ｚ为等效跨径，简支梁的ｚ 等于其计算跨度，连续梁：跨度中央部（Ｉ）ｚ— ｏ．８Ｌ。；跨度中央部（Ⅱ）ｚ＝ｏ．６Ｌ２；中间支点Ｌ＝０．２· （Ｌ１＋Ｌｚ）。
■一
图６有效宽度示意
跨度中央部（Ｉ）
跨度中央部（Ⅱ）
’
ｌ一
獭 笏镢‘
ｌ
Ｉ
ｌ
《｝＝［ｊ＆（二二跚士 ｋ。４刍堡出竺№虬丝业纠陋．

《正交异性钢桥面板焊接工艺参数研究》篇一一、引言随着交通运输业的快速发展，钢桥因其优良的力学性能和经济性在桥梁建设中得到广泛应用。

其中，正交异性钢桥面板以其高强度、轻量化和良好的抗疲劳性能等特点，在大型桥梁工程中占据重要地位。

然而，正交异性钢桥面板的制造过程中，焊接工艺是关键环节之一，其焊接质量直接影响到桥梁的安全性和使用寿命。

因此，对正交异性钢桥面板焊接工艺参数进行研究，对于提高桥梁建设质量和安全性具有重要意义。

二、焊接工艺概述正交异性钢桥面板的焊接工艺主要包括焊前准备、焊接过程和焊后处理三个阶段。

焊前准备阶段包括材料选择、焊缝设计、焊接坡口加工等；焊接过程涉及焊接方法、焊接速度、焊接电流等参数的选择；焊后处理则包括焊缝检验、热处理等。

本文重点研究焊接过程中的工艺参数，以优化焊接质量。

三、焊接工艺参数研究1. 焊接方法选择正交异性钢桥面板的焊接方法主要有熔化极气体保护焊、电弧焊等。

在选择焊接方法时，需考虑钢板厚度、材料性能、施工环境等因素。

一般情况下，对于较厚的钢板，采用熔化极气体保护焊；对于较薄的钢板，则可采用电弧焊。

2. 焊接电流与电压焊接电流和电压是影响焊接质量的关键参数。

电流过大或过小都会导致焊缝成形不良，电压过高或过低则会影响电弧的稳定性。

因此，在焊接过程中，需根据钢板厚度、材料性能等因素，合理选择焊接电流和电压。

3. 焊接速度焊接速度直接影响焊缝的冷却速度和热输入量。

焊接速度过快，会导致焊缝未完全熔合，降低焊缝强度；焊接速度过慢，则会导致焊缝过热，产生热裂纹等问题。

因此，在保证焊缝质量的前提下，应选择合适的焊接速度。

4. 坡口角度与间隙坡口角度和间隙的大小直接影响焊缝的成形和质量。

坡口角度过大或过小都会导致焊缝成形不良，间隙过大则会导致焊缝填充不饱满，间隙过小则会增加焊接难度。

因此，在焊前准备阶段，需根据钢板厚度和材料性能等因素，合理设计坡口角度和间隙。

四、实验研究为研究正交异性钢桥面板的焊接工艺参数，我们进行了系列实验。

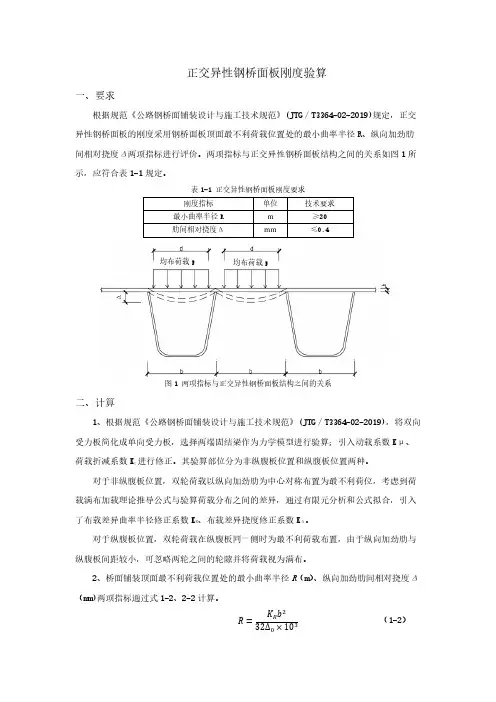
正交异性钢桥面板刚度验算一、要求根据规范《公路钢桥面铺装设计与施工技术规范》(JTG／T3364-02-2019)规定，正交异性钢桥面板的刚度采用钢桥面板顶面最不利荷载位置处的最小曲率半径R、纵向加劲肋间相对挠度Δ两项指标进行评价。

两项指标与正交异性钢桥面板结构之间的关系如图1所示，应符合表1-1规定。

表1-1 正交异性钢桥面板刚度要求刚度指标单位技术要求最小曲率半径R m ≥20肋间相对挠度Δmm ≤0.4图1 两项指标与正交异性钢桥面板结构之间的关系二、计算1、根据规范《公路钢桥面铺装设计与施工技术规范》(JTG／T3364-02-2019)，将双向受力板简化成单向受力板，选择两端固结梁作为力学模型进行验算；引入动载系数Kμ、荷载折减系数K t进行修正。

其验算部位分为非纵腹板位置和纵腹板位置两种。

对于非纵腹板位置，双轮荷载以纵向加劲肋为中心对称布置为最不利荷位，考虑到荷载满布加载理论推导公式与验算荷载分布之间的差异，通过有限元分析和公式拟合，引入了布载差异曲率半径修正系数K R、布载差异挠度修正系数KΔ。

对于纵腹板位置，双轮荷载在纵腹板同一侧时为最不利荷载布置，由于纵向加劲肋与纵腹板间距较小，可忽略两轮之间的轮隙并将荷载视为满布。

2、桥面铺装顶面最不利荷载位置处的最小曲率半径R（m）、纵向加劲肋间相对挠度Δ（mm)两项指标通过式1-2、2-2计算。

R=K R b232Δ0×103（1-2）均布荷载p 均布荷载p ΔΔ=K ΔΔ0式中：K R ——曲率半径布载差异修正系数，验算纵腹板位置时，取K R=1；非纵腹板位置按式(2-3)计算：K R =[1−13(b −d b )3]bdb ——纵向加劲肋板间距（mm ）（当加劲肋为U 型时，加劲肋与顶板的任意一个联结位置视为独立的加劲肋板位置)；Δ0——两端固结梁在均布荷载作用下跨中产生的挠度理论值（mm ）,按下式(2-4)计算：Δ0=k t K μ38412pb 4∑E i ℎi 3i=1,2,3K Δ——挠度布载差异修正系数，验算纵腹板位置时，取 K Δ=1；非纵腹板位置按式（2-5）计算：K Δ=(1.390+p ——验算荷载的接地压力值，标准验算荷载取0.81 MPa ；E i ——钢顶板或铺装材料的弹性模量，i =1、i =2、 i =3 依次对应钢桥面顶板、保护层、磨耗层的弹性模量（MPa ）；ℎi ——钢顶板或铺装材料的弹性模量，i =1、i =2、 i =3 依次对应钢桥面顶板、保护层、磨耗层的厚度（mm ）；k t ——理论计算的荷载折减系数，验算部位紧邻纵腹板时，取 k t =0.7；其他部位取0.5；k μ——动载系数，取1.3；d ——验算荷载单轮横向接地宽度，取200 mm 。

正交异性板和钢箱梁 研究报告
51、没有哪个社会可以制订一部永远 适用的 宪法， 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
谢谢！
51、 天 下 之 事 常成 于困约 ，而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸，生 命是活 动。——卢 梭
53、 伟 大 的 事 业，需 要决心 ，能力 ，组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起

关 键词 ： 箱梁 ； 交异性 桥 面板 地接 头 ； 验 钢 正 工 试
ｌ钢 桥 而扳—地 接头构 造 细节 的演变历 程 Ｆ
１ 钢桥面板的构造细节 对于大跨度悬索桥和斜托桥 ， １ 钢箱梁自重约 为ｌ ｃ箱粱 自最的 １ ～／５ ／ １ ．。正交 异性 钢板结 构 桥面板 的 自垂约 为钢 筋混 ５ ６ 凝土 桥面板 或预制 莉 监 混凝 土桥 面板 白重 的 ｌ 一／。所 以 ， 自最影 响 力 ／ ｌ ２ ３ 受 很 大 的大跨 度桥梁 ， 交异性 板铜箱 粱是 非常有 利 的结 构形 式 制造 时 ， 全 桥分成若 干 段在 工 厂组拼 ， 吊装后 在 桥上进 行 ｉ段 间的 ｒ地连 接 通 常 ７ 所 有 纵 向角焊 缝 （ 向肋 和 纵隔 扳等 ） 纵 贯通 ， 隔板 与 纵 向焊 缝 、 肋 翼 横 纵 缘相交处 切割成弧形缺口与其避开。 ｌ ２正交异性钢桥面板的疲劳及其工地接头构造细节的改进 、 钢桥面 板 作 为主粱 的上翼缘 ， 同时又 直接承 受车辆 的轮 载作用 。￣ｌ ｆ ， 挢 面 ｔＪ 述 钢 ｔ 板 是 Ｅ面板 、 和 横助三 种 薄板件 焊接 而成 ， 焊缝 交义 处 没弧 彤缺 ｕ、 ｈ 纵肋 在 其 构造细 节很 复杂 。当－ Ｎ通过 时 ， ￣ ｔ ｃ 轮载在 各部件 上产 生的腑 ， 在各 以及 部 件交 叉处产 生的 局部应 力 和变 形也非 常复 杂 ， 以钢桥 面板 的疲 劳 问题 所
４、 ．３当在焊 栓 接头 处加 载 时 ， 两个 试 件的 实 例应 力进行 比较 ， ２ 将 就会
发现 ：
ａ 件 Ｉ 助圆弧 缺 口附近 而板 Ｌ０ 试 ｕ形 白瞄向 ｆ力 比试件 Ⅱ大 ， 值较 越 但数 小， 在其 他 测点 ， 试 件而板 上 的实 测横 向应 力基 本上 一致 ， 试 件中心 两个 在 线与 焊栓 接头 中心线 的交点 附近 ，两 个试 件 面扳上 的横 向臆 力者； 大 ． ｌ 较 但 也不超过设 汁容许应力 ．． Ⅱ Ｉ ］ 试件 焊栓接头附近而扳上的纵向』 比试件 ｌ 膏 大 、 其他 测点 ， 试 件 的实测 纵 向应力 基 本 Ｌ 致 试 件 川 形 肋 圆弧 在 两个 一 缺 【附近的应力比试件 Ⅱ大， ｊ 但数值均较小。这表明 弧缺 ［的大小对试 １ 件应力的影响仅限于 ｕ形肋圆弧缺口附近，而目 ｕ形肋圆弧缺口宽度为 ５ ￣ｏ ｍｍ都是 安全 的 。 ｏ １ｏ

１９９７年 ，郑凯锋教授提 出建立 与实现大跨钢桥全桥全壳 单 元 模 型 的方 法 ，同 时分 析指 出 这 一 结 构 分 析 计 算 新 方 法 所 具有 的通用性 … 。１９９９年 ，王应 良等 采用 梯形 纵 向加劲 肋 的钢桥面板第二体系应力计算 的等效 格子梁法 ，推导 了等效 分配梁的刚度 ，编写 了正交异 性板 钢桥 面 的结 构分析 程序 ， 分析 了正交异性板 的第二体 系的应力 Ｊ。为 了分析方便 ，何 畏等将钢桥划分为 以下三个结 构体 系 进 行研 究 ，即 ：在 轴 力作用下 ，桥面板参 与主梁轴 向受力 并通过剪 力引起横 梁面 外弯 曲的第一体系 ；在竖 向荷 载作 用下 ，作 为纵 、横梁 承担弯 矩的上翼缘部 分 的第 二体 系 ；作 为 弹性支 承 的各 向同性 薄 板 ，在纵 、横梁 位 移 下 引 起 薄膜 应 力 的第 三 体 系 。２００４ 年 ，陈玉骥通过下 承式板 桁结 合梁模 型试 验 ，对 主桁 和纵 梁 的挠 度 ，横梁 的竖 向、水平 位移 ，纵 、横梁 、主桁 各 杆 的应力 ， 混凝 土板 上的应力 、裂缝 分布及 宽度 进行 了分 析 ，研 究 了混 凝 土板与 主桁 结 点是 否 直 接 相 连 以及 制 动 撑对 结 构 的 影 响 Ｊ。２００８年 ，韩衍 群等 采用 有 限元法 对该 类 型桥 面结 构 中桥 面荷 载的传递情况进行分析计算 和试 验研究 ，分析 了影 响传力 比（路径传递 的荷 载与一 个节 间总荷载 的 比）的主要 因素 Ｊ。２０１０年 ，张敏 等采用空 间有 限单元法 和模 型试验 ， 研究南京 大胜关长江大桥三 主桁 （拱 ）密布 横梁体 系钢正 交 异性板整 体桥 面结构 的受力行 为 Ｊ。罗如登提 出了正交 异 性整体 钢 桥 面 系 杆 平 面 梁 简 化 计 算 方 法 ，并 给 出 了计 算 参 数 。

０ 前 言
钢桥桥跨结构一般 由主要 承重结构 、 面系 、 桥 联 结系和支座 四部分组成 ，无论 哪种桥 梁体 系都 需 要 有 一 个 直 接 承 受 车 辆 荷 载 的桥 面 系 ，通 过 它 把荷载传人主要承重结构 中去 ，最后通 过支座把 荷 载传 递 给下 部 结构 。 钢 桥 面 板 不 仅 作 为 桥 面 系 直 接 承受 车 轮 荷 载 作用 ， 而且 还 作 为 主 梁 的 一 部 分 与 主梁 共 同受 力 ， 因此其力学行为十分复杂 。正交异性钢 桥面板 以 重量轻 、 省钢材 、 节 承载能力高等优点在世界各 国 桥 梁 尤 其 是 大 跨度 桥 梁 中得 到 广 泛 的应 用 。
横 梁 。 当荷 载作 用 在 横 肋 之 间 时 ， 载 的传 递 途 径 荷 为 ：桥 面 铺 装 盖板 纵 肋 横 肋 一 主梁 腹 板 ； 当 荷 载 直接 作 用 在 横 肋 上 时 ， 载 的传 递 途 径 为 ：桥 荷 面铺 装 一 盖 板 一 横 肋 主梁 腹 板 。 因此 ， 肋 可 以 纵
理论求 出的计算值大得多 ，这个问题 已被实 验证 实 ， 以 ， 钢 桥 面 板 静 力 强 度 计 算 中 ， 三 结 构 所 在 第
系 的应 力 可 以忽 略 不计 。
１ 正 交异性 钢桥 面板 的力 学特性
正 交 异 性 钢 桥 面 板 是 用 纵 横 向互 相 垂 直 的加
成 的结 构 系 组 成 主 梁 的 上 翼 缘 ，是 主梁 的 一 个 组 成 部 分 ， 与 主梁 共 同受 力 ， 构计 算 以 主 梁 为 研 参 结 究 对 象 ，钢 桥 面 板 的 内力 计 算 与 一 般 梁 桥 结 构 的 内力 计 算 相 同。 （ ） 二 结 构 系 （ 面 体 系 ） 由 纵 肋 、 肋 和 ２第 桥 ： 横 顶 板 组 成 的 结 构 系 ， 板 被 看 成 纵肋 、 肋 上 翼 缘 顶 横

论文的第三部分着重对第三体系的计算方法进行研究，结果表明，在正常使用荷载下盖板膜 效应对桥面板受力的影响不大，分析了叠加原理的适用范围及在正常使用荷载下盖板上膜应力及 弯曲应力的分布规律。 关键词：钢桥面板，斜拉桥，钢结构，有限无
镪霸梁正交异性桥面板受力特性及计算方法分析研究
串请同济大学硕士学位论文
ｔｈｉｓ ｓｔｒｕｃｔｕｒｅ ｈａｓ ｂｅｅｎ ａｄｏｐｔｅｄ ｂｙ ｍａｎｙ ｃｏｕｎｔｒｙ．Ｎｏｗ ｉｔ ｉｓ ａ ｕｎｉｖｅｒｓａｌｌｙ ｕｓｅｄ ｂｒｉｄｇｅ ｄｅｃｋ ｓｔｒｕｃｔｕｒｅ ｉｎ
ｌａｒｇｅ ａｎｄ ｍｉｄｄｌｉｎｇ ｓｐａｎ ｓｔｅｅｌ ｂｒｉｄｅ．Ｂｅｃａｕｓｅ Ｏｒｔｈｏｔｒｏｐｉｃ ｓｔｅｅｌ ｄｅｃｋ’。ｓｔｒｅｓｓ ｉｓ ｖｅｒｙ ｃｏｍｐｌｉｃａｔｅｄ，ｎｏｗ
１．２钢桥及钢箱形粱的发展现状
钢桥是一座桥的上部结构的主要承重受力部分是由钢材制成的。二次世界大战后，随着强度 高、韧性好、抗疲劳和耐腐蚀性能好的钢材的出现，以及用焊接平钢板和用角钢、板钢材等加劲 所形成轻而高强的正交异性板桥面的出现，高强度螺栓的应用等，钢桥有很大发展。
钢板梁和箱形钢梁同混凝土相结合的桥型，以及把正交异性板桥面同箱形钢粱相结合的桥型， 在大、中跨径的桥梁上广泛运用。１９５１年联邦德国建成的杜塞尔多夫至诺伊斯桥，是一座正交异 性板桥面箱形梁，跨径２０６米。１９５７年联邦德国建成的杜塞尔多夫北桥，是座６孔７２米钢板梁结台
正交异性钢桥面板的受力分析通常可归结为以下三个基本受力结构体系：作为主粱截面的一 部分承受车辆运营荷载（第一结构体系）；臼纵横向加劲肋组成桥面结构，承受车辆轮轴荷载（第 二结构体系）；支承在纵横加劲肋上的钢盖板直接承受车辆轮载（第三结构体系）。传统的简化计 算方法是把三个结构体系分别加以计算并进行应力叠加。

《正交异性钢桥面板焊接工艺参数研究》篇一一、引言随着现代桥梁建设的不断发展，正交异性钢桥面板因其具有优异的承载能力和良好的施工性能，在桥梁工程中得到了广泛应用。

焊接工艺作为正交异性钢桥面板施工的关键环节，其参数的选择直接影响到桥梁的质量和安全。

因此，对正交异性钢桥面板焊接工艺参数进行研究，对于提高桥梁建设质量和保障交通运营安全具有重要意义。

本文将针对正交异性钢桥面板的焊接工艺参数进行深入研究，分析不同参数对焊接质量的影响，为实际工程提供理论依据和指导。

二、正交异性钢桥面板概述正交异性钢桥面板是一种常用的桥梁结构形式，其由纵横交叉的加劲肋和桥面板板构成，具有较好的承载能力和稳定性。

在施工过程中，需要采用焊接工艺将各部分连接起来，因此焊接工艺参数的选择至关重要。

三、焊接工艺参数研究1. 焊接方法正交异性钢桥面板的焊接方法主要包括熔化极气体保护焊、药芯焊丝电弧焊等。

不同焊接方法具有不同的特点和适用范围，需要根据具体情况选择合适的焊接方法。

2. 焊接电流焊接电流是影响焊接质量的重要因素。

电流过大或过小都会对焊接质量产生不良影响。

适当的焊接电流能够保证焊缝的熔深和熔宽，提高焊缝的强度和韧性。

3. 焊接速度焊接速度是指单位时间内焊缝的移动距离。

焊接速度过快或过慢都会导致焊缝质量下降。

适当的焊接速度能够保证焊缝的均匀性和致密性，提高焊缝的力学性能。

4. 焊接温度焊接温度是影响焊缝成型和性能的重要因素。

过高的焊接温度会导致焊缝过烧、晶粒粗大等问题，而过低的焊接温度则会导致焊缝未熔合、夹渣等缺陷。

因此，需要合理控制焊接温度，以保证焊缝的质量。

四、实验研究为了研究不同焊接工艺参数对正交异性钢桥面板焊接质量的影响，可以进行一系列实验。

通过改变焊接电流、焊接速度和焊接温度等参数，观察焊缝的成型、力学性能和外观质量等指标，分析各参数对焊接质量的影响规律。

五、结果与讨论根据实验结果，可以发现不同焊接工艺参数对正交异性钢桥面板的焊接质量具有显著影响。

正交异性钢桥面板大跨度简支钢桁梁桥设计研究胡步毛【摘要】兰渝铁路新井口嘉陵江双线特大桥位于重庆市井口镇，该桥跨越既有渝怀铁路和襄渝铁路，受线路交角及桥下净空限制而采用128 m下承式简支钢桁梁。

文章主要介绍了主桁结构形式、正交异性钢桥面系结构特点和施工方案；建立了平面简化计算模型和空间整体计算模型，对比分析了主桁杆件的受力情况、结构变形情况和桥面系的受力特点，探讨了正交异性钢桥面板有效宽度的计算方法。

并通过研究，对于整体正交异性钢桥面板的钢桁梁桥，可采用平面模型进行快速计算，其精度可基本满足初步设计要求，进一步考虑正交异性钢桥面板有效宽度后，采用平面计算模型可得到更为准确的结果。

%The new Jialing River Bridge on Lanzhou-Chongqing railway is located in Chongqing Jingkou Town, the bridge spans both the Chongqing-Huaihua railway and Xiangyang-Chongqing railway. Limited by line angle and bridge clear-ance, it uses a 128 m simply-supported steel truss girder bridge. This article describes the main form of truss structure, the structural features of orthotropic steel deck and construction programs;establishes a plane finite element model and a three-dimensional finite element model. It also comparatively analyzes the forces, the structure deformation and mechan-ical characteristics of the orthotropic steel deck, discusses the calculation method of effective width of orthotropic steel deck. For steel truss girder bridge with orthotropic steel deck, the aecuracy of the result calculated with graphic model can basically satisfy the demand in the preliminarydesign. After we take the valid width of steel deck, accurate results can be obtained by using the plane model.【期刊名称】《高速铁路技术》【年(卷),期】2014(000)006【总页数】6页(P75-79,90)【关键词】正交异性钢桥面板;简支钢桁梁桥;计算模型【作者】胡步毛【作者单位】中铁二院工程集团有限责任公司，成都610031【正文语种】中文【中图分类】U442.5+3随着我国铁路事业的发展, 钢桥被广泛应用于铁路建设中，其中下承式简支钢桁梁桥以其跨越能力较大、自重小、建筑高度低等优点，特别适合于线路需要跨越道路及净空受限的地方。

加 了两倍 ，而且可以与面板上的焊接接头共同工 细节都有可靠的工作性能。在满足施工要求的条 １ 、加载方案 尽管该部 件 下，建议Ｕ 我国 公路桥梁设计通用规范》 （Ｔ ０ １ 作 ，从而增加 了焊栓接头部位的刚度 ， Ｊ Ｊ２ — 形肋圆弧缺 口不要过大 ，实际结构 形肋下面开 了 一个施工进手孔，但并不影响 上Ｕ形助圆弧缺口宽度为７ｍｍ。 ８ ）规 定汽 车一 ２ 级荷 载 中５ ０ ９ 超 ０ ５ ｋＮ的重车 位Ｕ ０
日 程术 技
有限元计算结果可以看出，两个试件对应部位的 挠度完全一致 ， 这说明缺 口的大小对试件的刚度 没有影响。 李艳丰 大庆市平通公路工程有限责任公司 ２ 、局部应力 （）实例应力基本上随着荷载的增加而呈 １ ４ｋＮ，后轮着 地面积为宽 长 囊嘲 ｉ大 路钢箱梁 异 魁 ０ 型公 正交 性桥面 后轴重 力为２ １０ 板 线性增加，而且基本上与计算值相吻合。 ６０ ＊０ｍ ０ｍｍ ２０ ｍ。本试验中 加载点的接触面积参 工地接头即箱梁节段之间的连接 ，过去均采用 （）在外加荷载作用下 ，两个试件的大多 ２ 考该规范选定 ， 考虑试件为单肋 ， 故将本试验的 全焊或高强度螺栓连接 。各 国实桥运营经验表 数对称测点的实测应力基本对称 。 明，这两种连接方 式各有不足。所 以，随着施 加载宽度折减为４０ ０ｍｍ，即介于单轮与双轮宽度 （）当在焊拴接头处加载时，将两个试件 ３ 工 技 术 的 不 断进 步 ，钢 桥 面板 工地 接 头构 造 细 之间。试验中以一块宽｛ 厚＝ ２ｍ ｝２０ ｍ 长｝ ４０ ｍ ０ｒ ａ 的实例应力进行比 ，就会发现 ：①试件Ｉ 形助 较 Ｕ 节也 再 演 变。 本 文介 绍 了大 型 公路 钢 箱 梁 正 交 ｌ ｍｍ的钢板模拟桥面铺 装层，以宽 厚 ２ 长 Ｉ 大，但 异性桥 面板工地接 头构造细节的演变，并通过 ４０ ｍ ｝３０ｕ ｝５ｍ 的橡胶块模拟车轮进 圆弧缺口附近面板上的横向应力比试件 Ｉ ０ｍ ０ｎ ｎ ０ｍ 两个试件面板上的实测 两个 足 足 试 件的 静 载和 疲 劳试 验 ， 以及 有 限 元 行加载，试验机为ＭＴ ３０ Ｎ电液伺服试验机， 数值较小 ，在其他测点 ， Ｓ０ｋ 分析 ，证 明正 交异 性桥 面板 ：￣ ．－ 采 用 焊拴 ｒ ｔ头 － ｔ 横向应力基本上一致 ，在试件中心线与焊栓接头 加载频率为３０ ／ ｉ。 ０次 ｍ ｎ 连接 具有 足 够 的刚度 、承 载 力和 耐 久 性 。 中心线的交点附近，两个试件面板上的横向应力 ２ 、测点布置 都较大 ， 但也不超过设汁容许应力；②试件 Ⅱ 焊 薯≤嘲 ≮ 钢 粱正 异 桥 板工 接 箱 交性 面 地 为研究缺 口 附近面板上 的应 力分布情况 ， 头 试验 栓接头附近面板上的纵向应力比试件Ｉ 大，在其他 在缺 口 附近面板上密集布置测点，其中面板焊缝 测点，两个试件的实测纵向应力基本上一致 ；③ 附近的ｌ个测点贴双向应变片测量纵、根双向应 ２ 试件Ｉ 形肋圆弧缺口附近的应力比试件 Ⅱ ， Ｕ 大 但 钢桥面板工地接头构造细节的演变历程 力。除了缺 Ｆ Ｉ 附近布置测点外，在试件跨中及与 数值均较小 。这表明圆弧缺 口 的大小对试件应力 １ 钢桥面板的构造细节 、 试 件焊 栓接 头对称的位置 ，也相应地布置 了测 的影响仅限于Ｕ 形肋圆弧缺 口附近 ，而且Ｕ形肋 对于大跨度悬索桥和斜拉桥 ，钢箱梁 自重 点。 圆弧缺口宽度为５ －１ ｒ 都是安全的。 ０ ０ａ ０ｍ 约为 Ｐ 箱梁 自 Ｃ 重的１５ ／ ．。正交异性钢板 ／ ～１６５ ３ 、静载试验 五， 有限元分析 结构桥面板的 自重约为钢筋混凝土桥面板或预制 两个试件都作静载试验 。静载试验分两种 １ 、计算模型 预应力混凝土桥面板 白重的１ ２ ／ 。所以，受 加载方案 ，一种是在焊栓接头处加载，另一种是 ／ ～１ ３ 计算采用４ 节点板单元，假定焊栓接头处的 自重影响很大的大跨度桥梁 ， 正交异性板铜箱梁 在跨中加载。根据有限元计算，当试件跨中作用 拼接板与Ｕ型助之间不产生滑动，即作为整体共 是非常有利的结构形式。制造时 ，全桥分成若干 １０ Ｎ ４ｋ 的荷载时 ，试件最大应力处 （ 中Ｕ 跨 形肋 同工作 ，不考虑桥面铺装层的影响。 节段在工厂组拼，吊装后在桥上进行节段间的工 下表面 ）的应力达到设计容许应力２０ ａ ０ＭＰ ，试 ２ 、计算结果分析 地连接。通常所有纵向角焊缝 （ 纵向肋和纵隔板 验中考虑到较实际受力情况更不利的状态，将最 （ １ ）在两种轮载作用下，圆弧缺 口处的变 等）贯通，横隔板与纵 向 焊缝 、纵肋下翼缘相交 大静载加到 １５ Ｎ ７ｋ ，为实际轴重力的 ２５ ．倍，使 形。在Ｕ 型肋与面板的连接处 ，Ｕ 型助产生向外 处切割成弧形缺口与其避开。 试件的最大计算应力达到钢材流动极限的７％。 ５ 的面外变形。 ２ 、正交异性钢桥面板的疲劳及其工地接头 加裁等级分四级和五级。 （ ）面板 下表面焊栓 接头线上的纵 向应 ２ 构造细节的改进 ４ 、疲劳试验 力。在两种轮载作用下，试件 Ⅱ 的纵向应力比试 钢桥面板作为主梁的上翼缘 ，同时又直接承 选 取试件 Ｉ 进行疲 劳试验 ，疲劳试验加 载 件Ｉ 的大 ，但应力的数值都较小，在对称轮载作 受车辆的轮载作用。如上所述 ，钢桥面板是由面 位置为焊拴接头处 ，荷载范围４ ～９ｋ Ｏ ０ Ｎ，循环 用下 ，试件Ｉ 和试件 Ⅱ 的纵向应 力最大值分别为 板、纵肋和横助三种薄板件焊接而成 ， 在焊缝交 次数为 ２０ ０万次。根据有限元计算 ， 试件跨中加 １． ａ ２ ． ４６ ＭＰ 和 ０ ５ ａ ＭＰ ，在偏心轮载作用下， 试 ０ Ｎ 形肋下表面的最大应 叉处设弧形缺 １ 其构造细节很复杂。当车辆通 ４ ｋ 荷载时，试件跨 中 Ｕ ３， 件Ｉ 和试件 Ⅱ 的纵向应力最大值分别为２ ． ａ ５６ 和 ＭＰ 过时 ， 轮载在各部件上产生的应力 ， 以及在各部 力与桥梁恒载作用下产生的最大应力相当 ，当加 ３ ．ＭＰ 。除 了 ０９ ａ 在焊栓接头中心线与Ｕ 型肋的交 ０Ｎ 件交叉处产生的局部应力和变形也非常复杂，所 ９ ｋ 荷载时，其最大应力与桥梁恒载、活载共同 线附近有差别外，两个试件纵 向应力分布的规律 故选取以上疲劳试 以钢桥面板的疲劳问题是设计考虑的重点之一。 作用下产生的最大应力相 当， 大体一致。 验加载范围。 改进后的构造细节既克服了工地接头纵 向Ｕ （ ）对称轮载和偏心轮载作用下两个试件 ３ 四．试验结果分析 形肋嵌补段的仰焊对接 ，从而改善了疲劳性能， 面板下表面焊栓接头中心线上的主应力分布。共 １ ． 竖向挠度 又避免 了面板栓接拼接对桥面铺装 层的不利影 同特点是 ，当轮载靠近和离开 圆弧缺 口 ，最大 时 实测各测点在不同荷载等级下的竖向挠度。 响。 主应力基本上相 同，当轮载离开圆弧缺口时，最 可以得出以下结论 ： ＝、 试件设计和制造 小主应力比靠近 圆弧缺 口时稍大 ；当两种轮载正 （ ）各测点的挠度与作用荷载的大小基本 好压在圆弧缺 口 １ 根据 《 美国公路桥梁 设计规 范》 ，用于计 上面时 ，两个试件的最大主应力 ’ 算正交异性钢桥面板刚度和恒载引起的弯曲效应 上呈线性关系。 达到极值，且数值基本上相同。 （ ）实测值与计算值基本接近，表明实测 ２ 时，与纵肋共同作用的钢桥面板的有效宽度取纵 正交异性钢桥面板工地接头中面板采用全熔 肋间距。钢箱梁工地接头处桥面板采用单面焊双 值基本可信。 透对接焊 、ｕ 形肋在两侧肋板采用摩擦型高强度 （ ）在跨中作用荷载时 ，有限元计算结果 螺栓拼接后，通过两个足尺试件的静载和疲劳试 ３ 面成型焊接工艺 ， 面板内侧需贴陶瓷衬垫 ，因此

正交异性钢桥面板构造优化及疲劳性能研究的开题报告一、研究背景和意义钢桥面板在桥梁工程中起着重要的作用，它是承受车辆荷载的重要承载构件。

然而，目前钢桥面板在设计时常常存在构造不合理、疲劳性能不足等问题。

因此，对钢桥面板构造和疲劳性能进行研究，具有重要的现实意义和工程应用价值。

本研究重点探究正交异性钢桥面板的构造优化以及其疲劳性能的提升。

正交异性钢桥面板由于其特殊的构造形式，其承载能力较强，但也存在一些缺陷，如制造工艺要求高，实用性较差等问题。

因此，开展正交异性钢桥面板构造优化和疲劳性能研究，将有助于进一步完善钢桥面板的结构设计及其工程应用。

二、研究内容和目标本研究拟从以下两个方面展开研究：1. 正交异性钢桥面板构造优化研究正交异性钢桥面板是一种新型材料，其独特的结构形式能够使得其承载能力得到优化。

但是当前正交异性钢桥面板在研究和应用过程中还存在一些问题，如制造难度大、材料成本较高等。

因此，需要深入研究正交异性钢桥面板的材料性能，优化其结构设计，使其能够更好地应用于桥梁工程中。

本研究将通过建立正交异性钢桥面板的数学模型，对其进行数据分析，并借助有限元分析软件进行模拟仿真。

通过优化分析，得出正交异性钢桥面板的最优设计方案，并进行实验验证。

2. 正交异性钢桥面板疲劳性能研究钢桥面板在长期使用过程中，常常会受到重复荷载的作用，从而导致疲劳损伤。

因此，对钢桥面板的疲劳性能进行研究，有助于提高其使用寿命和安全性能。

本研究将通过疲劳试验以及数值模拟方法，研究正交异性钢桥面板的疲劳性能，并分析其损伤机理。

同时，将探究不同材料和结构设计对正交异性钢桥面板疲劳性能的影响，为其应用于实际工程提供参考和指导。

三、研究方法和技术路线本研究将采用以下主要方法和技术：1. 数学建模方法：建立正交异性钢桥面板的数学模型，对其进行分析和优化设计。

2. 有限元分析技术：借助有限元分析软件，对正交异性钢桥面板进行模拟仿真。

3. 疲劳试验技术：通过实验室疲劳试验，研究正交异性钢桥面板的疲劳行为，并对其进行损伤分析。

摘要
本次演示对正交异性钢桥面板的疲劳问题进行了系统性的研究综述。通过收 集和分析相关文献，文章总结了关于正交异性钢桥面板疲劳性能的各种研究现状、 研究方法、研究成果和不足之处。本次演示旨在为后续研究提供参考，从而推动 正交异性钢桥面板疲劳问题的进一步解决。
引言
随着交通事业的快速发展，桥梁作为重要的交通设施之一，其安全性和耐久 性备受。正交异性钢桥面板作为一种常见的桥梁结构形式，具有较高的承载能力 和良好的疲劳性能。然而，在长期承受载荷的过程中，正交异性钢桥面板可能会 出现疲劳损伤，
总之，正交异性钢箱梁局部稳定分析理论及模型试验研究对于保障桥梁结构 的安全性和稳定性具有重要意义。通过不断完善研究方法和拓展研究领域，有望 为未来桥梁工程的发展提供有力支持。
参考内容
随着桥梁工程技术的不断发展，正交异性板扁平钢箱梁（Flat-plate Steel Box Girder）在桥梁结构中得到了广泛应用。本次演示将针对正交异性板扁平钢 箱梁的若干问题进行研究，并提出相应的解决方案。
固措施，以延长桥梁的使用寿命？ 3）在桥梁设计和施工过程中，如何优化 设计方案和施工工艺，以降低正交异性钢桥面板的疲劳损伤风险？ 4）如何利用 先进的无损检测技术和数值模拟方法对正交异性钢桥面板的疲劳损伤进行早期诊 断和预测？
这些问题的解决将有助于提高正交异性钢桥面板的耐久性和安全性，降低桥 梁维护和加固的成本，并为桥梁设计和施工提供更加科学的依据。因此，未来的 研究应该这些问题的解决，以期取得更加深入的研究成果。
然后分析局部稳定问题，建立相应的分析理论，最后通过模型试验验证理论 的有效性。
一、背景介绍
正交异性钢箱梁是一种由上下翼板和腹板组成的轻型钢结构，具有自重轻、 跨度大、施工方便等优点，被广泛应用于公路、铁路、城市桥梁等领域。然而， 在服役过程中，正交异性钢箱梁常常受到荷载的作用，如车辆、地震、风载等，