关于水稻产量影响因素的多元回归分析

影响粮食产量的因素分析The document was finally revised on 2021影响我国粮食产量的因素分析摘要:通过时1990一2012年间我国粮食产量的分析,在影响我国粮食产量的诸多原因中选出了3个主要影响因素,建立了多元线性回归模型，利用模型对粮食产量情况进行多元线性回归分析,研究了这些影响因素对粮食产量的影响与作用,最后,在此基础上提出了提高我国粮食产量的对策建议.关键词:粮食产量;影响因素;回归分析;建议一、研究意义粮食安全问题是一个关系到国计民生的重要战略问题! 它影响到经济的发展" 人民生活质量的提高和社会的稳定#尽管我国粮食总体上虽然保持了较高的自给率! 但大豆进口量近年来持续快速增长! 目前我国超过70% 的大豆依赖进口 ! 而其中30%以上进口自美国$当前的形势提醒我们! 必须进一步加强对粮食安全问题的重视$ 而对我国这样一个人口众多的农业大国来说! 粮食供给必须首先立足于国内生产$ 随着我国粮食需求日益增长! 以及城市化和工业化的加速推进! 大量资源不断流向城市! 农业可耕地面积日益萎缩! 使得粮食生产面临较为严峻的形势$ 粮食生产问题如果解决不好! 就会给我国的经济发展和社会稳定带来制约和冲击粮食是人民生存之本、经济发展之柱，对稳定社会、经济具有重要的作用。

粮食问题是一个关系到国计民生的重要战略问题，它更影响到经济的发展和社会的稳定。

中国是世界上的农业大国，同时又是一个农业相对落后的国家。

近几年世界粮食价格的大范围浮动，应该引起我们的注意，大起大落更使我们重新审视起粮食生产的重要性。

同时只有抓住了影响粮食产量的主要因素，改府才能正确的做出举措来将粮食生产引向健康合理的发展路线并且实现农业的现代化。

二、文献回顾影响粮食产量的因素很多,我国学者从不同角度研究了粮食生产问题.于法稳选择有效灌溉面积、化肥施用量、农业机械总动力、粮食播种面积和受灾面积等5个指标作为影响粮食生产的因素,并采用灰色关联分析的方法对这5个因素进行了分析,指出有效灌溉面积、农机总动力和粮食播种面积是影响粮食生产的3个最主要因素;肖海峰将影响粮食综合生产能力的影响因素选择为粮食播种面积、其他物质费用、成灾面积、劳动力和化肥费用,通过柯布一道格拉斯生产函数证实了粮食播种面积是影响粮食产量最重要的因素;熊华等人应用灰色关联分析和C一D生产函数相结合的分析方法证实了化肥施用量、粮食作物播种面积和有效灌溉面积均对粮食生产具有重要影响[’〕;此外,xinagL采用粗糙集理论,张建平、Yun zhang和Wu Y等人运用灰色关联分析与BP神经网络相结合的方法,在对影响粮食产量的因素中又加人了农村用电量、地膜覆盖面积、水电建设投资和支农支出等因素,从多种角度验证了这些影响因素对粮食产量的重要性。

粮食产量影响因素回归分析粮食产量是一个复杂的系统工程，受到多个因素的影响，包括自然因素和人为因素。

为了深入了解这些影响因素，可以运用回归分析方法对其进行量化分析。

下面将详细介绍粮食产量影响因素回归分析的步骤和应用。

回归分析是一种统计学方法，用于确定自变量与因变量之间的关系。

在粮食产量影响因素回归分析中，因变量是粮食产量，自变量则包括多个可能的因素，如天气、土壤条件、农业技术等。

首先，需要收集相关的数据，包括粮食产量的历史数据和可能的影响因素的数据。

对于年度产量数据，可以从农业统计年鉴等公开渠道获取，而对于自变量数据，可以通过相关研究或者实地调查获得。

接下来，对数据进行预处理，包括缺失值填充、异常值处理、数据标准化等。

这些步骤可以提高回归模型的准确性和可靠性。

然后，选择适当的回归模型进行分析。

根据问题的具体情况，可以选择线性回归模型、多项式回归模型、逻辑回归模型等。

线性回归模型是一种常用的回归模型，假设因变量与自变量之间存在线性关系。

而多项式回归模型可以描述因变量和自变量之间的非线性关系。

逻辑回归模型则用于因变量为分类变量的情况。

在建立回归模型后，需要对模型进行拟合和评估。

拟合是指找到最佳的回归系数，使得模型对数据的误差最小化。

评估包括解释模型的统计显著性、对模型的拟合优度进行检验等。

常用的评估指标包括R平方、调整R平方、F统计量等。

最后，根据回归模型得到的结果，可以分析各个自变量对粮食产量的影响程度和方向。

通过回归系数的正负来判断自变量对因变量的增益或减益作用。

此外，还可以进行模型的预测和验证，对未来的粮食产量进行预测，并与实际数据进行比较以验证模型的准确性。

总之，粮食产量影响因素回归分析是一种有效的量化分析方法，可以深入了解粮食产量背后的驱动因素，为农业生产提供科学指导。

这一方法在农业经济学、农业科学等领域具有广泛应用前景。

水稻产量预测模型的研究与应用随着人们生活水平的提高，对粮食的需求量逐渐增加。

水稻作为我国主要的粮食作物之一，拥有着广泛的种植面积和高产量的特点。

因此，对于水稻产量的预测与掌握是极为重要的。

而在现代技术的支持下，水稻产量预测模型的研究与应用已经成为了一个热门的话题。

一、水稻种植与产量影响因素水稻作为一种生态环境敏感的作物，其种植过程中受到的环境因素影响很大。

由于我国南北气候差异较大，不同地区对于水稻的种植也有所不同。

以南方地区为例，其中的水稻种植主要受到气温、降水、光照等气象因素的影响。

除此之外，还有土壤肥力、气候变化和病虫害等因素会对水稻产量造成影响。

因此，在进行水稻产量预测之前，必须深入了解水稻种植的影响因素。

二、水稻产量预测模型基于各种水稻生长因素和环境因素，我们可以得出以下水稻产量预测模型：WaterRice = f(Water, Soil, Air, Sunshine, Pests)。

其中Water、Soil、Air、Sunshine、Pests代表实际环境中水、土、气温、光照和病虫害等因素。

该预测模型被广泛应用于全国的水稻产量预测。

除此之外，还有许多其他的水稻产量预测模型，如基于后缀回归的模型、BP神经网络模型等。

这些模型均基于相关因素建立，精度和可靠性在实践应用中得到了证明。

尤其是在人工智能技术的支持下，这些模型在水稻产量预测中逐渐得到推广和应用。

三、水稻产量预测模型的应用水稻产量预测模型的应用主要体现在数据收集、决策支持和区域化水稻生产指导等方面。

利用水稻产量预测模型，可以及时得到水稻生长环境中重要因素的变化情况，及时发现问题并进行调整。

此外，还可以在不同的生态环境下得出更为准确的水稻产量预测，为农业生产的决策和规划提供参考依据。

例如，在某一地区中，历史数据表明该地区水稻生长环境的最佳温度为18~25摄氏度，而在某一年中，该地区的气温较高、降水较少，为预测该年水稻产量的变化，我们只需利用相关预测模型，根据实际气候数据计算出该年的产量指数，即可得出较为准确的预测结果。

水稻产量与品质关键因素分析与优化水稻作为我国的重要粮食作物之一，其产量和品质关乎着国家的粮食安全和人民的饮食健康。

对于提升水稻产量和品质，有着诸多的因素影响。

本文将对水稻产量与品质的关键因素进行分析和优化，以期能够提高水稻的产量和品质。

一、水稻产量关键因素1. 水肥管理水肥管理是影响水稻产量的关键因素之一。

在水稻的生长期内，水肥管理的恰当与否将会对产量有着直接的影响。

例如，过量的用水和肥料会导致水稻过度生长，从而影响水稻的发育和产量。

而缺水和缺肥则会限制水稻的生长和发育，从而导致产量的降低。

因此，在水肥管理方面，应该根据不同的生长期和不同的地理位置而采取不同的措施。

同时，还需注意选用优质的肥料，以及在灌溉和施肥过程中合理控制用水和肥料的用量，以达到最佳的肥料利用率，提高水稻的产量。

2. 生物学措施生物学措施同样也是影响水稻产量的重要因素。

生物学措施包括病虫害的防治、植物营养和土地改良等方面。

病虫害的防治包括药物或者生物治疗等措施，以保护水稻作物免受病虫害的危害。

而植物营养和土地改良则可以促进水稻的生长，提高产量。

在选择生物措施时，应该注意选择符合当地土地、气候和作物习惯的生物措施，以充分发挥生物措施的效果。

同时，还需注意及时清理草、夯实土壤，以便于水稻的成长，提高产量。

3. 种植方式种植方式也会影响水稻的产量。

一种优秀的种植方式能够在短时间内有效的提高水稻产量。

而错误或不适当的种植方式则会导致产量的降低。

在选择种植方式时，应该根据当地的土质、气候、水源等因素，选择适合当地条件的种植方式。

例如，在土壤肥力较高的地区，可以采用直播种植方式，以提高水稻的产量。

而在土质相对偏瘠或乾旱的地区，则应该采用适合的栽培方式，以促进水稻的生长。

二、水稻品质关键因素1. 稻种品种的选择稻种品种的选择是影响水稻品质的一个关键因素。

在不同的气候、土质和地理条件下，选用不同的稻种品种，可以使水稻产出的品质得到充分的发挥。

目录摘要1、研究背景及意义2、问题的提出3、模型的建立和求解3.1 相关分析—简单散点图3.2 多元回归分析—参数估计3.3 三种检验3.3.1 回归方程的拟合优度检验3.3.2 回归方程的显著性检验—F 检验3.3.3 参数显著性检验—t 检验4、多重共线性检验分析5、自相关分析6、模型的修正6.1 逐步修正法关于水稻产量影响因素的多元线性回归分析摘要本文的主要内目的是对影响水稻产量的因素进行分析，主要运用了SPSS18，采用多元线性回归分析的方法对我国最近18 年影响水稻产量的主要因素进行了分析，建立了以水稻产量为因变量，水稻播种面积、化肥施用量、生猪存栏量和降水量四种影响因素为自变量的多元线性回归模型，利用模型对各个因素进行了统计分析，并且对模型进行了修正检验，在此基础上提出一些提高水稻产量的合理化建议。

关键词：SPSS18 水稻产量多元回归线性分析1、研究背景及意义我国是一个人口大国，众所周知，很多偏远地方的人们仍然处在饥饿的边缘，水稻产量的提高首先可以很好的改善部分地区的粮食紧张问题，为我国经济的发展和社会的稳定提供有效的保障，其次，水稻产量的提高有利于稳定粮食的价格。

因此，对影响水稻产量的因素进行多元回归线性分析可以得出各个因素的影响程度，从而采取正确的措施，以最少的投入得到最大的产量，这对于农业的科学发展是十分必要的。

2、问题的提出下面的表格给出了我国最近18 年来水稻产量与影响和制约水稻产量的主要因素的有关数据。

表1 18 年来水稻产量和相关影响数据水稻播种面化肥施用量生猪存栏量降水量水稻总产量（万积（万亩）（万公斤）（万口）（10mm ）公斤）147.00 2.00 15.00 27.00 154.50 148.00 3.00 26.00 38.00 200.00154.00 5.00 33.00 20.00 227.50 157.00 9.00 38.00 99.00 260.00 153.00 6.50 41.00 43.00 208.00 151.00 5.00 39.00 33.00 229.50 151.00 7.50 37.00 46.00 265.50 154.00 8.00 38.00 78.00 229.00 155.00 13.50 44.00 52.00 303.50 155.00 18.00 51.00 22.00 270.50 156.00 23.00 53.00 39.00 298.50 155.00 23.50 51.00 28.00 229.00 157.00 24.00 51.00 46.00 309.50 156.00 30.00 52.00 59.00 309.00 159.00 48.00 52.00 70.00 371.00 164.00 95.50 57.00 52.00 402.50 164.00 93.00 68.00 38.00 429.50 156.00 97.50 74.00 32.00 427.50 数据来源：中国国家统计局，《中国统计年鉴》在现实生活中，影响水稻产量的因素有很多，但是不能一一列举，我们只是选择了水稻播种面积、化肥施用量、生猪存栏量和降水量 4 个影响因素作为解释变量进行了回归分析。

2017年月（中）行政事业资产财务与粮食产量出现明显的加速上升，但是在2006年以后粮食产量逐渐趋于平稳增长。

2.因素分析影响粮食产量的因素是多方面的，粮食生产能力是一个受自然条件、经济环境以及社会条件制约的综合系统，单单的从一个特定的指标出发来研究问题只能反映其特定视角对粮食产量的影响，因此粮食生产能力指标的选择上必须考虑综合因素，采取不同的指标从不同的角度来进行分析。

首先需要对影响河南省粮食产量的各个因素进行详细的定性分析，确定影响河南省粮食产量的主要因素，然后再根据这些具体影响粮食产量的因素通过使用最小二乘法，将这些影响河南省粮食产量的主要因素作为影响粮食产量的自变量，将河南省的粮食产量作为因变量构建数学模型。

本文在综合考虑前人的研究成果，根据量化可得与全面代表性原则，考虑针对产量有重要影响的土地利用率（粮食播种面积X1）、农业科技进步水平（化肥使用量X2、有效灌溉面积X3和农用机械总动力X4）、自然资源（受灾面积X5）以及劳动力成本（农业从业人员X6），本文采用这几个指数指标作为自变量，把河南省的粮食产量作为因变量，建立多元线性回归模型，使用Eviews 软件对其进行分析。

在进行分析是选取河南1978-2014年的年度数据(以上数据来源于《河南省统计年鉴》)。

设定粮食产量与其影响因素之间的回归模型为：ln Y =+1ln X 1+2ln X 2+3ln X 3+4ln X 4+5ln X 5+6ln X 63.模型建立与检验利用eviews7.0对河南省的粮食产量Y 关于X 1、X 2、X 3、X 4、X 5和X 6进行多元线性回归分析，拟合结果显示，决定系数R 2=0.976463，可以看出回归模型高度显著。

又由F 统计量为207.4353，P 值为0.00000，表明回归模型通过了F 检验，6个自变量整体对因变量Y 产生显著线性影响的判断所犯错误的概率仅为0.0000，说明回归方程式显著的。

影响水稻产量的因素篇一：拖累水稻产量的因素与利空因素分蘖期的管理影响水稻产量的因素与分蘖期的阻碍管理水稻产量是由单位面积穗数、每穗实粒数和千粒重三个因素所构成，这三个因素分别在相同生育时期形成，相辅相成相互促进决定着水稻的高低。

农作物产量是由单位面积穗数、每穗实粒数和千粒重三个因素所构成，这两个因素分别在不同生育风险因素时期形成。

单位面积穗数是由主茎数、单株分蘖数、分蘖成穗率三者组成的。

主茎数取决于插秧的密度及移栽成活率，其基础是在秧田期，所以育好秧，育壮秧，才能确保插秧返青快、分蘖早、成穗多。

逼不得已单位面积穗数的国土面积关键时期是在分蘖期。

在壮秧、合理密植的基础上，每亩穗数多少，便取决于单株分蘖数的成穗率。

一般分蘖越早，成穗的可能性越大;后期出生的分蘖，不容易成穗。

所以积极促进前期抽穗，适当控制后期分蘖，是水稻分蘖期栽培的基本要求。

水稻分蘖期的影响风险因素因素和管理要点番木瓜水稻分蘖实质上是水稻茎秆的分枝，幼苗多发生在基部节间极短的分蘖节上，主茎上所的分枝称一级分蘖，一级分蘖上的分枝称二级分蘖，依此类推。

水稻大葱的发生是有规律的。

正常情况从第一完成叶的丁叶腋伸出分蘖。

但是，特殊情况下也有分蘖不轨迹现象，如健壮秧苗有时分蘖从不完全叶长出，细弱秧苗出现蘖位较低、分蘖晚或不分蘖等情况。

一、影响分蘖的因素1.分蘖发生与秧苗营养状况有关：秧田期由于播种较密，养分、光照不足，基部节上的一直处于分蘖梢大都处于休眠状态。

瘤果以后生长中心转移，走向市场上部节的分蘖芽也都潜伏而不萌发，所以一般只有中位节上的分蘖节可以发育。

秧苗营养充足，生长粗壮，移栽质量保证，低位蘖多，成穗率高。

2.分蘖爆发与温度有关：分蘖生长最适热量为30～32℃，低于20℃或高于37℃对分蘖生长不利，16℃以下分蘖终止生长发育。

3.分蘖遭遇与光照有关：在自然光照下，水稻返青后3天开始分蘖；自然光照为50％时，返青后13天开始分蘖；当光强降到自然光强光照强度的5％时，分蘖不发生，主茎也会死亡。

关于中国粮食相关投入对中国粮食产量影响回归分析一、研究的目的和要求民以食为天，粮食对一个国家是非常重要的，因为粮食安全始终是国家安全的重要基石，是社会稳定的压舱石。

根据粮食年产量统计和粮食进出口统计，我国粮食年总产量居世界第一，粮食进口量仍居世界第一。

粮食是粮农的重要经济来源，也是很多工业产品的原料。

充足的粮食供应，对国民经济长期稳定发展意义具有重大意义。

我国人多地少，农业资源总量不足，人均资源量远低于世界平均水平，确保国家粮食安全具有极端的重要性和紧迫性。

从理论上说，粮食增产是多种综合因素共同作用的结果，研究粮食相关投入对粮食产量的影响对于增加粮食产量具有重要的现实意义。

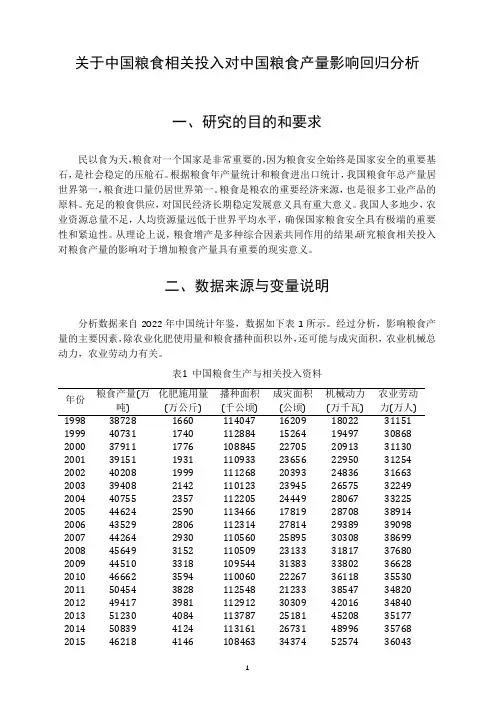
二、数据来源与变量说明分析数据来自2022年中国统计年鉴，数据如下表1所示。

经过分析，影响粮食产量的主要因素，除农业化肥使用量和粮食播种面积以外，还可能与成灾面积，农业机械总动力，农业劳动力有关。

表1中国粮食生产与相关投入资料年份粮食产量(万化肥施用量播种面积成灾面积机械动力农业劳动吨)(万公斤)(千公顷)(公顷)(万千瓦)力(万人)1998387281660114047162091802231151 1999407311740112884152641949730868 2000379111776108845227052091331130 2001391511931110933236562295031254 2002402081999111268203932483631663 2003394082142110123239452657532249 2004407552357112205244492806733225 2005446242590113466178192870838914 2006435292806112314278142938939098 2007442642930110560258953030838699 2008456493152110509231333181737680 2009445103318109544313833380236628 2010466623594110060222673611835530 2011504543828112548212333854734820 2012494173981112912303094201634840 2013512304084113787251814520835177 2014508394124113161267314899635768 20154621841461084633437452574360432016452644254106080317935517236513 2017457064339103891273195793036870 201843070441299410325166038736546 2019469474637101606162976402835269 2020484024766104278199666839833970 2021498044928104958246327252232561 2022501605108105638250647659031444三、模型构建3.1数据预处理本文对整理的数据进行了数据预处理。

计量经济学论文影响粮食产量的因素分析影响粮食产量的因素分析我国土地资源稀缺，人口多而粮食需求量大，因此粮食产量的稳定增长，直接影响着人民生活和社会的稳定与发展。

本文严格按照计量经济分析方法,以1996-2021年中国粮食产量及其重要因素的时间序列数据为样本,对影响中国粮食生产的多种因素进行了分析。

一、模型的建立以Y i=粮食产量、X1=粮食播种面积、X2=农用化肥施用量、X3=农用机械总动力、X4=农、林、牧、渔业劳动力、X5=耕地灌溉面积，设定Y i=c+β1X1i+β2X2i+β3X3i+β4X4i+β5X5i+u i理论模型。

由经济规律知β1、β2、β3、β4、β5都应大于零。

三、模型的参数估计利用Eviews8得到结果如下：Dependent Variable: YMethod: Least SquaresDate: 06/01/17 Time: 20:10Sample: 1996 2021Included observations: 20Variable Coefficient Std. Error t-Statistic Prob.C -66773.87 37106.01 -1.799543 0.0935X1 0.790068 0.119139 6.631499 0.0000X2 1.768843 8.059923 0.219462 0.8295X3 -0.028692 0.338671 -0.084720 0.9337X4 -0.087017 0.051349 -1.694614 0.1123X5 0.477765 0.663745 0.719802 0.4835R-squared 0.976250 Mean dependent var 51861.43 Adjusted R-squared 0.967768 S.D. dependent var 5548.066 S.E. of regression 996.0571 Akaike info criterion 16.88881 Sum squared resid 13889816 Schwarz criterion 17.18753 Log likelihood -162.8881 Hannan-Quinn criter. 16.94712 F-statistic 115.0958 Durbin-Watson stat 1.811852 Prob(F-statistic) 0.000000由此数据看出，可决系数和修正可决系数为0.976250和0.967768，F的检验值为115.0958，明显显著，拟合效果还可以。