归纳柯西不等式的典型应用

柯西不等式的应用技巧
柯西不等式是指对于凸的函数f的任何实数可以进行如下不等式的谓词：f(x) ≤ f(y) + f'(y)*(x-y)，这里f'(y)表示y点处函数f的导数。

柯西不等式可以
用来推断函数f在任何给定点处拥有特定属性，其特性更适用于凸函数。

柯西不等式可以用于求凸函数的极值，其可以把函数的极值分解为一系列的数
学运算，只有当所有的函数值都子满足柯西不等式的限制时，才能够换取到函数的极值。

柯西不等式其极大值点和极小值点也可以由其求出，而不需要考虑函数可能存在的复杂变化。

柯西不等式可以用来求解优化问题，可以把未知数量和变量映射到相应的函数，如果不满足柯西不等式，则可以构建一个优化问题求解未知变量，此时优化问题可以被视为最小化或最大化某一函数。

柯西不等式可以确保求解的可行性，同时可以加快优化的速度，将复杂的多变量求解转变为更简单的一维求解。

柯西不等式广泛应用于概率计算。

在概率论中，可以根据柯西不等式计算出概
率变量以及其相关的定义域范围，这允许概率论家以可视化的方式解决复杂的统计问题。

换句话说，只要满足某种柯西不等式，这些分析问题就可以被解决，比如联合概率分布，条件概率分布等。

总而言之，柯西不等式是一种极其重要的基础工具，其可用于求凸函数的极值，求解优化问题，甚至在概率计算上也有极大的作用。

一
是 ： 一 去 ， 一 去 ， ｚ — ， 即 ｚ 一 告 ， 一 告 ， ｚ — ， （ 号， ｏ ） ， ｃ （ ， ） ， 从
据 题 意 不 难 得 出
＋
∑
２ 利用柯 西不 等式解 决 平面 几何 问题
例２ Ｐ 为 △ ＡＢ Ｃ内一 点 ， Ｄ， Ｅ， Ｆ 分 别 为 Ｐ 到
‘ ． ． 一
２ ＋ 号＋ 一 ２ ｚ ＋ 号＋ 一 ２ ｘ ＋ 詈一（ ｚ
（ １ ）
一
１ ） ＋ （ 一 １ ） ＋ （ ｚ 一１ ） ＋ （ ７ ｃ 一３ ） ≤０
。 ． ．
又。 ． ‘（ ｚ一 １ ） ＋ （ ｙ－ －１ ） ＋ （ ｚ 一１ ） ≥ ０ ， （ ７ ｃ 一３ ） ＞０
‘ ．
例ｌ ： 证 明√ ２ 为无理数 ．
证明 ： 假 设√ ２ 为有理数 ， 则
一
。 ＿ ≤ 拓， 两边同时立方， 得口 ≤６． ’ ． 逆否命题成立
原命 题 如 果 ａ ＞ｂ ， 那 ３ ， ３ 一．
暑（ ｍ ， 为 既 约 分 数 ， 亦ｍ ， 互 质 ）
～ ｚ
也就是 Ｐ Ｄ— Ｐ Ｅ— ＰＦ ） 时等 号成 立 ， 因而 使而 Ｂ Ｃ＋
＋ Ａ Ｂ为最 小
≤
两
的 Ｐ 点 是 △ ＡＢ ｃ的 内心
．
锄
一 一
～
ｉ
１ １ 一
‘
… ，
３ 柯 西不等 式 求解解 析几 何 问题
例 ３ 设抛物线 ｖ ｚ 一２ 缸 （ 由 ＞０ ） 的 焦 点 为 Ｆ。 终 讨
（ ２ ｐ ２ ｐ Ｂ＼ ｐ
，
＿ ｙ
最小值．
￣ ． ： ｌ ＝ｘ ｑ － － ｙ ＋ｚ ＝ １・

柯西不等式各种形式的证明及其应用柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。

但从历史的角度讲，该不等式应当称为Cauchy-Buniakowsky-Schwarz 不等式，因为，正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。

柯西不等式非常重要，灵活巧妙地应用它，可以使一些较为困难的问题迎刃而解。

柯西不等式在证明不等式、解三角形、求函数最值、解方程等问题的方面得到应用。

一、柯西不等式的各种形式及其证明 二维形式在一般形式中，12122,,,,n a a a b b c b d =====令，得二维形式()()()22222bd ac d c b a+≥++等号成立条件：()d c b a bc ad //== 扩展：()()()222222222123123112233nn n n a a a a b b b b a b a b a b a b +++⋅⋅⋅++++⋅⋅⋅+≥+++⋅⋅⋅+等号成立条件：1122000::::,1,2,3,,i i i i n n i i a b a b a b a b a b a b i n ==⎛⎫==⋅⋅⋅= ⎪=⋅⋅⋅⎝⎭当或时，和都等于，不考虑二维形式的证明：()()()()()()22222222222222222222222,,,220=ab c d a b c d R a c b d a d b c a c abcd b d a d abcd b c ac bd ad bc ac bd ad bc ad bc ++∈=+++=+++-+=++-≥+-=等号在且仅在即时成立三角形式ad bc=等号成立条件：三角形式的证明：222111nn n k k k k k k k a b a b ===⎛⎫≥ ⎪⎝⎭∑∑∑()()22222222222222222-2a b c d a b c d ac bd a ac c b bd d a c b d =++++≥+++++≥-+++=-+-≥注：表示绝对值向量形式()()()()123123=,,,,,,,,2=n n a a a a b b b b n N n R αβαβαββαλβλ≥⋅⋅⋅⋅=⋅⋅⋅∈≥∈，等号成立条件：为零向量，或向量形式的证明：()()123123112233222222312322222222112233123123=,,,,,,,,,cos ,cos ,cos ,1n n n n n n n n n nm a a a a n b b b b m n a b a b a b a b m n m na a ab b b b m nm n a b a b a b a b a a a a b b b b =⋅=++++==++++++++≤∴++++≤++++++++令一般形式211212⎪⎭⎫ ⎝⎛≥∑∑∑===n k k k nk k nk k b a b a 1122:::n n i i a b a b a b a b ==⋅⋅⋅=等号成立条件：，或 、均为零。

3.1 配方法
。
由此证明了 且得等号成立的条件为：
.这等价于连比式 [8]。
3.2 判别式法
当 或 时，不等式显然成立
令 ，当 中至少有一个不为零时，可知A>0
构造二次函数 ，展开得： 故 的判别式
移项得 ，得证。
3.3 数学归纳法
) 当n=1时，有 ，不等式成立。
当n=2时，
因为 ，故有
当且仅当 ，即 时等号成立。
ii）假设n=k时不等式成立，即
当且仅当 时等号成立。
那么当n=k+1时，
当且仅当 , , 时等号成立，
即 时等号成立。
于是n=k+1时不等式成立。
由 ) ii）可得对于任意的自然数n，柯西不等式成立。
3.4 基本不等式法
运用基本不等式 。
记 , , , 。
则柯西不等式就等价于 ，也等价于 。
，当且仅当 ，即 时等号成立；
，当且仅当 ，即 时等号成立；
……
，当且仅当 ，即 时等号成立。
把以上 个式子相加得
。
当且仅当 时等号成立，则等价命题成立。
故柯西不等式成立。
3.5 运用推广不等式
若 为正数， 为非负数， ，实数 ，则
（当且仅当 时等号成立）。
在以上推广不等式中取 。
有 。
化简得， 。
当 为零或几个为零（ 处于对称位置），不等式显然成立。
2 柯西不等式的诠释
柯西是18世纪法国、巴黎著名的数学家，他的一生获得了多项重要的成果。本文介绍的柯西不等式便是他的一个非常重要的成果。除此之外他在数学的很多领域都进行了深刻的研究，其中包括数论、代数、数学分析和微分方程等，为数学的发展做出的突出的贡献。

柯西不等式在中学数学中的应用（重庆市大足中学402360）龙定源中学数学基本上是初等数学知识，但是初等数学是高等数学的基础，而高等数学是初等数学的发展，高等数学对初等数学和中学数学具有一定的指导作用，为了解决学生从中学到大学这一突变所产生的诸多不适应问题，在中学教材和教学中适当地蕴含一些高等数学知识是必要的，事实上，中学教材和教辅读物中有不少地方都有一些高等数学知识的皱型和影子，这体现了我们教育家们的远见卓识，基于此，本文拟以柯西不等式为例，谈谈它在中学数学中的一些应用。

本文所说的柯西（Cauchy）不等式是指( i=1，2,……，n) （1）当且仅当时，等号成立。

这也是Holder不等式（其中k>1，k/>1，且，、，I=1，2，……，n）当k=2，k/=2时的情形。

不等式(1)的证明方法很多，中学生能接受的方法就有配方法、判别式法、数学归纳法等，这里不必赘述。

下面仅谈谈它在中学数学中的应用。

导出重要公式1、证明n个实数平方平均数不小于这n个数的算术平均数，即若，则(2)证明：由柯西不等式所以故(2)式中当n=2时，为，这就是中学数学课本(下册)P15第11题。

不等式(2)把中学教材中仅有的“算术平均”，“几何平均”问题拓广到了“二次幂平均”问题，即，这不仅拓宽了中学生的眼界，而且为解决许多不等式的问题开辟了一条新路。

2、导出点到直线的距离公式，即点P(x0，y0)到直线l：Ax+By+C=0的距离上述非严格不等式仅在B(x1-x0)=A(y1-y0)，即PQ⊥l时取等号。

故公式，获证。

2证明不等式利用柯西不等式证明某些不等式显得特别方便，在现行的高中教材中就有不少这样的题目，例如高中代数下册(必修)P32复习题五的第11题：已知，求证，此题的题设和题断一看就知道具有柯西不等式的开工，因而利用柯西不等式证明十分箪捷，(证略)。

又如P16第19题：已知a、b、c∈R+，求证，简证为：由柯西不等式，左边=。

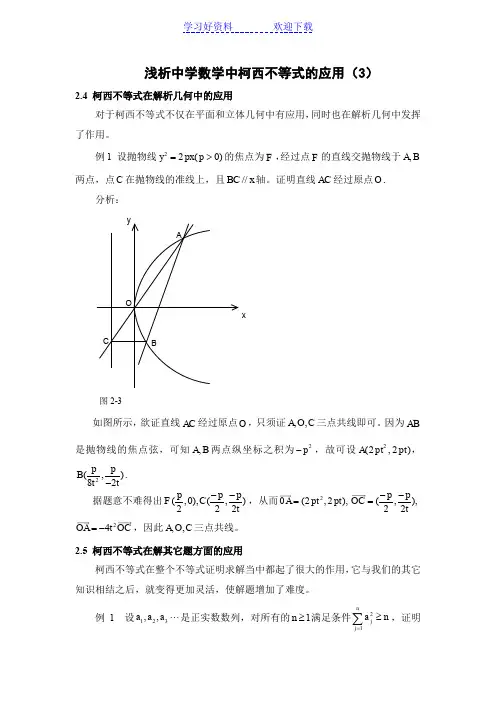
浅析中学数学中柯西不等式的应用（3）2.4 柯西不等式在解析几何中的应用对于柯西不等式不仅在平面和立体几何中有应用，同时也在解析几何中发挥了作用。

例1 设抛物线22(0)y px p =>的焦点为F ，经过点F 的直线交抛物线于,A B 两点，点C 在抛物线的准线上，且//BC x 轴。

证明直线AC 经过原点O .分析：xyOABC图2-3如图所示，欲证直线AC 经过原点O ，只须证,,A O C 三点共线即可。

因为AB 是抛物线的焦点弦，可知,A B 两点纵坐标之积为2p -，故可设2(2,2)A pt pt ，2(,)82p p B t t-. 据题意不难得出(,0),(,)222p p p F C t --，从而20(2,2),A pt pt =(,),22p pOC t--=24OA t OC =-，因此,,A O C 三点共线。

2.5 柯西不等式在解其它题方面的应用柯西不等式在整个不等式证明求解当中都起了很大的作用，它与我们的其它知识相结之后，就变得更加灵活，使解题增加了难度。

例1 设123,,a a a ⋅⋅⋅是正实数数列，对所有的1n ≥满足条件21nj j a n =≥∑，证明对所有1n ≥，有21111(1)42nj j a n=≥++⋅⋅⋅+∑ 证明：先证一个更一般的命题：设12,,n a a a ⋅⋅⋅和12,,n b b b ⋅⋅⋅都是正数， 且12n b b b >>⋅⋅⋅> （2-1）若对所有1,2,,k n =⋅⋅⋅，11kkj j j j b a ==≤∑∑ （2-2）则有2211k kj j j j b a ==≤∑∑（2-3）事实上，设10n b +=，由（2-1）和（2-2）可得111111()()nk n kkk j k k j k j k j bb b b b a ++====-≤-∑∑∑∑改变求和次序得1111()()nnnnj k k j k k j k jj k jb b b a b b ++====-≤-∑∑∑∑由此可得211nnjj jj j b a b ==≤∑∑由柯西不等式，有222111()nnnj j jjj i j a b ab===≤∑∑∑所以22221111()()n n nnjj j jjj j j j b a b ab====≤≤∑∑∑∑ 即2211nnj j j j b a ==≤∑∑令1,2,,)j b j n ===⋅⋅⋅则211111(1)42nnnj j j j a n ===≥>=++⋅⋅⋅+∑ 例 2 试问：当且仅当实数01,,,(2)n x x x n ⋅⋅⋅≥满足什么条件时，存在实数01,,,n y y y ⋅⋅⋅，使得2222012n z z z z =++⋅⋅⋅+成立，其中222k k k z x iy =+，i 为虚数单位，0,1,,k n =⋅⋅⋅.证明你的结论。

柯西不等式的证明、推广及应用2 柯西不等式的推广2.1 命题1若级数∑∑==ni i ni i b a 1212与收敛，则有不等式∑∑∑===≤⎪⎭⎫ ⎝⎛ni i n i i n i i i b a b a 121221。

证明：∑∑==ni i n i i b a 1212, 收敛，⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛≤⎪⎭⎫ ⎝⎛≤∑∑∑===n i i n i i n i i i b a b a 1212210i ni i b a ∑=∴1收敛，且∑∑∑=∞→=∞→=∞→≤⎪⎭⎫ ⎝⎛ni i n n i i n n i i i n b a b a 121221lim lim lim从而有不等式∑∑∑===≤⎪⎭⎫ ⎝⎛ni i n i i n i i i b a b a 121221成立。

2.2 命题2[3]若级数∑∑==ni i ni i b a 1212与收敛，且对N n ∈∀有∑∑∑===≤⎪⎭⎫ ⎝⎛ni i n i i n i i i b a b a 121221，则对定义在[]b a ,上的任意连续函数()()x g x f ,有不等式()()()()dx x g dx x f dx x g x f ba b ab a ⎰⎰⎰≤⎪⎭⎫ ⎝⎛222证明：因为函数()()x g x f ,在区间[]b a ,上连续，所以函数()()()()x g x fx g x f 22、、与在[]b a ,上可积，将[]b a ,区间n 等分，取每个小区间的左端点为i ξ，由定积分的定义得：()()()()()()()()xg dx x g x f dx x f xg dx x g x f dx x f i ni n bai ni n bani in bani in ba∆=∆=∆=∆=∑⎰∑⎰∑⎰∑⎰=∞→=∞→=∞→=∞→ξξξξ12212211lim ,lim lim ,lim令()()12211221,ξξg bfa ==，则∑∑==ni i n i i b a 1212与收敛，由柯西不等式得()()()()()()()()⎪⎭⎫ ⎝⎛∆⎪⎭⎫ ⎝⎛∆≤⎪⎭⎫ ⎝⎛∆⎪⎭⎫ ⎝⎛∆⎪⎭⎫ ⎝⎛∆≤⎪⎭⎫ ⎝⎛∆∑∑∑∑∑∑=∞→=∞→=∞→===ni i n n i i n ni i i n n i i n i i n i i i x g x f x g f x g x f x g f 121221121221lim lim lim ,ξξξξξξξξ从而有不等式()()()()dx x g dx x f dx x g x f ba b ab a ⎰⎰⎰≤⎪⎭⎫ ⎝⎛222。

柯西不等式的工程运用一、引言柯西不等式是数学中的一个重要定理，它在工程运用中也有着广泛的应用。

本文将从几个方面介绍柯西不等式在工程运用中的具体应用。

二、柯西不等式的基本概念1. 柯西不等式的定义柯西不等式是指对于任意两个向量a和b，有如下不等式成立：|a·b| ≤ ||a||·||b||其中，a·b表示向量a和向量b的内积，||a||表示向量a的模长。

2. 柯西不等式的证明柯西不等式可以通过几何方法、代数方法、微积分方法进行证明。

其中最常见的证明方法是通过几何方法进行证明。

3. 柯西不等式的应用前提柯西不等式只适用于欧几里得空间中，即只适用于实数域或复数域上定义的向量空间。

三、柯西不等式在工程运用中的具体应用1. 信号处理领域中的应用在信号处理领域中，柯西不等式被广泛地应用于信号分析、滤波器设计和通信系统设计等方面。

例如，在频谱估计问题中，可以利用柯西不等式来估计信号的功率谱密度。

2. 电力系统中的应用在电力系统中，柯西不等式被用来分析电路中的电流和电压之间的关系。

例如，在直流电路中，可以利用柯西不等式来估计电路中的功率损耗。

3. 机器学习领域中的应用在机器学习领域中，柯西不等式被广泛地应用于模型选择、特征提取和分类问题等方面。

例如，在分类问题中，可以利用柯西不等式来评估分类器的精度和鲁棒性。

4. 图像处理领域中的应用在图像处理领域中，柯西不等式被用来分析图像之间的相似性和差异性。

例如，在图像匹配问题中，可以利用柯西不等式来评估两幅图像之间的相似度。

5. 数值计算领域中的应用在数值计算领域中，柯西不等式被广泛地应用于求解线性方程组、优化问题和微积分问题等方面。

例如，在线性方程组求解问题中，可以利用柯西不等式来评估求解过程的稳定性和收敛速度。

四、结论总之，柯西不等式在工程运用中有着广泛的应用，它不仅可以帮助我们更好地理解和分析问题，还可以指导我们进行实际的工程设计和应用。

柯西重要不等式在实际问题应用柯西重要不等式是数学分析中的一个基本定理，它广泛应用于各个领域的实际问题中。

本文将详细探讨柯西重要不等式在实际问题中的应用，并通过具体案例进行说明。

一、简介柯西重要不等式是由法国数学家柯西在19世纪提出的，它是数学分析领域中的一项重要定理。

该不等式描述了两个函数的平方积与它们各自平方积之和的关系。

具体表述如下：对于任意实数a1, a2, …, an 和b1, b2, …, bn，有如下不等式成立：(a1^2 + a2^2 + … + an^2)(b1^2 + b2^2 + … + bn^2) ≥ (a1b1 + a2b2 + … + anbn)^2二、应用领域柯西重要不等式广泛应用于实际问题中的各个领域，如信号处理、金融数学、物理学等。

下面将具体介绍其中的几个应用案例。

1. 信号处理在信号处理领域，柯西重要不等式可用于评估信号的相关性。

通过对信号的样本进行求平方积和求积的操作，可以得到信号之间的相关系数。

这对于信号处理算法的设计和优化非常重要。

2. 金融数学在金融数学中，柯西重要不等式可用于衡量不同投资组合的风险。

通过计算投资组合中各项资产的相关关系，可以评估整体组合的波动性和风险水平。

这对于投资者的决策和风险管理至关重要。

3. 物理学在物理学领域，柯西重要不等式可用于分析力学问题。

例如，通过运用柯西不等式，可以证明质点在受力作用下的动能与势能之间满足能量守恒定律。

这对于解决物理学中的问题具有重要意义。

三、具体案例为了更好地理解柯西重要不等式的应用，下面将介绍一个具体案例。

在某家庭聚会上，有一桌上放着各种美味的食物，其中包括苹果、橙子和葡萄。

现在我们想知道不同食物之间的相关性如何。

假设有两个人分别吃苹果和橙子，并记录下每天吃的数量。

其中一个人吃了3个苹果和2个橙子，另一个人吃了4个苹果和5个橙子。

现在我们想通过柯西重要不等式来评估苹果和橙子的相关性。

根据柯西重要不等式，我们可以计算出苹果和橙子的平方积和它们各自平方积之和如下：(3^2 + 4^2)(2^2 + 5^2) ≥ (3×2 + 4×5)^2简化计算得：(9 + 16)(4 + 25) ≥ (6 + 20)^225 × 29 ≥ 26^2725 ≥ 676由此可见，苹果和橙子的相关性是较强的。

柯西不等式各种形式的证明及其应用柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。

但从历史的角度讲，该不等式应当称为Cauchy-Buniakowsky-Schwarz 不等式，因为，正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。

柯西不等式非常重要，灵活巧妙地应用它，可以使一些较为困难的问题迎刃而解。

柯西不等式在证明不等式、解三角形、求函数最值、解方程等问题的方面得到应用。

一、柯西不等式的各种形式及其证明 二维形式在一般形式中，12122,,,,n a a a b b c b d =====令，得二维形式()()()22222bd ac d c b a+≥++等号成立条件：()d c b a bc ad //== 扩展：()()()222222222123123112233nn n n a a a a b b b b a b a b a b a b +++⋅⋅⋅++++⋅⋅⋅+≥+++⋅⋅⋅+等号成立条件：1122000::::,1,2,3,,i i i i n n i i a b a b a b a b a b a b i n ==⎛⎫==⋅⋅⋅= ⎪=⋅⋅⋅⎝⎭当或时，和都等于，不考虑二维形式的证明：()()()()()()22222222222222222222222,,,220=ab c d a b c d R a c b d a d b c a c abcd b d a d abcd b c ac bd ad bc ac bd ad bc ad bc ++∈=+++=+++-+=++-≥+-=等号在且仅在即时成立三角形式ad bc=等号成立条件：三角形式的证明：222111nn n k k k k k k k a b a b ===⎛⎫≥ ⎪⎝⎭∑∑∑()()22222222222222222-2a b c d a b c d ac bd a ac c b bd d a c b d =++++≥+++++≥-+++=-+-≥注：表示绝对值向量形式()()()()123123=,,,,,,,,2=n n a a a a b b b b n N n R αβαβαββαλβλ≥⋅⋅⋅⋅=⋅⋅⋅∈≥∈，等号成立条件：为零向量，或向量形式的证明：()()123123112233222222312322222222112233123123=,,,,,,,,,cos ,cos ,cos ,1n n n n n n n n n nm a a a a n b b b b m n a b a b a b a b m n m na a ab b b b m nm n a b a b a b a b a a a a b b b b =⋅=++++==++++++++≤∴++++≤++++++++令一般形式211212⎪⎭⎫ ⎝⎛≥∑∑∑===n k k k nk k nk k b a b a 1122:::n n i i a b a b a b a b ==⋅⋅⋅=等号成立条件：，或 、均为零。

柯西不等式的推广及其应用1 柯西不等式的定义 定义1[1](1)P 如果1212,,,,,,n n a a a b b b 为两组实数，则21122()n n a b a b a b +++ ≤ 2222221212()()n n a a a b b b ++++++并且仅当1221133111n n n n a b a b a b a b a b a b ---=-==-时，等式成立．2 柯西不等式的证明证法一 (利用均值不等式)[2](12)P P -A=21ni i a =∑，B=21ni i b =∑，C=1ni i i a b =∑，只需证明A ≥2C B由均值不等式有222111122C C a b a b B B +≥， 222222222C C a b a b B B+≥22222n n n n C C a b a b B B+≥n 个式子相加得222C CA B C B B+≥，即2C A B≥．当且仅当(1,2,,)i i a kb i n ==，等号成立．证法二 （比值证明法）[2](12)P P -要证222111()n n ni i i i i i i a b a b ===≤∑∑∑只需证明2ni i a b ⎛⎫⎪∑1≤ （2.1）2ni ia b⎛⎫⎪∑=21ni=⎛⎫⎪⎝2222211112ni in nii ii ia ba b===⎡⎤⎛⎫⎢⎥⎪⎢⎥⎪≤+⎢⎥⎪⎪⎢⎥⎝⎭⎣⎦∑∑∑=21(11)2⎡⎤+⎢⎥⎣⎦=1(2.1)式得证，故结论成立．证法三（差值法）[2](12)P P-222111()n n ni i i ii i ia b a b===-∑∑∑221111n n n ni j i j j ii j i ja b a b a b=====-∑∑∑∑22221111111(2)2n n n n n ni j j i i j j ii j i j i ja b a b a b a b=======+-∑∑∑∑∑∑2222111(2)2n ni j i j j i j ii ja b a b a b a b===-+∑∑2111()2n ni j j ii ja b a b===-∑∑≥．当且仅当i j j ia b a b=，即(1,2,)jii jaai nb b==时等式成立．证法四（利用Cauchy-schwarz不等式）[2](12)P P-在nR里，对任意两个向量1212(,,,),(,,,)n nx x x y y yξη==,ξη1122n nx y x y x y+++，因而n R对于上述定义的内积来说作成一个欧氏空间，则有不等式2,,,ηξηη≤令1212(,,),(,,)n na a ab b bξη==从而就有222222*********()()()n n n n a b a b a b a a a b b b +++≤++++++当且仅当ξ与η线性相关时等式成立．即(1,2,,)i i a kb i n ==等号成立．3 柯西不等式的几种变形变形一[3](1)P设,0(1,2,,)i i a R b i n ∈>=，则22111n i ni i ni iii a a b b===⎛⎫⎪⎝⎭≥∑∑∑，当且仅当i i b a λ=时取等号．变形二[3](1)P设,i i a b ，同号且不为零（1,2,,i n =），则2111ni n i i ni ii ii a a b a b===⎛⎫⎪⎝⎭≥∑∑∑，当且仅当12n b b b ===时取等号．变形三[3](1)P对任意数12,(1,2,,)i i a a R i n ∈=，有不等式2221212111n n n i i i i i i i a a a a ===⎡⎤⎡⎤⎡⎤≤⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦∑∑∑成立，当且仅当12(1,2,)i i a a i n λ==时等号成立．变形四[3](1)P对任意1212,,,;,,,n n a a a R b b b R ∈∈，则有112222111nnn i i i i i i i a b a b ===⎡⎤⎡⎤≥⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑．变形五[4](2)P对于任意两个正实数组i a ，(1,2,,)i b i n =，有不等式1122111()()nn ni i i i i i i a b a b ===≤∑∑∑成立，当且仅当i a 与i b 成比例时等号成立．4 柯西不等式的推广推广一[4](2)P设对于由任意正实数构成的m 个数组，12,,(1,2,,)i i mi a a a i n =，有不等式1112121111()()nnnnmmii mi i i mi i i i i aa a a a a ====⋅⋅⋅≤⋅⋅⋅∑∑∑∑ (4.1)成立，当且仅当1i a :2i a ::mi a =1i b :2i b ::mi b 时等号成立．证明 根据算术－几何平均不等式，有下述几个不等式成立1112112111m nnniimii i i a a a aaa===+++∑∑∑11112112111mm n n ni imi i i i a a a m aa a ===⎛⎫⎪⎪≥⋅⋅⋅ ⎪ ⎪⎝⎭∑∑∑； 2122212111m nnniimii i i a a a aaa===+++∑∑∑12122212111mm n n ni imi i i i a a a m aa a ===⎛⎫ ⎪⎪≥⋅⋅⋅ ⎪ ⎪⎝⎭∑∑∑；1212111nnmnnnniimii i i a a a aaa===+++∑∑∑11212111mn n mn n n ni imi i i i a a a m aa a ===⎛⎫⎪⎪≥⋅⋅⋅ ⎪ ⎪⎝⎭∑∑∑． 将上述n 个不等式相加，整理后即得(4.1)式． 当上述n 个不等式等号成立时，(4.1)式等号才成立． 当且仅当各组数对应成比例时，(4.1)式等号成立．推广二[5](2)P 柯西不等式另一个很好的推广，即著名的Hölder 不等式设110,0(1,2,,),0,0,1,i i a b i n p q p q>>=>>+=则 11111nnnpqpq i i ii i i i a b a b ===⎛⎫⎛⎫≤ ⎪⎪⎝⎭⎝⎭∑∑∑， 当且仅当p qi i a b λ=时等号成立．证明 令11npp i i a M =⎛⎫= ⎪⎝⎭∑，11nqq i i b N =⎛⎫= ⎪⎝⎭∑则有11,nnppq q ii i i aM b N ====∑∑．由于函数()ln (0)f x x x =>为凹函数 因此有1111ln ln ln ,(1,2,,)p qp q i i i i a b a b i n p M q N p M q N ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+≤+=⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦．从而有11ln ln p q i ii i a b a b MN p M q N ⎡⎤⎛⎫⎛⎫≤+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦因此11p qi i i i a b a b MN p M q N ⎛⎫⎛⎫≤+ ⎪ ⎪⎝⎭⎝⎭，(1,2,,)i n =所以11111p qnn n i i i i i i i a b a b MNp M q N ===⎛⎫⎛⎫≤+ ⎪ ⎪⎝⎭⎝⎭∑∑∑ =1111nnp qiii i Pqab p Mq N ==+∑∑=11p q+ =1．即1ni i i a b MN =≤∑当且仅当p i a 与qi b 成比例时等号成立．推广三[4](3)P已知,(1,2,,,1,2,,)ji j a R i n j m α+∈==，且11mj j α==∑则有12121mni i mi i a a a ααα=⋅⋅⋅∑1212111mn n n i i mi i i i a a a ααα===⎛⎫⎛⎫⎛⎫≤⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑． 证明 对m 用数学归纳法 1） 当2m =时，命题成立． 2） 假设当m k =时，命题成立． 则当1m k =+时，因111k jj α+==∑，记12k j j s α+==∑，则11s α+=注意()23111k sααα++++=，有112121,1k ni i k i i a a a ααα++=⋅⋅⋅∑121121,1k sns si i k ii a a a ααα++=⎛⎫=⋅⋅ ⎪⎝⎭∑ 121121,111sk n nns si i k ii i i a a a αα++===⎛⎫⎛⎫≤⋅⋅ ⎪ ⎪⎝⎭⎝⎭∑∑∑ 121121,111k snn n s si i k i i i i a a a ααα++===⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥≤⋅⋅ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑∑∑ 121121,111k n n n i i k i i i i a a a ααα++===⎛⎫⎛⎫⎛⎫=⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑综上所述命题得证．5 柯西不等式的应用应用柯西不等式解一般题目的关键是将原问题变形使之适合柯西不等式的形式，而能否成功运 用柯西不等式的关键在于可否根据问题自身固有的特点对照柯西不等式的标准形式，构造出两组适当的数据演12,,,n a a a ；12,,,n b b b 的角色．例1 已知,x y R +∈，且44sin cos 1x y x y αα+=+，证明88333sin cos 1()x yx y αα+=+ 证明 由柯西不等式可得4422sin cos ()()1x y x y αα⎫++≥= 即44sin cos 1x y x yαα+≥+且当且仅当2α=时等号成立，即22sin cos x yαα= （5.1） 由已知44sin cos 1x y x yαα+=+ （5.2） 由（5.1）和（5.2）式解得22sin ,cos x yx y x yαα==++ 所以有8833sin cos x yαα+443311()()x y x x y y x y =+++ 31()x y =+． 例2 已知正数,,x y z 满足1x y z ++=，证明2223333x y z x y z ++++≥．证明 利用柯西不等式2222()x y z ++3131312222222()x x y y z z =++()333222222()()()x y z x y z ⎡⎤≤++++⎢⎥⎣⎦=3332()()x y z x y z ++++(1x y z ++=)，又因为222x y z xy yz zx ++≥++在此不等式两边同乘以2， 再加上222x y z ++得2222()3()x y z x y z ++≤++，因为2222333()()x y z x y z ++≤++⨯2223()x y z ++故2223333x y z x y z ++++≥．例3 求函数11sin cos (,0,,(0,)2n ny a b a b n N πααα=+>∈∈的最大值．解 由[6](2)12121122()()()()n n n n n n n P n n n n a a a b b b a b a b a b +≤+++可得112(sin cos )nnna b αα+111111112212121212121(sin cos )n n n n nn n n naaabbbαα------=+（21n -）个 （21n -）个2221222121()(sin cos )n nn n n abαα---≤++=22212121()n nn n n ab---+所以11222121212sin cos ()n n n n n n n na b abαα---+≤+当且仅当11112121:sin :cos n n n na bαα--=，即21arc ()n n a tg bα-=时等号成立．所以222121212max ()n n n n n ny ab---=+．例4 已知2221,,,x y z x y z ++=是实数，求证：112xy yz zx -≤++≤． 证明 因为22()(111)x y z x y z ++=⨯+⨯+⨯所以由柯西不等式2222222()(111)()3x y z x y z ++≤++++=又由于22220()2()12()3x y z x y z xy yz zx xy yz zx ≤++=+++++=+++≤所以012()3xy yz zx ≤+++≤即112xy yz zx -≤++≤．例5 求证三角形三边上正方形的面积之和不小于该三角形面积的222a b c ++≥，其中,,,a b c 为三角形三边的长，∆为三角形的面积．证明 由三角形面积公式可得2()()()s s a s b s c ∆=---其中2a b cs ++=，于是 216()()()()a b c b c a c a b a b c ∆=+++-+-+-2222224442()b c c a a b a b c =++---由柯西不等式，有22222224444444442()()()()b c c a a b b c a c a b a b c ++≤++++=++即222222444b c c a a b a b c ++≤++当且仅当222222b c a c a b==，即a b c ==时等号成立．于是4442222224()4()a b c b c c a a b ++≥++变形为444222222222a b c b c c a a b +++++2222224443(222)b c c a a b a b c ≥++---即22222()316a b c ++≥⨯∆所以222a b c ++≥，当且仅当a b c ==时等式成立．例6 设P 为ABC ∆内的一点，M ，N ，H ，分别为P 到各边所引垂线的垂足，求所有BC CA AB PM PN PH++为最小值的点P ． AB MC图1解 如图1，设ABC ∆的面积为S ，则S 111222BC PM CA PN AB PH =⨯+⨯+⨯（5.3） 由柯西不等式可知222222⎡⎤⎡⎤++++⎢⎥⎣⎦⎣⎦2≥ (5.4) 将（5.3）代入（5.4）得2()2BC CA AB BC CA AB PM PN PH S++++≥== 时等号成立， 即PM PN PH ==又S 和()AB BC CA ++分别是ABC ∆的面积和周长，故为定值， 即P 为ABC ∆内心时BC CA ABPM PN PH++为最小值．参考文献：[1] 鞠建恩．柯西不等式在初等数学中的应用[J]．南平师专学报，2002，02[2] 赵朋军．柯西不等式的多种证法推广及其应用[J]．商洛师范专科学校学报，2004，03 [3] 王晓凤．对柯西不等式探讨[J]．通化师范学院学报，2006，03 [4] 黄 毅．柯西不等式的一个变形及其推广[J]．数学教学通讯，2003，1 [5] 林银河．关于Minkowshi 不等式的讨论[J]．丽水师范专科学校学报，2003，10 [6] 徐幼明．柯西不等式的推广及其应用[J]．数学通讯，1996，12[7] T ．Damm ．A unified version of Cauchy-Schwarz and Wielandt inequality [J] ．School of Information and Mathematics ，2007，1111。

柯西不等式应用举例
嘿，朋友们！今天咱就来讲讲柯西不等式的应用举例，这可真的是超有意思的哦！
你想想看，就好比我们要建一座房子，柯西不等式就是那坚固的框架，让一切都能稳稳当当的。

比如说在数学竞赛中，有个题目是要找出两个数的最大乘积。

这时候，柯西不等式就闪亮登场啦！好比你有两个向量，一个是(3, 4)，另一个是(1, 2)，那用柯西不等式一算，就能找到它们乘积的一个范围，是不是很神奇？
再比如在实际生活中，我们安排任务。

假设有两个人，A 做事特别快但质量一般，B 做事慢但质量超高。

那怎么分配任务才能让效果最好呢？这时候柯西不等式就像个聪明的军师，能帮我们找到最佳方案。

“哎呀，要是没有柯西不等式，那可咋办呀！”
还有啊，我们在解决一些优化问题的时候。

比如说要把一些物品装到箱子里，怎样装才能最节省空间呢？哈哈，柯西不等式又来大显身手啦！
柯西不等式就像一把万能钥匙，能打开好多难题的大门呢！它能让复杂的问题变得简单易懂，让我们在数学的海洋里畅游无阻！
总之，柯西不等式的应用真是无处不在，从小小的数学题到大大的实际问题，它都能发挥巨大的作用。

它就像是我们的秘密武器，只要我们懂得运用它，就能解决好多看似无解的难题。

所以啊，朋友们，一定要好好掌握柯西不等式，让它为我们的学习和生活增添更多的精彩！你们说是不是呀！。

柯西不等式(应用版)题型分类柯西不等式是数学中一种重要的不等式，具有广泛的应用领域。

在使用柯西不等式解题时，根据不等式的具体应用背景和题目给定条件的不同，可以将题型进行分类。

以下是柯西不等式应用题的常见分类：1. 点积问题柯西不等式最常见的应用是求解点积问题。

点积问题通常给出两个向量，要求计算它们的点积的范围或最大值/最小值。

例如，已知向量 $\mathbf{a}=(a_1, a_2, \ldots, a_n)$ 和向量$\mathbf{b}=(b_1, b_2, \ldots, b_n)$，求证 $\mathbf{a} \cdot\mathbf{b} \leq \|\mathbf{a}\| \cdot \|\mathbf{b}\|$。

这是柯西不等式的基本形式，反映了两个向量的点积与它们的模长之间的关系。

2. 三角函数问题柯西不等式在三角函数问题中也有广泛的应用。

例如，已知$\theta \in [0, \pi/2]$，求证 $\sin^2\theta+\cos^2\theta \leq 1$。

这是一个典型的三角函数问题，可以通过柯西不等式证明。

3. 函数积分问题柯西不等式还可以用于求解函数积分问题。

例如，已知函数$f(x)$ 在区间 $[a, b]$ 上连续且非负，函数 $g(x)$ 在该区间上也是连续函数，且满足 $g(x) \leq M$。

求证 $\left(\int_a^bf(x)g(x)dx\right)^2 \leq M^2 \int_a^b [f(x)]^2dx$。

这是一个函数积分问题，可以利用柯西不等式进行证明。

将$f(x)$ 和 $g(x)$ 视为两个向量，在柯西不等式中应用积分运算。

4. 概率问题柯西不等式在概率问题中也有应用。

例如，已知 $X$ 和$Y$ 是两个随机变量，求证 $E(XY) \leq \sqrt{E(X^2)E(Y^2)}$。

这里的期望值表示随机变量的数学期望。

柯西施瓦茨不等式数学归纳法全文共四篇示例，供读者参考第一篇示例：柯西施瓦茨不等式是数学中一个非常重要的不等式，它广泛应用于数学分析、线性代数、概率论等领域。

柯西施瓦茨不等式在数学研究中扮演着重要的作用，其证明方法之一就是利用数学归纳法。

本文将介绍柯西施瓦茨不等式的定义及证明过程，并探讨数学归纳法在证明过程中的应用。

让我们来了解一下柯西施瓦茨不等式的定义。

柯西施瓦茨不等式是指对于任意两个向量a和b，都有如下不等式成立：\[|a \cdot b| \leq \|a\| \cdot \|b\|\]a和b分别是两个n维向量，acdot b表示a和b的点积，||a||表示a的范数，也就是a的长度。

柯西施瓦茨不等式告诉我们，两个向量的点积的绝对值不会大于它们长度的乘积。

接下来，我们将使用数学归纳法来证明柯西施瓦茨不等式。

数学归纳法是一种证明方法，在证明某个数学命题时，首先证明当n=1时命题是否成立，然后假设n=k时命题成立，再证明n=k+1时命题也成立，这样就证明了对于所有自然数n都成立。

我们来证明当n=1时柯西施瓦茨不等式成立。

设a和b分别是一维向量，即a=(a1)和b=(b1)，那么根据柯西施瓦茨不等式的定义，我们有：这就证明了当n=1时柯西施瓦茨不等式成立。

接下来，我们假设当n=k时柯西施瓦茨不等式成立，即对于任意k 维向量a和b有：现在我们来证明当n=k+1时柯西施瓦茨不等式也成立。

设a和b 分别是(k+1)维向量，即a=(a1,a2,...,ak,ak+1)和b=(b1,b2,...,bk,bk+1)，那么我们可以将a拆分成两部分，a=(a1,a2,...,ak)和(a(k+1))，同样将b拆分成两部分b=(b1,b2,...,bk)和(b(k+1))。

根据柯西施瓦茨不等式的性质，我们有：\[|a \cdot b|^2 = (a1b1 + a2b2 + ... + akbk + a(k+1)b(k+1))^2\]第二篇示例：柯西施瓦兹不等式是数学中的一个重要不等式，也是线性代数中的经典定理之一。

，所以 1 sin2A
=
4R2 a2
，同
理1 sin2B
=
4R2 b2
，1 sin2C
=
4R2 c2
于是左边
≥ ≥ ≥ ≥ =(a2+b2+c2)
4R2 a2
+
4R2 b2
+
4R2 c2
≥
a·2R a
+b·2R b
+c·2R c
2
=36R2
4、利用柯西不等式解方程
例 4 在实数集内解方程
≤x2+y2+z2= 9 4 - 8x+6y- 24y=39
— 405 —
（上接第 404 页） 来控制其进行自检，从而方便用户检修与维护。 边界扫描测试不仅可以用来测试芯片或电路板的功能，还可以用
来测试芯片或电路板之间的连接是否有问题。边界扫描测试技术在 CUT 核心部分的每一个输入端和输出端都设置了一个寄存器，叫做边 界扫描单元，这些寄存器均可以输入和输出数据，而且串联成一个移位 寄存器链。当测试电路的功能时，将电路输入端的寄存器设为输出方 式，输出端的寄存器设为输入方式，在控制电路的控制下，把测试激励 通过输入端的寄存器驱动 CUT，并将测试响应采集到输出端的寄存器。 当测试连线时，可将连线一端的寄存器设为输出方式，另一端设为输入 方式，再按一定的方式施加测试激励并捕捉响应，比较这两个寄存器中
22 22
a2 b3 +a3 b2 ≥2a2 b2 a3 b3（当且仅当 a2 b3 =a3 b2 时，等号成立）
222 2 2 2
2
故(a1 +a2 +a3 )(b1 +b2 +b3 )≥(a1 b1 +a2 b2 +a3 b3 )