中考复习函数专题10 一次函数中的四边形问题(老师版)

一次函数与四边形1、如图所示，把矩形纸片 OABC 放入直角坐标系 xOy 中，使 OA 、OC 分别落在x 、y 轴的正半轴上，连接AC，且AC =OC/OA=1/2（1）求AC 所在直线的解析式；（2）将纸片OABC 折叠，使点A 与点C 重合（折痕为EF ），求折 叠后纸片重叠部分的面积．（3）求EF 所在的直线的函数解析式．2、如图，直线364y x =+与x 轴、y 轴分别相交于点E 、F ，点A 的坐标为（－6，0），P （x ，y ）是直线364y x =+上一个动点． （1）在点P 运动过程中，试写出△OPA 的面积s 与x 的函数关系式；（2）当P 运动到什么位置，△OPA 的面积为278，求出此时点P 的坐标； （3）过P 作EF 的垂线分别交x 轴、y 轴于C 、D ．是否存在这样的点P ，使△COD ≌△FOE ？若存在，直接写出此时点P 的坐标；若不存在，请说明理由．3、如图，平面直角坐标系中，直线l 交x 轴、y 轴于A 、B 两点，点A 坐标为（1，0）∠ABO=30°，过点B 的直线m x y +=33与x 轴交于点C 。

（1）求直线l 的解析式及点C 的坐标.（2）点D 在x 轴上从点C 向点A 以每秒1个单位长的速度运动（0 ＜t ＜ 4 ），过点D 分别作DE ∥AB ，DF ∥BC ，交BC 、AB 于点E 、F ，连接EF ，点G 为EF 的中点.①判断四边形DEBF 的形状并证明；②求出t 为何值时线段DG 的长最短.（3）点P 是y 轴上的点，在坐标平面内是否存在点Q ，使以A 、B 、P 、Q 为顶点的四边形是菱形？若点的坐标；若不.备用图4、如图，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知A点坐标为（a，0），B点坐标为（0，b），且a，b满足+|2a﹣b﹣2|=0．D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动，当点P与点B重合时停止运动，运动时间为t秒．（1）当点P经过点C时，求直线DP的函数解析式；（2）①求△OPD的面积S关于t的函数解析式；②如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．（3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．5、如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，且OA=8、OB=6，∠ABO的平分线交x轴于点C过点C作AB的垂线，垂足为点D，交y轴于点E．（1）求线段AB的长；（2）求直线CE的解析式；（3）若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．6、平面直角坐标系中，直线y＝3x＋6与x轴、y轴分别交于点B、C，不论k为何值，直线l：y ＝kx－2k都经过x轴上点A(1) 如图1，若直线l过点C，求直线l的解析式和点A的坐标(2) 如图2，将线段BC沿某个方向平移，点B、C对应的点M、N恰好在直线l和直线y＝2x－4上，当k＝1时，请你判断四边形BMNC的形状，并说明理由(3) 如图3，点P由点C向下平移个单位得到，点Q是x轴上的动点，以P、Q为顶点作菱形PRQT，且∠T＝60°．直线l经过顶点R，当点Q在x轴上运动（点R不与点A重合）时，k的值是否会发生变化？若不变，求出k的值；若变化，请说明理由。

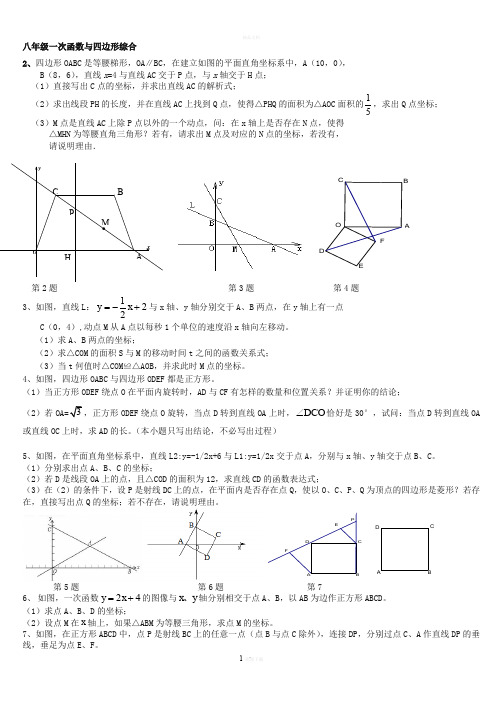
xyOABCPHM八年级一次函数与四边形综合2、四边形OABC 是等腰梯形，OA ∥BC ，在建立如图的平面直角坐标系中，A （10，0），B （8，6），直线x =4与直线AC 交于P 点，与x 轴交于H 点； （1）直接写出C 点的坐标，并求出直线AC 的解析式； （2）求出线段PH 的长度，并在直线AC 上找到Q 点，使得△PHQ 的面积为△AOC 面积的51，求出Q 点坐标； （3）M 点是直线AC 上除P 点以外的一个动点，问：在x 轴上是否存在N 点，使得△MHN 为等腰直角三角形？若有，请求出M 点及对应的N 点的坐标，若没有， 请说明理由．FEDC BAO第2题 第3题 第4题 3、如图，直线L ：221+-=x y 与x 轴、y 轴分别交于A 、B 两点，在y 轴上有一点 C （0，4）,动点M 从A 点以每秒1个单位的速度沿x 轴向左移动。

（1）求A 、B 两点的坐标；（2）求△COM 的面积S 与M 的移动时间t 之间的函数关系式； （3）当t 何值时△COM ≌△AOB ，并求此时M 点的坐标。

4、如图，四边形OABC 与四边形ODEF 都是正方形。

（1）当正方形ODEF 绕点O在平面内旋转时，AD 与CF 有怎样的数量和位置关系？并证明你的结论；（2）若ODEF 绕点O 旋转，当点D 转到直线OA 上时，DCO ∠恰好是30°，试问：当点D 转到直线OA 或直线OC 上时，求AD 的长。

（本小题只写出结论，不必写出过程）5、如图，在平面直角坐标系中，直线L2:y=-1/2x+6与L1:y=1/2x 交于点A ，分别与x 轴、y 轴交于点B 、C 。

（1）分别求出点A 、B 、C 的坐标；（2）若D 是线段OA 上的点，且△COD 的面积为12，求直线CD 的函数表达式；（3）在（2）的条件下，设P 是射线DC上的点，在平面内是否存在点Q ，使以O 、C 、P 、Q 为顶点的四边形是菱形？若存在，直接写出点Q 的坐标；若不存在，请说明理由。

一次函数中的四边形存在性问题【题型1 平行四边形的存在性问题】1．（2023•襄阳模拟）如图，直线l 1：y =−34x +b 分别与x 轴、y 轴交于A 、B 两点，与直线l 2：y ＝kx ﹣6交于点C （2，32）． （1）点A 坐标为（ ， ），B 为（ ， ）（2）在线段BC 上有一点E ，过点E 作y 轴的平行线交直线l 2于点F ，设点E 的横坐标为m ，若四边形OBEF 是平行四边形时，求出此时m 的值．【分析】（1）先将点C 坐标代入直线l 1中，求出直线l 1的解析式，令x ＝0和y ＝0，即可得出结论；（2）先求出直线l 2的解析式，表示出点E ，F 的坐标，在判断出OB ＝EF ，建立方程求解，即可得出结论；【解答】解：∵点C（2，32）在直线l1：y=−34x+b上，∴−34×2+b=32，∴直线l1的解析式为y=−34x+3，令x＝0，∴y＝3，∴B（0，3），令y＝0，∴−34x+3＝0，∴x＝4，∴A（4，0），故答案为：4，0，0，3；（2）∵点C（2，32）在直线l2：y＝kx﹣6上，∴2k﹣6=32，∴k=154，∴直线l2的解析式为y=154x﹣6，∵EF∥y轴，点E的横坐标为m，∴点F的横坐标为m，∵点E l1上，∴E（m，−34m+3），∵点F在直线l2：y=154x﹣6上，∴F（m，154m﹣6），∵四边形OBEF是平行四边形，且BO∥EF，∴OB＝EF，EF=−34m+3﹣（154m﹣6）＝3，∴m=4 3；【点评】此题是一次函数综合题，主要考查了待定系数法，平行四边形的性质，三角形的面积公式，利用方程的思想解决问题是解本题的关键．2．（2022春•涟水县校级月考）如图，平行四边形ABCD 在直角坐标系中，点B 、点C 都在x 轴上，其中OA ＝8，OB ＝6，AD ＝12，E 是线段OD 的中点．（1）直接写出点C ，D 的坐标；（2）求直线AE 的关系式；（3）平面内是否存在一点F ，使以A 、D 、E 、F 为顶点的四边形是平行四边形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．【分析】（1）根据平行四边形的性质得AD ＝BC ＝12，AD ∥BC ，根据题意可得OC ＝6，点A 的坐标为（0，8），点D 的坐标为（12，8），即可得点C 的坐标为（6，0）；（2）根据E 是线段OD 的中点得E （6，4），设直线AE 的关系式为：y ＝kx +b ，根据直线AE 经过点A ，点E ，即可得{b =86x +b =4，进行计算即可得； （3）分情况讨论：①当EF 为平行四边形的边时，根据对边相等即可得；②当EF 为平行四边形的对角线时，根据对角线互相平分即可得．BC【解答】解：（1）∵四边形ABCD 是平行四边形，∴AD ＝BC ＝12，AD ∥BC ，∵点B 、C 都在x 轴上，点A 在y 轴上，OA ＝8，OB ＝6，∴OC ＝BC ﹣OB ＝12﹣6＝6，点A 的坐标为（0，8），点D 的坐标为（12，8），∴点C 的坐标为（6，0）；（2）∵E 是线段OD 的中点，∴E （6，4），设直线AE 的关系式为：y ＝kx +b ，∵直线AE 经过点A ，点E ，∴{b =86x +b =4， 解得{b =8k =−23， ∴直线AE 的关系式：y =−23x +8；（3）存在，F坐标为（﹣6，4）或（18，4）或（6，12），①如图所示，当EF为平行四边形的边时，EF＝AD＝12，∴点F的坐标为：（﹣6，4）或（18，4），②如图所示，当EF为平行四边形的对角线时，则DG＝AG＝6，FG＝GE＝4，即点F的坐标为：（6，12），综上，点F的坐标为：（﹣6，4）或（18，4）或（6，12）．【点评】本题考查了平行四边形的判定与性质，一次函数的性质，解题的关键是掌握并灵活运用这些知识点．3．（2022春•昌江县期末）如图，直线y＝﹣x+4分别交x轴、y轴于A、B两点，直线BC与x轴交于点C （﹣2，0），P是线段AB上的一个动点（点P与A、B不重合）．（1）求直线BC所对应的函数表达式；（2）设动点P的横坐标为t，△POA的面积为S．①求出S与t的函数关系式，并写出自变量t的取值范围；②在线段BC上存在点Q，使得四边形COPQ是平行四边形，求此时点Q的坐标．【分析】（1）根据直线y ＝﹣x +4分别交x 轴、y 轴于A 、B 两点，直线BC 与x 轴交于点C （﹣2，0），可以得到点B 的坐标，从而可以得到直线BC 的函数表达式；（2）①根据题意，可以用含t 的代数式表示出点P 的坐标，从而可以得到S 与t 的函数关系式，并写出自变量t 的取值范围；②根据题意和平行四边形的性质，可以用含t 的代数式表示出点Q 的坐标，再根据OC ＝PQ ，即可得到点Q 的坐标．【解答】解：（1）∵直线y ＝﹣x +4分别交x 轴、y 轴于A 、B 两点，∴点A 的坐标为（4，0），点B 的坐标为（0，4），设直线BC 所对应的函数表达式为y ＝kx +b ，{b =4−2k +b =0， 解得，{k =2b =4， 即直线BC 所对应的函数表达式是y ＝2x +4；（2）①∵点O （0，0），点A （4，0），∴OA ＝4，∵动点P 的横坐标为t ，△POA 的面积为S ，P 是线段AB 上的一个动点（点P 与A 、B 不重合）， ∴动点P 的纵坐标为﹣t +4，∴S =4×(−t+4)2=−2t +8， 即S 与t 的函数关系式是S ＝﹣2t +8（0＜t ＜4）；②过点P 作PQ ∥x 轴，交BC 于点Q ，∵点P 的坐标为（t ，﹣t +4），∴点Q 的纵坐标为﹣t +4，∵点Q 在直线y ＝2x +4上，∴﹣t +4＝2x +4，得x ＝﹣0.5t ，∵四边形COPQ是平行四边形，OC＝2，∴OC＝PQ，∴2＝t﹣（﹣0.5t），解得，t=4 3，∴点Q的坐标为（−23，83）．【点评】本题是一道一次函数综合题，主要考查一次函数的性质、平行四边形的性质、待定系数法求一次函数解析式，三角形的面积，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．4．（2023春•鲤城区校级期中）如图1，在平面直角坐标系中，直角梯形OABC的顶点A的坐标为（4，0），直线y=−14x+3经过顶点B，与y轴交于顶点C，AB∥OC．（1）求顶点B的坐标；（2）如图2，直线l经过点C，与直线AB交于点M，点O'与点O关于直线l对称，连接CO′并延长交直线AB于第一象限的点D，当CD＝5时，求直线l的解析式；（3）在（2）条件下，点P在直线l上运动，点Q在直线OD上运动，当四边形PBCQ是平行四边形时，求点P的坐标．【分析】（1）根据AB∥OC，可得点B的横坐标为4，再代入y=−14x+3，即可求解；（2）过C点作CN⊥AB于N，可得到∠DCM＝∠DMC，从而得到CD＝MD＝5，再求出OC＝3，DN＝3，从而得到NM＝5﹣3＝2，继而得到AM＝1，可得到点M（4，1），即可求解；（3）连接OD，先求出D点坐标为（4，6），可得直线OD解析式为y=32x，设P点坐标为(a，−12a+3)，Q点坐标为(b，32b)，然后根据平行四边形对角线互相平分，即可求解．【解答】解：（1）∵A（4，0），AB∥OC，∴点B的横坐标为4，把x＝4代入y=−14x+3中，得y＝2，∴B（4，2）；（2）如图，过C点作CN⊥AB于N，∵AB∥OC，∴∠OCM＝∠DMC，∵点O'为点O关于直线l的对称点，∴∠DCM＝∠OCM，∴∠DCM＝∠DMC，∴CD＝MD＝5，∵y=−14x+3，当x＝0时，y＝3，∴点C（0，3），∴OC＝3，∵CN＝OA＝4，∴DN=√CD2−CN2=√52−42=3，∴NM＝5﹣3＝2，∴AM＝AN﹣NM＝3﹣2＝1，∴M（4，1），设直线l解析式y＝kx+b把C（0，3），M（4，1）代入得：{3=b 1=4k +b， 解得：{k =−12b =3，∴直线l 的解析式为：y =−12x +3；（3）如图，连接OD ，∵AD ＝AM +MD ＝1+5＝6，AD ∥OC ，A 点坐标为（4，0），∴D 点坐标为（4，6），设OD 直线解析式为y ＝kx ，将（4，6）代入可得4k ＝6，解得k =32，∴直线OD 解析式为y =32x ，∵点P 在直线l 上运动，点Q 在直线OD 上运动，∴设P 点坐标为(a ，−12a +3)，Q 点坐标为(b ，32b)，∵四边形PBCQ 是平行四边形，∴平行四边形对角线互相平分，{4+b 2=a+022+32b 2=−12a+3+32， 解得：{a =5b =1， 当a ＝5时，−12a +3=−12×5+3=12，∴P 点坐标为(5，12)．【点评】本题主要考查了一次函数与四边形的综合题，熟练掌握一次函数的图象和性质，平行四边形的性质是解题的关键．【题型2 矩形的存在性问题】1．如图，在平面直角坐标系xOy中，已知直线l与直线y＝2x平行，且直线l与x、y轴分别交于点A（﹣1，0）、点B，点C（1，a）在直线l上．（1）求直线l的表达式以及点C的坐标；（2）点P在y轴正半轴上，点Q是坐标平面内一点，如果四边形P AQC为矩形，求点P、Q的坐标．【分析】（1）根据题意设直线l的解析式为y＝2x+b，代入A（﹣1，0）求得b，即可求得直线l的解析式，然后代入C（1，a），就可求得a的值；（2）先证得Q在y轴上，根据勾股定理求得AB，然后根据矩形的性质即可求得P、Q的坐标．【解答】解：（1）∵直线l与直线y＝2x平行，∴直线l的斜率为2，设直线l的解析式为y＝2x+b，∵直线l经过A（﹣1，0），∴2×（﹣1）+b＝0，解得b＝2，∴直线l的表达式为y＝2x+2，∵点C（1，a）在直线l上，∴a＝2×1+2＝4；（2）∵y＝2x+2，∴B（0，2），∵A（﹣1，0），C（1，4），∴AB＝BC，∵四边形P AQC为矩形，点P在y轴正半轴上，∴Q点在y轴负半轴上，∵A（﹣1，0），∴AB=√12+22=√5，∴PB＝QB=√5，∴P（0，2+√5），Q（0，2−√5）．【点评】本题考查了两条直线相交或平行问题，待定系数法求一次函数的解析式，矩形的性质，熟练掌握矩形的对角线相等且互相平分是解题的关键．2．（2023•阜阳三模）如图，四边形OABC是矩形，点A、C分别在x轴、y轴上，△ODE是△OCB绕点O 顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，点B的坐标为（﹣2，4）．（1）求直线BD的表达式；（2）求△DEH的面积；（3）点M在x轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）根据矩形的性质和旋转的性质可得点D坐标，再利用待定系数法求直线BD的表达式即可；（2）先利用待定系数法求出直线OE 的解析式，再联立{y =12x y =−23x +83，求出点H 坐标，再根据△DEH 的面积=12DE ⋅HG 求解即可；（3）先求出点F 坐标，以点D 、F 、M 、N 为顶点的四边形是矩形，分情况讨论：①当FD 是矩形的对角线时，②当FD 为矩形的边时，分别求出点M 的坐标，根据平移的性质即可确定点N 坐标．【解答】解：（1）在矩形ABCO 中，∠OCB ＝90°，∵点B 坐标为（﹣2，4），∴OC ＝4，BC ＝2，根据旋转的性质可得，OD ＝OC ＝4，DE ＝BC ＝2，∠ODE ＝∠OCB ＝90°，∴点D 坐标为（4，0），点E 坐标为（4，2），设直线BD 的解析式为y ＝kx +b （k ≠0，k ，b 为常数），代入点B （﹣2，4），点D （4，0），得{−2k +b =44k +b =0， 解得{k =−23b =83， ∴直线BD 的解析式为y =−23x +83；（2）过点H 作HG ⊥DE 于点G ，如图所示：设直线OE 的解析式为y ＝mx （m ≠0，m 为常数），代入点E （4，2），得4m ＝2，解得m =12， ∴直线OE 的解析式为y =12x ，联立{y =12x y =−23x +83，解得{x =167y =87， ∴点H 坐标为（167，87）， ∴HG ＝4−167=127， ∵DE ＝2，∴△DEH 的面积=12DE ⋅HG =12×2×127=127； （3）存在点N ，点N 坐标为（4，83）或（209，−83），理由如下： 当x ＝0时，y =−23x +83=83，∴点F 坐标为（0，83）， 以点D 、F 、M 、N 为顶点的四边形是矩形，分情况讨论：①当FD 是矩形的对角线时，如图所示：此时M 点与点O 重合，∴N 点坐标为（4，83）； ②当FD 为矩形的边时，如图所示：设OM ＝m ，在Rt △OMF 中，根据勾股定理，得MF 2=m 2+(83)2，∵DF 2=42+(83)2，MF ＝4+m ， 在Rt △MDF 中，根据勾股定理，得MF 2+DF 2＝DM 2，∴m 2+(83)2+42+(83)2=(m +4)2，解得m =169， ∴点M 坐标为（−169，0）， 根据平移的性质，可得点N 坐标为（209，−83）， 综上所述，点N 坐标为（4，83）或（209，−83）． 【点评】本题考查了一次函数的综合题，涉及待定系数法求解析式，旋转的性质，矩形的性质，三角形的面积，存在性问题等，本题综合性较强，难度较大．3．（2020春•香坊区校级月考）如图，在平面直角坐标系中，矩形OABC 的顶点A 、C 分别落在x 轴、y 轴正半轴上，点E 在边OA 上，点F 在边OC 上，且AE ＝EF ，已知B （6，8），F （0，2√3 ）．（1）求点E 的坐标；（2）点E 关于点A 的对称点为点D ，点P 从C 点出发，以每秒1个单位的速度沿射线CB 运动，设P 点的运动时间为t 秒，△PBD 的面积为S ，用含t 的代数式表示S ；（3）在（2）的条件下，点M 为平面内一点，点P 在线段BC 上运动时，作∠PDO 的平分线交y 轴于点N ，t 为何值时，四边形DPNM 为矩形？并求此时点M 的坐标．【分析】（1）先确定出点A 的坐标，进而得出OA ，最后在Rt △OEF 中，利用勾股定理求出OE 即可得出点E 的坐标；（2）分两种情况，用三角形的面积公式即可解决问题；（3）先利用对称求出点D 的坐标，进而得出OD ，由角平分线的性质定理得出DP ＝OD 求出点P 的坐标，进而求出直线PD ，MD 的解析式，再利用勾股定理求出点N 的坐标，进而得出直线MN 的解析式，联立直线DM和MN的解析式即可得结论．【解答】解：（1）在矩形OABC中，BC∥OA，B（6，8），∴A（6，0），∴OA＝6，设OE＝a，∴EF＝AE＝OA﹣OE＝6﹣a，∵F（0，2√3），∴OF＝2√3，在Rt△AEF中，根据勾股定理得，OE2+OF2＝EF2，∴a2+12＝（6﹣a）2，∴a＝2，∴E（2，0）；（2）由（1）知，E（2，0），∴AE＝4，∵点D是点E关于点A的对称点，∴D（10，0），∵BC∥OA，B（6，8），OC＝AB＝8，∴P（t，8），PB＝|t﹣6|①当点P在边BC上时，如图1，∴0≤t＜6，∴PB＝6﹣t，∴S＝S△PBD=12PB•OC=12×（6﹣t）×8＝﹣4t+24，②当点P在CB的延长时，如图2，∴t＞6，∴PB＝t﹣6，∴S＝S△PBD=12PB•OC=12×（t﹣6）×8＝4t﹣24，即：S={−4t+24(0＜t＜6) 4t−24(t＞6)，（3）如图3，由（2）知，D（10，0），∴OD ＝10，∵四边形DPNM 是矩形，∴∠DPN ＝90°＝∠DON ，∴NP ⊥DP ，NO ⊥OD ，∵DN 是∠PDO 的平分线，∴NO ＝NP ，在Rt △NDO 和Rt △NDP 中，{DN =DN NO =NP， ∴Rt △NDO 和Rt △NDP （HL ），∴DP ＝OD ＝10，∵P （t ，8），D （10，0），∴DP 2＝（t ﹣10）2+64＝100，∴t ＝16（由于点P 在线段BC 上，所以舍去）或t ＝4，∴P （4，8），∵D （10，0），∴DP 的解析式为y =−43x +403，∵DM ⊥DP ，∴直线DM 的解析式为y =34x 152①，设N （0，n ），∴ON ＝n ，∴PN ＝n ，CN ＝OC ﹣ON ＝8﹣n ，∵P （4，8），∴CP ＝4，在Rt △CNP 中，根据勾股定理得，CN 2+CP 2＝PN 2，∴（8﹣n ）2+16＝n 2，∴n ＝5，∴N （0，5），∵PD ∥NM ，∴直线NM 的解析式为y =−43x +5②，联立①②解得，x＝6，y＝﹣3，∴M（6，﹣3）．【点评】此题是四边形综合题，主要考查了矩形的性质，角平分线的性质定理，待定系数法，勾股定理，解（1）的关键是利用勾股定理求出OE，解（2）的关键是分两种情况讨论计算，解（3）的关键是求出点P的坐标．【题型3 菱形的存在性问题】1．（2023春•江阴市期中）将矩形OABC如图所示放置在第一象限，点B的坐标为（3，4），一次函数y=−23x+b的图象与边OC、AB分别交于点D、E，并且满足OD＝BE，点M是线段DE上的一个动点．（1）填空：b＝；（2）设点N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点M的坐标．【分析】（1）分别表示出D和E点的坐标，根据OD＝BE列出等式即可求出b的值；（2）分当OD为菱形一边时和当OD为菱形一条对角线时两种情况，根据菱形邻边相等或对角线的对称性等特点找到等量列出等式即可求出M点坐标．【解答】解：（1）∵点B的坐标为（3，4），矩形OABC放置在第一象限，∴A（3，0），C（0，4），D（0，b），E（3，b﹣2），∵OD＝BE，∴b＝4﹣（b﹣2），∴b＝3；（2）①当OD 为菱形一边时，OD ＝OM ，如图所示：设M(m ，3−23m)， ∴m 2+(3−23m)2=32，解得，m =3613＜3或m ＝0（不合题意，舍去），∴M(3613，1513)；②当OD 为菱形一条对角线时，过OD 中点P 作PM ⊥OD 交直线CE 于点M ，∴点M 的纵坐标为32， ∴32=−23c +3， ∴c =94＜3，∴点M(94，32)，综上，符合条件的点M 有两个，其坐标分别为(94，32)或(3613，1513)．【点评】本题属于一次函数综合题，考查了一次函数基本性质以及菱形的基本性质等知识，熟练掌握好一次函数的基本性质以及平面直角坐标系中点的综合变化，并能将菱形特点与平面直角坐标系坐标变化相互结合，灵活运用是解决本题的关键．2．（2023•赫山区校级一模）如图，在平面直角坐标系中，直线y =12x +3分别与x 轴、y 轴交于点B ，C ，且与直线y =−12x 交于A ．（1）分别求出A ，B ，C 的坐标；（2）若D 是线段OA 上的点，且△COD 的面积为3，求直线CD 的函数解析式；（3）在（2）的条件下，设P 是射线CD 上的点，在平面内是否存在点Q ，使以O ，C ，P ，Q 为顶点的四边形是菱形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．【分析】（1）由函数图象上点的坐标特征直接求解即可；（2）求出D 点坐标，再由待定系数法求解即可；（3）设P （t ，t +3），Q （x ，y ），根据对角线的情况，再分三种情况讨论即可．【解答】解：（1）令x ＝0，y ＝3，∴C （0，3），令y ＝0，x ＝﹣6，∴B （﹣6，0），联立方程组{y =12x +3y =−12x ， 解得{x =−3y =32， ∴A （﹣3，32）； （2）由 S △COD =12OC ⋅ℎOC =12×3ℎOC =3，∴h OC ＝2，∴当x ＝﹣2时，y ＝1，∴D （﹣2，1），设直线CD 的函数解析式为y ＝kx +b （k ≠0），∴{b =3−2k +b =1， 解得{k =1b =3， ∴直线CD 的函数解析式为y ＝x +3；（3）存在点Q ，使以O ，C ，P ，Q 为顶点的四边形是菱形，理由如下：设P （t ，t +3），Q （x ，y ），①当PQ 为菱形对角线时，OP ＝PC ，∴{t +x =0t +3+y =3t 2+(t +3)2=t 2+t 2，解得{ t =−32x =32y =32， ∴Q （32，32）； ②当PO 为菱形对角线时，CO ＝PC ，∴{t =xt +3=y +39=t 2+t 2，解得{ t =32√2x =32√2y =32√2（舍）{ t =−32√2x =−32√2y =−32√2， ∴Q （−32√2，−32√2）；③当PC 为菱形对角线时，OP ＝OC ，∴{t =xt +6=y t 2+(t +3)2=9，解得{t =0x =0y =6（舍）或{t =−3x =−3y =3，∴Q （﹣3，3）；综上所述：满足条件的点Q 的坐标是（32，32）或（−32√2，−32√2）或（﹣3，3）． 【点评】本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，菱形的判定及性质，分类讨论是解题的关键．3．（2023春•新吴区期中）如图矩形OABC 的顶点A 、C 分别在x 轴、y 轴的正半轴上，点B 的坐标为（5，7），一次函数y =−13x +5的图象与边OC 、AB 分别交于D 、E 两点，点M 是线段DE 上的一个动点．（1）则BE 的长为 ；（2）连接OM ，若△ODM 的面积为152，求点M 的坐标；（3）在（2）的条件下，设点P 是x 轴上一动点，点Q 是平面内的一点，以O 、M 、P 、Q 为顶点的四边形是菱形，直接写出点Q 的坐标．【分析】（1）把点E 的横坐标代入一次函数解析式求出纵坐标得到AE 的长度，进而得到BE ＝AB ﹣AE 的长度；（2）根据△ODM 的面积为152列方程求解即可；（3）画出菱形，找到点Q 的位置，根据菱形的性质分情况分别计算即可．【解答】解：（1）∵四边形OABC 是矩形，∴AB ⊥x 轴，∵B （5，7），AB ＝7，∴E 点的横坐标为5，∵一次函数y =−13x +5的图象过点E ，∴当x ＝5时，y =−53+5=103，∴AE =103，∴BE ＝AB ﹣AE ＝7−103=113，故答案为：113；（2）∵一次函数y =−13x +5的图象交y 轴于点D ，∴当x ＝0时，y ＝5，∴D （0，5），∴OD ＝5，∵△ODM的面积为15 2，∴12×5×x M=152，∴x M＝3，当x＝3时，y=−13×3+5＝4，∴M（3，4）；（3）∵M（3，4），∴OM=√32+42=5，如图，当OM为菱形的边长时，QM∥x轴，QM＝OM＝5，∴Q（﹣2，4）或（8，4）；如图，当OP是菱形的对角线时，MQ⊥x轴于点F，FQ＝FM＝4，∴Q（3，﹣4）；如图，当OM是菱形对角线时，QM∥x轴，QM＝OQ，设Q（q，4），∵QM2＝OQ2，∴（3﹣q）2＝q2+42，解得：q=−7 6，∴Q （−76，4）；综上所述，点Q 的坐标为：（﹣2，4）或（8，4）或（3，﹣4）或（−76，4）． 【点评】本题考查一次函数综合题，考查分类讨论的思想，画出菱形，找到点Q 的位置，根据菱形的性质分情况分别计算是解题的关键．4．（2022春•荔湾区校级期中）如图1，在平面直角坐标系中，直线L 2：y =−12x +6与L 1：y =12x 交于点A ，分别与x 轴、y 轴交于点B 、C ．（1）分别求出点A 、B 、C 的坐标；（2）若D 是线段OA 上的点，且△COD 的面积为12，求直线CD 的函数表达式；（3）在（2）的条件下，设P 是直线CD 上的点，在平面内是否存在其它点Q ，使以O 、C 、P 、Q 为顶点的四边形是菱形？若存在，求出点Q 的坐标；若不存在，请说明理由．【分析】（1）构建方程组确定交点A 的坐标，利用待定系数法确定B ，C 两点坐标即可．（2）设D （m ，12m ），利用三角形的面积公式，构建方程求出m 的值，再利用待定系数法即可解决问题． （3）分三种情形：根据OC ＝PC ，设P （m ，12m ），利用两点间距离公式，构建方程求出m 即可．如图2﹣1中，当OC 为菱形的对角线时，OC 垂直平分线段P ′Q ′，利用对称性解决问题即可．当OC ＝OP 时，P ″（6，0），Q ″（6，6）．【解答】解：（1）由{y =−12x +6y =12x，解得{x =6y =3， ∴A （6，3）．∵y =−12x +6与分别与x 轴、y 轴交于点B 、C ， ∴C （0，6），B （12，0）；（2）设D （m ，12m ）， 由题意：OC ＝6，△COD 的面积为12，∴12×6×m ＝12， ∴m ＝4，∴D （4，2），∵C （0，6），设直线CD 的解析式为y ＝kx +b ，则有{4k +b =2b =6， 解得{k =−1b =6， ∴直线CD 的解析式为y ＝﹣x +6；（3）当四边形OCPQ ∴OC ＝PC ＝6，设P （m ，﹣m +6），∴m 2+m 2＝36，∴m ＝3√2或﹣3√2，∴P （3√2，﹣3√2+6），∵PQ ∥OC ，PQ ＝OC ，∴Q （3√2，﹣3√2），如图2﹣1中，当OC 为菱形的对角线时，OC 垂直平分线段P ′Q ′，易知P ′（3，3），Q ′（﹣3，3），∴满足条件的点Q ′的坐标为（﹣3，3）．当OC ＝OP 时，P ″（6，0），Q ″（6，6）．综上所述，满足条件的点Q 的坐标为（3√2，﹣3√2）或（﹣3，3）或（6，6）．【点评】本题属于一次函数综合题，考查了待定系数法，三角形的面积，菱形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．【题型4 正方形的存在性问题】1．（2022•前进区二模）△P AC在平面直角坐标系中的位置如图所示，AP与y轴交于点B（0，2），点P的坐标为（﹣1，3），线段OA，OC的长分别是方程x2﹣9x+14＝0的两根，OC＞OA．（1）求线段AC的长；（2）动点D从点O出发，以每秒1个单位长度的速度沿x轴负半轴向终点C运动，过点D作直线l与x轴垂直，设点D运动的时间为t秒，直线l扫过四边形OBPC的面积为S，求S与t的关系式；（3）M为直线l上一点，在平面内是否存在点N，使以A，P，M，N为顶点的四边形为正方形？若存在，请直接写出点的坐标；若不存在，请说明理由．【分析】（1）解方程可求得OA，OC的长，则可求得A、C的坐标，利用两点之间的距离公式即可求解；（2）分两种情况：①当0＜t≤1时；②当1＜t≤7时，利用梯形的面积公式即可求解；（3）分两种情况：①AP为正方形的对角线时，②AP为正方形的边时，根据正方形以及等腰直角三角形的性质，可求得N点坐标．【解答】解：（1）解方程x2﹣9x+14＝0可得x＝2或x＝7，∵线段OA，OC的长分别是方程x2﹣9x+14＝0的两根，且OC＞OA，∴OA＝2，OC＝7，∴AC＝2+7＝9，∴线段AC的长为：7；（2）①如图，当0＜t≤1时，点E（﹣t，t+2），∴S=S梯形OBDE =12t(2+t+2)=12t2+2t（0＜t≤1）；②如图，当1＜t≤7时，设直线CP解析式为：y＝mx+n，∵C（﹣7，0），点P的坐标为（﹣1，3），代入得{−7m+n=0−m+n=3，解得：{m=12n=72，∴直线CP解析式为：y=12x+72；设E（﹣t，−12t+72），∴DE=−12t+72，∴S＝S梯形OBPH+S梯形HPED=12×（2+3）×1+12（t﹣1）（−12t+72+3）=−14t2+72t−34（1＜t≤7），∴S=12t2+2t(0＜t≤1)或S=−14t2+72t−34(1＜t≤7)；（3）存在，分两种情况：①AP为正方形的对角线时，如图，∵A（2，0），B（0，2），∴∠OAB＝45°，∵四边形AMPN是正方形，∴∠P AN＝45°，∠NAM＝90°，∴∠OAB+∠P AN＝90°，∴点M在x轴上，NA⊥x轴，NP∥c轴，∴N（2，3）；②AP为正方形的边时，如图，∵∠OAB＝45°，四边形AMPN是正方形，∴∠NAO＝∠OAB＝45°，AP＝AN，∴HN＝PH＝3，∴N（﹣1，﹣3），∵MH＝AH＝3，∴M（﹣4，0），∴N（﹣4，0）或（﹣1，﹣3），综上可知，存在满足条件的N点，其坐标为（2，3）或（﹣4，0）或（﹣1，﹣3）．【点评】本题考查了一次函数的性质、一元二次方程、勾股定理、待定系数法、正方形的性质等知识．在（1）中求得OA、OC的长是解题的关键，在（2）中求得P点坐标是解题的关键，在（3）中分类思想的运用是解题的关键．2．如图，在平面直角坐标系中，OB和OC的长是方程x2﹣15x+36＝0的两个根，且OB＜OC．∠BAC＝90°，D是x轴上一点，且将△ADC沿AD翻折，AC恰好落在y轴上的AE处．（1）求点A的坐标；（2）求直线CE的解析式；（3）M是直线AC上一点，在平面上是否存在一点N，使以A，B，M，N为顶点的四边形为正方形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）解方程得出OB和OC的值，证△AOB∽△COA，根据线段比例关系求出OB即可确定B 点的坐标；（2）由（1）得出C点和E点的坐标，用待定系数法求出直线CE的解析式即可；（3）用待定系数法求出直线AC的解析式，平移AC过B点，设出N点坐标，根据BN＝AB确定N点坐标即可．【解答】解：（1）解方程x2﹣15x+36＝0，得x＝3或x＝12，∵OB＜OC，∴OB＝3，OC＝12，∵∠BAO+∠ABO＝90°，∠BAO+∠CAO＝90°，∴∠ABO ＝∠CAO ，又∵∠AOB ＝∠COA ＝90°，∴△AOB ∽△COA ，∴OB OA =OA OC ，∴OA =√OB ⋅OC =√3×12=6，∴A （0，6）；（2）由（1）知A （0，6），C （12，0），∴AC =√62+122=6√5，∴OE ＝AC ﹣OA ＝6√5−6，∴E （0，6﹣6√5），设直线CE 的解析式为y ＝kx +b ，代入C 点和E 点坐标得{12k +b =0b =6−6√5， 解得{k =12√5−12b =6−6√5， ∴直线CE 的解析式为y ＝（12√5−12）x +6﹣6√5；（3）存在点N ，使以A ，B ，M ，N 为顶点的四边形为正方形，理由如下：①若M 点在线段AC 上，∵∠BAM ＝90°，∴存在四边形ABNM 为正方形，设直线AC 的解析式为y ＝sx +t ，代入A 点和C 点的坐标得{t =612s +t =0， 解得{s =−12t =6，∴直线AC 的解析式为y =−12x +6，平移直线AC与直线BN重合，则直线BN得解析式为y=−12x+m，∵B（﹣3，0），∴m=−3 2，即直线BN得解析式为y=−12x−32，设N（n，−n2−32），∵四边形ABNM是正方形，∴BN2＝AB2，即（n+3）2+（−n2−32）2＝32+62，解得n＝3或n＝﹣9（舍去），故N点得坐标为（3，﹣3），②若M点在CA延长线上，由①知，此时N点也在直线y=−12x−32上，设N（p，−p2−32），∵四边形ABNM是正方形，∴BN2＝AB2，即（p+3）2+（−p2−32）2＝32+62，解得p＝3（舍去）或p＝﹣9，故N点得坐标为（﹣9，3），∴点N的坐标为（3，﹣3）或（﹣9，3）时四边形ABNM是正方形．【点评】本题主要考查一次函数的综合题型，熟练掌握待定系数法求函数解析式及一次函数的性质是解题的关键．3．（2021春•柳南区校级期末）如图，直线L 1：y ＝x +1与直线L 2：y ＝﹣x +5相交于点C 直线L 1与x 轴相交于点A ，直线L 2与x 轴相交于点B ．（1）求三角形ABC 的面积；（2）若经过点C 的一条直线交x 轴于D ，直线CD 把三角形ABC 分成两个三角形，且这两个三角形面积的比为1：2，请直接写出点D 的坐标；（3）假设G 是直线y ＝x +1上的点，在坐标平面上是否存在一点Q ，使以A ，B ，Q ，G 为顶点的四边形是正方形，若存在求出点Q 的坐标，若不存在请说明理由．【分析】（1）利用待定系数法求出A 、B 、C 三点坐标即可解决问题；（2）分两种情形分别求解即可；（3）分两种情形讨论①在L 1上取点G （G 异于A ），且CG ＝CA ，在L 2上取点Q （Q 异于B ），且CQ ＝CB ，可以证明四边形ABGQ ②当G 与C 重合时，以AB 为对称轴作G 的对称点Q ，于是四边形AQBG 为正方形．【解答】解：（1）在y ＝x +1中，当y ＝0时，则x ＝﹣1∴A （﹣1，0）在y ＝﹣x +5中当y ＝0时，则x ＝5B （5，0）∴AB ＝OA +OB ＝6，由{y =x +1y =−x +5解得{x =2y =3， ∴C （2，3）∴作CE⊥x轴于E．∴E（2，0）∴CE＝3∴S△ABC=12•AB•CE=12×6×3＝9，（2）由题意A（﹣1，0），B（5，0），AD＝2BD或BD＝2AD，可得D（1，0）或D（3，0）．（3）设y＝x+1交y轴于F，则F（0，1）．∴OF＝OA∴∠OAF＝45°同理∠ABC＝45°∴∠ACB＝90°∴CA＝CB，在L1上取点G（G异于A），且CG＝CA，在L2上取点Q（Q异于B），且CQ＝CB∴CG＝CA＝CQ＝CB，又∵AG⊥BQ，∴四边形ABGQ为正方形，又∵A（﹣1，0）AB＝AQ＝6当G与C重合时，以AB为对称轴作G的对称点Q，于是四边形AQBG为正方形．又∵G（2，3），∴Q（2，﹣3）综合上述：Q（﹣1，6）或Q（2，﹣3）．【点评】本题考查一次函数综合题、三角形的面积、正方形的性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题，属于中考压轴题．【题型5 四边形存在性的压轴题】1．（2023春•宜兴市期中）如图，在平面直角坐标系中，已知A（0，4），点B、C都在x轴上，BC＝12，AD∥BC，CD所在直线的函数表达式为y＝﹣x+9，E是BC的中点，点P是BC边上一个动点．（1）当PB＝时，以点P、A、D、E为顶点的四边形为平行四边形；（2）点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形能否构成菱形？试说明理由．【分析】（1）若以点P、A、D、E为顶点的四边形为平行四边形，则AD＝PE，有两种情况：①当P在E的左边，利用已知条件可以求出BP的长度；②当P在E的右边，利用已知条件也可求出BP的长度；（2）以点P、A、D、E为顶点的四边形能构成菱形．由（1）知，当BP＝11时，以点P、A、D、E为顶点的四边形是平行四边形，根据已知条件分别计算一组邻边，证明它们相等即可证明是菱形．【解答】解：（1）∵AD∥BC，点A坐标是（0，4），CD所在直线的函数关系式为y＝﹣x+9，∴D点的纵坐标为4，y＝4时，4＝﹣x+9，x＝5，∴D点的横坐标为5，∵CD所在直线的函数关系式为y＝﹣x+9，y＝0时，0＝﹣x+9，x＝9，∴C（9，0），∴OC＝9，作DN⊥BC交于N，如图1所示，则四边形OADN为矩形，∴CN＝OC﹣ON＝OC﹣AD＝9﹣5＝4，DN＝4，∴△DNC为等腰直角三角形，∴CD=√42+42=4√2，若以点P、A、D、E为顶点的四边形为平行四边形，则AD＝PE＝5，有两种情况：①当P在E的左边，∵E是BC的中点，∴BE＝6，∴PB＝BE﹣PE＝6﹣5＝1；②当P在E的右边，PB＝BE+PE＝6+5＝11；故当PB＝1或11时，以点P、A、D、E为顶点的四边形为平行四边形，故答案为：1或11；（2）点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形能构成菱形，理由如下：①当BP＝1时，此时CN＝DN＝4，NE＝5﹣3＝2，∴DE=√DN2+NE2=√42+22=2√5≠AD，故不能构成菱形．②当BP＝11时，以点P、A、D、E为顶点的四边形是平行四边形，∴EP＝AD＝5，过D作DN⊥BC于N，如图2所示：由（1）得：DN＝CN＝4，∴NP＝BP﹣BN＝BP﹣（BC﹣CN）＝11﹣（12﹣4）＝3．∴DP=√DN2+NP2=√42+32=5，∴EP＝DP＝AD＝5，故此时平行四边形PDAE是菱形，即以点P、A、D、E为顶点的四边形能构成菱形．【点评】本题是一次函数综合题，考查了等腰直角三角形的判定与性质、勾股定理、平行四边形的判定、矩形的判定、菱形的判定等知识，解题的关键是学会用分类讨论的思想思考问题，灵活运用所学知识解决问题，属于中考压轴题．2．如图，已知直线y=−1x+3与x轴，y轴分别交于点A，B，以AB为直角边，∠B为直角作等腰直角三2角形ABC（点C在第一象限）．（1）求点A，B，C坐标；（2）点D A，B，C，D四点围成的四边形为正方形时，求点D坐标；（3）点P为x轴上一动点，点Q为线段AC上一动点，是否存在四边形BP AQ为平行四边形？若存在，求出P，Q点的坐标，若不存在，说明理由．【分析】（1）利用待定系数法求出A，B的坐标，过点C作CH⊥y轴于点H．构造全等三角形求出点C 的坐标；（2）利用正方形的性质，平移变换的性质求解即可；（3）求出直线AC 的解析式，再利用平行四边形的性质求解即可．【解答】解：（1）对于直线y =−12x +3，令y ＝0，得到x ＝6，∴A （6，0），令x ＝0，得到y ＝3，∴B （0，3），∴OA ＝6，OB ＝3，过点C 作CH ⊥y 轴于点H ．∵∠BHC ＝∠CBA ＝∠AOB ＝90°，∴∠CBH +∠ABO ＝90°，∠ABO +∠BAO ＝90°，∴∠CBH ＝∠BAO ，在△BHC 和△AOB 中，{∠BHC =∠AOB∠CBH =∠BAO BC =AB，∴△BHC ≌△AOB （AAS ），∴CH ＝OB ＝3，BH ＝AO ＝6，∴OH ＝9，∴C （3，9）；（2）∵四边形ABCD 是正方形，∴BC ＝AD ，BC ∥AD ，∵点B 向右平移3个单位，向上平移6个单位得到点C ，∴点A 向右平移3个单位，向上平移6个单位得到点D ，∴D （9，6）；（3）∵A （6，0），C （3，9），设直线AC 的解析式为y ＝kx +b ，则有{6k +b =03k +b =9， 解得{k =−3b =18， ∴直线AC 的解析式为y ＝﹣3x +18，∵四边形APBQ 是平行四边形，∴BQ ∥AP ，BQ ＝AP ，∴Q（5，3），∴BQ＝AP＝5，∴P（1，0）．【点评】本题属于一次函数综合题，考查了一次函数的性质，正方形的性质，平行四边形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3．（2023•武陵区一模）如图，在平面直角坐标系中，直线AB交x轴于点A（﹣2，0），交y轴于点B（0，4），直线y＝kx+b经过点B且交x轴正半轴于点C，已知△ABC面积为10．（1）点C的坐标是（，），直线BC的表达式是；（2）如图1，点E为线段AB中点，点D为y轴上一动点，连接DE，以DE为直角边作等腰直角三角形△EDF，且DE＝DF，在点的运动过程中，当点F落在直线BC上时，求点D的坐标；（3）如图2，若G为线段BC上一点，且满足S△ABG＝S△ABO，点M为直线AG上一动点，在x轴上是否存在点N，使以点B，C，M，N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）由△ABC 面积为10，可得AC ＝5，即可求C 点坐标，再将点B 与C 代入y ＝kx +b ，解二元一次方程组可求y =−43x +4；（2）当D 点在E 上方时，过点D 作MN ⊥y 轴，过E 、F 分别作ME 、FN 垂直与x 轴，与MN 交于点M 、N ，由△EDF 是等腰直角三角形，可证得△MED ≌△NDF （AAS ），设D （0，y ），F （m ，−43m +4），E （﹣1，2），由ME ＝y ﹣2，MD ＝1，DN ＝y ﹣2，NF ＝1，得到m ＝y ﹣2，y ＝1+（−43m +4）＝5−43m ，求出D （0，237）；当点D 在点E 下方时，过点D 作PQ ⊥y 轴，过P 、Q 分别作PE 、FQ 垂直与x 轴，与PQ 交于点P 、Q ，同理可证△PED ≌△QDF （AAS ），设D （0，y ），F （m ，−43m +4），得到PE ＝2﹣y ，PD ＝1，DQ ＝2﹣y ，QF ＝1，所以m ＝2﹣y ，1=−43m +4﹣y ，求得D （0，﹣1）； （3）连接OG ，由S △ABG ＝S △ABO ，可得OG ∥AB ，求出AB 的解析式为y ＝2x +4，所以OG 的解析式为y＝2x ，可求出G （65，125），进而能求出AG 的解析式为y =34x +32，设M （t ，34t +32），N （n ，0）， ①当BC 、MN 分别为对角线时，BC 的中点为（32，2），MN 的中点为（t+n 2，38t +34），求得N （−13，0）；②当BM 、CN 分别为对角线时，BM 的中点为（t 2，38t +114），CN 的中点为（3+n 2，0），求得N （−313，0）；③当BN 、CM 分别为对角线时，BN 的中点为（n 2，2），CM 的中点为（t+32，38t +34），求得N （193，0）．【解答】解：（1）∵△ABC 10，∴12×AC ×OB =12×AC ×4＝10， ∴AC ＝5，∵A （﹣2，0），∴C （3，0），将点B 与C 的坐标代入y ＝kx +b ，可得{b =43k +b =0， ∴{k =−43b =4，∴y =−43x +4，故答案为（3，0），y =−43x +4；（2）当D 点在E 上方时，过点D 作MN ⊥y 轴，过E 、F 分别作ME 、FN 垂直于x 轴，与MN 交于点M 、N ，。

2024年中考数学专题复习：一次函数的图像与性质一、选择题（本大题共10道小题）1. (2023•沈阳)一次函数y ＝-3x+1的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限2. (2023八上·太原期中)课堂上,同学们研究正比例函数y=-x 的图象时,得到如下四个结论,其中错误的是( )A.当x=0时,y=0,所以函数y=-x 的图象经过原点B.点P(t,-t)一定在函数y=-x 的图象上C.当x>0时,y<0,当x<0时,y>0,所以函数y=-x 的图象经过二、四象限D.将函数的图象向左平移2个单位,即可得到函数y=-x+2的图象3. (2023·太原模拟)已知y 是x 的正比例函数,当x ＝3时,y ＝－6,则y 与x 的函数关系式为( )A.y ＝2xB.y ＝－2xC.y ＝12 xD.y ＝－12x 4. (2023•柳州)若一次函数y ＝kx+b 的图象如图所示,则下列说法正确的是( )A.k ＞0B.b ＝2C.y 随x 的增大而增大D.x ＝3时,y ＝0 5. (2023·贵州毕节·二模)已知正比例函数y=kx(k ≠0)的图象过点(2,3),把正比例函数y=kx(k ≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )A. B. C.D. 6. (2023秋•会宁县)已知关于x 的一次函数y ＝(k 2+1)x-2图象经过点A(3,m)、B(-1,n),则m,n 的大小关系为( )A.m ≥nB.m ＞nC.m ≤nD.m ＜n7. (2023·随州模拟)如图,在平面直角坐标系中,动点A,B 分别在x 轴上和函数y ＝x 的图象上,AB ＝4,CB ⊥AB,BC ＝2,则OC 的最大值为( )A.222B.224C.2 5D.2528. (2023·鄂州中考)数形结合是解决数学问题常用的思想方法.如图,直线y ＝2x －1与直线y ＝kx ＋b(k ≠0)相交于点P(2,3).根据图象可知,关于x 的不等式2x －1＞kx ＋b 的解集是( )A.x ＜2B.x ＜3C.x ＞2D.x ＞39. (2023•贵阳)小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线y ＝k n x+b n (n ＝1,2,3,4,5,6,7),其中k 1＝k 2,b 3＝b 4＝b 5,则他探究这7条直线的交点个数最多是( )A.17个B.18个C.19个D.21个10. (2023·湖南永州·中考真题)已知点P(x 0,y 0)和直线y=kx+b,求点P 到直线y=kx+b 的距离d 可用公式0021kx y b d k -+=+计算.根据以上材料解决下面问题:如图,⊙C 的圆心C 的坐标为(1,1),半径为1,直线l 的表达式为y=-2x+6,P 是直线l 上的动点,Q 是⊙C 上的动点,则PQ 的最小值是( )A.355B.3515-C.6515-D.2二、填空题（本大题共8道小题）11. (2023•毕节市)将直线y ＝-3x 向下平移2个单位长度,平移后直线的解析式为 .12. (2023·四川成都市)在正比例函数y=kx 中,y 的值随着x 值的增大而增大,则点P(3,k)在第_____象限.13. (2023·贵州黔西·二模)如图,平面直角坐标系中,经过点B(-4,0)的直线y ＝kx+b 与直线y ＝mx+2相交于点3(,1)2A --,则关于x 的方程mx+2＝kx+b 的解为________.14. (2023秋•宁化县)若函数y ＝4x ﹣1与y ＝﹣x+a 的图象交于x 轴上一点,则a 的值为( )A.4B.﹣4C.D.±415. (2023黔西南州)如图,正比例函数的图象与一次函数y ＝－x ＋1的图象相交于点P,点P 到x 轴的距离是2,则这个正比例函数的解析式是 .16. (2023·湖南湘西·中考真题)在平面直角坐标系中,O 为原点,点A(6,0),点B 在y 轴的正半轴上,∠ABO=30o .矩形CODE 的顶点D,E,C 分别在OA,AB,OB 上,OD=2.将矩形CODE 沿x 轴向右平移,当矩形CODE 与△ABO 重叠部分的面积为63时,则矩形CODE 向右平移的距离为___________.17. (2023•毕节市)如图,在平面直角坐标系中,点N 1(1,1)在直线l:y ＝x 上,过点N 1作N 1M 1⊥l,交x 轴于点M 1;过点M 1作M 1N 2⊥x 轴,交直线于N 2;过点N 2作N 2M 2⊥l,交x 轴于点M 2;过点M 2作M 2N 3⊥x 轴,交直线l 于点N 3;…,按此作法进行下去,则点M 2023的坐标为 .18. (2023•泰安)如图,点B 1在直线l:y ＝21x 上,点B 1的横坐标为2,过点B 1作B 1A 1⊥l,交x 轴于点A 1,以A 1B 1为边,向右作正方形A 1B 1B 2C 1,延长B 2C 1交x 轴于点A 2;以A 2B 2为边,向右作正方形A 2B 2B 3C 2,延长B 3C 2交x 轴于点A 3;以A 3B 3为边,向右作正方形A 3B 3B 4C 3,延长B 4C 3交x 轴于点A 4;…;照这个规律进行下去,则第n 个正方形A n B n B n+1∁n 的边长为 (结果用含正整数n 的代数式表示).三、解答题（本大题共6道小题）19. (2023秋•安徽月考)已知经过点A(4,-1)的直线y ＝kx+b 与直线y ＝-x 相交于点B(2,a),求两直线与x 轴所围成的三角形的面积.20. (2023春•西丰县)如图,一次函数y＝kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.(1)求k,b的值,并写出一次函数的解析式;(2)求点C的坐标.21. (2023秋•兰州)如图,直线l1:y＝-x+4分别与x轴,y轴交于点D,点A,直线l2:y x+1与x轴交于点C,两直线l1,l2相交于点B,连AC.(1)求点B的坐标和直线AC的解析式;(2)求△ABC的面积.22. (2023•滨州)如图,在平面直角坐标系中,直线y x﹣1与直线y＝﹣2x+2相交于点P,并分别与x轴相交于点A、B.(1)求交点P的坐标;(2)求△PAB的面积;(3)请把图象中直线y＝﹣2x+2在直线y x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.23. (2023·河北中考真题)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l ,如图.而某同学为观察k,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l '.(1)求直线l 的解析式; (2)请在图上画出．．直线l '(不要求列表计算),并求直线l '被直线l 和y 轴所截线段的长; (3)设直线y=a 与直线l ,l '及y 轴有三个不同的交点,且其中两点关于第三点对称,直接．．写出a 的值.24. (2023•黑龙江)如图,矩形ABOC 在平面直角坐标系中,点A 在第二象限内,点C 在y 轴正半轴上,OA 2-9x+20＝0的两个根.解答下列问题:(1)求点A 的坐标;(2)若直线MN 分别与x 轴,AB,AO,y 轴交于点D,M,F,N,E,S △AMN ＝2,tan ∠AMN ＝1,求直线MN 的解析式;(3)在(2)的条件下,点P 在第二象限内,使以E,F,P,Q 为顶点的四边形是正方形？若存在;若不存在,请说明理由.。

一次函数与四边形教学目标：知识与技能：1.利用一次函数比例系数k 值特征证明直线位置关系与四边形的形状；2.利用平行四边形的性质，求一次函数解析式.过程与方法：通过一次函数与四边形的想和转换，感受数形结合的思想方法. 情感态度与价值观：通过思考，让学生体会学习数学方法对于学习数学的重要性.教学重难点：教学重点：一次函数比例系数k 值与平行四边形的性质与判定的相互转换. 教学难点：利用数形结合思想解决函数与几何问题.教学过程：课前一练：1.若一次函数的图像经过点），（01A 和点），（22-B ，则这个一次函数的解析式为 .2.已知直线b kx y l +=11：与直线x y l 2:22=相互平行，且经过点）（1,2，则直线1l 的函数解析式为 .知识回顾：问题1：平面直角坐标系中求一次函数解析式的方法？ 问题2：待定系数法求一次函数解析式的两种常见类型？一、利用一次函数证明四边形的形状例1：如图，直线b kx y +=经过），（3203-A 、），（45-B 两点，过点A 作x AD ⊥轴点D ，过点B 作y BC ⊥轴于点C ，AB 与x 轴相交于点E .（1）求点E 坐标；（2）证明：AB CD ∥；（3）判断四边形BCDE 的形状.二、利用特殊四边形的性质求一次函数解析式例2：如图，一次函数4y的图象与x、y轴=x2+分别相交于点A、B，以AB为边在直线AB右侧作正方形四边形ABCD．（1）求点A、B、D的坐标；（2）求直线BD的函数解析式；（3）求直线AC的函数解析式．例3：如图所示，矩形ABCD中，5AD，==AB，3点A的坐标为）=：.l+（1,2，作直线bykx（1）当3k时，若直线l与矩形ABCD相交，求-=b的取值范围；（2）在（1）的条件下，若直线l平分矩形ABCD 面积，求直线l的解析式；（3）当2b时，若直线l平分矩形ABCD面积，=-求直线l的解析式；（4）在（3）的条件下，若直线l与矩形ABCD相交，求k的取值范围.。

中考数学复习考点知识讲解与练习专题15 一次函数与四边形一次函数与几何问题是考试中的常考点，也是是考热点，对刚进入一次函数学习的学生来讲，让其体会到了几何图形与函数结合在一起解决问题具有十分重要的意义，本中考数学复习考点知识讲解与练习 专题在平面坐标系下把直线与几何图形融入一体，充分体现数形结合的思想，本中考数学复习考点知识讲解与练习 专题的题型特点：从单一知识点到多个知识点，从简单图形到复杂图形，让几何图形性质与函数的性质有机结合，汇集了一次函数与四边形相关的题型，对拓展学生思维，对提升学生的综合能力十分有益。

一、单选题1．如图，在平面直角坐标系中，四边形OABC 为菱形，()0,0O ，()4,0A ，60AOC ∠=，则对角线交点E 的坐标为( )A ．(B ．)2C ．)D ．(2．如图，在平面直角坐标系中，点()() 30 0,4A B -，，，将AOB 沿x 轴向右平移得DEC ,此时四边形ABCD 是菱形，则点C 的坐标是（）A ．()5,4B ．()4,5C ．()5,3D ．()3,53．如图，在平面直角坐标系xOy 中，一次函数142y x =-+的图象与x 轴、y 轴分别相交于点A ，B ，点P 的坐标为(1,1)m m +-，且点P 在ABO ∆的内部，则m 的取值范围是（）A ．13m <<B ．15mC ．15mD ．1m 或3m <4．如图，在平面直角坐标系中，四边形OABC 是菱形，点C 的坐标为()2,3，则菱形OABC 的面积是（ ）A B C D ．5．如图，在平面直角坐标系xOy 中，四边形ABCD 是菱形，120ABC ∠=︒，点B 的坐标为(0,2)-，则菱形ABCD 的面积为（）A ．16B ．32C ．D ．6．如图，在平面直角坐标系xOy 中，将四边形ABCD 向下平移，再向右平移得到四边形1111A B C D ，已知1(3,5),(4,3),(3,3)A B A --，则点1B 坐标为（）A ．(1,2)B ．(2,1)C ．(1,4)D ．(4,1)二、填空题 7．如图，在平面直角坐标系中，四边形AOBC 是菱形．若点A 的坐标是(3，4)，则点B 的坐标是__________．8．如图，在平面直角坐标系xOy 中，已知点A 0），B （1，1）．若平移点B 到点D ，使四边形OADB 是平行四边形，则点D 的坐标是_____．9．如图，在平面直角坐标系中，点A 在x 轴上，点B 的坐标为（4，2），若四边形OABC 为菱形，则点C 的坐标为．10．如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点B 的坐标为（5，4），点P 为线段BC 上动点，当△POA 为等腰三角形时，点p 坐标为______________．11．如图，平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点B 的坐标为(10，6)，点P 为BC 边上的动点，当△POA 为等腰三角形时，点P 的坐标为_________．12．如图，在平面直角坐标系中，点B 在x 轴上，AOB 是等腰三角形，5AO AB ==，6OB =，则点A 的坐标是______．13．如图，在平面直角坐标系x O y 中，四边形0ABC 是平行四边形，且A(4，0)，B(6，2)，则直线AC 的解析式为___________.14．如图，在平面直角坐标系中，点B 在x 轴上，AOB 是等边三角形，AB 2 ，则点A 的坐标为______．15．如图，在平面直角坐标系中，四边形OABC 是正方形，点A 的坐标是（2，1），则点C 的坐标是_____．16．已知在平面直角坐标系中，等腰直角三角形ABC 的斜边AB 的端点,A B 分别在y 轴和x 轴上，且点(0,4)A ，(3,0)B ，直角顶点C 在第一象限，则点C 的坐标为__________．17．如图，在平面直角坐标系中，四边形AOBC 是菱形．若点A 的坐标是（6，8），则点C 的坐标是_____．18．如图，在平面直角坐标系中，将直角三角形的直角顶点放在点()3,3P 处，两直角边分别与坐标轴交于点A 和点B ，则OA OB +的值为___________.19．如图，在平面直角坐标系中，O 为原点，四边形OABC 是长方形，点A ，C 的坐标分别为(10,0)，(0,3)，D 是OA 的中点，点P 在边BC 上运动，当ODP ∆是腰长为5的等腰三角形时，点P 的坐标为_______.20．在平面直角坐标系xOy 中，已知点(2,2)P ，点Q 在y 轴上，PQO ∆是等腰三角形，则满足条件的点Q 共有______个．21．如图，在平面直角坐标系中，四边形ABCD 是菱形，60ABC ︒∠=，且点A 的坐标为(0,1)，则点,,B C D 的坐标分别为_______．22．如图，在平面直角坐标系中，四边形OABC 是菱形，若点A 的坐标是()1,2，则点B 的坐标是________．23．如图，将平行四边形OABC 放置在平面直角坐标系xoy 中，O 为坐标原点，若点C 的坐标是()1,3，点A 的坐标是()5,0，则点B 的坐标是________．24．如图，在平面直角坐标系中，O 为坐标原点，四边形ABCD 是平行四边形，点,,A B C 的坐标分别为(0,2)A ，(1,0)B -，(4,0)C ，点E 是BC 的中点，点P 为线段AD 上的动点，若BEP △是等腰三角形，则点P 的坐标为_____．25．如图，在平面直角坐标系xOy 中，一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ，则正方形OABC 的面积为____．26．如图，在平面直角坐标系中，一次函数y ＝2x ﹣5的图象经过正方形OABC 的顶点A 和C ，则正方形OABC 的面积为_____．27．如图，在平面直角坐标系中，四边形OABC 是平行四边形，O （0，0），A （1，-2），B （3，1）则C 点坐标为．28．如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是长方形，BC ∥OA ，点A 、C 的坐标分别为(10,0)A ，(0,4)C ，M 是OA 的中点，点P 在BC 边上运动．当OPM ∆是腰长为5的等腰三角形时，则点P 的坐标为________________．29．在平面直角坐标系中，将直角三角形的直角顶点放在点()8,8P 处，两直角边与坐标轴交于如图所示的点A 和点B ，则OA OB -的值为______.30．如图，平面直角坐标系中，四边形OABC 为菱形，点A 在x 轴正半轴上，点A 的坐标为()4,0,60AOC ∠=︒，对角线,OB AC 相交于点E ，则点E 的坐标为______．31．如图，在平面直角坐标系中，四边形OABC 是边长为8的正方形，()8,M s 、(),8N t 分别是边AB 、BC 上的两个动点，且OM MN ⊥，当ON 最小时，s t +=________．32．如图，在平面直角坐标系中，△OAB 是等腰直角三角形，∠OAB=90°，已知点A （4，3），点B 在第四象限，则点B 的坐标是_____．33．如图，在平面直角坐标系中，等腰直角三角形OAB 的斜边OA 与x 轴负半轴的夹角为60︒，若OAB 的面积是5，则点B 的坐标为_________.34．如图，在平面直角坐标系中，已知四个定点()30A -,、()1,1B -、()0,3C 、()1,3D -，点P 在四边形ABCD 内，则到四边形四个顶点的距离的和PA PB PC PD +++最小时的点P 的坐标为______．三、解答题35．如图，在平面直角坐标系中，一次函数y kx b =+的图象经过点(6,0)A ，与y 轴交于点(0,3)B -，与正比例函数2y x =的图象相交于点C ．（1）求此一次函数的解析式；（2）求出OBC 的面积；（3）点D 在此坐标平面内，且知以O 、B 、C 、D 为顶点四边形是平行四边形，请直接写出符合条件的点D 的坐标．36．如图，在平面直角坐标系xOy 中，已知一次函数24y x =-+的图像与x 轴相交于点A ，与y 轴相交于点B ．（1）求点A 坐标和点B 坐标；（2）点C 是线段AB 上一点，点O 为坐标原点，点D 在第二象限，且四边形BCOD 为菱形，求点D 坐标；（3）在（2）的条件下，点P 为平面直角坐标系中一点，以B 、D 、A 、P 为顶点的四边形是平行四边形，请直接写出所有满足条件的P 点坐标．37．如图，在平面直角坐标系中xOy 中，()4,0A ，OA OC =，60AOC ︒∠=且//CB OA ，OB 平分AOC ∠，点P 是四边形OABC 的内部的一点，且点P 到四边形OABC 的四条边的距离相等。

2020年中考数学《一次函数》专题复习(名师精选全国真题，值得下载练习)一．选择题1．（2019•辽阳）若ab＜0且a＞b，则函数y＝ax+b的图象可能是（）A．B．C．D．2．（2019•大庆）正比例函数y＝kx（k≠0）的函数值y随着x增大而减小，则一次函数y ＝x+k的图象大致是（）A．B．C．D．3．（2019•娄底）如图，直线y＝x+b和y＝kx+2与x轴分别交于点A（﹣2，0），点B（3，0），则解集为（）A．x＜﹣2 B．x＞3 C．x＜﹣2或x＞3 D．﹣2＜x＜3 4．（2019•雅安）如图，在平面直角坐标系中，直线l1：y＝x+1与直线l2：y＝x 交于点A1，过A1作x轴的垂线，垂足为B1，过B1作l2的平行线交l1于A2，过A2作x轴的垂线，垂足为B2，过B2作l2的平行线交l1于A3，过A3作x轴的垂线，垂足为B3…按此规律，则点A n的纵坐标为（）A．（）n B．（）n+1 C．（）n﹣1+D．5．（2019•鄂尔多斯）在“加油向未来”电视节目中，王清和李北进行无人驾驶汽车运送货物表演，王清操控的快车和李北操控的慢车分别从A，B两地同时出发，相向而行．快车到达B地后，停留3秒卸货，然后原路返回A地，慢车到达A地即停运休息，如图表示的是两车之间的距离y（米）与行驶时间x（秒）的函数图象，根据图象信息，计算a、b的值分别为（）A．39，26 B．39，26.4 C．38，26 D．38，26.4 6．（2019•遵义）如图所示，直线l1：y＝x+6与直线l2：y＝﹣x﹣2交于点P（﹣2，3），不等式x+6＞﹣x﹣2的解集是（）A．x＞﹣2 B．x≥﹣2 C．x＜﹣2 D．x≤﹣2 7．（2019•锦州）如图，一次函数y＝2x+1的图象与坐标轴分别交于A，B两点，O为坐标原点，则△AOB的面积为（）A．B．C．2 D．48．在平面直角坐标系中，函数y＝kx+b的图象如图所示，则下列判断正确的是（）A．k＞0 B．b＜0 C．k•b＞0 D．k•b＜09．（2019•鞍山）如图，若一次函数y＝﹣2x+b的图象与两坐标轴分别交于A，B两点，点A的坐标为（0，3），则不等式﹣2x+b＞0的解集为（）A．x＞B．x＜C．x＞3 D．x＜3 10．（2019•辽阳）一条公路旁依次有A，B，C三个村庄，甲乙两人骑自行车分别从A 村、B村同时出发前往C村，甲乙之间的距离s（km）与骑行时间t（h）之间的函数关系如图所示，下列结论：①A，B两村相距10km；②出发1.25h后两人相遇；③甲每小时比乙多骑行8km；④相遇后，乙又骑行了15min或65min时两人相距2km．其中正确的个数是（）A．1个B．2个C．3个D．4个11．（2019•桂林）如图，四边形ABCD的顶点坐标分别为A（﹣4，0），B（﹣2，﹣1），C（3，0），D（0，3），当过点B的直线l将四边形ABCD分成面积相等的两部分时，直线l所表示的函数表达式为（）A．y＝x+B．y＝x+C．y＝x+1 D．y＝x+ 12．（2019•包头）如图，在平面直角坐标系中，已知A（﹣3，﹣2），B（0，﹣2），C（﹣3，0），M是线段AB上的一个动点，连接CM，过点M作MN⊥MC交y轴于点N，若点M、N在直线y＝kx+b上，则b的最大值是（）A．﹣B．﹣C．﹣1 D．0 13．（2019•广元）如图，过点A0（0，1）作y轴的垂线交直线l：y＝x于点A1，过点A1作直线l的垂线，交y轴于点A2，过点A2作y轴的垂线交直线l于点A3，…，这样依次下去，得到△A0A1A2，△A2A3A4，△A4A5A6，…，其面积分别记为S1，S2，S3，…，则S100为（）A．（）100B．（3）100C．3×4199D．3×2395 14．（2019•聊城）某快递公司每天上午9：00﹣10：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为（）A．9：15 B．9：20 C．9：25 D．9：30 15．（2019•鄂州）如图，在平面直角坐标系中，点A1、A2、A3…A n在x轴上，B1、B2、B3…B n在直线y＝x上，若A1（1，0），且△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形，从左到右的小三角形（阴影部分）的面积分别记为S1、S2、S3…S n．则S n可表示为（）A．22n B．22n﹣1C．22n﹣2D．22n﹣3二．填空题16．（2019•济南）某市为提倡居民节约用水，自今年1月1日起调整居民用水价格．图中l1、l2分别表示去年、今年水费y（元）与用水量x（m3）之间的关系．小雨家去年用水量为150m3，若今年用水量与去年相同，水费将比去年多元．17．如图，在平面直角坐标系中，点A，C分别在x轴、y轴上，四边形ABCO是边长为4的正方形，点D为AB的中点，点P为OB上的一个动点，连接DP，AP，当点P满足DP+AP的值最小时，直线AP的解析式为．18．（2019•阜新）甲、乙两人分别从A，B两地相向而行，匀速行进甲先出发且先到达B地，他们之间的距离s（km）与甲出发的时间t（h）的关系如图所示，则乙由B地到A地用了h．19．（2019•鄂尔多斯）如图，有一条折线A1B1A2B2A3B3A4B4…，它是由过A1（0，0），B1（4，4），A2（8，0）组成的折线依次平移8，16，24，…个单位得到的，直线y ＝kx+2与此折线有2n（n≥1且为整数）个交点，则k的值为．20．（2019•大连）甲、乙两人沿同一条直路走步，如果两人分别从这条直路上的A，B 两处同时出发，都以不变的速度相向而行，图1是甲离开A处后行走的路程y（单位：m）与行走时间x（单位：min）的函数图象，图2是甲、乙两人之间的距离y（单位：m）与甲行走时间x（单位：min）的函数图象，则a﹣b＝．21．（2019•娄底）已知点P（x0，y0）到直线y＝kx+b的距离可表示为d＝，例如：点（0，1）到直线y＝2x+6的距离d＝＝．据此进一步可得两条平行线y＝x和y＝x﹣4之间的距离为．22．（2019•本溪）如图，点B1在直线l：y＝x上，点B1的横坐标为2，过B1作B1A1⊥l，交x轴于点A1，以A1B1为边，向右作正方形A1B1B2C1，延长B2C1交x轴于点A2；以A2B2为边，向右作正方形A2B2B3C2，延长B3C2交x轴于点A3；以A3B3为边，向右作正方形A3B3B4C3，延长B4C3交x轴于点A4；…；按照这个规律进行下去，点∁n的横坐标为（结果用含正整数n的代数式表示）23．（2019•贵阳）在平面直角坐标系内，一次函数y＝k1x+b1与y＝k2x+b2的图象如图所示，则关于x，y的方程组的解是．24．（2019•东营）如图，在平面直角坐标系中，函数y＝x和y＝﹣x的图象分别为直线l1，l2，过l1上的点A1（1，）作x轴的垂线交l2于点A2，过点A2作y 轴的垂线交l1于点A3，过点A3作x轴的垂线交l2于点A4，…依次进行下去，则点A2019的横坐标为．25．（2019•天门）如图，在平面直角坐标系中，四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，点A1，A2，A3，…都在x轴上，点C1，C2，C3，…都在直线y＝x+上，且∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，OA1＝1，则点C6的坐标是．26．（2019•徐州）函数y＝x+1的图象与x轴、y轴分别交于A、B两点，点C在x轴上．若△ABC为等腰三角形，则满足条件的点C共有个．三．解答题27．（2019•恩施州）某县有A、B两个大型蔬菜基地，共有蔬菜700吨．若将A基地的蔬菜全部运往甲市所需费用与B基地的蔬菜全部运往甲市所需费用相同．从A、B两基地运往甲、乙两市的运费单价如下表：甲市（元/吨）乙市（元/吨）A基地20 25B基地15 24（1）求A、B两个蔬菜基地各有蔬菜多少吨？（2）现甲市需要蔬菜260吨，乙市需要蔬菜440吨．设从A基地运送m吨蔬菜到甲市，请问怎样调运可使总运费最少？28．（2019•沈阳）在平面直角坐标系中，直线y＝kx+4（k≠0）交x轴于点A（8，0），交y轴于点B．（1）k的值是；（2）点C是直线AB上的一个动点，点D和点E分别在x轴和y轴上．①如图，点E为线段OB的中点，且四边形OCED是平行四边形时，求▱OCED的周长；②当CE平行于x轴，CD平行于y轴时，连接DE，若△CDE的面积为，请直接写出点C的坐标．29．（2019•大连）如图，在平面直角坐标系xOy中，直线y＝﹣x+3与x轴，y轴分别相交于点A，B，点C在射线BO上，点D在射线BA上，且BD＝OC，以CO，CD为邻边作▱COED．设点C的坐标为（0，m），▱COED在x轴下方部分的面积为S．求：（1）线段AB的长；（2）S关于m的函数解析式，并直接写出自变量m的取值范围．30．（2019•徐州）如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点A．甲从中山路上点B出发，骑车向北匀速直行；与此同时，乙从点A出发，沿北京路步行向东匀速直行．设出发xmin时，甲、乙两人与点A的距离分别为y1m、y2m．已知y1、y2与x之间的函数关系如图②所示．（1）求甲、乙两人的速度；（2）当x取何值时，甲、乙两人之间的距离最短？31．（2019•宁夏）在综合与实践活动中，活动小组对学校400米的跑道进行规划设计，跑道由两段直道和两端是半圆弧的跑道组成．其中400米跑道最内圈为400米，两端半圆弧的半径为36米．（π取3.14）．（1）求400米跑道中一段直道的长度；（2）在活动中发现跑道周长（单位：米）随跑道宽度（距最内圈的距离，单位：米）的变化而变化．请完成下表：跑道宽度/米0 1 2 3 4 5 …跑道周长/米400 …若设x表示跑道宽度（单位：米），y表示该跑道周长（单位：米），试写出y与x的函数关系式：（3）将446米的跑道周长作为400米跑道场地的最外沿，那么它与最内圈（跑道周长400米）形成的区域最多能铺设道宽为1.2米的跑道多少条？32．（2019•哈尔滨）如图，在平面直角坐标系中，点O为坐标原点，直线y＝x+4与x 轴交于点A，与y轴交于点B，直线BC与x轴交于点C，且点C与点A关于y轴对称；（1）求直线BC的解析式；（2）点P为线段AB上一点，点Q为线段BC上一点，BQ＝AP，连接PQ，设点P 的横坐标为t，△PBQ的面积为S（S≠0），求S与t之间的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，点E在线段OA上，点R在线段BC的延长线上，且点R的纵坐标为﹣，连接PE、BE、AQ，AQ与BE交于点F，∠APE＝∠CBE，连接PF，PF的延长线与y轴的负半轴交于点M，连接QM、MR，若tan∠QMR＝，求直线PM的解析式．参考答案一．选择题1．解：∵ab＜0，且a＞b，∴a＞0，b＜0，∴函数y＝ax+b的图象经过第一、三、四象限．故选：A．2．解：∵正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，∴k＜0，∵一次函数y＝x+k的一次项系数大于0，常数项小于0，∴一次函数y＝x+k的图象经过第一、三象限，且与y轴的负半轴相交．故选：A．3．解：∵直线y＝x+b和y＝kx+2与x轴分别交于点A（﹣2，0），点B（3，0），∴解集为﹣2＜x＜3，故选：D．4．解：联立直线l1与直线l2的表达式并解得：x＝，y＝，故A1（，）；则点B1（，0），则直线B1A2的表达式为：y＝x+b，将点B1坐标代入上式并解得：直线B1A2的表达式为：y3＝x﹣，将表达式y3与直线l1的表达式联立并解得：x＝，y＝，即点A2的纵坐标为；同理可得A3的纵坐标为，…按此规律，则点A n的纵坐标为（）n，故选：A．5．解：速度和为：24÷（30﹣18）＝2米/秒，由题意得：，解得：b＝26.4，因此慢车速度为：＝0.8米/秒，快车速度为：2﹣0.8＝1.2米/秒，快车返回追至两车距离为24米的时间：（26.4﹣24）÷（1.2﹣0.8）＝6秒，因此a＝33+6＝39秒．故选：B．6．解：当x＞﹣2时，x+6＞﹣x﹣2，所以不等式x+6＞﹣x﹣2的解集是x＞﹣2．故选：A．7．解：一次函数y＝2x+1中，当x＝0时，y＝1；当y＝0时，x＝﹣0.5；∴A（﹣0.5，0），B（0，1）∴OA＝0.5，OB＝1∴△AOB的面积＝0.5×1÷2＝故选：A．8．解：∵一次函数y＝kx+b的图象经过一、二、四象限，∴k＜0，b＞0．∴kb＜0，故选：D．9．解：∵一次函数y＝﹣2x+b的图象交y轴于点A（0，3），∴b＝3，令y＝﹣2x+3中y＝0，则﹣2x+3＝0，解得：x＝，∴点B（，0）．观察函数图象，发现：当x＜时，一次函数图象在x轴上方，∴不等式﹣2x+b＞0的解集为x＜．故选：B．10．解：由图象可知A村、B村相离10km，故①正确，当1.25h时，甲、乙相距为0km，故在此时相遇，故②正确，当0≤t≤1.25时，易得一次函数的解析式为s＝﹣8t+10，故甲的速度比乙的速度快8km/h．故③正确当1.25≤t≤2时，函数图象经过点（1.25，0）（2，6）设一次函数的解析式为s＝kt+b 代入得，解得∴s＝8t+10当s＝2时．得2＝8t﹣10，解得t＝1.5h由1.5﹣1.25＝0.25h＝15min同理当2≤t≤2.5时，设函数解析式为s＝kt+b将点（2，6）（2.5，0）代入得，解得∴s＝﹣12t+30当s＝2时，得2＝﹣12t+30，解得t＝由﹣1.25＝h＝65min故相遇后，乙又骑行了15min或65min时两人相距2km，④正确．故选：D．11．解：由A（﹣4，0），B（﹣2，﹣1），C（3，0），D（0，3），∴AC＝7，DO＝3，∴四边形ABCD分成面积＝AC×（|y B|+3）＝＝14，可求CD的直线解析式为y＝﹣x+3，设过B的直线l为y＝kx+b，将点B代入解析式得y＝kx+2k﹣1，∴直线CD与该直线的交点为（，），直线y＝kx+2k﹣1与x轴的交点为（，0），∴7＝×（3﹣）×（+1），∴k＝或k＝0，∴k＝，∴直线解析式为y＝x+；故选：D．12．解：连接AC，则四边形ABOC是矩形，∴∠A＝∠ABO＝90°，又∵MN⊥MC，∴∠CMN＝90°，∴∠AMC＝∠MNB，∴△AMC∽△NBM，∴，设BN＝y，AM＝x．则MB＝3﹣x，ON＝2﹣y，∴，即：y＝x2+x∴当x＝﹣＝﹣时，y最大＝×（）2+＝，∵直线y＝kx+b与y轴交于N（0，b）当BN最大，此时ON最小，点N（0，b）越往上，b的值最大，∴ON＝OB﹣BN＝2﹣＝，此时，N（0，）b的最大值为．故选：A．13．解：∵点A0的坐标是（0，1），∴OA0＝1，∵点A1在直线y＝x上，∴OA1＝2，A0A1＝，∴OA2＝4，∴OA3＝8，∴OA4＝16，得出OA n＝2n，∴A n A n+1＝2n•，∴OA198＝2198，A198A199＝2198•，∵S1＝（4﹣1）•＝，∵A2A1∥A200A199，∴△A0A1A2∽△A198A199A200，∴＝（）2，∴S＝2396•＝3×2395故选：D．14．解：设甲仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y1＝k1x+40，根据题意得60k1+40＝400，解得k1＝6，∴y1＝6x+40；设乙仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y2＝k2x+240，根据题意得60k2+240＝0，解得k2＝﹣4，∴y2＝﹣4x+240，联立，解得，∴此刻的时间为9：20．故选：B．15．解：∵△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形，∴A1B1∥A2B2∥A3B3∥…∥A n B n，B1A2∥B2A3∥B3A4∥…∥B n A n+1，△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形，∵直线y＝x与x轴的成角∠B1OA1＝30°，∠OA1B1＝120°，∴∠OB1A1＝30°，∴OA1＝A1B1，∵A1（1，0），∴A1B1＝1，同理∠OB2A2＝30°，…，∠OB n A n＝30°，∴B2A2＝OA2＝2，B3A3＝4，…，B n A n＝2n﹣1，易得∠OB1A2＝90°，…，∠OB n A n+1＝90°，∴B1B2＝，B2B3＝2，…，B n B n+1＝2n﹣1，∴S1＝×1×＝，S2＝×2×2＝2，…，S n＝×2n﹣1×2n﹣1＝；故选：D．二．填空题（共11小题）16．解：设当x＞120时，l2对应的函数解析式为y＝kx+b，，得，即当x＞120时，l2对应的函数解析式为y＝6x﹣240，当x＝150时，y＝6×150﹣240＝660，由图象可知，去年的水价是480÷160＝3（元/m3），故小雨家去年用水量为150m3，需要缴费：150×3＝450（元），660﹣450＝210（元），即小雨家去年用水量为150m3，若今年用水量与去年相同，水费将比去年多210元，故答案为：210．17．解：∵四边形ABCO是正方形，∴点A，C关于直线OB对称，连接CD交OB于P，连接P A，PD，则此时，PD+AP的值最小，∵OC＝OA＝AB＝4，∴C（0，4），A（4，0），∵D为AB的中点，∴AD＝AB＝2，∴D（4，2），设直线CD的解析式为：y＝kx+b，∴，∴，∴直线CD的解析式为：y＝﹣x+4，∵直线OB的解析式为y＝x，∴，解得：x＝y＝，∴P（，），设直线AP的解析式为：y＝mx+n，∴，解得：，∴直线AP的解析式为y＝﹣2x+8，故答案为：y＝﹣2x+8．18．解：由图可得，甲的速度为：36÷6＝6（km/h），则乙的速度为：＝3.6（km/h），则乙由B地到A地用时：36÷3.6＝10（h），故答案为：10．19．解：∵A1（0，0），A2（8，0），A3（16，0），A4（24，0），…，∴A n（8n﹣8，0）．∵直线y＝kx+2与此折线恰有2n（n≥1且为整数）个交点，∴点A n+1（8n，0）在直线y＝kx+2上，∴0＝8nk+2，解得：k＝﹣．故答案为：﹣．20．解：从图1，可见甲的速度为＝60，从图2可以看出，当x＝时，二人相遇，即：（60+V乙）×＝120，解得：乙的速度V乙＝80，∵乙的速度快，从图2看出乙用了b分钟走完全程，甲用了a分钟走完全程，a﹣b＝＝，故答案为．21．解：当x＝0时，y＝x＝0，即点（0，0）在直线y＝x上，因为点（0，0）到直线y＝x﹣4的距离为：d＝＝＝2，因为直线y＝x和y＝x﹣4平行，所以这两条平行线之间的距离为2．故答案为2．22．解：过点B1、C1、C2、C3、C4分别作B1D⊥x轴，C1D1⊥x轴，C2D2⊥x轴，C3D3⊥x轴，C4D4⊥x轴，……垂足分别为D、D1、D2、D3、D4……∵点B1在直线l：y＝x上，点B1的横坐标为2，∴点B1的纵坐标为1，即：OD＝2，B1D＝1，图中所有的直角三角形都相似，两条直角边的比都是1：2，∴点C1的横坐标为：2++（）0，点C2的横坐标为：2++（）0+（）0×+（）1＝+（）0×+（）1点C3的横坐标为：2++（）0+（）0×+（）1+（）1×+（）2＝+（）0×+（）1×++（）2点C4的横坐标为：＝+（）0×+（）1×+（）2×+（）3……点∁n的横坐标为：＝+（）0×+（）1×+（）2×+（）3×+（）4×……+（）n﹣1＝+[（）0+（）1×+（）2+（）3+（）4……]+（）n﹣1＝＝故答案为：23．解：∵一次函数y＝k1x+b1与y＝k2x+b2的图象的交点坐标为（2，1），∴关于x，y的方程组的解是．故答案为．24．解：由题意可得，A1（1，），A2（1，﹣），A3（﹣3，﹣），A4（﹣3，3），A5（9，3），A6（9，﹣9），…，可得A2n+1的横坐标为（﹣3）n∵2019＝2×1009+1，∴点A2019的横坐标为：（﹣3）1009＝﹣31009，故答案为：﹣31009．25．解：∵OA1＝1，∴OC1＝1，∴∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，∴C1的纵坐标为：sin60°•OC1＝，横坐标为cos60°•OC1＝，∴C1（，），∵四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，∴A1C2＝2，A2C3＝4，A3C4＝8，…，∴C2的纵坐标为：sin60°•A1C2＝，代入y＝x+求得横坐标为2，∴C2（2，），C3的纵坐标为：sin60°•A2C3＝2，代入y＝x+求得横坐标为5，∴C3（5，2），∴C4（11，4），C5（23，8），∴C6（47，16）；故答案为（47，16）．26．解以点A为圆心，AB为半径作圆，与x轴交点即为C；以点B为圆心，AB为半径作圆，与x轴交点即为C；作AB的中垂线与x轴的交点即为C；故答案为4；三．解答题（共6小题）27．解：（1）设A、B两基地的蔬菜总量分别为x吨、y吨．于是有：，解得：，答：A、B两基地的蔬菜总量分别为300吨和400吨；（2）由题可知：，∴0≤m＜260，∵w＝20m+25（300﹣m）+15（260﹣m）+24[400﹣（260﹣m）]＝4m+14760，∵4＞0，∴w随m的增大而增大，∴w最小＝14760答：当A基地运300吨到乙市，B基地运260吨到甲市，B基地运140吨到乙市时，总运费最少为14760元．28．解：（1）将A（8，0）代入y＝kx+4，得：0＝8k+4，解得：k＝﹣．故答案为：﹣．（2）①由（1）可知直线AB的解析式为y＝﹣x+4．当x＝0时，y＝﹣x+4＝4，∴点B的坐标为（0，4），∴OB＝4．∵点E为OB的中点，∴BE＝OE＝OB＝2．∵点A的坐标为（8，0），∴OA＝8．∵四边形OCED是平行四边形，∴CE∥DA，∴＝＝1，∴BC＝AC，∴CE是△ABO的中位线，∴CE＝OA＝4．∵四边形OCED是平行四边形，∴OD＝CE＝4，OC＝DE．在Rt△DOE中，∠DOE＝90°，OD＝4，OE＝2，∴DE＝＝2，∴C平行四边形OCED＝2（OD+DE）＝2（4+2）＝8+4．②设点C的坐标为（x，﹣x+4），则CE＝|x|，CD＝|﹣x+4|，∴S△CDE＝CD•CE＝|﹣x2+2x|＝，∴x2﹣8x+33＝0或x2﹣8x﹣33＝0．方程x2﹣8x+33＝0无解；解方程x2﹣8x﹣33＝0，得：x1＝﹣3，x2＝11，∴点C的坐标为（﹣3，）或（11，﹣）．29．解：（1）当x＝0时，y＝3，当y＝0时，x＝4，∴直线y＝﹣x+3与x轴点交A（4，0），与y轴交点B（0，3）∴OA＝4，OB＝3，∴AB＝，因此：线段AB的长为5．（2）当CD∥OA时，如图，∵BD＝OC，OC＝m，∴BD＝m，由△BCD∽△BOA得：，即：，解得：m＝；①当＜m≤3时，如图1所示：过点D作DF⊥OB，垂足为F，此时在x轴下方的三角形与△CDF全等，∵△BDF∽△BAO，∴，∴DF＝，同理：BF＝m，∴CF＝2m﹣3，∴S△CDF＝＝（2m﹣3）×＝m2﹣2m，即：S＝m2﹣2m，（＜m≤3）②当0＜m≤时，如图2所示：DE＝m≤，此时点E在△AOB的内部，S＝0 （0＜m≤）；③当﹣3＜m≤0时，如图3所示：同理可得：点D（﹣m，m+3）设直线CD关系式为y＝kx+b，把C（0，m）、D（﹣m，m+3）代入得：，解得：k＝﹣，b＝m，直线CD关系式为y＝﹣x+m，当y＝0时，0＝﹣x+m，解得x＝m2F（，0）∴S△COF＝OC•OF＝（﹣m）×＝﹣m3，即：S＝﹣m3，（﹣3＜m≤0）④当m＜﹣3时，如图4所示：同理可得：点D（﹣m，m+3）此时，DF＝﹣m﹣3，OC＝﹣m，OF＝﹣，∴S梯形OCDF＝（﹣m﹣3﹣m）×（﹣）＝即：S＝（m＜﹣3）综上所述：S与m的函数关系式为：S＝．30．解：（1）设甲、乙两人的速度分别为am/min，bm/min，则：y1＝y2＝bx由图②知：x＝3.75或7.5时，y1＝y2，∴，解得：∴y1＝1200﹣240x，令y1＝0，则x＝5∴y1＝y2＝80x答：甲的速度为240m/min，乙的速度为80m/min．（2）设甲、乙之间距离为d，则d2＝（1200﹣240x）2+（80x）2＝64000（x﹣）2+144000，∴当x＝时，d2的最小值为144000，即d的最小值为120；答：当x＝时，甲、乙两人之间的距离最短．31．解：（1）400米跑道中一段直道的长度＝（400﹣2×36×3.14）÷2＝86.96 米，答：400米跑道中一段直道的长度约为86.96米．（2）当跑道宽度为1米时，此时弯道的半径为36+1＝37米，周长为86.96×2+2×3.14×37＝406.28米，当跑道宽度为2米时，此时弯道的半径为36+2＝38米，周长为86.96×2+2×3.14×38＝412.56米，当跑道宽度为3米时，此时弯道的半径为36+3＝39米，周长为86.96×2+2×3.14×39＝418.84米，当跑道宽度为4米时，此时弯道的半径为36+4＝40米，周长为86.96×2+2×3.14×40＝425.12米，当跑道宽度为5米时，此时弯道的半径为36+1＝41米，周长为86.96×2+2×3.14×41＝431.4米，表格填写如下：y与x的函数关系式为：y＝2πx+400＝6.28x+400；（3）当y＝446时，即6.28x+400＝446，解得：x≈7.32 m7.32÷1.2≈6 条∴最多能铺设道宽为1.2米的跑道6条．32．解：（1）∵y＝x+4，∴A（﹣3，0）B（0，4），∵点C与点A关于y轴对称，∴C（3，0），设直线BC的解析式为y＝kx+b，将B（0，4），C（3，0）代入，，解得k＝﹣，b＝4，∴直线BC的解析式y＝﹣；（2）如图1，过点A作AD⊥BC于点点D，过点P作PN⊥BC于N，PG⊥OB于点G．∵OA＝OC＝3，OB＝4，∴AC＝6，AB＝BC＝5，∴sin∠ACD＝，即，∴AD＝，∵点P为直线y＝x+4上，∴设P（t，t+4），∴PG＝﹣t，cos∠BPG＝cos∠BAO，即，∴，∵sin∠ABC＝，∴PN＝＝，∵AP＝BQ，∴BQ＝5+，∴S＝，即S＝；（3）如图，延长BE至T使ET＝EP，连接AT、PT、AM、PT交OA于点S．∵∠APE＝∠EBC，∠BAC＝∠BCA，∴180°﹣∠APE﹣∠BAC＝180°﹣∠EBC﹣∠ACB，∴∠PEA＝∠BEC＝∠AET，∴PT⊥AE，PS＝ST，∴AP＝AT，∠TAE＝∠P AE＝∠ACB，AT∥BC，∴∠TAF＝∠FQB，∵∠AFT＝∠BFQ，AT＝AP＝BQ，∴△ATF≌△QBF，∴AF＝QF，TF＝BF，∵∠PSA＝∠BOA＝90°，∴PT∥BM，∴∠TBM＝∠PTB，∵∠BFM＝∠PFT，∴△MBF≌△PTF，∴MF＝PF，BM＝PT，∴四边形AMQP为平行四边形，∴AP∥MQ，MQ＝AP＝BQ，∴∠MQR＝∠ABC，过点R作RH⊥MQ于点H，∵sin∠ABC＝sin∠MQR＝，设QR＝25a，HR＝24a，则QH＝7a，∵tan∠QMR＝，∴MH＝23a，BQ＝MQ＝23a+7a＝30a，BR＝BQ+QR＝55a，过点R作RK⊥x轴于点K．∵点R的纵坐标为﹣，∴RK＝，∵sin∠BCO＝，∴CR＝，BR＝，∴，a＝，∴BQ＝30a＝3，∴5+＝3，t＝，∴P（），∴，∵BM＝PT＝2PS＝，BO＝4，∴OM＝，∴M（0，），设直线PM的解析式为y＝mx+n，∴，解得，∴直线PM的解析式为y＝．。

一次函数与四边形存在性【学习目标】1．熟练运用一次函数解决特殊四边形存在问题；2．体会数形结合的思想方法；体会一次函数与几何图形的内在联系．平行四边形问题:（注意点的顺序）1.给三点，先连接三点构成三角形；然后以每边为对角线构造平行四边形；以中点公式或者平移法求点坐标。

2.给两点，分为边和对角线讨论，充分利用平行四边形对边平行且相等，对角线平分两个全等三角形来做。

1.在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为．（1）如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为．（2）在直角坐标系中，有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．2.已知点A、B、C、D可以构成平行四边形，且点A（－1，0），点B（0，3），点C（3，0），则第四个顶点D的坐标为_________________________；xy BCA O举一反三：1.如图，在平面直角坐标系xOy 中，直线交y 轴于点A ，交x 轴于点B ，以线段AB 为边作菱形ABCD （点C 、D 在第一象限），且点D 的纵坐标为9． （1）求点A 、点B 的坐标； （2）求直线DC 的解析式；（3）除点C 外，在平面直角坐标系xOy 中是否还存在点P ，使点A 、B 、D 、P 组成的四边形是平行四边形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．2.如图，在平面直角坐标系中，函数122+=x y 的图像分别交x 轴、y 轴于A 、B 两点．过点A 的直线交y 轴正半轴于点C ，且点C 为线段OB 的中点． （1）求直线AC 的表达式；（2）如果四边形ACPB 是平行四边形，求点P 的坐标．3. 如图10，直线102+-=x y 与x 轴交于点A ，又B 是该直线上一点，满足OA OB =， （1）求点B 的坐标；（2）若C 是直线上另外一点，满足AB=BC ，且四边形OBCD 是平行四边形，试画出符合要求的大致图形，并求出点D 的坐标.4.已知：如图，平面直角坐标系中有一个等腰梯形ABCD ，且AD ∥BC ，AB=CD ，点A 在y 轴正半轴上，点B 、C 在x 轴上（点B 在点C 的左侧），点D 在第一象限，AD=3，BC=11，梯形的高为2，双曲线y=经过点D ，直线y=kx +b 经过A 、B 两点．O BA x yD（1）求点A、B、C、D的坐标；（2）求双曲线y=和直线y=kx+b的解析式；（3）点M在双曲线上，点N在y轴上，如果四边形ABMN是平行四边形，求点N的坐标．5.如图1，在平面直角坐标系中，点A的坐标为（﹣4，4），点B的坐标为（0，2）．（1）求直线AB的解析式；（2）以点A为直角顶点作∠CAD=90°，射线AC交x轴的负半轴于点C，射线AD交y轴的负半轴于点D．当∠CAD绕着点A旋转时，OC﹣OD的值是否发生变化？若不变，求出它的值；若变化，求出它的变化范围；（3）如图2，点M（﹣4，0）是x轴上的一个点，点P是坐标平面内一点．若A、B、M、P四点能构成平行四边形，请写出满足条件的所有点P的坐标（不要解题过程）．菱形问题:（注意点的顺序）一般给两点，一动点在某直线上，另一点在平面直角坐标系中。

中考数学高频考点突破——一次函数与四边形综合1.如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA，OC的长分别是m，n且满足(m−6)2+√n−8=0．点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E 处．(1) 求OA，OC的长．(2) 求直线AD的解析式．(3) 点M在直线DE上，在x轴的正半轴上是否存在点N，使以M，A，N，C为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．x+3与x轴，y轴相交于A，B两点，2.如图1，在平面直角坐标系中，直线y=−12点C在线段OA上，将线段CB绕着点C顺时针旋转90∘得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．(1) 求证：△BOC≌△CED;(2) 如图2，将△BCD沿x轴正方向平移得△BʹCʹDʹ,当BʹCʹ经过点D时，求△BCD平移的距离及点D的坐标；(3) 若点P在y轴上，点Q在直线AB上，是否存在以C，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的P点的坐标；若不存在，请说明理由．3.对于平面直角坐标系xOy中的图形M和点P（点P在M内部或M上），给出如下定义：如果图形M上存在点Q，使得0≤PQ≤2，那么称点P为图形M的和谐点．已知点A(−4,3)，B(−4,−3)，C(4,−3)，D(4,3)．(1) 在点P1(−2,1)，P2(−1,0)，P3(3,3)中，矩形ABCD的和谐点是；(2) 如果直线y=12x+32上存在矩形ABCD的和谐点P，直接写出点P的横坐标t的取值范围；(3) 如果直线y=12x+b上存在矩形ABCD的和谐点E，F，使得线段EF上的所有点（含端点）都是矩形ABCD的和谐点，且EF>2√5，直接写出b的取值范围．4.如图（1），在平面直角坐标系中，直线y=−12x+2交坐标轴于A，B两点．以AB 为斜边在第一象限作等腰直角三角形ABC，C为直角顶点，连接OC．(1) 求线段AB的长度．(2) 求直线BC的解析式．(3) 如图（2），将线段AB绕B点沿顺时针方向旋转至BD，且OD⊥AD，直线DO交直线y=x+3于P点，求P点坐标．5.已知：如图，在平面中直角坐标系xOy中，直线y=−34x+6与x轴、y轴的交点分别为A，B两点，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x 轴于点C．(1) 求点A，B，C的坐标．(2) 点D(6,−2)在第四象限，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由．(3) 在直线BC上存在点Q，使∣QA−QO∣∣最大，请直接写出点Q的坐标．6.如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D(0,0)，B(3,4)，矩形ABCD沿直线EF折叠，点B落在AD边上的G处，E，F分别在BC，AB边上且F(1,4)．(1) 求G点坐标．(2) 求直线EF解析式．(3) 点N在坐标轴上，直线EF上是否存在点M，使以M，N，F，G为顶点的四边形是平行四边形？若存在，求出M点坐标；若不存在，说明理由．7.在平面直角坐标系中，一次函数y=3x+6的图象与x轴负半轴交于点A，与y轴正半轴交于点C，点D为直线AC上一点，CD=AC，点B为x轴正半轴上一点，连接BD，△ABD的面积为48．(1) 如图1，求点B的坐标；(2) 如图2，点M，N分别在线段BD，BC上，连接MN，MB=MN，点N的横坐标为t，点M的横坐标为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；(3) 在（2）的条件下，如图3，连接AN，∠BAN=∠ACO，点F为x轴正半轴上点B右侧一点，点H为第一象限内一点，FH⊥NH，∠NFH=2∠NFB，FH=85√10，延长FN交AC于点G，点R为OB上一点，直线y=mx+3(m<0)经过点R和点G，过点F作FE∥AD，交直线RG于点E，连接AE，请你判断四边形AEFG的形状，并说明理由．8.【背景知识】研究平面直角坐标系，我们可以发现一条重要的规律：若平面直角坐标系上有两个不同的点A(x A,y A)，B(x B,y B)，则线段AB的中点坐标可以表示为(x A+x B2,y A+y B2)．(1) 【简单应用】如图1，直线AB与y轴交于点A(0,3),与x轴交于点B(4,0)，过原点O的直线L将△ABO分成面积相等的两部分，请求出直线L的解析式．(2) 【探究升级】小明发现“若四边形一条对角线平分四边形的面积，则这条对角线必经过另一对角线的中点”，①如图2，在四边形ABCD中，对角线AC，BD相交于点O，S△ABD=S△BCD，试说明AO=CO．②【综合运用】如图3，在平面直角坐标系中A(1,4)，B(3,−2)，C(2m,−m+5)，若OC恰好平分四边形OACB的面积，求点C的坐标．x+4分别交x，y轴于B，A两点，将9.如图，在平面直角坐标系中，直线l1:y=−23△AOB沿直线l2:y=2x−9折叠，使点B落在y轴上的点C处．2(1) ①点A的坐标为，点B的坐标为．②求点C的坐标．(2) ①点D在线段BA上，当△CDB与△CDO面积相等时，求OD所在直线的解析式．②如图，在①的条件下，以OD为一边作正方形OPQD（点Q在第二象限），则点Q的坐标为．(3) 在射线BA上是否还存在其它的点Dʹ，使得△CDʹB与△CDʹO面积相等？若存在，求出点Dʹ的坐标；若不存在，请说明理由．10.如图，在平面直角坐标系中，O为坐标原点，直线l1:y=kx+4与y轴交于点A，与x轴交于点B．(1) 请直接写出点A的坐标：．(2) 点P为线段AB上一点，且点P的横坐标为m，现将点P向左平移3个单位，再向下平移4个单位，得点Pʹ在射线AB上．①求k的值．②若点M在y轴上，平面内有一点N，使四边形AMBN是菱形，请求出点N的坐标．③将直线l1绕着点A顺时针旋转45∘至直线l2，求直线l2的解析式．11.如图1，直线y=−x+3交x轴于点B，交y轴于点C．点A在x轴负半轴上且∠CAO=30∘．(1) 求直线AC的解析式；(2) 如图2，边长为3的正方形DEFG，G点与A点重合，现将正方形以每秒1个单位地速度向右平移，当点G与点O重合时停止运动．设正方形DEFG与△ACB重合部分的面积为S，正方形DEFG运动的时间为t，求s关于t的函数关系式；(3) 如图3，已知点Q(1,0)，点M为线段AC上一动点，点N为直线BC上一动点，当三角形QMN为等腰直角三角形时，求M点的坐标．x+6的图象分别交x轴、y轴于A，B两点，点P从12.如图，已知一次函数y=√33点A出发沿AO方向以每秒√3单位长度的速度向终点O匀速运动，同时点Q从点B出发沿BA方向以每秒2个单位长度向终点A匀速运动，当其中一点到达终点时，另一点也停止运动，设运动时间为t秒，过点Q作QC⊥y轴，连接PQ，PC．(1) 点A的坐标为，点B的坐标为，AB=．(2) 当点Q运动到AB中点时，求此时PC所在直线的解析式．(3) 若点D(0,2)，点N在x轴上，直线AB上是否存在点M，使以M，N，B，D为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．13.如图，在直角坐标系中，矩形ABCD的一边CD在x轴上，点D坐标为(m,0)，其中m>0，边AB=a，BC=b，且a，b满足b2−16b+64=√a−10+√20−2a，将矩形折叠，使B落在边CD（含端点）上，落点记为E，这时折痕与边AD或边AB （含端点）交于点F．(1) 求矩形ABCD的边AB，BC的长．(2) 如图1，当点F与点A重合时，连接OA，若△OAE是等腰三角形，求m的值．的图象上，请你在图2中画出分析，△BEF是否存(3) 若点B，D在函数y=kx−85在面积最大值？若存在，说明理由，并求出此时点E的坐标；若不存在，说明理由．14.如图，在平面直角坐标系中，O为坐标原点，矩形OABC的顶点A(12,0)，C(0,9)，将矩形OABC的一个角沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与x轴交于点D．(1) 线段OB的长度为；(2) 求直线BD所对应的函数表达式；(3) 若点Q在线段BD上，在线段BC上是否存在点P，使以D，E，P，Q为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．15.如图1，矩形OABC摆放在平面直角坐标系中，点A在x轴上，点C在y轴上，OA=3，OC=2，过点A的直线交矩形OABC的边BC于点P，且点P不与点B，C重合，过点P作∠CPD=∠APB，PD交x轴于点D，交y轴于点E．(1) 若△APD为等腰直角三角形．①求直线AP的函数解析式．②在x轴上另有一点G的坐标为(2,0)，请在直线AP和y轴上分别找一点M，N，使△GMN的周长最小，并求出此时点N的坐标和△GMN周长的最小值．(2) 如图2，过点E作EF∥AP交x轴于点F，若以A，P，E，F为顶点的四边形时平行四边形，求直线PE的解析式．16.如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，B，D分别在y轴负半轴、x轴正半轴上，点E是x轴的一个动点，连接CE，以CE为边，在直线CE的右侧作正方形CEFG．(1) 如图1，当点E与点O重合时，请直接写出点F的坐标为，点G的坐标为．(2) 如图2，若点E在线段OD上，且OE=1，求正方形CEFG的面积．(3) 当点E在x轴上移动时，点F是否在某条直线上运动？如果是，请求出相应直线的表达式；如果不是，请说明理由．x+3交x轴于点A，交y轴于点B，17.如图，平面直角坐标系xOy中，直线y=−34点P是线段OA上一动点（不与点A重合），过点P作PC⊥AB于点C．(1) 当点P是OA中点时，△APC的面积是．(2) 连接BP，若BP平分∠ABO，求此时点P的坐标．(3) 设点D是x轴上方的坐标平面内一点，若以点O，B，C，D为顶点的四边形是菱形，求点D的坐标及此时OP的长．x+3交x轴于点A，交y轴于点B，18.如图，平面直角坐标系xOy中，直线y=−34点P是线段OA上一动点（不与点A重合），过点P作PC⊥AB于点C．(1) 当点P是OA中点时，求△APC的面积；(2) 连接BP，若BP平分∠ABO，求此时点P的坐标；(3) 设点D是x轴上方的坐标平面内一点，若以点O，B，C，D为顶点的四边形是菱形，求点D的坐标及此时OP的长．19.在平面直角坐标系中，点A(−3,0)，B(0,4)．(1) 直接写出直线AB的解析式．(2) 如图1，过点B的直线y=kx+b交x轴于点C，若∠ABC=45∘，求k的值．(3) 如图2，点M从A出发以每秒1个单位的速度沿AB方向运动，同时点N从O出发以每秒0.6个单位的速度沿OA方向运动，运动时间为t秒（0<t<5），过点N作ND∥AB交y轴于点D，连接MD，是否存在满足条件的t，使四边形AMDN为菱形，判断并说明理由．20.在平面直角坐标系xOy中，点Р和图形W的“中点形”的定义如下：对于图形W上的任意一点Q，连接PQ，取PQ的中点，由所以这些中点所组成的图形，叫做点Р和图形W的“中点形”．已知C(−2,2)，D(1,2)，E(1,0)，F(−2,0)．(1) 若点О和线段CD的“中点形”为图形G，则在点H1(−1,1)，H2(0,1)，H3(2,1)中，在图形G上的点是；(2) 己知点A(2,0)，请通过画图说明点A和四边形CDEF的“中点形”是否为四边形？若是，写出四边形各顶点的坐标，若不是，说明理由；(3) 点B为直线y=2x上一点，记点B和四边形CDEF的中点形为图形M，若图形M与四边形CDEF有公共点，直接写出点B的横坐标b的取值范围．答案1. 【答案】(1) ∵(m −6)2+√n −8=0，∴m =6，n =8，∴OA =6，OC =8．(2) ∵ 翻折，∴AO =AE =6，OD =DE ，设 OD =x ，则 DE =x ，CD =8−x ，在 Rt △AOC 中，AO =6，CO =8，∴AC =√AO 2+OC 2，∴AC =10，∴CE =4，在 Rt △CDE 中，CD 2=DE 2+CE 2，∴(8−x )2=x 2+16，即 64−16x +x 2=x 2+16，即 64−16x +x 2=x 2+16，解得 x =3，∴D (3,0)， 设直线 AD 的解析式为 y =kx +b ，把 A (0,6)，D (3,0) 代入解 {b =6,3k +b =0, 解得 {b =6,k =−2,∴y =−2x +6．(3) N (12,0)或(312,0)．【解析】(3) 假设存在这样的 N 点，设 N 为 (a,0)，∵DE ⊥AC ，∴k DE ⋅k AC =−1， ∴k DE =43，∴DE 的直线解析式为 y =43x −4，设 M (c,43c −4)， ①若 AC 为对角线时，有 {x A +x C =x M +x N ,y A +y C =y M +y N, 即 {0+8=c +a,6+0=43c +0, 解得 {c =152,a =12,∴N (12,0)．②若 AM 为对角线时，有 {x M +x A =x C +x N ,y M +y A =y C +y N, 即 {c +0=8+a,43c −4+6=0+0, 解得 {c =−32,a =−192, ∴N (−192,0)．③若 AN 为对角线时，有 {x A +x N =x M +x C ,y A +y N =y M +y C,即 {0+a =c +8,6+0=43c −4+0, 解得 {c =152,a =312,∴N (312,0)， ∵N 在 x 轴正半轴上，∴N (12,0)或(312,0)．2. 【答案】(1) ∵∠BOC =∠BCD =∠CED =90∘，∴∠OCB +∠OBC =90∘，∠OCB +∠ECD =90∘，∴∠OBC =∠ECD .∵ 将线段 CB 绕着点 C 顺时针旋转 90∘ 得到 CD ，∴BC =CD ． 在 △BOC 和 △CED 中，{∠BOC =∠CED =90∘,∠OBC =∠ECD,BC =CD.∴△BOC ≌△CED (AAS )． (2) ∵ 直线 y =−12x +3 与 x 轴，y 轴相交于 A ，B 两点， ∴ 点 B 的坐标为 (0,3)，点 A 的坐标为 (6,0)．设 OC =m ，∵△BOC ≌△CED ，∴OC =ED =m ，BO =CE =3，∴ 点 D 的坐标为 (m +3,m )． ∵ 点 D 在直线 y =−12x +3 上，∴m =−12(m +3)+3，解得：m =1， ∴ 点 D 的坐标为 (4,1)，点 C 的坐标为 (1,0)．∵ 点 B 的坐标为 (0,3)，点 C 的坐标为 (1,0)，∴ 直线 BC 的解析式为 y =−3x +3．设直线 BʹCʹ 的解析式为 y =−3x +b ，将 D (4,1) 代入 y =−3x +b ，得：1=−3×4+b ，解得：b =13．∴ 直线 BʹCʹ 的解析式为 y =−3x +13， ∴ 点 Cʹ 的坐标为 (133,0)， ∴CCʹ=133−1=103， ∴△BCD 平移的距离为103．(3) (0,12) 或 (0,112)．【解析】 (3) 设点 P 的坐标为 (0,m )，点 Q 的坐标为 (n,−12n +3)．分两种情况考虑，如图 3 所示：①若 CD 为边，当四边形 CDQP 为平行四边形时，∵C (1,0)，D (4,1)，P (0,m )，Q (n,−12n +3)， ∴{1+n =0+4,0−12n +3=m +1. 解得：{m =12,n =3.∴ 点 P 1 的坐标为 (0,12)；当四边形 CDPQ 为平行四边形时，∵C (1,0)，D (4,1)，P (0,m )，Q (n,−12n +3)， ∴{1+0=n +4,0+m =−12n +3+1. 解得：{m =112,n =−3. ∴ 点 P 2 的坐标为 (0,112)； ②若 CD 为对角线，∵C (1,0)，D (4,1)，P (0,m )，Q (n,−12n +3)，∴{1+4=0+n,0+1=m −12n +3. 解得：{m =12,n =5.∴ 点 P 的坐标为 (0,12)． 综上所述：存在，点 P 的坐标为 (0,12) 或 (0,112)．3. 【答案】(1) P 1，P 3(2) −4≤t ≤−2 或 −1≤t ≤3．(3) 2≤b <3 或 −3<b ≤−2．【解析】(1) 如图 1 中，根据点 P 为图形 M 的和谐点的定义，观察图象可知 P 1，P 3 是矩形ABCD 的和谐点．(2) 如图 2 中，当直线y=12x+32上的点P到直线AB的距离为2时，可得P2(−2,12)，同时P4(−4,−12)也满足条件，由题意此时P1，P4是矩形的和谐点，观察图象可知：当−4≤t≤−2时，点P是矩形的和谐点，当直线y=12x+32上的点P到直线AD的距离为2时，可得P3(−1,1)，同时P1(3,3)也满足条件，观察图象可知：当−1≤t≤3时，点P是矩形的和谐点．综上所述，满足条件的t的值为−4≤t≤−2或−1≤t≤3．(3) 如图3中，当b=3时，图中线段EF上的点都是和谐点，且EF=2√5．当b=2时，图中线段EʹFʹ上的点都是和谐点，且EF>2√5．观察图象可知：满足条件的b的值为2≤b<3．根据对称性，同法可证，当−3<b≤−2时，也满足条件．综上所述，满足条件的b的值为：2≤b<3或−3<b≤−2．4. 【答案】(1) 对于直线y=−12x+2，令x=0，得到y=2，可得B(0,2)，令y=0，得到x=4，可得A(4,0)，∴OA=4，OB=2，∴AB=√OA2+OB2=2√5．(2) 如图1中，作CE⊥x轴于E，作CF⊥y轴于F，∴∠BFC=∠AEC=90∘，∵∠EOF=90∘，∴四边形OECF是矩形，∴CF=OE，CE=OF，∠ECF=90∘，∵∠ACB=90∘，∴∠BCF=∠ACE，∵BC=AC，∴△CFB ≌△CEA ，∴CF =CE ，AE =BF ，∴ 四边形 OECF 是正方形，∴OE =OF =CE =CF ，∴OE =OA −AE =OA −BF =OA −OF +OB =4−OE +2，∴OE =3，∴OF =3，∴C (3,3)，设直线 BC 的解析式为 y =kx +b ，则有 {3k +b =3,b =2, 解得 {k =13,b =2,∴ 直线 BC 的解析式为 y =13x +2．(3) 如图 2 中，延长 AB ，DP 相交于 Q ，由旋转知，BD =AB ，∴∠BAD =∠BDA ，∵AD ⊥DP ，∴∠ADP =90∘，∴∠BDA +∠BDQ =90∘，∠BAD +∠AQD =90∘，∴∠AQD =∠BDQ ，∴BD =BQ ，∴BQ =AB ，∴ 点 B 是 AQ 的中点，∵A (4,0)，B (0,2)，∴Q (−4,4)，∴ 直线 DP 的解析式为 y =−x, ⋯⋯①∵ 直线 DO 交直线 y =x +3, ⋯⋯② 于 P 点， 联立①②解得，x =−32，y =32，∴P (−32,32)．5. 【答案】 (1) 把 x =0 代入 y =−34x +6 得 y =6，把 y =0 代入 y =−34x +6 得 x =8，∴A (8,0)，B (0,6)，∴OA =8，OB =6，根据勾股定理，AB 2=OA 2+OB 2，∴AB =√OA 2+OB 2=√82+62=10，连接 CH ，根据折叠性质，△DBC ≌△HBC ，∴BO =BH =6，∠BHC =∠BOC =90∘，CO =CH ，∴AH =AB −BH =10−6=4，∠AHC =90∘，设 OC =x ，则 CH =x ，AC =OA −OC =8−x ，在 Rt △ACH 中，AC 2=CH 2+AH 2，∴(8−x )2=x 2+42，解得 x =3，∴OC =3，∴C (3,0)．(2) 设直线 BC 解析式 y =kx +b ， 把 B (0,6)，C (3,0) 代入 {b =6,3k +b =0, 解得 {k =−2,b =6,∴ 直线 BC 解析式为 y =−2x +6，设 P 坐标 (x,−2x +6)，作 OP ∥AD ，连接 AP ，AD ，OD ，作 PM ⊥x 轴于 M ，DN ⊥x 轴于 N ，∵OP ∥AD ，∴∠POM =∠DAN ，∴tan∠POM =tan∠DAN ， ∴PM OM =DN AN ，∵P (x,−2x +6)，D (6,−2)，∴PM =−2x +6，OM =x ，DN =2，AN =8−6=2， ∴−2x+6x =32， ∴x =2，此时 P (2,2)，OP =2√2，AD =2√2，∴OP =AD ，∴ 四边形 OPAD 是平行四边形．(3) Q (0,6)．【解析】(3) 根据折叠性质得，O ，H 关于 BC 对称，∴QO =QH ，∴∣QA −QO∣∣ 最大，即 ∣QA −QH∣∣ 最大， ∵A ，H ，Q 共线时，QA −QH =AH ，A ，H ，Q 不共线时，QA −QH <AH ，∴A ，H ，Q 共线时，∣QA −QH∣∣ 最大，此时点 B 即 Q 点， ∴Q (0,6)．6. 【答案】(1) 由题意得：AB =3，AF =1，则 FB =AB −AF =2=GF ，则 AG =√GF 2−AF 2=√22−12=√3∴G(0,4−√3)．(2) 由对称性：EF ⊥BG ，则 K EF ×K GB =−1，又 K BG =4−(4−√3)3−0=√33， ∴K EF =−√3，又 F (1,4)，则直线 EF 解析式：y =−√3x +√3+4． (3) 设 M(m,−√3m +√3+4)，G(0,4−√3)，F (1,4)，①当 N 在 x 轴上时，设 N (n,0)， 当 FG 为对角线时，则 {1+0=m +n,4+4−√3=−√3m +√3+4+0, 则 {m =2−43√3,n =43√3−1,∴M (2−43√3,8−√3)．当 FM 为对角线时，则 {1+m =0+n,4−√3+0=−√3m +√3+4, 则 {m =2+43√3,n =3+43√3,∴M (2+43√3,−√3)．当 FN 为对角线时，则 {1+n =0+m,4+0=−√3m +√3+4+4,则 {m =43√3,n =43√3−1,∴M (43√3,√3)．②当 N 在 y 轴上时，设 N (0,n )， 当 FG 为对角线时，则 {1+0=m +0,4+4−√3=−√3m +√3+4+n,则 {m =1,n =4−√3,∴M (1,4)（舍去）．当 FM 为对角线时，则 {1+m =0+0,4−√3+m =−√3m +√3+4+4,则 {m =−1,n =4+3√3,∴M(−1,4+2√3)，当 FN 为对角线时，则 {1+0=0+m,4+n =−√3m +√3+4+4−√3,则 {m =1,n =4−√3,∴M (1,4)（舍去）．综上所述：M 1(2−43√3,8−√3)，M 2(2+43√3,−√3)，M 3(43√3,√3)或 M 4(−1,4+2√3)．7. 【答案】(1) 令 x =0，y =6，令 y =0，x =−2，∴A (−2,0)，B (0,6)，∴AO =2，CO =6，作 DL ⊥y 轴垂足为 L 点，DI ⊥AB 垂足为 I ，∴∠DLO =∠COA =90∘，∠DCL =∠ACO ，DC =AC ，∴△DLC ≌△AOC (AAS )，∴DL =AO =2，∴D 的横坐标为 2，把 x =2 代入 y =3x +6 得 y =12，∴D (2,12)，∴DI =12，∵S △ABD =12AB ⋅DI =48，∴AB =8；∵OB =AB −AO =8−2=6，∴B (6,0)．(2) ∵OC =OB =6，∴∠OCB =∠CBO =45∘，∵MN =MB ，∴ 设 ∠MNB =∠MBN =α，作 NK ⊥x 轴垂足为 K ，MQ ⊥AB 垂足为 Q ，MP ⊥NK ，垂足为 P ；∴∠NKB =∠MQK =∠MPK =90∘，∴ 四边形 MPKQ 为矩形，∴NK ∥CO ，MQ =PK ；∵∠KNB =90∘−45∘=45∘，∴∠MNK =45∘+α，∠MBQ =45∘+α，∴∠MNK =∠MBQ ，∵MN =MB ，∠NPM =∠MQB =90∘，∴△MNP ≌△MQB (AAS )，∴MP =MQ ；∵B (6,0)，D (2,12)，∴ 设 BD 解析式为 y =kx +b (k ≠0)， ∴{6k +b =0,2k +b =12,解得：k =−3，b =18， ∴BD 的解析式为 y =−3x +18，∵ 点 M 的纵坐标为 d ， ∴MQ =MP =d ，把 y =d 代入 y =−3x +18 得 d =−3x +18，解得 x =18−d 3，∴OQ =18−d3；∵N 的横坐标为 t ，∴OK =t ，∴OQ =OK +KQ =t +d ， ∴18−d 3=t +d ， ∴d =−34t +92． (3) 作 NW ⊥AB 垂足为 W ，∴∠NWO =90∘，∵∠ACN =45∘+∠ACO ，∠ANC =45∘+∠NAO ，∵∠ACO =∠NAO ，∴∠ACN =∠ANC ，∴AC =AN ，又 ∵∠ACO =∠NAO ，∠AOC =∠NOW =90∘，∴△ANW ≌△CAO (AAS )，∴AO =NW =2，∴WB =NW =2，∴OW =OB −WB =6−2=4，∴N (4,2)；延长 NW 到 Y ，使 NW =WY ，∴△NFW ≌△YFW (SAS )，∴NF =YF ，∠NFW =∠YFW ，又 ∵∠HFN =2∠NFO ，∴∠HFN =∠YFN ，作 NS ⊥YF ，∵∠FH ⊥NH ，∴∠H =∠NSF =90∘，∵FN =FN ，∴△FHN ≌△FSN (AAS )， ∴SF =FH =85√10，NY =2+2=4， 设 YS =a ，FY =FN =a +85√10，在 Rt △NYS 和 Rt △FNS 中：NS 2=NY 2−YS 2；NS 2=FN 2−FS 2；NY 2−YS 2=FN 2−FS 2， ∴42−a 2=(a +85√10)2−(85√10)2，解得 a =25√10， ∴FN =25√10+85√10=2√10； 在 Rt △NWF 中，WF =√FN 2−NR 2=√(2√10)2−22=6，∴FO =OW +WF =4+6=10，∴F (10,0)，∴AW =AO +OW =2+4=6，∴AW =FW ，∵NW ⊥AF ，∴NA =NF ，∴∠NFA =∠NAF ，∵∠ACO =∠NAO ，∴∠NFA =∠ACO ，设 GF 交 y 轴于点 T ，∠CTF =∠ACO +∠CGF =∠COF +∠GFO ，∴∠CGF =∠COF =90∘，设 FN 的解析式为 y =px +q (p ≠0)，把 F (10,0)，N (4,2) 代入 y =px +q ，得 {12p +q =0,4p +q =2, 解得 {p =−13,q =103,∴y =−13x +103，∴ 联立 {y =−13x +103,y =3x +6,解得：{x =−45,y =185, ∴G (−45,185)，把 G 点代入 y =mx +3，得 −45m +3=185，得 m =−34， ∴y =−34x +3， 令 y =0，得 0=−34x +3，x =4， ∴R (4,0)，∴AR =AO +OR =2+4=6，RF =OF −OR =10−4=6，∴AR =RF ，∵FE ∥AC ，∴∠FEG =∠AGE ，∠GAF =∠EFA ，∴△GRA ≌△EFR (AAS )，∴EF =AG ，∴ 四边形 AGFE 为平行四边形，∵∠AGF =180∘−∠CGF =180∘−90∘=90∘，∴平行四边形AGFE为矩形．8. 【答案】(1) ∵直线L将△ABO分成面积相等的两部分，∴直线L必过相等AB的中点，设线段AB的中点为E，∵A(0,3)，B(4,0)，∴E(4+02,3+02)，∴E(2,32)，∵直线L过原点，∴设直线L的解析式为y=kx，∴2k=32，∴k=34，∴直线L的解析式为y=34x．(2) ① 如图2，过点A作AF⊥BD于F，过点C作CG⊥BD于G，∴S△ABD=12BD⋅AF，S△CBD=12BD⋅CG，∵S△ABD=S△BCD，∴12BD⋅AF=12BD⋅CG，∴AF=CG，在△AOF和△COG中，{∠AOF=∠COG,∠AFO=∠CGO=90∘, AF=CG.∴△AOF≌△COG(AAS)，∴OA=OC．②如图3，由【探究升级】知，若四边形一条对角线平分四边形的面积，则这条对角线必经过另一条对角线的中点，∵OC恰好平分四边形OACB的面积，∴OC过四边形OACB的对角线OA的中点，连接AB，设线段AB的中点为H，∵A(1,4)，B(3,−2)，∴H(2,1)，设直线OC的解析式为y=kʹx，∴2kʹ=1，∴kʹ=12，∴ 直线 OC 的解析式为 y =12x ，∵ 点 C (2m,−m +5) 在直线 OC 上，∴−m +5=12×2m ， ∴m =52，∴C (5,52)．9. 【答案】(1) ① (0,4)；(6,0)②由题意知，C 点为 B 点关于直线 l 2:y =2x −92的对称点，连接 BC ，则可知直线 BC 与直线 l 2 垂直，且与直线 l 2 交点为 BC 中点． ∴ 设直线 BC 解析式为 y =kx +b ，则解析式满足：{k ×2=−1,0=k ×6+b, 解之得：{k =−12,b =3. 故 BC 解析式为 y =−12x +3． ∴ 可知直线 BC 与直线 l 2 交点满足：{y =−12x +3,y =2x −92,解之得：{x =3,y =32. 故交点为 (3,32)．∴ 设点 C 的坐标为 (x 1,y 1)，则由 BC 中点为交点有： {x 1+6=3×2,y 1+0=32×2,解之得：{x 1=0,y 1=3,故 C 点坐标为 (0,3)．(2) ①点 D 在线段 BA 上，故可设点 D 坐标为 (a,−23a +4)，且 0≤a ≤6， ∴ △CDO 可看为以 OC 为底，D 到 y 轴距离为高的三角形，故 S △CDO =3×a ×12=32a ．又 S △CDB =S △ABO −S △BCO −S △ADC =6×4×12−6×3×12−(4−3)×a ×12=3−12a.∵△CDB 与 △CDO 面积相等，故 32a =3−12a ，解之得 a =32．∴ 可知 D 坐标为 (32,3) .设直线 OD 解析式为 y =k 1x +b ，将 O ，D 两点代入有：{3=32×k 1+b 1,0=k 1×0+b 1,解之得：{b 1=0,k 1=2, 故 OD 解析式为 y =2x ．② (−32,92)．(3) 由 (2) 中①问情况为 D 在线段 BA 上，即 D 为 BA 在第一象限点，∴ 若射线 BA 上存在其它点 Dʹ，使得 △CDʹB 与 △CDʹO 面积相等，则此 Dʹ 应该在第二象限，∴ 可设 Dʹ 坐标为 (c,−23c +4)，(c <0)． ∴ 可知 S △CDʹO =3×∣c ∣×12=−32c ．S △CDʹB =S △CADʹ+S △CBA =(4−3)×∣c ∣×12+(4−3)×6×12=−12c +3.∴ 可知 S △CDʹO =S △CDʹB 时，有 −32c =−12c +3，解之得 c =−3．∴ 此时，Dʹ 坐标为 (−3,6)， ∴ 存在 Dʹ，Dʹ 坐标为 (−3,6)． 【解析】(1) ① ∵ 直线 l 1:y =−23x +4 分别与 x ，y 轴交于 B ，A 两点， ∴ 当 x =0 时，y =−23×0+4=4，故 A 坐标 (0,4)． 当 y =0 时，0=−23x +4，解之得 x =6，故 B 坐标 (6,0)．(2) ②由①可知 D (32,3)，OD 的解析式为 y =2x ． ∵ODQP 为正方形且 OD =√(32)2+32=3√52，∴ 可知 OD ∥QP ，且 D 到 QP 的距离 d =3√52． ∴ 设直线 QP 解析式为 y =k 3x +b 3，故解析式满足： {k 3=2,d =∣∣∣∣∣k ×32+b −3√k 3+C−D 2∣∣∣∣∣=3√52, 解之得：{k 3=2,b 3=±152.∵ 点 Q 在第二象限，故 b 3>0，b 3=152． ∴QP 解析式为 y =2x +152．此时又有直线 DQ 垂直于 QP ，∴ 设直线 DQ 解析式为 y =k 4x +b 4，故有： {k 4×2=−1,3=k 4×32+b 4, 解之得：{k 4=−12,b 4=154,故 DQ 解析式为 y =−12x +154， ∴Q 为 DQ 与 QP 交点，故有： {y =−12x +154,y =2x +152, 解之得：{x =−32,y =92. 故 Q 点的坐标为 (−32,92)．10. 【答案】(1) (0,4)(2) ①由题意得：P (m,km +4)， ∴Pʹ(m −3,km )，∵Pʹ(m −3,km ) 在射线 AB 上， ∴k (m −3)+4=km ，解得：k =43．②如图 1 中，作 AB 的中垂线与 y 轴交于 M 点，连接 BM ，分别作 AM ，BM 的平行线，相交于点 N ，则四边形 AMBN 是菱形． 设 M (0,t )，则 AM =BM =4−t ， 在 Rt △BOM 中，OB 2+OM 2=BM 2， 即 32+t 2=(4−t )2，解得：t =78， ∴M (0,78)，∴OM =78，BN =AM =4−78=258，∴N (−3,258)．③如图 2 中，过点 B 作 BC ⊥l 1，交 l 2 于点 C ，过点 C 作 CD ⊥x 轴于 D ． 则 ∠AOB =∠BDC =90∘， ∵∠BAC =45∘，∴△ABC 是等腰直角三角形，∴AB =BC ，∠ABO +∠CBD =90∘， 又 ∠ABO +∠BAO =90∘， ∴∠BAO =∠CBD ，∴△AOB ≌△BDC (AAS )，∴AO =BD =5，OB =DC =3， ∴OD =OB +BD =3+4=7， ∴C (−7,3)，设直线 l 2 的解析式为：y =ax +4， 则 −7a +4=3，解得：a =17．∴ 直线 l 2 的解析式为：y =17x +4． 【解析】(1) ∵y =kx +4 与 y 轴交于点 A ， ∴A (0,4)．11. 【答案】(1) 直线 y =−x +3 交 x 轴于点 B ，交 y 轴于点 C ，则点 B ，C 的坐标为 (3,0)，(0,3)，∵∠CAO =30∘，则 AC =2OC =6，则 OA =3√3，将点 A ，C 的坐标代入一次函数表达式：y =kx +b 并解得：直线 AC 的表达式为：y =√33x +3； (2) 如图 2 所示： ①当 0≤t ≤3 时，（左侧图），正方形的 DA 边交 AC 于点 H ，点 A 运动到点 M 处， 则点 M(−3√3+t,0)，则点 H (−3√3+t,√33t)，S =S △AHM =12×AM ×HM =12×t ×√33t =√36t 2， ②当 3<t ≤3√3 时，（右侧图），正方形的 DA 边交 AC 于点 H ，点 A 运动到点 G 处，E ，F 交直线 AC 于点 R ，S ， AG =t ，则 AS =t −3，则 RS =√33(t −3)，同理 HG =√33t ， 同理可得：S =S 梯形RSHG =12×3×(√33t √33t −√3)=√3t −3√32；故：S ={√36t 2(0≤t ≤3),√3t −3√32(3<t ≤3√3);(3) ∵ 点 M 为线段 AC 上一动点，经画图，∠MQN 分别为 90∘ 时，点 M 不在线段 AC 上，① NMQ =90∘ 时，三角形 QMN 为等腰直角三角形，过点 M 作 y 轴的平行线交 x 轴于点 G ，过点 N 作 x 轴的平行线交 MG 于点 R 、交 y 轴于点 H ，设点 M ，N 的坐标分别为 (m,√33m +3)，(n,3−n )，∵∠NMR +∠RNM =90∘，∠MNR +∠GMQ =90∘， ∴∠GMQ =∠RNM ，∠NRM =∠MGO =90∘，MR =MQ ， ∴△NRM ≌△MGO (AAS )， 则 MG =RN ，GQ =RM ， 即：n −m =√33m +3，3−n −(√33m +3)=1−m ，解得：m =−2√3，故点 M 的坐标为 (−2√3,1)； ②当 ∠MNQ =90∘ 时， 同理可得：点 M(−√3,2)；综上，点 M 的坐标为：(−2√3,1) 或 (−√3,2)．12. 【答案】(1) (−6√3,0)；(0,6)；12(2) 当由题可知，QC ⊥OB ，AO ⊥OB ， ∴QC ∥AO ，∵Q 为 AB 中点， ∴C (0,3)，∴2t=122，t=3，∴AP=3√3，PO=6√3−3√3=3√3，点P(−3√3,0)，设PC解析式为y=kx+b(k≠0)，把P(−3√3,0)和C(0,3)代入，解得：{k=√33, b=3,故PC解析式为y=√33x+3．(3) 存在点M使以M，N，B，D为顶点四边形的平行四边形，M坐标为(−2√3,4)或(−10√3,−4)或(2√3,8)．【解析】(1) 把x=0代入解析式，求得：y=6，故B(0,6)，把y=0代入解析式，求得，x=−6√3，故A(−6√3,0)，AB=√(6√3)2+62=12．(3) 由题已知A(−6√3,0)，B(0,6)，可求AB解析式为y=√33x+6，BD=4，当BD为平行四边形时，① MN=BD=4，MN⊥x轴，把y=4代入AB解析式得：4=√33x+6，解得：x=−2√3，∴M(−2√3,4)．②把y=−4代入，得−4=√33x+6，解得：x=−10√3，∴M2(−10√3,−4)．③当BD为平行四边形对角线时，过点M3作M3G⊥y轴，∴M3B=DN，GB=OD=2，∴GM3=ON=2√3，GO=2+6=8，∴M3(2√3,8)．综上所述，存在点M使以M，N，B，D为顶点四边形的平行四边形，M坐标为(−2√3,4)或(−10√3,−4)或(2√3,8)．13. 【答案】(1) ∵b2−16b+64=√a−10+√20−2a，∴(b −8)2=√a −10+√20−2a ， ∴ 由非负性易得 a =10，b =8， ∴AB =10，BC =8．(2) ∵ 点 D 的坐标为 (m,0)， ∴OD =m ．由（1）知，AD =BC =8，AE =AB =10． ①当 OA =OE 时，DE =√AE 2−AD 2=6， ∴OA =m +6，∴OA 2=OD 2+AD 2，即 (m +6)2=m 2+82，解得 m =73．②当 OA =AE 时，OA =10，则 OD =√OA 2−AD 2=6，即 m =6， ③当 AE =OE 时，则 OE =10， ∴DE =10−m ．∵AD 2+DE 2=AE 2，即 82+(10−m )2=102， 解得 m =4 或 m =−6（舍去）．综上，m 的值为 73或 6 或 4．(3) ①若 F 在 AD 上时，此时 S △BEF ≤12S 矩形ABCD ， 当 E 在点 C 时，S △BEF =12S 矩形ABCD =12×10×8=40，此时 E (12,0)．②若 F 在 AB 上时，此时 S △BEF ≤12S 矩形ABCD ， 此时 S △BEF =12S 矩形ABCD =12×10×8=40， 此时 E (8,0)．∴ 综上所述：存在最大值，E (12,0) 或 E (8,0)．14. 【答案】(1) 15(2) 如图，设 AD =x ，则 OD =OA =AD =12−x ，根据轴对称的性质，DE =x ，BE =AB =9，又 OB =15， ∴OE =OB −BE =15−9=6，在 Rt △OED 中，OE 2+DE 2=OD 2，即 62+x 2=(12−x )2，解得 x =92，∴OD =OA −AD =12−92=152，∴ 点 D (152,0)，设直线 BD 所对应的函数表达式为：y =kx +b (k ≠0)则 {12k +b =9,152k +b =0, 解得 {k =2,b =−15,∴ 直线 BD 所对应的函数表达式为：y =2x −15．(3) 过点 E 作 EP ∥BD 交 BC 于点 P ，过点 P 作 PQ ∥DE 交 BD 于点 Q ， 则四边形 DEPQ 是平行四边形，再过点 E 作 EF ⊥OD 于点 F ，由 12⋅OE ⋅DE =12⋅DO ⋅EF ，得 EF =6×92152=185，即点 E 的纵坐标为 185，又点 E 在直线 OB:y =34x 上， ∴185=34x ，解得 x =245，∴E (245,185)，由于 PE ∥BD ，∴ 可设直线 PE:y =2x +n ， ∵E (245,185)，在直线 EP 上∴185=2×245+n ，解得 n =−6，∴ 直线 EP:y =2x −6，令 y =9，则 9=2x −6，解得 x =152， ∴P (152,9)．【解析】(1) 在 Rt △ABC 中， ∵OA =12，AB =9，∴OB =√OA 2+AB 2=√92+122=15．15. 【答案】(1) ① ∵ 矩形 OABC ，OA =3，OC =2， ∴A (3,0)，C (0,2)，B (3,2)，AO ∥BC ，AO =BC =3，∠B =90∘，CO =AB =2， ∵△APD 为等腰直角三角形， ∴∠PAD =45∘， ∵AO ∥BC ，∴∠BPA =∠PAD =45∘， ∵∠B =90∘，∴∠BAP =∠BPA =45∘， ∴BP =AB =2， ∴P (1,2)，设直线 AP 解析式为 y =kx +b ， ∵ 过点 A ，点 P ，∴{2=k +b,0=3k +b,∴{k =−1,b =3,∴ 直线 AP 解析式为 y =−x +3．②如图所示：作 G 点关于 y 轴对称点 Gʹ(−2,0)，作点 G 关于直线 AP 对称点 Gʺ(3,1)，连接 GʹGʺ 交 y 轴于 N ，交直线 AP 于 M ， 此时 △GMN 周长最小， ∵Gʹ(−2,0)，Gʺ(3,1)，∴ 直线 GʹGʺ 解析式 y =15x +25，当 x =0 时，y =25，∴N (0,25)，∵GʹGʺ√GʹA 2+AGʺ2=√52+12=√26， ∴△GMN 周长的最小值为 √26． (2) 如图，作 PM ⊥AD 于 M ， ∵BC ∥OA ，∴∠CPD =∠PDA 且 ∠CPD =∠APB ， ∴PD =PA ，且 PM ⊥AD ， ∴DM =AM ，∵ 四边形 PAEF 是平行四边形， ∴PD =DE ，又 ∵∠PMD =∠DOE ，∠ODE =∠PDM ， ∴△PMD ≌△EOD ，∴OD =DM ，OE =PM ， ∴OD =DM =MA ， ∵PM =2，OA =3， ∴OE =2，OM =2， ∴E (0,−2)，P (2,2)，设直线 PE 的解析式 y =mx +n {n =−2,2=2m +n, ∴{m =2,n =−2,∴ 直线 PE 解析式 y =2x −2．16. 【答案】(1) (4,4)；(8,0)(2) 过点 E 作 EH ⊥BC 于 H ， ∵OE =1，OD =OB =4， ∴DE =3=CH ，在 Rt △EHC 中，CE =√32+42=5， ∴S 正方形CEFG =CE 2=52=25．(3) 过点 F 做 FH ⊥x 轴于 H ， 在 △FEH 和 △ECD 中， {∠FEH =∠ECD,∠FHE =∠EDC =90∘,FE =EC,∴△EFH ≌△CED (AAS )，①当 E 向 x 轴正半轴移动时，设 H (x,0)，由（1）得 x >4， 则 EH =CD =4，FH =DE =x −4， ∴F (x,x −4)，∴ 点 F 在 y =x −4 图象上．②当 E 向 x 轴正半轴移动时，设 H (x,0)，由（1）得 x <4， 则 EH =CD =4，FH =DE =4−x ， ∴F (x,4−x )，∴ 点 F 在 y =4−x 图象上． 【解析】(1) 连接 DF ，∵四边形CEFG为正方形，四边形OBCD为正方形，∴DF=DC=4，∴F(4,4)，又DG=DE=4，∴G(8,0)．17. 【答案】(1) 2425(2) ∵BP平分∠ABO，又∵PO⊥OB，PC⊥AB，∴PC=PO．设PO=x，则PC=x，PA=4−x，∵∠ACP=∠AOB=90∘，∠PAC=∠BAO，∴△ACP∽△AOB，∴APAB =PCBO，即：4−x5=x3，∴x=32，即：P(32,0)．(3) ①若四边形OCBD是菱形，∴OC=BC=BD=DO，∴CD，BO互相垂直平分，∴y C=y D=12BO=32，即：−34x C+3=32，∴x=2，∴C(2,32)，∵D，C关于y轴对称，∴D(−2,32)，此时，C是AB中点，∵△ACP∽△AOB，∴APAB =ACAO，即AP5=524，∴AP=258，∴OP=78．②若四边形 OCDB 是菱形，∴OC =CD =BD =BO ，延长 DC 交 x 轴于 E ，∵DE ∥y 轴，设 C (m,−34m +3)， 在 Rt △OCE 中 OE =m ，CE =3−34m ，OC =3，∴m 2+(3−34m)2=32，∴m 1=7225 或 m 2=0（舍去），∴C (7225,2125)， ∴D (7225,9625)，∵OB =OC ，∴∠OBC =∠OCB ，∴∠OAC =∠OCP ，又 ∠AOC =∠COP ， ∴△AOC ∽△COP ， ∴OC OP =AO CO ，即 3OP =43，∴OP =94．③若四边形 OBCD 是菱形，∴OB =BC =CD =DO ，OD ∥BC ，此时，点 D 在第四象限，不合题意，舍去．∴ 综上所述，符合条件的点 D 1(−2,32)，此时 OP 1=78；点 D 2(7225,9625)，此时 OP 2=94．【解析】(1) S △ACP =2425．18. 【答案】(1) 如图，连接 BP ． ∵ 直线 y =−34x +3 交 x 轴于点 A ，交 y 轴于点 B ， ∴ 点 A (4,0)，点 B (0,3)，∴AO =4，OB =3，∴AB =√OB 2+OA 2=√16+9=5，∵ 点 P 是 OA 中点，∴AP =OP =2， ∵S △ABP =12×AP ×OB =12×AB ×CP ，∴CP =65，∴AC =√PA 2−PC 2=√4−3625=85，∴S △APC =12×AC ×PC =2425．(2) ∵BP 平分 ∠ABO ，∴∠OBP =∠CBP ，又 ∵BP =BP ，∠BOP =∠BCP =90∘，∴△BOP≌△BCP(AAS)，∴BO=BC=3，OP=CP，∴AC=AB−BC=5−3=2，∵AP2=PC2+AC2，∴(4−OP)2=OP2+4，∴OP=32，∴点P(32,0)．(3) 若OB为边，如图2，设点C(a,−34a+3)，连接OD，∵四边形OCDB是菱形，∴OC=CD=BD=OB=3，BO∥CD，OD⊥BC，∴(a−0)2+(−34a+3−0)2=9，∴a1=0（不合题意舍去），a2=7225，∴点C(7225,2125)，∵BO∥CD，OB=CD=3，∴点D(7225,9625)，∴直线OD解析式为：y=43x，∵PC∥OD，∴设直线PC解析式为y=43x+b，∴2125=43×(7225)+b，∴b=−3，∴直线PC解析式为y=43x−3，∴当y=0时，x=94，∴点P(94,0)，∴OP=94；若OB为对角线，如图3，设点C(a,−34a+3)，连接CD，∵四边形OCBD是菱形，∴OB与CD互相垂直平分，∴点C在OB的垂直平分线上，∴32=−34a+3，∴a=2，∴点C(2,32)，∵BO垂直CD，∴点D(−2,32)，设直线PC解析式为y=43x+b，∴32=43×2+b，∴b=−76，∴设直线PC解析式为y=43x−76，当y=0时，x=78，∴ 点 P (78,0)，∴OP =78． 综上所述：当 OP =78 时，点 D (−2,32) 或当 OP =94 时，点 D (7225,9625)．19. 【答案】 (1) y =43x +4． (2) 若点 C 在直线 AB 右侧，如图 1，过点 A 作 AD ⊥AB ，交 BC 的延长线于点 D ，过点 D 作 DE ⊥AC 于 E ，∵∠ABC =45∘，AD ⊥AB ，∴∠ADB =∠ABC =45∘，∴AD =AB ，∵∠BAO +∠DAC =90∘，且 ∠BAO +∠ABO =90∘，∴∠ABO =∠DAC ，AB =AD ，∠AOB =∠AED =90，∴△ABO ≌△DAE (AAS )∴AO =DE =3，BO =AE =4，∴OE =1，∴ 点 D (1,−3)，∵ 直线 y =kx +b 过点 D (1,−3)，B (0,4)． ∴{−3=k +b,4=b,∴k =−7；若点 C 在点 A 右侧时，如图 2，同理可得 k =17，综上所述：k =−7 或 17． (3) 设直线 DN 的解析式为：y =43x +n ，且过点 N (−0.6t,0)，∴0=−0.8t +n ，∴n =0.8t ，∴ 点 D 坐标 (0,0.8t )，且过点 N (−0.6t,0)，∴OD =0.8t ，ON =0.6t ，∴DN =√ON 2+OD 2=1，∴DN =AM =1，且 DN ∥AM ，∴ 四边形 AMDN 为平行四边形，当 AN =AM 时，四边形 AMDN 为菱形，∵AN =AM ，∴t =3−0.6t ， ∴t =158， ∴ 当 t =158 时，四边形 AMDN 为菱形．【解析】(1) 设直线 AB 解析式为：y =mx +n ， 根据题意可得：{0=−3m +n,n =4, ∴{m =43,n =4, ∴ 直线 AB 解析式为：y =43x +4．20. 【答案】(1) H1，H2．(2) 点A和四边形CDEF的“中点形”是四边形．各顶点的坐标为：(0,0)、(0,1)、(32,0)、(32,1)．(3) −1≤b≤0或1≤b≤2．。