空间几何中的平行与垂直关系

§3.2立体几何中的向量方法 (一>——平行与垂直关系的向量证法知识点一求平面的法向量已知平面α经过三点A(1,2,3>，B(2,0，－1>，C(3，－2，0>，试求平面α的一个法向量．解∵A(1,2,3>，B(2,0，－1>，C(3，－2,0>，＝(1，－2，－4>，错误!＝(1，－2，－4>，设平面α的法向量为n＝(x，y，z>．依题意，应有n·=0，n·错误!=0.即错误!，解得错误!.令y＝1，则x＝2.b5E2RGbCAP∴平面α的一个法向量为n＝(2,1,0>．【反思感悟】用待定系数法求平面的法向量，关键是在平面内找两个不共线向量，列出方程组，取其中一组解(非零向量>即可．p1EanqFDPw Array在正方体ABCD-A1B1C1D1中，E，F分别是BB1，DC的中点，求证：是平面A1D1F的法向量.DXDiTa9E3d 证明设正方体的棱长为1，建立如图所示的空间直角坐标系，则是平面A1D1F的法向量．证明A(1,0,0>，E错误!，RTCrpUDGiTF错误!，A1(1,0,1>．jLBHrnAILg∵·＝错误!·错误!＝错误!－错误!＝0，LDAYtRyKfE知识点二利用向量方法证平行关系在正方体ABCD—A1B1C1D1中，O是B1D1的中点，求证：B1C∥平面ODC1.∴ B∴B1C∥A1D，又A1D面ODC1，∴B1C∥面ODC1.方法二∵ = += + + + = +.∴，，共面.方法三建系如图，设正方体的棱长为1，则可得B1(1,1,1>，C(0,1,0>，O错误!，C1(0,1,1>，dvzfvkwMI1＝(－1,0，－1>，＝错误!，rqyn14ZNXI＝错误!.EmxvxOtOco设平面ODC1的法向量为n＝(x0，y0，z0>，则得错误!SixE2yXPq5令x0＝1，得y0＝1，z0＝－1，∴n＝(1,1，－1>．又·n＝－1×1＋0×1＋(－1>×(－1>＝0，∴⊥n，∴B1C∥平面ODC1.【反思感悟】证明线面平行问题，可以有三个途径，一是在平面ODC1内找一向量与共线；二是说明能利用平面ODC1内的两不共线向量线性表示，三是证明与平面的法向量垂直．6ewMyirQFL如图所示，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF，∠BCF＝∠CEF＝90°，AD＝错误!，EF＝2.kavU42VRUs 求证：AE∥平面DCF.证明如图所示，以点C为坐标原点，以CB、CF和CD所在直线分别作为x轴、y轴和z轴，建立空间直角坐标系C—xyz.y6v3ALoS89设AB＝a，BE＝b，CF＝c，则C(0,0,0>，A(错误!，0，a>，B(错误!，0,0>，E(错误!，b,0>，F(0，c,0>．错误!＝(0，b，－a>，＝(错误!，0,0>，M2ub6vSTnP＝(0，b,0>，所以·错误!=0，· =0，从而CB⊥AE，CB⊥BE.0YujCfmUCw所以CB⊥平面ABE.因为CB⊥平面DCF，所以平面ABE∥平面DCF.故AE∥平面DCF.知识点三利用向量方法证明垂直关系在正方体ABCD—A1B1C1D1中，E，F分别是棱AB，BC的中点，试在棱BB1上找一点M，使得D1M⊥平面EFB1.eUts8ZQVRd 解建立空间直角坐标系D—xyz，设正方体的棱长为2，则E(2,1,0>，F(1,2,0>，D1(0,0,2>，B1(2,2,2>．sQsAEJkW5T设M<2，2，m），则 =<1，1，0），错误!=<0，1，2），GMsIasNXkA=<2，2，m2）.∵⊥平面EFB1，∴⊥EF，⊥B1E，∴· =0且·错误!=0，于是∴m＝1，故取B1B的中点为M就能满足D1M⊥平面EFB1.【反思感悟】证明直线与平面垂直有两种方法：(1>用直线与平面垂直的判定定理；(2>证明该直线所在向量与平面的法向量平行．TIrRGchYzg在正三棱柱ABC—A1B1C1中，B1C⊥A1B.求证：AC1⊥A1B.证明建立空间直角坐标系C1—xyz，设AB＝a，CC1＝b.则A1错误!，B(0，a，b>，B1(0，a,0>，C(0,0，b>，A错误!，7EqZcWLZNXC1(0,0,0>．于是 =错误! =<0， a，b），lzq7IGf02E＝错误!.zvpgeqJ1hk∵B1C⊥A1B，∴·＝－错误!＋b2＝0,而·＝错误!a2－错误!a2－b2＝错误!－b2＝0NrpoJac3v1∴⊥即AC1⊥A1B.课堂小结：1．用待定系数法求平面法向量的步骤：(1>建立适当的坐标系．(2>设平面的法向量为n＝(x，y，z>．(3>求出平面内两个不共线向量的坐标a＝(a1，b1，c1>，b＝(a2，b2，c2>．(4>根据法向量定义建立方程组错误!.1nowfTG4KI(5>解方程组，取其中一解，即得平面的法向量.2．平行关系的常用证法＝λ错误!.证明线面平行可转化为证直线的方向向量和平面的法向量垂直，然后说明直线在平面外，证面面平行可转化证两面的法向量平行．fjnFLDa5Zo3．垂直关系的常用证法要证线线垂直，可以转化为对应的向量垂直．要证线面垂直，可以转化为证明这条直线与平面内两条相交直线垂直．要证面面垂直，可以转化为证明两个平面的法向量垂直．一、选择题1.已知A<3，5，2），B<-1，2，1），把按向量a＝(2,1,1>平移后所得的向量是( >A．(－4，－3,0> B．(－4，－3，－1>C．(－2，－1,0> D．(－2，－2,0>答案B＝(－4，－3，－1>．平移后向量的模和方向是不改变的． 2．平面α的一个法向量为(1,2,0>，平面β的一个法向量为(2，－1,0>，则平面α与平面β的位置关系是( >tfnNhnE6e5 A．平行B．相交但不垂直C．垂直D．不能确定答案C解读∵(1,2,0>·(2，－1,0>＝0，∴两法向量垂直，从而两平面也垂直．3．从点A(2，－1,7>沿向量a＝(8,9，－12>的方向取线段长AB＝34，则B点的坐标为( >HbmVN777sLA．(－9，－7,7> B．(18,17，－17>C．(9,7，－7> D．(－14，－19,31>答案B解读，设B<x，y，z），=<x2，y+1，z7）=λ<8，9， 12），λ>0.故x2=8λ,y+1=9λ,z7=12λ，又<x22+<y+12+<z72=342，得<17λ）2=342，∵λ>0,∴λ=2.∴x=18,y=17,z=17,即B<18，17， 17）.4．已知a＝(2,4,5>，b＝(3，x，y>分别是直线l1、l2的方向向量，若l1∥l2，则( >V7l4jRB8HsA．x＝6，y＝15B．x＝3，y＝错误!C．x＝3，y＝15D．x＝6，y＝错误!答案D解读∵l1∥l2，∴a∥b，则有错误!＝错误!＝错误!，解方程得x＝6，y＝错误!.5．若直线l的方向向量为a＝(1,0,2>，平面α的法向量为u ＝(－2,0，－4>，则( >A．l∥αB．l⊥αC．lαD．l与α斜交答案B解读∵u＝－2a，∴a∥u，∴l⊥α.二、填空题6．已知A(1,1，－1>，B(2,3,1>，则直线AB的模为1的方向向量是________________．83lcPA59W9答案错误!或错误!mZkklkzaaP解读， =<1，2，2），| |=3.模为1的方向向量是±,7．已知平面α经过点O(0,0,0>，且e＝(1,1,1>是α的法向量，M(x，y，z>是平面α内任意一点，则x，y，z满足的关系式是________________．AVktR43bpw答案x＋y＋z＝0解读·e=<x，y，z）·<1，1，1）=x+y+z=0.8．若直线a和b是两条异面直线，它们的方向向量分别是(1,1,1>和(2，－3，－2>，则直线a和b的公垂线(与两异面直线垂直相交的直线>的一个方向向量是________．ORjBnOwcEd 答案(1,4，－5>(答案不唯一>解读设直线a和b的公垂线的一个方向向量为n＝(x，y，z>，a与b的方向向量分别为n1，n2，由题意得错误!即：错误! 2MiJTy0dTT解之得：y＝4x，z＝－5x，令x＝1，则有n＝(1,4，－5>．三、解答题9．已知正方体ABCD－A1B1C1D1的棱长为2，E、F分别是BB1、DD1的中点，求证：(1>FC1∥平面ADE；(2>平面A DE∥平面B1C1F.证明如图所示建立空间直角坐标系Dxyz，则有D(0,0,0>、A(2,0,0>，C(0,2,0>，C1(0,2,2>，E(2,2,1>，F(0,0,1>，B1(2,2,2>，所以 =<0，2，1），=<2，0，0）， =<0，2，1）.<1）设n1=<x1,y1,z1）是平面ADE的法向量,则n1⊥，n1⊥，即得令z1＝2，则y1＝－1，所以n1＝(0，－1,2>．因为错误!·n1＝－2＋2＝0，所以错误!⊥n1.gIiSpiue7A又因为FC1平面ADE，所以FC1∥平面ADE.<2）∵=<2，0，0），设n2 =(x2,y2,z2>是平面B1C1F的一个法向量.由n2⊥错误!,n2⊥,得得得令z2＝2得y2＝－1，所以n2＝(0，－1,2>，因为n1＝n2，所以平面ADE∥平面B1C1F.10.如图所示，在棱长为1的正方体ABCD—A′B′C′D′中，AP＝BQ＝b (0<b<1>，截面PQEF∥A′D，截面PQGH∥AD′.uEh0U1Yfmh(1>证明：平面PQEF和平面PQGH互相垂直；(2>证明：截面PQEF和截面PQGH面积之和是定值，并求出这个值；(3>若b＝错误!，求D′E与平面PQEF所成角的正弦值．解以D为原点，射线DA、DC、DD′分别为x、y、z轴的正半轴建立如图(2>所示的空间直角坐标系D—xyz，由已知得DF＝1－b，故A(1,0,0>，A′(1,0,1>，D(0,0,0>，IAg9qLsgBXD′(0,0,1>，P(1,0，b>，Q(1,1，b>，E(1－b,1,0>，F(1－b,0,0>，G(b,1,1>，H(b,0,1>．WwghWvVhPE(1>，证明在所建立的坐标系中,可得=(0,1,0>,=(b,0,b>, =(b1,0,1b>,=(1,0,1>, =(1,0, 1>,因为· =0，·=0，所以是平面PQEF的法向量.因为· =0，· =0，所以是平面PQGH的法向量.所以平面PQEF和平面PQGH互相垂直.(2>证明，因为=(0, 1,0>,所以∥,| |=||,又⊥,所以四边形PQEF为矩形,同理四边形PQGH为矩形.在所建立的坐标系中可求得||= (1-b>,||=b,所以||+||=,又||=1,所以截面PQEF和截面PQGH的面积之和为,是定值.(3>解由(1>知＝(－1,0,1>是平面PQEF的法向量．由P为AA′的中点可知，Q、E、F分别为BB′、BC、AD的中点．所以E<，1，0,），＝错误!，因此D′E与平面PQEF所成角的正弦值等于|cos〈错误!,> ＝错误!.asfpsfpi4k申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

空间几何的平行与垂直解析几何的基本性质几何学是数学的一个分支，研究空间中的各种形状、大小、相对位置以及与它们相关的性质。

空间几何是其中的一个重要分支，主要研究空间中的点、线、面以及它们之间的关系。

平行与垂直是空间几何中的重要概念，下面将介绍平行和垂直的解析几何的基本性质。

一、平行线的解析几何性质平行线是指在同一个平面上永不相交的两条直线。

在解析几何中，我们可以利用坐标系来描述平行线的性质。

1. 两直线平行的判定条件在平面直角坐标系中，两条直线平行的条件为斜率相等。

假设直线L1的斜率为k1，直线L2的斜率为k2，若k1=k2，则直线L1与直线L2平行。

2. 平行线的性质（1）平行线之间的距离相等：设直线L1和直线L2分别为y=k1x+b1和y=k2x+b2，斜率相等且截距不相等，则直线L1与直线L2平行。

设点P1(x1, y1)和点P2(x2, y2)分别在直线L1和直线L2上，则点P1到直线L2的距离等于点P2到直线L1的距离。

（2）平行线的夹角为0度：两条平行线之间的夹角为0度。

二、垂直线的解析几何性质垂直线是指两条直线相交时互相垂直的性质。

同样，在解析几何中，我们可以利用坐标系来描述垂直线的性质。

1. 两直线垂直的判定条件在平面直角坐标系中，两条直线垂直的条件为斜率的乘积为-1。

假设直线L1的斜率为k1，直线L2的斜率为k2，若k1*k2=-1，则直线L1与直线L2垂直。

2. 垂直线的性质（1）直线与其法线的斜率互为相反数：设直线L的斜率为k1，直线L的法线的斜率为k2，则k1*k2 = -1。

（2）两条垂直线之间的夹角为90度：两条垂直线之间的夹角为90度。

三、平行与垂直的应用平行和垂直的概念在几何学中有广泛的应用。

在建筑、工程、地理学和艺术等领域中，平行和垂直关系的运用非常常见。

以建筑为例，建筑设计师在绘制平面图时需要准确地描述建筑物之间的相对位置。

这时，平行和垂直的概念就派上了用场。

设计师可以利用解析几何的性质来判断各个建筑物之间的平行和垂直关系，从而保证建筑的结构稳定和美观。

空间向量的垂直与平行解析几何的几何关系空间向量在解析几何中具有广泛的应用，它们可以描述物体在空间中的位置、方向和运动等属性。

在学习空间向量时，了解其垂直与平行的几何关系是非常重要的。

本文将通过几何解析的方式，深入探讨空间向量垂直与平行的性质及其应用。

一、垂直向量在空间中，当两个向量的数量积为零时，我们称这两个向量是垂直的。

数学上可以表达为：两个向量的数量积等于零，则它们垂直。

设有两个向量a和b，它们的坐标分别表示为(a1, a2, a3)和(b1, b2, b3)，则向量a与向量b垂直的条件可以表示为：a1 * b1 + a2 * b2 + a3 * b3 = 0这个条件求解出的结果就是两个向量垂直的充要条件。

垂直向量在几何上有许多重要的应用。

例如在平面几何中，两条直线互相垂直，则它们的方向向量必然垂直；在立体几何中，两个平面互相垂直，其法向量也必然垂直。

因此，熟练掌握垂直向量的性质对于解析几何的应用非常重要。

二、平行向量在空间中，当两个向量之间存在倍数关系时，我们称这两个向量是平行的。

数学上可以表达为：两个向量之间存在倍数关系，则它们平行。

设有两个向量a和b，它们的坐标表示为(a1, a2, a3)和(b1, b2, b3)，则向量a与向量b平行的条件可以表示为：a1/b1 = a2/b2 = a3/b3 = k (k为常数)其中k为两个向量平行的倍数关系。

平行向量的性质可以应用于线段、直线和平面的平行关系的判断。

例如，在平面几何中，两个直线互相平行，则它们的方向向量之间必然存在倍数关系；在立体几何中，平面与直线平行，则平面的法向量与直线的方向向量必然平行。

三、垂直与平行向量的应用举例1. 垂直向量的应用考虑一个示例问题：已知一条直线L的向量方程为(r - r1) · n = 0，其中r1为已知点，n为已知向量。

求直线L上与已知点A垂直的点B 的坐标。

解析：根据向量方程可以得知，L上的任意点P满足向量n与r - r1垂直的关系。

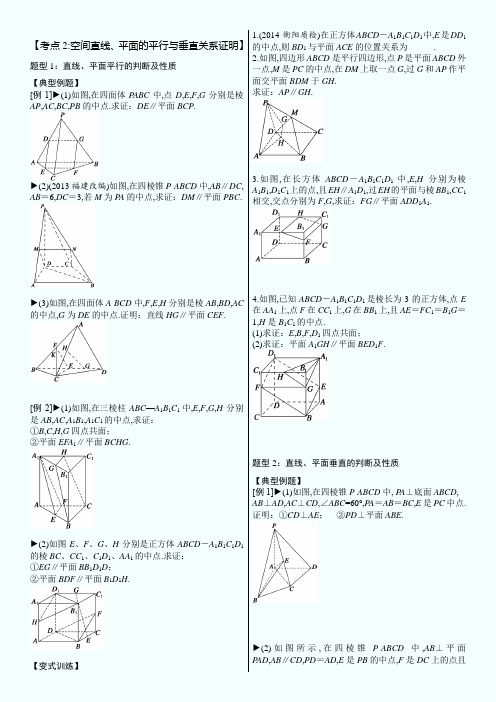
【考点2:空间直线、平面的平行与垂直关系证明】题型1：直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证：DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB＝6,DC＝3,若M为P A的中点,求证：DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明：直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证：①B,C,H,G四点共面；②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD－A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证：①EG∥平面BB1D1D；②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD－A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证：AP∥GH .3.如图,在长方体ABCD－A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证：FG∥平面ADD1A1.4.如图,已知ABCD－A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE＝FC1＝B1G＝1,H是B1C1的中点.(1)求证：E,B,F,D1四点共面；(2)求证：平面A1GH∥平面BED1F .题型2：直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A＝AB＝BC,E是PC中点. 证明：①CD⊥AE；②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD＝AD,E是PB的中点,F是DC上的点且DF＝12AB,PH为△P AD中AD边上的高.①证明：PH⊥平面ABCD；②证明：EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB＝BC＝BD＝2,∠ABC＝∠DBC＝120°,E,F,G分别为AC,DC,AD的中点.(I)求证：EF⊥平面BCG；(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB＝90°,AC＝BC＝12AA1,D是棱AA1的中点.(I)证明：平面BDC1⊥平面BDC；(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD＝DC＝BC＝1,AB＝2,AB∥DC,∠BCD＝90°.①求证：PC⊥BC；②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证：CE⊥平面P AD；(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证：CD⊥平面ABD；(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A＝PB＝AB ＝BC,∠PBC＝90°,D为AC的中点,AB⊥PD.(1)求证：平面P AB⊥平面ABC；(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明：B1C⊥AB；(2)若AC⊥AB1,∠CBB1＝60°,BC＝1,求三棱柱ABC-A1B1C1的高.☆题型3：直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β；②若l⊂α,l∥β,α∩β＝m,则l∥m；③若α∥β,l∥α,则l∥β；④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β＝l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题：①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1＝AC＝2,BC＝1,E,F分别为A1C1,BC的中点.(I)求证：平面ABE⊥平面B1BCC1；(II)求证：C1F∥平面ABE；(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A＝6,BC＝8,DF＝5. 求证：(I)直线P A∥平面DEF；(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积；(II)证明：四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C＝90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证：DE∥平面A1CB；(II)求证：A1F⊥BE；(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ？说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β＝c.给出下列命题：①若a与b是异面直线,则c至少与a,b中的一条相交；②若a不垂直于c,则a与b一定不垂直；③若a∥b,则必有a∥c；④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD ＝2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证： (1)P A ⊥底面ABCD ； (2)BE ∥平面P AD ；(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB ＝BC＝12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC －A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明：BC 1∥平面A 1CD ；(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证：BC ⊥平面P AC ； (2)设Q 为P A 的中点,G 为△AOC 的重心,求证：QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明：PB ∥平面AEC ；(2)设AP ＝1,AD ＝3,三棱锥P - ABD 的体积V ＝34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC ＝CC 1.设AB 1的中点为D ,B 1C ∩BC 1＝E . 求证：(1)DE ∥平面AA 1C 1C ； (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC ＝4,AB ＝6,BC ＝3. (1)证明：BC ∥平面PDA ； (2)证明：BC ⊥PD ；(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB ＝16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)； (2)求平面α把该长方体分成的两部分体积的比值．16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点．将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE ． (Ⅰ)证明：CD ⊥平面A 1OC ；(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值．17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE ＝CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置． (1)证明：AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′­ABCFE 的体积．18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB ＝AD ＝AC ＝3,P A ＝BC ＝4,M 为线段AD 上一点,AM ＝2MD ,N 为PC 的中点． (1)证明MN ∥平面P AB ；(2)求四面体N -BCM 的体积．19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP ＝∠CDP ＝90°.(1)证明：平面PAB ⊥平面PAD ； (2)若PA =PD =AB =DC ,∠ADP ＝90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明：直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。

完整版)立体几何中平行与垂直证明方法归纳本文系统总结了立体几何中平行与垂直证明方法，适合高三总复时学生构建知识网络、探求解题思路、归纳梳理解题方法。

以下是常见证明方法：一、“平行关系”常见证明方法一）直线与直线平行的证明1.利用平行四边形的对边互相平行的特性；2.利用三角形中位线性质；3.利用空间平行线的传递性（即公理4）；4.利用直线与平面平行的性质定理；5.利用平面与平面平行的性质定理；6.利用直线与平面垂直的性质定理；7.利用平面内直线与直线垂直的性质；8.利用定义：在同一个平面内且两条直线没有公共点。

二）直线与平面平行的证明1.利用直线与平面平行的判定定理；2.利用平面与平面平行的性质推论；3.利用定义：直线在平面外，且直线与平面没有公共点。

三）平面与平面平行的证明1.利用平面与平面平行的判定定理；2.利用某些空间几何体的特性；3.利用定义：两个平面没有公共点。

二、“垂直关系”常见证明方法一）直线与直线垂直的证明1.利用直角三角形的两条直角边互相垂直的特性；2.看夹角：两条共（异）面直线的夹角为90°，则两直线互相垂直；3.利用直线与平面垂直的性质：如果一条直线与一个平面垂直，则这条直线垂直于此平面内的所有直线。

1.利用空间几何体的特性：例如长方体侧棱垂直于底面。

2.观察直线与平面所成角度：若直线与平面所成角为90度，则该直线垂直于平面。

3.利用直线与平面垂直的判定定理：若一条直线与一个平面内的两条相交直线垂直，则该直线垂直于此平面。

4.利用平面与平面垂直的性质定理：若两个平面互相垂直，则在这两个平面内分别作垂直于交线的直线，则这两条直线互相垂直。

5.利用常用结论：例如若一条直线平行于一个平面的垂线，则该直线也垂直于此平面。

空间直线的平行与垂直关系直线的平行与垂直关系是几何学中的基本概念之一，这个概念在我们日常生活中也是无处不在的。

在建筑、设计、城市规划、工程等领域中，了解直线的平行与垂直关系至关重要。

本文将介绍直线的平行与垂直的定义、性质以及应用。

首先，我们来看直线的平行关系。

当两条直线在平面上永不相交，且在同一平面上的任意两点之间连线都与这两条直线相交，我们可以说这两条直线是平行的。

以字母 "||" 表示直线的平行关系，如果直线a || 直线b，则可以写作 a || b。

直线的平行关系有以下几个重要性质：1. 平行性质一：如果两条直线都与同一平面上的第三条直线平行，那么这两条直线必定平行。

2. 平行性质二：如果两条直线分别与同一平面上的两条平行线平行，那么这两条直线也平行。

3. 平行性质三：如果直线a与b平行，直线b与c平行，那么直线a与c平行。

直线的垂直关系与平行关系相对应。

当两条直线在平面上相交且交角为90度，我们可以说这两条直线是垂直的。

以一个类似于 "⊥" 的符号表示直线的垂直关系，如果直线a ⊥直线b，则可以写作 a ⊥ b。

直线的垂直关系也有几个重要性质：1. 垂直性质一：如果两条直线都与同一平面上的第三条直线垂直，那么这两条直线必定垂直。

2. 垂直性质二：如果一条直线与平面上的一条直线垂直，那么与该平面上的另一条直线平行的直线也与该直线垂直。

3. 垂直性质三：如果直线a与b垂直，直线b与c垂直，那么直线a与c平行。

直线的平行与垂直关系在很多领域中都有广泛的应用。

以下是几个常见的应用实例：1. 建筑和设计：在建筑和设计中，了解平行和垂直关系对于设计合理的建筑和室内布局至关重要。

例如，在设计房间时，我们应该确保墙壁平行或垂直于地面，以获得更美观的效果。

2. 道路和交通：平行和垂直关系在规划和设计道路和交通系统时也非常重要。

道路的平行布局可以提高交通流畅性，而垂直的交叉路口可以确保交通的安全。

微专题14 空间中的平行与垂直关系 (几何法、向量法) 高考定位 1.以选择题、填空题的形式考查线线、线面、面面位置关系的判定与性质定理，对命题的真假进行判断，属基础题.2.空间中的平行、垂直关系的证明也是高考必考内容，多出现在立体几何解答题中的第(1)问.

1.(2022·全国乙卷)在正方体ABCD－A1B1C1D1中，E，F分别为AB，BC的中点，则( ) A.平面B1EF⊥平面BDD1 B.平面B1EF⊥平面A1BD C.平面B1EF∥平面A1AC D.平面B1EF∥平面A1C1D 答案 A 解析 对于选项A，在正方体ABCD－A1B1C1D1中，因为B1B⊥平面ABCD，EF⊂平面ABCD，所以B1B⊥EF.因为E，F分别为AB，BC的中点，所以EF⊥BD，

又B1B∩BD＝B，B1B，BD⊂平面BDD1，所以EF⊥平面BDD1，又EF⊂平面B1EF，

所以平面B1EF⊥平面BDD1，故选项A正确；

对于选项B，因为平面A1BD∩平面BDD1＝BD，由选项A知，平面B1EF⊥平面

A1BD不成立，故选项B错误； 对于选项C，由题意知直线AA1与直线B1E必相交，故平面B1EF与平面A1AC

不平行，故选项C错误； 对于选项D，连接AB1，B1C(图略)，易知平面AB1C∥平面A1C1D，又平面AB1C与平面B1EF有公共点B1，所以平面AB1C与平面B1EF不平行，所以平面A1C1D

与平面B1EF不平行，故选项D错误.故选A.

2.(2020·全国Ⅲ卷)如图，在长方体ABCD－A1B1C1D1中，点E，F分别在棱DD1，BB1上，且2DE＝ED1，BF＝2FB1.证明：

(1)当AB＝BC时，EF⊥AC； (2)点C1在平面AEF内. 证明 (1)如图，连接BD，B1D1. 因为AB＝BC，所以四边形ABCD为正方形，故AC⊥BD. 又因为BB1⊥平面ABCD，AC⊂平面ABCD，于是AC⊥BB1.

高中数学总复习-第七章立体几何-空间中的平行和垂直关系【知识结构图】第3课空间中的平行关系【考点导读】1．掌握直线和平面平行、两个平面平行的判定定理和性质定理。

2．明确定义与定理的不同，定义是可逆的，既是判定也是性质，而判定定理与性质定理多是不可逆的。

3．要能灵活的对“线线平行”、“线面平行”和“面面平行”进行转化。

【基础练习】1．若ba、为异面直线，直线c∥a，则c与b的位置关系是异面或相交2．给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行.③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行. ④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线. 其中假．命题的个数是 4 个。

3．对于任意的直线l 与平面a ,在平面a 内必有直线m ,使m 与l 垂直 。

4. 已知a 、b 、c 是三条不重合的直线，α、β、r 是三个不重合的平面，下面六个命题：①a ∥c ，b ∥c ⇒a ∥b ；②a ∥r ，b ∥r ⇒a ∥b ；③α∥c ，β∥c ⇒α∥β； ④α∥r ，β∥r ⇒α∥β；⑤a ∥c ，α∥c ⇒a ∥α；⑥a ∥r ，α∥r ⇒a ∥α． 其中正确的命题是 ①④ 。

【范例导析】例1．如图，在四面体ABCD 中，截面EFGH 是平行四边形． 求证：AB ∥平面EFG ． 证明 ：∵面EFGH 是截面．∴点E ，F ，G ，H 分别在BC ，BD ，DA ，AC 上． ∴EH面ABC ，GF面ABD ，由已知，EH ∥GF ．∴EH ∥面ABD ． 又 ∵EH 面BAC ，面ABC ∩面ABD=AB∴EH ∥AB ． ∴AB ∥面EFG ．例2． 如图，在正方体ABCD —A 1B 1C 1D 1中，点N 在BD 上，点M 在B 1C 上，并且CM=DN.求证:MN ∥平面AA 1B 1B.分析：“线线平行”、“线面平行”、“面面平行”是可以互相转化的。