阻抗变换.
- 格式:pptx
- 大小:1.40 MB
- 文档页数:4
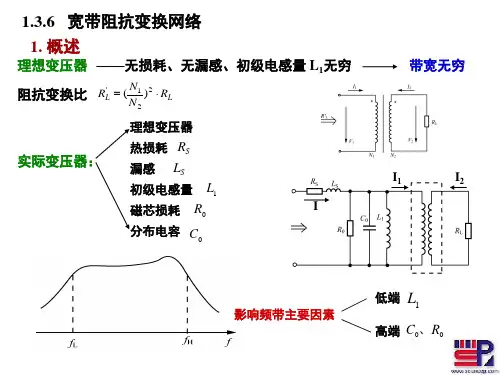


变压器的阻抗变换介绍及其性质
变压器阻抗介绍
变压器阻抗,是指变压器里的线圈的绕组的阻抗,包括电阻,感抗,容抗。
变压器的标准对阻抗、损耗都有明确规定。
有些用户增加或减小阻抗电压后,损耗还按标准要求是不合理的。
如果阻抗电压变小,合理的变化是:空载损耗变大,负载损耗变小;如果阻抗电压变大,合理的变化是:空载损耗变小,负载损耗变大;
变压器阻抗变化介绍
变压器就像是一个水管的变径。
既然一头是细的,另一头是粗的,当然对水的阻力是不一样的。
变压器初级线细,匝数多,所以电感(抗)就大,(输入的电压高,电流小。
)。


阻抗星三角变换公式好的,以下是为您生成的文章:咱今天来聊聊阻抗星三角变换公式,这玩意儿在电学里可有着重要的地位呢!还记得我当年在学校学习这个公式的时候,那可真是费了一番功夫。
当时我们的电学老师,是一个特别严谨又有点小幽默的人。
有一次上课,他为了让我们更清楚地理解这个公式,特意带来了一堆电线、电阻啥的,就在讲台上摆弄起来。
他一边接线路,一边给我们讲解:“同学们,你们看,这就好比是一个电路的迷宫,而阻抗星三角变换公式就是我们走出这个迷宫的钥匙。
” 我们都瞪大了眼睛,盯着老师的操作。
老师接着说:“星型连接的时候,三个阻抗分别是 Z1、Z2、Z3,而三角型连接的时候,对应的阻抗就是 Z12、Z23、Z31。
它们之间的关系,就像是一场巧妙的变形秀。
”咱们先来说说星型连接到三角型连接的变换公式。
Z12 = (Z1 * Z2 +Z2 * Z3 + Z3 * Z1) / Z3 ,Z23 = (Z1 * Z2 + Z2 * Z3 + Z3 * Z1) / Z1 ,Z31 = (Z1 * Z2 + Z2 * Z3 + Z3 * Z1) / Z2 。
这看起来是不是有点复杂?别着急,咱们来举个例子。
假设 Z1 =3Ω,Z2 = 4Ω,Z3 = 5Ω ,那咱们算算 Z12 是多少。
先把数值代入公式,Z12 = (3×4 + 4×5 + 5×3) / 5 = 8.2Ω 。
再来说说三角型连接到星型连接的变换公式。
Z1 = Z12 * Z31 / (Z12 + Z23 + Z31) ,Z2 = Z12 * Z23 / (Z12 + Z23 + Z31) ,Z3 = Z23 * Z31 /(Z12 + Z23 + Z31) 。
咱们还是用刚才的数值来算一下,Z1 = 8.2×7.5 / (8.2 + 10 + 7.5) ≈2.5Ω 。
在实际的电路分析中,这个阻抗星三角变换公式用处可大了。
比如说,我们要计算复杂电路中的电流和电压,如果直接计算很困难,这时候通过变换连接方式,用这个公式就能让问题变得简单许多。

射频电路设计实训报告设计题目阻抗变换器设计系别年级专业设计组号学生姓名/学号指导教师摘要:射频设计的主要工作之一,就是使电路的某一部分与另一部分相匹配,在这两部分之间实现最大功率传输,这就需要在射频电路中加入阻抗变换器从而达到阻抗匹配的目的。
阻抗变换器就是起到将压电传感器的高阻抗变换为信号放大处理部分需要的低阻抗。
本设计是关于阻抗匹配和阻抗转换器的一些阻抗匹配电路以及阻抗匹配的方法,用以实现匹配以及50Ω到75Ω以及75Ω到50Ω的阻抗转换器。
从而得到所需要的输出阻抗以达到变换的目的。
本次实验以2个无源阻抗匹配器为例,分别采用简单的电容电感的方式设计所需要的阻抗转换器,整理出实物并进行测试。
Abstract: One of the main RF design is a part of the circuit and the other part of the match between the two parts to achieve maximum power transfer, which requires adding the RF circuit impedance converter to achieve impedance matching purposes. Impedance transformer is played to a high impedance piezoelectric sensor signal amplification process is transformed into some of the needs of low impedance. This design is about impedance matching and impedance converter circuit and impedance matching impedance matching some of the methods used to achieve matching and 50Ω to 75Ω and 75Ω to 50Ω impedance converter. In order to get the required output impedance of achieving the purpose of transformation. The experiment with two passive impedance matching device, for example, capacitance and inductance, respectively, a simple way to design the required impedance converter to produce a physical and tested. 关键词: 射频设计 阻抗变换器 阻抗匹配 无源一、基本阻抗匹配理论当负载阻抗与传输线特性阻抗不相等或连接两段特性阻抗不同的传输线时,由于阻抗不匹配会产生反射现象,从而导致传输系统的功率容量和传输效率下降,负载不能获得最大功率。

实验六 滤波器一、实验要求设计一节4节切比雪夫匹配变换器,以匹配40Ω的传输线到60Ω的负载,在整个通带上最大允许的驻波比值为1.2,求出其带宽,并画出输入反射系数与频率的关系曲线。
二、实验目的(1) 掌握切比雪夫电路的原理及其基本设计方法。
(2) 利用Microwave Office 或Ansoft Designer 软件进行相关电路设计和仿真。
三、预习内容(1)切比雪夫的相关原理。
(2)切比雪夫匹配变换器的设计方法。
四、理论分析切比雪夫变换器是以通带内的波纹为代价得到最佳带宽的。
若能容忍这种通带特性的话,对于给定节数,切比雪夫变换器的带宽将明显其他变换器的带宽。
切比雪夫变换器是通过使Γ与切比雪夫多项式相等的方法设计的,因为切比雪夫多项式具有这类变换器所需的最佳特性。
1、切比雪夫多项式第n 阶切比雪夫多项式是用()x T n 表示的n 次多项式。
前4阶切比雪夫多项式是188341224433221+-=-=-==x x T x x T x T x T从而得到切比雪夫的递推公式:()()()x T x xT x T n n n 112-+-=现在令θcos =x ,得切比雪夫表达式可表示为:θθn T n cos )(cos =或者更一般的表达式()()()⎪⎩⎪⎨⎧>⋅≤⋅=--11cos cos 11x x ch n ch x xn x T n因为θncos 可展开为θ)2cos(m n -形式的多项和,从而切比雪夫又可改写为:上面的结果用于高到4节的匹配变换器的设计。
2、切比雪夫变换器的设计 我们现在通过使)(θΓ正比于()θθcos sec m N T 来综合切比雪夫的等波纹通带,此处N 是变换节数。
()()(){}()θθθθθθθθcos sec 2cos 2cos cos 210m N jN n jN T Ae n N N N e --=+-Γ++-Γ+Γ=ΓL L我们可令θ=0求出常数A ,于是有所以,我们有现在,若通带内最大允许的反射系数的幅值为m Γ,则有A m =Γ。
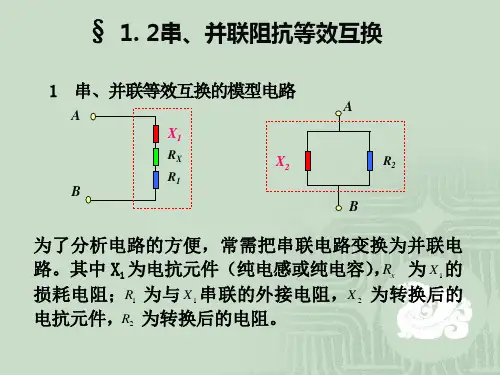

变压器的阻抗变换关系
如图6-3 所示,当变压器的次级负载阻抗Z2 发生变化时,初级阻抗Z2会立即受到次级的反射而变化。
这种阻抗的变化关系,可以通过下面公式的推导得出。
根据欧姆定律,下式成立:
如果不考虑变压器的损耗,则输入功率P1等于输出功率P2,即
从上面的公式推导可以得出.变压器的初、次级阻抗比等于初、次级匝数比的平方。
因此,变压器可以通过改变初、次级匝数的方法居到变换阻抗的作用。
当电子电路输入端阻抗与信号源、内阳相等时,信号掘可以把信号功率最大限度地传送给电路。
当负载阻抗与电子电路的输出阻抗相等时,负载上得到的功率最大。
这种情况在电子电路中称为阻抗匹配变压器的阻抗变换功能,在阻抗匹配中可发阵作用。
1.生活如意,事业高升。
2.前程似锦,美梦成真。
3.年年今日,岁岁今朝。
4.百事大吉,万事顺利。
5.愿与同僚,共分此乐。
6.事业有成,幸福快乐。
7.生日快乐,幸福安康。
8.幸福快乐,与君同在。

buck电路的阻抗变换为了了解buck电路的阻抗变换,我们首先需要了解什么是buck电路以及它的工作原理。
buck电路是一种DC-DC转换器,用于将输入电压降低到较低的输出电压。
这种电路通常由开关管、电感和负载组成,工作原理是通过周期性地开关开和关来控制电感和电容的充放电过程,从而实现输入电压到输出电压的降压转换。
在buck电路中,输入电压经过开关管控制,与电感和电容相互作用,最终输出为较低的电压。
因此,buck电路的阻抗变换主要是指在输入和输出端的阻抗变化。
在实际应用中,我们需要对buck电路的阻抗进行匹配,以确保电路正常工作和高效转换。
在buck电路中,输入阻抗取决于开关管和电感的特性,而输出阻抗取决于负载的特性。
电感和电容在电路中起到了储能和滤波的作用,因此对于输入阻抗的变换,我们需要考虑电感和电容的影响。
电感在电路中的作用类似于电阻,但是它会随着频率的变化而产生阻抗变化。
而电容在电路中的作用主要是滤波和储能,其阻抗也会随着频率的变化而变化。
当输入电压频率较高时,电感的阻抗会变得较低,从而对电路的输入阻抗产生影响。
而输出阻抗则取决于负载的特性,例如电阻、感性负载和电容负载。
当负载发生变化时,输出阻抗也会发生相应的变化。
在实际的应用中,我们通常需要对buck电路的阻抗进行匹配,以确保电路的稳定性和高效性。
在设计阶段,我们需要根据输入和输出端的阻抗特性,选择合适的电感和电容,并进行合理的匹配。
此外,我们还需要考虑开关管的导通和关断特性,以充分利用电路的阻抗特性。
另外,对于大功率的buck电路,我们还需要考虑电路的阻抗匹配与散热、功率损耗的关系。
高功率buck电路通常需要较大的电感和电容,以降低输入和输出端的阻抗,同时提高电路的稳定性和功率转换效率。
此外,散热和功率损耗也会影响电路的阻抗匹配,需要在设计过程中进行合理的考虑。
在实际应用中,buck电路的阻抗变换是一个复杂的问题,需要综合考虑电感、电容、开关管、负载等因素。

变压电路工作原理
一、电压变换
电压变换是变压电路最基本的功能之一。
通过改变变压器原副边匝数比,可以将输入电压升高或降低,以满足不同电路对电压的需求。
在理想情况下,原副边匝数比等于原副边电压比,即原边电压与副边电压成正比。
二、电流变换
电流变换也是变压电路的重要功能之一。
通过改变变压器原副边的匝数比,可以将输入电流增大或减小,以满足不同电路对电流的需求。
在理想情况下,原副边电流与匝数成反比,即原边电流与副边电流成反比。
三、阻抗变换
阻抗变换是指通过变压器将输入端的阻抗值进行变换,使其与输出端的阻抗值相匹配。
当输出端的阻抗值大于输入端的阻抗值时,变压器起到了升压的作用;当输出端的阻抗值小于输入端的阻抗值时,变压器起到了降压的作用。
阻抗变换的实现主要是利用了变压器的线性耦合特性。
四、相位变换
相位变换是指通过变压器改变信号的相位。
在交流电系统中,相位的变化会影响到系统的正常运行。
通过相位变换,可以解决一些系统中的相位不匹配问题,使系统正常运行。
相位变换的实现主要是利用了变压器的磁芯的磁导率随磁场强度的变化而变化的特性。
五、隔离作用
隔离作用是变压电路的重要功能之一。
通过变压器可以将输入端和输出端隔离,避免输入端和输出端之间的电气连接,从而起到保护作用。
在高压电路中,隔离变压器可以保护操作人员的人身安全。
滤波器设计中的阻抗匹配与阻抗转换技术在滤波器设计中,阻抗匹配和阻抗转换技术是至关重要的。
阻抗匹配是指在电路中将两个不同阻抗之间的电能传递最大化的过程,而阻抗转换则是将一个阻抗值转换为另一个阻抗值的方法。
本文将介绍阻抗匹配和阻抗转换技术在滤波器设计中的应用。
一、阻抗匹配的原理和方法阻抗匹配的目的是为了消除信号源与负载之间的阻抗不匹配,使信号能够有效地传递到负载。
阻抗匹配可以通过使用传输线、变压器和阻抗匹配电路等方法来实现。
下面将具体介绍几种常见的阻抗匹配方法。
1. 传输线阻抗匹配传输线阻抗匹配是一种常用的阻抗匹配方法。
通过调整传输线的特性阻抗来实现信号源与负载之间的阻抗匹配。
例如,在微波电路设计中,常用的传输线有微带线和同轴线,通过调整它们的几何参数,可以实现阻抗匹配。
2. 变压器阻抗匹配变压器阻抗匹配是一种通过变压器来实现阻抗匹配的方法。
变压器有不同的匝数比例,通过调整匝数比例可以实现信号源与负载之间的阻抗匹配。
变压器阻抗匹配能够实现比较宽频段的阻抗匹配,但需要注意设计时的功率损耗。
3. 阻抗匹配电路阻抗匹配电路是一种通过电路元件来实现阻抗匹配的方法。
常见的阻抗匹配电路有L型匹配电路和π型匹配电路。
L型匹配电路是由一个电感和一个电容组成,而π型匹配电路则是由一个电感和两个电容组成。
通过合理选择电感和电容的参数,可以实现阻抗的精确匹配。
二、阻抗转换的原理和方法阻抗转换是指将一个阻抗值转换为另一个阻抗值的过程。
在滤波器设计中,经常需要将滤波器的输入阻抗转换为输出阻抗,或者将输出阻抗转换为负载阻抗。
下面将介绍几种常用的阻抗转换方法。
1. 阻抗转换器阻抗转换器是一种能够将输入阻抗转换为输出阻抗的电路。
常见的阻抗转换器有共源共栅极电路、共发射极共基极电路等。
通过合理选择电路的参数,可以实现输入阻抗与输出阻抗之间的阻抗转换。
2. 负载变换器负载变换器是一种能够将输出阻抗转换为负载阻抗的电路。
通过合理选择变换器的参数,可以使输出阻抗与负载阻抗匹配,从而实现信号传输的最优化。
5.4 阻抗与导纳及其等效变换一、阻抗1.阻抗的定义及表示形式如下图(a)所示的单口无源线性两端网络N 0,设端口电压为2sin()u u U t ωϕ=+,对应的相量.u U U ϕ=∠,端口电流为2sin()i i I t ωϕ=+,对应的相量.i I I ϕ=∠。
则其端口电压相量与电流相量之比定义为该网络的阻抗Z ,即..()u i U UZ Z I Iϕϕϕ==∠-=∠ 由上式可得 u i U Z Iϕϕϕ⎫=⎪⎬⎪=-⎭说明:(1)Z 是一个复数,所以又称为复阻抗,Z 是阻抗的模,ϕ为阻抗角,它是电压与电流的相位差。
复阻抗的图形符号与电阻的图形符号相似,如上图(b)所示。
复阻抗的单位为Ω。
(2)阻抗Z 用代数形式表示时,可写为:j Z R X =+R :Z 的实部,称为阻抗的电阻分量,单位:Ω,R 一般为正值;X :Z 的虚部,称为阻抗的电抗分量,单位:Ω,X 的值可能为正,亦可能为负。
阻抗的代数形式与极坐标形式之间的互换公式:22arctan Z R X X R ϕ⎫=+⎪⎬=⎪⎭cos sin R Z X Z ϕϕ=⎫⎪⎬=⎪⎭由阻抗Z 的代数形式可知,由于R 一般为正值,所以有π2ϕ≤,且R 、X 和Z 三者之间的关系可用一个直角三角形表示,如上图(c )所示。
2.阻抗的性质由于阻抗Z Z ϕ=∠而arctan XRϕ=,电路结构、参数或频率不同时,阻抗角ϕ可能会出现三种情况:(1)0ϕ>(即0X >)时,称阻抗的性质为感性,电路为感性电路; (2)0ϕ=(即0X =)时,称阻抗性质为电阻性,电路为阻性电路; (3)0ϕ<(即0X <)时,称阻抗性质为容性,电路为容性电路。
3.单口无源网络的串联等效电路由.......R X (j )j U Z I R X I R I XI U U ==+=+=+,可知.R U 与.I 同相位,.X U 与.I 相差π2。
5.4 阻抗与导纳及其等效变换一、阻抗1.阻抗的定义及表示形式如下图(a)所示的单口无源线性两端网络N 0,设端口电压为2sin()u u U t ωϕ=+,对应的相量.u U U ϕ=∠,端口电流为2sin()i i I t ωϕ=+,对应的相量.i I I ϕ=∠。
则其端口电压相量与电流相量之比定义为该网络的阻抗Z ,即..()u i U UZ Z I Iϕϕϕ==∠-=∠ 由上式可得 u i U Z Iϕϕϕ⎫=⎪⎬⎪=-⎭说明:(1)Z 是一个复数,所以又称为复阻抗,Z 是阻抗的模,ϕ为阻抗角,它是电压与电流的相位差。
复阻抗的图形符号与电阻的图形符号相似,如上图(b)所示。
复阻抗的单位为Ω。
(2)阻抗Z 用代数形式表示时,可写为:j Z R X =+R :Z 的实部,称为阻抗的电阻分量,单位:Ω,R 一般为正值;X :Z 的虚部,称为阻抗的电抗分量,单位:Ω,X 的值可能为正,亦可能为负。
阻抗的代数形式与极坐标形式之间的互换公式:22arctan Z R X X R ϕ⎫=+⎪⎬=⎪⎭cos sin R Z X Z ϕϕ=⎫⎪⎬=⎪⎭由阻抗Z 的代数形式可知,由于R 一般为正值,所以有π2ϕ≤,且R 、X 和Z 三者之间的关系可用一个直角三角形表示,如上图(c )所示。
2.阻抗的性质由于阻抗Z Z ϕ=∠而arctan XRϕ=,电路结构、参数或频率不同时,阻抗角ϕ可能会出现三种情况:(1)0ϕ>(即0X >)时,称阻抗的性质为感性,电路为感性电路; (2)0ϕ=(即0X =)时,称阻抗性质为电阻性,电路为阻性电路; (3)0ϕ<(即0X <)时,称阻抗性质为容性,电路为容性电路。
3.单口无源网络的串联等效电路由.......R X (j )j U Z I R X I R I XI U U ==+=+=+,可知.R U 与.I 同相位,.X U 与.I 相差π2。