无源RLC网络与阻抗变换

阻抗变换原理
阻抗变换原理，又称为阻抗匹配原理，是电路中常用的一种技术，用于将电路的输入和输出阻抗匹配，以提高电路的性能和效果。

阻抗变换的基本原理是利用电路元件的特性，将一种阻抗转换为另一种阻抗，使得输入阻抗和输出阻抗之间能够达到最佳匹配。

这种匹配可以通过适当地选择电阻、电容、电感等元件的数值来实现。

在电路中，当输入和输出之间的阻抗不匹配时，会出现反射和功率损耗等问题。

阻抗变换可以通过将输入和输出之间的阻抗变换为相等或者接近的数值，减小阻抗不匹配带来的问题。

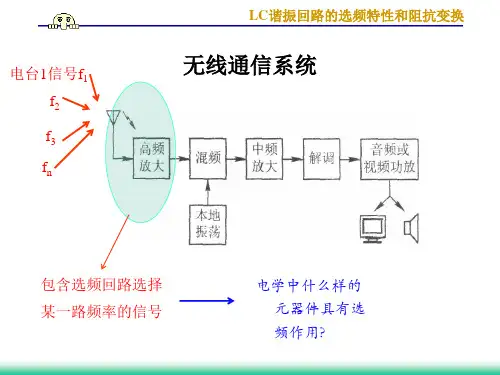
阻抗变换常用于放大器、滤波器、天线系统等电子电路中。

在放大器中，阻抗变换可以提高输入和输出之间的耦合效率，增加信号的传输效果。

而在滤波器中，阻抗变换可以实现滤波器对特定频率范围的阻抗适配，提高滤波器的精确度和性能。

总之，阻抗变换原理是一种重要的电路设计技术，能够利用电路元件的特性，实现输入和输出阻抗之间的匹配，从而提高电路的性能和效果。

通过合理选择电阻、电容、电感等元件的数值，能够实现阻抗的变换，使得电路能够更好地适应不同的工作条件和需求。

§1-5 无源网络的等效变换图1-5-1所示的方框P 表示一个由电阻元件组成的任意复杂的网络，称为无源一端口电阻网络，也称为无源二端电阻网络。

如果在端口施加电压U 时，其端电流为I ，那么在端口电压、电流取为关联参考方向的情况下，端电压与端电流之比，称为该一端口电阻网络的输入电阻，也称为入端电阻或等效电阻。

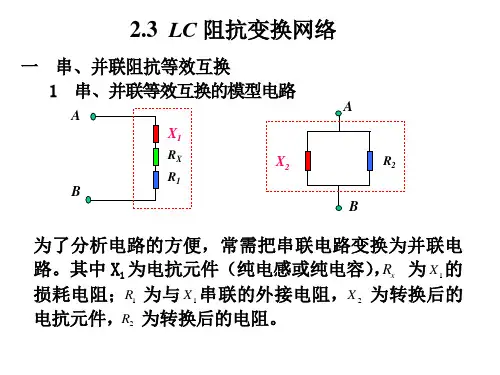
一、电阻的串并联及平衡电桥图1-5-2所示为一桥型电阻电路。

假设：11R =Ω，22R =Ω，32R =Ω，43R =Ω，56R =Ω。

由于四个桥臂满足平衡条件1524R R R R =，所以a 、b 两点的电位恒等。

当a 、b 两点短接时，1R 与2R 并联，4R 与5R 并联，两个并联后的等效电阻再串联，得到：45121245123612368()3cd R R R R R R R R R =+++⨯⨯=+++=Ω 当a 、b 两点开路时，1R 与4R 串联，2R 与5R 串联，两个串联后的等效电阻再并联，得到：14251425()()()()(13)(26)(13)(26)8()3cd R R R R R R R R R ++=+++++=+++=Ω图1-5-1图1-5-2二、Y -∆变换如图1-5-5()()a b 所示，图()a 中有三个节点，每两个节点间均联接有一个电阻支路，三条电阻支路组成一个回路，这种联接方式称为三角形（∆形）联接方式；图()b 中有三条电阻支路，这三条支路的一个端点联于一个公共点，另一个端点与电路其他部分联接，这种联接方式称为星形（Y 形）联接方式。

121212323231233131123G G G G G G G G G G G G G G G G G G ⎫=⎪++⎪⎪⎪=⎬++⎪⎪=⎪++⎪⎭ （式1-5-1） 122331123122331231122331312R R R R R R R R R R R R R R R R R R R R R R R R ⎫++=⎪⎪⎪++=⎬⎪⎪++=⎪⎪⎭ （式1-5-2） （式1-5-1）和（式1-5-2）就是由已知星形联接的电导、电阻推求与之等效的三角形联接的电导、电阻的公式。

rlc串联谐振电路阻抗公式
（原创版）
目录
1.RLC 串联谐振电路的概念
2.RLC 串联谐振电路的阻抗公式
3.阻抗公式的应用
4.RLC 串联谐振电路的特点
正文
一、RLC 串联谐振电路的概念
RLC 串联谐振电路是一种由电阻（R）、电感（L）和电容（C）三个元件串联组成的电路。

当电路中的电流和电压频率达到一定值时，电路的阻抗将呈现谐振现象，即阻抗最小，电流最大。

这种电路在电气工程领域中具有广泛的应用，例如在通信、广播和音响设备中。

二、RLC 串联谐振电路的阻抗公式
在 RLC 串联谐振电路中，阻抗公式可以表示为：
Z = R + j(ωL - 1/ωC)
其中，Z 表示阻抗，R 表示电阻，ω表示角频率，L 表示电感，C 表示电容。

三、阻抗公式的应用
阻抗公式可以用于分析 RLC 串联谐振电路在不同频率下的阻抗特性。

在实际应用中，通过调整电路中的电阻、电感和电容参数，可以实现对电路阻抗的控制，从而达到特定的性能要求。

四、RLC 串联谐振电路的特点
1.阻抗谐振：当电路中的电流和电压频率达到一定值时，电路的阻抗
最小，电流最大。

2.电流超前：在 RLC 串联谐振电路中，电流相位领先于电压相位 90 度。

3.谐振频率：当电路中的频率为谐振频率时，电路的阻抗最小，电流最大。

4.品质因数：RLC 串联谐振电路的品质因数（Q 值）与电路中的电阻、电感和电容参数有关，它决定了谐振电路的性能。

总之，RLC 串联谐振电路是一种具有特殊阻抗特性的电路，其阻抗公式可以帮助我们分析电路在不同频率下的性能。

毕业论文开题报告电子信息工程RLC-CRD变换法有源RC滤波器的设计与研究一、课题研究意义及现状从上世纪二十年代至六十年代，滤波器主要由无源元件R、L、C构成，称为无源滤波器。

为了提高无源滤波器的质量，要求所用的电感元件具有较高的品质因数Q L，但同时又要求有一定的电感量，这就必然增加电感元件的体积，重量与成本。

这种矛盾在低频时尤为突出。

为了解决这一矛盾，五十年代有人提出用由电阻、电容与晶体管组成的有源网络替代电感元件，由此产生了用有源元件和无源元件(一般是R和C)共同组成的电滤波器，称为有源滤波器。

六十年代末由分立元件组成的有源滤波器得到应用。

七十年代以来，由薄膜电容、薄膜电阻和硅集成电路运算放大器构成的薄膜混合集成电路提供了大量质优价廉的小型和微型有源RC滤波器。

集成电路技术的出现和迅速发展给有源滤波器赋予巨大的生命力。

集成电路有源滤波器不但从根本上克服了R、L、C无源滤波器在低频时存在的体积和重量上的严重问题，而且成本低、质量可靠及寄生影响小。

和无源滤波器相比，它的设计和调整过程较简便，此外还能提供增益。

随着小型通信机的迅速发展，在由电子管向晶体管演变的过程中，滤波器在载波机里所占的比例，无论在体积上、质量上，还是在成本上，均占有重要的地位，而且不要很久，大部分晶体管，电阻，电容就将被导体集成电路，薄膜集成电路所代替，因而虽然在磁性材料的发展上下了不少功夫，但目前的LC滤波器在体积，价格方面和其他部件仍然不相称，这时有源RC滤波器就满足了这一要求，现在使用半导体集成电路和薄膜集成电路，不仅能够减轻制品的重量和小型化，而且由于半导体集成电路价格低廉和薄膜集成电路产量提高，这就使成本低，稳定性好的有源RC滤波器有了制成的可能。

几年来，我们把重点放在使用运算放大器的制造方法上，并对制品进行了试用。

二、课题研究的主要内容和预期目标1、了解掌握RLC-CRD变换法有源RC滤波器的设计方法。

在LC无源网络中，如果能通过变换的方法，将电感L变换为其它的无源或有源元件，就可以实现有源RC滤波器。

开题报告
电子信息工程
RLC-CRD变换法有源RC滤波器的设计与研究
图1 各元件的变换关系
预期目标：掌握RLC-CRD变换法有源RC滤波器的设计方法，制作出相应的滤波器电路，通过计算机仿真电路，并对RLC-CRD变换法有源RC滤波器的设计进行研究。

三、课题研究的方法及措施
首先，通过查找资料熟悉并掌握RLC-CRD变换法技术的基本原理，并且掌握RLC-CRD 变换法有源RC滤波器的设计方法。

再，动手制作出相应的滤波器电路。

然后，熟悉OrCAD Relaese 9的开发环境，了解绘图和仿真电路，通过学习和仿真成功集成电路，来实现用RLC-CRD变换法来实现有源RC滤波器的设计。

最后，对RLC-CRD变换法有源RC滤波器的设计进行研究。

四、课题研究进度计划
毕业设计期限：自2011年9月至2012年2月。

第一阶段（2周）：分析任务，收集资料，系统总体方案设计。

第二阶段（2周）：完成开题报告、文献综述、外文翻译。

第三阶段（6周）：设计与写论文，硬件电路的设计与制作，撰写设计报告与论文。

第四阶段（2周）：设计作品完善，论文修改。

五、参考文献
[1] 杨志民,马义德.现代电路理论与设计[M].清华大学出版社,2009,2
[2] 邱关源.现代电路理论[M].北京：高等教育出版社,2001
[3] Sesra A S,Brackett P.O. Filter theory and design:active and passive[M]. Matrix
publishers,Inc.,1978.。

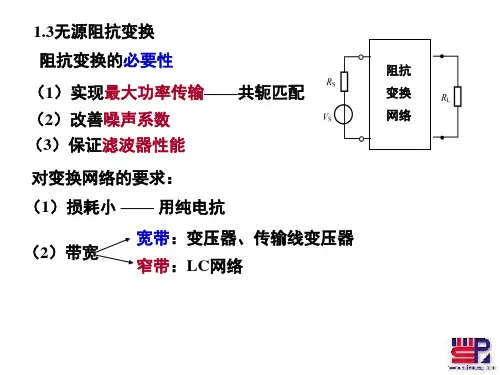
阻抗变换几乎每本介绍与高频相关的书都会涉及到阻抗变换这个概念，但大都只是蜻蜓点水，介绍得都不太详细，而且对于阻抗变换的计算也一直是困扰大家的一个问题，我在这里针对这个问题谈谈自己的理解；阻抗变换网络的种类很多，在这里我重点说一下抽头式、L型、π型、T型阻抗变换网络。

说一下他们的区别与联系。

以下图片除去信号源及内阻和负载后，剩下的才是L型网络的庐山真面目；L型()a()b()c()d()e()f()g()hL 型网络是最基本的阻抗变换网络，它分为两类：第一类即网络中电感和电容都有（即上图前四个），这些基本单元可以再搭建出各种T 型网络，π型网络甚至更为复杂的滤波匹配网络；第二类是只含有电容或电感（即上图后四个），这些是抽头式阻抗变换网路的主要构成部分，也参与组成T 型或π型网络等；以上L 网络进行阻抗变换的根基都是串并联阻抗互换公式；串并联阻抗互换公式书本上都会有比较详细的介绍；这里就不再赘述；第一类L 型阻抗变换如图（a ）：要将信号源内阻Rs 与负载RL 匹配计算过程如下。

已知：将信号源Rs 与负载RL 在频率为f 时进行匹配；解：第一类L 型网络在在进行阻抗变换时，为了达到阻抗匹配，那么左边的电抗与电阻的品质因数应当与右边的电抗与电阻的品质因数相等，否则无法达到匹配。

如图左边的Rs 与L 串联，由串联转换为并联的阻抗变换公式知；()2211L L LZ Rs R Rs Rs Q R ⎡⎤⎛⎫+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+= 即 则：1LR Q Rs=- 然后可求得：LR Zc Q=L Z Rs Q =• 则：12C Zc f π=•2LZ L fπ=一旦知道了Rs 和RL ，那么两边的品质因数便确定了，那么匹配网络的带宽也便确定了，它是窄带变换网络，此网络只可以使得小的Rs 与大的RL 相匹配，反之则不行。

因为10RLRs->。

其他三种的计算方式与此相同，这里就不再赘述。

()a第二类L 型阻抗变换如图（b ），这是典型的抽头式阻抗变换网络，也可以把它看成π型阻抗变换网络，而其中最重要的部分便c1与c2构成第二类L 型阻抗变换网络。