最大熵模型

多维最大熵模型及其在海岸和海洋工程中的应用研究多维最大熵模型及其在海岸和海洋工程中的应用研究引言：随着经济的发展和人口的增长，海洋资源的开发利用以及海岸和海洋工程领域的建设不断扩大，越来越多的人们开始关注如何有效地预测和管理海洋和海岸工程中的各种复杂问题。

多维最大熵模型，作为一种基于统计学原理和最优化方法的数据挖掘技术，已经在海岸和海洋工程中得到广泛应用。

本文旨在阐述多维最大熵模型的基本原理和方法，并深入探讨其在海岸和海洋工程中的应用研究。

一、多维最大熵模型的基本原理和方法多维最大熵模型是基于最大熵原理和条件最大熵原理的统计模型，通过最大化系统的不确定性和满足已知约束来对数据进行建模和预测。

最大熵原理认为，当我们对某个系统的知识有限时，应该选择满足已知条件的最均匀的概率分布。

在多维最大熵模型中，我们可以通过最小化训练数据的信息熵和最大化观测数据的期望来构建最优模型。

多维最大熵模型主要包括以下步骤：1）选择合适的特征函数和约束；2）确定特征函数的权重；3）通过迭代算法对模型进行优化；4）对模型进行预测。

二、多维最大熵模型在海岸和海洋工程中的应用1. 海岸泥沙输运预测海岸泥沙输运是海岸和海洋工程中一个重要的问题，对于海岸线的维护和海岸工程的设计具有重要意义。

然而，由于受到多种因素的影响，包括海洋水文、波浪、潮汐和风向等，海岸泥沙输运的预测一直是一个困难的问题。

多维最大熵模型可以结合多个特征函数来对泥沙输运进行建模，通过最大熵原理来构建最优的预测模型。

通过实际案例分析，发现多维最大熵模型在海岸泥沙输运预测中相比传统方法具有更高的预测准确性和稳定性。

2. 海洋水质评估海洋水质评估是保护海洋环境和促进可持续发展的重要任务之一。

通过收集和分析海洋水质数据，可以评估海洋生态系统的健康状况以及海洋生物多样性的丰富度。

多维最大熵模型可以通过最大熵原理和已知约束来对海洋水质数据进行建模和预测。

通过实际案例分析，发现多维最大熵模型在海洋水质评估中能够提供准确的预测结果，并能够识别出影响海洋水质的主要因素。

机器学习中的最大熵原理及应用随着人工智能、大数据时代的到来，机器学习作为一种重要的人工智能技术，受到了越来越多的关注和研究。

机器学习中有一种常用的模型叫做最大熵模型，其理论基础是最大熵原理。

本文将介绍最大熵原理的概念和应用在机器学习中的方法和优点。

一、最大熵原理概述最大熵原理源自于热力学中的熵概念，熵在热力学中表示一种宏观上的无序状态。

而在信息论中，熵被定义为信息的不确定性或者混乱度。

最大熵原理认为，在没有任何先验知识的情况下，我们应该将分布的不确定性最大化。

也就是说，在满足已知条件下，选择最均匀的分布，最大程度上表示了对未知情况的不确定性，也就是最大的熵。

二、最大熵模型基本形式最大熵模型通常用于分类问题，基本形式为：$$f(x)=\arg \max_{y} P(y / x) \text{ s.t. } \sum_{y} P(y / x)=1$$其中，$x$表示输入的特征，$y$表示输出的类别，$P(y|x)$表示输出类别为$y$在输入特征为$x$的条件下的概率。

通过最大熵原理，我们要求在满足已知条件下，使输出类别分布的熵最大。

三、最大熵模型参数估计最大熵模型参数估计的方法采用最大似然估计。

在训练集中，我们存在$n$个输入特征向量和对应的输出类别标签，即：$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$。

对于给定的每个$x_i$，我们可以得到相应的条件概率$P(y_i|x_i)$，用于计算最大熵模型的参数。

最终的目标是最大化训练集的对数似然函数：$$L(\boldsymbol{\theta})=\sum_{i=1}^{n} \log P(y_i |x_i)=\sum_{i=1}^{n} \log \frac{\exp \left(\boldsymbol{\theta}^{T}\cdot \boldsymbol{f}(x_i, y_i)\right)}{Z(x_i, \boldsymbol{\theta})} $$其中，$\boldsymbol{\theta}$表示最大熵模型的参数向量，$\boldsymbol{f}(x_i,y_i)$表示输入特征$x_i$和输出类别$y_i$的联合特征，$Z(x_i,\boldsymbol{\theta})$表示规范化常数，也就是对数值进行标准化。

最大熵模型算法今天我们来介绍一下最大熵模型系数求解的算法IIS算法。

有关于最大熵模型的原理可以看专栏里的这篇文章。

有关张乐博士的最大熵模型包的安装可以看这篇文章。

最大熵模型算法 1在满足特征约束的条件下，定义在条件概率分布P(Y|X)上的条件熵最大的模型就认为是最好的模型。

最大熵模型算法 23. IIS法求解系数wi先直接把算法粘贴出来，然后再用Python代码来解释。

这里也可以对照李航《统计学习方法》P90-91页算法6.1来看。

这个Python代码不知道是从哪儿下载到的了。

从算法的计算流程，我们明显看到，这就是一个迭代算法，首先给每个未知的系数wi赋一个初始值，然后计算对应每个系数wi的变化量delta_i，接着更新每个wi，迭代更新不断地进行下去，直到每个系数wi都不再变化为止。

下边我们一点点儿详细解释每个步骤。

获得特征函数输入的特征函数f1,f2,...,fn，也可以把它们理解为特征模板，用词性标注来说，假设有下边的特征模板x1=前词, x2=当前词, x3=后词 y=当前词的标记。

然后，用这个特征模板在训练语料上扫，显然就会出现很多个特征函数了。

比如下边的这句话，我/r 是/v 中国/ns 人/n用上边的模板扫过，就会出现下边的4个特征函数(start，我，是，r)(我，是，中国，v)(是，中国，人，ns)(中国，人，end，n)当然，在很大的训练语料上用特征模板扫过，一定会得到相同的特征函数，要去重只保留一种即可。

可以用Python代码得到特征函数def generate_events(self, line, train_flag=False):"""输入一个以空格为分隔符的已分词文本，返回生成的事件序列:param line: 以空格为分隔符的已分词文本:param train_flag: 真时为训练集生成事件序列；假时为测试集生成事件:return: 事件序列"""event_li = []# 分词word_li = line.split()# 为词语序列添加头元素和尾元素，便于后续抽取事件 if train_flag:word_li = [tuple(w.split(u'/')) for w inword_li if len(w.split(u'/')) == 2]else:word_li = [(w, u'x_pos') for w in word_li]word_li = [(u'pre1', u'pre1_pos')] + word_li + [(u'pro1', u'pro1_pos')]# 每个中心词抽取1个event，每个event由1个词性标记和多个特征项构成for i in range(1, len(word_li) - 1):# 特征函数a 中心词fea_1 = word_li[i][0]# 特征函数b 前一个词fea_2 = word_li[i - 1][0]# 特征函数d 下一个词fea_4 = word_li[i + 1][0]# 构建一个事件fields = [word_li[i][1], fea_1, fea_2, fea_4] # 将事件添加到事件序列event_li.append(fields)# 返回事件序列return event_li步进值 \delta_{i} 的求解显然delta_i由3个值构成，我们一点点儿说。

最⼤熵1. 最⼤熵原理最⼤熵原理是概率模型学习的⼀个准则，其认为学习概率模型时，在所有可能的概率模型中，熵最⼤的模型是最好的模型。

通常⽤约束条件来确定概率模型的集合，然后在集合中选择熵最⼤的模型。

直观地，最⼤熵原理认为要选择的概率模型⾸先必须满⾜已有的事实，即约束条件。

在没有更多信息的情况下，那些不确定的部分都是等可能的。

最⼤熵原理通过熵的最⼤化来表⽰等可能性，因为当X服从均匀分布时熵最⼤。

2. 最⼤熵模型最⼤熵原理应⽤到分类得到最⼤熵模型。

给定训练集T=(x1,y1),(x2,y2),...,(x N,y N)，联合分布P(X,Y)以及边缘分布P(X)的经验分布都可以由训练数据得到：˜P(X=x,Y=y)=count(X=x,Y=y)N˜P(X=x)=count(X=x)N⽤特征函数f(x,y)描述输⼊x和输出y之间的某⼀个事实，特征函数是⼀个⼆值函数，当x与y满⾜某⼀事实时取1，否则取0。

例如，可以令特征x与标签y在训练集出现过时取1，否则取0。

特征函数f(x,y)关于经验分布˜P(X=x,Y=y)的期望值为：E˜P(f)=∑x,y˜P(x,y)f(x,y)特征函数f(x,y)关于模型P(Y|X)与经验分布˜P(x)的期望值为：E P(f)=∑x,y˜P(x)P(y|x)f(x,y)如果模型能够获取训练数据中的信息，那么就可以假设这两个期望值相等，即：∑x,y ˜P(x,y)f(x,y)=∑x,y˜P(x)P(y|x)f(x,y)将上式作为模型学习的约束条件，条件数量对应特征函数个数，设所有满⾜约束条件的模型集合为：C={P|∑x,y˜P(x,y)fi(x,y)=∑x,y˜P(x)P(y|x)fi(x,y),i=1,2,...,n}其中n为特征函数个数。

定义在条件概率分布P(Y|X)上的条件概率熵为：H(P)=−∑x,y˜P(x)P(y|x)ln P(y|x)模型集合C中条件熵H(P)最⼤的模型称为最⼤熵模型。

第五节最大熵模型最大熵模型（Entropy Model）也是随机概率模型之一。

典型的最大熵模型有Wilson模型和佐佐木(Sasaki)模型，以下分别讲述。

1．Wilson模型Wilson模型是由A.G.Wilson提出的方法，它以英国为中心，在区域科学方面的应用例较多，其模型如下式所示。

(4-5-1)式中，T：对象地区的生成交通量。

即，OD交通量的组合数由求E的最大得到。

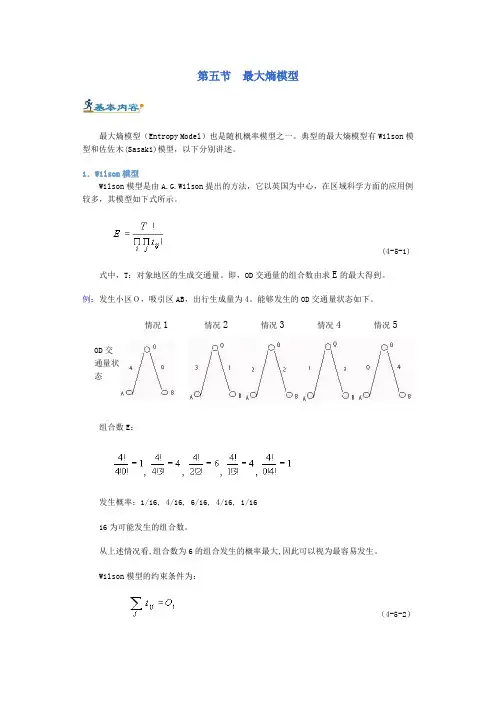
例：发生小区Ｏ，吸引区AB，出行生成量为4。

能够发生的OD交通量状态如下。

OD交通量状态情况1 情况2 情况3 情况4情况5组合数E：,,,,发生概率：1/16, 4/16, 6/16, 4/16, 1/1616为可能发生的组合数。

从上述情况看,组合数为6的组合发生的概率最大,因此可以视为最容易发生。

Wilson模型的约束条件为：（4-5-2）（4-5-3）(4-5-4)式中，的交通费用；总交通费用。

最大熵模型一般用以下对数拉格朗日方法求解。

(4-5-5)式中，，，为拉格朗日系数。

应用Stirling公式近似，得，(4-5-6) 代入（4-5-5）式，并对求导数，得，令，得，(4-5-7)∵∴(4-5-8)同样，(4-5-9)这里，令，则（4-5-7）为：(4-5-10）可以看出，式(4-5-10）为重力模型。

Wilson模型的特点：(1)能表现出行者的微观行动；(2)总交通费用是出行行为选择的结果，对其进行约束脱离现实；(3)各微观状态的概率相等，即各目的地的选择概率相等的假设没有考虑距离和行驶时间等因素。

计算步骤：第1步给出第2步给出，求出第3步用求出的，求出第4步如果，非收敛，则返第2步；反之执行第5步。

第5步将，，代入式（4-5-7)求出，这时，如果总用条件（ 4-5-4）满足，则结束计算，反之，更新值返回第1步。

2．佐佐木(Sasaki)模型分别设定i区的发生概率和j区的吸引（选择）概率。

, （）－－发生守恒条件(4-5-11), （）－－吸引守恒条件(4-5-12), () (4-5-13)式中，为i区的发生交通量被j区有吸引的概率。

基于最大熵原则的汉语语义角色分类随着自然语言处理技术的不断发展和深入研究，语义角色标注在语言表达分析中扮演着越来越重要的角色。

语义角色是指在句子中扮演特定语义角色的成分，如主语、宾语、施事、受事等等。

语义角色标注可以帮助我们更好地理解自然语言文本中的意义，并为自然语言处理任务（如问答系统、机器翻译、信息提取等）提供支持。

本文将探讨一种基于最大熵原则的汉语语义角色分类方法。

一、最大熵模型与汉语语义角色分类最大熵模型（Maximum Entropy Model）是一种概率模型，它的学习过程是基于最大熵原则的。

最大熵原则是指在给定约束条件下选择最简单的概率分布，也就是使信息熵最大的概率分布。

在自然语言处理中，最大熵模型是一种经典的机器学习模型，被广泛应用于词性标注、命名实体识别、情感分析等任务中。

汉语语义角色分类任务是指将给定的汉语句子中的每个成分打上相应的语义角色标签。

例如，在句子“骑士将剑交给了国王”中，骑士是施事角色，剑是传达角色，国王是受事角色。

最大熵模型可以用来解决这个问题。

具体来说，我们可以将句子中每个成分所在的上下文作为特征，将语义角色标签作为分类标签，然后运用最大熵模型对汉语语义角色进行分类。

二、特征选择在最大熵模型中，特征选择是非常关键的一步。

选定好的特征可以大大提高模型的性能。

在汉语语义角色分类任务中，我们可以根据经验、分析和语言学知识，选取一些有代表性的特征，如：1.句法特征。

包括成分在句子中的位置、所属词性、前后成分的关系等等。

2.语义特征。

包括成分的词义、是否具有指示意义等等。

3.上下文特征。

包括成分前后的其他成分、句子的主谓宾结构等等。

4.词语的前缀和后缀等等。

在汉语语义角色分类中，特征选择不是单纯的选择多少，而是要选取能够表征成分、句法和语义属性的特征。

更具体点，主要是选择一些代表性的、能够区分成分、角色类型的特征，并且这些特征是具有语言学含义的。

在特征选择方面，根据不同的任务和语料库，选择的特征也可能不同。

经典的自然语言处理模型
1. 隐马尔可夫模型（Hidden Markov Model，HMM）
- HMM是一种基于状态转移概率和观测概率对序列进行分析
和预测的统计模型，常用于语音识别和自然语言处理中的分词、标注和语法分析等任务。

- HMM的基本思想是将待分析的序列看作是由一系列不可观
测的隐含状态和一系列可观测的输出状态组成的，通过观测状态推断隐含状态，从而实现对序列的分析和预测。

2. 最大熵模型（Maxent Model）
- 最大熵模型是一种用于分类和回归分析的统计模型，常用于
文本分类、情感分析、命名实体识别等自然语言处理任务中。

- 最大熵模型的核心思想是最大化熵的原则，即在满足已知条
件的前提下，使模型的不确定性最大化，从而得到最优的预测结果。

3. 支持向量机（Support Vector Machine，SVM）
- SVM是一种用于分类和回归分析的机器学习模型，常用于文本分类、情感分析、命名实体识别等自然语言处理任务中。

- SVM的基本思想是将特征空间映射到高维空间，通过寻找能够最大化不同类别之间的margin（间隔）的超平面来完成分
类或回归分析，从而实现优秀的泛化能力和低复杂度。

4. 条件随机场（Conditional Random Field，CRF）
- CRF是一种用于标注和序列预测的统计模型，常用于实体识别、词性标注、句法分析等自然语言处理任务中。

- CRF的基本思想是基于马尔可夫假设，采用条件概率模型来
表示序列中每个位置的标签和相邻位置的标签间的依赖关系，从而实现对序列的标注和预测。

基于最大熵模型的聚类分析技术研究在大数据时代，数据处理和分析变得日益重要。

而对于这些庞杂的数据，聚类分析技术是十分必要的。

最大熵模型则是一种应用广泛、效果良好的聚类算法之一。

一、什么是聚类分析技术？聚类分析技术是指将数据集中的样本按照某种距离度量进行分组，使得组内数据之间的相似度越高，组间数据之间的差异度则越大。

对于大数据分析而言，聚类分析技术可以帮助我们快速地发现数据中的规律和模式，对于数据分析有重要的帮助作用。

聚类分析技术还广泛应用于社交网络分析、广告推荐、金融风险评估等领域。

二、最大熵模型的基本思想和特点最大熵模型是一种基于信息论的统计模型，其应用范围非常广泛。

在聚类分析领域中，最大熵模型将每个样本看作一个随机变量，样本间的关系可以通过条件熵衡量。

模型的目标是在保证系统有确定约束下，通过熵的最大值来确定模型的参数，从而使得样本的信息熵最大化。

最大熵模型的特点是能够控制输出规则的数量，从而降低了过拟合的风险。

三、最大熵模型在聚类中的应用最大熵模型可以应用于不同的聚类问题，包括有监督和无监督的聚类问题。

在有监督的聚类问题中，我们可以利用预先标注好的训练数据，从而学习到对于未标注样本需要聚类的规则。

而在无监督的聚类问题中，我们可以根据最大熵模型学习到样本之间的关系，从而找到针对该数据集最优的聚类方案。

最大熵模型在实际应用中非常有效，有许多开源代码库可以供大家使用。

四、最大熵模型的优缺点最大熵模型以最大化信息熵作为目标，可以用较少的规则来描述问题，从而降低了过拟合的风险。

同时，最大熵模型可以将所有的约束都融合到模型中来，并且可以进行高维数据的处理和学习。

但是最大熵模型也存在着一些缺点，比如它无法做多分类问题，并且不同的学习算法会导致不同的结果，从而难以比较。

五、总结在大数据时代，聚类分析技术越来越重要。

而最大熵模型则是一个效果很好的聚类算法之一。

最大熵模型以最大化信息熵作为目标，可以控制规则数量，降低过拟合的风险，同时可以处理高维数据。