偏心变径(大小头)手工放样展开步骤详解
- 格式:docx
- 大小:397.77 KB
- 文档页数:10

在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
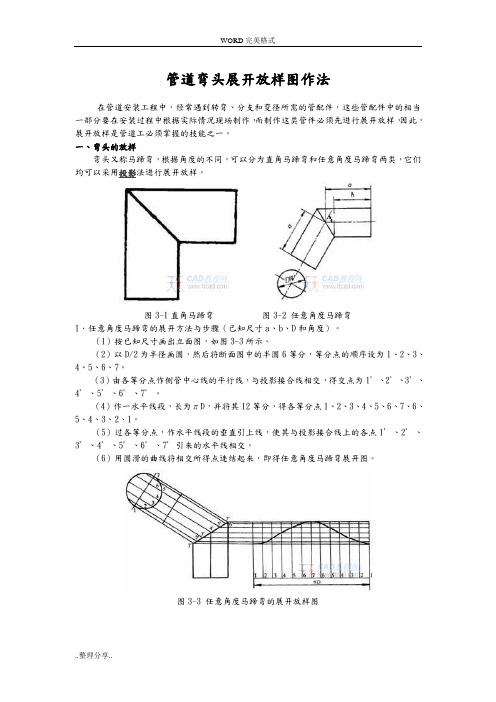
图3-1直角马蹄弯图3-2任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。

管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。

管道弯头展开放样图作法管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。

大小头放样计算最简单的方法大小头放样是一种在模型制作和图纸绘制中常用的技术,它使得在平面上绘制的图形可以在3D空间中呈现出立体的效果。
在实际应用中,大小头放样方法是解决复杂形状的工程问题的一种常用技术。
本文将介绍大小头放样的基本原理和最简单的计算方法。
一、大小头放样的原理大小头放样是指在绘制平面轮廓图时,为了使图形可以在3D空间中形成立体效果,需要通过放样操作将平面图形转换为3D结构。
其原理基于几何关系和投影原理,主要包括以下几个步骤:确定基准面、平移、旋转和尺寸变化。
1.确定基准面:基准面是放样操作的参考平面,通常是平面图形的底部或顶部。
确定基准面后,可以方便地进行平移、旋转和尺寸变换操作。
2.平移:根据实际情况确定平移的方向和距离。
平移操作可以将平面图形在基准面上的投影沿着指定的方向进行移动,以达到放样的效果。
3.旋转:根据实际情况确定旋转的角度和轴线。
旋转操作可以将平面图形绕指定的轴线进行旋转,使其呈现出立体的效果。
4.尺寸变化:根据实际需要,可以在放样过程中对图形的尺寸进行缩放或拉伸操作。
这样可以使放样后的图形更加符合实际需求。
二、大小头放样的计算方法在具体计算大小头放样时,需要根据实际情况选择不同的计算方法。
下面将介绍最简单的大小头放样计算方法,该方法适用于简单的放样操作,如平移和缩放。
1.平移计算:平移操作是指将平面图形在基准面上的投影沿着指定方向进行移动。
平移的计算方法很简单,只需要确定平移的距离和方向即可。
例如,如果需要将图形在水平方向上向右平移10个单位,只需要在水平坐标上加上10即可。
2.缩放计算:缩放操作是指对图形的尺寸进行放大或缩小。
缩放的计算方法也很简单,只需要确定缩放因子即可。
例如,如果需要将图形在x轴方向上放大2倍,则可以将图形的x坐标乘以2。
需要注意的是,大小头放样的计算方法一般适用于简单的放样操作,对于复杂的放样操作,可能需要借助专业计算软件或技术进行计算。
三、大小头放样的应用场景大小头放样方法在工程领域有着广泛的应用。
管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。

管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一.一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯(1)按已知1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
ﻫ尺寸画出立面图,如图3-3所示。
ﻫ(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
ﻫ(3)由各等分点作侧管中心(4)线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
ﻫ作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
ﻫ(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3—3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4直角弯展开图二、虾壳弯的展开放样ﻫ虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:ﻫ(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一局部要在安装过程中根据实际情况现场制作,而制作这类管件必须先进展展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进展展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤〔己知尺寸a、b、D和角度〕。
〔1〕按尺寸画出立面图,如图3-3所示。
〔2〕以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
〔3〕由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
〔4〕作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
〔5〕过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
〔6〕用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样〔己知直径D〕由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由假设干个带斜截面的直管段组成,有两个端节及假设干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:〔1〕作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
〔2〕将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
偏心变径(人小头)手工放样展开步骤详解
b见图h席变径的主视图和俯视图画出来(L1),俯视图大.小圆进行U等分〈等分长度分别为t和,如尺寸太大,可按一定比例缩小匾图
2、如图2,将主视图两边母线向上延伸,相交于一点O,见图2虚线部分, 垂直向下和俯视图中心线相交于O点』连接各个两圆对应的等分点
3、如图3,等分点连线的延长线应相交干O点的。
按图标上等分点序号
I .
9
4、如图乩下一步要求出0 0“ 06 OT、0J > ............................ OJU O'11
的实际长度〈各条母线的实际长度)』为放样展开中常用方法,请牢记
下面以求解0W. 04实际长度为例,详细说明此方法a)如下图,画】条互相垂宜的直线
b)在竖直线上截取长度为图4主视图中H和h的丄点在水平线上戡取长度为图4俯视图中0J和04的】点
连接对应的点,就得到CH车的实际长度(:蓝线〉和的实际长度(红线)
e>其虑理如下立体图,三角形0Q4是宜角三角形,0 0=h , 0J皋俯视图的投影,0T就是母线的突际长度(求0寸用上面的小直角三角形)
图5
天圆地方也是这样求解每条母统的实际长度的,还有很多的放样展幵,所以此方法是学习放样展幵必须掌握的方法
灵下一步开始画展开图F如图■烙变径从0V处剖幵
a)画一条水平直线,左端点为◎,截取长度00〔己在第4步求出)』标记『点:截取长度0P〔己在第4步求出),标记0点(见图6〉
b)以c为圆心,以cn (己在第4步求出?为半径iffi弧线,以o点为圆心’ 以t为半径画弧线.两弧线相交点即为点1 (见图力
图7
匚)以CT为圆心,以OP (己在第4步求出)为半径画弧线;以1点为圆心, 以t为半径画弧线‘两弧线相交点即为点2 (见图小
图8
1)以cr为圆心,以0口〔已在第」步求出〉为半径画弧线;以2点为圆心, 以t为半径画弧线,两弧线相交点即为点3 (见图9)
o501
a以此类推,再求出卜11点。
注意:最后一点还是o点(见图io〉
D连接点0:到各个点的直线'在对应的直线上戡取了竹03 0审O订P I见图o连接各个点形战的扇形区域,即为所求展幵图
说明:在上下圆直径比较接近时』h 的数值会很大,手工在纸上画图误差 会比较大,不宜采用此种方法
此时姜用到一种叫三角形放样展开法,如下图,也是用到第*步求解母线 实际尖度的方法」有宾趣的朋友可仔细体会一下
01 0*
为方便看圉,立体图只i®到
图12。