放样计算公式(借鉴材料)

弯头放样方法弯头放样公式
弯头放样是专业人员在制图过程中必须要掌握的知识，但对于弯头放样方法、弯头放样步骤等专业知识很多人都并不了解，那么今天装修界小编就给大家讲讲弯头放样方法，弯头放样步骤以及弯头放样公式等知识，希望对大家有所帮助哦。

弯头介绍弯头放样，现代
水暖安装中一种常用的连接管件，它主要用来连接两根公称通径相同或不同的管子，使管件
做一定角度的弯转，从而改变管道方向。

弯头一般有45°、90°、180°三种最常用的角度，不过也有根据工程需要定制的60°等其他非正常角度弯头。

弯头放样又名直角弯、90度弯头等，它的制作材料常有铸铁、不锈钢、合金钢、可锻铸铁、碳钢、有色金属及塑料等。

而弯头与管件连接的方式有直接焊接、法兰连接、热熔连接、电熔连接、螺纹连接及承插式连接等。

按生产工艺弯头可分为焊接弯头、冲压弯头、推制弯头、铸造弯头、对焊弯头等几大类。

弯头放样方法弯头是用于管道转弯处的一种管件，在管道系统所使用的全部管件中，弯头所占比例总是最大的，通常都在80%左右。

而对于弯头放样方法、步骤是什么，很多人都不太了解，弯头放样在制图中必须掌握的，那么下面看看装修界小编为大家提供一些简单的弯头放样计算方法、步骤吧。

弯度90度，直径300MM，是这样下料：划一根直线长为∏(d-t)，其中d为圆管外径，t为板厚。

把该线段16等分，两节等径直角弯头放样计算式：Yn=r cosα，当0°≤αn≤90°时，Yn=1/2(d-2t)cosα;当90°。

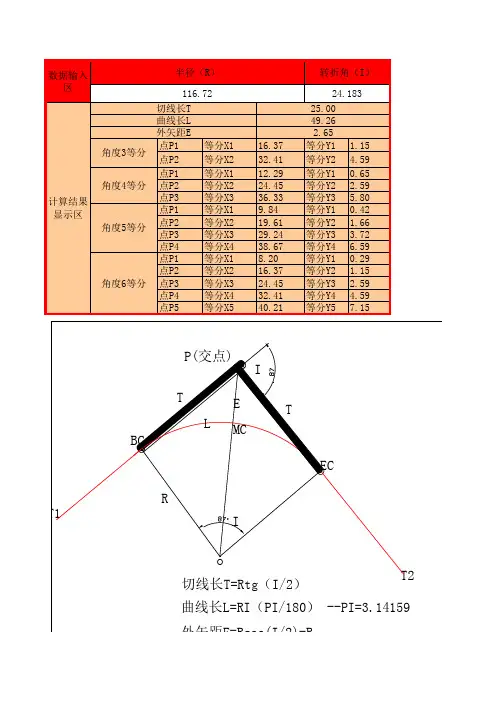
第1篇一、极坐标法放样公式极坐标法放样是一种常用的施工放样方法，主要用于测量平面位置。

其基本公式如下：X = x0 + R cos(α)Y = y0 + R sin(α)其中：X、Y 为目标点的平面坐标；x0、y0 为已知控制点的平面坐标；R 为控制点到目标点的距离；α 为控制点与目标点连线的方位角。

二、全站仪坐标法放样公式全站仪坐标法放样是利用全站仪进行三维坐标测量的施工放样方法。

其基本公式如下：X = Xs + d cos(β)Y = Ys + d sin(β)Z = Zs + h其中：X、Y、Z 为目标点的三维坐标；Xs、Ys、Zs 为已知控制点的三维坐标；d 为控制点到目标点的距离；β 为控制点与目标点连线的方位角；h 为控制点到目标点的高程差。

三、交会法放样公式交会法放样是通过两个或多个已知控制点来确定目标点的平面位置。

其基本公式如下：X = (x1 y2 - y1 x2) / (x1 y3 - y1 x3)Y = (x2 y1 - x1 y2) / (x2 y3 - x1 y3)其中：X、Y 为目标点的平面坐标；x1、y1、x2、y2、x3、y3 为已知控制点的平面坐标。

四、GPS RTK放样公式GPS RTK放样是利用全球定位系统（GPS）进行高精度三维坐标测量的施工放样方法。

其基本公式如下：X = Xs + d cos(β)Y = Ys + d sin(β)Z = Zs + h其中：X、Y、Z 为目标点的三维坐标；Xs、Ys、Zs 为已知控制点的三维坐标；d 为控制点到目标点的距离；β 为控制点与目标点连线的方位角；h 为控制点到目标点的高程差。

在实际施工过程中，根据工程需求选择合适的放样公式，可以确保工程质量和进度。

同时，要注意以下几点：1. 确保控制点的精度，提高放样结果的准确性；2. 根据实际情况，选择合适的放样方法；3. 在放样过程中，注意操作规范，确保施工安全。

总之，工程施工放样公式是工程实践中不可或缺的工具，熟练掌握各种放样公式，有助于提高施工效率和质量。

斜栏杆放样计算公式斜杠放样计算公式。

在建筑设计和施工中，斜杠放样是一个常见的计算方法，用于确定斜面或倾斜物体的尺寸和角度。

斜杠放样计算公式是一个基本的工程数学公式，它可以帮助工程师和设计师准确地计算出斜面的尺寸和角度，从而确保建筑物的结构和外观都符合设计要求。

斜杠放样计算公式的基本原理是利用三角函数来计算斜面的长度、高度和角度。

在斜杠放样中，我们通常会用到正弦、余弦和正切等三角函数，以及勾股定理和正弦定理等几何定理。

通过这些数学工具，我们可以准确地计算出斜面的各种参数，从而为建筑设计和施工提供准确的数据支持。

斜杠放样计算公式的具体应用包括但不限于以下几个方面：1. 斜面的长度和高度计算，通过斜杠放样计算公式，可以准确地计算出斜面的长度和高度，从而为斜面的设计和施工提供准确的数据支持。

这对于建筑物的结构设计和施工进度的控制都非常重要。

2. 斜面的角度计算，斜杠放样计算公式还可以用来计算斜面的角度，这对于确定斜面的倾斜程度和与其他构件的连接方式都非常重要。

通过准确地计算出斜面的角度，可以确保建筑物的外观和结构都符合设计要求。

3. 斜面的切割和连接计算，在建筑设计和施工中，斜面通常需要进行切割和连接，以满足设计要求和施工需要。

通过斜杠放样计算公式，可以准确地计算出斜面的切割和连接参数，从而为斜面的加工和安装提供准确的数据支持。

在实际的建筑设计和施工中，斜杠放样计算公式通常会与CAD软件和数值模拟工具相结合，以实现对斜面的精确设计和计算。

通过这些工具的辅助，工程师和设计师可以更加高效地进行斜面的设计和计算，从而确保建筑物的结构和外观都符合设计要求。

需要指出的是，斜杠放样计算公式虽然是一个基本的工程数学公式，但在实际应用中也存在一些限制和局限性。

例如，在计算过程中需要考虑到斜面的实际情况和复杂性，以及斜面与其他构件的连接方式和加工精度等因素。

因此，在实际应用中，工程师和设计师需要综合考虑多种因素，并结合实际情况进行合理的计算和设计。

板金展开图样一般都采用相贯线法放样，没有计算公式。

制图软件绘制比较方便。

多节的弯头叫作“虾米腰”。

手工放样步骤：（以一节为例，其余方法相同）1）先按实际尺寸画出弯头侧面投影。

包括接缝线。

2）按线把每一个封闭线框图形分割成独立的图形。

（可以裁剪，也可以单独再画。

3）取一个图样，（将中心线垂直的设置）画在另一张纸上，沿图样高度画两条上下平行的横线，并与中心线垂直，长度正好是图样直径的圆周长。

（封闭的长方形）4）将图样垂直方向作等分，并作好标记，然后将这些等分线垂直的画到刚才画的展开的长方形内，注意展开图上的点一定要对应投影图样上的点。

5）将图样上斜线沿水平方向作等分。

并平行的拉到展开的图样上，并对应相应的点。

把展开样上得到的交点圆滑连接，就是展开的曲线。

等分作的越密，曲线越准。

6）放出咬口的量，和板厚处理。

弯头展开图反映了弯头的真实尺寸，对于生产加工有很大的指导意义。

弯头展开图绘制的步骤都大致相同，下面，世界工厂泵阀网为大家汇总弯头展开图大全，以供学习参考。

圆管弯头展开图图为任意节角度90°圆管弯头的立体图和投影视图。

圆管直径φ300，弯头半径R300，弯头由两个端节和三个中间节组成，端节的夹角分别为5°、10°，中间节的夹角分别为20°、25°、30°。

要绘制弯头的平面展开图，必须求出所有五个节的母线实长，整体放样。

三节圆管弯头的放样展开图等径直角弯头展开图弯头各节斜口的展开曲线可按上例斜口圆管展开图的画法作出，如图所示。

在实际生产中，若用钢板制作弯管，不必画出完整的弯管正面投影，只需要求出斜口角度，画出下端半节的展开图，再以它为样板画出其余各节的下料曲线。

& BASIC中国化学工程第四建设公司高用全目录前言…………………………………………………………………………………（ 3 ）第一部分两体相贯展开………………………………………………………………（ 5 ）1 ．封头与圆管相贯………………………………………………………………… （5 ）2 ．方管与封头垂直体相贯………………………………………………………… （9 ）3 ．直管与封头水平相贯…………………………………………………………… （12 ）4 ．直角二节弯头…………………………………………………………………… （14 ）5 ．任意角度二节弯头……………………………………………………………… （15 ）6 ．任意角度四节弯头……………………………………………………………… （17 ）7 ．虾米弯管托……………………………………………………………………… （19 ）8 ．圆锥体弯头……………………………………………………………………… （21 ）9 ．圆筒上直管……………………………………………………………………… （24 ）10 ．圆管与圆筒中心线平行相贯及开孔……………………………………………（25 ）11 ．圆台与圆筒相贯…………………………………………………………………（28 ）12 ．直管与圆筒体斜相贯……………………………………………………………（32 ）13 ．特殊形状圆变方与圆筒相贯……………………………………………………（34 ）14 ．特殊形体圆变圆与圆筒相贯一…………………………………………………（38 ）15 ．特殊形体圆变圆与圆筒相贯二…………………………………………………（41 ）16 ．圆锥与直管垂直相贯……………………………………………………………（45 ）17 ．直管与圆锥水平相贯……………………………………………………………（48 ）18 ．直管与圆锥相贯开孔……………………………………………………………（50 ）19 ．圆管与圆台中心线平行相贯……………………………………………………（53 ）20 ．球体与圆柱相贯（球罐柱腿）…………………………………………………（55 ）第二部分单形体展开…………………………………………………………………（58 ）21 ．天圆地方…………………………………………………………………………（58 ）22 ．倾斜天圆地方……………………………………………………………………（60 ）23 ．天圆地方二………………………………………………………………………（63 ）24 ．圆台体大圆弧展开法……………………………………………………………（66 ）25 ．偏心大小头 (69)26 ．马蹄形体 (72)27 ．斜圆台 (75)附：BASIC 语言程序计算值……………………………………………………………… 78)第一部分两体相贯展开1 ．封头与圆管相贯已知：R 、r 、 a 、b 、H ，求：圆管素线实长（展开圆管实形）椭圆封头上的节管是石油化工容器设备上常见的一种，这里计算的是节管的下料长度。

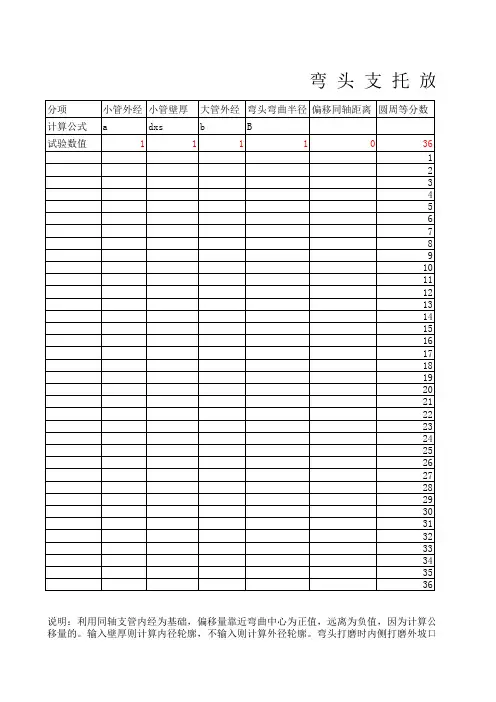
天方地圆计算公式和放样好的，以下是为您生成的一篇关于“天方地圆计算公式和放样”的文章：在咱们的日常生活和各种工程建设中，常常会碰到需要制作天方地圆这种形状的构件的时候。

这可不像做个普通的方形或者圆形物件那么简单，这里面藏着不少的数学玄机和实际操作的技巧。

先来说说这天方地圆的计算公式。

其实啊，这就像是解一道复杂的数学谜题。

假设我们有一个方形，边长是 a 和 b ，然后要把它过渡到一个圆形，半径是 R 。

这时候，计算展开图的尺寸就需要用到一些巧妙的公式啦。

比如说，展开图中扇形的半径 L ，可以通过一个这样的公式来算：L = √[ ( a / 2 )² + ( b / 2 )² ] 。

这公式看起来是不是有点让人头疼？别着急，咱们慢慢理解。

就拿我之前参与的一个小项目来说吧。

那是给一个小型工厂制作通风管道的接头，就是天方地圆的形状。

厂里给的方形尺寸是 50 厘米乘80 厘米，要连接的圆形管道半径是 30 厘米。

按照公式算下来，扇形的半径大约是 40 厘米多一点。

接下来就是放样啦。

放样这活儿，讲究的是精细和耐心。

首先得在一块平整的大板子上，把方形的轮廓画出来，边边角角都要画得直直的。

然后根据算好的尺寸，在方形的四个角上，画出过渡到圆形的弧线。

这弧线画起来可不容易，得一点点地比划，稍有偏差，后面做出来的东西就可能不贴合，影响使用效果。

我记得当时我拿着软尺和铅笔，蹲在那块板子前面，眼睛死死地盯着尺子上的刻度，手还不敢抖一下。

画完弧线后，再把多余的部分裁掉，一个天方地圆的初步形状就出来啦。

但是，这还没完呢。

接下来还要对边缘进行打磨和修整，让它更加光滑和平整。

这时候就得用上各种工具，像砂轮机、锉刀什么的。

打磨的时候，那火星子四溅，还得小心别被烫着。

等把边缘都处理好了，还得检查一下尺寸是不是准确。

这时候就得靠量具啦，游标卡尺、直尺都得上阵。

要是尺寸有偏差，还得继续修整，直到完全符合要求为止。

总之啊，天方地圆的计算公式和放样虽然有点复杂，但只要掌握了方法，加上足够的细心和耐心，就能做出满意的构件来。

（一）长方形截面塔身计算A 正面上根开（边对边）B 正面下根开（边对边）E 侧面上根开（边对边）F 侧面下根开（边对边）H 垂高K=(B－A)÷2 正面比值K[27]=(F－E)÷2 侧面比值C=Pol（K[27]，H) ⍓正面一次高R=J 正面一次角L=Pol(K,C) ⍓二次高W=J ⍓正面二次角C[27]=Pol(K,H) ⍓侧面一次高R[27]=J ⍓侧面一次角L=Pol(K[27],C[27]) ⍓二次高W[27]=J ⍓侧面二次角Lbl 0{D} 塔段垂高D[27]=(L÷H)D ⍓塔段二次高Goto 0（二）塔身任意高度下的根开计算K=2COS О⍓ K为比值数；О为塔面二次角。

Lbl 1{D B} D为塔段二次高；B为塔下根开。

L=D+L ⍓ L为累积值A=B－LK ⍓A为所求根开Goto 1（三）余弦公式计算（已知二边及其夹角）C=(A2+B2-2AB COSО) ⍓A[27]=COS-1((C2+B2-A2)÷(2CB)) ⍓B[27]=COS-1((C2+A2-B2)÷(2CA)) ⍓A、B为已知边，C[27]为A、B边夹角。

（四）余弦公式计算（已知三边）C[27]=COS-1((A2+B2-C2)÷(2AB)) ⍓A[27]=COS-1((C2+B2-A2)÷(2BC)) ⍓B[27]=COS-1((C2+A2-B2)÷(2AC)) ⍓（五）塔材负头计算О 0°<0<90°L=(X COSО+Y+K)÷SinО（六）塔身斜材计算L=(AB+C2) ⍓E=LA÷（A+B）⍓F=LB÷（A+B）⍓A[27]=COS-1((L2+C2-A2)÷(2LC)) ⍓B[27]=COS-1((L2+C2-B2)÷(2LC)) ⍓C[27]=COS-1((L2+B2-C2)÷(2LB)) ⍓M=(A÷2）tan C[27] ⍓N=(B÷2）tan C[27]副材横隔面D朝向：正面长度－a+主材准线+横材准线－横材准线COS WC朝向：正面长度－a+主材准线－横材准线－横材准线COS WB朝向：正面长度－a+主材准线+横材准线+横材准线COS W（一）长方形截面塔身计算A 正面上根开（边对边）B 正面下根开（边对边）E 侧面上根开（边对边）F 侧面下根开（边对边）H 垂高K=(B－A)÷2 正面比值K[27]=(F－E)÷2 侧面比值C=Pol（K[27]，H) ⍓正面一次高R=J 正面一次角L=Pol(K,C) ⍓二次高W=J ⍓正面二次角C[27]=Pol(K,H) ⍓侧面一次高R[27]=J ⍓侧面一次角L=Pol(K[27],C[27]) ⍓二次高W[27]=J ⍓侧面二次角Lbl 0{D} 塔段垂高D[27]=(L÷H)D ⍓塔段二次高Goto 0（二）塔身任意高度下的根开计算K=2COS О⍓ K为比值数；О为塔面二次角。

一、对称曲线1、曲线要素计算(α表示偏角、l s表示缓和曲线长，R表示半径) 切线角：内移值：（当曲线为大半径时可忽略后两项）切线增量：（当曲线为大半径时可忽略后一项）切线长：曲线长：外矢距：切曲差：2、曲线主点里程计算3、曲线中桩计算（1）当点在ZH→HY之间时（l i为该点里程减去ZH点里程）（为该点切线方位角，为ZH点的切线方位角）（2）当点在HY→QZ之间时（l i为该点里程减去ZH点里程）（为该点切线方位角，为ZH点的切线方位角）（3）当点在QZ→YH之间时（l i为HZ点里程减去该点里程）（为该点切线方位角，为HZ点的切线方位角）（4）当点在YH→HZ之间时（l i为HZ点里程减去该点里程）（为该点切线方位角，为HZ点的切线方位角）4、曲线中桩计算（1）当点在ZH→HY、HY→QZ时（2）当点在QZ→YH、YH→HZ之间时二、不对称曲线1、曲线要素计算(α表示偏角、l s1表示前缓和曲线长，l s2表示后缓和曲线长，R表示半径)切线角：内移值：（当曲线为大半径时可忽略后两项）切线增量：（当曲线为大半径时可忽略后一项）切线长：圆曲线长：曲线长：外矢距：切曲差：2、曲线主点里程计算3、曲线中桩计算（1）当点在ZH→HY之间时（l i为该点里程减去ZH点里程）（为该点切线方位角，为ZH点的切线方位角）（2）当点在HY→QZ之间时（l i为该点里程减去ZH点里程）（为该点切线方位角，为ZH点的切线方位角）（3）当点在QZ→YH之间时（l i为HZ点里程减去该点里程）（为该点切线方位角，为HZ点的切线方位角）（4）当点在YH→HZ之间时（l i为HZ点里程减去该点里程）（为该点切线方位角，为HZ点的切线方位角）4、曲线中桩计算（1）当点在ZH→HY、HY→QZ时（2）当点在QZ→YH、YH→HZ之间时。