当前位置：文档之家 › 第9章 9.7.5 小桥孔径水力计算

第9章 9.7.5 小桥孔径水力计算

  • 格式：ppt
  • 大小：488.50 KB
  • 文档页数：32

下载文档原格式

  / 32

合集下载

[讲义]小桥涵水力计算经典讲义(71页 涵洞 倒虹吸)

[讲义]小桥涵水力计算经典讲义(71页 涵洞 倒虹吸)

1.水流类型
水流的类型有临界流、缓流、急流三类。
当计算基线通过河底时，
位能： Ep H
动能： 能率：
Ek

v2 2g
E0 Ep Ek
H v2 2g

H

Q2
2 g 2
17
小桥涵水流状态
当流量及流水断面形状为已知时，能率为水深的函数：
E0 f (H )
E0
C点的能率最小，称为临界点。
13
公路桥涵水毁的成因分析
（4）小桥涵进水口紧接较陡的山坡，进水口处的路基及防 护构造物由于洪水急流的顶冲而被摧毁，或因为淘刷基 础造成了水毁。
（5）受资金、材料的限制，公路标准低、质量差，缺少 排水和防护构造物；平原地区的路基标高太低，填土高 度较小；多年来农、林、水和公路建设欠协调，破坏了 生态平衡，同时公路桥涵的抗灾能力降低，严重的则发 生了水毁。
9
三、小桥涵孔径计算的一般要求
（1）小桥涵孔径必须保证设计洪水、流水和漂流物等的安全通 过；必须满足交通、农田灌溉、排涝和排碱等的合理需要；同 时要考虑桥涵前积水影响路堤的稳定和农田村舍的受淹影响， 通过全面分析，从而选定孔径。 （2）小桥涵孔径不应单凭流量计算资料来确定，其他如流域水 文特征、沟槽形态、地质特点、冲淤情况、人类活动等对桥涵 孔径大小都会产生影响，在确定孔径时，应充分给与考虑。 （3）小桥涵孔径应采用标准孔径，并应大于规定的最小孔径要 求。 （4）小桥宜设计为非自由出流状态，涵洞应设计为无压力式。
15
小桥涵水毁的防治
（4）对上游蜿蜒曲折的河沟段，可裁弯取直，改善水流条 件。有时还可以在桥涵前河沟的上游，加设消力池等消能 设施，以达到降低流速，沉积泥沙的目的。 由上述分析可见，孔径是影响小桥涵水毁的重要因素，

小桥涵水力计算讲座

小桥涵水力计算讲座
11
四、小桥涵孔径与水毁
1. 公路桥涵水毁的成因分析 2. 小桥涵水毁的防治
12
公路桥涵水毁的成因分析
从小桥涵水毁实况，可归纳其水毁主要成因： （1）较大孔径的小桥、涵洞，由于基础的埋置深度不够或
未设必要的调治防护构造物，而致桥台及涵洞进出口被冲 毁。
沪陕高速大桥桥墩受损 严重 商州水务局称洪 水冲刷所致
大中桥孔径计算以冲刷系数作控制条件，容许桥下发生一 定的冲刷，采用天然河槽断面平均流速作为桥孔设计流速 ，并按自由出流条件，由计算的过水面积推求桥孔长度； 小桥孔径计算则以容许不冲刷流速作为控制条件，河床不 容许发生冲刷，但容许有较大的桥前壅水高度，须考虑桥 孔的出流状态，按此确定桥孔长度。
7
三、小桥涵孔径计算的一般要求
水流的类型有临界流、缓流、急流三类。
当计算基线通过河底时，
位能： E p H
动能：
Ek

v2 2g
能率： E 0EpE kH2 vg 2H2Q g 22
（1）小桥涵孔径必须保证设计洪水、流水和漂流物等的安全通 过；必须满足交通、农田灌溉、排涝和排碱等的合理需要；同 时要考虑桥涵前积水影响路堤的稳定和农田村舍的受淹影响， 通过全面分析，从而选定孔径。 （2）小桥涵孔径不应单凭流量计算资料来确定，其他如流域水 文特征、沟槽形态、地质特点、冲淤情况、人类活动等对桥涵 孔径大小都会产生影响，在确定孔径时，应充分给与考虑。 （3）小桥涵孔径应采用标准孔径，并应大于规定的最小孔径要 求。 （4）小桥宜设计为自由出流状态，涵洞应设计为无压力式。
10
三、小桥涵孔径计算的一般要求
（5）有压涵洞水压力较大，沉陷缝处容易漏水，危及基础和 路堤，所以涵洞应设计为无压的，仅在特殊情况下，有充分的 技术经济比较依据时，方可采用有压涵洞。 （6）涵洞可设计成单孔或双孔。由于多孔涵洞流量分配不均 匀，使个别涵孔通过流量有可能超过设计标准，故不宜修建， 只有个别情况在技术和经济上均属适宜时，方可采用多孔。 （7）小桥涵孔径式样，在同一区段内应力求简化，以便于施 工及养护维修。

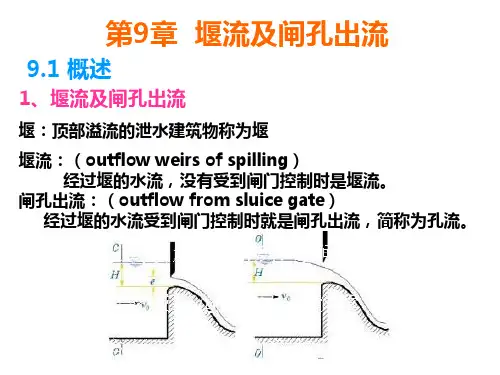
水力学第9章 堰流及闸孔出流-2015

水力学第9章 堰流及闸孔出流-2015
Q 1.4H 5 2
梯形薄壁堰：
H 越大，水面B越宽，适合量测稍
大的流量，如Q >0.1 m3/s
Q 1.856bH 3 2
9.5 实用堰的水力计算
1、曲线型实用堰的剖面形状
克里格尔- -奥菲采洛夫剖面，简称 克 - -奥剖面。
长研型剖面
WES(Waterw ays Experiment Station) 剖面
考虑侧收缩和淹没出流的堰流的基本公式
Q mB 2 g H 0
3/ 2
9.4 薄壁堰的水力计算
薄壁堰可分为：
矩形薄壁堰的流量计算： 将行进流速放在流量系数 内考虑
（1）计算流量系数
Q m0 B 2 g H
3/ 2
雷保克（T .Rehbock) 公式
H 1 m0 0.4034 0.0534 a 1610 H 4.5
0为闸墩系数（查表 9.1 ）
k为边墩系数（查表 9.2）
H0 H0 如果 1 按 1 计算 b b
(3)淹没系数
实用堰发生淹没出流的条件 （1）下游水位高于堰顶； （2）堰下游发生淹没水跃
淹没出流的条件
hs a 0.15 及 1 2.0 H0 H0
（二）折线型实用堰
a H
( z )c a1
例9.2某曲线型实用堰，堰高 a 6.5m,堰的设计水头 H d 0.9m， 设计流量系数 md 0.49, 堰宽与渠宽相同 b 5.0m. 设泄流时下游发生远离 式水跃，求过堰流量。
解：
由题给条件 1.0， 1.0
设H 0 H
Q1 mB 2g H 1.5 1.0 1.0 0.49 5.0 2 9.81 0.91.5 9.266(m3 / s)

桥涵孔径计算课件

桥涵孔径计算课件

操作流程
桥涵孔径计算软件的操作流程一 般包括数据输入、计算过程和结 果输出三个步骤。
功能特点
软件应具备界面友好、操作简单 、计算准确等特点，同时应具备 数据存储和查询功能。
软件应用实例及效果展示
应用实例
以某高速公路桥涵为例，采用计算机 程序进行孔径计算，相比传统手工计 算方法，大大缩短了计算时间，提高 了效率。
桥涵孔径计算课件
目 录
• 桥涵孔径计算概述 • 桥涵孔径计算的前期准备 • 桥涵孔径计算的数学模型 • 桥涵孔径计算的实例分析 • 桥涵孔径计算的软件应用 • 桥涵孔径计算的发展趋势与展望
01
桥涵孔径计算概述
桥涵孔径的概念与重要性
桥涵孔径是指桥涵流水断面上垂直于 流线的直线长度，是桥涵设计中的重 要参数之一。
桥涵孔径的大小直接影响着桥涵的过 水能力、水流状态、河床冲刷和河床 演变等，对于桥梁和涵洞的安全和使 用性能具有重要意义。
桥涵孔径计算的原理与依据
桥涵孔径计算的原理主要是基于水力学和流体力学的原理，通过分析桥涵处的地 形、地质、水流条件等因素，确定合适的孔径大小。
桥涵孔径计算的主要依据包括桥涵设计规范、水文资料、地质勘察报告、洪水计 算成果等。
02
根据桥涵设计的规范和标准，确 定计算方法和标准，如采用水力 学公式或计算机程序进行计算。
建立计算模型与数据库
根据桥涵设计的具体情况，建立合适的计算模型，如堰流模 型、孔口模型等。
建立桥涵孔径计算的数据模型和数据库，包括数据采集、处 理、存储和查询等功能，以便进行计算和管理。
03
桥涵孔径计算的数学模型
桥涵孔径计算的基本步骤
01
02
03
04
收集和分析桥涵设计规范、水 文资料、地质勘察报告、洪水

小桥涵水文计算

小桥涵水文计算

QS (h z) F
3 2
4 5
确定计算参数

1）频率P： 三级公路小桥涵 （表1-6） P=

2）地貌系数ψ：依据F＝12，I=20‰，查附表3—8，ψ=
3）径流深度h ： 根据A 查附表3-11，得知汇流时间τ= 4) 根据土壤为粘土，附表3-9，定吸水类属为Ⅱ类 5)第12暴雨分区，附表3-12，径流深度h＝ 6)植物洼地拦蓄厚度z ：附表3-13，山地水稻田z=
（1） 当有地形图可利用时，根据等高地形图 作出构造物至分分水岭沿河沟的纵断面图，然后依 其 等面积切割 的坡度即主河沟平均坡度 。
（2）当无地形图可利用时，当主河沟长度大于 500米，以河沟形成处与桥涵处高差除以其水平距 离。
3）汇水区平均宽度B及横向平均坡度 利用地形图，先勾绘出汇水区范围线，近似求 出汇水面积的形心c，垂直主河沟作一直线， 交汇水区边界的a，b两点，取此两点间距离即 为汇水区平均宽度B。 确定系数降雨不均匀系数。
第四章 小桥涵水文计算
第一节 小流域水文计算概要 小流域：指汇水面积小于100平方公里的流域。 一、特征： 1 洪水暴涨暴落； 2 缺少观测资料； 3 流量小，历时短； 4 暴雨是形成洪峰流量的主要原因。




汇水面积小，洪峰流量淹没范围小，洪水历时短，没 有水文观测资料，难以找到一种普遍适用于全国的计算 方法和公式。 通常采用的方法有：暴雨推理法、径流形成法、形态调 查法、直接类比法以及暴雨推理法。
损失参数 : (mm/h)

北方
K1 S P
1 2


南方：
K2SP A
K1、K2 ———附表3-3
1, 2 , ———附表3-3

第9章道路排水设计

第9章道路排水设计

能太长；
排水设施有较好的耐久性。
9-1 概述
9-1 概述
二. 排水设计的一般原则
1. 根据公路沿线条件，进行系统分析，拟定排水系统 的总体思路。 2. 要因地制宜、全面规划、综合治理、讲究实效，并 充分利用有效地形和自然水系。 3. 应与农田水利相配合。 4. 应进行调查研究，做到综合设计和分期修建。
二、地下排水设备
3. 渗沟
洞式渗沟：
二、地下排水设备
3. 渗沟 管式渗沟： • 管道：陶土或混
凝土预制管
• 管内径：水力计算而定， 一般为0.4～0.6m
二、地下排水设备
4. 渗井 设置条件：
属于水平方向的地下排水设备，当地下存在多层 含水层，其中影响路基的上部含水层较薄，排水量 不大，且平式渗沟难以布置时，采用渗井。
一、 路面表面排水
1. 拦水带的设置 •拦水带的顶面：应略高于过水断面的设计水 位高 •设计水位高：水面不漫过右侧车道边缘或中 心线的要求 •拦水带高度：一般不超过15cm。 9-3 路面排水设计
一、 路面表面排水
2 路肩排水沟 设置情况：
在硬路肩宽度较窄、爬坡车道占用了过水断面
设置作用： 路面的汇水量较大，拦水带的流水断面不足时， 可在路肩上设置由U型水泥混凝土预制件铺筑的路 肩排水沟。 9-3 路面排水设计
2. 暗沟（盲沟） 盲沟设置及作用： 拦截流向路基的层间水
防止路基边坡滑坍和毛细水上升危及路基
二、地下排水设备
2. 暗沟（盲沟） 盲沟设置及作用： 降低地下水位
防止毛细水上升 至路基工作区，造 成冻胀或翻浆
二、地下排水设备
2. 暗沟（盲沟） 盲沟设置及作用： 拦截和排除路堑下面层间水或小股泉水 保持路堤填土不受水害

实用堰水力计算公式

1、 游水位较低，水流在流出堰顶时将产生第二次跌落。

2、 4、 10>H δ时，用明渠流理论解决不能用堰流理论。

f h不可忽略。

同一堰，当堰上水头H 较大时，视为实用堰；当堰上水头较小时，视为宽顶堰。

§8-2 堰流的基本方程以宽顶堰为例来推求堰流的基本方程 取渐变流断面1-1C-C （近似假设渐变流） 以堰顶为基准面， 列两断面能量方程：g v g v h g v H c c c 22222000ςαα++=+ 0002H g vH =+α作用水头c h 与H 有关，引入一修正系数k 。

则00H h k c =机0kH h co =。

修正系数k 取决于堰口的形状和过流断面的变化。

代入上式，整理得：021211gH k gH k v c -=++=ϕςα23021H g b k k b RH v b h v Q c c c -===ϕ 2302H g mb = 式中：b ——堰宽 ϕ——流速系数ςαϕ+=1m ——流量系数，k k m -=1ϕ适用：堰流无侧向收缩注：堰流存在侧向收缩或堰下游水位对堰流的出水能力产生影响时，可对此公式进行修正。

§8-3 薄壁堰一、一、分类：矩形薄壁堰→较大流量按堰口形状： 三角形薄壁堰→较小流量梯形薄壁堰→较大流量1、 1、 矩形薄壁堰① ① 矩形薄壁堰的自由出流；在无侧向收缩的影响时，其流量公式为： 2302H g mb Q =上式为关于流速的隐式方程，了；两边均含有流速，一般计算法进行计算，较复杂，于是，为计算简便，将上式改写成： 2302H g b m Q =0m ——已考虑流速影响的薄壁堰的流量系数 0m 的确定：矩形薄壁8的流量系数由1898年法国工程师Basin 提出经验公式为：])(55.01)[0027.0405.0(20p H H H m +++=式中：H ——堰上水头（m ）p ——上游堰高 （m ）适用条件：m H 24.1~25.0= m p 75.0~24.0= m b 0.2~2.0=2、 2、 三角形薄壁堰：当流量较小时，堰上水头较小时，采用三角形薄壁堰 ⑴公式：取微元，则流量表达式为：db h g m dQ 2302= （*） 设h 为db 处水头，则由几何关系：2)(θtgh H b -=dhtgdb 2θ-=代入*式，得dhh g tgm dQ 23022θ-= 积分得：dhh g tgm Q H⎰-=0230222θ2502254H g tg m θ=当90=θ，m H 25.0~05.0=时，实验得395.00=m 。

第三节-小桥孔径计算

word 专业资料-可复制编辑-欢迎下载
教 案用纸
学 路基 第七章 路面
科 工程 第三节
小桥涵孔径确定及形式布置 小桥孔径计算
审批签字
授课时数
授课方法
教具
授课班级
1、了解小桥孔径长度 L、桥前水深 H、桥头路堤及桥面最低标高的计算公式 教学目的
2、掌握桥孔径长度 L、桥前水深 H、桥头路堤及桥面最低标高的及计算方法
跨径和孔数，按自由出流和淹没出流两种情况分别计算。
一、小桥孔径度 Bk 和孔径 L 的计算： 1）当考虑桥台和桥墩侧向束挟水流对桥下过水面积减小的影响，以式（7-4）和
（7-5）计算需要的桥下水面宽度 Bk ：
Bk
QP • g • vk3
N •d
式中： —桥梁的挤压系数，查表 6-21 可得；
2、通过拟建小桥处的设计流量 QP ，用计算法或公式法求桥下天然水深 ht ；
3、先按自由出流计算，由 v y 查表 7-3，即可求得：孔径系数 、桥下临界水
深 ht 和桥前水深 H ；
4、水力图式的判别：1）当 ht 1.3hk 时，确定桥下水流为自由出流，则计算桥
下水面宽度 Bk ：
Bk • QP N • d
教案用纸附页
教学内容、方法和过程
附记
word 专业资料-可复制编辑-欢迎下载
3)若桥孔断面为梯形，则桥孔长度为(如图 7-2)： L Bk 2mh 式中：m —桥台处锥坡的边坡系数；
（7-6）
△h —小桥上部结构底面高出水面的高度（m）， h H hk l
l —自积水时的壅水位到上部结构底面的净高，取值为：一般不通航时为 0.5m,有流水的河沟为 0.75m，通航时按通航净空高度计算。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。