解耦控制
- 格式:ppt
- 大小:1.64 MB
- 文档页数:42


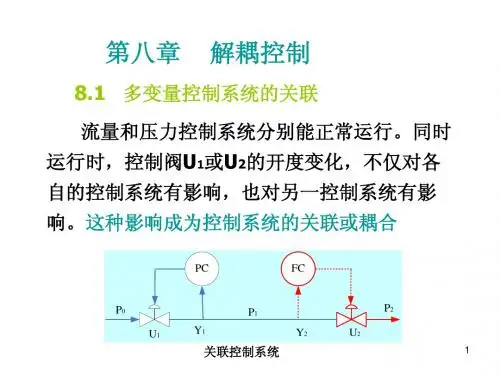
一、引言
随着电力电子技术的不断发展,电力电子器件的应用范围越来越广泛,特别是在工业自动化、电力传输、新能源等领域,电力电子器件起到了至关重要的作用。
然而,电力电子器件的开关操作会产生高频噪声和电磁干扰,对于其他电子设备和系统的正常工作产生负面影响。
因此,如何降低电力电子器件的电磁干扰,成为当前电力电子技术研究的热点之一。
二、电流解耦控制原理
电流解耦控制(DQ控制)是一种常用的电力电子器件控制策略,它可以有效地降低电磁干扰。
DQ控制的基本思想是将三相交流电压或电流转换为d轴电压或电流和q轴电压或电流,从而实现对电力电子器件的控制。
其中,d轴电压或电流代表着直流分量,q轴电压或电流代表着交流分量。
在DQ控制中,d轴和q轴的控制是相互独立的。
因此,通过对d轴和q轴的控制,可以实现对电力电子器件的精确控制。
具体来说,可以通过控制d轴电流来实现对电力电子器件的直流分量控制,通过控制q轴电流来实现对电力电子器件的交流分量控制。
三、DQ控制的应用
DQ控制已经广泛应用于各种电力电子器件的控制中,例如交流电机驱动器、变频器、电力电容器等。
以电机驱动器为例,DQ控制可以实现对电机的高精度控制,提高电机的效率和稳定性。
同时,DQ控制还可以降低电机的电磁噪声和振动,减少对周围环境和人员的影响。
四、结论
DQ控制是一种有效的电力电子器件控制策略,可以降低电磁干扰,提高电力电子器件的控制精度和稳定性。
随着电力电子技术的不断发展,DQ控制将会得到更广泛的应用,成为电力电子器件控制的重要手段之一。


多变量解耦控制方法多变量解耦控制(Multivariable Decoupling Control)是一种用于多变量控制系统的控制方法,旨在解决多变量系统中变量之间相互影响的问题,以实现对个别变量的独立控制。
本文将重点介绍多变量解耦控制的基本原理、应用领域以及实现方法。
多变量解耦控制的基本原理是将多变量控制系统转化为一组耦合度相对较小的单变量子系统,从而能够实现对这些单变量子系统的相对独立控制。
在多变量控制系统中,由于变量之间存在相互耦合的影响,当控制一些变量时,其他变量的变化也会受到影响,导致控制效果不理想。
多变量解耦控制通过重新设计系统的控制结构,使得系统中的耦合影响尽可能减小,从而实现对每个变量的独立控制。
多变量解耦控制在许多工业领域中得到广泛应用,如化工过程控制、能源系统控制、飞行器控制等。
这些系统通常由多个变量组成,变量之间存在耦合关系。
例如,在化工过程控制中,系统的温度、压力、流量等变量相互影响,为了实现对每个变量的独立控制,需要采用多变量解耦控制方法。
多变量解耦控制的实现方法有多种,其中最常用的方法是基于传递函数模型的解耦控制设计。
这种方法通常包括两个步骤:模型建立和解耦控制器设计。
首先,通过系统辨识方法获得多变量系统的传递函数模型,然后根据系统的传递函数模型设计解耦控制器。
在解耦控制器设计中,通常采用频域设计方法,通过对系统的传递函数进行频域分析,确定解耦控制器的参数。
除了基于传递函数模型的解耦控制方法,还有一些其他的多变量解耦控制方法,如基于状态空间模型的解耦控制、模型预测控制、自适应控制等。
这些方法基于不同的控制原理和数学模型来实现多变量系统的解耦控制,可以根据实际需要选择适当的方法。
总结起来,多变量解耦控制是一种用于多变量控制系统的控制方法,通过重新设计系统的控制结构,实现对每个变量的独立控制。
它在工业领域中得到广泛应用,可以通过基于传递函数模型、状态空间模型、模型预测控制、自适应控制等方法来实现。




第三章复杂控制系统的仿真研究3.4 解耦控制系统3.4.1 系统分析及控制策略随着工业的发展,生产规模越来越复杂,而且在一个过程中,需要控制的变量以及操作变量常不止一对,一个生产装置要求若干个控制回路来稳定各被控量。
一个过程变量的变化必然会波及到其它过程变量的变化,这种现象称之为耦合。
严重耦合的系统对于工程实际很不利,直接影响控制质量甚至导致系统无法运行。
例如,对于一个精馏塔而言,其顶部产品成分和流量、回流、送料量、上下塔板温度等,都是一些彼此有关的量,那么在这种情况下,对某一个参数的控制不可避免地要考虑另一些有关联的参数或操作变量的影响,因此这些单个参数的控制系统之间就必定有通道互相交错,就涉及到多变量控制的问题,必须进行解耦控制。
常规解耦方法有前馈补偿法、对角矩阵法和单位矩阵法[2]。
1、前馈补偿法前馈补偿是自动控制里最早出现的一种克服干扰的方法,它同样适用于解耦控制系统,方框图如图3-12。
图3-12 前馈解耦控制方框图其中D21和D12是补偿器,利用补偿器原理:K21g21(s) + D21K22g22(s) = 0K12g12(s) + D12K11g11(s) = 0- 33 -第三章 复杂控制系统的仿真研究- 34 -解得补偿器的数学模型为:)()(2222212121s g K s g K D -= )()(1111121221s g K s g K D -= (3-9) 采用前馈解耦,解耦器形控制器环节比较简单。
2、对角矩阵法对角矩阵法与单位矩阵法类似,不同之处在于其使系统传递函数矩阵成为如下形式:⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)()()(00)()()(21221121s M s M s G s G s Y s Y c c 同样可以求得解耦器为:⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-)(00)()()()()()()()()(221112221121122211211s G s G s G s G s G s G s D s D s D s D (3-10)加入解耦器后,各回路保持前向通道特性,互相不再关联影响。
解耦控制的基本原理解耦控制是一种常用的软件设计原则,旨在减少系统中各个模块之间的依赖关系,提高系统的灵活性和可维护性。
本文将介绍解耦控制的基本原理,并探讨其在软件开发中的应用。
解耦控制的基本原理是将一个复杂的系统拆分成多个相互独立的模块,各模块之间通过接口进行通信。
这样做的好处是,当一个模块发生变化时,只需要修改该模块的代码,而不会影响到其他模块。
这样可以降低系统的耦合度,使系统更易于维护和扩展。
在软件开发中,解耦控制的应用非常广泛。
首先,在模块化的架构设计中,我们可以将系统划分为多个模块,每个模块负责不同的功能。
通过定义清晰的接口和协议,各个模块之间可以独立开发和测试,最后再进行集成。
这种模块化的设计可以提高开发效率,同时也方便后续的维护和升级。
在分布式系统中,解耦控制也非常重要。
分布式系统由多个独立的节点组成,节点之间通过网络进行通信。
为了实现解耦控制,我们可以使用消息队列等中间件来实现节点之间的异步通信。
通过将消息发送到队列中,发送方和接收方之间是解耦的,可以独立进行扩展和修改。
这种解耦控制的设计可以提高系统的可伸缩性和容错性。
在前后端分离的架构中,解耦控制也是非常重要的。
通过将前端和后端拆分成独立的两个模块,前端负责用户界面的展示,后端负责逻辑处理和数据存储。
通过定义良好的接口和协议,前后端之间可以独立开发和测试,最后再进行集成。
这种解耦控制的设计可以提高开发效率,同时也方便前后端的升级和替换。
解耦控制是一种重要的软件设计原则,可以提高系统的灵活性和可维护性。
通过将系统拆分成多个相互独立的模块,并通过接口进行通信,可以降低系统的耦合度,使系统更易于维护和扩展。
在模块化的架构设计、分布式系统和前后端分离的架构中,解耦控制都有着广泛的应用。
因此,掌握解耦控制的原理和方法,对于软件开发人员来说是非常重要的。