资金时间价值与等值计算例题2(含答案)

第四章建设工程决策阶段投资控制第二节资金时间价值综合练习与答案一、单选题1、某购房人从银行贷款50万元，贷款期限10年，按月等额还本付息，贷款年利率6%，每月计息一次，其每月应向银行还款的数额为（）元。

A.4917B.5551C.7462D.7581【参考答案】：B【试题解析】：根据公式，贷款月利率=6%/12=0.5%，n=120，可得每月应向银行还款的数额=5551元。

2、资金的数量会随时间的推移而变动，变动的这部分资金就是原有资金的（）。

A.投资价值B.货币价值C.时间价值D.变化价值【参考答案】：C【试题解析】：将一笔资金存入银行会获得利息，进行投资可获得收益（也可能会发生亏损）。

而向银行借贷，也需要收付利息。

这反映出资金在运动中，其数量会随着时间的推移而变动，变动的这部分资金就是原有资金的时间价值。

3、有现金流量图如下图所示，且已知（F/A，i，n）＝1.333，F＝100万元，则A应为（）万元。

A.100B.133.3C.75D.25【参考答案】：C【试题解析】：（万元）。

4、设名义利率为r，在一年中计算利息m次，则当m大于1时，实际利率i将（）名义利率r。

A.不确定B.小于C.等于D.大于【参考答案】：D【试题解析】：当名义利率为r时，实际利率的公式为：i=I/P=[P（1＋r/m）m-P]/P=（1＋r/m）m－1，由上式可知，当m=1时，实际利率i等于名义利率r；当m 大于1时，实际利率i将大于名义利率r；而且m越大，二者相差也越大。

5、某公司在第3年末应偿还一笔100万元的债务，按年利率2.79%计算，该公司从现在起连续3年每年末应向银行存入（）万元，才能使其本利和正好偿清这笔债务。

A.32.42B.30.52C.16.21D.20.18【参考答案】：A【试题解析】：本题中，F=100万元，i=2.79%，n=3。

将数据带入偿债系数公式，得每年末应存入款额：6、某建设单位的开发项目，建设期两年，建设投资为8000万，期初一次性投入，其中60%来自银行贷款。

项目二资金的时间价值与等值计算练习题一、单项选择题1．资金时间价值的习惯表示方式是( )。

A.利息B．利率C．利润D．终值2．利息是表示资金时间价值的（）。

A.相对尺度B．绝对尺度C．重要依据D．两者无必然联系3．把一个时间点发生的资金额转换成另一个时间点等值的资金额，这个计算过程称为资金的( )。

A.利率折算B．价值转换C．时间价值性D．等值计算4．单利与复利的区别在（）。

A、单利考虑计息周期，复利不考虑计息周期B、单利只对本金计算利息，复利对本金与利息要再计息C、两者计息周期不同D、复利计算时名义利率等于实际利率5、某工程向银行贷款100万元，年利率10％，借期4年，求按单利计算4年后需要向银行偿还本利（）万元。

A、F=100×(4×10%+1)B、F=100×4×(10%+1)C、F＝100×(10%+1)4D、缺少条件不能计算6、下列有关名义利率与实际利率正确的是（）。

A、当给定利率的时间单位与计息周期不一致时，不同的计息周期所得的利息不同，就是因为存在实际利率与名义利率B、在单利计息的情况下，名义利率等同于实际利率C、名义利率是周期利率与名义利率包含的单位时间内计息周期数的乘积D、名义利率与实际利率可以通过一定的公式进行转换E、名义利率是名义的利率，实际利率是真正的利率7、名义利率与实际利率的转换方法是（）。

A、i=（1+r/m）m+1B、i=（1+r/m）m-1C、i=（1+m/r）m-1D、i=（1+m/r）m+1其中：r名义利率、i实际利率、m每年计息次数8、工程经济学中的现金流量（CF,CashFlow)是指（）。

A、反映项目计算期内各年的现金流入、现金流出和净现金流量的表格B、在项目寿命周期内流入、流出的货币C、是指把评价方案作为一各独立的系统，在一定时间内流出、流入系统的活动D、产品销售收入、回收固定资产残值、回收流动资金9、净现金流量是指（）。

第二章资金的时间价值与等值计算作业（说明：作业采用百分制计分，本次作业共计100分。

）1、下列等额支付的年金终值和年金现值各为多少？（12分）(1)年利率为6%．每年年末借款500元，连续借款12年；（3分）(2)年利率为9%，每年年初借款4200元，连续借款43年；（3分）(3)年利率为8%，每季度计息1次，每季度末借款1400元，连续借款16年；（3分）(4)年利率为10%，每半年计息1次，每月月末借款500元，连续借款2年。

（3分）2、下列终值的等额支付为多少？（12分）(1)年利率为12%．每年年末支付1次，连续支付8年，8年未积累金额15000元；（3分）(2)年利率为9%，每半年计息1次，每年年末支付1次，连续支付11年，11年年末积累4000元；（3分）(3)年利率为12%，每季度计息1次，每季度末支付1次，连续支付8年，8年年末积累金额15000元；（3分）(4)年利率为8%，每季度计息1次，每月月末支付1次，连续支付15年，15年年末积累17000元。

（3分）3、下列现值的等额支付为多少？（12分）(l)借款5000元，得到借款后的第1年年末开始归还，连续5年，分5次还清，年利率按4%计算；（6分）(2)借款37000元，得到借款后的第1个月月末开始归还，连续5年，分60次还清，年利率为9%，每月计息1次。

（6分）4、下列现金流量序列的年末等额支付为多少？（12分）(l)第1年年末借款1000元，以后3年每年末递增借款100元，按年利率5%计息；（3分）(2)第1年年末借款5000元，以后9年每年末递减借款200元，按年利率12%计息；（3分）(3)第1年年末借款2000元，以后3年每年末借款比上一年末递增2%，按年利率5%计息；（3分）(4)第1年年末借款3000元，以后6年每年末借款是上一年的1.1倍，年利率5%计息。

（3分）5、某企业获得8万元贷款，偿还期4年，年利率为10%，试就以下4种还款方式，分别计算每年还款额、4年还款总额及还款总额的现值：22分）(1)每年年末还2万元本金和所欠利息；（6分）(2)每年末只还所欠利息，本金在第4年末一次还清；（6分）(3)每年末等额偿还本金和利息；（6分）(4)第4年末一次还清本金和利息。

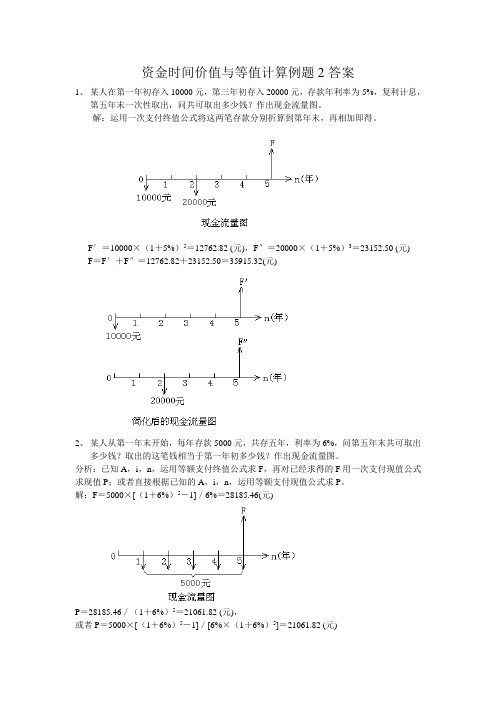
资金时间价值与等值计算例题2答案1、某人在第一年初存入10000元，第三年初存入20000元，存款年利率为5%，复利计息，第五年末一次性取出，问共可取出多少钱？作出现金流量图。

解：运用一次支付终值公式将这两笔存款分别折算到第年末，再相加即得。

F′＝10000×（1＋5%）5＝12762.82 (元)，F″＝20000×（1＋5%）3＝23152.50 (元) F＝F′＋F″＝12762.82＋23152.50＝35915.32(元)2、某人从第一年末开始，每年存款5000元，共存五年，利率为6%，问第五年末共可取出多少钱？取出的这笔钱相当于第一年初多少钱？作出现金流量图。

分析：已知A，i，n，运用等额支付终值公式求F，再对已经求得的F用一次支付现值公式求现值P；或者直接根据已知的A，i，n，运用等额支付现值公式求P。

解：F＝5000×[（1＋6%）5－1]／6%＝28185.46(元)P＝28185.46／（1＋6%）5＝21061.82 (元)，或者P＝5000×[（1＋6%）5－1]／[6%×（1＋6%）5]＝21061.82 (元)3、某人准备在三年后用100000元购买一辆轿车，若从现在起每年年末存入银行等额的钱，存期三年，利率为4%，这笔等额的钱是多少？如果是在第一年初一次性存入一笔钱用于三年后买车，应存多少？作出现金流量图。

分析：已知F，i，n，运用等额支付偿债基金公式求A，运用一次支付现值公式求P。

解：A＝100000×4% ／[（1＋4%）3－1]＝32034.85(元)P＝100000／（1＋4%）3＝88899.64 (元)。

4、某人投资1000000元，投资收益率为8%，每年等额收回本息，共六年全部收回，问每年收回多少钱？作出现金流量图。

分析：已知P，i，n，运用等额支付投资回收公式求A。

解：A＝1000000×8%×（1＋8%）6／[（1＋8%）6－1]＝216315.39(元)5、某人欲从今年起，每年末得到10000元，共二十年。

淮海工学院工管工程经济学习题01-资金的时间价值、等值计算习题一（资金的时间价值、等值计算）一、单选题:1、某项目投资来源中，项目资本金2000万元，借入银行资金1000万元，建设期借款利息200万元。

在编制项目财务现金流量表时，建设期现金流出的投资应为（）万元。

A.1200B.2000C.3000D.32002、年名义利率为i，一年内计息周期数为m，则年有效利率为（）。

A.(1+i)m-1B.(1+i/m)m-1C.(1+i)m-iD.(1+i*m)m-i3、某施工企业向银行借款100万元，年利率8%，半年复利计息一次，第三年末还本付息，则到期时企业需偿还银行（）万元。

A.124.00B.125.97C.126.53D.158.694、折旧基数随着使用年限变化而变化的折旧方法是（）。

A.平均年限法B.工作量法C.双倍余额递减法D.年数总和法5、某施工机械预算价格为100万元，折旧年限为10年，年平均工作225个台班，残值率为4%，则该机械台班折旧费为（）元。

A.426.67B.444.44C.4266.67D.4444.446、某债券面值为100元，期限为3年，年利率为10％，按单利计算，则到期后的本息和为（）。

A．133元B．130元C．330元D．121元7、在利率、现值相同的情况下，若计息期数n=l，则复利终值和单利终值的数量关系是（）。

A．前者大于后者 B．前者等于后者 C．前者小于后者 D．无法判断8、假如以复利方式借入1000元，年利率8％，第四年末偿还，则第二年年末利息之和为（）元。

A．80 B．1080 C．166.4 D．1166.49、某企业贷款50000元，利率为9%，期限5年，每年末应等额偿还（）元。

A．12000 B．13535 C．14500 D．1285410、下列是回收系数表示符号的是（）。

A．（A／F，i，n）B．（A／P，i，n）C．（F／A，i，n）D．（P/A，i，n）11、每半年末存款2000元，年利率4%，每季复利计息一次。

【例题1·单选】某企业前3年每年初借款1000万元，按年复利计息，年利率为8%，第5年末还款3000万元，剩余本息在第8年末全部还清，则第8年末需还本付息（）万元。

【2017】A.981.49B.990.89C.1270.83D.1372.49【答案】 D【解析】第8年末需还本付息金额F=[1000×（F/A，8%，3）×（F/P，8%，3）－3000]×（F/P，8%，3）=1372.49万元。

【考点来源】第四章第一节资金的时间价值及计算【例题2·单选】某企业年初借款2000万元，按年复利计息，年利率8%。

第3年末还款1200万元，剩余本息在第5年末全部还清，则第5年末需还本付息（）万元。

【2016】A.1388.80B.1484.80C.1538.98D.1738.66【答案】C【解析】2000×（1+8%）5 -1200×（1+8%）2 =1538.98（万元）。

【考点来源】第四章第一节资金的时间价值及计算【例题3·单选】某工程建设期为2年，建设单位在建设期第1年初和第2年初分别从银行借入700万元和500万元，年利率8％，按年计息。

建设单位在运营期前3年每年末等额偿还贷款本息，则每年应偿还（）万元【2014】A.452.16B.487.37C.526.36D.760.67【答案】C【解析】A=[700×(F/P，8%，2)+500×(F/P，8%，1)] ×(A/P，8%，3)= 526.36。

【考点来源】第四章第一节资金的时间价值及计算【例题4·单选】某工程建设期2年，建设单位在建设期第一年初和第二年初分别从银行借入资金600万元和400万元，年利率8%，按年计息，建设单位在运营期第三年末偿还了贷款500万元后，自运营期第五年末应偿还（）万元，才能还清贷款本息。

【2013】A.925.78B.956.66C.1079.84D.1163.04【答案】C【解析】运营期第五年末应偿还=[600×（1+8%）5+400×（1+8%）4-500] ×（1+8%）2=1079.84万元。

正保远程教育旗下品牌网站美国纽交所上市公司(NYSE:DL)职业培训教育网职业人的网上家园中级经济师考试辅导《房地产专业知识与实务》第六章第二节讲义2资金的时间价值及等值计算【典型例题】将1000元存入银行，年利率为6%，如果按复利计算，则三年后的本利和为多少？[答疑编号2526060105]【解析】按单利计算：1000×（1+6%×3）=1180按复利计算：1000×（1+6%）3=1191.023.6 复利的种类■ 间断复利－按期计算复利的方法（实际中采用）■ 连续复利－按瞬时计算复利的方法3.7 周期利率、名义利率和实际利率3.8 名义利率和实际利率的关系■ 当n＝1时，名义利率等于实际利率■ 当n＞1时，且一年中计复利的次数越多，实际利率高于名义利率越高■ 当n＜1时，实际利率小于名义利率■ 当n 趋于无穷大时，一年中计算期无限多，得出连续复利的一次性支付公式【典型例题】下列关于名义利率与实际利率的表述中，正确的有（）。

A.当计算周期为一年时，年名义利率等于年实际利率B.实际利率真实地反映了资金的时间价值C.名义利率真实地反映了资金的时间价值D.名义利率相同时，计息周期越短，名义利率与实际利率的差值就越大E.计息周期相同时，名义利率越小，名义利率与实际利率的差值就越大[答疑编号2526060106]【答案】ABD【解析】实际利率真实地反映了资金的时间价值，所以C项错误；计息周期相同时，名义利率越大，名义利率与实际利率的差值就越大，所以E项错误。

参见教材P106。

4.资金等效值及其计算4.1 资金等效值的概念■ 发生在不同时点的等额资金，价值会不相同。

正保远程教育旗下品牌网站 美国纽交所上市公司(NYSE:DL)
职业培训教育网 职业人的网上家园
中级经济师考试辅导《房地产专业知识与实务》第六章第二节讲义3
资金的时间价值及等值计算
■ 系数名称
☆ 等额分付终值系数（Ｆ/Ａ，i ，n ）
5.4 终值换算为年值 F ～A
（等额分付偿债基金公式） ■ 公式
■ 形象记忆
☆ （存款、养老保险）已知最后要取出一笔钱，每年应等额存入多少钱。

年轻时定期等额支付养老金，想到一定年龄一次性取出一定钱数，问年轻时每月应存入多少钱。

■ 系数名称
☆ 等额分付偿债基金系数（Ａ/Ｆ，i, n ）
【典型例题】
◆ 某设备估计尚可使用5年，为此准备5年后进行设备更新，所需资金估计为30万元，若存款利率为5%，从现在开始每期末均等地存款，则应存款（ ）万元。

已知（A/F,5%,5）=0.18097
A.6.426
B.5.429
C.4.846
D.5.868
[答疑编号2526060203]
【答案】B
【解析】F ～A
A=F （A/F,i,n ）=30×（A/F,5%,5）=30×0.18097=5.429（万元）。

5.5 年值换算为现值 A ～P
（等额分付现值公式）
■ 公式
■ 形象记忆
☆ （养老金,房地产估价收益法，抵押求借款额）一次性存入一大笔钱，以后每年可获得等额的养老金，如已知养老金的数额，问最初一次性需存入多少钱。

■ 系数名称
☆ 等额分付现值系数（Ｐ/Ａ，i, n ）
5.6 现值换算为年值 P ～A （等额分付资本回收公式）
■ 公式。

资⾦的时间价值与等值计算第⼆章资⾦的时间价值与等值计算⼀、基本概念资⾦的时间价值资⾦等值(计算) 利息利润本⾦利率单利复利名义利率实际利率间断计息连续计息折现贴现现值终值⼆、思考题1.什么是资⾦的时间价值？资⾦为什么具有时间价值？2.资⾦增值的前提条件是什么？3.资⾦时间价值⼤⼩主要由哪些因素决定？4.名义利率与实际利率的关系是怎样的？5.利息的计算⽅法有哪两种？6.如何理解资⾦等值？什么是决定资⾦等值的三要素？7.资⾦等值计算⽅法有哪些？8.怎样计算资⾦偿还年限？三、计算题（本部分习题如不特别指明，均按复利计算）（⼀）例题1.某公司从银⾏贷款600万元，利率为10%，第10年末⼀次偿清本利和。

试分别⽤单利法和复利法计算本利和各是多少？解：单利法 F=P(1+i×n)=1 000(1+10%×10)=2 000(万元)复利法 F=P(1+i)n =1 000×(1+10%)10=2 594(万元)2.求下列各题未知数的值800万元(1)100万元解: (1)F=P(F/P,15%,5)=100×2.011=201.1(万元)(2)P=500(P/F,10%,5)+800(P/F,10%,8)=684.1(万元)(3)F10=1 000(F/P,10%,10)-100(P/A,10%,4)(F/P,10%,7)=1 976.173.某⼯程项⽬预计需投资⼈民币350亿元(其中：60%⾃筹，40%从国外贷款，贷款利率为10%),⼯程建设期18年。

试计算:(1)建设期期末时，⽋国外贷款利息多少？(2)所⽋贷款利息是贷款本⾦的⼏倍？(3)建设期期末共⽋国外贷款本利和是多少？解：(1)建设期末⽋国外贷款利息350×40%×(F/P,10%,18)-350×40%=638.4(亿元)(2)所⽋贷款利息是本⾦的 638.4/(350×40%)=4.56倍(3)建设期末⽋国外贷款的本利和 350×40%×(F/P,10%,18)=778.4元4.在孩⼦第4个⽣⽇最好投⼊⼀笔钱，以便孩⼦从第18到第22个⽣⽇（包括这两个⽣⽇在内），每个⽣⽇都可提取2000元。