2018版数学新导学同步选修2-2人教A版：课时作业2导数的几何意义含解析

课时跟踪检测（四） 导数的运算法则层级一 学业水平达标1．已知函数f (x )＝ax 2＋c ，且f ′(1)＝2，则a 的值为( )A ．1 B. 2 C ．－1D ．0 解析：选A ∵f (x )＝ax 2＋c ，∴f ′(x )＝2ax ，又∵f ′(1)＝2a ，∴2a ＝2，∴a ＝1.2．函数y ＝(x ＋1)2(x －1)在x ＝1处的导数等于( )A ．1B ．2C ．3D ．4 解析：选D y ′＝[(x ＋1)2]′(x －1)＋(x ＋1)2(x －1)′＝2(x ＋1)·(x －1)＋(x ＋1)2＝3x 2＋2x －1，∴y ′|x ＝1＝4.3．曲线f (x )＝x ln x 在点x ＝1处的切线方程为( )A ．y ＝2x ＋2B ．y ＝2x －2C ．y ＝x －1D ．y ＝x ＋1 解析：选C ∵f ′(x )＝l n x ＋1，∴f ′(1)＝1，又f (1)＝0，∴在点x ＝1处曲线f (x )的切线方程为y ＝x －1.4. 已知物体的运动方程为s ＝t 2＋3t(t 是时间，s 是位移)，则物体在时刻t ＝2时的速度为( )A.194 B.174 C.154 D.134解析：选D ∵s ′＝2t －3t 2，∴s ′|t ＝2＝4－34＝134. 5．设曲线y ＝ax －ln(x ＋1)在点(0,0)处的切线方程为y ＝2x ，则a ＝( )A ．0B ．1C ．2D ．3 解析：选D y ′＝a －1x ＋1，由题意得y ′|x ＝0＝2，即a －1＝2，所以a ＝3. 6．曲线y ＝x 3－x ＋3在点(1,3)处的切线方程为________．解析：∵y ′＝3x 2－1，∴y ′|x ＝1＝3×12－1＝2.∴切线方程为y －3＝2(x －1)，即2x －y ＋1＝0.答案：2x －y ＋1＝07．已知曲线y 1＝2－1x与y 2＝x 3－x 2＋2x 在x ＝x 0处切线的斜率的乘积为3，则x 0＝________.解析：由题知y ′1＝1x 2，y ′2＝3x 2－2x ＋2，所以两曲线在x ＝x 0处切线的斜率分别为1x 20，3x 20－2x 0＋2，所以3x 20－2x 0＋2x 20＝3，所以x 0＝1.答案：18．已知函数f (x )＝f ′⎝ ⎛⎭⎪⎫π4cos x ＋sin x ，则f ⎝ ⎛⎭⎪⎫π4的值为________．解析：∵f ′(x )＝－f ′⎝ ⎛⎭⎪⎫π4sin x ＋cos x ，∴f ′⎝ ⎛⎭⎪⎫π4＝－f ′⎝ ⎛⎭⎪⎫π4×22＋22，得f ′⎝ ⎛⎭⎪⎫π4＝2－1.∴f (x )＝(2－1)cos x ＋sin x .∴f ⎝ ⎛⎭⎪⎫π4＝1.答案：19．求下列函数的导数：(1)y ＝x sin 2x ；(2)y ＝e x＋1e x －1；(3)y ＝x ＋cos xx ＋sin x ；(4)y ＝cos x ·sin 3x .解：(1)y ′＝(x )′sin 2x ＋x (sin 2x )′＝sin 2x ＋x ·2sin x ·(sin x )′＝sin 2x ＋x sin 2x . (2)y ′＝e x ＋1′e x －1－e x＋1e x －1′e x －12＝－2exe x －12 . (3)y ′＝x ＋cos x ′x ＋sin x －x ＋cos x x ＋sin x ′x ＋sin x 2＝1－sin x x ＋sin x －x ＋cos x 1＋cos xx ＋sin x 2＝－x cos x －x sin x ＋sin x －cos x －1x ＋sin x 2.(4)y ′＝(cos x ·sin 3x )′＝(cos x )′sin 3x ＋cos x (sin 3x )′＝－sin x sin 3x ＋3cos x cos 3x＝3cos x cos 3x －sin x sin 3x .10．偶函数f (x )＝ax 4＋bx 3＋cx 2＋dx ＋e 的图象过点P (0,1)，且在x ＝1处的切线方程为y ＝x －2，求f (x )的解析式．解：∵f (x )的图象过点P (0,1)，∴e ＝1.又∵f (x )为偶函数，∴f (－x )＝f (x )．故ax 4＋bx 3＋cx 2＋dx ＋e ＝ax 4－bx 3＋cx 2－dx ＋e .∴b ＝0，d ＝0.∴f (x )＝ax 4＋cx 2＋1.∵函数f (x )在x ＝1处的切线方程为y ＝x －2，∴切点为(1，－1)．∴a ＋c ＋1＝－1.∵f ′(x )|x ＝1＝4a ＋2c ，∴4a ＋2c ＝1.∴a ＝52，c ＝－92. ∴函数f (x )的解析式为f (x )＝52x 4－92x 2＋1. 层级二 应试能力达标1．若函数f (x )＝ax 4＋bx 2＋c 满足f ′(1)＝2，则f ′(－1)等于( )A ．－1B ．－2C ．2D ．0 解析：选B ∵f ′(x )＝4ax 3＋2bx 为奇函数，∴f ′(－1)＝－f ′(1)＝－2.2．曲线y ＝x ex －1在点(1,1)处切线的斜率等于( ) A ．2eB ．eC ．2D ．1 解析：选C 函数的导数为f ′(x )＝e x －1＋x e x －1＝(1＋x )e x －1，当x ＝1时，f ′(1)＝2，即曲线y ＝x ex －1在点(1,1)处切线的斜率k ＝f ′(1)＝2，故选C. 3．已知函数f (x )的导函数为f ′(x )，且满足f (x )＝2xf ′(e)＋ln x ，则f ′(e)＝( )A ．e －1B ．－1C ．－e －1D ．－e解析：选C ∵f (x )＝2xf ′(e)＋ln x ，∴f ′(x )＝2f ′(e)＋1x， ∴f ′(e)＝2f ′(e)＋1e ，解得f ′(e)＝－1e，故选C.4．若f (x )＝x 2－2x －4ln x ，则f ′(x )＞0的解集为( )A ．(0，＋∞)B ．(－1,0)∪(2，＋∞)C ．(2，＋∞)D ．(－1,0) 解析：选C ∵f (x )＝x 2－2x －4ln x ，∴f ′(x )＝2x －2－4x＞0， 整理得x ＋x －x ＞0，解得－1＜x ＜0或x ＞2，又因为f (x )的定义域为(0，＋∞)，所以x ＞2.5．已知直线y ＝2x －1与曲线y ＝ln(x ＋a )相切，则a 的值为________________． 解析：∵y ＝ln(x ＋a )，∴y ′＝1x ＋a，设切点为(x 0，y 0)， 则y 0＝2x 0－1，y 0＝ln(x 0＋a )，且1x 0＋a ＝2， 解之得a ＝12ln 2. 答案：12ln 2 6．曲线y ＝x 2x －1在点(1,1)处的切线为l ，则l 上的点到圆x 2＋y 2＋4x ＋3＝0上的点的最近距离是____________．解析：y ′＝－1x －2，则y ′| x ＝1＝－1，∴切线方程为y －1＝－(x －1)，即x ＋y －2＝0，圆心(－2,0)到直线的距离d ＝22，圆的半径r ＝1，∴所求最近距离为22－1.答案：22－17．已知曲线f (x )＝x 3＋ax ＋b 在点P (2，－6)处的切线方程是13x －y －32＝0.(1)求a ，b 的值；(2)如果曲线y ＝f (x )的某一切线与直线l ：y ＝－14x ＋3垂直，求切点坐标与切线的方程．解：(1)∵f (x )＝x 3＋ax ＋b 的导数f ′(x )＝3x 2＋a ，由题意可得f ′(2)＝12＋a ＝13，f (2)＝8＋2a ＋b ＝－6，解得a ＝1，b ＝－16.(2)∵切线与直线y ＝－14x ＋3垂直， ∴切线的斜率k ＝4.设切点的坐标为(x 0，y 0)，则f ′(x 0)＝3x 20＋1＝4，∴x 0＝±1.由f (x )＝x 3＋x －16，可得y 0＝1＋1－16＝－14， 或y 0＝－1－1－16＝－18.则切线方程为y ＝4(x －1)－14或y ＝4(x ＋1)－18. 即y ＝4x －18或y ＝4x －14.8．设f n (x )＝x ＋x 2＋…＋x n－1，x ≥0，n ∈N ，n ≥2.(1)求f n ′(2)；(2)证明：f n (x )在⎝ ⎛⎭⎪⎫0， 23内有且仅有一个零点(记为a n )，且0＜a n －12＜2n3n ＋1.解：(1)由题设f n ′(x )＝1＋2x ＋…＋nx n －1.所以f n ′(2)＝1＋2×2＋…＋(n －1)2n －2＋n ·2n －1，① 则2f n ′(2)＝2＋2×22＋…＋(n －1)2n －1＋n ·2n ，② ①－②得，－f n ′(2)＝1＋2＋22＋…＋2n －1－n ·2n＝1－2n1－2－n ·2n ＝(1－n )·2n －1，所以f n ′(2)＝(n －1)·2n＋1.(2)因为f (0)＝－1＜0，f n ⎝ ⎛⎭⎪⎫23＝23⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫23n1－23－1＝1－2×⎝ ⎛⎭⎪⎫23n ≥1－2×⎝ ⎛⎭⎪⎫232＞0，因为x ≥0，n ≥2.所以f n (x )＝x ＋x 2＋…＋x n －1为增函数， 所以f n (x )在⎝ ⎛⎭⎪⎫0， 23内单调递增，因此f n (x )在⎝ ⎛⎭⎪⎫0， 23内有且仅有一个零点a n .由于f n (x )＝x －x n ＋11－x －1，所以0＝f n (a n )＝a n －a n ＋1n1－a n－1，由此可得a n ＝12＋12a n ＋1n ＞12，故12＜a n ＜23.所以0＜a n －12＝12a n ＋1n ＜12×⎝ ⎛⎭⎪⎫23n ＋1＝2n 3n ＋1.。

课时作业（五)基本初等函数的导数公式及导数的运算法则A组基础巩固1．函数f(x)＝ln x－错误!x2，则f（x）的导函数f′(x）的奇偶性是( )A．奇函数B．偶函数C．既奇又偶函数D．非奇非偶函数解析:f(x）的定义域是(0，＋∞)，不关于原点对称．答案：D2．已知函数f(x)＝2x n－nx2，且f′(2）＝0，则n的值为( ) A．1 B．2C．3 D．4解析：由已知得f′(x)＝2nx n－1－2nx.∵f′(2）＝0,∴2n·2n－1－2n·2＝0,即n·2n－4n＝0。

当n＝2时，2×22－4×2＝0成立．故选B。

答案：B3．若f（x）＝x2－2x－4ln x，则f′(x）＞0的解集为（）A．（0,＋∞）B．（－1，0)∪（2，＋∞)C．（2，＋∞）D．(－1，0）解析：∵f(x)＝x2－2x－4ln x，∴f′（x)＝2x－2－错误!＞0，整理得错误!＞0，解得－1＜x＜0或x＞2，又因为f（x)的定义域为｛x｜x＞0｝，故选C。

答案：C4．若函数f(x）＝ax4＋bx2＋c满足f′（1)＝2，则f′(－1)等于（)A．－1 B．－2B组能力提升11．已知f错误!＝错误!,则f′（x）＝( ）A.11＋x B．－错误!C。

错误!D．－错误!解析：令错误!＝t，则f(t）＝错误!＝错误!，∴f(x)＝错误!，∴f′（x）＝错误!′＝－错误!。

答案：D12．若函数f（x)＝x2＋bx＋c的图象的顶点在第四象限,则函数f′(x)的图象是（）A B C D解析：由函数f（x)＝x2＋bx＋c的图象的顶点在第四象限,得b ＜0。

又f′（x）＝2x＋b在R上是增函数且在y轴上的截距小于0，故选A。

答案：A13．已知f（x）＝错误!x3＋bx2＋cx（b，c∈R)，f′(1)＝0,x∈[－1，3］时，曲线y＝f（x）的切线斜率的最小值为－1,求b,c的值．解析：f′(x)＝x2＋2bx＋c＝（x＋b)2＋c－b2，且f′(1）＝1＋2b＋c＝0.①（1)若－b≤－1，即b≥1，f′（x）在[－1，3］上是增函数，所以f′（x)min＝f′（－1)＝－1，即1－2b＋c＝－1，②由①②解得b＝14，不满足b≥1,故舍去．(2)若－1＜－b＜3，即－3＜b＜1,f′(x)min＝f′（－b）＝－1,即b2－2b2＋c＝－1，③由①③解得b＝－2，c＝3，或b＝0，c＝－1.。

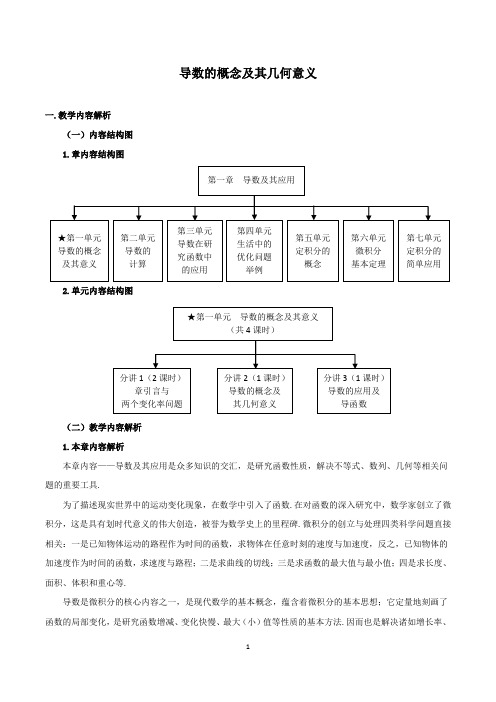
导数的概念及其几何意义一.教学内容解析（一）内容结构图1.章内容结构图2.单元内容结构图（二）教学内容解析1.本章内容解析本章内容——导数及其应用是众多知识的交汇，是研究函数性质，解决不等式、数列、几何等相关问题的重要工具.为了描述现实世界中的运动变化现象，在数学中引入了函数.在对函数的深入研究中，数学家创立了微积分，这是具有划时代意义的伟大创造，被誉为数学史上的里程碑.微积分的创立与处理四类科学问题直接相关：一是已知物体运动的路程作为时间的函数，求物体在任意时刻的速度与加速度，反之，已知物体的加速度作为时间的函数，求速度与路程；二是求曲线的切线；三是求函数的最大值与最小值；四是求长度、面积、体积和重心等.导数是微积分的核心内容之一，是现代数学的基本概念，蕴含着微积分的基本思想；它定量地刻画了函数的局部变化，是研究函数增减、变化快慢、最大（小）值等性质的基本方法.因而也是解决诸如增长率、膨胀率、效率、密度、加速度等实际问题的基本工具.2.本单元内容解析在本单元——导数的概念及其意义中，学生将通过实际情境，经历用平均变化率和瞬时变化率刻画实例的过程，感受数学的极限思想，抽象生成导数的概念，并通过函数图像直观感受导数的几何意义，感受“以直代曲”的极限思想.能够用导数的概念解释生活中的现象，体会用导数的知识研究函数的思想方法.通过具体实例感受导数在研究函数和解决实际问题中的作用，体会导数的意义.本单元设计了三个分讲，共计4课时，分别是章引言与两个变化率问题（2课时），导数的概念及其几何意义（1课时），导数的应用及导函数（1课时）.3. 课时内容解析本课时内容选自人教社A 版《选修2-2》第一章导数及其应用中第一单元导数的概念及其意义中的单元分讲2——导数的概念及其几何意义，用时1课时.本课时内容是在学生已经学习了分讲1——章引言和两个变化率问题，即：已经研究了物理学中的平均速度和瞬时速度，几何学中的割线斜率和切线斜率的基础上，通过数学抽象，生成导数的概念及其表达.从“数”的角度理解导数概念的本质就是瞬时变化率.从“形”的角度，类比分讲1中曲线2()f x x =在点(0,0)处的切线的斜率就是函数2()f x x =在0x =处的导数的几何意义，抽象生成一般曲线()y f x =在0x x =处的导数的几何意义. 通过信息技术，直观感受“以直代曲”的极限思想，感受“数”与“形”的相辅相成.由质疑“切线的原始定义”为出发点，类比分讲1中曲线2()f x x =在点(0,0)处的切线定义，抽象生成一般曲线()y f x =在点00(,())x f x 处的切线定义. 体会微积分的重要思想——用运动变化的观点解决问题.课时中的两个生活实例，意在引导学生用导数的概念解决 “原油的瞬时变化率”问题，用导数的几何意义解决运动员“高台跳水”不同时刻的变化情况，感受数学源于生活，用于生活的价值.培养学生用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界，提升分析问题、解决问题的能力，提升数学抽象和直观想象的数学核心素养.基于以上分析，确定本课时的教学重点：抽象生成导数的概念，直观感受导数的几何意义，体会“以直代曲”的极限思想.二.教学目标设置（一）本章教学目标1.通过实例分析，经历由平均变化率到瞬时变化率的过程，了解导数概念的实际背景，知道导数是关于瞬时变化率的数学表达，体会导数的内涵与思想，体会极限思想.通过函数图像直观理解导数的几何意义，体会“以直代曲”的极限思想.2.能根据导数定义求函数231,,,,,y c y x y x y x y y x======.能利用给出的基本初等函数的导数公式和导数的四则运算法则，求简单函数的导数；能求简单的复合函数（限于形如()f ax b +）的导数.3.结合实例，借助几何直观了解函数的单调性与导数的关系；能利用导数研究函数的单调性；对于多项式函数，能求不超过三次的多项式函数的单调区间.借助函数的图像，了解函数在某点取得极值的必要条件和充分条件；能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值；体会导数与单调性、极值、最大（小）值的关系.4.知道微积分创立过程，以及微积分对数学发展的作用.提升数学抽象、数学运算、直观想象、数学建模和逻辑推理的核心素养.（二）本单元教学目标1.了解微积分的创立背景，感受引入导数的必要性.经历由平均变化率到瞬时变化率的过程，理解导数的本质就是瞬时变化率，体会极限思想.经历由形到数的关系，理解导数的几何意义，体会“以直代曲”的思想，理解函数的单调性与导数的关系.2.经历抽象概括不同领域变化率问题的数学共性，体会微积分的重要思想——用运动变化的观点解决问题.经历探究具体实例和知识的形成过程，感受导数在研究函数和解决问题中的作用，体会导数的意义.3.经历提出问题——分析问题——解决问题的过程，体会从特殊到一般、从具体到抽象的研究方法的一般性和有效性.发展学生观察、类比、概括的数学能力,提升学生数学抽象、直观想象、逻辑推理的数学核心素养.4.经历从实际情境抽象出数学概念，培养学生敢于质疑、勇于探索的学习习惯，激发学生的学习兴趣与求知欲，让学生感受数学源于生活，用于生活.引导学生会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界，让学生体验成功，提高课堂参与度与成就感.（三）课时教学目标1.经历解决生活中不同领域的瞬时变化率问题，通过探究它们的数学共性，抽象生成导数的概念及其数学表达.通过类比探究，抽象概括导数的几何意义，生成一般曲线在某一点处的切线的定义.应用信息技术，直观感受“以直代曲”的极限思想.体会微积分的重要思想——用运动变化的观点解决问题.2.理解导数的概念，明确求导数的基本方法，能够运用导数的概念和几何意义解决生活中与瞬时变化率有关的问题.3.经历导数概念的形成和几何意义的探究，经历“数”与“形”相辅相成的过程，体会从特殊到一般、从具体到抽象在解决数学问题中的一般性和有效性.发展学生观察、类比、概括的数学能力,提升学生数学抽象、直观想象、逻辑推理的数学核心素养.4.经历从实际情境抽象出数学概念，激发学生的学习兴趣与求知欲，让学生感受数学源于生活，用于生活.引导学生会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界.应用自主探究、合作交流的学习模式，培养学生敢于质疑、勇于探索的学习习惯，在学习过程中提升发现问题、分析问题、解决问题的能力.让学生体验成功，提高课堂参与度与成就感.三.学生学情分析1.已具备的认知基础本课时的教学对象是天津市耀华中学的学生.耀华中学是天津市的直属重点中学，学生具有良好的知识储备和较强的学习能力.在物理中学生已经学习了平均速度和瞬时速度等概念，并会计算平均速度.在数学中学生对函数已经有了系统的学习与认知，理解函数是刻画客观世界两个变量相互关系的重要模型，可以通过列表、图像、解析式三种方式表示、研究函数.学生已经学习了与直线斜率和直线方程相关的知识.学生具备一定的探究意识和团队合作意识，有较好的语言表达能力，积累了一定的数学活动经验，能够运用图形计算器及几何画板等数学工具，具有一定的动手实践能力.2.可能存在的认知困难导数的概念是由物理中的瞬时速度和几何中的切线斜率以及学生搜集的有关变化率问题中的数学共性抽象生成，其本质就是瞬时变化率，是应用了重要的极限.而“极限”的概念学生尚未学习.因此，抽象生成导数的概念是学生可能存在的认知困难之一.在研究导数的几何意义与一般曲线在某一点处的切线定义时，要引导学生通过类比上一分讲中特殊的函数和特殊的曲线的探究方式，进行抽象概括.需要运用微积分中的重要思想——运动变化的观点解决问题.这是突破了学生的“惯性思维”.因此，探究导数的几何意义与一般曲线的切线定义是本节课的难点之二.基于以上分析，本节课的教学难点确定为：用运动变化的观点解决问题和对导数的概念及其几何意义的探究.突破难点的关键：问题链引导与应用信息技术辅助教学.四.教学策略分析1.教法分析结合本课时的内容特点和学情分析，采用PBL（Problem-based Learning）的教学模式，即：基于问题链的教学模式.本课时以提升学生的数学抽象与直观想象的核心素养为根本出发点，以抽象生成导数的概念和直观感受导数的几何意义为明线，以感受“用运动变化的观点研究问题”、感受“以直代曲”的极限思想、体会“类比概括”、“数形结合”的研究方法为暗线，以用导数的概念解释“原油温度的瞬时变化率”和用导数的几何意义研究“高台跳水运动员的瞬时变化率”作为课堂反馈，以完成《课堂目标检测》与阅读《割圆术》的著作作为课堂的延伸和拓展，充分体现数学发展过程中的新旧知识的结合，理论与实际的结合，为学生指引学习的方向，使课堂摆脱知识的束缚，成为学生学习能力成长的发源地.为了引导学生理解导数的本质就是瞬时变化率，教师遵循“观察——归纳——抽象——概括”四个层次.为了引导学生理解导数的几何意义就是切线的斜率，教师遵循“类比——探究——归纳”三个层次.本课时教师将内容设计成“温故知新，建构导数概念——学以致用，解决典型问题——自主探究，获得几何意义——小结提升，布置分层作业”四个环节.2.学法分析学生采取小组合作探究的学习模式.在课堂教学中鼓励学生独立思考、敢于质疑，通过小组合作、交流分享，突破难点，提升学生的合作探究意识，提高分析问题、解决问题的能力.在课堂教学中始终以学生为核心，教师组织、适时引导，有效地提升学生的课堂参与度，使学生在开放的活动中获取直接的数学经验.学生经历思考、观察、分析、实践、归纳的认知过程，深刻体会知识的形成过程，提升知识迁移、解决问题的能力.3.教学支持条件本节课通过PPT演示的方式为学生导入情境.在课堂教学中，教师为学生精心设计了导学案，提升学生的学习效率，直观呈现出本节课的重点和知识的形成过程. 教师应用几何画板动态演示“逼近”与“放大”，巧妙突破难点.教师使用“希沃授课助手”同屏软件，实时地展示学生的探究过程和结果，充分发挥生生互评、师生互评的评价效能，引发学生更加深入的思考，加深对新知的理解与应用.课堂中，学生每人手持手机或ipad，用几何画板软件探究导数的几何意义，激发求知欲和学习兴趣的同时，大大提高了探究效率，增强动手实践能力，积累数学活动经验，直观感受知识的形成过程.五.教学过程设计本节课设计了四个教学环节，逐步达成教学目标，完成教学任务.1.温故知新，建构导数概念教师引言（1）：上周开始，我们进入了一个新单元的学习——导数及其意义.上两节课我们学习了章引言，并探究了两个变化率问题.这节课让我们接续探究导数的概念及其几何意义.【师生活动】教师板书，如下：1.1.2 导数的概念及其几何意义教师引言（2）：让我们首先重温上节课的两个情境.情境1——高台跳水问题，涉及物理学中的平均速度和瞬时速度，情境2——抛物线的切线问题，涉及到几何学中的割线斜率和切线斜率.上节课，老师布置了课前作业，请同学们以学习小组为单位，每个小组写出一个与“变化率”有关的实例，写出具体问题与解答过程.请三个小组的同学进行分享.【师生活动】教师用PPT展示情境.如下：课前，教师收上七个小组的“变化率”实例，筛选出“非同质性”的实例有三个，请这三个小组的代表进行分享.教师提前将小组作业拍照，用PPT播放如下，学生解说.【设计意图】让学生搜集“变化率”实例，写出完整的解答过程，能够较好地反馈学生对上一单元分讲中平均变化率和瞬时变化率的掌握与理解.学生课前搜集，教师提前筛选，提高课堂效率的同时，使得实例涉及不同领域，对数学共性的说明更具说服力，为引出导数概念做好充分铺垫.探究1：虽然上面的五个实例涉及不同领域，但从数学的角度思考上述五个实例，在“过程与方法”、“结果的形式”上有哪些共性？【师生活动】教师要着重引导学生从“数学的角度”观察问题的一致性，从“过程与方法”和“结果的形式”进行归纳小结.学生小组合作探究，教师巡视，深入小组活动，倾听学生交流.教师请小组代表分享交流，其他组进行补充.教师用PPT 展示“数学共性”，如下：【设计意图】培养学生的观察、概括能力.让学生体会微积分的重要思想——用运动变化的观点研究问题.体会极限思想.感受用“平均变化率”趋近“瞬时变化率”的研究方法.关注结果形式的一致性——都是一个确定的数值.引导学生用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界. 问题（1）：如果研究更一般的问题，对于函数()y f x =在0x x =处的瞬时变化率如何表示？【师生活动】教师提问，学生回答. 教师要关注学生的数学表达，让学生感受从具体到一般的抽象过程和研究方法. 教师板书，如下：【设计意图】让学生深刻体会概念的建构过程.教师引言（3）：其实函数()y f x =在0x x =处的瞬时变化率就称为函数()y f x =在0x x =处的导数，这就是导数的概念.【师生活动】教师板书，如下： 对于函数()y f x =在0x x =处的瞬时变化率为： 00()()lim lim x x y f x x f x x x ∆→∆→∆+∆-=∆∆问题（2）：让我们应用导数的概念，再来重温两个情境.如何用导数表示运动员在2t =时的瞬时速度(2)v 如何用导数表示抛物线2()f x x =在点(0,0)P 处的切线的斜率k ？它们的意义是什么？【师生活动】教师要注意引导学生用导数的表达形式'0()f x 来表示(2)v 和k .用导数的本质——瞬时变化率解释两个情境的意义.教师用PPT 展示问题与答案（如下）.学生独立思考、回答问题.【设计意图】理解导数的概念，体会导数的本质就是瞬时变化率.问题（4）：问题（4）：同样，抛物线2y x =在点P(1,1)处的切斜斜率是谁的导数？它的意义是什么？【设计意图】让学生理解导数的概念，体会导数的本质就是瞬时变化率.2. 学以致用，解决典型问题教师引言（4）：下面，让我们学以致用，来解决一道数学问题.例1. 设2()f x x=，求'(1)f -. 问题（3）：请问'(1)f -表示什么？1. 导数的概念 对于函数()y f x =在0x x =处的瞬时变化率为： 0''000()()()lim lim x x x x y f x x f x f x y x x =∆→∆→∆+∆-==∆∆= 叫函数()y f x =在0x x =处的导数.追问：如何用导数的定义求'(1)f -【师生活动】教师要引导学生关注导数的符号表达,引导学生用导数的定义解决问题，体会导数的求解步骤.教师提问，学生独立思考、作答在学案上，教师巡视，请学生回答，并板书，如下：【设计意图】让学生学以致用，加深对导数概念的理解，明确求导数的步骤.教师板书，示范解题格式，展示数学的严谨.教师引言（5）：让我们再来解决一道实际问题.例2. 将原油精炼为汽油.柴油.塑胶等各种不同产品，需要对原油进行冷却和加热.已知在第x h 时，原油的温度（单位：C 。

导数的几何意义一、选择题1．如果曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为x ＋2y －3＝0，那么( )A ．f ′(x 0)＞0B ．f ′(x 0)＜0C ．f ′(x 0)＝0D ．f ′(x 0)不存在 [答案] B[解析] 切线x ＋2y －3＝0的斜率k ＝－12，即f ′(x 0)＝－12＜0.故应选B. 2．曲线y ＝12x 2－2在点⎝⎛⎭⎪⎫1，－32处切线的倾斜角为( ) A ．1B.π4C.54π D ．－π4 [答案] B[解析] ∵y ′＝li m Δx →0 [12(x ＋Δx )2－2]－(12x 2－2)Δx＝li m Δx →0 (x ＋12Δx )＝x ∴切线的斜率k ＝y ′|x ＝1＝1.∴切线的倾斜角为π4，故应选B. 3．在曲线y ＝x 2上切线的倾斜角为π4的点是( ) A ．(0,0)B ．(2,4) C.⎝ ⎛⎭⎪⎫14，116 D.⎝ ⎛⎭⎪⎫12，14 [答案] D [解析] 易求y ′＝2x ，设在点P (x 0，x 20)处切线的倾斜角为π4，则2x 0＝1，∴x 0＝12，∴P ⎝ ⎛⎭⎪⎫12，14. 4．曲线y ＝x 3－3x 2＋1在点(1，－1)处的切线方程为( )A ．y ＝3x －4B ．y ＝－3x ＋2C ．y ＝－4x ＋3D ．y ＝4x －5[答案] B[解析] y ′＝3x 2－6x ，∴y ′|x ＝1＝－3.由点斜式有y ＋1＝－3(x －1)．即y ＝－3x ＋2.5．设f (x )为可导函数，且满足lim x →0 f (1)－f (1－2x )2x＝－1，则过曲线y ＝f (x )上点(1，f (1))处的切线斜率为( )A ．2B ．－1C ．1D ．－2[答案] B[解析] lim x →0 f (1)－f (1－2x )2x ＝lim x →0 f (1－2x )－f(1)－2x＝－1，即y ′|x ＝1＝－1，则y ＝f (x )在点(1，f (1))处的切线斜率为－1，故选B.6．设f ′(x 0)＝0，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线( )A ．不存在B ．与x 轴平行或重合C ．与x 轴垂直D ．与x 轴斜交[答案] B[解析] 由导数的几何意义知B 正确，故应选B.7．已知曲线y ＝f (x )在x ＝5处的切线方程是y ＝－x ＋8，则f (5)及f ′(5)分别为( )A ．3,3B ．3，－1C ．－1,3D ．－1，－1[答案] B[解析] 由题意易得：f (5)＝－5＋8＝3，f ′(5)＝－1，故应选B.8．曲线f (x )＝x 3＋x －2在P 点处的切线平行于直线y ＝4x －1，则P 点的坐标为( )A ．(1,0)或(－1，－4)B ．(0,1)C ．(－1,0)D ．(1,4)[答案] A[解析] ∵f (x )＝x 3＋x －2，设x P ＝x 0，∴Δy ＝3x 20·Δx ＋3x 0·(Δx )2＋(Δx )3＋Δx ，∴ΔyΔx ＝3x 20＋1＋3x 0(Δx )＋(Δx )2，∴f ′(x 0)＝3x 20＋1，又k ＝4，∴3x 20＋1＝4，x 20＝1.∴x 0＝±1，故P (1,0)或(－1，－4)，故应选A.9．设点P 是曲线y ＝x 3－3x ＋23上的任意一点，P 点处的切线倾斜角为α，则α的取值范围为() A.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π B.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫56π，πC.⎣⎢⎡⎭⎪⎫23π，πD.⎝ ⎛⎦⎥⎤π2，56π[答案] A[解析] 设P (x 0，y 0)，∵f ′(x )＝li m Δx →0 (x ＋Δx )3－3(x ＋Δx )＋23－x 3＋3x －23Δx＝3x 2－3，∴切线的斜率k ＝3x 20－3，∴tan α＝3x 20－3≥－ 3. ∴α∈⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π.故应选A. 10．(2010·福州高二期末)设P 为曲线C ：y ＝x 2＋2x ＋3上的点，且曲线C 在点P 处切线倾斜角的取值范围为[0，π4]，则点P 横坐标的取值范围为( ) A ．[－1，－12] B ．[－1,0] C ．[0,1]D ．[12，1] [答案] A[解析] 考查导数的几何意义．∵y ′＝2x ＋2，且切线倾斜角θ∈[0，π4]， ∴切线的斜率k 满足0≤k ≤1，即0≤2x ＋2≤1，∴－1≤x ≤－12. 二、填空题11．已知函数f (x )＝x 2＋3，则f (x )在(2，f (2))处的切线方程为________．[答案] 4x －y －1＝0[解析] ∵f (x )＝x 2＋3，x 0＝2∴f (2)＝7，Δy ＝f (2＋Δx )－f (2)＝4·Δx ＋(Δx )2∴Δy Δx ＝4＋Δx .∴li m Δx →0 Δy Δx ＝4.即f ′(2)＝4. 又切线过(2,7)点，所以f (x )在(2，f (2))处的切线方程为y －7＝4(x －2)即4x －y －1＝0.12．若函数f (x )＝x －1x，则它与x 轴交点处的切线的方程为________． [答案] y ＝2(x －1)或y ＝2(x ＋1)[解析] 由f (x )＝x －1x＝0得x ＝±1，即与x 轴交点坐标为(1,0)或(－1,0)．∵f ′(x )＝li m Δx →0 (x ＋Δx )－1x ＋Δx －x ＋1x Δx ＝li m Δx →0 ⎣⎢⎡⎦⎥⎤1＋1x (x ＋Δx )＝1＋1x 2. ∴切线的斜率k ＝1＋11＝2. ∴切线的方程为y ＝2(x －1)或y ＝2(x ＋1)． 13．曲线C 在点P (x 0，y 0)处有切线l ，则直线l 与曲线C 的公共点有________个．[答案] 至少一[解析] 由切线的定义，直线l 与曲线在P (x 0，y 0)处相切，但也可能与曲线其他部分有公共点，故虽然相切，但直线与曲线公共点至少一个．14．曲线y ＝x 3＋3x 2＋6x －10的切线中，斜率最小的切线方程为________．[答案] 3x －y －11＝0[解析] 设切点P (x 0，y 0)，则过P (x 0，y 0)的切线斜率为，它是x 0的函数，求出其最小值． 设切点为P (x 0，y 0)，过点P 的切线斜率k ＝＝3x 20＋6x 0＋6＝3(x 0＋1)2＋3.当x 0＝－1时k 有最小值3，此时P 的坐标为(－1，－14)，其切线方程为3x －y －11＝0.三、解答题 15．求曲线y ＝1x －x 上一点P ⎝⎛⎭⎪⎫4，－74处的切线方程． [解析] ∴y ′＝lim Δx →0 ⎝ ⎛⎭⎪⎫1x ＋Δx －1x －(x ＋Δx －x )Δx＝lim Δx →0 －Δx x (x ＋Δx )－Δx x ＋Δx ＋x Δx＝lim Δx →0 ⎝ ⎛⎭⎪⎫－1x (x ＋Δx )－1x ＋Δx ＋x ＝－1x 2－12x . ∴y ′|x ＝4＝－116－14＝－516， ∴曲线在点P ⎝⎛⎭⎪⎫4，－74处的切线方程为： y ＋74＝－516(x －4)．即5x ＋16y ＋8＝0.16．已知函数f (x )＝x 3－3x 及y ＝f (x )上一点P (1，－2)，过点P 作直线l .(1)求使直线l 和y ＝f (x )相切且以P 为切点的直线方程；(2)求使直线l 和y ＝f (x )相切且切点异于点P 的直线方程y ＝g (x )．[解析] (1)y ′＝li m Δx →0 (x ＋Δx )3－3(x ＋Δx )－3x 3＋3x Δx＝3x 2－3. 则过点P 且以P (1，－2)为切点的直线的斜率 k 1＝f ′(1)＝0，∴所求直线方程为y ＝－2.(2)设切点坐标为(x 0，x 30－3x 0)，则直线l 的斜率k 2＝f ′(x 0)＝3x 20－3，∴直线l 的方程为y －(x 30－3x 0)＝(3x 20－3)(x －x 0)又直线l 过点P (1，－2)，∴－2－(x 30－3x 0)＝(3x 20－3)(1－x 0)，∴x 30－3x 0＋2＝(3x 20－3)(x 0－1)，解得x 0＝1(舍去)或x 0＝－12. 故所求直线斜率k ＝3x 20－3＝－94， 于是：y －(－2)＝－94(x －1)，即y ＝－94x ＋14. 17．求证：函数y ＝x ＋1x图象上的各点处的切线斜率小于1. [解析] y ′＝li m Δx →0 f (x ＋Δx )－f (x )Δx＝li m Δx →0⎝ ⎛⎭⎪⎫x ＋Δx ＋1x ＋Δx －⎝ ⎛⎭⎪⎫x ＋1x Δx ＝li m Δx →0x ·Δx (x ＋Δx )－Δx (x ＋Δx )·x ·Δx ＝li m Δx →0 (x ＋Δx )x －1(x ＋Δx )x＝x 2－1x 2＝1－1x 2＜1， ∴y ＝x ＋1x图象上的各点处的切线斜率小于1. 18．已知直线l 1为曲线y ＝x 2＋x －2在点(1,0)处的切线，l 2为该曲线的另一条切线，且l 1⊥l 2.(1)求直线l 2的方程；(2)求由直线l 1、l 2和x 轴所围成的三角形的面积．[解析] (1)y ′|x ＝1＝li m Δx →0 (1＋Δx )2＋(1＋Δx )－2－(12＋1－2)Δx＝3， 所以l 1的方程为：y ＝3(x －1)，即y ＝3x －3.设l 2过曲线y ＝x 2＋x －2上的点B (b ，b 2＋b －2)，y ′|x ＝b ＝li m Δx →0 (b ＋Δx )2＋(b ＋Δx )－2－(b 2＋b －2)Δx＝2b ＋1，所以l 2的方程为：y －(b 2＋b －2)＝(2b ＋1)·(x －b )，即y ＝(2b ＋1)x －b 2－2.因为l 1⊥l 2，所以3×(2b ＋1)＝－1，所以b ＝－23，所以l 2的方程为：y ＝－13x －229. (2)由⎩⎪⎨⎪⎧ y ＝3x －3，y ＝－13x －229，得⎩⎪⎨⎪⎧ x ＝16，y ＝－52，即l 1与l 2的交点坐标为⎝ ⎛⎭⎪⎫16，－52. 又l 1，l 2与x 轴交点坐标分别为(1,0)，⎝ ⎛⎭⎪⎫－223，0. 所以所求三角形面积S ＝12×⎪⎪⎪⎪⎪⎪－52×⎪⎪⎪⎪⎪⎪1＋223＝12512.。