第七章 直线与圆测试

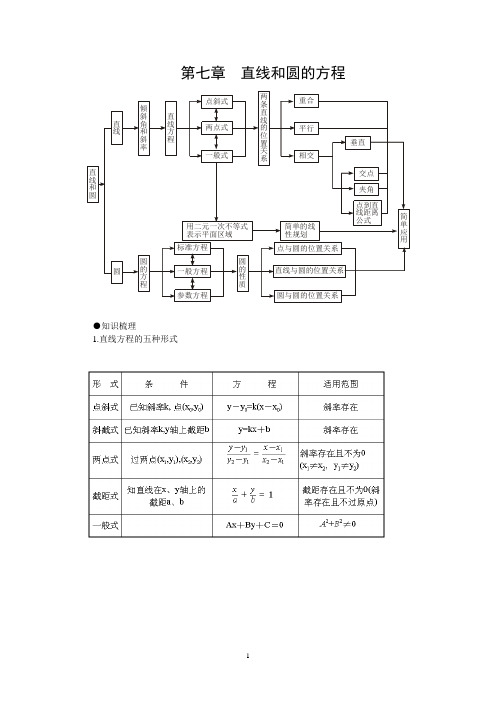
第七章直线和圆的方程●知识梳理1.直线方程的五种形式2.直线的倾斜角、斜率及直线的方向向量及位置关系:（1）直线的倾斜角在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角.直线和x 轴平行或重合时，直线的倾斜角为0°,直线倾斜角取值范围0°≤α＜180°. （2）直线的斜率倾斜角α不是90°的直线，它的倾斜角的正切叫做这条直线的斜率，常用k 表示，即k =tan α（α≠90°）.倾斜角是90°的直线没有斜率；倾斜角不是90°的直线都有斜率，其取值范围是（－∞，+∞）.（4）求直线斜率的方法①定义法：已知直线的倾斜角为α，且α≠90°，则斜率k =tan α.②公式法：已知直线过两点P 1（x 1，y 1）、P 2（x 2，y 2），且x 1≠x 2，则斜率k =1212x x y y --.平面直角坐标系内，每一条直线都有倾斜角，但不是每一条直线都有斜率. 对于直线上任意两点P 1（x 1，y 1）、P 2（x 2，y 2），当x 1=x 2时，直线斜率k 不存在，倾斜角α=90°；当x 1≠x 2时，直线斜率存在，是一实数，并且k ≥0时，α=arctan k ，k ＜0时，α=π+arctan k .（5）到角与夹角：若直线l 1, l 2的斜率分别为k 1, k 2，将l 1绕它们的交点逆时针旋转到与l 2重合所转过的最小正角叫l 1到l 2的角；l 1与l 2所成的角中不超过900的正角叫两者的夹角。

若记到角为θ，夹角为α，则tan θ=21121k k k k +-,tan α=21121k k k k +-.（6）平行与垂直：若直线l 1与l 2的斜率分别为k 1, k 2。

且两者不重合，则l 1//l 2的充要条件是k 1=k 2；l 1⊥l 2的充要条件是k 1k 2=-1。

高三数学练习十九一、填空题：（每小题5分，共70分）1．已知直线m 的倾斜角是直线0333=--y x 的倾斜角的2倍，且直线m 在x 轴上的截距是3-，则直线m 的方程是2．圆1C ：222880x y x y +++-=与圆2C 224420x y x y +-+-=的位置关系是3．如果直线0121=+-ay x l ：与直线07642=-+y x l ：平行，则a 的值为4．到直线3410x y --=的距离为2的直线方程是5．与直线01:2=--y m mx l 垂直于点(2,1)P 的直线方程是6．与圆8)3()3(22=-+-y x 相切，且在y x 、轴上截距相等的直线有 条7．过原点的直线与圆03422=+++x y x 相切，若切点在第三象限，则该直线的方程是8．若直线:10 (0,0)l ax by a b ++=>>始终平分圆M ：228210x y x y ++++=的周长，则14a b+的最小值为 9. 设,x y 满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩，则231x y x +++取值范围是 10. 00(,)M x y 为圆222x y a+=()0a >内异于圆心的一点，则直线200x x y y a +=与该圆的位置关系是11．已知圆的方程是x 2＋y 2＝1，则在y 轴上截距为2的切线方程为 12．圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4)A -，(0,2)B -，则圆C 的方程为13．已知实数x 、y 满足方程22410x y x +-+=，则xy 的最大值为 14．如图，已知()4,0A 、()0,4B ，从点()2,0P 射出的光线经直线AB 反向后再射到直线OB 上，最后经直线OB 反射后又回到P 点，则光线所经过的路程是二、解答题：本大题共6小题，共90分．15. (14分)求经过两条直线04:1=-+y x l 和02:2=+-y x l 的交点，且分别与直线012=--y x （1）平行， （2）垂直的直线方程.16. (14分)圆的方程为x 2+y 2－6x －8y ＝0，过坐标原点作长为8的弦，求弦所在的直线方程.17. (14分)一圆与y 轴相切，圆心在直线03=-y x 上，在x y =上截得的弦长为72，求此圆的方程.18. (16分)已知关于x ,y 的方程C :04222=+--+m y x y x .（1）当m 为何值时，方程C 表示圆.（2）若圆C 与直线l :x +2y －4=0相交于M ,N 两点，且MN =,求m 的值19. (16分)设有半径为3km 的圆形村落，A 、B 两人同时从村落中心出发，B 向北直行，A 先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B 相遇.设A 、B 两人速度一定，其速度比为3:1，问两人在何处相遇？20. (16分)已知可行域0,20,0,y x y ≥⎧⎪+≥⎨+-≤的外接圆C 与x 轴交于点1A 、2A ，椭圆1C 以线段12A A为长轴，离心率2e =． （1）求圆C 及椭圆1C 的方程；（2）设椭圆1C 的右焦点为F ，点P 为圆C 上异于1A 、2A 的动点，过原点O 作直线PF的垂线交直线x =Q ，判断直线PQ 与圆C 的位置关系，并给出证明．。

题目 第七章直线和圆的方程高考要求1．掌握直线和圆的位置关系、圆与圆的位置关系等知识，能够从代数特征（解或讨论方程组）或几何性质去考虑2．会运用半径长、半径、弦心距构成的直角三角形减少运算量知识点归纳1研究圆与直线的位置关系最常用的方法：①判别式法；②考查圆心到直线的距离与半径的大小关系。

直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种，若22BA C Bb Aa d +++=，则0<∆⇔⇔>相离r d ;0=∆⇔⇔=相切r d ; 0>∆⇔⇔<相交r d2两圆位置关系的判定方法设两圆圆心分别为O 1，O 2，半径分别为r 1，r 2，d O O =21 ①条公切线外离421⇔⇔+>r r d ②条公切线外切321⇔⇔+=r r d ③条公切线相交22121⇔⇔+<<-r r d r r ④条公切线内切121⇔⇔-=r r d ⑤无公切线内含⇔⇔-<<210r r d3直线和圆相切：这类问题主要是求圆的切线方程求圆的切线方程主要可分为已知斜率k 或已知直线上一点两种情况，而已知直线上一点又可分为已知圆上一点和圆外一点两种情况①过圆上一点的切线方程：圆),(00222y x P r y x 的以=+为切点的切线方程是200r y y x x =+。

当点00(,)P x y 在圆外时，200r y y x x =+表示切点弦的方程。

一般地，曲线)(00022y x P F Ey Dx Cy Ax ，的以点=++-+为切点的切线方程是：0220000=++⋅++⋅-+F y y E x x D y Cy x Ax 。

当点00(,)P x y 在圆外时，0220000=++⋅++⋅-+F y y E x x D y Cy x Ax 表示切点弦的方程。

这个结论只能用来做选择题或者填空题，若是做解答题，只能按照求切线方程的常规过程去做。

第七章 直线与圆的方程7.1～7.4单元检测题（A ）卷一、 选择题（每小题6分，共48分）1、 已知直线l 过)2,1(A 和)6,4(B 两点，则直线l 的斜率为（ ）（A ）43 （B ）43-（C ）34 （D ）34-2、 直线0632=-+y x 的斜率为k ，在x 轴上的截距为a ，则（ ）（A ）2,32=-=a k （B ）3,32=-=a k （C ）2,23=-=a k （D ）3,23=-=a k3、 如果0>AC ，0<BC ，那么直线0=++C By Ax 不经过（ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 4、 若直线022=-+y ax 与直线023=--y x 平行，那么a 等于（ ）（A ）－3 （B ）－6 （C ）23-（D ）325、 到直线0143=+-y x 的距离为3，且与此直线平行的直线方程为（ ）（A ）0443=+-y x （B ）02430443=--=+-y x y x 或 （C ）01643=+-y x （D ）0144301643=--=+-y x y x 或 6、 原点和点（1，1）在直线a y x =+的两侧，则a 的取值范围是（ ）（A ）20><a a 或 （B ）02==a a 或（C ）20<<a （D ）20≤≤a7、 若直线025=++y ax 和直线032=++y x 互相垂直，那么a 等于（ ）（A ）－6 （B ）－8 （C ）－10 （D ）108、 直线0),(:=y x f C 关于直线0=-y x 的对称直线/C 的方程为（ ）（A ）0),(=-x y f （B ）0),(=-x y f（C ）0),(=x y f （D ）0),(=--x y f二、 填空题（每小题6分，共24分）9、 直线032=+-y x 到直线023=-+y x 的角为_______________。

第5节 圆的切线、切点弦结论知识与方法1求过圆()()222:C x a y b r -+-=上一点()00,P x y 的圆C 的切线的步骤如下：（1）先验证经过点P 且垂直于x 轴的直线是否和圆C 相切，若是，如图1所示，所求切线为0x x =，问题求解完毕；若否，则进行下一步；（2）设切线斜率为k ，如图2所示，由PC ⊥切线，求出k ，用点斜式写出切线的方程，问题求解完毕.上述问题的结论：圆C 上点P 处的切线的方程为()()()()200x a x a y b y b r --+--=. 2求过圆()()222:C x a y b r -+-=外一点()00,P x y 的圆C 的切线的步骤如下：（1）先验证过点P 且垂直于x 轴的直线是否和圆相切，若是，如图3所示，其中一条切线为0x x =（2）设切线的斜率为k ，用点斜式写出切线的方程，由圆心到切线的距离d r =，解出k ，求得切线方程.3.过圆()()222:C x a y b r -+-=外一点()00,P x y 作圆C 的两条切线，切点分别为A 和B ，如图4所示，则切点弦AB 所在直线的方程为()()()()200x a x a y b y b r --+--=典型例题【例l 】圆()22:14C x y -+=在点(3P 处的切线方程为______.变式1 圆22:230C x y x +--=在点()2,3P -处的切线方程为______. 变式2 已知圆()22:14C x y -+=，则： （1）圆C 的过点()2,0P -的切线方程为_______；（2）圆C 的过点()3,1Q 的切线方程为_______【例2】已知圆22:4O x y +=外一点()2,3P ，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为_______变式1 已知圆22:2410C x y x y +--+=外一点()2,1P -，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.变式2 已知圆22:4Q x y +=，P 为直线:4l y x =+上一点，过点P 作圆O 的两条切线，切点分别为A 和B ，若四边形PAOB 的面积为12，则直线AB 的方程为______. 变式3 已知圆22:4O x y +=，P 为直线:260l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，当四边形PACB 的面积最小时，则直线AB 的方程为______. 变式4 已知直线:4l y x =+与x 轴交于点T ，过直线l 上的动点P 作圆22:4O x y +=的两条切线，切点分别为A 、B ，设AB 中点为M ，则TM 的最小值为（ ） A.22 B.3217 D.3强化训练1.（★★）圆22:40C x y x +-=在点(3P 处的切线方程为（ ） A.320x y +-= B.340x y -=C.340x +=D.320x -+= 2.（★★）已知圆()22:11C x y +-=，则：（1）圆C 的过点()0,2P -的切线方程为______；（2）圆C 的过点()1,1Q -的切线方程为______.3.（★★）已知圆()22:12C x y -+=外一点()2,2P ，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.4.（★★）已知圆()()22:129C x y -+-=外一点()4,2P -，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.5.（★★）已知圆22:2440C x y x y +---=外一点()4,1P --，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.6.（★★★）已知圆22:2440C x y x y +---=，P 为直线:20l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，若四边形PACB 的面积为12，则直线AB 的方程为______.7.（★★★）已知圆22:2440C x y x y +---=，P 为直线:20l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，当四边形PACB 的面积最小时，则直线AB 的方程为______.8.（★★★★）已知P 为抛物线2:4C y x =上的动点，过P 作圆()22:44M x y -+=的两条切线，切点分别为A 和B ，则当四边形PAMB 的面积最小时，直线AB 的方程为______.9.（★★★★）已知圆22:2440C x y x y +---=，P 为直线:20l x y ++=上的动点，过点P 作圆C 的两条切线，切点分别为A 和B ，AB 的中点为Q ，若点T 的坐标为111,1010⎛⎫ ⎪⎝⎭，则TQ 的最小值为______.。

第七章直线与圆的方程7.5～7.6单元检测题（A ）卷一、 选择题（本大题共8个小题，每小题6分，共48分）1、 若曲线C 上的点的坐标都是方程0),(=y x f 的解，则（ ）（A ）曲线C 的方程是0),(=y x f（B ）以方程0),(=y x f 的解为坐标的点都在曲线C 上（C ）不在曲线C 上的点的坐标都不是方程0),(=y x f 的解（D ）坐标不是方程0),(=y x f 的解的点都不在曲线C 上2、 到两坐标轴的距离之和为6的点的轨迹方程是（ ）（A ）6=+y x （B ）6=±y x （C ）6||||=+y x （D ）6||=+y x3、 方程0222=++-+k y x y x 是圆的方程，则实数k 的取值范围是（ ）（A ）5<k （B ）45<k （C ）45>k （D ）5>k 4、 圆0744:221=+-++y x y x C 与圆013104:222=+--+y x y x C （ ）（A ）相交 （B ）内切 （C ）外切 （D ）相离5、 动点P 到点（1,－2）的距离为3，则点P 的轨迹方程为（ ）（A ）9)2()1(22=-++y x （B ）9)2()1(22=++-y x（C ）3)2()1(22=-++y x （D ）3)2()1(22=++-y x6、 下列各点中，不在方程0122=++-y xy x 的图形上的是（ ）（A ）（1，－2） （B ）（2，－3） （C ）（3，10） （D ）（－3，－2） 7、 已知圆C ：⎩⎨⎧+=+=θθsin 22cos 2y a x （θ,0>a 为参数）及直线l ：03=+-y x ，若直线l 被圆C 截得的弦长为32，则a 的值为（ ）（A ）2 （B ）22- （C ）12- （D ）12+8、 已知曲线241x y -+=与直线4)2(+-=x k y 有两个不同的交点，则k 的取值范围是（ ）（A ）]43,125( （B ）),125(+∞ （C ）]43,31( （D ）)125,0( 二、 填空题（本大题共4个小题，每小题6分，共24分）9、 直线y x y x ==+-2012和曲线的交点坐标为_________________。

1．(2013·河南第二次联考)已知p ：“x 2＋y 2＋2x ＝F 为一圆的方程(F ∈R )”，q ：“F >0”，则p 是q 的( )A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件解析：x 2＋ y 2 ＋2x ＝F 为一圆的方程(F ∈R )，则有22＋4F ＞0，即F ＞－1；反之，若F＞0，则22＋4F ＞0一定成立，所以， x 2＋ y 2＋2x ＝F 为一圆的方程(F ∈R )，故p 是q 的必要不充分条件．故选C.答案：C2．以两点A (－3，－1)和B (5,5)为直径端点的圆的方程是( )A ．(x －1)2＋(y ＋2)2＝100B ．(x －1)2＋(y －2)2＝100C ．(x －1)2＋(y －2)2＝25D ．(x ＋1)2＋(y ＋2)2＝25答案：C3．动点A 在圆x 2＋y 2＝1上移动时，它与定点B (3,0)连线的中点的轨迹方程是( )A ．(x ＋3)2＋y 2＝4B ．(x －3)2＋y 2＝1C ．(2x －3)2＋4y 2＝1 D.⎝ ⎛⎭⎪⎫x ＋322＋y 2＝12解析：设中点M (x ，y )，由中点公式得点A (2x －3,2y )，∵A 在圆x 2＋y 2＝1上，∴(2x －3)2＋(2y )2＝1，即(2x －3)2＋4y 2＝1.故选C. 答案：C4．过点M (1,2)的直线l 将圆(x －2)2＋y 2＝9分成两段弧，当其中的劣弧最短时，直线的方程是( )A ．x ＝1B ．y ＝1C ．x －y ＋1＝0D ．x －2y ＋3＝0解析：设圆心为C ，当CM ⊥l 时，圆截l 的弦最短，其所对的劣弧最短，又k CM ＝－2，所以k l ＝12.所以直线l 的方程为y －2＝12(x －1)，即x －2y ＋3＝0.答案： D5．在平面直角坐标系内，若曲线C ：x 2＋y 2＋2ax －4ay ＋5a 2－4＝0上所有的点均在第二象限内，则实数a 的取值范围为( )A ．(－∞，－2)B ．(－∞，－1)C ．(1，＋∞)D ．(2，＋∞)解析：曲线C ：x 2＋y 2＋2ax －4ay ＋5a 2－4＝0，即(x ＋a )2＋(y －2a )2＝4表示以(－a,2a )为圆心，2为半径的圆，当－a <－2且2a ＞2， 即a >2时，曲线C 上所有的点均在第二象限内．故选D. 答案：D6．(2013·天津卷)已知过点P (2,2)的直线与圆(x －1)2＋y 2＝5相切，且与直线ax －y ＋1＝0垂直，则a 等于( )A ．－12B ．1C ．2 D.12解析：圆心为O (1,0)，由于P (2,2)在圆(x －1)2＋y 2＝5上，所以P 为切点，OP 与P 点处的切线垂直．所以K OP ＝2－02－1＝2，又过点P 处的切线与直线ax －y ＋1＝0垂直．所以a ＝K OP ＝2.故选C.答案：C7．(2013·吉林模拟)圆x 2＋y 2－2x ＋6y ＋5a ＝0关于直线y ＝x ＋2b 成轴对称图形，则a －b 的取值范围是( )A ．(－∞，4)B ．(－∞，0)C ．(－4，＋∞)D ． (4，＋∞)解析：由题意得，圆心(1，－3)在直线y ＝x ＋2b 上，得b ＝－2，由圆成立的条件可得(－2)2＋62－4×5a >0，解得a <2，∴a －b <4，故选A.答案：A8．圆x 2＋y 2－4x －4y －10＝0上的点到直线x ＋y －14＝0的最大距离与最小距离的差是( )A ．36B ．18C ．6 2D ．5 2解析：圆x 2＋y 2－4x －4y －10＝0的圆心为(2,2)，半径为32，圆心到直线x ＋y －14＝0的距离为|2＋2－14|2＝52>32，圆上的点到直线的最大距离与最小距离的差是2R ＝6 2.故选C.答案：C9．(2013·佛山、江门二模)已知圆C 经过点A (0,3)和B (3,2)，且圆心C 在直线y ＝x 上，则圆C 的方程为__________．解析：设圆心坐标为C (a ，a )，则由题意可得半径r ＝a 2＋a －2＝a －2＋a －2，解得 a ＝1，故圆C 的方程为(x －1)2＋(y －1)2＝5.答案：(x －1)2＋(y －1)2＝510．过点(－1，－2)的直线l 被圆x 2＋y 2－2x －2y ＋1＝0截得的弦长为2，则直线l 的斜率为____________．解析： 由题意，直线与圆要相交，斜率必须存在，设为k ，则直线l 的方程为y ＋2＝k (x ＋1)．又圆的方程为(x －1)2＋(y －1)2＝1，圆心为(1,1)，半径为1，所以圆心到直线的距离d ＝|k －1＋k －2|1＋k 2＝ 1－⎝⎛⎭⎪⎫222＝22，解得k ＝1或177. 答案：1或17711．(2013·温州模拟)若直线2ax ＋by －2＝0(a ，b 为正实数)平分圆x 2＋y 2－2x －4y －6＝0，则2a ＋1b的最小值是________．解析：圆心为(1,2)，代入直线方程得a ＋b ＝1，则2a ＋1b ＝⎝ ⎛⎭⎪⎫2a ＋1b (a ＋b )＝3＋a b ＋2ba≥3＋2 2.等号成立的条件为a ＝2－2，b ＝2－1.答案：3＋2 212．(2012·北京西城区二模)已知曲线C 的方程是⎝⎛⎭⎪⎫x －|x |x 2＋⎝ ⎛⎭⎪⎫y －|y |y 2＝8，给出下列三个结论：①曲线C 与两坐标轴有公共点；②曲线C 既是中心对称图形，又是轴对称图形； ③若点P ，Q 在曲线C 上，则|PQ |的最大值是6 2. 其中，所有正确结论的序号是________．解析：显然x ≠0，y ≠0，所以①错误．分四种情况去掉绝对值，可画出其图形，其图形是圆(x －1)2＋(y －1)2＝8在第一象限的圆弧关于x ，y 和原点对称而形成的封闭图形，其图形上两点间的最大距离是圆半径的3倍，即62，所以②③正确．答案：②③ 13．求过A (1,4)，B (3,2)两点，且圆心在直线y ＝0上的圆的标准方程，并判断点M 1(2,3)，M 2(2,4)与圆的位置关系．解析：根据圆的标准方程，只要求得圆心坐标和圆的半径即可．因为圆过A ，B 两点，所以圆心在线段AB 的垂直平分线上．由k AB ＝4－21－3＝－1，AB 的中点为(2,3)，故AB 的垂直平分线的方程为y －3＝x －2，即x －y ＋1＝0.又圆心在直线y ＝0上，因此圆心坐标是方程组⎩⎪⎨⎪⎧x －y ＋1＝0，y ＝0的解，即圆心坐标为(－1,0)，半径r ＝－1－2＋－2＝20，所以得所求圆的标准方程为(x ＋1)2＋y 2＝20.因为M 1到圆心C (－1,0)的距离为＋2＋－2＝18，|M 1C |<r ，所以M 1在圆C 内；而点M 2到圆心C 的距离|M 2C |＝＋2＋－2＝25>20，所以M 2在圆C 外．14．在直角坐标系xOy 中，以O 为圆心的圆与直线x －3y ＋4＝0相切． (1)求圆O 的方程；(2)圆O 与x 轴相交于A 、B 两点，圆内的动点P 使|PA →|，|PO →|，|PB →|成等比数列，求PA →·PB →的取值范围．解析：(1)依题设，圆O 的半径r 等于原点O 到直线x －3y ＋4＝0的距离，即r ＝41＋3＝2.所以圆O 的方程为x 2＋y 2＝4.(2)不妨设A (x 1,0)，B (x 2,0)，x 1<x 2.由x 2＝4即得A (－2,0)，B (2,0)．设P (x ，y )，由|PA →|，|PO →|，|PB →|成等比数列， 得x ＋2＋y 2·x －2＋y 2＝x 2＋y 2，即x 2－y 2＝2. PA →·PB →＝(－2－x ，－y )·(2－x ，－y )＝x 2－4＋y 2＝2(y 2－1)．由于点P 在圆O 内，故⎩⎪⎨⎪⎧x 2＋y 2＜4，x 2－y 2＝2，由此得y 2<1. 所以PA →·PB →的取值范围为[－2,0).15．已知以点C ⎝ ⎛⎭⎪⎫t ，2t (t ∈R ，t ≠0)为圆心的圆与x 轴交于点O ，A ，与y 轴交于点O ，B ，其中O 为原点．(1)求证：△OAB 的面积为定值；(2)设直线y ＝－2x ＋4与圆C 交于点M ，N ，若|OM |＝|ON |，求圆C 的方程．（1)证明：∵圆C 过原点O ，∴|OC |2＝t 2＋4t2.∴圆C 的方程是(x －t )2＋⎝⎛⎭⎪⎫y －2t 2＝t 2＋4t2.令x ＝0，得y 1＝0，y 2＝4t；令y ＝0，得x 1＝0，x 2＝2t .∴S △OAB ＝12|OA |·|OB |＝12×⎪⎪⎪⎪⎪⎪4t ×|2t |＝4，即△OAB 的面积为定值．(2)解析：∵|OM |＝|ON |，|CM |＝|CN |， ∴OC 垂直平分线段MN .∵k MN ＝－2，∴k OC ＝12.∴直线OC 的方程是y ＝12x .∴2t ＝12t ，解得t ＝2或t ＝－2. 当t ＝2时，圆心C 的坐标为(2,1)，|OC |＝5，此时C 到直线y ＝－2x ＋4的距离d ＝15<5，满足圆C 与直线y ＝－2x ＋4相交于两点．当t ＝－2时，圆心C 的坐标为(－2，－1)，|OC |＝5，此时C 到直线y ＝－2x ＋4的距离d ＝95> 5.此时圆C 与直线y ＝－2x ＋4不相交，∴t ＝－2不符合题意，舍去．∴圆C 的方程为(x －2)2＋(y －1)2＝5.。

第七章 第五节 圆及直线与圆的位置关系1.(2009·重庆高考) ( )A ．x 2＋(y －2)2＝1B ．x 2＋(y ＋2)2＝1C ．(x －1)2＋(y －3)2＝1D ．x 2＋(y －3)2＝1解析：由题意知圆心为(0,2)，则圆的方程为x 2＋(y －2)2＝1.答案：A2．(2010·潍坊模拟)已知圆C 与直线x －y ＝0及x －y －4＝0都相切，圆心在直线x ＋y ＝0上，则圆C 的方程为 ( )A ．(x ＋1)2＋(y －1)2＝2B ．(x －1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2D ．(x ＋1)2＋(y ＋1)2＝2解析：由圆心在直线x ＋y ＝0上．不妨设为C (a ，－a )．∴r ＝|a －(－a )|2＝|a －(－a )－4|2， 解得a ＝1，r ＝ 2.∴C ：(x －1)2＋(y ＋1)2＝2.答案：B3．若圆x 2＋y 2＋(a 2－1)x ＋2ay －a ＝0关于直线x －y ＋1＝0对称，则实数a 的值为 ________．解析：依题意知直线x －y ＋1＝0经过圆x 2＋y 2＋(a 2－1)x ＋2ay －a ＝0的圆心(－a 2－12，－a )， 所以－a 2－12＋a ＋1＝0，解得a ＝3或a ＝－1， 当a ＝－1时，方程x 2＋y 2＋(a 2－1)x ＋2ay －a ＝0不能表示圆，所以只能取a ＝3. 答案：34.直线x ＋y ＝1与圆x ( )A ．(0，2－1)B ．(2－1，2＋1)C ．(－2－1，2＋1)D ．(0，2＋1)解析：圆心(0，a )，半径r ＝a .∴|a －1|2>a ，∴0<a <2－1. 答案：A5．直线2x －y ＝0与圆C ：(x －2)2＋(y ＋1)2＝9相交于A ，B 两点，则△ABC (C 为圆心) 的面积等于 ( )A ．2 5B ．2 3C ．4 3D ．4 5解析：由已知，C (2，－1)，∴点C 到直线2x －y ＝0的距离d ＝55＝5， 由题意知，(|AB |2)2＋d 2＝9， ∴|AB |＝4，∴S △ABC ＝12×4×5＝2 5. 21 答案：A6．(2009·全国卷Ⅱ)已知AC 、BD 为圆O ：x 2＋y 2＝4的两条相互垂直的弦，垂足为 M (1，2)，则四边形ABCD 的面积的最大值为________．解析：设圆心O 到AC 、BD 的距离为d 1、d 2，垂足分别为F 、E ，则四边形OEMF为矩形，则有d 21＋d 22＝3.由平面几何知识知 |AC |＝24－d 21，|BD |＝24－d 22， ∴S 四边形ABCD ＝12|AC |·|BD | ＝24－d 21·4－d 22≤(4－d 21)＋(4－d 22)＝8－(d 21＋d 22)＝5，即四边形ABCD 的面积的最大值为5.答案：57．已知圆x 2＋y 2＋2ax －2ay ＋2a 2－4a ＝0(0＜a ≤4)的圆心为C ，直线l ：y ＝x ＋m .(1)若m ＝4，求直线l 被圆C 所截得弦长的最大值；(2)若直线l 是圆心C 下方的切线，当a 在(0,4]上变化时，求m 的取值范围． 解：(1)∵x 2＋y 2＋2ax －2ay ＋2a 2－4a ＝0，∴(x ＋a )2＋(y －a )2＝4a ，∴圆心为C (－a ，a )，半径为r ＝2a ，设直线l 被圆C 所截得的弦长为2t ，圆心C 到直线l 的距离为d ，m ＝4时，直线l ：x －y ＋4＝0，圆心C 到直线l 的距离d ＝|－a －a ＋4|2＝2|a －2|， t 2＝(2a )2－2(a －2)2＝－2a 2＋12a －8＝－2(a －3)2＋10，又0＜a ≤4，∴当a ＝3时，直线l 被圆C 所截得弦长的值最大，其最大值为210.(2)圆心C 到直线l 的距离d ＝|－a －a ＋m |2＝22|2a －m |， ∵直线l 是圆C 的切线，∴d ＝r ，即|m －2a |2＝2a ， ∴m ＝2a ±22a ，∵直线l 在圆C 的下方，∴m ＝2a －22a ＝(2a －1)2－1，∵a ∈(0,4]，∴m ∈[－1,8－42]．8.已知半径为1( )A ．(x －5)2＋(y ＋7)2＝25B ．(x －5)2＋(y ＋7)2＝3或(x －5)2＋(y ＋7)2＝15C ．(x －5)2＋(y ＋7)2＝9D ．(x －5)2＋(y ＋7)2＝25或(x －5)2＋(y ＋7)2＝9解析：当动圆圆心在定圆外时，动圆圆心(x ，y )到(5，－7)的距离为5，∴(x －5)2＋(y ＋7)2＝25，当动圆圆心在定圆内时，动圆圆心(x ，y )到(5，－7)的距离为3，∴(x －5)2＋(y ＋7)2＝9.答案：D9．已知0＜r ＜2＋1，则圆x 2＋y 2＝r 2与(x －1)2＋(y ＋1)2＝2的位置关系是 ( )A ．外切B ．内含C ．相交D ．相离解析：两圆连心线长|O 1O 2|＝2，r 1＋r 2＝r ＋2，|r 1－r 2|＝|2－r |，因为0＜r ＜2＋1，所以2＜r ＋2＜22＋1，－2＜r －2＜1，所以|2－r |＜|O 1O 2|＜r ＋2，所以两圆相交．答案：C10.(2010·唐山模拟)x ＋y ＋m ≥0恒成 立，则实数m 的取值范围是________．解析：据题意圆x 2＋(y －1)2＝1上所有的点都在直线x ＋y ＋m ≥0的右上方．∴⎩⎪⎨⎪⎧ 1＋m ≥0，|1＋m |2≥1.∴m 的取值范围是m ≥－1＋ 2. 答案：m ≥－1＋ 211．若实数x 、y 满足(x －2)2＋y 2＝3，则y x的最大值为________． 解析：y x ＝y －0x －0，即连结圆上一点与坐标原点的直线的斜率，因此y x的最值即为过原 点的直线与圆相切时该直线的斜率．设y x ＝k ，则kx －y ＝0.由|2k |1＋k 2＝3，得k ＝±3， 结合图形可得(y x )max ＝3，(y x)min ＝－ 3. 答案： 312．已知圆M 过两点A (1，－1)，B (－1,1)，且圆心M 在x ＋y －2＝0上．(1)求圆M 的方程；(2)设P 是直线3x ＋4y ＋8＝0上的动点，P A 、PB 是圆M 的两条切线，A 、B 为切点， 求四边形P AMB 面积的最小值．解：(1)设圆M 的方程为：(x －a )2＋(y －b )2＝r 2(r >0)，根据题意得：⎩⎪⎨⎪⎧ (1－a )2＋(－1－b )2＝r 2(－1－a )2＋(1－b )2＝r2a ＋b －2＝0，解得：a ＝b ＝1，r ＝2，故所求圆M 的方程为：(x －1)2＋(y －1)2＝4.(2)由题知，四边形P AMB 的面积为S ＝S △P AM ＋S △PBM ＝12|AM ||P A |＋12|BM ||PB |.又|AM|＝|BM|＝2，|P A|＝|PB|，所以S＝2|P A|，而|P A|＝|PM|2－|AM|2＝|PM|2－4，即S＝2|PM|2－4.因此要求S的最小值，只需求|PM|的最小值即可，即在直线3x＋4y＋8＝0上找一点P，使得|PM|的值最小，所以|PM|min＝|3×1＋4×1＋8|32＋42＝3，所以四边形P AMB面积的最小值为S＝2|PM|2－4＝232－4＝2 5.。