141有理数的乘法法则

有理数的四则运算法则
有理数是指可以表示为两个整数的比值的数，包括正整数、负
整数、零和分数。

有理数的四则运算包括加法、减法、乘法和除法，下面将详细介绍有理数的四则运算法则。

一、有理数的加法
1. 同号相加：两个正数相加，结果为正数；两个负数相加，结
果为负数。

例如：3 + 5 = 8，(-3) + (-5) = -8。

2. 异号相加：一个正数和一个负数相加，结果的绝对值等于两
个数的绝对值之差，符号取绝对值大的数的符号。

例如：3 + (-5) = -2，(-3) + 5 = 2。

二、有理数的减法
有理数的减法可以转化为加法，即a - b = a + (-b)。

例如：
3 - 5 = 3 + (-5) = -2。

三、有理数的乘法
1. 同号相乘：两个正数或两个负数相乘，结果为正数。

例如：3 * 5 = 15，(-3) * (-5) = 15。

2. 异号相乘：一个正数和一个负数相乘，结果为负数。

例如：3 * (-5) = -15，(-3) * 5 = -15。

四、有理数的除法
有理数的除法可以转化为乘法，即 a ÷ b = a * (1/b)。

例如：3 ÷ 5 = 3 * (1/5)。

需要注意的是，在有理数的除法中，除数不能为0，即 b ≠ 0。

以上就是有理数的四则运算法则，通过以上规则，我们可以轻
松地进行有理数的加减乘除运算。

希望以上内容能够帮助大家更好
地理解有理数的四则运算法则，提高数学运算能力。

有理数的运算法则
一、有理数的加减法法则：
1. 两个有理数同号，相加后仍为同号，即正加正得正，负加负
得负；
2. 两个有理数异号，相加后正数的绝对值大于负数的绝对值，
结果的符号与绝对值较大的数相同；
3. 有理数的加法满足交换律，即 a + b = b + a。

二、有理数的乘除法法则：
1. 两个有理数同号，相乘后为正，即正乘正得正，负乘负得正；
2. 两个有理数异号，相乘后为负，即正乘负得负，负乘正得负；
3. 有理数的乘法满足交换律，即 a × b = b × a；
4. 有理数相乘，可以先化简再计算，如分子分母都可以约去公
因数；
5. 有理数相除，可以先取倒数再进行乘法运算。

三、有理数的混合运算法则：
1. 先进行括号内的运算；
2. 依次进行乘除法；
3. 依次进行加减法。

四、有理数的运算与绝对值：
1. 一个有理数的相反数和该有理数的绝对值具有相同的绝对值；
2. 任何与零相等的有理数绝对值为零。

以上是有理数的运算法则，在进行数学运算时，请按照这些规
则进行操作，以确保得到正确的结果。

有理数四则运算法则
【原创实用版】
目录
1.有理数的加法法则
2.有理数的减法法则
3.有理数的乘法法则
4.有理数的除法法则
正文
有理数是指可以表示为两个整数之比的数，包括整数、分数和无理数。

在数学中，有理数的四则运算是非常基础和重要的内容。

下面我们将分别介绍有理数的加法、减法、乘法和除法法则。

1.有理数的加法法则
有理数的加法法则非常简单，只需将两个有理数的分子相加，分母保持不变。

如果相加得到的结果可以约分，那么应该将其约分为最简形式。

例如，对于两个分数 1/2 和 1/4，它们的和为 (1+1)/4=2/4，可以约分为 1/2。

2.有理数的减法法则
有理数的减法法则是将减数取相反数后与被减数相加。

例如，对于两个分数 1/2 和 1/4，它们的差为 1/2-(1/4)=1/2+(-1/4)=(2-1)/4=1/4。

3.有理数的乘法法则
有理数的乘法法则是将两个有理数的分子相乘，分母相乘。

如果相乘得到的结果可以约分，那么应该将其约分为最简形式。

例如，对于两个分数 1/2 和 1/3，它们的积为 (1*1)/(2*3)=1/6。

4.有理数的除法法则
有理数的除法法则是将除数的分子与被除数的分母相乘，分母与分子相乘。

如果相除得到的结果可以约分，那么应该将其约分为最简形式。

例如，对于两个分数 2/3 和 3/4，它们的商为 (2*4)/(3*3)=8/9。

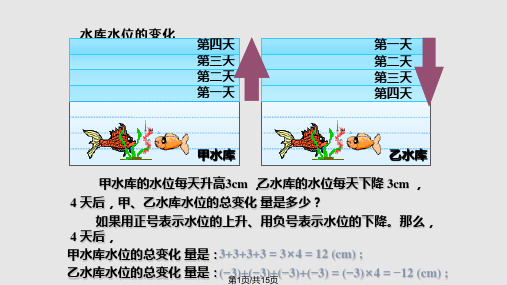
1 .4.1有理数的乘法（一）一、创设情境，引入新课说说小学我们学过了数的乘法的意义？比如说3×4，(1/5) ×10，……一个数乘以整数是求几个相同加数的简便运算，一个数乘以分数是求这个数的几分之几是多少？我们已经对正数及0的乘法运算很熟悉了，引入负数之后呢，有理数的乘法应该怎么运算？这节课我们就来学习有理数的乘法。

（板书课题）二、讲授新课问题：如图,一只蜗牛沿直线L爬行，它现在的位置恰好是L上的点O，求：（1）若蜗牛一直以每分2cm的速度向右爬行，3分后它在什么位置？（2）若蜗牛一直以每分2cm的速度向左爬行，3分后它在什么位置？（3）若蜗牛一直以每分2cm的速度向右爬行，3分前它在什么位置？（4）若蜗牛一直以每分2cm的速度向左爬行，3分前它在什么位置？规定：向左为负，向右为正，同样规定：现在前为负，现在后为正。

学生回答：（1）3分钟后蜗牛应在O点的右边6cm处。

可以表示为：(＋2)×(＋3) ＝＋6;(2) 3分钟前蜗牛应在O点的右边6cm处。

可以表示为：(－2)×(－3) ＝6(3) 3分钟后蜗牛应在O点的左边6cm处。

可以表示为：(－2)×(＋3) ＝－6(4) 3分钟前蜗牛应在O点的左边6cm处。

可以表示为：(＋2)×(－3) ＝－6问题：当一个因数为０时,积是多少？学生回答：积为0根据上面结果可知：1.正数乘正数积为＿＿数;负数乘负数积为＿＿数;2.负数乘正数积为＿＿数;正数乘负数积为＿＿数;3.乘积的绝对值等于各乘数绝对值的＿＿.4.零与任何数相乘或任何数与零相乘结果是。

师生归纳：1、有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；2、任何数同0相乘，都得0。

讨论：(1)若a＜0,b＞0,则ab 0 ;(2)若a＜0,b＜0,则ab 0 ;(3)若ab＞0,则a、b应满足什么条件？(4)若ab＜0,则a、b应满足什么条件？随堂练习：典例精析：（1）9×6 （2）（－9）×6 （3）3×（－4）（4）（－3）×（－4）注意：1、上面的法则是对于只有两个因子相乘而言的。