并联机构

3-UPUUPU并联机构刚度求解与优化的开题报告
1. 研究目的
UPU并联机构被广泛应用于机器人领域，其具有结构简单、运动灵活、刚度高等优点。

然而，UPU并联机构的刚度受到其结构特性的限制，因此需要进行刚度的求解和优化。

本研究旨在通过理论分析和仿真实验
的方式，对UPU并联机构的刚度进行求解和优化，为其在工程实践中的
应用提供理论依据。

2. 研究内容
（1）UPU并联机构刚度的理论分析：根据UPU并联机构的特点和
运动规律，推导其刚度表达式，分析其刚度特性和影响因素。

（2）UPU并联机构刚度的仿真实验：采用SolidWorks和ADAMS软件对UPU并联机构进行建模和仿真，验证理论分析结果的正确性，并进
一步探究结构优化的方向。

（3）UPU并联机构的刚度优化研究：根据理论分析和仿真实验结果，分析UPU并联机构的设计缺陷和不足，提出刚度优化的方向，进一步改
进其结构、材料等方面的参数。

3. 研究意义
UPU并联机构是机器人领域中常用的一种六自由度并联机构，其刚
度对机器人的性能和精度影响极大。

本研究通过理论分析和仿真实验的
方式，深入研究了UPU并联机构的刚度特性和影响因素，提出刚度优化
的方向，对机器人领域的精度控制、运动规划等方面的研究具有重要的
理论意义和实际应用价值。

并联机构工作空间方法的分析引入并联机构的定义以及其具有的优点。

相对串联机构，并联机构刚性好，具有高的稳定性;惯性较小、动态响应好、累积误差小等特点成为学者的研究热点。

并联机构的工作空间是机构性能的重要指标。

文中总结并联机构工作空间求解的方法以及各种方法的特点及区别，为并联机构的应用和研究提供理论意义和实用价值。

标签：并联机构;工作空间;求解方法并联机构是机械、电子及计算机控制相结合的产物，是机器人学的一个重要分支。

并联机构的定义：由2个或2个以上的独立运动链连接动平台和静平台，通过并联方式驱动的闭环系统。

与串联机构相比，并联机构具有的优点：闭环支链结构刚度大，稳定性较好;运动惯性小、动态响应快、累积误差小、精度较高等;其中对于完全对称的并联机构具有较好的各向同性，可以避开机构的奇异点等，使得并联机构得到广泛的应用及发展[1]。

最早并联机构由学者Stewart提出的6自由度Stewart平台机构，该机构具有输出精度高，承载能力强以及易于控制，将其应用在飞行三维空间模拟器中。

由学者Fichter和Sugimoto将此平台用于操作器和力矩传感器。

并联机构中包含一类自由度小于6称少自由度并联机构，为并联机构中的重要分支[2]。

相对于6自由度并联机构，少自由度并联机构具有结构简单、造价低，易于控制优点。

Hunt提出一种3自由度并联平台机构，该并联机构动平台末端输出为2个转动自由度和1个移动自由度。

Gosselin提出了平面和球面3自由度机器人。

黄真和赵铁石综合出一种4-URU对称4自由度并联机构，可以实现3个移动自由度和1个转动自由度。

少自由度并联机构适合应用在模块化可重组制造系统中。

可用来构造串、并联机构、微动机构特殊用途机器人，从而进一步促进并联机构的实用性。

1 并联机构工作空间的定义及分类并联机构的工作空间定义[3]为：当给并联机构的驱动构件输入驱动时，动平台输出末端的参考点的所有运动区域，也即为此并联机构的工作空间。

并联机构总结CNKI 2011.6-2011.12题目：3-PPRR并联分拣机器人机构的运动学建模与仿真（2011.6）优点及用途：与串联机构相比, 3-PPRR 并联机构将驱动装置安装在机架上, 在很大程度上降低了机构的质量, 使动平台能够获得很高的速度和加速度。

因此3-PPRR 并联机器人在轻工业领域中的高速分拣、抓放等操作方面具有明显优势。

模型：图1 3-PPRR并联机构图2单支链示意题目：3-PRRU并联机构的解析雅可比矩阵优点及用途：模型：题目：3 － PRR 平面并联机构精度分析优点及用途：模型：题目：3-PRR微动操作机器人刚度及工作空间分析优点及用途：模型：题目：3 － PRS 并联式钻尖刃磨机床运动学研究优点及用途：模型：题目：3 PTT 串并联数控机床构型设计与位姿分析优点及用途：模型：题目：3-RPS 并联机构运动与静力特性分析*优点及用途：模型：题目：3—RRC 机器人的动力学分析探究优点及用途：模型：题目：3 － RRR 型并联机构运动学研究优点及用途：模型：题目：3- RUC 并联机构的运动分析优点及用途：该机构对称性好, 加工方便、造价低且易于控制。

模型：题目：3-UPS/S 并联转台球铰链的优化研究优点及用途：模型：题目：3-UPU-SPS 并联机构及关节的分析*优点及用途：提出了一种新型三平移一转动4 自由度空间并联机构，分析了机构运动输出特性，并计算了机构的自由度和耦合度，给出了该并联机构的正、反解，并讨论了该机构的工作空间。

模型：题目：3DOF 并联机构的分析优点及用途：模型：题目：优点及用途：模型：题目：4SPS+ UPU 并联机床法向加工自由曲面的研究与仿真优点及用途：模型：题目：6-PU S/ UPU 并联机器人冗余驱动力控制仿真优点及用途：模型：题目：6-RSS并联机构的运动学、动力学分析优点及用途：模型：题目：6-TPS 并联坐标测量机结构设计与实体建模优点及用途：模型：题目：PRS- XY 混联数控机床运动学仿真件开发优点及用途：模型：题目：RRR UPRR RPUR 球面转动并联机构运动学分析优点及用途：模型：题目：Tricept 并联机构的奇异性分析优点及用途：模型：题目：Tripod 并联定位器刚度分析及其在飞机装配中的应用优点及用途：模型：题目：并联６－ＵＰＳ稳定平台瞬态分析与谱分析优点及用途：模型：题目：车辆并联机构座椅三维减振研究优点及用途：模型：题目：3－RRR 并联机优点及用途：模型：题目：二平移并联机构位置分析及运动学仿真优点及用途：模型：题目：基于Adams 的3-( 2SPS) 并联机构的配重平衡分析优点及用途：模型：题目：基于ADAMS的3-P4R并联打磨机器人运动学仿真优点及用途：模型：题目：基于Matlab技术的4-RP（RR）R并联机构的运动仿真优点及用途：模型：题目：基于反螺旋理论的2-PTR＆PSR 并联机器人的奇异位形研究优点及用途：模型：题目：一种新型6PTS并联机器人工作空间分析优点及用途：模型：题目：一种新型３－ＲＰＲ并联机构及其运动学分析优点及用途：模型：题目：二自由度球面并联换档机构运动学分析及仿真优点及用途：模型：题目：风洞模型并联机构工作空间分析与仿真优点及用途：模型：题目：混合驱动柔索并联机器人的设计与分析优点及用途：模型：题目：混联式石材加工机械手3-TPS/TP型工作头的运动特性分析优点及用途：模型：题目：基于概率分布的3-UPU 机构误差影响敏感度*优点及用途：模型：题目：基于几何法的3-PCR 平移并联分拣机器人工作空间研究优点及用途：模型：题目：髋关节试验机中3SPS+1PS并联机构有限元分析优点及用途：模型：题目：一种3-PRP共平面并联微动平台的研究优点及用途：模型：题目：优点及用途：模型：题目：一种2SPS + UPR 并联机构的位置与工作空间分析优点及用途：模型：题目：一种新型2T2R 并联机构及其运动学分析优点及用途：模型：题目：一种新型3-UPS 并联机构及其工作空间分析优点及用途：模型：题目：一种2PUU+ 2PUS 并联机构的位置与工作空间分析优点及用途：模型：题目：一种两转动一平移并联机构的运动学分析优点及用途：模型：题目：新型并联运动振动筛的筛分效率及其试验研究*优点及用途：模型：题目：平面2 自由度并联机构弹性振动的最优控制优点及用途：模型：题目：优点及用途：模型：题目：优点及用途：模型：题目：优点及用途：模型：。

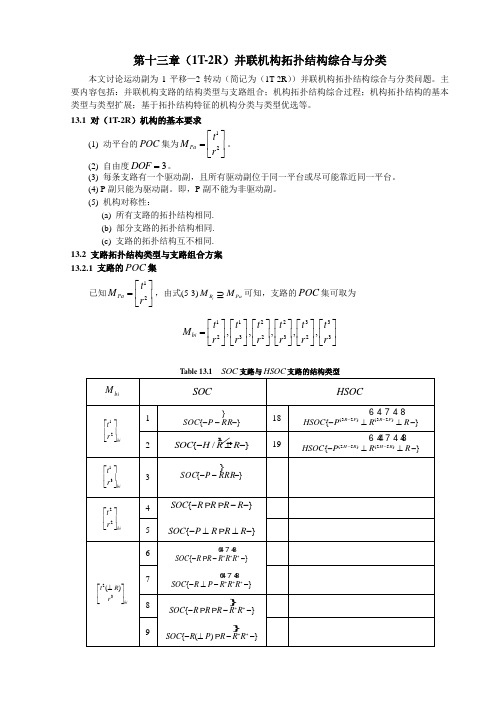
第十三章（1T-2R）并联机构拓扑结构综合与分类本文讨论运动副为1平移—2转动（简记为（1T-2R））并联机构拓扑结构综合与分类问题。

主要内容包括：并联机构支路的结构类型与支路组合；机构拓扑结构综合过程；机构拓扑结构的基本类型与类型扩展；基于拓扑结构特征的机构分类与类型优选等。

13.1 对（1T-2R）机构的基本要求(1) 动平台的POC集为12PatMr⎡⎤=⎢⎥⎣⎦。

(2) 自由度3DOF=。

(3) 每条支路有一个驱动副，且所有驱动副位于同一平台或尽可能靠近同一平台。

(4) P副只能为驱动副。

即，P副不能为非驱动副。

(5) 机构对称性：(a) 所有支路的拓扑结构相同.(b) 部分支路的拓扑结构相同.(c) 支路的拓扑结构互不相同.13.2 支路拓扑结构类型与支路组合方案13.2.1 支路的POC集已知12PatMr⎡⎤=⎢⎥⎣⎦，由式(5-3)iB PaM M⊇可知，支路的POC集可取为112233232323,,,,,bit t t t t tMr r r r r r⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦Table 13.1 支路与支路的结构类型(25)}H RR R-⊥-}R R R--}R R R⊥⊥-}R R R R***--}P R R R***⊥--}R R R R**--)P R R R*⊥-((,*))R R ◊**}R R R R --**}R P R R ---3t ⎡⎤ {}SOC H S S ----13.2.2 简单支路的结构类型由上节得到的支路的6种POC 集，简单支路(SOC )的结构类型可从表(8-1)的dim.()S DOF M =中直接选取，如表13.1的No.1-No.19所示。

13.2.3 复杂支路的结构类型仅讨论只含一个回路的复杂支路(HSOC)的结构类型。

(1) 含平面五杆(32)R P -回路的复杂支路在平面五杆(32)R P -回路的连架13R R 、副之间, 串联一个转动副2R ，得到一个含平面五杆(32)R P -回路的HSOC 支路，如图13-1所示，记为(32)(32){}R P R P HSOC P R R ---⊥⊥-(表13-1之No.18)，该HSOC 支路的POC 集为12bi t M r ⎡⎤=⎢⎥⎣⎦。

并联机构雅可比矩阵的求法及其计算精度研究并联机构雅可比矩阵的求法及其计算精度研究随着机器人技术的不断发展，机构的并联化设计越来越重要，而雅可比矩阵作为描述机构运动状态的重要工具，其精度的确保对于机构的运动控制和优化至关重要。

本文研究了并联机构雅可比矩阵的求法及其计算精度，为机构的设计和控制提供一定的理论参考。

用于求解并联机构雅可比矩阵的方法主要有两种：解析法和数值法。

解析法是根据机构的几何结构及其运动学方程，直接推导出雅可比矩阵的表达式。

但是这种方法的局限性很大，只适用于几何结构简单的机构，对于复杂的机构无法直接求解。

而数值法则是通过数值微分的方法，近似求解机构的雅可比矩阵，可以适用于各种类型的机构。

本文首先介绍了并联机构的基本概念和运动学方程，然后详细阐述了解析法和数值法两种求解雅可比矩阵的方法及其优缺点。

在此基础上，本文又针对数值法中常用的有限差分法和基于逆向微分的方法进行了比较，分析了它们的精度和计算速度。

研究表明，基于逆向微分的方法计算速度更快，精度更高，但需要对机构进行求导，且对于动态模型的求解不适用。

而有限差分法则是一种通用、易于实现的方法，适用于各种机构及其动态模型，但需要更小的步长和更高的阶数以保证精度。

最后，通过对比实验验证了不同方法的计算精度，并提出了提高并联机构雅可比矩阵计算精度的方法。

研究结果表明，在有限差分法中采用更高的阶数和更小的步长，能够有效提高计算精度，同时在基于逆向微分的方法中，采用更高的多项式阶数和更小的时间窗口，也能够提高计算精度。

总之，本文对并联机构雅可比矩阵的求法及其计算精度进行了研究和探索，提供了一定的理论基础和实验验证，为机构的设计和控制提供了参考。

但是，由于机构的复杂性和多样性，对于不同的机构类型和控制需求，需要采用不同的方法进行求解，并结合实际情况进行优化。