2014年春季学期新版新人教版七年级数学下册8.3实际问题与二元一次方程组学案3
- 格式:doc
- 大小:137.50 KB
- 文档页数:2


8.3.1实际问题与二元一次方程组简介:本节课的内容是人教版义务教育教科书《数学》七年级(下)§8.3实际问题与二元一次方程组,主要内容是掌握用二元一次方程组解决实际问题,了解二元一次方程组是解决实际问题的非常有效的数学模型.在本节学习之前,学生在学习消元法解二元一次方程组的同时已经接触过一些应用问题,学生已经对应用二元一次方程组解实际问题有了一定的认识,会用二元一次方程组表示问题中的数量关系。
本节内容是探究用二元一次方程组解决生活中有关总量和数字的实际问题,使学生能够熟练地用二元一次方程组解决此类问题,使学生会根据实际问题中的数量关系列方程组解决问题。
教材分析本节课是用二元一次方程组解实际应用问题,深入理解方程组的应用思想,通过对有关总量和数字的问题的探究解决,使学生进一步掌握二元一次方程组的应用。
老师要引导学生分析总结归纳,让学生熟练掌握用二元一次方程组解实际问题的一般步骤。
本节课教学重点为:分析实际问题,并列二元一次方程组解决。
教学难点:分析实际问题,寻找问题中的等量关系列方程。
教学目标1、知识与技能经历如何列二元一次方程组解实际问题的探究过程.2、过程与方法熟练掌握列方程组解实际问题的一般步骤,培养和提高学生运用方程组模型分析并解决实际问题能力。
3、情感态度与价值观进一步体会方程是刻画现实世界的有效数学模型重点难点教学重点:用代入法、加减法解二元一次方程组. 教学难点:会用二元一次方程组解决实际问题教学方法引导比较发现法、小组合作探究法。
教学准备教学过程设计程序时间创教师行为期望的学生行为(要素)设情景创设情境引入新课8分钟创设问题情境知识回顾1复习解二元一次方程组及练习解简单的实际问题。
2.前面我们已经学习了二元一次方程组的解法,也初步接触了列二元一次方程组解应用题.列二元一次方程组解应用题的一般步骤是什么?第一、理解题意并设未知数;(怎么设?)第二、找等量关系并列方程组;(怎么列?)第三、解方程组,检验是否符合实际;(为什么要检验呀?)第四、回答实际问题。
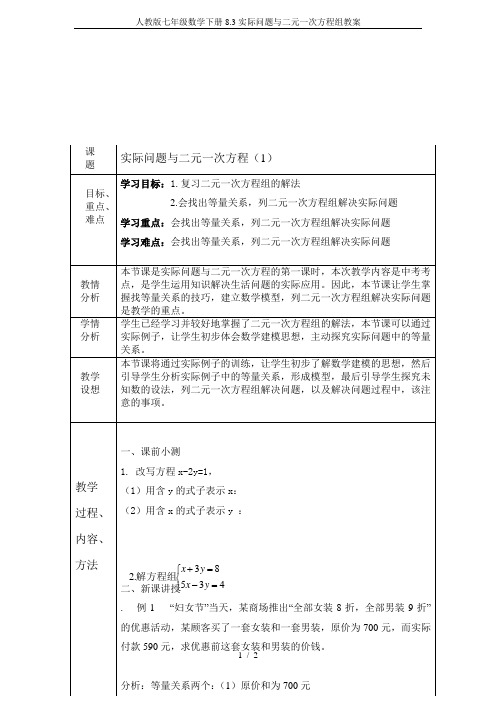



8.3 实际问题与二元一次方程组第1课时【教学目标】知识技能目标1.能够找出实际问题中的已知数和未知数,分析它们之间的等量关系,列出方程组,并解决生活中一些实际问题.2.在列方程组的建模过程中,强化方程的模型思想.过程性目标让学生进一步经历和体验列方程组解决实际问题的过程,体会方程(组)是刻画现实世界的有效数学模型,培养学生数学应用能力.情感态度目标通过列方程组解决实际问题,培养应用数学意识,提高学习数学的趣味性、现实性、科学性.【重点难点】重点:根据简单应用题的题意列出二元一次方程组.难点:将实际情景中的数量关系抽取出来,并用二元一次方程组表示.【教学过程】一、创设情境知识回顾:列二元一次方程组解决实际问题的一般步骤是什么?进一步提问:如何解二元一次方程组的应用问题?解决实际问题的基本思路:二、新知探究探究点1:和差倍分问题例题讲解例1 (教材P99【探究1】)请同学们讨论以下各题:(1)你有什么办法检验李大叔估计的值是否准确?(2)问题中有几个未知数?(3)能写出题目中的等量关系吗?(4)能用等式表示出来吗?引导学生独立思考,培养学生自主学习的能力.让学生自己动手解答问题,检验知识的掌握情况.【方法指导】解答“和、差、倍、分”问题要善于抓关键词,如“谁比谁大、小、多、少,谁是谁的几倍或几分之几.在谁的基础上增加或减少”等,分析题意,准确找出等量关系.探究点2:行程问题例2 1.(教材P101习题8.3 T2变形)一艘轮船顺流航行时,每小时行32 km;逆流航行时,每小时行28 km,则轮船在静水中的速度是每小时行_______km.(轮船在静水中的速度大于水流速度)2.甲乙两人在400 m的环形跑道上练习赛跑,如果两人同时同地反向跑,经过25秒第一次相遇;如果两人同时同地同向跑,经过250秒甲第一次追上乙.则甲、乙两人的平均速度分别是每秒_______m.要点归纳:环形问题的等量关系1.同时同地反向跑:(v甲+v乙)×t相遇=环长.2.同时同地同向跑:(v甲-v乙)×t追上=环长.解决顺逆流(风)行程问题常用的两个等量关系1.往返路程相等,即顺流(风)速度×顺流(风)时间=逆流(风)速度×逆流(风)时间.2.轮船(飞机)本身速度不变,即顺流(风)速度-水(风)速度=逆流(风)速度+水(风)速度.【方法技巧】行程问题中的两个重要相等关系(1)相遇问题:两人各自走的路程之和等于两地间的距离.(2)追及问题:两人同地不同时,同向而行,直至后者追上前者,两人所走路程相等;两人同时不同地,同向而行,直至后者追上前者,两人所走路程差等于两地的距离.例3 (教材P99探究2)问题1:本题研究的是长方形面积的分割问题,你能画出示意图帮助自己理解吗?问题2:长度涉及的数量关系?问题3:产量比与种植面积的比有什么关系?问题4:你能根据数量关系列出方程组,并解决这个问题吗?问题5:你还能设计其他种植方案吗?三、检测反馈1.甲、乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )A. B.C. D.2.某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1 225元,设其中有x张成人票,y张儿童票,根据题意,下列方程组正确的是 ( )A. B.C. D.3.我校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y 组,则列方程组为( )A. B.C. D.4.如图,用12块相同的小长方形瓷砖拼成一个大的长方形,则每个小长方形瓷砖的面积是( )A.175 cm2B.300 cm2C.375 cm2D.336 cm25.某校去年有学生1000名,今年比去年增加5.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x名,走读学生y名,则可列出方程组为_______.6.一个两位数,个位上的数字比十位上的数字大4,交换位置后,所得的新两位数比原两位数的4倍少9,则原两位数是_______.7.为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一);某农户承包了一片山坡地种树种草,所得到国家的补偿如表(二),问:该农户种树、种草各多少亩?表(一)种树、种草每亩每年补粮补钱情况表表(二)该农户收到乡政府下发的种树种草亩数及年补偿通知单8.甲、乙两人从相距36 km的两地相向而行,如果甲比乙先动身2 h,那么他们在乙动身2.5 h后相遇;如果乙比甲先动身2 h,那么他们在甲动身3 h后相遇,问甲、乙两人每小时各走多少km?四、本课小结这节课学了什么知识?列二元一次方程组解决实际问题的一般步骤(1)审题.(2)设两个未知数,找两个等量关系.(3)根据等量关系列方程,联立方程组.(4)解方程组.(5)检验并作答.五、布置作业课本第101页第1,2,3题六、板书设计七、教学反思在这节课之前的学习中,学生已经掌握了用方程组表示问题中的条件及解方程组的相关知识,而且探究了用方程组解决具有现实意义的实际问题.(比如92页例2、95页例4).这一节安排了两个实际问题,这些问题比前面的问题更接近现实,数量关系相对比较隐蔽,因此这些问题的分析解决难度比以前的问题也要大些.这节课更为关注建立二元一次方程组数学模型的“探索”过程.它不仅为解决实际问题提供了重要的策略,而且为数学交流提供了有效的途径,它的模型化的方法,合理优化的思想意识为学生解决实际问题提供了理论上的科学依据.所以设计本节课的重点应该是使学生在探究如何用二元一次方程组解决实际问题的过程中,进一步提高分析问题中的数量关系、设未知数、列方程组并解方程组、检验结果的合理性等能力,感受建立数学模型的作用.教学中我应该根据学生的实际,选取学生熟悉的背景,让学生体会数学建模的思想.在教学中应发挥学生自主学习的积极性,引导学生先独立探究,再进行合作交流.如有侵权请联系告知删除,感谢你们的配合!如有侵权请联系告知删除,感谢你们的配合!。
8.3《实际问题与二元一次方程组(2)》课后习题含答案1.木工厂有28名工人,每名工人一天加工桌子数与加工椅子数的比是9:20,现在如何安排劳动力能使生产的一张桌子与四个椅子配套.2.有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨.5辆大货车与6辆小货车一次可以运货35吨.则3辆大货车与5辆小货车,一次可以运货多少吨?3.足球表面是由一些呈正五边形和正六边形的皮块缝合而成的,共计32块,已知正五边形块数比正六边形块数的一半多2.问两种皮块各有多少?4.两个水池共存水40吨,如果再往甲池注进水4吨,再往乙池注进水8吨,则两池的水一样多,那么两池原来分别有水多少吨?5.用一根绳子环绕一棵大树,若环绕大树3周,则绳子还多4尺.若环绕大树4周,则绳子少了3尺,求这根绳子长多少尺?参考答案1.解:设安排x人加工桌子,安排y人加工椅子,由题可知:x+y=289x:20y=1:4解得: x=10y=18答:安排10人加工桌子,安排18人加工椅子可以使生产的1张桌子与4个椅子配套。
2.解:设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,由题可知:2x+3y=15.55x+6y=35解得: x=4y=2.5则3辆大货车与5辆小货车,一次可以运货的吨数为3×4+5×2.5=24.5(吨)答:3辆大货车与5辆小货车,一次可以运货24.5吨。
3.解:设正五边形x块,正六边形y块,由题可知:x+y=32½ y+2=x解得: x=12y=20答:正五边形12块,正六边形20块。
4.解:设甲水池原有水x吨,乙水池原有y吨,由题可知:x+y=40x+4=y+8解得: x=22y=18答:甲水池原有水22吨,乙水池原有18吨。
5.解:设绳子长为x尺,大树周长为y尺,由题可知:x-3y=44y-x=3解得: x=25y=7答:绳子长为25尺,大树周长为7尺。
8.3实际问题与二元一次方程组(第1课时)学案
编者:平邑仲里中学 公晓红 【学习目标】
1.知道用方程组解决实际问题的一般步骤.
2.会找出简单的实际问题中的数量关系,列出方程组,得出问题的解答.
【重点难点】 重点:会用列方程组的方法解决实际问题.
难点:会找出简单的实际问题中的数量关系.
【学前准备】
1.你还记得列方程解应用题的步骤吗?
(1)_______________
(2)_______________
(3)_______________
(4)_______________
(5)_______________
2.买12支铅笔和5本练习本,铅笔每支x 元,练习本每本y 元,共需4.9元,则列关于的二元一次方程是_____________________ .
3.30只大牛和15只小牛1天约用饲料675kg ,若每只大牛1天约用饲料x kg,,每只小牛1天约用饲料y kg ,列方程为____________________________ .又购进12只大牛和5只小牛,这时1天约用饲料940 k g ,此时列方程为 __________________________ .
【课中探究】 看一看 课本105页探究1 想一想 问题1:你能用自己的语言清晰、条理的把问题叙述一遍吗?
问题2:问题中有哪些已知量?哪些未知量?
问题3:问题中等量关系有哪些?
本题的等量关系是(1)30只大牛和15只小牛一天需用饲料为675kg
(2)____________________________________________ . 做一做 如何解这个应用题?
解:设每只大牛和每只小牛1天各约用饲料为x kg 和y kg
根据上面的两种情况的饲料用料,找出相等关系,列方程,得
_______________________________(1)_______________________________(2)⎧⎨⎩
解这个方程组得
⎩⎨⎧==__________________y x
答:每只大牛和每只小牛1天各约需饲料为20 kg 和5 kg ,因此饲养员李大叔估计每天大牛约需饲料18~20千克较准确,每只小牛一天约需饲料7~8千克偏高.
说一说
1.你认为应用方程组求解实际问题应该怎么做?
2.结合探究一和你的经验谈一下估算在计算中的作用.
【尝试应用】
有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨,3辆大车与5辆小车一次可以运货多少吨?
完成后与小组同学交流,说说你找出的等量关系.小组间交流.
【学习体会】
1.我的收获:
2.我的疑惑:
【当堂达标】
1.甲乙两数的和为10,其差为2,若设甲数为x,乙数为y,则可列方程组为
2.今年哥哥的年龄是妹妹的2倍,2年前哥哥的年龄是妹妹的3倍,求2年前哥哥和妹妹的年龄,设2年前哥哥x岁,妹妹y岁,依题意,得到的方程组是()
A.
23(2),
2
x y
x y
+=+
⎧
⎨
=
⎩
B.
23(2),
2
x y
x y
-=-
⎧
⎨
=
⎩
C.
22(2),
3
x y
x y
+=+
⎧
⎨
=
⎩
D.
23(2),
3
x y
x y
-=-
⎧
⎨
=
⎩
3.某学校现有甲种材料35㎏,乙种材料29㎏,制作A、B两种型号的工艺品,用料情况如下表:
(1)利用这些材料能制作A、B两种工艺品各多少件?
(2)若每公斤甲、乙种材料分别为8元和10元,问制作A、B两种型号的工艺品各需材料多少钱?。