同样签订“广场协议”,货币大幅升值100%以上,为什么只有日本败了,这个国家却安然无恙

函蜘郎长芒邻茶栩2023"-'2024学年安徽县中联盟高二10月联考数学试题考生注意：l．满分150分，考试时间120分钟。

2．考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B铅笔把答超卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

3．本卷命题范困：人教版必修第一册、第二册，选择性必修笫一册2.2结束。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的．L已知i是虚数单位，－a+bi=2b-i,a,bER，则la一如＝A．我B．戎 C.22．已知直线l的一个方向向批为（烈，－3），则直线l的倾斜角a=A. 30•B. so· c. 120° o. 1so03．在棱长为2的正方体ABCD-A心C1D1中，E、F,G、H分别为AIBl、B心、A1D1、BB1的中．盲盲点，则IGF+GH+2EGI=A../6B.2屈D../5C．月D.2我l4.已知直线l1y=-工+1与y轴交千点P，将l绕点P逆时针旋转45°后与工轴交千点Q，要使2直线l平移后经过点Q，则应将直线l1A．向左平移一个单位长度 16B．向右平移一个单位长度65C．向左平移一个单位长度 53 D．向右平移一个单位长度3一酝• 盲• • 5．巳知向批OA=(0,1,2),0B=（一1,0,l),0C=(2,1，入），若O,A,B,C共而，则0C在OB上的投影向址的桢为A.q B．我c．孚过6．光线通过点A(2,3)，在直线l,工＋y+l=O上反射，反射光线经过点B(2,2)，则反射光线所.(f: ·1'［线方程为A. 6:r-5y-2=0C. 5:r－6y+2=0认6.1·+Sy-22=0D.釭＋6y-22=0［抖二J O丿l联打·数学卷第1页（共4页）RJ】4048B7.已知向俅a=(2,1),b= (0,2),c=（一1,1)，集合A=｛，m m=a＋入b},B={nl n=b+入2c}，其中入1山ER，则A.AnB=0B.An B={2,0}C．若d EAn B，则（a，心为钝角D．若dEA nB，则l b=d2＆已知a=/1了一』了，b=6斗，c=logs3-¾log克则9A.a<b<cB. b<c<aC. b<a<cD. c<a<b二、选择题：本题共4小题，每小题5分，共20分。

2. Role play the conversation in front of the class.
一、单项选择
1.—___A_____people travel every year?
—Perhaps when we are talking about it, more than
100 planes have taken off around the world.
8.How many c_l_a__s_s_e_s_(class) do you have at school? 9.I buy crayontso________(paint)． 10.How about _mp_ia_xi_in_nt_g__(mix) these colours?
本节课主要学习了以下重点内容: （1）重点单词：want, paint, make, look等。 （2）重点短语：mix…and…, in the sky等。 （3）重点句式：I don’t like red. How about…?
3.MiHxowbltuoemaankde ygerleleonw?.
I am a rainbow. Look at me.
How many colors do you see?
I am red, orange and blue.
I am green, yellow and purple, too.
want之后加动词不 the park
定式to do表示想 tomorrow.我想明
做某事。
天去公园。
want sb. to do I want Jenny to
sth.想让某人做某 go with me.我想
事。
让詹妮和我一起

苏科版七年级数学下册直线平行的条件和探索【直线平行的条件和性质】【学习目标】1.同位角、内错角、同旁内角的识别；2.会判定两条直线平行；3.平行线的性质.【基础知识梳理】1．如图，同位角的是；内错角的是；同旁内角的是．2．直线平行的条件：（1）基本事实：，两直线平行；（2）定理：，两直线平行；（3）定理：，两直线平行．3．平行线的性质：（1）基本事实：两直线平行，；（2）定理：两直线平行，；（3）定理：两直线平行，．【典型例题】一、三线八角模型例1：如图所示，同位角一共有对，分别是；内错角一共有对，分别是；同旁内角一共有对，分别是．【变式】已知：如图是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角．跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如：从起始位置∠1跳到终点位置∠3写出其中两种不同路径，路径1：∠1一同旁内角→∠9一内错角→∠3．路径2：∠1一内错角→∠12一内错角→∠6一同位角→∠10一同旁内角→∠3．试一试：（1）从起始∠1跳到终点角∠8；（2）从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点∠8？二、平行线的判定例2：如图，点E在AC的延长线上，给出四个条件：①∠1＝∠2；②∠3＝∠4：③∠A＝∠DCE；④∠D+∠ABD＝180°．其中能判断AB∥CD的有．（填写所有满足条件的序号）三、平行线的性质例3：如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，求图2中∠AEF的度数.【变式】如图，AB⊥BC，DC⊥BC，E是BC上一点，EM⊥EN，∠EMA和∠END的平分线交于点F，求∠F的度数.四、综合运用例4：填空并完成以下证明：已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H，求证：CD⊥AB．证明：FH⊥AB（已知）∴∠BHF＝．∵∠1＝∠ACB（已知）∴DE∥BC（）∴∠2＝．（）∵∠2＝∠3（已知）∴∠3＝．（）∴CD∥FH（）∴∠BDC＝∠BHF＝．°（）∴CD⊥AB．例5：（1）如图(1)，若∠B+∠D＝∠BED，试猜想AB与CD的位置关系，并说明理由；（2）如图(2)，要想得到AB∥CD，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．【变式】问题情境：如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【拓展应用】例6：如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．【能力提升】1．如图所示，下列结论中不正确的是（）A．∠1和∠2是同位角B．∠2和∠3是同旁内角C．∠1和∠4是同位角D．∠2和∠4是内错角2．在同一个平面内，不相邻的两个直角，如果它们有一条边共线，那么另一边互相（）A．平行B．垂直C．共线D．平行或共线3．如图，F A⊥MN于A，HC⊥MN于C，指出下列各判断中，错误的是（）A．由∠CAB＝∠NCD，得AB∥CD B．由∠DCG＝∠BAC，得AB∥CDC．由∠MAE＝∠ACG，∠DCG＝∠BAE，得AB∥CD D．由∠MAB＝∠ACD，得AB∥CD4．如图，在△ABC中，以点C为顶点，在△ABC外画∠ACD＝∠A，且点A与D在直线BC的同一侧，再延长BC至点E，在所作的图形中，∠A与是内错角；∠B与是同位角；∠ACB与是同旁内角．5．如图，已知∠1＝（3x +24）°，∠2＝（5x +20）°，要使m ∥n ，那么∠1＝ （度）．6．如图，BE ∥CF ，则∠A +∠B +∠C +∠D ＝ 度．7.如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，求∠2的度数.8.（1）如图①，若∠B +∠D ＝∠BED ，试猜想AB 与CD 的位置关系，并说明理由；（2）如图②，要想得到AB ∥CD ，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．9.如图，AD ∥BC ，∠DAC ＝120°，∠ACF ＝20°，∠EFC ＝140°．求证：EF ∥AD ．10.【探究】如图①，∠AFH 和∠CHF 的平分线交于点O ，EG 经过点O 且平行于FH ，分别与AB 、CD 交于点E 、C ．（1）若∠AFH ＝60°，∠CHF ＝50°，则∠EOF ＝ 度，∠FOH ＝ 度．（2）若∠AFH +∠CHF ＝100°，求∠FOH 的度数．【拓展】如图②，∠AFH 和∠CHI 的平分线交于点O ，EG 经过点O 且平行于FH ，分别与AB 、CD 交于点E 、G ．若∠AFH +∠CHF ＝α，直接写出∠FOH 的度数．（用含α的代数式表示）【能力提升】答案第1题 第3题 第4题 第5题 第6题1．如图所示，下列结论中不正确的是（）A．∠1和∠2是同位角B．∠2和∠3是同旁内角C．∠1和∠4是同位角D．∠2和∠4是内错角解：A、∠1和∠2是同旁内角，故本选项错误，符合题意；B、∠2和∠3是同旁内角，故本选项正确，不符合题意；C、∠1和∠4是同位角，故本选项正确，不符合题意；D、∠3和∠4是内错角，故本选项正确，不符合题意；故选：A．2．在同一个平面内，不相邻的两个直角，如果它们有一条边共线，那么另一边互相（）A．平行B．垂直C．共线D．平行或共线解：如图所示：不相邻的两个直角，如果它们有一条边共线，内错角相等，或同旁内角互补，那么另一边互相平行或共线．故选：D．3．如图，F A⊥MN于A，HC⊥MN于C，指出下列各判断中，错误的是（）A．由∠CAB＝∠NCD，得AB∥CDB．由∠DCG＝∠BAC，得AB∥CDC．由∠MAE＝∠ACG，∠DCG＝∠BAE，得AB∥CDD．由∠MAB＝∠ACD，得AB∥CD解：A、正确，同位角∠CAB＝∠NCD，故AB∥CD；B、错误，∠DCN＝∠BAC不是同位角，所以B不对；C、正确，∠MAE＝∠ACG，∠DCG＝∠BAE，可得同位角∠BAN＝∠DCN，故AB∥CD；D、正确，同位角∠MAB＝∠ACD，故AB∥CD．故选：B．4．如图，在△ABC中，以点C为顶点，在△ABC外画∠ACD＝∠A，且点A与D在直线BC的同一侧，再延长BC至点E，在作的图形中，∠A与是内错角；∠B与是同位角；∠ACB与是同旁内角．解：如图所示，∠A与∠ACD、∠ACE是内错角；∠B与∠DCE、∠ACE是同位角；∠ACB与∠A、∠B是同旁内角．5．如图，已知∠1＝（3x+24）°，∠2＝（5x+20）°，要使m∥n，那么∠1＝75（度）．解：如图所示：∠1+∠3＝180°，∵m∥n，∴∠2＝∠3，∴∠1+∠2＝180°，∴3x+24+5x+20＝180°，解得：x＝17，则∠1＝（3x+24）°＝75°．6．如图，BE∥CF，则∠A+∠B+∠C+∠D＝180度．解：如图所示，由图知∠A+∠B＝∠BPD，∵BE∥CF，∴∠CQD＝∠BPD＝∠A+∠B，又∵∠CQD+∠C+∠D＝180°，∴∠A+∠B+∠C+∠D＝180°.7.如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，求∠2的度数.解：如图，∵∠ACB＝90°∴∠1+∠3＝90°，∵∠1＝30°，∴∠3＝60°，∵a∥b，∴∠2＝∠3＝60°.8.（1）如图①，若∠B+∠D＝∠BED，试猜想AB与CD的位置关系，并说明理由；（2）如图②，要想得到AB∥CD，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．解：（1）AB∥CD，理由：如图（1），延长BE交CD于F．∵∠BED＝∠B+∠D，∠BED＝∠EFD+∠D，∴∠B＝∠EFD，∴AB∥CD；（2）∠1＝∠2+∠3．理由如下：如图（2），延长BA交CE于F，∵AB∥CD（已知），∴∠3＝∠EF A（两直线平行，同位角相等），∵∠1＝∠2+∠EF A，∴∠1＝∠2+∠3．9.如图，AD∥BC，∠DAC＝120°，∠ACF＝20°，∠EFC＝140°．求证：EF∥AD．证明：∵AD∥BC，∴∠DAC+∠ACB＝180°，∵∠DAC＝120°，∴∠ACB＝60°，又∵∠ACF＝20°，∴∠BCF＝∠ACB－∠ACF＝40°，又∵∠EFC＝140°，∴∠BCF+∠EFC＝180°，∴EF∥BC，∵AD∥BC，∴EF∥AD．10. 【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF ＝α，直接写出∠FOH的度数．（用含α的代数式表示）解：【探究】（1）∵∠AFH＝60°，OF平分∠AFH，∴∠OFH＝30°，又∵EG∥FH，∴∠EOF＝∠OFH＝30°；∵∠CHF＝50°，OH平分∠CHF，∴∠FHO＝25°，∴△FOH中，∠FOH＝180°－∠OFH－∠OHF＝125°；故答案为：30，125；（2）∵FO 平分∠AFH ，HO 平分∠CHF ，∴∠OFH ＝12 ∠AFH ，∠OHF ＝12∠CHF ． ∵∠AFH +∠CHF ＝100°，∴∠OFH +∠OHF ＝12 （∠AFH +∠CHF ）＝12×100°＝50°． ∵EG ∥FH ，∴∠EOF ＝∠OFH ，∠GOH ＝∠OHF ．∴∠EOF +∠GOH ＝∠OFH +∠OHF ＝50°．∵∠EOF +∠GOH +∠FOH ＝180°，∴∠FOH ＝180°－（∠EOF +∠GOH ）＝180°－50°＝130°．【拓展】∵∠AFH 和∠CHI 的平分线交于点O ，∴∠OFH ＝12 ∠AFH ，∠OHI ＝12∠CHI ， ∴∠FOH ＝∠OHI －∠OFH＝12（∠CHI －∠AFH ） ＝12（180°－∠CHF －∠AFH ） ＝12（180°－α） ＝90°－12α．。

淮南市2023届高三第二次模拟考试学试题数本试卷分为第I卷（选择题〉和第E卷〈非选择题〉两部分．考试时间120分钟．第I卷，．．．．．．． 3、N··一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，有且只有一项符合题目要求．1己知全集U=R ，集合A＝�eRly＝�｝，则CuA=<D . {x i x 三－1}C .{x lx 豆－1}B .{x lx <O }A .{x lx <-1}2己知复数z 满足（2-i)·z = i2023,(i 是虚数单位），则复数z 在复平面内所对应的点位于〉A.第一象限B.第二象限c.第三象限 D.第四象限3.四位同学各自在“五一”劳动节五天假期中任选一天参加公益活动，则甲在5月1日、乙不在5D .-25c 土25月1日参加公益活动的概率为（4 B. -54己知函数f(x )=A s 叫ω＋的，［A ＞阳〉喇〈立的相邻两个对称中心距离为2且图\2)象经过Ml 乏，A i ，若将f(x ）图象上的所有点向右平移至个单位长度得到函数g(x ）的图象，飞。

）6则函数g(x ）的单调递减区间是〈 B.[k π中π刽k eZ［叶，kπ叶ke ZA.D.[k 什叶十εZC.[k 7r,ktr +f J.k eZ〉〉汩。

A ..!_52,r5.在A ABC中，己知LACB＝一－，BC=4,AC=3,D是边AB的中点，点E满足3一－3一－1一一一一一『A E=-AB+-AC，则CD·DE=()4 4A.－三B.l c ..!.8 2 86.我国古代数学在宋元时期达到繁荣的顶点，涌现了一大批卓有成就的数学家，其中朱世杰与秦九韶、杨辉、李冶被誉为我国“宋元数学四大家”朱世杰著有《四元玉鉴》和《算学启蒙》等，在《算学启蒙》中，最为引人入胜的问题莫过于堆垛问题，其中记载有以下问题：“今有三角、四角果子垛各一所，共积六百八十五个，只云三角底子一面不及四角底子一面七个，问二垛底子一面几何？”其中“积”是和的意思，“三角果子垛”是每层都是正三角形的果子垛，自上至下依次有I,3, 6, 10, 15, ...，个果子，“四角果子垛”是每层都是正方形的果子垛，自上至下依次有L4, 9, 16, ...，个果子，“底子一面”指每垛最底层每条边”根据题意，可知该三角、四角果子垛最底层每条边上的果子数是〈（参考公式：川山·＋n2＝巾＋俨1))A.4,11B.5,12 c.6,137.如圈，αiβ，αnβ＝l,Aeα，Beβ，点A,B在棱l上的射影分别是码，B i，若AA1=BB1 =2, AB=4，则异面直线AB1与A1B所成角的余弦值为D.7,14A.主B.I第7题图5521c.一D.一338.定义在R上的函数f(x）满足f(-x)+f(x)+2cosx=0，当x�O时，J'(x)>sinx，则不等式f(x)+2cosx>f（π－x）的解集为A.(J, +co)B.（斗） c.（－咒） D.（一∞，π）二、多项选择踵I;I 尔踵共4,J、踵，每小题5分，共20分．在每小踵给出的选项中，有多项符合匾目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.己知单位向盘a,b ，则下列命题正确的是（A. (;i+b ）土（;i -b )B剖＝（－手，J.b -(coC若｜二－bl 川，记向盘二，5的夹角为θ，则θ的最小值为子’－－‘’霄『－．－D 若（a.b) ＝二，则向盘b栩如上的投影向盘是γ飞’I 3IO.己知圆M 的方程为：x 2+y 2+ax ＋咿－2a-4=o,(a εR ），点P(l,l ），给出以下结论其中正确的有（A.过点P 的任意直线与圆M都相交B若因l M 与直线川＋川无交点则ae （÷棉）C.四M 面积最小时的圆与圆Q:x 2+ y 2 +6x-10y+16=0有三条公切线D.无论。

0到100分设计测试用例摘要：一、测试用例设计的重要性1.软件测试的基本概念2.测试用例的作用3.测试用例设计的原则二、0到100分设计测试用例的方法1.等价类划分法2.边界值分析法3.错误推测法4.场景法5.因果图法6.判定表驱动法7.功能图法三、测试用例设计的实践与优化1.确定测试目标2.分析需求和功能3.选择合适的测试用例设计方法4.制定测试计划5.执行测试用例6.分析测试结果7.优化测试用例设计四、总结1.测试用例设计在软件测试中的重要性2.不同测试用例设计方法的优缺点3.如何提高测试用例设计的质量和效率正文：一、测试用例设计的重要性软件测试是保证软件质量的关键环节，而测试用例设计则是软件测试的核心。

测试用例是测试人员进行测试的依据，通过对软件的各种输入和操作进行验证，以发现潜在的缺陷和问题。

一个好的测试用例设计可以有效提高软件的质量和稳定性，减少开发和维护成本，提升用户体验和满意度。

二、0到100分设计测试用例的方法1.等价类划分法：将可能的输入数据分为相似的组，每组中的数据都能使被测程序产生相同的输出。

等价类划分法可以有效减少测试用例数量，提高测试效率。

2.边界值分析法：针对程序的边界条件进行测试，边界值分析法有助于发现程序在边界情况下的逻辑错误和异常行为。

3.错误推测法：基于程序员的经验和直觉，推测程序中可能存在的错误，设计测试用例进行验证。

4.场景法：根据实际场景和用户需求，模拟用户操作和程序运行过程，设计测试用例。

5.因果图法：通过分析程序输入与输出之间的因果关系，设计测试用例。

6.判定表驱动法：根据程序的逻辑判断条件，设计测试用例，用于验证程序的分支和循环逻辑。

7.功能图法：通过绘制程序功能图，分析各功能模块之间的接口和调用关系，设计测试用例。

三、测试用例设计的实践与优化1.确定测试目标：明确测试的目的和范围，为测试用例设计提供依据。

2.分析需求和功能：深入了解软件需求和功能，找出潜在的测试需求和风险点。

资料来自货车电器电子交流联盟总群65026188
欢迎同行加入交流只限货车电工加入
本群主修：欧曼、豪沃、德龙、解放系列、奥威、北奔重卡.解放J6、陕汽德龙、江淮、JAC、东风天龙、陕汽奥龙、豪沃A7、华凌、徐工汽车、三一重工、中国一托东方红、红岩杰狮、东风系列大型货车电路、车身自带电脑版、电子仪表、CAN、欧三电喷、等等。

解放J6锡柴电装系统故障码大揭密
资料来自货车电器电子交流联盟总群65026188
欢迎同行加入交流只限货车电工加入
本群主修：欧曼、豪沃、德龙、解放系列、奥威、北奔重卡.解放J6、陕汽德龙、江淮、JAC、东风天龙、陕汽奥龙、豪沃A7、华凌、徐工汽车、三一重工、中国一托东方红、红岩杰狮、东风系列大型货车电路、车身自带电脑版、电子仪表、CAN、欧三电喷、等等。

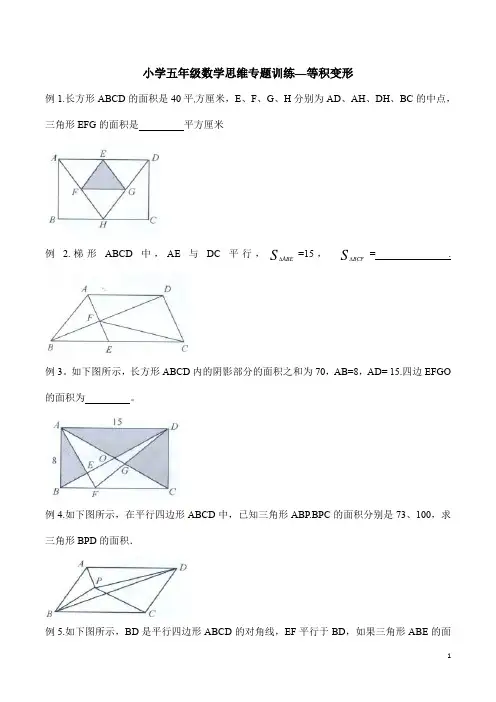
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米，E、F、G、H分别为AD、AH、DH、BC的中点，三角形EFG的面积是平方厘米例 2.梯形ABCD中，AE与DC平行，S ABE∆=15，S BCF∆= .例3。

如下图所示，长方形ABCD内的阴影部分的面积之和为70，AB=8，AD= 15.四边EFGO 的面积为。

例4.如下图所示，在平行四边形ABCD中，已知三角形ABP.BPC的面积分别是73、100，求三角形BPD的面积．例5.如下图所示，BD是平行四边形ABCD的对角线，EF平行于BD，如果三角形ABE的面积是12平方厘米，那么三角形AFD的面积是平方厘米。

例6.如下图所示，已知AE=EC，CD=DB，S ABC =60，求四边形FDCE的面积．例7.如右图所示，正方形ABC D和正方形ECGF并排放置，BF与CD相交于点H,已知AB=6厘米，则阴影部分的面积是平方厘米．例8.如下图所示，E、F、G、H分别是四边形ABCD各边的中点，EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积．试比较S1+S3与S2+S4的大小．例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份，长方形内任意一点与分点及顶点连结，如右图所示，则阴影部分的面积是 平方厘米．例10.右图所示ABCD 是个直角梯形（∠DAB=∠ABC= 900），以 ， AD 为一边向外作长方形ADEF ，其面积为6.36平方厘米，连接BE 交AD 于P ，再连接PC ．则图中阴影部分的面积是 平方厘米。

A.6.36B.3.18C.2.12D.1.59例11.如下图所示，平行四边形内有两个大小一样的正六边形，那么阴影部分的面积占平行四边形面积的 。

A ．21B ．32C ．52D ．125例12.如下图所示，矩形ABCD 的面积是24平方厘米，三角形ADM 与三角形BCN 的面积之和是7.8平方厘米，则四边形PMON 的面积是 平方厘米．例13.一个矩形分成4个不同的三角形（如下图），绿色三角形面积占矩形面积的15%，黄色三角形的面积是21平方厘米．问：矩形的面积是多少平方厘米？例14.如下图所示，正方形每条边上的三个点（端点除外）都是这条边的四等分点，则阴影部分的面积是正方形面积的。

like作动词时，意为“喜欢”；作介词时，意为“像”，可 与be或look连用。 eg：It is like a bird.
它像一只鸟。
5 difficult/'dɪfɪklt/ adj.困难的
辨析difficult和hard difficult与hard用作形容词时，均可表示“困难的”，其 反义词为easy。一般情况下能互换，但两者之间也有区别：
介词 用法
in
表示“月、季节、年、世纪”或泛指“上午、下午、晚 上”。eg：in May在五月，in the evening在晚上
表示“在具体的某一天”或“(在具体的某一天的)早上、
on
下午、晚上”等，“在星期几”或“在星期几的早上、下 午、晚上”等，“在某一节日”。eg: on Sunday morning
2：45读作：a quarter to three 表示“在某一时刻”，即“在某时间点”，应该用介词at。 eg：at three o'clock在3点钟
对时刻提问时，一般用what time。 eg：—What time is it now？现在几点了？
—It's half past seven.七点半。
3 maths/mæθs/n.数学
eg：Do you like maths？你喜欢数学吗？ maths是mathematics的缩写形式，英国英语中常用maths，美国英 语中常用math。 中学常见学科如下：Chinese语文 maths数学 English英语 physics 物理 chemistry化学 science科学 biology生物 politics政治 history历 史 geography地理 art美术 music音乐 PE (physical education)体育

结束语
若有不当之处，请指正，谢谢！
写作： 6 7
7在（个）位写上一写，，表示
读一读。
（ 7 ）个（ 一）。
读作： ___六_十___七___
67里面有（ 7 ）个一和（ 6 ）个十 2021/6/16
8
３５．２
1、看图写数。
百 十个 百 十个 百 十个
14
50 7 6
2021/6/16
9
３７.７
2、想一想，填一填。
27 28 29 30 31 32 33 34 35 36 37
2021/6/16
B 百位
C 个位
“95”这个数的最
高位是（ A ）
12
A 低
2021/6/16
B
C
高
个
读数和写数都
从（B ）位起。
13
A 左
2021/6/16
B
C
右
上
从（ B）边起，
第一位是个位， 第二位是十位，
14
23读作（二三 、 三十二 、二√十三）
90读作（九0、 九√十、
九）
58读作（五八、八十五、五√十八）
(2)写出3个个位是5的两位数。
１５、２５、３５
(3)写出4个十位是3的两位数。
３０、３１、３２、３３
2021/6/16
18
妹妹今年6岁，姐姐今年13岁，
50年后，姐姐比妹妹大( ７ )岁。 １３－６＝７（岁）
(探究题)填 空。
2021/6/16
19
2021/6/16
20
2021/6/16
21
16
填空
1、一个数个位上的数是3,十位 上的数比个位上的数多5,这个数

人教版七年级下册英语第二单元知识点归纳Unit 2 What time do you go to school?一、词汇与短语◆重点单词◆重点短语◆重点句子◆重点单词变形二、语法知识点A部分知识点1、 whattime/when引导的特殊疑问句在询问时间时，我们一般使用when或what time，表示什么时候或什么时间，他们有时能互相通用，但有些地方是不能通用的，区别很大。

◆问做某事的具体时间点（几点几分），两者可互换。

eg：— What time/when does he get up every morning？他每天早上什么时候起床？—At seven o'clock. 七点钟。

◆问钟表所指的具体时间时，就是问单纯的时间，几点几分，与事无关。

只能用what time。

eg：— Excuse me, what time is it？打扰一下，现在几点了？—It's 1 o'clock. 现在是1点钟了。

◆问事件发生的年份、月份、日期等，非钟点性时间，只能用when。

eg：—When is her birthday？她的生日什么时候？—It's on October 19th. 10月19日◆when可作连词，引导状语从语,“当……的时候”，但what time没有这种用法。

eg：My mother was cooking when I came back2、频度副词❶频度副词的含义：表示次数、频率的副词称为频度副词。

常用的频度副词按频率的高低依次为：always﹥usually﹥often﹥sometimes﹥seldom﹥hardly ever﹥nevereg：John always comes late. 约翰总是迟到。

He hardly ever exercises. 他几乎从不锻炼。

❷表示具体的频率、次数时,一次用once,两次用twice,三次及以上用“基数词+ times”表示。

日本食品农产品进口商名录香港进口商名录日本综合贸易商社ALC。

INC。

地址：东京都中央区新川1-23-5SHINKAWA-EAST，1-23-5，SHINKAWA，CHUO-KU，TOKYO Tel：0081-3-5541-2053 Fax：0081-3-5541-2140E-mail：YOUSIHARA@aicinc.co.jp社长：本村博志资本金：23，000万日元从业人数：175人设立：1979年1月业务内容：食品特色：消费物资输入各国（株）爱峰商会AIHOO TRADINGCO，LTD。

地址：奇玉县大宫市日进町3-493-23-493-2。

NISSHINCHO，OMIRATel：0081-48-668-5055 Fax：0081-48-668-1243社长：荻谷弘康复资本金：1，500万日元老派从业人数：4人设立：1983年6月业务内容：冷冻蔬菜等农业产业加工品特色：中国贸易的多年的业务经验有专业商社（株）葵源六甲AOLGEN-ROKKOCORP地址：京都府京都市南区久世高田町126Tel：0081-75-931-5525 Fax：0081-75-931-5584社长：杉山正义资本金：1000万日元老派从业人数：3人设立：1993年3月业务内容：食品青山贸易（株）http/AOYAMA TRADECO,LTD地址：兵车县姬路市青山14641464，AOYAMA，HIMEJI，HYOGOTel：0081-792-66-6035 Fax：0081-792-67—4624 E-mail:aoyamaz@siluer.ocn.ne.jp社长：赵善云资本金：1000万日元从业人数：15人设立：1992年10月业务内容：化学品（株）本铺AKACHAN HONPOCO，LTD地址：大阪府大阪市中央区南本町3-3-213-3-21 MINAMI-HONMACHI，CHUO-KU，OSAKATel：0081-6-6251-0625 Fax：0081-6-6251-3340社长：小原正司资本金：19000万日元从业人数：2700人设立：1941年2月业务内容：进口生活用品及生产资料朝阳贸易（株）ASAHI TRADINGCO，LTD地址：东京都中央区八丁堀4-10-4 白铜第一HKUDODALLTLBLDG，4-10-4，HATTYOBORL，CHUO-KU，TOKYO Tel：0081-3-3351-0771 Fax：0081-3-3351-2344社长：华井满资本金：9600万日元从业人数：50人设立：1968年9月业务内容：原料羽毛，进出口食品原料及健康食品（株）亚细亚交易AJAKOEKICO，LTD地址：大分县别府市原町18-2418-24，HARA-MACHI，BEPPU，OITATel：0081-977-21-0888 Fax：0081-977-21-2048 E-mail：tukasaki@mocha.ocn.ne.jp社长：圜田展久资本金：2000万日元从业人数：3人设立：1972年5月业务内容：进口竹制品制药（株）ASGENPHARMACEUTICAL CO，LTDhttp/www.asgen.cojp地址：爱知县名古屋市东区泉2-28-22-28-2，IZUML，HLGASHI-KU，NAGOYATel：0081-52-9031-1212 Fax：0081-52-931-1331E-mail:asgen@asgen.co.jp社长：水墅昌树资本金：1000万日元从业人数：60人设立：1968年1月业务内容：中药材，中成药，化工医药品，食品原料（株）甘栗太郎AMAGURITARO CO，LTD地址：东京都千代田区神田松永町1111，MATSUNAGACHO，KANDA，CHIYODA-KU，TOKYO Tel：0081-3-3251-9021 Fax：0081-3-3251-9280社长：田中康则资本金：1280万日元从业人数：130人设立：1956年11月业务内容：天津甘栗（株）新井清太郎商店SEITARO ARAICO，LTD地址：神奈川县横浜市中区尾上町1-81-8，ONOE-CHO-NAKA-KU，YOKOHANATel：0081-45-681-6729 Fax：0081-45-662-2357社长：新井光世资本金：2000万日元从业人数：100人设立：1888年4月业务内容：香辛料，辣椒干，脱水蔬菜，植物生产品，柳腾制品，轻工品。

版本变更记录版本号日期描述V1.0 2020年01月07日EG1205数据手册初稿目录1. 特性 (1)2. 描述 (1)3. 应用领域 (1)4. 引脚 (2)4.1 引脚定义 (2)4.2 引脚描述 (2)5. 内部电路图 (3)6. 典型应用电路 (4)7. 电气特性 (5)7.1 最大额定值 (5)7.2 典型参数 (6)8. 封装尺寸 (7)8.1 ESOP8封装尺寸 (7)EG1205芯片数据手册V1.01. 特性⏹双线性电源输出12V、5V⏹每路最大输出电流为100mA⏹低噪声⏹高纹波抑制比⏹温度保护⏹输出短路电流限制⏹集成过流保护三极管⏹集成功率三极管可驱动蜂鸣器、继电器2. 描述EG1205芯片内部集成2路线性电源、一个功率三极管可驱动蜂鸣器或继电器、一个保护三极管可做过流保护功能； 2路线性电源，其中一路12V输出，另一路5V输出，每路最大输出电流为100mA。

采用 ESOP8 的封装形式。

3. 应用领域⏹扭扭车控制器⏹平衡车控制器⏹电动车控制器⏹线性稳压源⏹声卡和电脑主板4. 引脚4.1 引脚定义图4-1. EG1205管脚定义4.2 引脚描述5. 内部电路图VINCO图5-1. EG1205内部电路图6. 典型应用电路VINMCU图6-1. EG1205典型应用电路图7. 电气特性7.1 最大额定值7.2 典型参数无另外说明:VIN=24V;TA=25℃; C1=C2=C3=1μF;8. 封装尺寸8.1 ESOP8封装尺寸。

版本变更记录版本号日期描述V1.0 2017年11月21日EG2104数据手册初稿V1.1 2017年11月23日输出电流能力修改目录1. 特性 (1)2. 描述 (1)应用领域 (1)3. 引脚 (2)3.1 引脚定义 (2)3.2 引脚描述 (2)4. 结构框图 (3)5. 典型应用电路 (3)6. 电气特性 (4)6.1 极限参数 (4)6.2 典型参数 (5)6.3 开关时间特性及死区时间波形图 (6)7. 应用设计 (7)7.1 Vcc端电源电压 (7)7.2 输入逻辑信号要求和输出驱动器特性 (7)7.3 自举电路 (8)8. 封装尺寸 (9)8.1 SOP8封装尺寸 (9)EG2104芯片数据手册V1.11. 特性⏹高端悬浮自举电源设计，耐压可达600V⏹适应5V、3.3V输入电压⏹最高频率支持500KHZ⏹低端VCC电压范围2.8V-20V⏹输出电流能力I O+/- 2A/2.5A⏹内建死区控制电路����输入通道低电平有效，关闭HO、LO输出。

⏹SD⏹外围器件少⏹静态电流小于1uA，非常适合电池场合⏹封装形式：SOP-82. 描述����功能的MOS管、IGBT管栅极驱动专用芯片，内部集成了逻辑信号输入处EG2104是一款高性价比的带SD理电路、死区时控制电路、电平位移电路、脉冲滤波电路及输出驱动电路，专用于无刷电机控制器、电源DC-DC中的驱动电路。

EG2104高端的工作电压可达600V，低端Vcc的电源电压范围宽2.8V～20V，静态功耗小于1uA。

该芯����内建了一个200K下拉电阻,在输入悬空时使上、下功率MOS 片输入通道IN内建了一个200K下拉电阻，SD管处于关闭状态,输出电流能力I O+/- 2/2.5A，采用SOP8封装。

3.应用领域⏹移动电源高压快充开关电源⏹无线充电驱动器变频水泵控制器⏹DC-DC电源⏹无刷电机驱动器⏹高压Class-D类功放4. 引脚4.1 引脚定义Vcc GNDSD图4-1. EG2104管脚定义4.2 引脚描述5. 结构框图LOGNDVccHOVS VB图5-1. EG2104内部电路图6. 典型应用电路+600VOUT图6-1. EG2104典型应用电路图7. 电气特性7.1 极限参数7.2 典型参数L7.3 开关时间特性及死区时间波形图图7-1. 低端输出LO 开关时间波形图图 7-2. 高端输出HO 开关时间波形图50%50%IN图7-3. 死区时间波形图8. 应用设计8.1 Vcc端电源电压针对不同的MOS管，选择不同的驱动电压，芯片电源电压范围2.8V-20V。

★了解同轴线的特性阻抗及分类。

1.4习题及参考解答[I. 1]设一特性阻抗为50 Q的均匀传输线终端接负4k/<=100 Q.求负我反对系数巧・在离负裁0.2入・0.25入及0.5入处的输入阳抗及反对系数分别为多少？解终端反射系数为=& - Z。

= 100 — 50 =丄11 _ K _ 100 + 50 _ T根拥传输线上任怠一恵的反肘糸数和输入阳抗的公贰r（z）= r lC ^和= z。

；兰：：二在离负载0.2入.0. 25A> 0.5入反射系数和输入阻抗分别为r（0.2A）= Y“初忌• r（0.25A）MZ.（0.2入）=29.43Z -23.79° Q・ Z in（0.25A） = 25 Q> Z lft（0.5A） = 100 Q[1.2]求内外导体直径分别为0.25 cm和0.75 cm的空气同轴线的持性阻抗。

若在两导体何塡充介电常数匕= 2.25的介质.求其特性阻抗及300 MHz时的波长。

解空气同轴线的持性阻抗为乙=60 In — = 65. 9 Qa塡充相对介电常数为€,=2.25的介质后.英持件阳抗为/=300 MHz时的波长为[1.3]设特性阻抗为乙的无耗传输线的址波比为"滾一个电爪波"•点离负我的距离为人讪.试证明此时终端负我应为r（0.5A） = Y证明根据输入阳抗公式Z： + jZ, tan" 乂Z o + jZ| tan/3 z在距负栈第一个波节点处的阻抗Z /（/“）=—P y Zl— j 乙I "1,3】Z.P将匕式整理即得17I318[I. 4] 何 持性阻抗为Z =50 Q 的无耗均匀传输线•导体间的媒质参敌为 £.=2.25 ・“, = 】，终瑞接仃&=】Q 的负我"/- 100 MHz 时•兀线长度为A/40试求： ①传输线实际长度'②负载终瑞反射系敌；③ 输入端反射系数'④ 输入瑞阻抗.解传输线上的波长= 2 m因而.传输线的实际长度/ = * = 0. 5 m4终瑞反射系数为…R]—Z 。

2023年人教版初中英语七年级上册Unit 5知识点讲义（含巩固练习）初中英语教研室整理Unit 5 Do you have a soccer ball?Section A1.Let’s = let us 译为“让我们...”Let (动词）“让”。

let常用在祈使句句首，常用短语为let sb. do sth. “让某人做某事”Eg: Let’s go to school together. “让我们一起去学校吧！”2.Go to + 地点表示去某地；但当后面的地点是home, here, there等地点副词时，to要省略Eg: go to Beijing “去北京”；go home “回家”；3.Be late “迟到”; be late for “迟到”Eg: I am late for school. “我上学迟到了。

”4.Get (动词) “得到；进入；抵达；懂了”等常用短语：get sb. to do “让某人做某事”Eg: I can’t get him to play the piano. “我无法让他弹钢琴。

”get sb./sth. Doing “让某人/物行动起来”Eg: I can’t get the car moving “我无法发动车子。

”get to “到达”Eg: I get to Beijing by plane. “我坐飞机到北京。

”Get up “起床”Eg: She gets up at 6:00 am. “她早上六点起床。

”Eg: I got your meaning. “我明白你的意思。

”Grammar语法：行为动词的一般现在时一、用法：（1）表示经常性或习惯性的动作或现在存在的状态（2）表示人的性格、能力、特征或爱好等。

（3）表示客观真理或普遍事实。

二、句式：（1）肯定句：主语 + 动词原形 + 其它Eg: I often go to school at 7:00.（2）否定句：主语+ don’t +动词原形 + 其它Eg: They don’t sing e very morning.（3）一般疑问句：Do + 主语 + 动词原形 + 其它肯定回答：Yes, 主语 + do. 否定回答：No, 主语+ don’t.Eg: Do they play football after school? Yes, they do./ No, they don’t.（4）特殊疑问句：疑问词 + do + 主语 + 动词原形 + 其它 ?Eg: What do you want to do?注意：1. 在一般现在时的句子中，行为动词前不能有be动词2. do除了作助动词，还可用作行为动词，译为“做”，变否定句时，不能再实义动词do后加not，要在前加don’t。

七年级百分比知识点总结本文档总结了七年级学生需要了解的百分比知识点。

一、百分比的概念百分比是一种表示比例或比率的方式，以百分数形式表示。

百分号（%）表示每一百的意思，通常用于表示一个数值相对于整体的比例或频率。

二、百分数的转换1. 将百分数转化为小数：将百分数除以100，即可得到相应的小数。

例如，75%可以转化为0.75。

2. 将小数转化为百分数：将小数乘以100，并加上百分号即可。

例如，0.8可以转化为80%。

3. 将百分数转化为分数：将百分数的值除以100，并将分子写在分数的上方，分母为100。

例如，25%可以转化为25/100或1/4。

三、百分比之间的关系1. 百分数增长：当一个数值增加了百分之几，可以通过将原数值乘以1加百分数的值来计算。

例如，将100增加20%，可以计算为100 * (1+0.20) = 120。

2. 百分数减少：当一个数值减少了百分之几，可以通过将原数值乘以1减去百分数的值来计算。

例如，将80减少30%，可以计算为80 * (1-0.30) = 56。

四、百分比的应用百分比在日常生活中有着广泛的应用。

例如：1. 购物打折：商家常常以百分比方式打折，让消费者享受更优惠的价格。

2. 考试成绩：考试成绩通常以百分数表示，便于学生了解自己的得分情况。

3. 统计数据：百分比用于表示调查结果、人口比例等统计数据，便于比较和分析。

总结：百分比是一种表示比例或比率的方式，通过将数值转化为百分数或小数来表示。

了解百分比的转换和计算方法，以及百分比之间的关系，有助于我们在日常生活和研究中更好地应用百分比知识。

以上是对七年级百分比知识点的简要总结。

第六章动态经济模型：自回归模型和分布滞后模型6.1 (1)错。

(2)对。

(3)错。

估计量既不是无偏的，又不是一致的。

(4)对。

(5)错。

将产生一致估计量，但是在小样本情况下，得到的估计量是有偏的。

(6)对。

6.2对于科克模型和适应预期模型，应用OLS法不仅得不到无偏估计量，而且也得不到一致估计量。

但是，部分调整模型不同，用OLS法直接估计部分调整模型，将产生一致估计值，虽然估计值通常是有偏的(在小样本情况下)。

6.3科克方法简单地假定解释变量的各滞后值的系数(有时称为权数)按几何级数递减,即：Yt=α+βXt÷β λ Xt-ι ÷β λ2χt.2 +...+ ut其中O<λ<l0这实际上是假设无限滞后分布，由于0<入<1, X的逐次滞后值对Y的影响是逐渐递减的。

而阿尔蒙方法的基本假设是，如果Y依赖于X的现期值和若干期滞后值, 则权数由一个多项式分布给出。

由于这个原因，阿尔蒙滞后也称为多项式分布滞后。

即在分布滞后模型工=α + β0X t + B1X—+∙∙∙ ++ %中，假定：βi =tz0 +tz1z + a2i2 H ------ F a p i p其中P为多项式的阶数。

也就是用一个P阶多项式来拟合分布滞后，该多项式曲线通过滞后分布的所有点。

6.4(1)估计的Y值是非随机变量X1和X2的线性函数，与扰动项v无关。

(2)与利维顿方法相比，本方法造成多重共线性的风险要小一些。

6.5(1)M∣= aγxγ2+ βλγλY t-∕3lχl(l-χ2)Y l.l+ β2γ2R t-β2r2(1 -∕1)R t.l ÷(2 - ∕l—χ2)μt-∖-(1-∕ι )(1-Yι)M t_2÷[u t—(2 —∕1-χ2)〃1 ÷(I -∕ι )(1-Yz )u t-21 其中&)是a、为和72的函数。

(2)第(1)问中得到的模型高度参数非线性，它的参数需采用非线性回归技术来估计。