湍流的数值模拟方法进展
- 格式:doc
- 大小:407.00 KB
- 文档页数:18

大气湍流机理及其模拟对于大气系统来说,湍流是一个非常重要的现象,它存在于大气中的许多过程中,如边界层的形成、天气系统的演变等。
湍流丰富了大气的物理现象,但同时也增加了对大气的模拟和预测的难度。
本文将介绍大气湍流的机理和模拟方法。
一、湍流的机理湍流的起因是流体在过程中受到扰动,这些扰动会引起流体的速度、密度等物理量发生变化。
在湍流发展的过程中,流体速度的各向异性和空间的不规则性增大,流体中的大尺度涡旋逐渐分裂成小尺度涡旋,这些小尺度涡旋不断转化能量,最终会被湍流耗散。
湍流的机理非常复杂,目前还没有完全解决。
基于大气湍流机理的研究,可以分为两个方向:传统的湍流建模和基于数据的机器学习方法。
传统湍流建模主要是基于质量、动量和能量守恒等定律,结合统计理论和实验数据,来建立起湍流的物理模型。
而基于数据的机器学习方法,是利用机器学习算法对海量数据进行分析,从而发现湍流的统计规律。
二、湍流的模拟方法湍流模拟的方法有很多,如数值模拟方法、直接数值模拟方法、大涡模拟方法等。
其中,数值模拟方法是目前使用最广泛的湍流模拟方法,主要分为Reynolds平均Navier-Stokes方程(RANS)和雷诺平均Navier-Stokes方程(LES)两类。
RANS方程是基于湍流平均的模型,将流场分解为平均流和湍流脉动,其中平均流体现了湍流的空间分布,湍流脉动则描述了湍流的时间变化。
RANS方程通过假设某些量在湍流平均后不变,来减少不可控因素的影响,从而简化了计算。
但是,由于RANS方程是基于平均流假设的,所以不能准确地模拟湍流的涡旋结构和流体运动过程。
LES方法是一种基于大涡模拟的方法,通过求解Navier-Stokes方程的高频分量,来描述湍流的小尺度结构和动态特征。
由于LES方法可以解决湍流脉动的时间变化,所以能够更精确地模拟湍流的涡旋结构和流体运动过程。
三、结论综上所述,湍流现象是大气系统的一个重要现象,对于天气系统的演变和边界层的形成有着巨大的影响。

湍流模型理论§3.1 引言自然界中的实际流动绝大部分是三维的湍流流动,如河流,血液流动等。
湍流是流体粘性运动最复杂的形式,湍流流动的核心特征是其在物理上近乎于无穷多的尺度和数学上强烈的非线性,这使得人们无论是通过理论分析、实验研究还是计算机模拟来彻底认识湍流都非常困难。
回顾计算流体力学的发展,特别是活跃的80年代,不仅提出和发展了一大批高精度、高分辨率的计算格式,从主控方程看相当成功地解决了Euler方程的数值模拟,可以说Euler方程数值模拟方法的精度已接近于它有效使用范围的极限;同时还发展了一大批有效的网格生成技术及相应的软件,具体实现了工程计算所需要的复杂外形的计算网格;且随着计算机的发展,无论从计算时间还是从计算费用考虑,Euler方程都已能适用于各种实践所需。
在此基础上,80年代还进行了求解可压缩雷诺平均方程及其三维定态粘流流动的模拟。
90年代又开始一个非定常粘流流场模拟的新局面,这里所说的粘流流场具有高雷诺数、非定常、不稳定、剧烈分离流动的特点,显然需要继续探求更高精度的计算方法和更实用可靠的网格生成技术.但更为重要的关键性的决策将是,研究湍流机理,建立相应的模式,并进行适当的模拟仍是解决湍流问题的重要途径。
要反映湍流流场的真实情况,目前数值模拟主要有三种方法:1。
平均N-S方程的求解,2。
大涡模拟(LES),3。
直接数值模拟(DNS)。
但是由于叶轮机械内部结构的复杂性以及目前计算机运算速度较慢,大涡模拟和直接数值模拟还很少用于叶轮机械内部湍流场的计算,更多的是通过求解平均N-S方程来进行数值模拟。
因为平均N-S方程的不封闭性,人们引入了湍流模型来封闭方程组,所以模拟结果的好坏很大程度上取决于湍流模型的准确度。
自70年代以来,湍流模型的研究发展迅速,建立了一系列的零方程、一方程、两方程模型和二阶矩模型,已经能够十分成功的模拟边界层和剪切层流动。
但是,对于复杂的工业流动,比如航空发动机中的压气机动静叶相互干扰问题,大曲率绕流,激波与边界层相互干扰,流动分离,高速旋转以及其他一些原因,常常会改变湍流的结构,使那些能够预测简单流动的湍流模型失效,所以完善现有湍流模型和寻找新的湍流模型在实际工作中显得尤为重要。


第1篇一、实验背景湍流作为一种复杂的流动现象,在工程、气象、环境等领域具有重要的应用价值。
为了更好地理解湍流流动的特性,本实验选取了典型的湍流模型进行分析,并通过对实验数据的处理和分析,验证模型的适用性和准确性。
二、实验目的1. 了解不同湍流模型的基本原理和适用范围。
2. 通过实验验证湍流模型在工程实际中的应用效果。
3. 分析湍流模型在计算精度和计算效率方面的差异。
三、实验设备与材料1. 实验设备:湍流测试系统、数据采集仪、计算机等。
2. 实验材料:空气、水等。
四、实验方法1. 实验一:验证湍流模型的基本原理- 采用标准K-ε湍流模型和Realizable K-ε湍流模型对一维圆管湍流流动进行模拟,并与实验数据进行对比。
- 通过对比分析,验证两种湍流模型的适用性和准确性。
2. 实验二:验证湍流模型在工程实际中的应用效果- 采用K-ε湍流模型对一维矩形管道内的流动进行模拟,分析管道内流速、湍流强度等参数的分布情况。
- 将模拟结果与实际测量数据进行对比,验证模型的工程应用效果。
3. 实验三:分析湍流模型在计算精度和计算效率方面的差异- 分别采用K-ε湍流模型、Realizable K-ε湍流模型和LES湍流模型对同一湍流流动进行模拟,对比分析不同模型的计算精度和计算效率。
五、实验结果与分析1. 实验一:验证湍流模型的基本原理- 通过对比分析,发现K-ε湍流模型和Realizable K-ε湍流模型在预测一维圆管湍流流动的流速、湍流强度等参数方面具有较高的准确性。
- 实验结果表明,Realizable K-ε湍流模型在预测湍流流动方面具有更好的性能。
2. 实验二:验证湍流模型在工程实际中的应用效果- 通过模拟一维矩形管道内的流动,发现K-ε湍流模型能够较好地预测管道内流速、湍流强度等参数的分布情况。
- 将模拟结果与实际测量数据进行对比,验证K-ε湍流模型在工程实际中的应用效果。
3. 实验三:分析湍流模型在计算精度和计算效率方面的差异- 通过对比分析,发现LES湍流模型在计算精度方面具有优势,但计算效率较低。

零方程模型:C-S模型,由Cebeci-Smith给出;B-L模型,由Baldwin-Lomax 给出。
一方程模型:来源由两种,一种从经验和量纲分析出发,针对简单流动逐步发展起来,如Spalart-Allmaras(S-A)模型;另一种由二方程模型简化而来,如Baldwin-Barth(B-B)模型。
二方程模型:应用比较广泛的两方程模型有Jones与Launder提出的标准k-e 模型,以及k-omega模型。
另外还有雷诺应力模型。
6湍流模型选取的准则:流体是否可压、建立特殊的可行的问题、精度的要求、计算机的能力、时间的限制。
为了选择最好的模型,你需要了解不同条件的适用范围和限制。
FLUENT软件中提供以下湍流模型:1Spalart-Allmaras 模型;2k-ε模型;3k-ω模型;4 雷诺应力模型(RSM);5 大涡模拟模型(LES)。
1 Spalart-Allmaras模型应用范围:Spalart-Allmaras模型是设计用于航空领域的,主要是墙壁束缚(wall-bounded)流动,而且已经显示出很好的效果。
在透平机械中的应用也愈加广泛。
在湍流模型中利用Boussinesq 逼近,中心问题是怎样计算漩涡粘度。
这个模型被Spalart-Allmaras提出,用来解决因湍流动粘滞率而修改的数量方程。
模型评价:Spalart-Allmaras模型是相对简单的单方程模型,只需求解湍流粘性的输运方程,不需要求解当地剪切层厚度的长度尺度;由于没有考虑长度尺度的变化,这对一些流动尺度变换比较大的流动问题不太适合;比如平板射流问题,从有壁面影响流动突然变化到自由剪切流,流场尺度变化明显等问题。
Spalart-Allmaras模型中的输运变量在近壁处的梯度要比k-ε中的小,这使得该模型对网格粗糙带来数值误差不太敏感。
Spalart-Allmaras模型不能断定它适用于所有的复杂的工程流体。
例如不能依靠它去预测均匀衰退,各向同性湍流。


流体流动中的湍流现象及其控制方法引言流体流动是一种自然现象,常见于大气环流、海洋洋流、河流水流、气候变化等多个领域。
在流体流动中,流体粒子会发生不规则的瞬时扰动,形成湍流。
湍流具有不稳定性和复杂性,对于一些工程和科学问题的研究和应用带来了挑战。
本文将介绍湍流现象的定义及其特点,讨论湍流的产生机制,并介绍一些湍流控制的方法。
湍流现象的定义及特点湍流是流体流动中的一种现象,其特点包括流速的不规则性、涡旋的形成和衰减、随机性等。
湍流流动的速度和方向时刻发生变化,无法通过简单的数学模型精确描述。
湍流的主要特点包括湍流能量的分层、湍流尺度的分布以及湍流建立和维持的能量交换过程。
湍流现象的定义可以通过雷诺数(Reynolds number)来描述。
雷诺数是流体力学中的一个无量纲数,用来表征流体流动的稳定性。
当雷诺数大于一定阈值时,流体流动将发生湍流现象。
湍流的产生与流体的运动速度、粘性和长度尺度有关。
湍流现象在自然界和工程领域具有广泛的应用。
在自然界中,湍流可以带动物种的迁移,产生大气环流、海洋洋流等自然现象。
在工程领域中,湍流可以影响飞机、汽车、船舶等流体力学性能,对于设计和优化这些工程系统至关重要。
湍流的产生机制湍流的产生机制主要包括不稳定性机制和能量耗散机制。
不稳定性机制是指当流体流动速度超过一定临界值时,流动将从稳定流动转变为湍流流动。
这种转变是由于流体粒子之间的相互作用导致的流动速度和方向的不规则变化。
能量耗散机制指的是湍流流动中由于摩擦引起的涡旋破裂和能量损失。
湍流的产生过程可以通过数值模拟和实验研究进行分析。
数值模拟通常基于流体动力学(computational fluid dynamics, CFD)方法,通过数值计算来模拟湍流流动的演化过程。
实验研究通常利用流体力学实验装置,在实验室中模拟湍流流动的产生和演化过程。
湍流控制的方法湍流控制是指通过改变湍流流动的性质和结构,来减小湍流的能量损失和不稳定性,提高流体流动的稳定性和效率。

气体流动中的湍流特性研究气体流动是自然界中一种普遍存在的现象,在很多领域都有着重要的应用价值。
湍流是气体流动中常见的流态,其特性与稳定流动存在显著差异。
本文将探讨气体流动中的湍流特性及其研究方向。
一、湍流的基本特性湍流是一种混乱不规则的流动状态,表现出无规则的变化和高度的不确定性。
其特点主要包括强烈的涡旋运动、流向的紊乱、速度和压力的不稳定性等。
湍流在气体流动中具有广泛的存在性,从天气系统到管道内部的气体传输,几乎都可观察到湍流现象。
二、湍流的数学描述湍流的数学描述是研究湍流特性的基础。
流体动力学方程是描述流动的基本方程,包括连续性方程、动量方程和能量方程。
由于湍流的复杂性,直接求解这些方程并不现实。
因此,研究者采用了不同的数值模拟方法,如雷诺平均Navier-Stokes方程(RANS)、大涡模拟(LES)和直接数值模拟(DNS)等,来描述湍流现象。
三、湍流模拟方法湍流模拟方法是湍流研究中的重要工具。
通过数值模拟,可以得到湍流中各个物理量的数值解,进而深入了解湍流的特性。
常用的湍流模拟方法包括雷诺平均Navier-Stokes方程模拟、湍流能量方程模拟、湍流结构模拟等。
这些方法不仅能够捕捉湍流现象的主要特征,还可以分析湍流的统计特性和流场结构。
四、湍流特性的实验研究实验研究是湍流研究中不可或缺的手段。
通过实验可以直接观测和测量湍流流动的各种参数,如湍流特征的统计规律、湍流能量谱、湍流结构等。
常用的实验方法包括热线和冷线测速技术、激光多普勒测速技术和烟雾轨迹可视化技术等。
这些实验手段为湍流特性的研究提供了重要的数据和分析依据。
五、湍流的应用领域湍流在工程和科学领域具有广泛的应用价值。
例如,在空气动力学中,湍流特性的研究对于改进飞机的设计和气动性能的优化具有重要意义。
此外,湍流的研究还能够帮助理解大气层中的气象现象、改善能源的利用效率、提高化工过程中的传热和传质性能等。
六、湍流特性的挑战与前景湍流的复杂性使得湍流特性的研究面临着诸多挑战,如流场的不稳定性、湍流能量传递机制的理解等。

湍流的名词解释湍流,是指在气体或者流体中,不同速度和方向的流动产生的一种混乱的、不规则的运动状态。
湍流是流体力学中重要且复杂的现象,既存在于大自然中的河流、海洋、大气层等环境中,也常常出现在工程和实验室中。
1. 湍流的特点湍流的主要特点有三个方面:不可预知性、非线性和不稳定性。
不可预知性指的是湍流过程中速度和压力分布变化快速且无规律可循。
这是由于湍流中气体或流体不同速度流动产生的涡旋相互作用,导致运动状态难以准确预测。
非线性是指湍流现象无法通过简单的线性方程来描述。
湍流运动中存在着复杂的相互作用、非线性扰动和不可控因素,这导致湍流无法通过简单的数学模型来精确描述。
不稳定性是指湍流状态很容易被外界的微小扰动所改变。
湍流中发生的各种涡旋交错运动,使得湍流处于一种非平衡状态,任何微小的扰动都会在流体中扩散并影响整个流体的运动。
2. 湍流的产生机制湍流的产生机制可以通过雷诺数(Reynolds number)来描述。
雷诺数是流体力学中用于表征流体流动性质、判断流动状态的一个无量纲数值,它由流体运动的惯性力和粘性力之比来决定。
当流体的雷诺数较小时,粘性效应主导,流体流动较为平稳,无湍流现象;当雷诺数超过一定阈值时,流体的惯性力开始占主导地位,湍流现象开始出现。
在工程和实验室中,湍流可以通过增加流体速度、改变管道和物体的形状以及引入不规则障碍物等方式来促使其发生。
3. 湍流的应用与挑战湍流的研究对许多领域具有重要意义,并且应用广泛。
例如,在航空航天中,湍流的存在对于飞机的气动力学、涡轮机械的设计和燃烧过程的优化都有重要的影响。
在能源领域,湍流的研究对于风力发电、水力发电和燃烧等方面都具有重要意义。
在环境科学中,湍流的理解可以帮助我们研究海洋和大气的流动特性。
然而,湍流的复杂性也带来了挑战。
由于湍流存在着不可预知性和非线性的特点,目前对湍流的研究仍然处于较为困难的阶段。
湍流模拟和预测的精确性仍然需要进一步提高,以满足实际应用的需求。

数值模拟方法在流体力学中的应用评价概述数值模拟方法是流体力学研究中的重要工具之一,它通过数值计算的方法,模拟流体的运动状态以及相应的力学特性。
本文将对数值模拟方法在流体力学中的应用进行评价,并探讨其优势和挑战。
一、数值模拟方法的优势1.1 精度和精细度数值模拟方法能够通过细致的离散化和精确的数值计算,精确地模拟流体在各种条件下的运动行为。
在空间和时间上的分辨率可以随需求进行调整,以获得更高的精度和精细度。
1.2 可视化和理解数值模拟方法可以将复杂的流体流动过程可视化展示,使得研究人员能够直观地观察和理解流体的动态行为。
这有助于研究人员深入探究流体力学中的各种现象,如湍流、边界层以及涡旋等。
1.3 低成本和高效率与实验方法相比,数值模拟方法具有较低的成本和高效率。
数值模拟方法不需要大量的实验设备和物质,减少了实验耗时和费用。
此外,数值模拟方法还能够通过并行计算的方式加速计算过程,提高研究效率。
二、数值模拟方法的应用评价2.1 流场分析与设计优化数值模拟方法在流体力学中的一个重要应用是流场分析与设计优化。
通过数值模拟方法,我们可以获得流体在不同条件下的速度、压力、温度等分布情况,为设计者提供流体力学特性方面的参考。
利用数值模拟方法,可以在流体力学领域中进行参数优化和设计优化,以提高流体系统的效率和可靠性。
2.2 海洋工程与环境模拟数值模拟方法在海洋工程和环境模拟方面也有广泛的应用。
例如,通过数值模拟方法,可以预测风暴潮、海浪和海流等海洋现象,为海上工程设计和沿海城市建设提供科学依据。
同时,数值模拟方法还可以模拟河流、湖泊和海洋污染的扩散与传播过程,有助于环境保护和污染防治。
2.3 气象预报与空气动力学模拟数值模拟方法在气象预报和空气动力学模拟方面应用广泛。
通过数值模拟方法,可以对大气环流、气象灾害等进行预测和分析,提供准确的天气预报和气候评估。
此外,数值模拟方法还可用于研究飞机机翼、汽车流场等空气动力学问题,为交通运输与工程领域的设计提供依据。
大气湍流中光传播的数值模拟* 马保科1,2, 郭立新1 吴振森1(1.西安电子科技大学,陕西西安 710071 2.西安工程大学,陕西西安 710048 )摘 要 光在大气湍流中传播时,受大气分子、气溶胶等粒子的相互作用,将发生光束扩展、漂移和相干性退化等大气湍流效应,这些因素严重影响了光波的远场特性。
文章从大气湍流中光传播的理论研究入手,分析了如何构造较为合理的大气湍流相位屏。
进而采用McGlamery 算法,对Kolmogorov 谱下的大气湍流随机相位屏进行了数值模拟,并分析了光波从发射机经湍流大气传播到达接收机时的远场变化特性。
研究表明,大气湍流的存在对光的远场传播质量造成很大的影响,研究结果也为大气湍流中与光传播相关的工程应用及自适应光学技术的完善提供了参考。
关键词 大气湍流;McGlamery 算法;相位屏模拟; 大气结构常数;中图分类号 TP391 文献标识码 A1 引言大气湍流是一个相当复杂的随机媒质系统,虽然物理学界对湍流的研究已经历了相当漫长的历史,但因涉及的因素千头万绪,其间的相互作用和关系也错综复杂,人们对其物理本质至今未能做到较为清楚的认识。
因此,光在大气湍流中传播问题的研究仍存在理论和实验上的挑战[1,2]。
通常,当光在湍流大气中传播时,光束截面内包含着许多的大气漩涡,这些漩涡各自对照射到它的那一部分光束形成衍射作用,可导致光束的强度和相位随机变化,进而表现出光束扩展,大气闪烁和相位起伏等大气湍流效应,从而严重降低了接收机的接收效率。
目前,突破大气湍流的影响仍是光在随机介质中传播所要解决的关键问题[3]。
早在20世纪中期,苏联的Obukhov 便采用Rytov 平缓微扰法由实验反演湍流特征。
在闪烁的饱和现象被发现之后,物理学界又将Markov 近似引入求解光场的统计矩,研究大气湍流下的光场特性[1]。
然而,在中等起伏条件下,目前仍没有找到很好的解析处理方法。
由于数值模拟能够从光的传播过程出发,较为清楚地反映出所涉及问题的物理本质,因而成为研究湍流效应的主要方法[4]。
fluent中常见的湍流模型及各自应用场合湍流是流体运动中的一种复杂现象,它在自然界和工程应用中都非常常见。
为了模拟和预测湍流的行为,数学家和工程师们开发了各种湍流模型。
在Fluent中,作为一种流体动力学软件,它提供了多种常见的湍流模型,每个模型都有其自己的适用场合。
1. k-ε 模型最常见的湍流模型之一是k-ε模型。
该模型基于雷诺平均的假设,将湍流分解为宏观平均流动和湍流脉动两个部分,通过计算能量和湍动量方程来模拟湍流行为。
k-ε模型适用于边界层内和自由表面流动等具有高湍流强度的情况。
它还适用于非压缩流体和对称或旋转流动。
2. k-ω SST 模型k-ω SST模型是基于k-ε模型的改进版本。
它结合了k-ω模型和k-ε模型的优点,既能够准确地模拟边界层流动,又能够提供准确的湍流边界条件。
SST代表了"Shear Stress Transport",意味着模型在对剪切流动的边界层进行处理时更为准确。
k-ω SST模型适用于各种湍流强度的流动,特别是在激烈湍流的边界层内。
3. Reynolds Stress 模型Reynolds Stress模型是一种基于雷诺应力张量模拟湍流的高级模型。
它考虑了流场中的各向异性和非线性效应,并通过解Reynolds应力方程来确定流场中的张应力。
由于对流场的湍流行为进行了更精确的建模,Reynolds Stress模型适用于湍流流动和涡旋流动等复杂的工程应用。
然而,由于模型的计算复杂度较高,使用该模型需要更多的计算资源。
4. Large Eddy Simulation (LES)Large Eddy Simulation是一种直接模拟湍流的方法,它通过将整个流场划分为大尺度和小尺度的涡旋来模拟湍流行为。
LES适用于高雷诺数的流动,其中小尺度涡旋的作用显著。
由于需要同时解决大尺度和小尺度涡旋的运动方程,LES计算的复杂度非常高,适用于需要高精度湍流求解的工程应用。
湍流流体力学的发展与应用展望1. 引言湍流流体力学是研究流体中的湍流现象及其动力学行为的学科领域。
湍流是一种非线性、非稳定的复杂现象,存在于自然界中的各种流动过程中,如海洋流、大气环流、河流、汽车行驶中的空气流动等。
湍流的研究对于增进对自然界和工程实践中流体运动的理解具有重要意义。
本文将探讨湍流流体力学的发展历程以及对工程领域的应用,并展望未来的发展方向。
2. 湍流流体力学的发展史湍流流体力学的研究始于19世纪末的流体动力学研究。
最早的湍流研究是基于实验观察和经验公式的。
然而,由于湍流的复杂性和不可预测性,这种经验研究方法很快遇到了困难。
随着计算机技术的发展,数值模拟成为湍流研究的重要手段。
20世纪后期,湍流模型的发展和大规模计算能力的提高加速了湍流流体力学的进展。
3. 湍流流体力学的基本理论湍流流体力学的基本理论主要包括雷诺平均Navier-Stokes方程(RANS)及其湍流模型、直接数值模拟(DNS)以及大涡模拟(LES)等。
3.1 雷诺平均Navier-Stokes方程及湍流模型雷诺平均Navier-Stokes方程是湍流流体力学研究的基础方程之一。
雷诺平均是指对流场进行时间平均处理。
湍流模型用于模拟流场中的湍流运动,其中最经典的是k-$\\varepsilon$模型和$k-\\omega$模型。
这些模型基于统计和实验数据,对湍流的运动和传输进行建模,从而实现对湍流运动的计算。
3.2 直接数值模拟直接数值模拟是通过求解Navier-Stokes方程组来模拟湍流流动。
在直接数值模拟中,湍流的小尺度结构和湍流涡旋被完全模拟,可以获得精确的流场解。
然而,直接数值模拟计算量巨大,只适用于小规模问题,限制了其在工程领域的应用。
3.3 大涡模拟大涡模拟是介于雷诺平均和直接数值模拟之间的一种模拟方法。
在大涡模拟中,通过将流场分解成大尺度涡旋和小尺度湍流结构,对大尺度涡旋进行模拟,而对小尺度湍流结构进行参数化处理。
大气湍流传输特性研究及模拟方法摘要:大气湍流传输特性是气象学和大气科学研究的重要课题之一,对于空气质量、气候变化以及环境污染等问题有着重要的影响。
本文将探讨大气湍流传输特性的研究方法和模拟方法,介绍湍流的形成机制和传输过程,并且分析现有的模拟方法及其应用领域。
通过深入研究大气湍流传输特性,有助于我们更好地了解和预测大气环境的变化。
1. 引言大气湍流传输特性是指大气中的湍流现象对物质传输的影响。
湍流是指流动介质中的无规则运动,具有剧烈的速度波动和能量传递。
大气湍流传输特性的研究对于理解大气环境变化以及对空气质量的影响具有重要意义。
2. 湍流的形成机制湍流的形成机制主要由湍流能量输入和湍流能量耗散两个过程共同决定。
湍流能量输入包括大气层之间的能量交换以及地表和大气之间的能量交换。
湍流能量的耗散主要通过黏性阻尼来实现。
3. 湍流传输过程湍流传输过程包括湍流扩散、湍流对流和湍流输运等几个方面。
湍流扩散主要指物质在湍流的作用下的横向扩散过程,湍流对流指因湍流引起的物体内部和外部的无规则运动,湍流输运是指物质在湍流流场中由于速度非均匀性而发生的输运。
4. 大气湍流传输特性的模拟方法现代大气科学研究中,模拟方法是一种常用的研究手段。
常见的大气湍流传输的模拟方法包括数值模拟和实验模拟两种。
4.1 数值模拟方法数值模拟方法是通过数学模型来模拟大气湍流传输特性。
常用的数值模拟方法有雷诺平均N-S方程模型(RANS)、大涡模拟(LES)和直接数值模拟(DNS)三种。
RANS方法是常用的湍流模拟方法,Les方法相对而言更加精确,DNS方法则是最为精确的模拟方法。
4.2 实验模拟方法实验模拟方法是通过实验设备来模拟大气中的湍流传输过程。
常见的实验模拟方法包括风洞实验、水洞实验和人工湍流实验等。
这些实验模拟方法可以精确测量大气湍流传输特性的相关参数,为湍流传输特性的研究提供了可靠的数据。
5. 模拟方法的应用领域大气湍流传输特性的模拟方法在空气质量、气候变化和环境污染等研究领域有着广泛的应用。
可压缩平板湍流边界层拟序结构的直接数值模拟作者:高慧来源:《价值工程》2013年第10期摘要:文中直接数值模拟了来流马赫数(M∞)为2.25的空间发展的可压缩平板湍流边界层。
研究了可压缩平板湍流边界层内的拟序结构的形成过程。
指出在粘性底层出现低速条带是触发拟序结构的第一个信息。
条带升起,开始发生振动,然后破裂,并伴随着产生强烈的湍流脉动,这便形成了湍流的猝发过程。
因此壁湍流拟序结构的重要意义在于它是生成湍流的重要机制。
条带的破裂还伴随着上抛和下扫现象,这是壁湍能生成和耗散的关键。
Abstract: A Direct numerical simulation of a spatially evolving compressible flat-plate turbulent boundary layer with incoming Mach number (M∞) of 2.25 was performed in this paper. The coherent structure forming process is studied. The low-speed strip appearing in the viscous sublayer is the first information to trig coherent structure. Strip rises, begin to vibrate, and rupture, and accompanied by strong turbulence, which will form the turbulent bursting process. Therefore the wall turbulent coherent structure is significant in that it is the important mechanism to generate turbulence. Strip rupture accompanied by up and down sweep phenomenon, it is the key of wall turbulent energy generation and dissipation.关键词:可压缩;平板湍流边界层;直接数值模拟;拟序结构Key words: compressible;flat-plate boundary layer;direct numerical simulation;coherent structure中图分类号:O35 文献标识码:A 文章编号:1006-4311(2013)10-0003-020 引言对湍流拟序结构的研究,使得人们在揭示湍流的物理本质方面寻觅到了一个新的有效的方向,从而得以有能力预测和控制湍流。
.专业整理. .学习帮手. 《高等计算流体力学》课程作业
湍流的数值模拟方法进展 .专业整理.
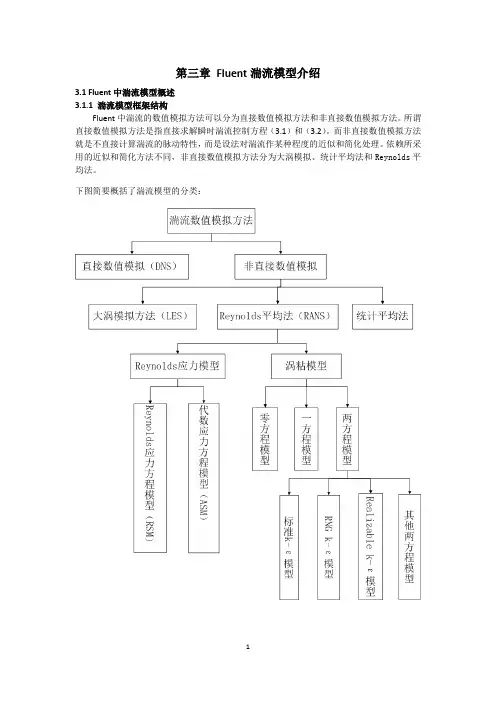
.学习帮手. 1概述 自然环境和工程装置中的流动常常是湍流,模拟任何实际过程首先遇到的就是湍流问题,而湍流问题本身又是流体力学理论上的难题。对于某些简单的均匀时均流场,如果湍流脉动是各向均匀及各向同性的,可以用经典的统计理论来分析,但实际上的湍流往往是不均匀的,给理论分析带来了极大困难。 湍流是空间上不规则和时间上无秩序的一种非线性的流体运动,表现出非常复杂的流动状态,主要表现在湍流流动的随机性、有旋性、统计性。传统计算流体力学中描述湍流的基础是Navier-Stokes(N-S)方程,根据N-S方程中对湍流处理尺度的不同,湍流数值模拟方法主要分为:直接数值模拟(DNS)、雷诺平均方法(RANS)和大涡模拟(LES)。 直接数值模拟可以获得湍流场的精确信息,是研究湍流机理的有效手段,但现有的计算资源往往难以满足对高雷诺数流动模拟的需要,从而限制了它的应用范围。雷诺平均方法可以计算高雷诺数的复杂流动,但给出的是平均运动结果,不能反映流场脉动的细节信息。大涡模拟基于湍动能传输机制,直接计算大尺度涡的运动,小尺度涡运动对大尺度涡的影响则通过建立模型体现出来,既可以得到比雷诺平均方法更多的诸如大尺度涡结构和性质等的动态信息,又比直接数值模拟节省计算量,从而得到了越来越广泛的发展和应用。
2 雷诺平均方法(RANS)
雷诺平均模拟(RANS)即应用湍流统计理论, 将非定常的N - S方程对时间作平均,求解工程中需要的时均量。利用湍流模式理论,对Reynolds应力做出各种假设,即假设各种经验的和半经验的本构关系,从而使湍流的平均Reynolds方程封闭。
2.1 控制方程 对非定常的N - S 方程作时间演算, 并采用Boussinesp 假设,得到Reynolds 方程 .专业整理. .学习帮手. ''21ijiiijijjjjjuuuuupufvtxxxxx
=0ii
ux
式中,附加应力可记为''ijijpuu
,称为雷诺应力。
这种方法只计算大尺度平均流动,而所有湍流脉动对平均流动的影响,体现到雷诺应力ij中。由于雷诺应力在控制方程中的出现,造成了方程不封闭,为使方程组封闭,必须建立湍流模型。
2.2 湍流模型 目前工程计算中常用的湍流模型从对模式处理的出发点不同,可以将湍流模式理论分类成两大类:一类引入二阶脉动项的控制方程而形成二阶矩封闭模型,或称为雷诺应力模型,另一类是基于Boussinesq 的涡粘性假设的涡粘性封闭模式,如零方程模型,一方程模型和二方程模型。
2.2.1雷诺应力模型 雷诺应力模型(RSM)从Reynolds应力满足的方程出发,直接建立以''ijuu为因变量的偏微分方程, 将方程右端未知的项(生成项,扩散项,耗散项等)用平均流动的物理量和湍流的特征尺度表示出来,并通过模化封闭。封闭目标是雷诺应力输运方程:
''''''
''''ijijji
kikjkijijij
kkk
uuuuuuuuuuuDtxxx
(7)
式中ij 是雷诺应力再分配项, ijD是雷诺应力扩散项, ij是雷诺应力耗
散项。 典型的平均流动的变量是平均速度和平均温度的空间导数。这种模式理论,由于保留了Reynolds应力所满足的方程,如果模拟的好,可以较好地反映Reynolds应力随空间和时间的变化规律,因而可以较好地反映湍流运动规律。因此,二阶矩模式是一种较高级的模式,但是,由于保留了Reynolds应力的方程,加上平均运动的方程整个方程组总计15个方程,应用这样一个庞大的方程组来解决实际工程问题,计算量很大,极大地限制了二阶矩模式的应用。 .专业整理. .学习帮手. 2.2.2涡粘性模型 涡粘性模型在工程湍流问题中得到广泛应用。这是由Boussinesq仿照分子粘性的思路提出的,即设Reynolds应力为,
,,,22()33ijTijjikkijijuuUUUk
这里12ijkuu是湍动能,T
称为涡粘性系数,这是最早提出的基准涡粘性模式,即假设
雷诺应力与平均速度应变率成线性关系,当平均速度应变率确定后,六个雷诺应力只需要通过确定一个涡粘性系数T
就可完全确定,且涡粘性系数各向同性,可以通过附加的湍流
量来模化,比如湍动能k,耗散率,比耗散率w以及其它湍流量/k,/2/3kl
,kq,根据引入的湍流量的不同,可以得到不同的涡粘性模式,比如常
见的k,k-w模式,以及后来不断得到发展的k,q-w,k-l等模式,涡粘性系数可以分别表示为 /2kCT
kCT
kCT
2q
CT
lkCT 雷诺平均方法的优点为 (1) 对计算机的要求较低,同时可以得到符合工程要求的计算结果。 (2)一旦给定合理的Reynolds应力模型,可以很容易地从RANS方程解出湍流的统计量,所需要的计算资源小。 (3)几乎能对所有雷诺数范围的工程问题求解,并得出一些有用的结果。 其不足之处在于: (1) 对不同类型的湍流,需要采用不同的Reynolds应力模型,甚至对于同.专业整理. .学习帮手. 一类型的问题,对应于不同的边界条件需要修改模型的常数。 (2) 由于不区分旋涡的大小和方向性,对旋涡的运动学和动力学问题考虑不足,不能用来对流体流动的机理进行描述。 (3) 对于非定常流动、大分离流动、逆压力梯度数值模拟等问题,受湍流模型条件的限制,很难得到满意的计算结果。 (4)严重依赖流场形状和边界条件,普适性差,计算很大程度上依赖于经验。
2.3 常用的湍流模型 常用的湍流模型有: 零方程模型:C-S模型,由Cebeci-Smith给出;B-L模型,由Baldwin-Lomax给出。 一方程模型:来源由两种,一种从经验和量纲分析出发,针对简单流动逐步发展起来,如Spalart-Allmaras(S-A)模型;另一种由二方程模型简化而来,如Baldwin-Barth(B-B)模型。 二方程模型:应用比较广泛的两方程模型有Jones与Launder提出的标准k-e模型,以及k-omega模型。
1、零方程模型 上世纪30年代发展的一系列湍流的半经验理论,如Prandtl的混合长度理论、Taylor的涡量输运理论、von Karman的相似性理论等,本质上即是零方程湍流模型。零方程模型直接建立雷诺应力与平均速度之间的代数关系,由于不涉及代数关系故称为零方程模型:
''m
uuvy
其中m称为涡粘系数,与分子的运动粘性系数有相同的量级。对于一般的三
维的情况,上式可写为: ''223ijmijijuvSK
K为单位质量的湍流脉动动能。为了发展上述方法,需要建立m与平均速度之
间的关系。1925年,普朗特提出混合长度理论,认为存在这样的长度l,在此.专业整理. .学习帮手. 长度内流体质点运动是自由的,l称为混合长度。由于湍流漩涡的作用,到达新位置后他会低于当地周围的平均速度,此即流向脉动速度'
10()()uUyUy,
显然,此速度差取决于当地的平均速度梯度Uy与微团沿y向跳动的距离l,即:
'Uuly
此l表示在此距离内微团沿y向脉动时基本不丧失其原有速度。实际测量表明,虽然一般情况下流向的脉动速度的均方根值大于法向值,但他们有相同的量级,因此有:
'Uvly
所以有:
''2uuuvlyy
由此可算出涡粘性系数为:
2m
uly
由此可见,若假设l不随速度变化,则可得出湍流切应力与平均速度平方成比例,这与实验结果是一致的。 混合长度理论已成功用于研究多种湍流剪切流,如流管、边界层和各种湍流剪切流。 目前应用最广泛的零方程模型是Baldwim-Lomax模型,该模型对湍流边界层的内层和外层采用不同的混合长度假设,在流体分离不严重的流场计算中结果较好。但是实际上,零方程湍流模型仅适用于局部平衡状态的湍流流动。
2,、一方程模型 一方程模型一般求解湍流动能或涡粘性系数的输运方程,精度较好,鲁棒性也比较好,B-B模型和S-A模型是典型的单方程模型。特别是S-A模型,从经验和量纲分析出发得出了涡粘性系数的输运方程,采用大量的实验结果标定模型系数,具有良好的鲁棒性和计算准确性,目前已经被集成在各种商业软件和科学计算的代码中,在航空航天领域的空气动力学计算中得到了十分广泛的应