2015年江西省高考模拟试题_江西省赣州市十二县市重点中学高三上学期期中联考数学(理)卷

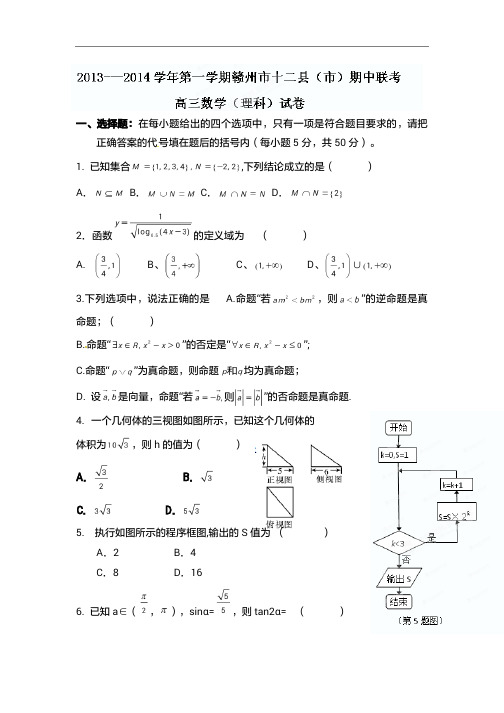
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）。

1.已知集合,下列结论成立的是（）A．B．C．D．2．函数的定义域为（）A.B、C、D、∪3.下列选项中，说法正确的是 A.命题“若，则”的逆命题是真命题；（）B.命题“”的否定是“”;C.命题“”为真命题，则命题均为真命题；D.设是向量，命题“若”的否命题是真命题.4.一个几何体的三视图如图所示，已知这个几何体的体积为，则h的值为（）A．B．C．D．5.执行如图所示的程序框图,输出的S值为（）A．2B．4C．8D．166.已知a∈（，），sinα=，则tan2α=（）A. B. C. D.7.如图，平行四边形ABCD 中，，点M在AB 边上，且等于（）A.B.C.D.18.函数（其中）的图象如图所示，为了得到的图像，则只要将的图像（）A ．向右平移个单位长度B ．向右平移个单位长度C ．向左平移个单位长度D ．向左平移个单位长度9、设为坐标原点，第一象限内的点的坐标满足约束条件，，若的最大值为40，则的最小值为（）（A ）（B ）（C ）1（D ）410.如图，线段=8，点在线段上，且=2，为线段上一动点，点绕点旋转后与点绕点旋转后重合于点.设=，的面积为.则的最大值为（）．A.B ．2C ．3D ．二、填空题：(本大题共4小题，每小题5分，共20分，把答案填在答题纸的相应位置．)11.在平面直角坐标系中，由直线与曲线围成的封闭图形的面积是A C P BD8题图12.,则13.若双曲线的左、右焦点分别为F1,F2，线段F1F2被抛物线的焦点分成5：3两段，则此双曲线的离心率为______.14.根据下面一组等式S1=1S2=2+3=5S3=4+5+6=15S4=7+8+9+10=34S5=11+12+13+14+15=65S6=16+17+18+19+20+21=111S7=22+23+24+25+26+27+28=175……………………可得三、选做题（在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分，本题共5分）15．(1)（选修4—4坐标系与参数方程）已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为（为参数），直线的极坐标方程为．则直线与曲线C的位置关系为(2)（选修4—5不等式选讲）不等式对任意实数恒成立,则实数的取值范围是____________.四、解答题：16、（本小题满分12分）已知向量，，．（Ⅰ）求函数的最小正周期及对称轴方程；（Ⅱ）在中，角A，B，C的对边分别是若，b=1，的面积为，求的值．17、（本小题满分12分）袋中有8个大小相同的小球，其中1个黑球，3个白球，4个红球.（I）若从袋中一次摸出2个小球，求恰为异色球的概率；（II）若从袋中一次摸出3个小球，且3个球中，黑球与白球的个数都没有超过红球的个数，记此时红球的个数为，求的分布列及数学期望E.18、（本小题满分12分）如图，已知直角梯形所在的平面垂直于平面，，，．（Ⅰ）点是直线中点，证明平面；（Ⅱ）求平面与平面所成的锐二面角的余弦值.19、（本小题满分12分）已知数列满足，（且）．（Ⅰ）求数列的通项公式；（Ⅱ）令，记数列的前项和为，若恒为一个与无关的常数，试求常数和.20、（本小题满分13分）已知抛物线的焦点为F2，点F1与F2关于坐标原点对称，以F1,F2为焦点的椭圆C过点.（Ⅰ）求椭圆C的标准方程；（Ⅱ）设点，过点F2作直线与椭圆C交于A,B两点，且，若的取值范围.21、（本小题满分14分）已知.（Ⅰ）求函数在上的最小值；（Ⅱ）对一切恒成立，求实数的取值范围；（Ⅲ）证明：对一切，都有成立.2013---2014学年第一学期赣州市十二县（市）期中联考高三数学（理科）试卷答案17、解：解:（Ⅰ）摸出的2个小球为异色球的种数为 (2)分从8个球中摸出2个小球的种数为………………3分故所求概率为………………………………6分（Ⅱ）符合条件的摸法包括以下三种：一种是有1个红球，1个黑球，1个白球，共有种………………………………7分一种是有2个红球，1个其它颜色球，共有种，………………………………8分一种是所摸得的3小球均为红球，共有种不同摸法，故符合条件的不同摸法共有种.………………………………10分由题意知，随机变量的取值为，，.其分布列为：123……………………12分18、（Ⅰ）证明：取的中点连结，则，，取的中点，连结，∵且，∴△是正三角形，∴．∴四边形为矩形，∴．………………4分又∵，∴且，四边形是平行四边形．∴，而平面，平面，∴平面． (6)分（Ⅱ）（法1）过作的平行线，过作的垂线交于，连结，∵，∴，是平面与平面所成二面角的棱．……8分∵平面平面，，∴平面，又∵平面，∴平面，∴，∴是所求二面角的平面角．………………10分设，则，，∴，∴．………12分（法2）∵，平面平面，∴以点为原点，直线为轴，直线为轴，建立空间直角坐标系，则轴在平面内（如图）．设，由已知，得，，．∴，，…………………8分ABCDE PMF G设平面的法向量为，则且，∴∴解之得取，得平面的一个法向量为.………10分又∵平面的一个法向量为．……10分．………12分19、（本小题满分12分）解:（Ⅰ）由题……①……②由①②得：，即…………………………………………3分当时，，，,所以，数列是首项为，公比为的等比数列故（）………………………………………………………………………6分（Ⅱ），，是以为首项，以为公差的等差数列， (8)分……………………………………………10分恒为一个与无关的常数，解之得：，………………………………………………………………12分20、解：（Ⅰ）设椭圆的半焦距为，由题意得，设椭圆的标准方程为，则③④将④代入③，解得或（舍去）所以故椭圆的标准方程为 (4)分（Ⅱ）方法一：容易验证直线的斜率不为0，设直线的方程为将直线的方程代入中得：.…………………6分设，则由根与系数的关系，可得：⑤⑥…………………7分因为，所以，且.将⑤式平方除以⑥式，得：由所以……………………………………………………………10分因为，所以，又，所以，故，令，所以所以，即，所以.而，所以.所以.………………………………………………13分方法二：1）当直线的斜率不存在时，即时，，，又，所以…………6分2）当直线的斜率存在时，即时，设直线的方程为由得设，显然，则由根与系数的关系，可得：，……………………7分⑤⑥因为，所以，且.将⑤式平方除以⑥式得：由得即故，解得………………………………………10分因为，所以，又，故…………………11分令，因为所以，即，所以.所以……………………12分综上所述：.……………………13分21、【解析】（Ⅰ）.当单调递减，当单调递增……2分①，即时，；………………4分②，即时，在上单调递增，．所以.……………………………………6分（Ⅱ），则，设，则，………………8分①单调递减，②单调递增，所以，对一切恒成立，所以.………………10分（Ⅲ）问题等价于证明，由（Ⅰ）可知的最小值是，当且仅当时取到.…12分设，则，易知，当且仅当时取到，从而对一切，都有成立.………………14分。

一、选择题（每题只有一个选项符合要求，每小题1.5分，共51分）1、下列关于细胞结构和功能的叙述正确的是A.D N A、R N A和蛋白质可通过核孔进出细胞核B.只有含叶绿体的细胞才能将无机物合成有机物C.分泌功能越强的细胞，高尔基体膜的更新速度越快D.蛋白质是细胞膜的主要组成成分且在膜上均匀分布2、人血红蛋白由两条α链和两条β链构成。

镰刀型细胞贫血症患者的β链第6位的谷氨酸替换为缬氨酸导致血红蛋白聚集为纤维状，红细胞形状随之改变。

下列叙述错误的是A．人血红蛋白至少有4个氨基和4个羧基B．该病是基因控制的蛋白质结构异常造成的C．患者体内编码β链的基因碱基数量改变D．氨基酸序列改变影响蛋白质的生理功能3、科学家把从小鼠胚胎干细胞中分离获得的4个基因通过病毒导入已分化的小鼠成熟细胞，发现成熟细胞返回到了未成熟的干细胞状态。

这种干细胞（i P S细胞）又能在不同条件下分化形成神经细胞等多种细胞。

下列叙述不正确的是A.此实验过程中病毒发挥了载体的功能B.此实验过程中运用了动物细胞培养技术C.分化形成的神经细胞能进行遗传信息的表达D.i P S细胞分化形成的多种细胞所含核基因不同4、某些植物在早春开花时，花序细胞的耗氧速率高出其它细胞100倍以上，但单位质量葡萄糖生成A T P的量却只有其它细胞的40%。

此时的花序细胞A．主要通过无氧呼吸生成A T P B．产生的热量远多于其它细胞C．线粒体基质不参与有氧呼吸D．没有进行有氧呼吸第三阶段5、将一份刚采摘的新鲜蓝莓用高浓度的C O2处理48h后，贮藏在温度为1℃的冷库内。

另一份则始终在l℃的冷库内贮藏。

从采后算起每10天取样一次，测定其单位时间内C O2释放量和O2吸收量，计算二者的比值得到下图所示曲线。

下列结论不正确的是A．比值大于1，表明蓝莓既进行有氧呼吸，又进行无氧呼吸B．第20天对照组蓝莓产生的乙醇量高于C O2处理组C．第40天对照组蓝莓有氧呼吸比无氧呼吸消耗的葡萄糖多D．贮藏蓝莓前用C O2短时处理，能抑制其在贮藏时的无氧呼吸6.下列过程不需要酶参与的是A.D N A转录成R N A的过程B.光合作用中C O2的固定C.细胞质壁分离与复原D.细胞质基质内糖酵解过程7、在D N A分子的一条单链中，相邻的碱基A与T是通过（）连接的A．肽键B．磷酸—脱氧核糖—磷酸C．氢键D．脱氧核糖—磷酸—脱氧核糖8、放射性同位素示踪法是生物学研究过程中常采用的技术手段。

相对原子质量：H—1、O—16、N—14、N a—23、S—32、F e—56、C u—64一、选择题（每小题只有一个正确选项，每小题3分，共48分）1、下列叙述正确的是（）A.溶液和胶体的本质区别是有无丁达尔效应B.明矾在水中能形成A l(O H)3胶体，可作净水剂C.玻璃、水泥和光导纤维的主要成分都是硅酸盐D.将S O2通入品红溶液，溶液褪色后加热恢复原色，将S O2通入溴水，溴水褪色后加热也恢复原色2、设N A为阿伏加德罗常数的数值，下列说法中正确的是（）A.标准状况下，22.4L C H C l3含有的分子数为N AB.0.1m o l/L的N H4N O3溶液中含有的氮原子数为0.2N AC.1m o l F e2+与足量的H2O2溶液反应，转移2N A个电子D.常温常压下，92g的N O2和N2O4混合气体含有的原子数为6N A3、下列离子方程式书写正确的是（）A.碳酸钙溶于醋酸：C a C O3+2H+＝C a2++C O2↑+H2OB.标准状况下将112m l氯气通入6ml1m o l/L的碘化亚铁溶液中3C l2+2F e2++4I-＝6C l-+2F e3++2I2C.漂白粉溶液中通入少量S O2：C a2++2C l O-+S O2+H2O＝C a S O3↓+2H C l OD.向澄清石灰水中加入过量碳酸氢钠溶液C a2++2O H-+2H C O3-＝C a C O3↓+2H2O+C O32-4、三氟化氮（N F3）是一种新型电子材料，它在潮湿的空气中与水蒸气能发生氧化还原反应，其反应的产物有：H F、N O和H N O3。

则下列说法错误的是()A．反应过程中，被氧化与被还原的元素的物质的量之比为1：2B．N F3是一种无色、无臭的气体，因此N F3在空气中泄漏时不易被察觉C．一旦N F3泄漏，可以用N a O H溶液喷淋的方法减少空气污染D．若反应中生成1.0m o l N O，转移的电子数目为6.02×10235、下列各组离子中可能大量共存的是（）A.在能使紫色石蕊试剂变红的溶液中：N a+、S O42-、C l-、H C O3-B.在强酸性溶液中：N H4+、B a2+、F e2+、B r-、N O3-C.在含有大量A l O2-的溶液中：N H4+、N a+、C l-、A l3+D.在水电离出的c(H+)＝1×10-13m o l/L的溶液中：N a+、K+、C O32-、N O3-6、下列实验能达到预期目的的是（）编号实验内容实验目的A 取两只试管，分别加入4m l0.01mo l/L K Mn O4酸性溶液，然后向一只试管中加入0.1m o l/L H2C2O4溶液2m l，向另一只试管中加入0.1m o l/L H2C2O4溶液4ml，记录褪色时间。

赣州市2015届高三上学期十二县（市）期中联考理科数学试题第Ⅰ卷（选择题 共50分）一、选择题（共50分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设复数11z i =+，22()z xi x R =+∈，若12z z R ⋅∈，则x 的值为( )A ．2-B ．1-C ．1D ．2 2．若20(23)0kx x dx -=⎰，则正数k 的值为( )A ．0B ．1C ．0或1D ．2 3.( )A．[)1,0 4.平面向量→a ，→b 的夹角为60︒，)0,2(=→a =→b 2（ ）A． 2 5. 已知113::<+≥x q k x p ，，如果p 是q 的充分不必要条件，则实数k 的取值范围是（ ）A. ),2[+∞B. ),2(+∞C. ),1[+∞D. ]1,(--∞6. 若10,0,cos(),cos()224342ππππβαβα<<-<<+=-=则cos()2βα+=（ ）A.7. 设x ，y 满足约束条件2208400,0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩，若目标函数()0,0z ax by a b =+>>的最大值为8，则ab 的最大值为( )A.1B.2C.3D.48．已知数列{}n a 是等差数列，若0,032015201420152013<⋅<+a a a a ，且数列{}n a 的前n 项和n S 有最大值，那么n S 取得最小正值时n 等于（ ）A ．4029B ．4028C ．4027D ．4026 9. 在实数集R 中定义一种运算“*”，R b a ∈∀,，a b *为唯一确定的实数，且具有性质： （1）对任意R a ∈，0a a *=； （2）对任意,R a b ∈，(0)(0)a b ab a b *=+*+*．关于函数1()()x x f x e e=*的性质，有如下说法：①函数)(x f 的最小值为3；②函数)(x f 为偶函数；③函数)(x f 的单调递增区间为(,0]-∞．其中正确说法的序号为（ ）A ．①B ．①②C ．①②③D ．②③10．如图，正△ABC 的中心位于点G （0，1），A （0，2），动点P 从A 点出发沿△ABC 的边界按逆时针方向运动，设旋转的角度∠AGP =x （0≤x ≤2π），向量OP 在(1,0)a =方向的投影为y （O 为坐标原点），则y 关于x 的函数y =f （x ）的图象是（ ）第Ⅱ卷（非选择题 共100分）二、填空题 (本大题共4小题，每小题5分，共20分，把答案填在答题纸的相应位置) 11.设集合}1,0,1{-=M ，},{2a a N =，若N N M =⋂,则a 的值是 ．12.若函数1212,0,()2,0,(3),0,x x f x x x x -⎧>⎪⎪=-=⎨⎪⎪+<⎩且(((0)))b f f f =,若24a a b y x --=是偶函数，且在(0,)+∞ 内是减函数，则整数a 的值是__________．13.已知函数()sin()(0,)2f x x πωϕωϕ=+><的部分图像如图，令),6(πn f a n =则=++++2014321a a a a ．14. 定义域为R 的偶函数)(x f 满足对任意x R ∈，有)1()()2(f x f x f -=+，且当]3,2[∈x 时，18122)(2-+-=x x x f ，若函数)1|(|log )(+-=x x f y a 在),0(+∞上至少有三个零点，则a的取值范围是 ．三、选做题（在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分，本题共5分）15. (1)（坐标系与参数方程选做题）在极坐标系中，圆θρcos 2=在点)0,2(M 处的切线方程为 ．(2)（不等式选讲选做题）已知函数a a x x f +-=|2|)(．若不等式6)(≤x f 的解集为{}32|≤≤-x x ，则实数a 的值为 ．四、解答题（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤） 16．（本小题满分12分）已知向量(sin ,1)m x =- ，向量1,)2n x =- ，函数()()f x m n m =+⋅ .(1)求()f x 的最小正周期T ；(2)已知a ，b ，c 分别为ABC D 内角A ，B ，C 的对边，A 为锐角，a =4c =， 且()f A 恰是()f x 在⎥⎦⎤⎢⎣⎡2,0π上的最大值，求A ，b 和ABC ∆的面积S .17. (本小题满分12分)已知函数b ax ax x g ++-=12)(2（0>a ）在区间]3,2[上有最大值4和最小值1． 设xx g x f )()(=． （1）求a 、b 的值；（2）若不等式02)2(≥⋅-x x k f 在]1,1[-∈x 上有解，求实数k 的取值范围.18．（本小题满分12分）2014年巴西世界杯的周边商品有80%左右为“中国制造”，所有的厂家都是经过层层筛选才能获此殊荣。

满分：150分做题时间：120分钟第一部分听力(共两节，满分30分)第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一小题，从题中所给的ABC三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题，每段对话仅读一遍。

1. How many words do Eskimos have for ice probably?A. Less than 33.B. Exactly 33.C. More than 33.2. Who is the woman?A. The man’s customer.B. The man’s secretary .C. The man’s boss.3. Where are the speakers?A. In a lab.B. In a classroom.C. In an office.4. When did the man go to Yellowstone National Park?A.This year.B. Last year.C. Three years ago.5. What does the woman mean?A. She is busy at the moment.B. She didn’t go out with Peter last night.C. She wants the man to hold on for a minute.第二节（共15小题：每小题1.5分，共22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给ABC三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答6、7题。

6. Where does the conversation take place?A. At a bus stop.B. In a newspaper office.C. In a coffee shop.7. What are the speakers mainly talking about?A. A letter.B. Public transportation.C. Road construction. 听第7段材料，回答第8、9题。

江西省赣州市十二县（市）2015届高三上学期期中联考数学文试题【试卷综评】本试卷注重对数学基础知识、基本技能、基本思想和方法的考查，突出了对数学的计算能力、逻辑思维能力等方面的考察。

紧扣考纲，注重双基 .本次期末考试有很多题目源于课本。

2、突出重点和数学思想. 试题对本部分各节知识考察较为全面，一方面突出了重点知识重点考察，另一方面突出数学知识和数学思想的考察。

对学生的综合能力要求较多，在知识交汇点处设置考题。

第Ⅰ卷（选择题 共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）【题文】1. 已知集合{|(1)(2)0}A x x x =+-≤，集合B 为整数集，则A B I =（ ）A 、{1,0}-B 、{0,1}C 、{2,1,0,1}--D 、{1,0,1,2}-【知识点】交集及其运算．A1【答案】【解析】D 解析：{|(1)(2)0}A x x x =+-≤={|12}x x ﹣≤≤，又集合B 为整数集，故A B I ={1,0,1,2}-，故选D ．【思路点拨】由题意，可先化简集合A ，再求两集合的交集． 【题文】2.设i 是虚数单位，复数=++iii 123（ ） A. 1 B. 1- C. i D. i -【知识点】复数代数形式的混合运算．L4 【答案】【解析】A 解析：复数=++i ii 123()()()()211111i i i i i i i i --+=-+-=+-． 故选：A ．【思路点拨】利用复数的运算法则即可得出．【题文】3.命题“0||,2≥+∈∀x x R x ”的否定是（ ）A.0||,2<+∈∀x x R xB. 0||,2≤+∈∀x x R xC. 0||,2000<+∈∃x x R x D. 0||,2000≥+∈∃x x R x【知识点】命题的否定．A2【答案】【解析】C 解析：根据全称命题的否定是特称命题，则命题“0||,2≥+∈∀x x R x ”的否定0||,2000<+∈∃x x R x ，故选：C ．【思路点拨】根据全称命题的否定是特称命题即可得到结论．【题文】4. 在ABC △中，3AB BC ==，60ABC ∠=︒，AD 是边BC 上的高，则AD ACu u u r u u u r ⋅的值等于（ ） A ．94-B ．94 C ．274D ．9【知识点】平面向量数量积的运算．F3【答案】【解析】C 解析：分别以BC ，AD 所在直线为x 轴，y 轴建立如图所示平面直角坐标系；根据已知条件可求以下几点坐标：A ⎛ ⎝，D ()0,0，C 3,02⎛⎫⎪⎝⎭；∴0,AD u u u r ⎛= ⎝，3,2AC u u u r ⎛= ⎝；∴274AD AC u u u r u u u r ⋅=．故选C ． 【思路点拨】根据已知条件可以分别以BC ，DA 所在直线为x ，y 轴建立平面直角坐标系，而根据已知的边长及角的值可求出向量AD u u u r ，AC u u ur 的坐标，根据数量积的坐标运算即可求出AD AC u u u r u u u r ⋅．【题文】5.设等差数列{}n a 的前n 项和为n S ，若363,15,S S ==则9S =（ ）A ．27B ．36C ．44D ．54 【知识点】数列的求和．D4【答案】【解析】B 解析：∵等差数列{}n a 的前n 项和为n S ，363,15,S S == ∴36396-S S S S S ，，﹣成等差数列．∴2（63-S S ）= 3S + 96S S ﹣．∴2×（15﹣3）=3+ 9S ﹣15，解得9S =36．故选：B ．【思路点拨】利用等差数列{}n a 的前n 项和为n S ，可得36396-S S S S S ，，﹣成等差数列．即可得出．【题文】6. 函数2()3ln f x x x =+-)f 处的切线斜率是（ ）A.-B.【知识点】利用导数研究曲线上某点切线方程．B11【答案】【解析】C 解析：由2()3ln f x x x =+-3()2f x x x'=+-∴f '=．故选：C ．【思路点拨】求出原函数的导函数，然后直接取x =得2()3ln f x x x =+-+在点)f 处的导数值，即切线的斜率．【题文】7. 若将函数sin 2c )s (o 2x x f x +=的图像向左平移ϕ个单位，得到偶函数，则ϕ的最小正值是（ ） A.8πB.4πC.83π D. 43π 【知识点】函数y=Asin （ωx+φ）的图象变换。

江西省赣州中学2015届高三上学期期中物理试卷一、选择题（每小题4分，共40分．第1～6小题只有一个选项正确，第7～10小题有多个选项正确；全部选对的得4分，选对但不全的得2分，有选错或不答的得零分）1．学习物理除了知识的学习外，还要领悟并掌握处理物理问题的思想与方法．下列关于物理学中的思想方法叙述正确的是( )A．万有引力定律和牛顿运动定律一样都是自然界普遍适用的基本规律B．在探究加速度与力、质量的关系实验中使用了理想化模型的思想方法C．库伦利用库伦扭秤巧妙地实现了他对电荷间相互作用力规律的研究D．伽利略用“月﹣地检验”证实了万有引力定律的正确性2．伽利略曾利用对接斜面研究“力与运动”的关系．如图，固定在水平地面上的倾角均为θ的两斜面，以光滑小圆弧相连接，左侧顶端有一小球，与两斜面的动摩擦因数均为μ．小球从左侧顶端滑到最低点的时间为t1，滑到右侧最高点的时间为t2．规定斜面连接处为参考平面，则小球在这个运动过程中速度的大小v、加速度的大小a、动能E k及机械能E随时间t 变化的关系图线正确的是( )A．B．C．D．3．如图所示，水平面B点以左是光滑的，B点以右是粗糙的，质量为m1和m2的两个小物块，在B点以左的光滑水平面上相距L，以相同的速度向右运动．它们先后进入表面粗糙的水平面后，最后停止运动．它们与粗糙表面的动摩擦因数相同，静止后两个质点的距离为x，则有( )A．若m1＞m2，x＞LB．若m1=m2，x=LC．若m1＜m2，x＞LD．无论m1、m2大小关系如何，都应该x=04．如图所示，将一个质量为m的球固定在弹性杆AB的上端，今用测力计沿水平方向缓慢拉球，使杆发生弯曲，在测力计的示数逐渐增大的过程中，AB杆对球的弹力方向为( )A．始终水平向左B．始终竖直向上C．斜向左上方，与竖直方向的夹角逐渐增大D．斜向左下方，与竖直方向的夹角逐渐增大5．如图所示，A、B两小球由绕过轻质定滑轮的细线相连，A放在固定的光滑斜面上，B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连，C球放在水平地面上．现用手控制住A，并使细线刚刚拉直但无拉力作用，并保证滑轮左侧细线竖直、右侧细线与斜面平行．已知A的质量为4m，B、C的质量均为m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放A后，A沿斜面下滑至速度最大时C恰好离开地面．下列说法正确的是( )A．斜面倾角α=60°B．A获得最大速度为2gC．C刚离开地面时，B的加速度最大D．从释放A到C刚离开地面的过程中，A、B两小球组成的系统机械能守恒6．如图所示，质量为m，带电量为q的粒子，以初速度v0，从A点竖直向上射入空气中的沿水平方向的匀强电场中，粒子通过电场中B点时，速率v B=2v0，方向与电场的方向一致，则A，B两点的电势差为( )A．B．C．D．7．如图所示，A、B分别为竖直放置的光滑圆轨道的最低点和最高点，已知小球通过A点时的速度大小为v A=2m/s 则该小球通过最高点B的速度值可能是( )A．10m/s B．m/s C．3m/s D．1.8m/s8．假设将来人类登上了火星，考察完毕后，乘坐一艘宇宙飞船从火星返回地球时，经历了如图所示的变轨过程，则有关这艘飞船的下列说法正确的是( )A．飞船在轨道Ⅰ上运动时的机械能大于飞船在轨道Ⅱ上运动时的机械能B．飞船在轨道Ⅱ上运动时，经过P点时的速度大于经过Q点时的速度C．飞船在轨道Ⅲ上运动到P点时的加速度等于飞船在轨道Ⅱ上运动到P点时的加速度D．飞船绕火星在轨道Ⅰ上运动的周期跟飞船返回地球的过程中绕地球以轨道Ⅰ同样的轨道半径运动的周期相同9．如图所示，一个由轻杆组成的等边三角形ABO的A点和B点分别固定着质量为m和2m 的小球，三角形ABO可绕光滑的水平转轴O自由转动，现使OA处于竖直位置，OB与水平方向的夹角为30°，此时将它们由静止释放，不考虑空气阻力作用，则( )A．B球到达最低点时速度为零B．A球向左摆动所能达到的最高点应高于B球开始运动时的最高点C．当它们从左向右回摆时，B球一定能回到起始位置D．B球到达最低点的过程中，B球机械能的减少量等于A球机械能的增加量10．如图所示，在场强大小为E的匀强电场中，一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是( )A．小球重力与电场力的关系是mg=EqB．小球重力与电场力的关系是Eq=mgC．球在B点时，细线拉力为T=mgD．球在B点时，细线拉力为T=2Eq二、实验题（2小题，第11题10分，第12题8分，共18分11．某实验小组在“探究加速度与物体质量、物体受力的关系”实验中，设计出如下的实验方案，其实验装置如图1所示．已知小车质量M=214.6g，砝码盘质量m0=7.8g，打点计时器所使用的交流电频率为f=50Hz．其实验步骤是A．按图所示安装好实验装置；B．调节长木板的倾角，轻推小车后，使小车能沿长木板向下做匀速运动；C．取下细绳和砝码盘，记下砝码盘中砝码的质量m；D．将小车置于打点计时器旁，先接通电源，再放开小车，打出一条纸带，由纸带求得小车的加速度a；E．重新挂上细绳和砝码盘，改变砝码盘中砝码的质量，重复A、B、C、D步骤，求得小车在不同合外力F作用下的加速度．回答下列问题：（1）按上述方案做实验，是否要求砝码和砝码盘的总质量远小于小车的质量？__________（填“是”或“否”）．（2）实验中打出的其中一条纸带如图2所示，由该纸带可求得小车的加速度a=__________ m/s2．（3）某同学将有关测量数据填入他所设计的表格中，如表：次数 1 2 3 4 5砝码盘中砝码的重力F/N 0.10 0.20 0.29 0.39 0.49小车的加速度a/（m•s﹣2）0.88 1.44 1.84 2.38 2.89他根据表中的数据画出a﹣F图象（如图3）．造成图线不过坐标原点的最主要原因是__________，从该图线延长线与横轴的交点可求出的物理量是__________，其大小为__________．12．某同学利用如图所示的实验装置验证机械能守恒定律．弧形轨道末端水平，离地面的高度为H．将钢球从轨道的不同高度h处静止释放，钢球的落点距轨道末端的水平距离为s．（1）若轨道完全光滑，s2与h的理论关系应满足s2=__________（用H、h表示）．（2）该同学经实验测量得到一组数据，如下表所示：h（10﹣1m） 2.00 3.00 4.00 5.00 6.00s2（10﹣1m2） 2.62 3.89 5.20 6.53 7.78请在坐标纸上作出s2﹣h关系图．（3）对比实验结果与理论计算得到的s2﹣﹣h关系图线（图中已画出），自同一高度静止释放的钢球，水平抛出的速率__________ （填“小于”或“大于”）理论值．（4）从s2﹣h关系图线中分析得出钢球水平抛出的速率差十分显著，你认为造成上述偏差的可能原因是__________．三、计算题（4小题，共42分．解题过程应写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分）13．如图AB两滑环分别套在间距为1m的两根光滑平直杆上，A和B的质量之比为1：3，用一自然长度为1m的轻弹簧将两环相连，在A环上作用一沿杆方向大小为20N的拉力F，当两环都沿杆以相同的加速度a运动时，弹簧与杆夹角为53°．（cos53°=0.6）求：（1）弹簧的劲度系数为多少？（2）若突然撤去拉力F，在撤去拉力F的瞬间，A的加速度为a′，a′与a之间比为多少？14．如图所示，M是水平放置的半径足够大的圆盘，可绕过其圆心的竖直轴OO′匀速转动，在圆心O正上方h处有一个正在间断滴水的容器，每当一滴水落在盘面时恰好下一滴水离开滴口．某次一滴水离开滴口时，容器恰好开始水平向右做速度为v的匀速直线运动，将此滴水记作第一滴水．不计空气阻力，重力加速度为g．求：（1）相邻两滴水下落的时间间隔；（2）要使每一滴水在盘面上的落点都在一条直线上，求圆盘转动的角速度；（3）第二滴和第三滴水在盘面上落点之间的距离最大可为多少？15．静电喷漆技术具有效率高，浪费少，质量好，有利于工人健康等优点，其装置示意图如图所示．A、B为两块平行金属板，间距d=0.30m，两板间有方向由B指向A、电场强度E=1.0×103N/C的匀强电场．在A板的中央放置一个安全接地的静电油漆喷枪P，油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒，油漆微粒的质量m=2.0×10﹣15kg、电荷量为q=﹣2.0×10﹣16C，喷出的初速度v0=2.0m/s．油漆微粒最后都落在金属板B上．微粒所受重力和空气阻力以及微粒之间的相互作用力均可忽略．试求：（1）微粒落在B板上的动能；（2）微粒从离开喷枪后到达B板所需的最短时间；（3）微粒最后落在B板上所形成图形的面积．16．质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A 点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑．B、C 为圆弧的两端点，其连线水平．已知圆弧半径R=1.0m圆弧对应圆心角θ=1060，轨道最低点为O，A点距水平面的高度h=0.8m．小物块离开C点后恰能无碰撞的沿固定斜面向上运动，0.8s后经过D点，物块与斜面间的滑动摩擦因数为μ1=（g=10m/s2，sin37°=0.6，cos37°=0.8）试求：（1）小物块离开A点的水平初速度v1（2）小物块经过O点时对轨道的压力（3）斜面上CD间的距离（4）假设小物块与传送带间的动摩擦因数为μ2=0.3，传送带的速度为5m/s，则PA间的距离是多少？江西省赣州中学2015届高三上学期期中物理试卷一、选择题（每小题4分，共40分．第1～6小题只有一个选项正确，第7～10小题有多个选项正确；全部选对的得4分，选对但不全的得2分，有选错或不答的得零分）1．学习物理除了知识的学习外，还要领悟并掌握处理物理问题的思想与方法．下列关于物理学中的思想方法叙述正确的是( )A．万有引力定律和牛顿运动定律一样都是自然界普遍适用的基本规律B．在探究加速度与力、质量的关系实验中使用了理想化模型的思想方法C．库伦利用库伦扭秤巧妙地实现了他对电荷间相互作用力规律的研究D．伽利略用“月﹣地检验”证实了万有引力定律的正确性考点：物理学史．分析：牛顿定律不是普适规律，具有局限性．运用控制变量法探究加速度与力、质量的关系．库仑发现了电荷间作用力的规律．牛顿用“月﹣地“检验法验证了牛顿定律的正确性，解答：解：A、牛顿第二定律不适用于微观粒子和高速运动的物体，万有引力定律是自然界普遍适用的基本规律，故A错误；B、在探究加速度与力、质量的关系实验中使用了控制变量法，不是理想化模型的思想方法；故B错误．C、库伦利用库伦扭秤实验，发现了电荷间相互作用力的规律，故C正确；D、牛顿用“月﹣地“检验法验证了万有引力定律的正确性，故D错误．故选：C点评：对于著名物理学家、经典实验和重要学说要记牢，还要学习他们的科学研究的方法．2．伽利略曾利用对接斜面研究“力与运动”的关系．如图，固定在水平地面上的倾角均为θ的两斜面，以光滑小圆弧相连接，左侧顶端有一小球，与两斜面的动摩擦因数均为μ．小球从左侧顶端滑到最低点的时间为t1，滑到右侧最高点的时间为t2．规定斜面连接处为参考平面，则小球在这个运动过程中速度的大小v、加速度的大小a、动能E k及机械能E随时间t 变化的关系图线正确的是( )A．B．C．D．考点：伽利略研究自由落体运动的实验和推理方法．专题：常规题型．分析：据牛顿第二定律求出上滑和下滑过程中的加速度大小，从而得出速度随时间的变化规律，根据动能与速度大小的关系得出动能与时间t变化的关系求解．解答：解：A、由牛顿第二定律可知，小球在两斜面的运动都是匀变速直线运动，两阶段的加速度都恒定不变，小球在左侧斜面下滑时的加速度：a1=gsinθ﹣μgcosθ小球在右侧斜面下滑时的加速度：a2=gsinθ+μgcosθ，小球在左侧斜面下滑时的加速度较小，故A错误，B正确；C、小球的动能与速率的二次方成正比，即E k=mv2，因此，动能与时间关系图象是曲线，故C错误；D、由于小球在两斜面运动时的加速度大小不相等，因此，小球机械能与时间的关系图象不是连续曲线，故D错误；故选：B．点评：解决本题的关键根据牛顿第二定律得出上滑和下滑的加速度，判断出物体的运动情况．3．如图所示，水平面B点以左是光滑的，B点以右是粗糙的，质量为m1和m2的两个小物块，在B点以左的光滑水平面上相距L，以相同的速度向右运动．它们先后进入表面粗糙的水平面后，最后停止运动．它们与粗糙表面的动摩擦因数相同，静止后两个质点的距离为x，则有( )A．若m1＞m2，x＞LB．若m1=m2，x=LC．若m1＜m2，x＞LD．无论m1、m2大小关系如何，都应该x=0考点：牛顿第二定律；匀变速直线运动的位移与时间的关系．专题：牛顿运动定律综合专题．分析：两物块进入粗糙水平面的初速度相同，末速度都为零，根据牛顿第二定律比较出两物块的加速度大小，即可比较出两物块在粗糙水平面上运行的位移大小，从而得出x．解答：解：根据牛顿第二定律得，物块进入粗糙水平面的加速度a=，知两物块的加速度相等，又进入粗糙水平面的初速度相同，末速度都为零，根据运动学公式，知两物块运行的位移s相等，则x=0．故D正确，A、B、C错误．故选D．点评：解决本题的关键掌握牛顿第二定律求出加速度，以及知道两物块的初末速度相等，加速度相等，所以在粗糙水平面上运行的位移相等．4．如图所示，将一个质量为m的球固定在弹性杆AB的上端，今用测力计沿水平方向缓慢拉球，使杆发生弯曲，在测力计的示数逐渐增大的过程中，AB杆对球的弹力方向为( )A．始终水平向左B．始终竖直向上C．斜向左上方，与竖直方向的夹角逐渐增大D．斜向左下方，与竖直方向的夹角逐渐增大考点：牛顿第三定律．专题：牛顿运动定律综合专题．分析：分析球的受力情况：重力、测力计的拉力和AB杆对球作用力，由平衡条件求出AB 杆对球弹力方向．解答：解：以球为研究对象，分析受力情况：重力G、测力计的拉力T和AB杆对球作用力F，由平衡条件知，F与G、T的合力大小相等、方向相反，作出力的合成图如图．则有G、T的合力方向斜向右下方，测力计的示数逐渐增大，T逐渐增长，根据向量加法可知G、T的合力方向与竖直方向的夹角逐渐增大，所以AB杆对球的弹力方向斜向左上方，与竖直方向的夹角逐渐增大，所以选项ABD错误，C正确．故选C．点评：本题是三力平衡问题，分析受力情况，作出力图是关键．难度不大．5．如图所示，A、B两小球由绕过轻质定滑轮的细线相连，A放在固定的光滑斜面上，B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连，C球放在水平地面上．现用手控制住A，并使细线刚刚拉直但无拉力作用，并保证滑轮左侧细线竖直、右侧细线与斜面平行．已知A的质量为4m，B、C的质量均为m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放A后，A沿斜面下滑至速度最大时C恰好离开地面．下列说法正确的是( )A．斜面倾角α=60°B．A获得最大速度为2gC．C刚离开地面时，B的加速度最大D．从释放A到C刚离开地面的过程中，A、B两小球组成的系统机械能守恒考点：机械能守恒定律；牛顿第二定律．专题：机械能守恒定律应用专题．分析：C刚离开地面时，弹簧的弹力等于C的重力，根据牛顿第二定律知B的加速度为零，B、C加速度相同，分别对B、A受力分析，列出平衡方程，求出斜面的倾角．A、B、C组成的系统机械能守恒，初始位置弹簧处于压缩状态，当B具有最大速度时，弹簧处于伸长状态，根据受力知，压缩量与伸长量相等．在整个过程中弹性势能变化为零，根据系统机械能守恒求出B的最大速度，A的最大速度与B相等．解答：解：A、A刚离开地面时，对A有：kx2=mg此时B有最大速度，即a B=a C=0则对B有：T﹣kx2﹣mg=0对A有：4mgsinα﹣T=0以上方程联立可解得：sinα=0.5，α=30°，故A错误；B、初始系统静止，且线上无拉力，对B有：kx1=mg由上问知x1=x2=，则从释放至A刚离开地面过程中，弹性势能变化量为零；此过程中A、B、C组成的系统机械能守恒，即：4mg（x1+x2）sinα=mg（x1+x2）+（4m+m）v Bm2以上方程联立可解得：v Bm=2g所以A获得最大速度为2g，故B正确；C、对B球进行受力分析可知，刚释放A时，B所受合力最大，此时B具有最大加速度，故C错误；D、从释放A到C刚离开地面的过程中，A、B、C及弹簧组成的系统机械能守恒，故D错误．故选：B．点评：本题关键是对三个物体分别受力分析，得出物体B速度最大时各个物体都受力平衡，然后根据平衡条件分析；同时要注意是那个系统机械能守恒．6．如图所示，质量为m，带电量为q的粒子，以初速度v0，从A点竖直向上射入空气中的沿水平方向的匀强电场中，粒子通过电场中B点时，速率v B=2v0，方向与电场的方向一致，则A，B两点的电势差为( )A．B．C．D．考点：电势差；动能定理的应用；带电粒子在匀强电场中的运动．专题：电场力与电势的性质专题．分析：微粒在匀强电场中受到重力和电场力两个力作用，根据动能定理求出AB两点间的电势差U AB解答：解：粒子，从A到B，根据动能定理得：qU AB﹣mgh=因为v B=2v0，若只考虑粒子在竖直方向，只受到重力，所以机械能守恒，则有mgh=由以上三式，则有U AB=故选：C点评：涉及到电势差的问题，常常要用到动能定理．本题的难点在于运动的处理，由于微粒受到两个恒力作用，运用运动的分解是常用的方法．7．如图所示，A、B分别为竖直放置的光滑圆轨道的最低点和最高点，已知小球通过A点时的速度大小为v A=2m/s 则该小球通过最高点B的速度值可能是( )A．10m/s B．m/s C．3m/s D．1.8m/s考点：牛顿第二定律；向心力．专题：牛顿第二定律在圆周运动中的应用．分析：小球在光滑的圆轨道内运动，只有重力做功，其机械能守恒，根据机械能守恒定律得到小球在最高点的速度表达式．小球要能到达最高点，向心力要大于重力，得到最高点速度的范围，再进行选择．解答：解：设小球到达最高点B的速度为v B．根据机械能守恒定律得mg•2R+=得到v B=①小球要能到达最高点，则在最高点B时，得到v B②由①②联立得≥解得gR≤代入得gR≤4代入①得v B≥2m/s又机械能守恒定律可知，v B＜v A=2m/s所以2m/s≤v B＜2m/s故选BC点评：本题是机械能守恒定律、向心力等知识的综合应用，关键是临界条件的应用：当小球恰好到达最高点时，由重力提供向心力，临界速度v0=，与细线的模型相似．8．假设将来人类登上了火星，考察完毕后，乘坐一艘宇宙飞船从火星返回地球时，经历了如图所示的变轨过程，则有关这艘飞船的下列说法正确的是( )A．飞船在轨道Ⅰ上运动时的机械能大于飞船在轨道Ⅱ上运动时的机械能B．飞船在轨道Ⅱ上运动时，经过P点时的速度大于经过Q点时的速度C．飞船在轨道Ⅲ上运动到P点时的加速度等于飞船在轨道Ⅱ上运动到P点时的加速度D．飞船绕火星在轨道Ⅰ上运动的周期跟飞船返回地球的过程中绕地球以轨道Ⅰ同样的轨道半径运动的周期相同考点：人造卫星的环绕速度．专题：人造卫星问题．分析：1、飞船从轨道Ⅰ转移到轨道Ⅱ上运动，必须在P点时，点火加速，使其速度增大做离心运动，即机械能增大．2、根据开普勒第二定律可知，飞船在轨道Ⅱ上运动时，在P点速度大于在Q点的速度．3、飞船在轨道Ⅰ上运动到P点时与飞船在轨道Ⅱ上运动到P点时，都由火星的万有引力产生加速度，根据牛顿第二定律列式比较加速度．4、根据万有引力等于向心力列式，比较周期．解答：解：A、飞船在轨道Ⅰ上经过P点时，要点火加速，使其速度增大做离心运动，从而转移到轨道Ⅱ上运动．所以飞船在轨道Ⅰ上运动时的机械能小于轨道Ⅱ上运动的机械能．故A错误．B、根据开普勒第二定律可知，飞船在轨道Ⅱ上运动时，在P点速度大于在Q点的速度．故B正确．C、飞船在轨道Ⅲ上运动到P点时与飞船在轨道Ⅱ上运动到P点时受到的万有引力大小相等，根据牛顿第二定律可知加速度必定相等．故C正确．D、根据G=m，得周期公式T=2π，虽然r相等，但是由于地球和火星的质量不等，所以周期T不相等．故D错误．故选BC．点评：本题要知道飞船在轨道Ⅰ上运动到P点时与飞船在轨道Ⅱ上运动到P点时受到的万有引力大小相等，根据牛顿第二定律可知加速度必定相等，与轨道和其它量无关．9．如图所示，一个由轻杆组成的等边三角形ABO的A点和B点分别固定着质量为m和2m 的小球，三角形ABO可绕光滑的水平转轴O自由转动，现使OA处于竖直位置，OB与水平方向的夹角为30°，此时将它们由静止释放，不考虑空气阻力作用，则( )A．B球到达最低点时速度为零B．A球向左摆动所能达到的最高点应高于B球开始运动时的最高点C．当它们从左向右回摆时，B球一定能回到起始位置D．B球到达最低点的过程中，B球机械能的减少量等于A球机械能的增加量考点：机械能守恒定律．专题：机械能守恒定律应用专题．分析：对于两球组成的系统只有重力做功，机械能守恒．根据机械能定律进行分析．解答：解：A、当B球到达最低点时，A上升到B球原来等高的位置，因为B减少的势能比A增加的势能要在，所以系统的重力势能减少，动能增加，A、B两者还具有相同大小的速度，故B 球到达最低点时速度不为零，故A错误．B、由上分析可知，当A向左摆到与B球开始时的高度时，B球到达最低点，由于此时仍有速度，还要向左摆动，可知A摆的高度比B球的高度要2014-2015学年高一些，故B正确．C、根据系统的机械能守恒可知当它们从左向右回摆时，B球一定能回到起始位置，故C正确．D、对于两球组成的系统只有重力做功，机械能守恒，根据系统机械能守恒得知：B球到达最低点的过程中，B球机械能的减少量等于A球机械能的增加量，故D正确．故选：BCD点评：本题是轻杆构成的系统机械能守恒，要正确分析动能和重力势能是如何转化，结合几何关系和对称性进行分析这类问题．10．如图所示，在场强大小为E的匀强电场中，一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是( )A．小球重力与电场力的关系是mg=EqB．小球重力与电场力的关系是Eq=mgC．球在B点时，细线拉力为T=mgD．球在B点时，细线拉力为T=2Eq考点：匀强电场；力的合成与分解的运用；向心力；动能定理的应用；电势能．专题：压轴题；电场力与电势的性质专题．分析：类比单摆，小球从A点静止释放，运动到B点速度为0，说明弧AB的中点是运动的最低点，对小球进行受力分析，小球处在弧线中点位置时切线方向合力为零，再根据几何关系可以求出Eq，球到达B点时速度为零，向心力为零，则沿细线方向合力为零，此时对小球受力分析，再根据几何关系即可解题．解答：解：（1）类比单摆，根据对称性可知，小球处在弧线中点位置时切线方向合力为零，此时细线与水平方向夹角恰为30°，根据三角函数关系可得：qEsin30°=mgcos30°，化简可知Eq=mg，选项A错误、B正确；（2）小球到达B点时速度为零，向心力为零，则沿细线方向合力为零，此时对小球受力分析可知：T=qEcos60°+mgsin60°，故细线拉力T=mg，选项C正确、D错误．故选BC．点评：本题要求同学们能正确进行受力，并能联想到已学的物理模型，根据相关公式解题．二、实验题（2小题，第11题10分，第12题8分，共18分11．某实验小组在“探究加速度与物体质量、物体受力的关系”实验中，设计出如下的实验方案，其实验装置如图1所示．已知小车质量M=214.6g，砝码盘质量m0=7.8g，打点计时器所使用的交流电频率为f=50Hz．其实验步骤是A．按图所示安装好实验装置；B．调节长木板的倾角，轻推小车后，使小车能沿长木板向下做匀速运动；C．取下细绳和砝码盘，记下砝码盘中砝码的质量m；D．将小车置于打点计时器旁，先接通电源，再放开小车，打出一条纸带，由纸带求得小车的加速度a；E．重新挂上细绳和砝码盘，改变砝码盘中砝码的质量，重复A、B、C、D步骤，求得小车在不同合外力F作用下的加速度．回答下列问题：（1）按上述方案做实验，是否要求砝码和砝码盘的总质量远小于小车的质量？否（填“是”或“否”）．（2）实验中打出的其中一条纸带如图2所示，由该纸带可求得小车的加速度a=0.88 m/s2．（3）某同学将有关测量数据填入他所设计的表格中，如表：次数 1 2 3 4 5砝码盘中砝码的重力F/N 0.10 0.20 0.29 0.39 0.49小车的加速度。

2014-2015学年第一学期赣州市十二县（市）期中联考高三年级化学试卷相对原子质量：H—1、C-12、N-14、O—16、Na—23、Al-27、S—32、Cl-35.5 、K-39、Cr-52、Fe—56、I-127、Ba-137一、选择题（每小题只有一个正确选项，每小题3分，共48分）1．下列实验方法能达到目的的是（）A．用氨水清洗试管内壁附着的银镜B．将NH4Cl溶液蒸干制备NH4Cl固体C．制备Fe(OH)3胶体，向盛有沸水的烧杯中滴加FeCl3饱和溶液并长时间煮沸D．可用K3［Fe(CN)6］溶液鉴定FeCl3溶液中是否存在Fe2+2．下列反应与Na2O2＋SO2==Na2SO4相比较，Na2O2的作用相同的是（）A．2Na2O2＋2CO2==2Na2CO3＋O2↑ B．2Na2O2＋2SO3==2Na2SO4＋O2↑C．Na2O2＋H2SO4==Na2SO4＋H2O2 D．3Na2O2＋Cr2O3==2Na2CrO4＋Na2O3．设N A表示阿伏加德罗常数的值,下列有关N A的叙述中不正确的有（）A.标准状况下,20 g重水(D2O)中含有的电子数为10N AB.乙烯和环丙烷组成的42 g混合气体中氢原子的个数为6N AC.22.4 L的N2的共用电子对数为3N AD.78gNa2O2固体中含有的阴离子数为N A4．25℃时，下列各组离子在指定溶液中一定能大量共存的是（）A．0.1mol·L－1 AlC13溶液中：H+、Na+、Cl－、SO42－B．含有0.1mol·L－1 Fe3+的溶液中：Na+、K+、SCN－、NO3－C．使甲基橙变红色的溶液中：Fe2+、K+、NO3－、SO42－D．由水电离产生的c(H+)=10－12mol·L－1的溶液中：NH4+、SO42－、HCO3－、Cl－5．M是一种治疗艾滋病的新药(结构简式见下图)，已知M分子中—NH—COO—(除H外)与苯环在同一平面内，关于M的以下说法正确的是（）A．该物质易溶于水B．M的分子式为C13H12O2NF4C．M能发生加聚反应D．M分子内至少有13个碳原子在同一平面内6．下列指定反应的离子方程式正确的是（）A．向苯酚钠溶液中通入少量的CO2：C6H5O－+CO2+H2O → C6H5OH+HCO3－B．FeS固体放入稀硝酸溶液中：FeS＋2H＋＝ Fe2+＋H2S↑C．(NH4)2Fe(SO4)2溶液与过量NaOH溶液反应制Fe(OH)2：Fe2++2OH－ = Fe(OH)2↓D．用惰性电极电解氯化钠溶液：2Cl－+2H+通电 H2↑+Cl2↑7．在1 L溶液中含有Fe(NO3)3和H2SO4两种溶质，其浓度分别为0.2 mol•L-1和1.5 mol•L-1，现向该溶液中加入39.2 g铁粉使其充分反应。

2014-2015学年江西省赣州市十二县（市）联考高三（上）期中数学试卷（文科）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知集合A={x|（x+1）（x﹣2）≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0}B．{0，1}C．{﹣2，﹣1，0，1}D．{﹣1，0，1，2} 2．（5分）设i是虚数单位，复数i3+=（）A．1 B．﹣1 C．i D．﹣i3．（5分）命题“∀x∈R，|x|+x2≥0”的否定是（）A．∀x∈R，|x|+x2＜0 B．∀x∈R，|x|+x2≤0C．∃x0∈R，|x0|+x02＜0 D．∃x0∈R，|x0|+x02≥04．（5分）在△ABC中，||=||=3，∠ABC=60°，AD是边BC上的高，则的值等于（）A．B．C．D．95．（5分）设等差数列{a n}的前n项和为S n，若S3=3，S6=15，则S9=（）A．27 B．36 C．44 D．546．（5分）函数f（x）=3lnx+x2﹣在点处的切线斜率是（）A．B．C．D．7．（5分）若将函数f（x）=sin2x+cos2x的图象向左平移φ个单位，得到偶函数，则φ的最小正值是（）A．B．C． D．8．（5分）已知函数，则函数y=f（x）的大致图象为（）A．B．C．D．9．（5分）函数f（x）=的图象关于原点对称，g（x）=lg（10x+1）+bx是偶函数，则a+b=（）A．1 B．﹣1 C．﹣ D．10．（5分）设x，y满足约束条件且，z=x+ay的最小值为17，则a=（）A．﹣7 B．5 C．﹣7或5 D．﹣5或7二、填空题：（本大题共5小题，每小题5分，共25分．）11．（5分）已知数列{a n}为等比数列，且a6=4，a10=64，则a8=．12．（5分）设0＜θ＜，向量=（sin2θ，cosθ），=（1，﹣cosθ），若•=0，则tanθ=．13．（5分）若函数f（x）=+（3﹣a）x+b有三个不同的单调区间，则实数a的取值范围是．14．（5分）设函数f（x）=，则使得f（x）≤2成立的x的取值范围是．15．（5分）已知实数a，b，c满足a+b+c=0，a2+b2+c2=1，则a的最大值是．三、解答题（本大题共6小题.解答应写出文字说明、证明过程或演算步骤.）16．（12分）记关于x的不等式的解集为P，不等式|x﹣1|≤1的解集为Q．（1）若a=3，求P；（2）若a＞0，且P∩Q=Q，求实数a的取值范围．17．（12分）已知函数f（x）=sin（2x+）+sin（2x﹣）﹣cos2x+a（a∈R，a 为常数）．（1）求函数f（x）的最小正周期和单调递增区间；（2）若x∈[0，]时，求函数f（x）的值域．18．（12分）在△ABC中，（1）求角B；（2）若tanA=，求sinC的值．19．（12分）数列{a n}满足a1=1，na n﹣1=（n﹣1）a n﹣n（n﹣1），n≥2且n∈N+（Ⅰ）证明：数列是等差数列；（Ⅱ）设b n=3n﹣1•，求数列{b n}的前n项和S n．20．（13分）已知函数f（x）=﹣alnx（a∈R）．（1）求f（x）的单调区间；（2）设g（x）=f（x）+2x，若g（x）在[1，e]上不单调且仅在x=e处取得最大值，求a的取值范围．21．（14分）已知函数f（x）=x3+3|x﹣a|（a＞0），若f（x）在[﹣1，1]上的最小值记为g（a）．（Ⅰ）求g（a）；（Ⅱ）证明：当x∈[﹣1，1]时，恒有f（x）≤g（a）+4．2014-2015学年江西省赣州市十二县（市）联考高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知集合A={x|（x+1）（x﹣2）≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0}B．{0，1}C．{﹣2，﹣1，0，1}D．{﹣1，0，1，2}【解答】解：A={x|（x+1）（x﹣2）≤0}={x|﹣1≤x≤2}，又集合B为整数集，故A∩B={﹣1，0，1，2}故选：D．2．（5分）设i是虚数单位，复数i3+=（）A．1 B．﹣1 C．i D．﹣i【解答】解：复数i3+=﹣i+=﹣i+i（1﹣i）=1．故选：A．3．（5分）命题“∀x∈R，|x|+x2≥0”的否定是（）A．∀x∈R，|x|+x2＜0 B．∀x∈R，|x|+x2≤0C．∃x0∈R，|x0|+x02＜0 D．∃x0∈R，|x0|+x02≥0【解答】解：根据全称命题的否定是特称命题，则命题“∀x∈R，|x|+x2≥0”的否定∃x0∈R，|x0|+x02＜0，故选：C．4．（5分）在△ABC中，||=||=3，∠ABC=60°，AD是边BC上的高，则的值等于（）A．B．C．D．9【解答】解：分别以BC，AD所在直线为x轴，y轴建立如图所示平面直角坐标系；根据已知条件可求以下几点坐标：A（0，），D（0，0），C（）；∴；∴．故选：C．5．（5分）设等差数列{a n}的前n项和为S n，若S3=3，S6=15，则S9=（）A．27 B．36 C．44 D．54【解答】解：∵等差数列{a n}的前n项和为S n，S3=3，S6=15，∴S3，S6﹣S3，S9﹣S6成等差数列．∴2（S6﹣S3）=S3+S9﹣S6．∴2×（15﹣3）=3+S9﹣15，解得S9=36．故选：B．6．（5分）函数f（x）=3lnx+x2﹣在点处的切线斜率是（）A．B．C．D．【解答】解：由f（x）=3lnx+x2﹣得f′（x）=，∴y′|x==2．故选：C．7．（5分）若将函数f（x）=sin2x+cos2x的图象向左平移φ个单位，得到偶函数，则φ的最小正值是（）A．B．C． D．【解答】解：由f（x）=sin2x+cos2x=sin（2x+），把该函数的图象左移φ个单位，所得图象对应的函数解析式为：y=sin[2（x+φ）+]=sin（2x++2φ）．又偶函数图象关于y轴对称，则+2φ=k，k∈Z．则φ=，k∈Z．∴当k=0时，φ有最小正值是．故选：A．8．（5分）已知函数，则函数y=f（x）的大致图象为（）A．B．C．D．【解答】解：函数y=f（x）是一个非奇非偶函数，图象不关于原点对称，故排除选项A、C，又当x=﹣1时，函数值等于0，故排除D，故选：B．9．（5分）函数f（x）=的图象关于原点对称，g（x）=lg（10x+1）+bx是偶函数，则a+b=（）A．1 B．﹣1 C．﹣ D．【解答】解：∵f（x）=关于原点对称，∴函数f（x）是奇函数，∴f（0）=0，∴a=1∵g（x）=lg（10x+1）+bx是偶函数，∴g（﹣x）=g（x）对任意的x都成立，∴lg（10﹣x+1）﹣bx=lg（10x+1）+bx，∴lg（）=lg（10x+1）+2bx∴﹣x=2bx对一切x恒成立，∴b=﹣，∴a+b=故选：D．10．（5分）设x，y满足约束条件且，z=x+ay的最小值为17，则a=（）A．﹣7 B．5 C．﹣7或5 D．﹣5或7【解答】解：作出不等式组对应的平面区域如图：联立，解得∴A（，）．①当a=0时A为（，），z=x+ay的最小值为，不满足题意；②当a＜0时，由z=x+ay得y=x+，要使z最小，则直线y=x+，在y轴上的截距最大，满足条件的最优解不存在；③当a＞0时，由z=x+ay得y=x+，由图可知，当直线过点A时直线y=x+，在y轴上的截距最小，z最小．此时z=+a•=．即a2+2a﹣35=0解得：a=5或a=﹣﹣7（舍）．故选：B．二、填空题：（本大题共5小题，每小题5分，共25分．）11．（5分）已知数列{a n}为等比数列，且a6=4，a10=64，则a8=16．【解答】解：因为已知数列{a n}为等比数列，且a6=4，a10=64，则a82=a6×a10=4×64=162，所以a8=16；故答案为：16．12．（5分）设0＜θ＜，向量=（sin2θ，cosθ），=（1，﹣cosθ），若•=0，则tanθ=．【解答】解：∵=sin2θ﹣cos2θ=2sinθcosθ﹣cos2θ=0，0＜θ＜，∴2sinθ﹣cosθ=0，∴tanθ=，故答案为：．13．（5分）若函数f（x）=+（3﹣a）x+b有三个不同的单调区间，则实数a的取值范围是a＞2或a＜﹣6．【解答】解：∵函数f（x）=+（3﹣a）x+b有三个不同的单调区间，∴y′=x2﹣ax+（3﹣a）的图象与x轴有两个交点，∴△=a2﹣4（3﹣a）＞0，∴a＞2或a＜﹣6，故答案为：a＞2或a＜﹣6．14．（5分）设函数f（x）=，则使得f（x）≤2成立的x的取值范围是[0，4] ．【解答】解：由题意，f（x）≤2得及，解得0≤x＜1及1≤x≤4，所以使得f（x）≤2成立的x的取值范围是[0，4]；故答案为：[0，4]；本题函数图象：15．（5分）已知实数a，b，c满足a+b+c=0，a2+b2+c2=1，则a的最大值是．【解答】解：∵a+b+c=0，a2+b2+c2=1，∴b+c=﹣a，b2+c2=1﹣a2，∴bc=•（2bc）=[（b+c）2﹣（b2+c2）]=a2﹣∴b、c是方程：x2+ax+a2﹣=0的两个实数根，∴△≥0∴a2﹣4（a2﹣）≥0即a2≤∴﹣≤a≤即a的最大值为故答案为：．三、解答题（本大题共6小题.解答应写出文字说明、证明过程或演算步骤.）16．（12分）记关于x的不等式的解集为P，不等式|x﹣1|≤1的解集为Q．（1）若a=3，求P；（2）若a＞0，且P∩Q=Q，求实数a的取值范围．【解答】解：（1）由，得（x﹣3）（x+1）＜0，即﹣1＜x＜3．∴P={x|﹣1＜x＜3}；（2）Q={x||x﹣1|≤1}={x|0≤x≤2}．由a＞0，得P={x|﹣1＜x＜a}，又P∩Q=Q，∴Q⊆P，∴a＞2．17．（12分）已知函数f（x）=sin（2x+）+sin（2x﹣）﹣cos2x+a（a∈R，a 为常数）．（1）求函数f（x）的最小正周期和单调递增区间；（2）若x∈[0，]时，求函数f（x）的值域．【解答】（本小题满分12分）解：（1）函数f（x）=sin（2x+）+sin（2x﹣）﹣cos2x+a==2∴f（x）的最小正周期为：T=令（k∈Z）解得：故函数f（x）的单调递增区间为：[]（k∈Z），（2）当，则：，∴∴f（x）值域为[a﹣1，a+2]18．（12分）在△ABC中，（1）求角B；（2）若tanA=，求sinC的值．【解答】解：（1）原式可化简为，由正弦定理知：a=sinA×2R，b=sinB×2R，c=sinC×2R，代入上式，∴，由余弦定理可知cosB==，∴∵（2）∵，A为锐角，sinA＞0，cosA＞0，，故有sinA=由于sinA2+cosA2=1，故有，∴，∴sinC=sin（A+B）=sinAcosB+cosAsinB==．19．（12分）数列{a n}满足a1=1，na n﹣1=（n﹣1）a n﹣n（n﹣1），n≥2且n∈N+（Ⅰ）证明：数列是等差数列；（Ⅱ）设b n=3n﹣1•，求数列{b n}的前n项和S n．【解答】（Ⅰ）证：由已知可得，即，∴是以为首项，1为公差的等差数列．（Ⅱ）解：由（Ⅰ）得，∴，从而，①②①﹣②得，=．∴．20．（13分）已知函数f（x）=﹣alnx（a∈R）．（1）求f（x）的单调区间；（2）设g（x）=f（x）+2x，若g（x）在[1，e]上不单调且仅在x=e处取得最大值，求a的取值范围．【解答】解：（Ⅰ）f′（x）=x﹣=（x＞0）﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）若a≤0，则f′（x）≥0，所以此时只有递增区间（0，+∞）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）若a＞0，当f′（x）＞0时，得x＞，当f′（x）＜0时，得0＜x＜，所以此时递增区间为：（，+∞），递减区间为：（0，）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（Ⅱ）g′（x）=x﹣+2=（x＞0），设h（x）=x2+2x﹣a（x＞0）若g（x）在[1，e]上不单调，则h（1）h（e）＜0，∴（3﹣a）（e2+2e﹣a）＜0∴3＜a＜e2+2e，同时g（x）仅在x=e处取得最大值，∴只要g（e）＞g（1）即可得出：a＜+2e﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）∴a的范围：（3，+2e﹣）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（15分）21．（14分）已知函数f（x）=x3+3|x﹣a|（a＞0），若f（x）在[﹣1，1]上的最小值记为g（a）．（Ⅰ）求g（a）；（Ⅱ）证明：当x∈[﹣1，1]时，恒有f（x）≤g（a）+4．【解答】（Ⅰ）解：∵a＞0，﹣1≤x≤1，①当0＜a＜1时，若x∈[﹣1，a]，则f（x）=x3﹣3x+3a，f′（x）=3x2﹣3＜0，故此时函数在（﹣1，a）上是减函数，若x∈（a，1]，则f（x）=x3+3x﹣3a，f′（x）=3x2+3＞0，故此时函数在（a，1）上是增函数，∴g（a）=f（a）=a3．②当a≥1，f（x）=x3+3|x﹣a|=x3﹣3x+3a，f′（x）=3x2﹣3＜0，故此时函数在[﹣1，1]上是减函数， 则g （a ）=f （1）=﹣2+3a ．综上：g （a ）=．（Ⅱ）证明：设h （x ）=f （x ）﹣g （a ）， ①当0＜a ＜1时，g （a ）=a 3，若x ∈[a ，1]，h （x ）=x 3+3x ﹣3a ﹣a 3，h′（x ）=3x 2+3， ∴h （x ）在[a ，1]上是增函数，∴h （x ）在[a ，1]上的最大值是h （1）=4﹣3a ﹣a 3，且0＜a ＜1，∴h （1）≤4，∴f （x ）≤g （a ）+4．若x ∈[﹣1，a ]，h （x ）=x 3﹣3x +3a ﹣a 3，h′（x ）=3x 2﹣3， ∴h （x ）在[﹣1，a ]上是减函数，∴h （x ）在[﹣1，a ]上的最大值是h （﹣1）=2+3a ﹣a 3，令t （a ）=2+3a ﹣a 3，则t′（a ）=3﹣3a 2，∴t （a ）在（0，1）上是增函数， ∴t （a ）＜t （1）=4∴h （﹣1）＜4，∴f （x ）≤g （a ）+4．②a ≥1时，g （a ）=﹣2+3a ，∴h （x ）=x 3﹣3x +2，∴h′（x ）=3x 2﹣3， ∴h （x ）在[﹣1，1]上是减函数，∴h （x ）在[﹣1，1]上的最大值是h （﹣1）=4， ∴f （x ）≤g （a ）+4；综上，当x ∈[﹣1，1]时，恒有f （x ）≤g （a ）+4．赠送—高中数学知识点【2.1.1】指数与指数幂的运算 （1）根式的概念①如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n n a n 是偶数时，正数a 的正的n n a 表示，负的n 次方根用符号n a -0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当n 为奇数时，a =；当n 为偶数时，(0)|| (0) nn a a a a a a ≥⎧==⎨-<⎩． （2）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mn m na a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义． 注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈【2.1.2】指数函数及其性质 （4）指数函数〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>． （2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）． （4）对数的运算性质 如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a a MM N N-= ③数乘：log log ()n a a n M M n R =∈ ④log a NaN =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质定义域 (0,)+∞值域 R过定点 图象过定点(1,0)，即当1x =时，0y =．奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<变化对图象的影响 在第一象限内，a 越大图象越靠低；在第四象限内，a 越大图象越靠高．x O(1,0)xO (1,0)。

江西省赣州市十二县（市）重点中学2015届高三上学期期中考试语文试题高三2013-11-12 18:59江西省赣州市十二县（市）重点中学2015届高三上学期期中考试语文试题本试卷分第I卷(选择题)和第Ⅱ卷两部分。

共1 5 0分，考试时间l 5 0分钟。

第I卷(选择题，共3 6分)一、(1 8分，每小题3分)1．下列词语中，加点字的读音完全正确的一组是 ( )A. 供给jǐ包庇bì框kuāng架随声附和（hè）B. 蹊qī跷提dī防翘qiào首乘（chéng）人之危C. 罹lí难悭qiān吝请帖tiě自怨自艾（yì）D. 浸渍zì破绽zhàn咋舌zhà不着（zhuó）边际2．下列词语中，没有错别字的一组是 ( )A．厮打照相机额手称庆原形毕露B．蹙缩必需品不明就理变幻无穷C．瓦楞金钢钻以逸待劳相辅相成D．蜷缩钓鱼竿分庭抗礼不悲不亢3．下列各句中，加点成语使用恰当的一项是 ( )A．昨天,南昌、九江等地400多位老知青在江西饭店欢聚一堂，共同回忆起了当年让人激情燃烧的蹉跎岁月。

B.教授李大潜院士认为，应用数学要真正取得成果，转化成生产力，有比较长的周期，所以校方和企业都要对此有耐心，不要趋利避害。

C.安检人员目不交睫地盯着安检显示仪，突然一个画面定格在工作人员面前：一个包裹里藏有一支枪!机场方面立即将该包裹扣押并报警。

D．在经历了几次进入国际大赛决赛却功败垂成之后，2012年李晓霞终于在伦敦奥运会上捧起了奥运会冠军奖杯。

4．依次填入下面一段文字横线处的语句，衔接最恰当的一组是（）。

人总是需要一点精神的,___ 。

①实现中国梦，要求我们不仅要在物质上强大起来，也要在精神上强大起来。

②一个国家和民族更是这样。

③物质贫乏不是社会主义，精神空虚也不是社会主义。

④没有人的精神的有力支撑，就没有全民族精神力量的充分发挥，⑤一个国家一个民族就不可能屹立世界民族之林。