下载文档原格式
第二章 超声波发射声场与——规则反射体的回波声压§2.1纵波发射声场一、圆盘声源辐射的纵波声场 1.波源轴线上的声压分布如图2.1所示,设液体介质中有一圆盘声源作连续活塞振动,辐射单一频率的连续正弦波。
图2.1圆盘声源轴线上的声压)(2220X X R Sin P P -+=λπR 一波源的半径,波源直径D=2R;当m>D(2R)时,(2.1)式可简化为:λπX DSinP P 8220=当X时，进一步简化：λX F P P 0=式中：F ——波源的面积，。
圆盘声源轴线上的声压分布规律如图2.2所示。
图2.2声学上把由子波的干涉在波源附近的轴线上产生一系列声压极大极小值的区域称为超声场的近场区,又称菲涅耳区。
波源轴线上最后一个声压极大值至波源的距离称为近场区长度,用N 表示。
近场区长度N 可以用下式来计算：λλλ44222D D N =-=2.超声场截面声压分布3.波束指向性与半扩散角超声波的能量主要集中在以内的锥形区域内，此区域称为主波束。
圆晶片辐射的波束半扩散角为:D Dλλθ7022.1arcsin 0==4.未扩散区与扩散区从理想化圆晶片辐射的声场(图 2.5)可以发现,超声波扩散波束并不是从波源开始扩散的,N b 64.1=式中：N 一近场区长度。
二、矩形波源辐射的纵波声场长为α、宽为b 的矩形波源作活塞振动,在液体介质中辐射的纵波声场类似于圆盘源，当x 3N 时,波束轴线上的声压为：λX Fp P 0=(a) (b)图2.6 矩形波源的指向性当a=b 时,波源为正方形。
波束在X 和Y 方向的半扩散角均为za aλλθ57arcsin0==（度）§2.2横波发射声场一、 假想波源图2.9横波声的与假想波源四、指向性和半扩散角图2.10横波声场半扩散声ββθ-2=上1-ββθ=下b a -=1sin β b a +=2sin β21)22.1(1sin Da L λβ-=αλCos DC C b L S L 12122.1=在通过声束轴线入射平面垂直的平面内，声束对称于轴线，这时半扩散角可按下式计算。
第二章超声波发射声场与规则反射体的回波声压超声波探头(波源)发射的超声场，具有特殊的结构。
只有当缺陷位于超声场内时，才有有可能被发现。
由于液体介质中的声压可以进行线性叠加，并且测试比较方便。
因此对声场的理论分析研究常常从液体介质入手，然后在一定条件下过渡到固体介质。
又由于实际探伤中广泛应用反射法，因此本章在讨论了超声波发射声场以后，还讨论了各种规则反射体的回波声压。
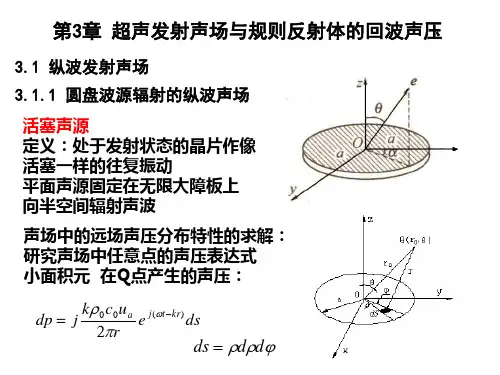
第一节纵波发射声场一、圆盘波源辐射的纵波声场1.波源轴线上声压分布在不考虑介质衰减的条件下，图2.1所示的液体介质中圆盘源上一点波源ds辐射的球面波在波源轴线上Q点引起的声压为式中 P o——波源的起始声压；d s——点波源的面积；λ——波长；r——点波源至Q点的距离；κ———波数，κ=ω/c=2π/λ；ω——圆频率，ω=2πf；‘t——时间。
根据波的迭加原理，作活塞振动的圆盘波源各点波源在轴线上Q点引起的声压可以线性迭加，所以对整个波源面积积分就可以得到波源轴线上的任意一点声压为其声压幅值为(2.1)式中 R s—波源半径；χ——轴线上Q点至波源的距离。
上述声压公式比较复杂，使用不便，特作如下简化。
当χ≥2R，时，根据牛顿二项式将(2.1)式简化为(2.2)根据sinθ≈θ(θ很小时)上式可简化为(2.3)式中 Fs——波源面积，(2.3)式表明，当χ≥3R；/A时，圆盘源轴线上的声压与距离成反比，与波源面积成正比。
波源轴线上的声压随距离变化的情况如图2.2所示。
(1)近场区：波源附近由于波的干涉而出现一系列声压极大极小值的区域，称为超声场的近场区，又叫菲涅耳区。
近场区声压分布不均，是由于波源各点至轴线上某点的距离不同，存在波程差，互相迭加时存在位相差而互相干涉，使某些地方声压互相加强，另一些地方互相减弱，于是就出现声压极大极小值的点。
波源轴线上最后一个声压极大值至波源的距离称为近场区长度，用N表示。
声压P有极大值，化简得极大值对应的距离为式中n=O、1、2、3、……<(D s-一x)/2λ的正整数，共有n+1个极大值，其中n=0为最后一个极大值。
超声波发射声场与规则反射体的回波声压第一节 纵波发射声场一、圆盘波源辐射的纵波声场(声源固定在无限大障板上) 1．波源轴线上声压)(2kh t j a e hds cu jk dp -=ωπρ112ρπρd ds = h 221x +=ρ声源在Q 点产生的总声压⎰-=akht j a d he ecu jk Q P 0113)(22)(ρπρπρω ⎰-=Rxjkh t j a e e cu jk ωρ=][jkx jkR t j a e e e cu ----ωρ][2)(2)(2R x jk R x jk x R jkt j a e e ee cu ---+---=ωρ]2/2/)([)](2sin[2πωρ++--=x R k t j a e x R kcu此处用到公式je e j j 2sin θθθ--=Q 点处的声压振幅P 可表示为)](sin[2220x x R P P s -+=λπ式中s R ——波源半径x ——轴线上Q 点至波源的距离 P 0——a cu ρ(1)近场区 a)当2)12()4(2πλπ+=-+n x x D s 时02P P =声压具有最大值,此声压为2倍平面波声压。
此位置)12(4)12(222++-=n n D x s n λλn=0,1,2 (2)λλ-s D 有(n+1)个值 其中n=0为距声源最远一个最大值，此时λλλ44222s s D D N ≈-=（条件λ>>s D ） N 称为近场长度。
近场区内，与声轴垂直且与声源面积相当的范围内，其平均声压等于平面波声压。
b)声压最小值点 当πλπn x x D s=-+)4(2时,该位置声压振幅P=0。
以'x 表示声压最小值点的位置,则λλn n D x s n8)2(22'-=，得n<[λ2s D ]取整，最小值个数为1、2、3…[λ2s D ]其中n=1相应于最远的最小值点，且此点的值为282822'1ND D x s s =≈-=λλλ c)N 内其他各点的声压介于0与02P 之间。
