求未知参数的置信区间的一般方法
- 格式:ppt
- 大小:900.51 KB
- 文档页数:11

置信区间估计的方法与应用引言:在统计学中,置信区间估计是一种常用的参数估计方法,用于给出未知总体参数的范围估计。
通过置信区间估计,我们可以在给定的置信水平下,对总体参数的取值范围作出合理的估计。
本文将介绍一些常见的置信区间估计方法及其应用。
一、均值的置信区间估计方法1. 正态总体的均值置信区间当总体是正态分布时,可以使用标准正态分布的性质得出均值的置信区间。
假设样本均值为x,样本标准差为s,样本容量为n,置信水平为1-α(α为显著性水平),则均值的置信区间为 [x - Z(α/2) * (s/√n), x + Z(α/2) * (s/√n)]。
其中,Z(α/2)为标准正态分布的上α/2分位数。
2. 大样本均值置信区间当样本容量较大(通常大于30)时,根据中心极限定理,样本均值近似服从正态分布。
此时可以使用大样本均值置信区间公式,即 [x - Z(α/2) * (σ/√n), x +Z(α/2) * (σ/√n)]。
其中,σ为总体标准差,n为样本容量。
二、比例的置信区间估计方法1. 正态总体比例的置信区间当总体满足正态分布假设时,比例的置信区间可以通过正态分布的性质得出。
假设样本比例为p,样本容量为n,置信水平为1-α,则比例的置信区间为 [p -Z(α/2) * √(p(1-p)/n), p + Z(α/2) * √(p(1-p)/n)]。
其中,Z(α/2)为标准正态分布的上α/2分位数。
2. 大样本比例置信区间当样本容量较大且样本比例接近0或1时,可以使用大样本比例置信区间。
此时,比例的置信区间可近似为 [p - Z(α/2) * √(p(1-p)/n), p + Z(α/2) * √(p(1-p)/n)]。
其中,p为样本比例,n为样本容量。
三、方差的置信区间估计方法1. 单个正态总体方差的置信区间当总体满足正态分布假设时,方差的置信区间可以通过卡方分布的性质得出。
假设样本方差为s^2,样本容量为n,置信水平为1-α,则方差的置信区间为 [(n-1) * s^2 / X^2(α/2, n-1), (n-1) * s^2 / X^2(1-α/2, n-1)]。

置信区间计算方法
置信区间,也称为可信区间,是用来估计参数真值的一个重要统
计学概念。
在统计学分析中,我们通常无法直接得到总体参数的真值,因此需要通过样本数据对其进行估计。
而置信区间指的是样本统计量
的一个范围,该范围内有一定置信度(通常为95%或99%)包含了总体
参数真值的可能性。
下面将介绍置信区间的计算方法。
置信区间的计算方法基于正态分布或者t分布,具体计算步骤如下:
1. 确定置信水平(通常为95%或99%),转换为显著性水平(通
常为0.05或0.01)。
2. 根据样本数据计算统计量的值,比如平均数或者比例等。
3. 计算标准误差,即统计量的标准差除以样本量的平方根。
4. 确定分布类型。
如果总体参数的分布已知且符合正态分布,应该使
用z分布;如果总体参数的分布未知或者不符合正态分布,应该使用t 分布。
5. 根据分布类型和显著性水平确定临界值。
临界值告诉我们在某个置
信水平下,多少的观测值会出现在计算得到的置信区间之外。
6. 计算置信区间。
统计量的值加减分布类型对应的临界值与标准误差
的乘积,即可得到置信区间的上限和下限。
以上是常见的置信区间计算方法,需要注意的是不同的分布类型
和显著性水平会影响置信区间的宽度和准确性。
因此,在使用置信区
间进行参数估计时,需要根据实际情况进行合理的选择和判断。

置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念,它们帮助我们在样本数据的基础上对总体参数进行估计,并给出估计的可靠性范围。
接下来,让我们深入探讨一下置信度和置信区间的计算方法以及相关的公式表。
首先,我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%、99%等。
它表示在多次重复抽样的情况下,得到的置信区间包含总体参数真值的概率。
例如,95%的置信度意味着,如果我们进行多次抽样并计算置信区间,大约有 95%的置信区间会包含总体参数的真实值。
而置信区间则是一个范围,它基于样本数据计算得出,旨在估计总体参数可能的取值范围。
常见的总体参数包括总体均值、总体比例等。
那么,如何计算置信区间呢?这就需要用到相应的公式。
对于总体均值的置信区间计算,当总体标准差已知时,使用以下公式:\\overline{x} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\overline{x}\)是样本均值,\(z_{\alpha/2}\)是对应于置信度的标准正态分布的分位数(例如,对于95%的置信度,\(\alpha =005\),\(z_{\alpha/2} =196\)),\(\sigma\)是总体标准差,\(n\)是样本容量。
当总体标准差未知,且样本容量较大(通常认为\(n \geq 30\))时,可以用样本标准差\(s\)代替总体标准差\(\sigma\),使用近似的公式:\\overline{x} \pm z_{\alpha/2} \frac{s}{\sqrt{n}}\而当样本容量较小(\(n < 30\))且总体服从正态分布时,需要使用 t 分布来计算置信区间,公式为:\\overline{x} \pm t_{\alpha/2, n 1} \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2, n 1}\)是自由度为\(n 1\)、对应于置信度的 t 分布的分位数。

置信区间估计方法
置信区间估计方法是统计学中一种常用的区间估计方法,它通过构造一个置信区间来估计未知参数的取值范围。
这个区间通常包含了未知参数的真实值,并且随着置信水平的提高,这个区间的长度也会相应地缩短。
在应用置信区间估计方法时,我们首先需要选择一个合适的置信水平,通常为95%或99%。
然后,根据样本数据和选定的置信水平,计算出置信区间的上下限。
这个计算过程可以通过一些常见的统计软件或在线工具来完成。
置信区间估计方法在许多领域都有广泛的应用。
例如,在医学研究中,我们可以通过置信区间估计方法来评估治疗效果的有效性,并确定治疗方案的适用范围。
在经济学中,置信区间估计方法可以用于预测模型的误差范围和评估政策效果的不确定性。
在社会科学中,它可以帮助我们了解社会现象的发展趋势和变化范围。
值得注意的是,置信区间估计方法也存在一些局限性。
例如,当样本量较小或者数据不符合正态分布时,置信区间估计的结果可能会存在较大的误差。
此外,置信区间估计方法也不能提供关于单个观测值的预测或决策。
综上所述,置信区间估计方法是一种实用的统计方法,它可以用于估计未知参数的取值范围,并且在许多领域都有广泛的应用。
然而,在使用置信区间估计方法时,我们也需要注意其局限性,并根据实际情况选择合适的方法来进行参数估计。

置信区间值置信区间(Confidence Interval)是统计学中一种常用的估计方法,用于估计总体参数的区间范围。
通过置信区间,我们可以对未知总体参数给出一个估计值,并且给出了一个相信该估计值的区间范围。
一、置信区间的定义和计算方法1. 置信区间的定义:置信区间是指对一个总体参数的估计范围,其通常表示为一个区间,该区间是在一定置信水平下,包含真实参数的概率。
2. 置信水平(Confidence Level):置信水平是指在统计推断中采用的一种信心水平,通常用来衡量置信区间的准确程度。
常见的置信水平有90%、95%和99%等。
3. 置信区间的计算方法:常见的计算方法有基于正态分布的置信区间和基于 t 分布的置信区间。
a. 基于正态分布的置信区间:用于大样本的估计,适用于总体参数的分布近似服从正态分布的情况。
计算公式为:估计值± Z * 方差b. 基于 t 分布的置信区间:用于小样本的估计,适用于总体参数的分布不近似服从正态分布的情况。
计算公式为:估计值± t * 标准误差二、置信区间的应用1. 总体均值的置信区间:在估计总体均值时,可以计算出一个置信区间,用来估计总体均值的真实范围。
置信区间可以帮助我们确定估计值的可信程度,从而做出合理的决策。
2. 总体比例的置信区间:在估计总体比例时,可以计算出一个置信区间,用来估计总体比例的真实范围。
置信区间可以帮助我们确定估计值的置信程度,从而做出合理的判断。
3. 其他总体参数的置信区间:除了均值和比例外,置信区间还可以应用于其他总体参数的估计,如方差、回归系数等。
三、置信区间的解释和应用注意事项1. 置信区间的解释:置信区间并不是总体参数的具体值,而是对其估计范围的一个区间。
例如,95%的置信区间为[10, 20],表示我们对总体参数的估计范围有95%的置信,而不是说总体参数的值一定在该区间内。
2. 置信区间的应用注意事项:a. 样本大小:样本越大,置信区间越窄,估计的准确程度越高。

置信区间求法什么是置信区间在统计学中,置信区间是用来估计一个参数真实值范围的一种统计方法。
置信区间表示了我们对于总体参数的不确定性,给出了一个范围,该范围内有一定的概率包含了真实的总体参数。
置信区间通常由两个值组成,下限和上限,表示了参数的估计范围。
置信区间的计算方法依赖于样本数据和所选择的置信水平。
置信水平置信水平是指在重复抽样的情况下,统计方法会产生包含真实参数的区间的频率。
常见的置信水平有95%和99%。
95%置信水平表示,在进行100次抽样时,大约有95次的置信区间会包含真实参数值。
同样地,99%置信水平表示,在进行100次抽样时,大约有99次的置信区间会包含真实参数值。
选择置信水平的大小需要根据具体的应用场景和对结果的要求来决定。
较高的置信水平会导致置信区间变宽,包含更多的可能取值,但也会增加错误估计的概率。
置信区间的计算方法置信区间的计算方法通常依赖于所研究的统计量和总体分布的已知信息。
以下是一些常见的置信区间计算方法:1. 样本均值的置信区间当总体的分布是正态分布,并且总体标准差已知时,可以使用以下公式计算样本均值的置信区间:其中,是样本均值,是总体标准差,是样本容量,是对应于所选置信水平的标准正态分布的临界值。
2. 样本均值的置信区间(总体标准差未知)当总体的分布是正态分布,但总体标准差未知时,可以使用以下公式计算样本均值的置信区间:其中,是样本均值,是样本标准差,是样本容量,是对应于所选置信水平和自由度的t分布的临界值。
3. 比例的置信区间当研究的统计量是比例时,可以使用以下公式计算比例的置信区间:其中,是样本比例,是样本容量,是对应于所选置信水平的标准正态分布的临界值。
置信区间的应用举例为了更好地理解置信区间的应用,我们可以通过一个实际的例子来说明。
假设我们想要估计一家电商平台上某商品的平均评分,我们从该平台上随机抽取了100个用户的评分数据。
我们想要计算出该商品评分的置信区间,以便了解该评分的可信程度。


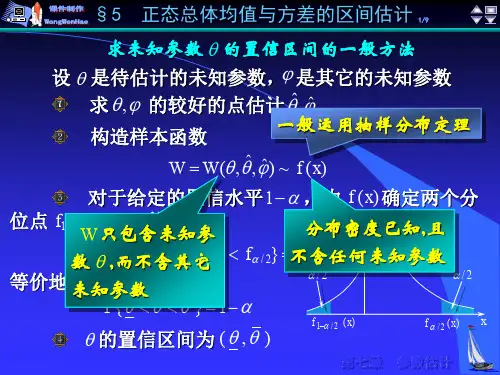
求未知参数置信区间一般方法未知参数的置信区间是统计学中一种重要的概念,用来衡量样本估计值的不确定性。
一般方法包括点估计、置信区间估计和假设检验。
在本文中,我们将重点介绍置信区间估计的一般方法。
置信区间估计是用样本估计值构造区间估计,以描述未知参数的可能取值范围。
它包括点估计和间隔估计两个部分。
点估计是用样本统计量估计未知参数的具体值,而置信区间估计则是在点估计基础上,给出未知参数可能的取值区间。
构造置信区间的一般步骤如下:1.选择一个合适的概率分布假设:在进行置信区间估计之前,需要选择适当的概率分布假设,以确定参数的分布。
一般来说,如果样本容量较大,可以使用正态分布进行近似;而对于小样本容量,可以使用t分布。
2.确定置信水平:置信水平描述了对参数估计的可信程度。
常见的置信水平有95%和99%。
一般来说,置信水平越高,置信区间就越宽。
3.计算样本统计量:使用给定的样本数据计算出所需的样本统计量,比如样本均值、样本比例等。
这些统计量可以作为点估计。
4.计算标准误差:标准误差是样本估计值与真实参数值之间的平均差异。
它可以用来估计置信区间的宽度。
标准误差可以使用公式计算,也可以通过抽样方法进行估计。
5.确定置信界限:根据所选的概率分布,计算出相应的临界值。
临界值分为两个,分别对应于置信区间的下限和上限。
一般使用正态分布或t 分布的分位数。
6.构造置信区间:使用估计值、标准误差和置信界限,可以构造出一个包含未知参数真实值的区间。
这个区间就是所求的置信区间。
需要注意的是,置信区间并不是参数的真实取值区间,而仅仅是对其可能取值的一个估计。
在统计学中,我们不能确定未知参数的真实值,只能通过样本数据进行估计。
总结起来,构造未知参数的置信区间所使用的一般方法包括:选择概率分布假设、确定置信水平、计算样本统计量、计算标准误差、确定置信界限和构造置信区间。
这些方法可以帮助我们理解样本估计值的不确定性,并提供了对未知参数可能取值范围的估计。


数值计算置信区间置信区间的计算涉及到样本均值、标准差和样本量等,根据总体分布的特点和样本的抽样方法,可以采用不同的计算方法。
下面将介绍几种常见的数值计算置信区间的方法。
1.正态分布的置信区间当样本的大小足够大,并且总体呈现近似正态分布时,可以采用正态分布的置信区间计算方法。
下面是正态分布置信区间的计算公式:置信区间=样本均值±Z*(标准差/√n)其中,Z是标准正态分布的分位数,可以根据所需的置信水平来确定。
例如,对于95%的置信水平,Z为1.96;对于99%的置信水平,Z为2.582.t分布的置信区间当样本的大小较小,总体的分布未知或总体不是正态分布时,可以采用t分布的置信区间计算方法。
下面是t分布置信区间的计算公式:置信区间=样本均值±t*(标准差/√n)其中,t是t分布的分位数,可以根据所需的置信水平和自由度来确定。
3.二项分布的置信区间当需要估计总体比例时,且样本符合二项分布时,可以采用二项分布的置信区间计算方法。
下面是二项分布置信区间的计算公式:置信区间=样本比例±Z*√((样本比例*(1-样本比例))/n)其中,Z是标准正态分布的分位数,可以根据所需的置信水平来确定。
除了上述方法外,还有其他一些适用于特定情况的置信区间计算方法,例如泊松分布的置信区间、贝叶斯置信区间等。
需要注意的是,置信区间是对总体参数的估计范围,不是总体参数的准确值。
置信区间的计算依赖于样本数据,不同的样本可能得到不同的置信区间。
因此,在进行置信区间的解释和应用时,需要考虑到置信区间的范围和置信水平的选择。
在实际应用中,数值计算置信区间可以帮助我们了解样本数据的可靠性和总体参数的不确定性,从而做出更准确的推断和决策。
可信区间的估计方法一、引言在统计学中,可信区间是用于估计未知参数的一种方法。
它提供了一个范围,该范围内有一定概率包含真实的参数值。
可信区间的估计方法是统计学中一个重要的概念,它在实际问题中具有广泛的应用。
本文将介绍可信区间的估计方法及其在实际问题中的应用。
二、点估计与区间估计在统计学中,点估计是一种估计未知参数的方法,它给出一个具体的数值作为估计值。
然而,点估计只能提供一个数值,无法反映估计值的不确定性。
为了解决这个问题,统计学引入了可信区间的估计方法。
可信区间是用于估计未知参数的一种区间估计方法。
它提供了一个范围,该范围内有一定概率包含真实的参数值。
可信区间的估计方法主要有频率派方法和贝叶斯方法。
三、频率派方法频率派方法是一种基于频率统计理论的可信区间估计方法。
它假设参数是固定的但未知的,并利用样本信息对参数进行估计。
常用的频率派方法有置信度法和最大似然估计。
1. 置信度法置信度法是一种常用的可信区间估计方法。
它通过构造置信区间来估计未知参数。
置信区间是一个区间,它有一定的概率包含真实的参数值。
置信度是指在重复抽样的情况下,置信区间包含真实参数的概率。
构造置信区间的方法主要有正态分布法和t分布法。
正态分布法适用于大样本情况,t分布法适用于小样本情况。
2. 最大似然估计最大似然估计是一种常用的可信区间估计方法。
它通过寻找最大化似然函数的参数值来估计未知参数。
最大似然估计得到的估计值具有一定的不确定性,因此可以构造可信区间来表示估计值的不确定性。
四、贝叶斯方法贝叶斯方法是一种基于贝叶斯统计理论的可信区间估计方法。
它假设参数是随机的,并利用先验分布和样本信息来估计参数。
贝叶斯方法通过后验分布来表示参数的不确定性。
贝叶斯方法的核心是贝叶斯公式,它将先验分布和似然函数结合起来,得到后验分布。
通过后验分布可以得到参数的可信区间。
五、实际应用可信区间的估计方法在实际问题中具有广泛的应用。
例如,在市场调查中,我们可以利用可信区间的估计方法来估计产品的市场份额。
置信区间计算方法(一)置信区间计算什么是置信区间?•置信区间是统计学中常用的概念,用于估计一个总体参数的范围。
•置信区间的计算依赖于样本数据,可以帮助我们对总体参数进行推断。
置信区间的计算方法1. 正态分布情况下的置信区间•对于大样本(样本量大于30)且总体近似服从正态分布的情况,常用的计算方法为Z分数方法。
•Z分数方法:假设总体均值为μ,样本均值为x̄,样本标准差为s,置信水平为1-α,置信区间为[x̄ - Z * , x̄ + Z * ],其中Z为标准正态分布的分位数。
2. 小样本或总体非正态分布情况下的置信区间•对于小样本(样本量小于30)或总体分布未知的情况,可以使用t分布进行置信区间的计算。
•t分布方法:假设总体均值为μ,样本均值为x̄,样本标准差为s,自由度为n-1,置信水平为1-α,置信区间为[x̄ - t_{} * , x̄ + t_{} * ],其中t为t分布的分位数。
3. 样本比例的置信区间•当我们想要估计一个总体比例时,可以使用二项分布进行置信区间的计算。
•二项分布方法:假设总体比例为p,样本比例为p̄,样本个数为n,置信水平为1-α,置信区间为[p̄ - Z * , p̄ + Z * ],其中Z为标准正态分布的分位数。
置信区间的应用•置信区间可以帮助我们对总体参数进行估计,例如总体均值、总体比例等。
•置信区间还可以用于比较不同样本之间的差异,例如两个样本均值的差异、两个样本比例的差异等。
•置信区间在市场调研、医学研究等领域都有重要的应用,在决策和推断中起到了至关重要的作用。
置信区间计算的注意事项•置信区间的计算结果是对总体参数范围的估计,并不是总体参数的准确值。
•置信区间的宽度受样本量和置信水平的影响,样本量越大、置信水平越高,置信区间越窄。
•在使用置信区间时,需要明确置信水平和适用的分布假设,否则可能得到不准确的结果。
以上就是置信区间计算的各种方法。
置信区间是统计学中常用的工具,可以帮助我们对总体参数进行推断和估计,具有广泛的应用价值。
置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念。
它们帮助我们在对总体参数进行估计时,给出一个可能包含真实参数值的范围,以及我们对这个范围的确定程度,也就是置信度。
首先,让我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%或 99%。
它反映了我们在多次重复抽样和估计的过程中,得到的置信区间能够包含真实总体参数值的比例。
比如说,95%的置信度意味着如果我们进行 100 次抽样和估计,大约有 95 次得到的置信区间能够包含真实的总体参数值。
而置信区间则是一个可能包含总体参数真实值的范围。
这个范围的宽窄取决于我们所选择的置信度、样本数据的特征以及样本量的大小。
接下来,我们重点介绍几种常见的置信区间计算方法和相应的公式。
对于正态总体均值的置信区间计算,当总体方差已知时,我们使用的公式是:\\bar{X} \pm Z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\bar{X}\)是样本均值,\(Z_{\alpha/2}\)是标准正态分布的双侧分位数(对应于置信度\(1 \alpha\)),\(\sigma\)是总体标准差,\(n\)是样本量。
例如,如果我们有一个样本均值为 50,总体标准差为 10,样本量为 100,并且想要计算 95%置信度下的置信区间,那么首先找到\(Z_{\alpha/2}\),对于 95%的置信度,\(\alpha = 005\),\(\alpha/2 = 0025\),对应的\(Z_{\alpha/2} \approx 196\)。
然后代入公式计算:\50 \pm 196 \times \frac{10}{\sqrt{100}}= 50 \pm 196\得到的置信区间就是 4804, 5196。
当总体方差未知时,我们用样本方差\(s\)来代替总体方差\(\sigma\),此时使用的是\(t\)分布,公式变为:\\bar{X} \pm t_{\alpha/2}(n 1) \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2}(n 1)\)是自由度为\(n 1\)的\(t\)分布的双侧分位数。
高考数学中的置信区间:概念、计算和解题方法一、什么是置信区间在统计学中,置信区间是一种用来估计未知参数的区间。
例如,我们想要估计某个班级的平均身高,但是我们没有办法测量每一个学生的身高,那么我们可以从这个班级中随机抽取一些样本,然后根据样本的平均值和标准差,计算出一个区间,这个区间就是置信区间。
我们可以说,我们有多大的置信水平(confidence level ),这个区间就包含了真实的平均身高。
二、如何计算置信区间一般来说,置信区间的计算公式是:x ±z α/2s √n其中,x 是样本平均值,z α/2 是标准正态分布的分位数,α 是置信水平的补数(例如,如果置信水平是 95%,那么 α 就是 0.05),s 是样本标准差,n 是样本容量。
例如,假设我们从一个班级中随机抽取了 30 个学生,测量了他们的身高(单位:厘米),得到了如下数据:我们可以用 Python 的 numpy 库来计算这些数据的平均值和标准差:输出结果是:如果我们想要以 95% 的置信水平估计这个班级的平均身高,那么我们可以查表得到 z α/2 的值是 1.96。
然后代入公式,得到:181.5±1.969.574√30简化后得到:181.5±3.41也就是说,我们以 95% 的置信水平估计这个班级的平均身高在 178.09 厘米到 184.91 厘米之间。
三、如何解释置信区间有时候,人们会误解置信区间的含义,认为它表示真实参数有多大的概率落在这个区间内。
其实,这是不正确的。
因为真实参数是一个固定的值,它要么在这个区间内,要么不在这个区间内,不存在概率的问题。
正确的理解方式是:如果我们重复进行同样的抽样和计算过程,那么有多大比例的置信区间会包含真实参数。
例如,在上面的例子中,我们以 95% 的置信水平估计了这个班级的平均身高在 178.09 厘米到 184.91 厘米之间,这并不意味着这个班级的平均身高有 95% 的概率在这个区间内,而是意味着如果我们重复进行 100 次抽样和计算,那么大约有 95次的置信区间会包含这个班级的真实平均身高。
方差未知时均值的置信区间的推导在统计学中,我们经常需要推断出一个总体的均值,但由于实际的样本容量有限,我们无法确定这个均值的真实值。
于是,我们需要通过样本来估计这个均值,并确定一个区间,来表示我们对这个均值可能的取值进行估计。
这个区间就是置信区间。
然而,当总体的方差未知时,我们该如何推导出均值的置信区间呢?接下来,让我们来一步步探索这个问题。
首先,我们需要知道一个重要的统计量——样本均值的标准误差。
这个标准误差被定义为样本均值的标准差除以样本容量的平方根。
即标准误差 = 样本标准差 / sqrt(样本容量)接下来,我们将会在置信水平α下,对于一个未知方差的总体,推导均值的置信区间。
这个置信水平α,通常取0.05或0.01。
令样本均值为x̄,样本容量为n,样本标准差为s,置信水平为α。
我们知道,样本均值符合t分布,其自由度为n-1,根据此,我们可以计算出样本均值的标准误差:标准误差 = s / sqrt(n)接下来,我们要计算出t分布表中的相应t值,这个t值的自由度为n-1。
我们可以通过查找t分布表,在这个自由度下,查找到对应α/2和自由度下t值的双尾概率。
假设这个概率为p,则有1-p的置信水平落在这个双尾概率的两侧。
即1-α = (1-p) x 2于是,我们就可以计算出双尾区间的t值为:t = t分布表中对应α/2和自由度n-1的值接下来,我们就可以计算出均值的置信区间了。
置信区间为:均值的置信区间 = x̄± t x 标准误差其中,x̄是样本均值,t是t分布表中对应双尾概率和自由度下的t值,标准误差是样本标准差除以样本容量的平方根。
需要注意的是,这个置信区间只适用于总体方差未知的情况。
如果总体方差已知,我们则应使用正态分布表来计算相应的z值,并应用z分布的置信区间计算公式。
在实际应用中,我们需要进行多次样本抽取,并根据不同的样本抽取结果,得出不同的置信区间。
这些置信区间中,有一定比例包含了总体真实均值,我们称其为“成功置信区间”,相应地,其余的置信区间我们则称为“失败置信区间”。