毕尔萨伐尔定律

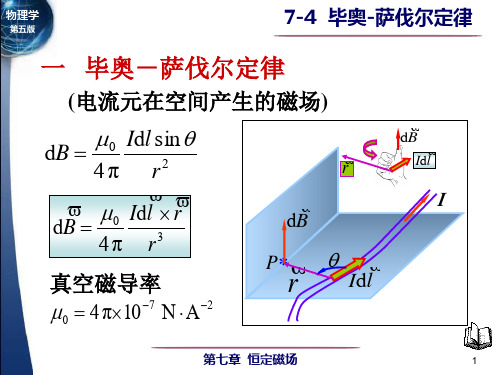
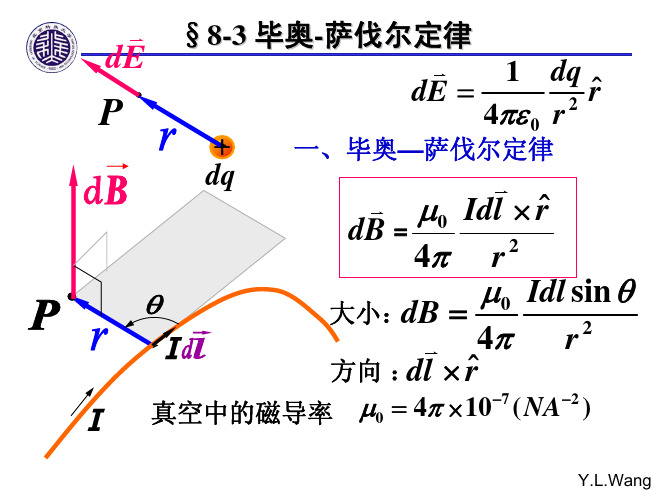
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。

微分形式为：整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。

磁感应线的方向服从右手定则，如图。

二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布：载流直导线；圆电流。

例1.载流长直导线的磁场解：建立如图坐标系，在载流直导线上，任取一电流元Idz，由毕-萨定律得元电流在P点产生的磁感应强度大小为：方向为垂直进入纸面。

所有电流元在P点产生的磁场方向相同，所以求总磁感强度的积分为标量积分，即：（1）由图得：,即：此外：，代入（1）可得：讨论：（1）无限长直通电导线的磁场：（2）半无限长直通电导线的磁场：（3）其他例子例2:圆形载流导线轴线上的磁场：设在真空中，有一半径为 R ，通电流为 I 的细导线圆环，求其轴线上距圆心 O 为 x 处的P点的磁感应强度。

解：建立坐标系如图，任取电流元，由毕-萨定律得：，方向如图：，所有dB形成锥面。

将dB进行正交分解：，则由由对称性分析得：，所以有:，因为： ,r=常量，所以：，又因为：所以：，方向：沿x轴正方向，与电流成右螺旋关系。

讨论：（1）圆心处的磁场：x=0 ，。

（2）当即P点远离圆环电流时，P点的磁感应强度为：。

例3：设有一密绕直螺线管。

半径为 R ，通电流 I。

总长度L，总匝数N（单位长度绕有n 匝线圈），试求管内部轴线上一点 P 处的磁感应强度。

解：建立坐标系，在距P 点 x 处任意截取一小段 dx ，其线圈匝数为: 电流为：。

其相当于一个圆电流，它在P点的磁感应强度为：。

因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右，所以整个螺线管在P点的磁感应强度的大小为：因为：代入上式得：所以：讨论：（1）管内轴线上中点的磁场:（2）当 L>>R时，为无限长螺线管。

此时,，管内磁场。

即无限长螺线管轴线上及内部为均匀磁场，方向与轴线平行满足右手定则。

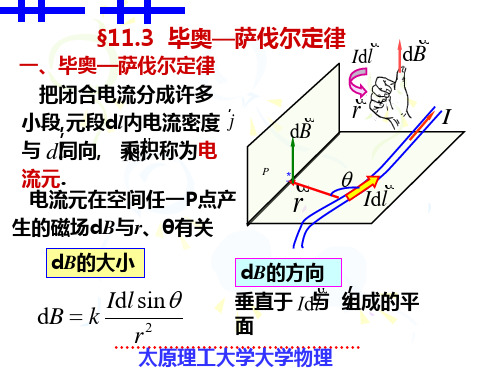
毕奥萨伐尔定律毕奥－萨伐尔定律指出: 磁场的是电流元，磁场随场点到电流元的距离平方而衰减，磁场遵从叠加原理，由任意形状通电导线所激发的总磁感应强度B 是由电流元所激发的磁感应强度dB 的矢量积分，任意形状的载流导线都可以看成由许多电流元Idl 组成，只要知道了电流元激发磁场的规律，再用叠加原理就可以求得任意载流导线激发的磁场分布。

载流导线的任一电流元Idl 在给定点P 所产生的磁感应强度dB 的大小与电流元的大小成正比，与电流元和由电流元到P 点的矢径r 之间夹角的正弦成正比，并与电流元到P 点的距离的平方成反比; dB 的方向垂直于dl 与r 所决定的平面，指向由右手螺旋法则决定，即当右手螺旋由Idl 经小于180°的角转向r 时螺旋前进的方向，如附图－1 所示。

其数学表达式为附图－1 电流元到P 点dB 的方向地球磁场起源理论式中: k 为比例系数，在真空中k =107T·m·A－1，不同的磁介质k 值不同。

为了使dB 的公式有理化，取k = μ/4π，μ为介质的磁导率，真空中μ= 4π×107T·m·A－1，这样，式( 附－1) 改为:地球磁场起源理论毕奥－萨伐尔定律的矢量表达式为:地球磁场起源理论任意形状载流导线在P 点产生的磁感应强度B，等于导线上各个电流元Idl 在该点处所产生的磁感应强度矢量和，即:地球磁场起源理论毕奥－萨伐尔定律给出了电流元Idl 对距离r 处的空间某一点P 处产生dB 的大小与方向，但由于电流元不可能单独存在，所以毕奥－萨伐尔定律不可能由实验直接加以验证。

毕奥－萨伐尔定律的正确性是通过间接的方法被证实的，因为由毕奥－萨伐尔定律推出的所有结果都能很好地与实验结果相符合。