交流电下的毕奥萨伐尔定律

.毕奥-萨伐尔定律摘要：1.引言2.毕奥- 萨伐尔定律的定义3.毕奥- 萨伐尔定律的公式表示4.毕奥- 萨伐尔定律的应用领域5.我国在毕奥- 萨伐尔定律研究方面的贡献6.结论正文：1.引言毕奥- 萨伐尔定律是电磁学中的一个基本定律，它描述了电流在磁场中的作用力。

这个定律是由法国物理学家毕奥和萨伐尔在19 世纪初提出的，为电磁学的发展奠定了基础。

2.毕奥- 萨伐尔定律的定义毕奥- 萨伐尔定律指出，一个电流在磁场中受到的磁场力与电流的大小、磁场的强度和电流与磁场之间的夹角有关。

具体来说，磁场力F 的大小与电流I、磁感应强度B 以及电流与磁场之间的夹角θ的关系可以表示为：F = I * (Bl * sinθ)。

3.毕奥- 萨伐尔定律的公式表示毕奥- 萨伐尔定律可以用数学公式表示为：F = I * (Bl * sinθ)，其中F 表示磁场力，I 表示电流，B 表示磁感应强度，l 表示电流元的长度，θ表示电流与磁场之间的夹角。

4.毕奥- 萨伐尔定律的应用领域毕奥- 萨伐尔定律在许多领域都有广泛的应用，如电磁制动、电磁起重机、磁悬浮列车等。

此外，这个定律还为研究电磁波、电磁感应和磁流体等现象提供了理论基础。

5.我国在毕奥- 萨伐尔定律研究方面的贡献我国科学家在毕奥- 萨伐尔定律研究方面取得了举世瞩目的成果。

例如，中国科学院物理研究所的科学家们通过对磁性材料的研究，为理解毕奥- 萨伐尔定律提供了新的视角。

此外，我国在磁悬浮列车、电磁制动等领域的研究也取得了重要突破，为国民经济的发展做出了巨大贡献。

6.结论毕奥- 萨伐尔定律是电磁学的基本定律之一，它对电磁学的发展产生了深远的影响。

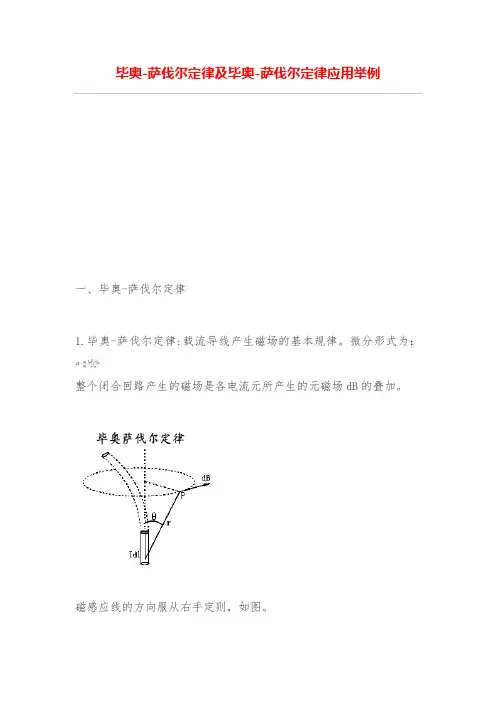
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。

微分形式为：整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。

磁感应线的方向服从右手定则，如图。

二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布：载流直导线；圆电流。

例1.载流长直导线的磁场解：建立如图坐标系，在载流直导线上，任取一电流元Idz，由毕-萨定律得元电流在P点产生的磁感应强度大小为：方向为垂直进入纸面。

所有电流元在P点产生的磁场方向相同，所以求总磁感强度的积分为标量积分，即：（1）由图得：,即：此外：，代入（1）可得：讨论：（1）无限长直通电导线的磁场：（2）半无限长直通电导线的磁场：（3）其他例子例2:圆形载流导线轴线上的磁场：设在真空中，有一半径为 R ，通电流为 I 的细导线圆环，求其轴线上距圆心 O 为 x 处的P点的磁感应强度。

解：建立坐标系如图，任取电流元，由毕-萨定律得：，方向如图：，所有dB形成锥面。

将dB进行正交分解：，则由由对称性分析得：，所以有:，因为： ,r=常量，所以：，又因为：所以：，方向：沿x轴正方向，与电流成右螺旋关系。

讨论：（1）圆心处的磁场：x=0 ，。

（2）当即P点远离圆环电流时，P点的磁感应强度为：。

例3：设有一密绕直螺线管。

半径为 R ，通电流 I。

总长度L，总匝数N（单位长度绕有n 匝线圈），试求管内部轴线上一点 P 处的磁感应强度。

解：建立坐标系，在距P 点 x 处任意截取一小段 dx ，其线圈匝数为: 电流为：。

其相当于一个圆电流，它在P点的磁感应强度为：。

因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右，所以整个螺线管在P点的磁感应强度的大小为：因为：代入上式得：所以：讨论：（1）管内轴线上中点的磁场:（2）当 L>>R时，为无限长螺线管。

此时,，管内磁场。

即无限长螺线管轴线上及内部为均匀磁场，方向与轴线平行满足右手定则。

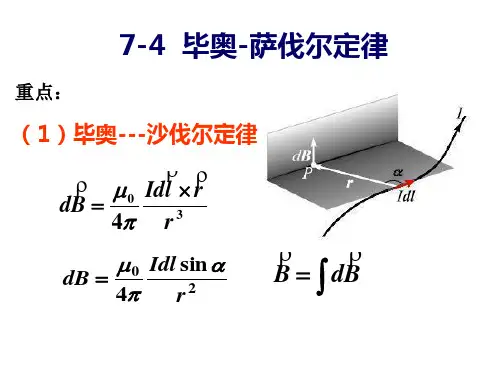
第4章基本要求•用毕-萨定律计算一段线电流在一点的磁场（大小、方向），面电流、体电流会用微积分处理。

•用环路定理计算对称性磁场（无限长直线电流，无限大均匀电流面等）。

•会计算运动电荷受到的磁场力，在磁场的轨迹方程及轨迹参数（周期，回旋半径，螺线螺距等）•会计算一段电流受到的安培力、线圈受到的力和力矩。

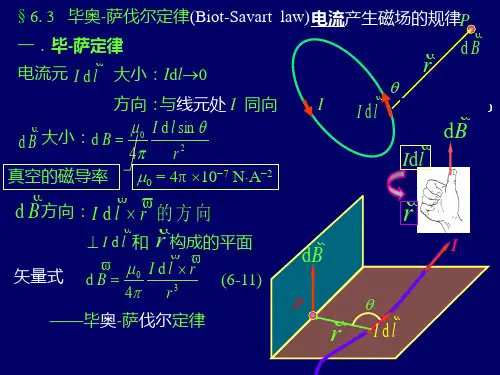
304RR l Id B d⨯=πμ毕奥－萨伐尔定律：34R R l Id B L⨯=⎰πμI dl i dS j dVIdlrαβdORθe re ze IP 1z例：无限长两平行电流（I 1＝I 2＝I ）中垂面上的磁场强度。

xyOI 1I 2B 1B2解：由安培环量定理得I 1、I 2在O 点的磁场大小为122IB B rμπ==B 1、B 2方向如图所示，分别与半径r 1、r 2垂直。

由对称性可知，B 1、B 2的合矢量沿y 方向r 2r 1θ111ˆ2sin B B yθ=稳恒磁场的基本性质⎪⎩⎪⎨⎧=⋅=⋅⎰∑⎰⎰Lk k0SI l d B 0S d B μ微分形式：积分形式：⎩⎨⎧=⨯∇=⋅∇jB 0B 0μ高斯定理和环路定理IBOrRL II ABC D C'D'(a)III(b)Bl Id F d⨯=若线圈的线度远小于外场非均匀度，则线圈在外磁场中的力和力矩分别为：Bm L ⨯=Bm F)(∇⋅=安培力:)(B v E q F ⨯+=洛仑兹力:θzxyθ=arcsin(V ⊥/V )dIB nqd IB U K==霍尔效应第5章基本要求●由环路定理计算线性各项同性介质中的磁场（磁感应强、磁场强度）、磁化强度、磁化电流●两类问题的处理●磁场在边界处的边值关系，界面磁化电流磁介质存在时的静磁场∑⎰⎰⎰=⋅=⋅0I l d H 0S d B MB H 0-=μnM i Mj⨯='⨯∇='本构方程基本方程磁化电流B H j ⎧∇⋅=⎪⎨∇⨯=⎪⎩0r B Hμμ=均匀各向同性边界条件nn B B 12=210()n H H i ⨯-=2121tg tg μμθθ=B B第6章电磁感应定律动生电动势与感生电动势互感与自感磁能dtd Φ-=ε⎰⋅⨯=Cld B v )(ε电磁感应定律动生电动势⎰⎰⎰⋅∂∂-=⋅=L Sd t Bl d E S旋ε感生电动势互感和自感⎪⎪⎩⎪⎪⎨⎧-==dt dI M I M 1212112121εΦ⎪⎩⎪⎨⎧-==dt dI L I L εψ,21H B m⋅=ω∑=Φ=Ni ii I W 121载流线圈系统的磁能两个线圈系统的磁能为212222112121I MI I L I L W m ++=自感磁能互感磁能磁场中的磁能密度似稳条件交流电路中的元件及其性质交流电路基本方程及其复数形式交流电路的电功率第7章平均功率为瞬时功率一个周期内的平均值平均功率是电路实际消耗的功率–其中V ，I 分别是电压和电流的有效值。