2018年北京市平谷区中考二模数学试卷及答案

代几综合题2018昌平二模28.在平面直角坐标系xOy 中，对于任意三点A 、B 、C 我们给出如下定义：“横长”a ：三点中横坐标的最大值与最小值的差，“纵长”b ：三点中纵坐标的最大值与最小值的差，若三点的横长与纵长相等，我们称这三点为正方点.例如：点A (2-,0) ，点 B (1,1) ，点 C (1-, 2-)，则A 、B 、C 三点的 “横长”a =|1(2)--|=3，A 、B 、C 三点的“纵长”b =|1(2)--|=3. 因为a =b ，所以A 、B 、C 三点为正方点.（1）在点R (3，5) ，S (3，2-) ，T (4-，3-)中，与点A 、B 为正方点的是 ； （2）点P (0，t )为y 轴上一动点，若A ，B ，P 三点为正方点，t 的值为 ； （3）已知点D (1，0).①平面直角坐标系中的点E 满足以下条件：点A ，D ，E 三点为正方点，在图中画出所有符合条件的点E 组成的图形； ②若直线l ：12y x m =+上存在点N ，使得A ，D ，N 三点为正方点，直接写出m 的取值范围．y xxy yx2018朝阳二模28. 对于平面直角坐标系xOy 中的点P 和直线m ，给出如下定义：若存在一点P ，使得点P 到直线m 的距离等于，则称P 为直线m 的平行点． （1）当直线m 的表达式为y =x 时， ①在点P 1（1，1），P 2（0，2），P 3（22-，22）中，直线m 的平行点是 ； ②⊙O 的半径为10，点Q 在⊙O 上，若点Q 为直线m 的平行点，求点Q 的坐标. （2）点A 的坐标为（n ，0），⊙A 半径等于1，若⊙A 上存在直线x y 3=的平行点，直接写出n 的取值范围．2018东城二模28. 研究发现，抛物线214y x =上的点到点F (0，1)的距离与到直线l ：1y =-的距离相等.如图1所示，若点P 是抛物线214y x =上任意一点，PH ⊥l 于点H ，则PH PF =.基于上述发现，对于平面直角坐标系x O y 中的点M ，记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ，称d 为点M 关于抛物线214y x =的关联距离；当24d ≤≤时，称点M 为抛物线214y x =的关联点.（1）在点1(20)M ，，2(12)M ，，3(45)M ，，4(04)M -，中，抛物线214y x =的关联点是______ ；（2）如图2，在矩形ABCD 中，点(1)A t ，，点(13)C t +， ①若t =4，点M 在矩形ABCD 上，求点M 关于抛物线214y x =的关联距离d 的取值范围；②若矩形ABCD 上的所有点都是抛物线214y x =的关联点，则t 的取值范围是__________.2018房山二模28. 已知点P，Q为平面直角坐标系xOy中不重合的两点，以点P为圆心且经过点Q作⊙P，则称点Q为⊙P的“关联点”，⊙P为点Q的“关联圆”.（1）已知⊙O的半径为1，在点E（1，1），F（－12，32），M（0，－1）中，⊙O的“关联点”为；（2）若点P（2，0），点Q（3，n），⊙Q为点P的“关联圆”，且⊙Q的半径为 5 ，求n的值；（3）已知点D（0，2），点H（m，2），⊙D是点H的“关联圆”，直线443y x=-+与x轴，y轴分别交于点A，B. 若线段AB上存在⊙D的“关联点”，求m的取值范围.2018丰台二模28．在平面直角坐标系xOy 中，将任意两点()11,y x P 与()22y x Q ，之间的“直距”定义为：2121y y x x D PQ -+-=.例如：点M （1，2-），点N （3，5-），则132(5)5MN D =-+---=. 已知点A (1，0)、点B (-1，4).（1）则_______=AO D ，_______=BO D ；（2）如果直线AB 上存在点C ，使得CO D 为2，请你求出点C 的坐标； （3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出EO D 的取值范围.2018海淀二模28．对某一个函数给出如下定义：若存在实数k ，对于函数图象上横坐标之差为1的任意两点1(,)a b ，2(1,)a b +，21b b k -≥都成立，则称这个函数是限减函数，在所有满足条件的k 中，其最大值称为这个函数的限减系数．例如，函数2y x =-+，当x 取值a 和1a +时，函数值分别为12b a =-+，21b a =-+，故211b b k -=-≥，因此函数2y x =-+是限减函数，它的限减系数为1-．（1）写出函数21y x =-的限减系数； （2）0m >，已知1y x=（1,0x m x -≤≤≠）是限减函数，且限减系数4k =，求m 的取值范围．（3）已知函数2y x =-的图象上一点P ，过点P 作直线l 垂直于y 轴，将函数2y x =-的图象在点P 右侧的部分关于直线l 翻折，其余部分保持不变，得到一个新函数的图象，如果这个新函数是限减函数，且限减系数1k ≥-，直接写出P 点横坐标n 的取值范围．2018平谷二模28．对于平面直角坐标系xOy 中的点P 和⊙M ，给出如下定义：若⊙M 上存在两个点A ，B ，使AB =2PM ，则称点P 为⊙M 的“美好点”． （1）当⊙M 半径为2，点M 和点O 重合时，○1点()120P -， ，()211P ，，()322P ，中，⊙O 的“美好点”是 ； ○2点P 为直线y=x+b 上一动点，点P 为⊙O 的“美好点”，求b 的取值范围； （2）点M 为直线y=x 上一动点，以2为半径作⊙M ，点P 为直线y =4上一动点，点P 为⊙M 的“美好点”，求点M 的横坐标m 的取值范围．2018石景山二模28．在平面直角坐标系xOy 中，对于任意点P ，给出如下定义：若⊙P 的半径为1，则称⊙P 为点P 的“伴随圆”． （1）已知，点()1,0P ，①点1,2A ⎛⎝⎭在点P 的“伴随圆” （填“上”或“内”或“外”）； ②点()1,0B -在点P 的“伴随圆” （填“上”或“内”或“外”）；（2）若点P 在x 轴上，且点P 的“伴随圆”与直线x y 33=相切，求点P 的坐标； （3）已知直线2+=x y 与x 、y 轴分别交于点A ，B ，直线2-=x y 与x 、y 轴分别交于点C ，D ，点P 在四边形ABCD 的边上并沿DA CD BC AB →→→的方向移动，直接写出点P 的“伴随圆”经过的平面区域的面积．2018西城二模28. 对于平面直角坐标系xOy 中的点(,)Q x y （x ≠0），将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”，记作Q L .如(1,2)Q -的“理想值”221Q L ==--. （1）①若点(1,)Q a 在直线4y x =-上，则点Q 的“理想值”Q L 等于_________；②如图，C ，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”Q L 的取值范围是 .（2）点D 在直线+3y =上，⊙D 的半径为1，点Q 在⊙D 上运动时都有0≤L Q ，求点D 的横坐标D x 的取值范围；（3）(2,)M m （m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤件的最大圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）2018怀柔二模28. A 为⊙C 上一点，过点A 作弦AB ，取弦AB 上一点P ，若满足131<≤ABAP ，则称P 为点A 关于⊙C 的黄金点．已知⊙C 的半径为3，点A 的坐标为（1，0）． (1)当点C 的坐标为（4，0）时，①在点D （3，0），E （4，1），F （7，0）中，点A 关于⊙C 的黄金点是 ； ②直线3333-=x y 上存在点A 关于⊙C 的黄金点P ，求点P 的横坐标的取值范围； (2)若y 轴上存在．．点A 关于⊙C 的黄金点，直接写出点C 横坐标的取值范围．2018门头沟二模28.在平面直角坐标系xOy中的某圆上，有弦MN，取MN的中点P，我们规定:点P到某点（直”表示.线）的距离叫做“弦中距”，用符号“d中以(3,0)W-为圆心，半径为2的圆上.（1）已知弦MN长度为2.①如图1：当MN∥x轴时，直接写出到原点O的d的长度；中的取值范围.②如果MN在圆上运动时，在图2中画出示意图，并直接写出到点O的d中（2）已知点(5,0)y x=-，求到直线2=-的dy xM-,点N为⊙W上的一动点，有直线2中备用图2018顺义二模28．已知边长为2a 的正方形ABCD ，对角线AC 、BD 交于点Q ，对于平面内的点P 与正方形ABCD ，给出如下定义：如果a ≤PQ，则称点P 为正方形ABCD 的“关联点”．在平面直角坐标系xOy 中，若A (-1，1)，B (-1，-1)，C (1，-1)，D (1，1) ．（1）在11(,0)2-P，21(2P，3P 中，正方形ABCD 的“关联点”有 ； （2）已知点E 的横坐标是m ，若点E在直线=y 上，并且E 是正方形ABCD 的“关联点”，求m 的取值范围；（3）若将正方形ABCD 沿x 轴平移，设该正方形对角线交点Q 的横坐标是n ，直线1=+y 与x 轴、y 轴分别相交于M 、N 两点．如果线段MN 上的每一个点都是正方形ABCD 的“关联点”，求n 的取值范围．代数综合题2018昌平二模26.在平面直角坐标系xOy 中，抛物线223(0)y ax ax a a =--≠，与x 轴交于A 、B 两点(点A 在点B 的左侧)． （1）求点A 和点B 的坐标；（2）若点P （m ，n ）是抛物线上的一点，过点P 作x 轴的垂线，垂足为点D ．①在0a >的条件下，当22m -≤≤时，n 的取值范围是45n -≤≤，求抛物线的表达式； ②若D 点坐标（4，0），当PD AD >时，求a 的取值范围.2018朝阳二模26.已知二次函数)0(222≠--=a ax ax y ．（1）该二次函数图象的对称轴是直线 ；（2）若该二次函数的图象开口向上，当-1≤x ≤5时，函数图象的最高点为M ，最低点为N ，点M 的纵坐标为211，求点M 和点N 的坐标；（3）对于该二次函数图象上的两点A （x 1，y 1），B （x 2，y 2），设t ≤ x 1 ≤ t +1，当x 2≥3时，均有y 1 ≥ y 2，请结合图象，直接写出t 的取值范围．2018东城二模26．在平面直角坐标系xOy 中，抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ，． （1）求该抛物线的表达式；（2）求直线AB 关于x 轴的对称直线的表达式；（3）点P 是x 轴上的动点，过点P 作垂直于x 轴的直线l ，直线l 与该抛物线交于点M ，与直线AB 交于点N ．当PM PN ＜时，求点P 的横坐标P x 的取值范围．2018房山二模26. 在平面直角坐标系xOy 中，二次函数2y ax bx c =++（0a ≠）的图象经过A （0，4），B （2，0），C （－2，0）三点.（1）求二次函数的表达式；（2）在x 轴上有一点D （－4，0），将二次函数的图象沿射线DA 方向平移，使图象再次经过点B .①求平移后图象顶点E 的坐标；②直接写出此二次函数的图象在A ，B 两点之间（含A ，B 两点）的曲线部分在平移过程中所扫过的面积.2018丰台二模26．在平面直角坐标系xOy 中，二次函数22y x hx h =-+的图象的顶点为点D ． （1）当1h =-时，求点D 的坐标； （2）当1x ≤≤≤1-≤1时，求函数的最小值m ．（用含h 的代数式表示m ）2018海淀二模26．在平面直角坐标系xOy 中，已知点(3,1)A -，(1,1)B -，(,)C m n ，其中1n >，以点,,A B C 为顶点的平行四边形有三个，记第四个顶点分别为123,,D D D ，如图所示.（1）若1,3m n =-=，则点123,,D D D 的坐标分别是（ ），（ ），（ ）； （2）是否存在点C ，使得点123,,,,A B D D D 在同一条抛物线上？若存在，求出点C 的坐标；若不存在，说明理由.2018平谷二模26．在平面直角坐标系中，点D 是抛物线223y ax ax a =--()0a >的顶点，抛物线与x轴交于点A ，B （点A 在点B 的左侧）． （1）求点A ，B 的坐标；（2）若M 为对称轴与x 轴交点，且DM =2AM ，求抛物线表达式； （3）当30°<∠ADM <45°时，求a 的取值范围．2018石景山二26．在平面直角坐标系xOy 中，抛物线()240y ax x c a =++≠经过点()34,A -和()02,B ．（1）求抛物线的表达式和顶点坐标；（2）将抛物线在A 、B 之间的部分记为图象M （含A 、B 两点）．将图象M 沿直线3x =翻折，得到图象N ．若过点()94,C 的直线y kx b =+与图象M 、图象N 都相交，且只有两个交点，求b 的取值范围．2018西城二模26. 抛物线M ：241y ax ax a =-+- (a ≠0)与x 轴交于A ，B 两点（点A 在点B 左侧），抛物线的顶点为D .（1）抛物线M 的对称轴是直线____________； （2）当AB =2时，求抛物线M 的函数表达式；（3）在（2）的条件下，直线l ：y kx b =+(k ≠0)经过抛物线的顶点D ，直线y n =与抛物线M 有两个公共点，它们的横坐标分别记为1x ，2x ，直线y n =与直线l 的交点的横坐标记为3x （30x >），若当2-≤n ≤1-时，总有13320x x x x ->->，请结合函数的图象，直接写出k 的取值范围.2018怀柔二模26.在平面直角坐标系xOy 中，二次函数C 1：()332--+=x m mx y （m ＞0）的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C . (1)求点A 和点C 的坐标； (2)当AB =4时，①求二次函数C 1的表达式；②在抛物线的对称轴上是否存在点D ，使△DAC 的周长最小，若存在，求出点D 的坐标，若不存在，请说明理由；(3)将(2)中抛物线C 1向上平移n 个单位，得到抛物线C 2，若当0≤x ≤25时，抛物线C 2与x 轴只有一个公共点，结合函数图象，求出n 的取值范围.2018门头沟二模26.在平面直角坐标系xOy 中，有一抛物线其表达式为222y x mx m =-+. （1）当该抛物线过原点时，求m 的值；（2）坐标系内有一矩形OABC ,其中(4,0)A 、(4,2)B . ①直接写出C 点坐标；②如果抛物线222y x mx m =-+与该矩形有2个交点，求m 的取值范围.x2018顺义二模26．在平面直角坐标系中，二次函数221y x ax a =+++的图象经过点 M （2，-3）． （1）求二次函数的表达式；（2）若一次函数(0)y kx b k =+≠的图象与二次函数221y x ax a =+++的图象经过x 轴上同一点，探究实数k ，b 满足的关系式；（3）将二次函数221y x ax a =+++的图象向右平移2个单位，若点P （x 0，m ）和Q （2，n ）在平移后的图象上，且m >n ，结合图象求x 0的取值范围．反比例综合题2018昌平二模22.如图，在平面直角坐标系xOy 中，一次函数+(0)y ax b a =≠与反比例函数ky k x=≠（0）的图象交于点A （4，1）和B （1-，n ）． （1）求n 的值和直线+y ax b =的表达式；（2）根据这两个函数的图象，直接写出不等式0kax b x+-<的解集．x2018朝阳二模21. 如图，在平面直角坐标系xOy 中，直线61+=x k y 与函数)0(2>=x xk y 的图象的两个交点分别为A （1，5），B . （1）求21,k k 的值；（2）过点P （n ，0）作x 轴的垂线，与直线61+=x k y 和函数)0(2>=x xk y 的图象的交点分别为点M ，N ，当点M 在点N 下方时，写出n 的取值范围.2018东城二模22. 已知函数1y x =的图象与函数()0y kx k =≠的图象交于点(),P m n .（1）若2m n =，求k 的值和点P 的坐标；（2）当m n ≤时，结合函数图象，直接写出实数k 的取值范围.2018房山二模22. 如图，在平面直角坐标系xOy 中，直线y kx m =+与双曲线2y x=-相交于 点A （m ，2）．（1）求直线y kx m =+的表达式； （2）直线y kx m =+与双曲线2y x=-的另一个交点为B ，点P 为x 轴上一点，若AB BP =，直接写出P 点坐标 ．2018丰台二模22．在平面直角坐标系xOy 中，直线l ：21(0)y mx m m =-+≠. （1）判断直线l 是否经过点M （2，1），并说明理由； （2）直线l 与反比例函数ky x=的图象的交点分别为点M ，N ，当OM =ON 时，直接写出点N 的坐标.2018海淀二模22．已知直线l 过点(2,2)P ，且与函数(0)ky x x=>的图象相交于,A B 两点，与x 轴、y 轴分别交于点,C D ，如图所示，四边形,ONAE OFBM 均为矩形，且矩形OFBM 的面积为3. （1）求k 的值；（2）当点B 的横坐标为3时，求直线l 的解析式及线段BC 的长； （3）如图是小芳同学对线段,AD BC 的长度关系的思考示意图.记点B 的横坐标为s ，已知当23s <<时，线段BC 的长随s 的增大而减小，请你参考小芳的示意图判断：当3s ≥时，线段BC 的长随s 的增大而 . （填“增大”、“减小”或“不变”）2018平谷二模21．如图，在平面直角坐标系xOy 中，函数()0ky k x=≠的图象与直线y =x －2交于点A （a ，1）． （1）求a ，k 的值；（2）已知点P （m ，0）（1≤m < 4），过点P 作平行于y 轴的直线，交直线y =x －2于点M （x 1，y 1），交函数()0ky k x=≠的图象于点N （x 1，y 2），结合函数的图象，直接写出12y y -的取值范围．2018石景山二模22．在平面直角坐标系xOy 中，直线1:2l y x b =-+与x 轴，y 轴分别交于点1(,0)2A ，B ，与反比例函数图象的一个交点为(),3M a . （1）求反比例函数的表达式；（2）设直线2:2l y x m =-+与x 轴，y 轴分别交于点C ,D ,且3OCD OAB S S ∆∆=，直接写出m 的值 .2018西城二模23. 如图，在平面直角坐标系xOy 中，函数my x=（0x <）的图象经过点(4,)A n -，AB ⊥x 轴于点B ，点C 与点A 关于原点O 对称， CD ⊥x 轴于点D ，△ABD 的面积为8.（1）求m ，n 的值；（2）若直线y kx b =+（k ≠0）经过点C ，且与x 轴，y 轴的交点分别为点E ，F ，当2CF CE =时，求点F 的坐标．2018怀柔二模23.在平面直角坐标系xOy 中，直线y =kx +b （k ≠0）与双曲线)0(≠=m xmy 相交于A ，B 两点，A 点坐标为（-3，2），B 点坐标为（n ，-3）. (1)求一次函数和反比例函数表达式；(2)如果点P 是x 轴上一点，且△ABP 的面积是5，直接写出点P 的坐标.2018门头沟二模20. 如图，在平面直角坐标系xOy 中，一次函数y x =与反比例函数ky x=（k ≠0）的图象相交于点(2,2)M . （1）求k 的值；（2）点(0,)P a 是y 轴上一点，过点P 且平行于x 轴的直线分别与一次函数y x =、反比例函数ky x=的图象相交于点1(,)A x b 、2(,)B x b ，当12x x <时，画出示意图并直接写出a 的取值范围.2018顺义二模20．如图，在平面直角坐标系xOy 中，函数ky x=（x >0）的图象与直线21y x =+交于点A （1，m ）．（1）求k 、m 的值；（2）已知点P （n ，0）（n ≥1），过点P 作平行于y 轴的直线，交直线21y x =+于点B ，交函数ky x=（x >0）的图象于点C ．横、纵坐标都是整数的点叫做整点． ①当3n =时，求线段AB 上的整点个数； ②若ky x=（x >0）的图象在点A 、C 之间的部分与线段AB 、BC 所围成的区域内（包括边界）恰有5个整点，直接写出n 的取值范围．函数操作题2018昌平二模25．有这样一个问题：探究函数3126y x x =-的图象与性质.小彤根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小彤探究的过程，请补充完整：（1）求m 的值为 ；（2）如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；（3）方程31226x x -=-实数根的个数为 ； （4）观察图象，写出该函数的一条性质 ； （5）在第（2）问的平面直角坐标系中画出直线12y x =，根据图象写出方程311262x x x -=的一个正数根约为 （精确到0.1）.2018朝阳二模25. 在数学活动课上，老师提出了一个问题：把一副三角尺如图1摆放，直角三角尺的两条直角边分别垂直或平行，60°角的顶点在另一个三角尺的斜边上移动，在这个运动过程中，有哪些变量，能研究它们之间的关系吗？小林选择了其中一对变量，根据学习函数的经验，对它们之间的关系进行了探究．下面是小林的探究过程，请补充完整：（1）画出几何图形，明确条件和探究对象；如图2，在Rt △ABC 中，∠C =90°，AC =BC =6cm ，D 是线段AB 上一动点，射线DE ⊥BC 于点E ，∠EDF = °，射线DF 与射线AC 交于点F ．设B ，E 两点间的距离为x cm ，E ，F 两点间的距离为y cm ．图1 图2（说明：补全表格时相关数据保留一位小数）（3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（4）结合画出的函数图象，解决问题：当△DEF为等边三角形时，BE的长度约为 cm.2018东城二模25. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园，妈妈问九年级的小强至少需要几米长的竹篱笆（不考虑接缝）.小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程，请补充完整：建立函数模型：设矩形小花园的一边长为x米，篱笆长为y米.则y关于x的函数表达式为 ;列表（相关数据保留一位小数）：根据函数的表达式，得到了x与y的几组值，如下表：描点、画函数图象：如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点， 根据描出的点画出该函数的图象； 观察分析、得出结论：根据以上信息可得，当x = 时，y 有最小值. 由此，小强确定篱笆长至少为 米.2018房山二模25. 有这样一个问题：探究函数3126y x x =-的图象与性质． 小东根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小东的探究过程，请补充完整： （1）函数3126y x x =-的自变量x 的取值范围是 ; (2) 下表是y 与x 的几组对应值则m的值为；(3) 如下图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；（4）观察图象，写出该函数的两条性质．2018丰台二模25．数学活动课上，老师提出问题：如图，有一张长4dm，宽3dm的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大.下面是探究过程，请补充完整：Array（1）设小正方形的边长为x dm，体积为y dm3，根据长方体的体积公式得到y和x的关系式：；（2）确定自变量x的取值范围是；（3）列出y与x的几组对应值.（说明：表格中相关数值保留一位小数）（4）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm时，盒子的体积最大，最大值约为 dm3.2018海淀二模25．小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。

1东城．在平面直角坐标系xOy 中，抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ，．（1）求该抛物线的表达式；（2）求直线AB 关于x 轴的对称直线的表达式；（3）点P 是x 轴上的动点，过点P 作垂直于x 轴的直线l ，直线l 与该抛物线交于点M ，与直线AB 交于点N ．当PM PN ＜时，求点P 的横坐标P x 的取值范围．2西城. 抛物线M ：241y ax ax a =-+- (a ≠0)与x 轴交于A ，B 两点（点A 在点B 左侧），抛物线的顶点为D .（1）抛物线M 的对称轴是直线____________； （2）当AB =2时，求抛物线M 的函数表达式；（3）在（2）的条件下，直线l ：y kx b =+(k ≠0)经过抛物线的顶点D ，直线y n =与抛物线M 有两个公共点，它们的横坐标分别记为1x ，2x ，直线y n =与直线l 的交点的横坐标记为3x （30x >），若当2-≤n ≤1-时，总有13320x x x x ->->，请结合函数的图象，直接写出k 的取值范围.3海淀．在平面直角坐标系xOy 中，已知点(3,1)A -，(1,1)B -，(,)C m n ，其中1n >，以点,,A B C 为顶点的平行四边形有三个，记第四个顶点分别为123,,D D D ，如图所示.（1）若1,3m n =-=，则点123,,D D D 的坐标分别是（ ），（ ），（ ）； （2）是否存在点C ，使得点123,,,,A B D D D 在同一条抛物线上？若存在，求出点C 的坐标；若不存在，说明理由.4朝阳.已知二次函数)0(222≠--=a ax ax y ．（1）该二次函数图象的对称轴是直线 ；（2）若该二次函数的图象开口向上，当-1≤x ≤5时，函数图象的最高点为M ，最低点为N ，点M 的纵坐标为211，求点M 和点N 的坐标；（3）对于该二次函数图象上的两点A （x 1，y 1），B （x 2，y 2），设t ≤ x 1 ≤ t +1，当x 2≥3时，均有y 1 ≥ y 2，请结合图象，直接写出t 的取值范围．5丰台．在平面直角坐标系xOy 中，二次函数22y x hx h =-+的图象的顶点为点D ．（1）当1h =-时，求点D 的坐标；（2）当1x -≤≤≤11x -≤≤≤1时，求函数的最小值m ． （用含h 的代数式表示m ）。

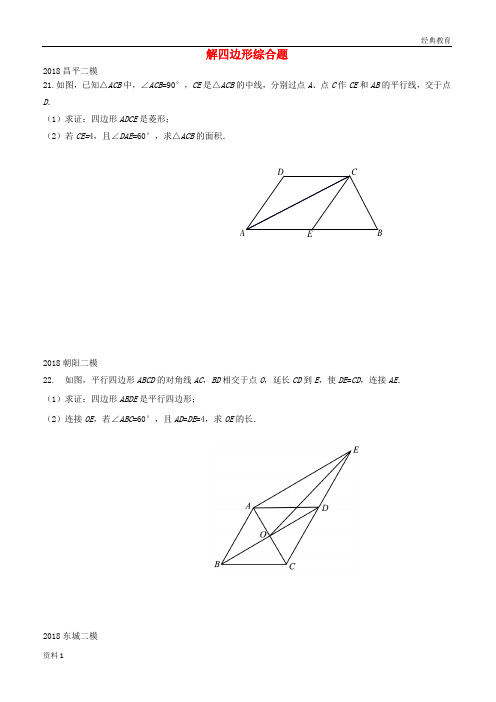
解四边形综合题2018昌平二模21.如图，已知△ACB 中，∠ACB =90°，CE 是△ACB 的中线，分别过点A 、点C 作CE 和AB 的平行线，交于点D ．（1）求证：四边形ADCE 是菱形；（2）若CE=4，且∠DAE =60°，求△ACB 的面积．2018朝阳二模22. 如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，延长CD 到E ，使DE =CD ，连接AE ． （1）求证：四边形ABDE 是平行四边形；（2）连接OE ，若∠ABC =60°，且AD =DE =4，求OE 的长．2018东城二模DECBA21．如图，在菱形ABCD 中，BAD α∠=，点E 在对角线BD 上. 将线段CE 绕点C 顺时针旋转α，得到CF ，连接DF .（1）求证：BE =DF ；（2）连接AC ， 若EB =EC ，求证：AC CF ⊥.2018房山二模21. 已知：如图，四边形ABCD 中，AD ∥BC ，AD =CD ，E 是对角线BD 上一点，且EA =EC ． （1）求证：四边形ABCD 是菱形；（2）如果∠BDC =30°，DE =2，EC =3，求CD 的长．2018丰台二模21．如图，BD 是△ABC 的角平分线，过点D 作DE ∥BC 交AB 于点E ，DF ∥AB 交BC 于点F ． （1）求证：四边形BEDF 为菱形；B（2）如果∠A = 90°，∠C = 30°，BD = 12，求菱形BEDF 的面积．2018海淀二模21．如图，在四边形ABCD 中，AB CD ， BD 交AC 于G ，E 是BD 的中点，连接AE 并延长，交CD于点F ，F 恰好是CD 的中点. （1）求BGGD的值； （2）若CE EB ，求证：四边形ABCF 是矩形.2018平谷二模22．如图，已知□ABCD ，延长AB 到E 使BE =AB ，连接BD ，ED ，EC ，若ED =AD ． （1）求证：四边形BECD 是矩形；（2）连接AC ，若AD=4，CD= 2，求AC 的长．F DECB AE G FA B CD2018石景山二模21．如图，在四边形ABCD 中，45A ∠=︒，CD BC =，DE 是AB 边的垂直平分线，连接CE ． （1）求证：DEC BEC ∠=∠；（2）若8AB =，BC =CE 的长．2018西城二模21.如图，在Rt △ABC 中，90ACB ∠=︒，CD ⊥AB 于点D ，BE ⊥AB于点B ，BE=CD ，连接CE ，DE ．（1）求证：四边形CDBE 为矩形； （2）若AC =2，1tan 2ACD ∠=，求DE 的长．ACD2018怀柔二模20.如图，四边形ABCD 是边长为2的菱形，E ，F 分别是AB ，AD 的中点，连接EF ，EC ，将△FAE 绕点F 旋转180°得到△FDM ．(1)补全图形并证明：EF ⊥AC ； (2)若∠B =60°，求△EMC 的面积．2018顺义二模22．如图，四边形ABCD 中，∠C =90°，AD ⊥DB ，点E 为AB 的中点，DE ∥BC ． （1）求证：BD 平分∠ABC ；（2）连接EC ，若∠A=30 ，DC EC 的长．2018门头沟二模21．如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BF=BE．（1）求证：四边形BDEF为平行四边形；（2）当∠C=45°，BD=2时，求D，F两点间的距离.。

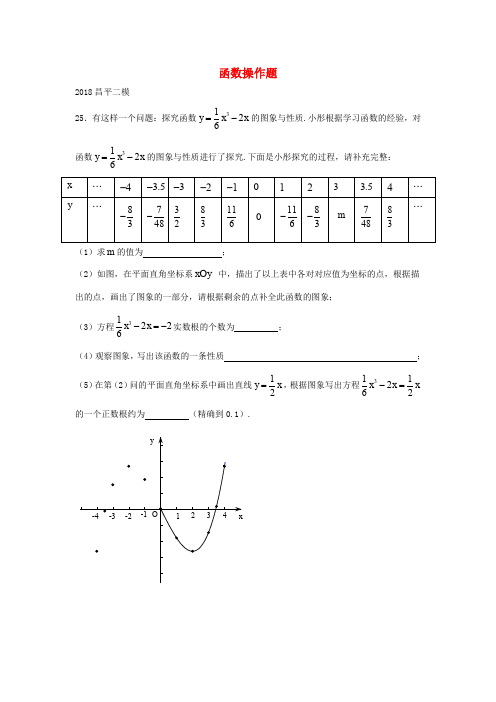
函数操作题2018昌平二模25．有这样一个问题：探究函数3126y x x =-的图象与性质.小彤根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小彤探究的过程，请补充完整：（1）求m 的值为 ；（2）如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象； （3）方程31226x x -=-实数根的个数为 ； （4）观察图象，写出该函数的一条性质 ； （5）在第（2）问的平面直角坐标系中画出直线12y x =，根据图象写出方程311262x x x -=的一个正数根约为 （精确到0.1）.25. 在数学活动课上，老师提出了一个问题：把一副三角尺如图1摆放，直角三角尺的两条直角边分别垂直或平行，60°角的顶点在另一个三角尺的斜边上移动，在这个运动过程中，有哪些变量，能研究它们之间的关系吗？小林选择了其中一对变量，根据学习函数的经验，对它们之间的关系进行了探究．下面是小林的探究过程，请补充完整：（1）画出几何图形，明确条件和探究对象；如图2，在Rt △ABC 中，∠C =90°，AC =BC =6cm ，D 是线段AB 上一动点，射线DE ⊥BC 于点E ，∠EDF = °，射线DF 与射线AC 交于点F ．设B ，E 两点间的距离为x cm ，E ，F 两点间的距离为y cm ．（2）通过取点、画图、测量，得到了x 与y 的几组值，如下表：（说明：补全表格时相关数据保留一位小数）（3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（4）结合画出的函数图象，解决问题：当△DEF 为等边三角形时，BE 的长度约为 cm.图1 图225. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园，妈妈问九年级的小强至少需要几米长的竹篱笆（不考虑接缝）.小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程，请补充完整：建立函数模型：设矩形小花园的一边长为x米，篱笆长为y米.则y关于x的函数表达式为 ;列表（相关数据保留一位小数）：根据函数的表达式，得到了x与y的几组值，如下表：描点、画函数图象：如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；观察分析、得出结论：根据以上信息可得，当x= 时，y有最小值.由此，小强确定篱笆长至少为米.25. 有这样一个问题：探究函数3126y x x =-的图象与性质． 小东根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小东的探究过程，请补充完整： （1）函数3126y x x =-的自变量x 的取值范围是 ; (2) 下表是y 与x 的几组对应值则m 的值为 ；(3) 如下图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；（4）观察图象，写出该函数的两条性质 ．25．数学活动课上，老师提出问题：如图，有一张长4dm ，宽3dm 的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大. 下面是探究过程，请补充完整：（1）设小正方形的边长为x dm ，体积为y dm 3，根据长方体的体积公式得到y 和x 的关系式： ；（2）确定自变量x 的取值范围是 ； （3）列出y 与x 的几组对应值.（说明：表格中相关数值保留一位小数）（4）在下面的平面直角坐标系xOy 中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm 时，盒子的体积最大，最大值约为 dm 3.25．小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。

北京市平谷区2018年中考模拟试卷2018.5一、选择题（本题共16分，每小题2分）1．风和日丽春光好，又是一年舞筝时。

放风筝是我国人民非常喜爱的一项户外娱乐活动．下列风筝剪纸作品中，不是．．轴对称图形的是A．B．C．D．2．下面四幅图中，用量角器测得∠AOB度数是40°的图是A．B．C．D．3．如图，数轴上每相邻两点距离表示1个单位，点A，B互为相反数，则点C表示的数可能是A．0 B．1 C．3 D．54．下图可以折叠成的几何体是A．三棱柱B．圆柱C．四棱柱D．圆锥5．中国有个名句“运筹帷幄之中，决胜千里之外”．其中的“筹”原意是指《孙子算经》中记载的“算筹”．算筹是古代用来进行计算的工具，它是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如右图）．当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间：个位、百位、万位数用纵式表示；十位，千位，十万位数用横式表示；“0”用空位来代替，以此类推．例如3306用算筹表示就是，则2022用算筹可表示为A． B. C. D.6．一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是A．3 B．4 C．6 D．127．“龟兔赛跑”是同学们熟悉的寓言故事．如图所示，表示了寓言中的龟、兔的路程S 和时间t的关系（其中直线段表示乌龟，折线段表示兔子）．下列叙述正确的是A．赛跑中，兔子共休息了50分钟B．乌龟在这次比赛中的平均速度是0.1米/分钟C．兔子比乌龟早到达终点10分钟D．乌龟追上兔子用了20分钟8．中小学时期是学生身心变化最为明显的时期，这个时期孩子们的身高变化呈现一定的趋势，7~15岁期间生子们会经历一个身高发育较迅速的阶段，我们把这个年龄阶段叫做生长速度峰值段，小明通过上网查阅《2016年某市儿童体格发育调查表》，了解某市男女生7~15岁身高平均值记录情况，并绘制了如下统计图，并得出以下结论：①10岁之前，同龄的女生的平均身高一般会略高于男生的平均身高；②10~12岁之间，女生达到生长速度峰值段，身高可能超过同龄男生；③7~15岁期间，男生的平均身高始终高于女生的平均身高；④13~15岁男生身高出现生长速度峰值段，男女生身高差距可能逐渐加大．以上结论正确的是A．①③B．②③C．②④D．③④二、填空题（本题共16分，每小题2分）9x 的取值范围是 ．10．林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中幼树成活率的统计图：估计该种幼树在此条件下移植成活的概率为 （结果精确到0.01）．11．计算：23222333m n ++++⨯⨯⨯个个= ．12．如图，测量小玻璃管口径的量具ABC 上，AB 的长为10毫米，AC 被分为60等份，如果小管口中DE 正好对着量具上20份处（DE ∥AB ），那么小管口径DE 的长是_________毫米．13．已知：24a a +=，则代数式()()()2122a a a a +-+-的值是 ． 14．如图，AB 是⊙O 的直径，AB ⊥弦CD 于点E ，若AB =10，CD =8，则BE = ．15．如图，在平面直角坐标系xOy 中，△OCD 可以看作是△ABO 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABO 得到△OCD 的过程： ．16．下面是“作已知角的角平分线”的尺规作图过程．请回答：该尺规作图的依据是 ． 三、解答题（本题共68分，第17~22题，每小题5分，第23题7分，第24题6分，第25题5分，第26题6分，第27题7分，第28题7分） 解答应写出文字说明、演算步骤或证明过程. 17．计算：(1112sin 603-⎛⎫-+-︒ ⎪⎝⎭π.18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．．19．如图，在△ABC 中，AB=AC ，点D 是BC 边上一点，EF 垂直平分CD ，交AC 于点E ，交BC 于点F ，连结DE ，求证：DE ∥AB ．20．关于x 的一元二次方程2210x x k ++-=有两个不相等的实数根． （1）求k 的取值范围；（2）当k 为正整数时，求此时方程的根．21．如图，在平面直角坐标系xOy 中，函数()0ky k x=≠的图象与直线y =x +1交于点A （1，a ）． （1）求a ，k 的值；（2）连结OA ，点P 是函数()0ky k x=≠上一点，且满足OP=OA ，直接写出点P 的坐标（点A 除外）．22．如图，在□ABCD 中，BF 平分∠ABC 交AD 于点F ，AE ⊥BF 于点O ，交BC 于点E ，连接EF ．（1）求证：四边形ABEF 是菱形；（2）连接CF ，若∠ABC=60°， AB= 4，AF =2DF ，求CF 的长．23．为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整. 收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析：甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91 乙 84 93 66 69 76 87 77 82 85 8890886788919668975988整理、描述数据按如下数据段整理、描述这两组数据分析数据两组数据的平均数、中位数、众数、方差如下表：的值是 ．得出结论a 若甲学校有400名初二学生，估计这次考试成绩80分以上人数为 .b 可以推断出 学校学生的数学水平较高，理由为. （至少从两个不同的角度说明推断的合理性）24．如图，以AB 为直径作⊙O ，过点A 作⊙O 的切线AC ，连结BC ，交⊙O 于点D ，点E 是BC 边的中点，连结AE ． （1）求证：∠AEB =2∠C ； （2）若AB =6，3cos 5B，求DE 的长．25．如图，在△ABC 中，∠C =60°，BC =3厘米，AC =4厘米，点P 从点B 出发，沿B →C →A 以每秒1厘米的速度匀速运动到点A ．设点P 的运动时间为x 秒，B 、P 两点间的距离为y 厘米．小新根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究． 下面是小新的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如下表：经测量m 的值是 （保留一位小数）．（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC 中画出点P 所在的位置．26．在平面直角坐标系xOy 中，抛物线223y x bx =-+-的对称轴为直线x =2． （1）求b 的值； （2）在y 轴上有一动点P （0，m ），过点P 作垂直y 轴的直线交抛物线于点A （x 1，y 1），B （x 2 ，y 2），其中 12x x <．①当213x x -=时，结合函数图象，求出m 的值；②把直线PB 下方的函数图象，沿直线PB 向上翻折，图象的其余部分保持不变，得到一个新的图象W ，新图象W 在0≤x ≤5 时，44y -≤≤，求m 的取值范围．27．在△ABC 中，AB=AC ，CD ⊥BC 于点C ，交∠ABC 的平分线于点D ，AE 平分∠BAC 交BD 于点E ，过点E 作EF ∥BC 交AC 于点F ，连接DF ． （1）补全图1；（2）如图1，当∠BAC =90°时，①求证：BE=DE ；②写出判断DF 与AB 的位置关系的思路（不用写出证明过程）； （3）如图2，当∠BAC=α时，直接写出α，DF ，AE 的关系．28. 在平面直角坐标系xOy 中，点M 的坐标为()11,x y ，点N 的坐标为()22,x y ，且12x x ≠，12y y ≠，以MN 为边构造菱形，若该菱形的两条对角线分别平行于x 轴，y 轴，则称该菱形为边的“坐标菱形”.（1）已知点A （2,0），B （），则以AB 为边的“坐标菱形”的最小内角为_______； （2）若点C （1,2），点D 在直线y =5上，以CD 为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙OP 的坐标为(3,m ) .若在⊙O 上存在一点Q ，使得以QP 为边的“坐标菱形”为正方形，求m 的取值范围．图1BB 图2北京市平谷区2018年中考统一练习（一）数学试卷参考答案及评分标准 2018.04二、填空题（本题共16分，每小题2分） 9．x ≥2；10．0.88； 11．23n m +；12．103；13．8；14．2；15．答案不唯一，如：将△ABO 沿x 轴向下翻折，在沿x 轴向左平移2个单位长度得到△OCD . 16．答案不唯一：到线段两端点距离相等的点在线段的垂直平分线上；等腰三角形三线合一．三、解答题（本题共68分，第17-22题，每小题5分，第23题7分，第24题6分，第25题5分，第26题6分，第27题7分，第28题7分） 解答应写出文字说明、演算步骤或证明过程. 17．解：(1112sin 603-⎛⎫-+--︒ ⎪⎝⎭π=3112--········································································· 4 =1 ···································································································· 5 18．解：3(1)4553 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． (1)解不等式②，得 x ＞-1． ....................................................................... 3 ∴原不等式组的解集为12x -<≤． ....................................................... 4 ∴适合原不等式组的整数解为0,1,2． ...................................................... 5 19．证明：∵AB=AC ， ∴∠B =∠C ． ................................................................................. 1 ∵EF 垂直平分CD ， ∴ED=EC ． ................................................................................... 2 ∴∠EDC =∠C ． ............................................................................. 3 ∴∠EDC =∠B ． ............................................................................. 4 ∴DF ∥AB ． . (5)20．解：（1）∵关于x 的一元二次方程有两个不相等的实数根．∴()2Δ2410k =--> (1)=8－4k >0. ∴2k < ··················································································· 2 （2）∵k 为正整数， ∴k =1． ··················································································· 3 解方程220x x +=，得120,2x x ==-． ········································· 5 21．解：（1）∵直线y =x +1经过点A （1，a ），∴a =2． ····················································································· 1 ∴A （1,2）．∵函数()0ky k x=≠的图象经过点A （1，2）， ∴k =2． (2)（2）点P 的坐标（2,1），（-1，-2），（-2，-1）． ......................................... 5 22．（1）证明：∵BF 平分∠ABC ， ∴∠ABF =∠CBF ． .. (1)∵□ABCD ，∴AD ∥BC ．∴∠AFB =∠CBF ．∴∠ABF =∠AFB ．∴AB=AF ．∵AE ⊥BF ，∴∠ABF +∠BAO =∠CBF +∠BEO =90°． ∴∠BAO =∠BEO ． ∴AB=BE ． ∴AF=BE ．∴四边形ABEF 是平行四边形． ∴□ABEF 是菱形． (2)（2）解：∵AD=BC ，AF=BE ，∴DF=CE ． ∴BE =2CE ． ∵AB =4，∴BE =4． ∴CE =2．过点A 作AG ⊥BC 于点G ． (3)∵∠ABC =60°，AB=BE ， ∴△ABE 是等边三角形． ∴BG=GE =2． ∴AF=CG =4． (4)∴四边形AGCF是平行四边形．∴□AGCF是矩形．∴AG=CF．在△ABG中，∠ABC=60°，AB=4，∴AG=∴CF= (5) (2)分析数据经统计，表格中m的值是88 ． (3)得出结论a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为300 . (4)b 答案不唯一，理由须支撑推断结论. (7)24．（1）证明：∵AC是⊙O的切线，∴∠BAC=90°． (1)∵点E是BC边的中点，∴AE=EC．∴∠C=∠EAC， (2)∵∠AEB=∠C+∠EAC，∴∠AEB=2∠C． (3)（2）解：连结AD．∵AB为直径作⊙O，∴∠ABD=90°．∵AB= 6，3 cos5B=，∴BD=185． (4)在Rt△ABC中，AB=6，3 cos5B=，∴BC=10．∵点E是BC边的中点，∴BE=5． (5)∴75DE=． (6)25．解：（1）3.0；························ (1)（2）如图所示； (4)（3）如图 (5)26．解：（1）∵抛物线223y x bx =-+-的对称轴为直线x =2， ∴b =2． ················································· 1 （2）①∴抛物线的表达式为243y x x =-+-． ∵A （x 1，y ），B （x 2 ，y ）， ∴直线AB 平行x 轴．∵213x x -=， ∴AB =3．∵对称轴为x =2，∴AC =12． ············································· 2 ∴当12x =时，54y m ==-． (3)②当y =m =-4时，0≤x ≤5时，41y -≤≤； (4)当y =m =-2时，0≤x ≤5 时，24y -≤≤； (5)∴m 的取值范围为42m -≤≤-． (6)27．解：（1）补全图1； (1)B（2）①延长AE ，交BC 于点H ． ················· 2 ∵AB=AC ， AE 平分∠BAC ，∴AH ⊥BC 于H ，BH=HC ．∵CD ⊥BC 于点C ， ∴EH ∥CD ． ∴BE=DE ． (3)②延长FE ，交AB 于点G ．由AB=AC ，得∠ABC =∠ACB ． 由EF ∥BC ，得∠AGF =∠AFG ． 得AG=AF ．由等腰三角形三线合一得GE=E F ． ·· (4)BB由∠GEB =∠FED ，可证△BEG ≌△DEF ．可得∠ABE =∠FDE ． (5)从而可证得DF ∥AB ． ························ 6 （3）tan 2DF αAE =． (7)28．解：（1）60；·························································································· 1 （2）∵以CD 为边的“坐标菱形”为正方形，∴直线CD 与直线y =5的夹角是45°． 过点C 作CE ⊥DE 于E ．∴D （4,5）或()2,5-． ........................................ 3 ∴直线CD 的表达式为1y x =+或3y x =-+． .. (5)（3）15m ≤≤或51m -≤≤-． (7)。

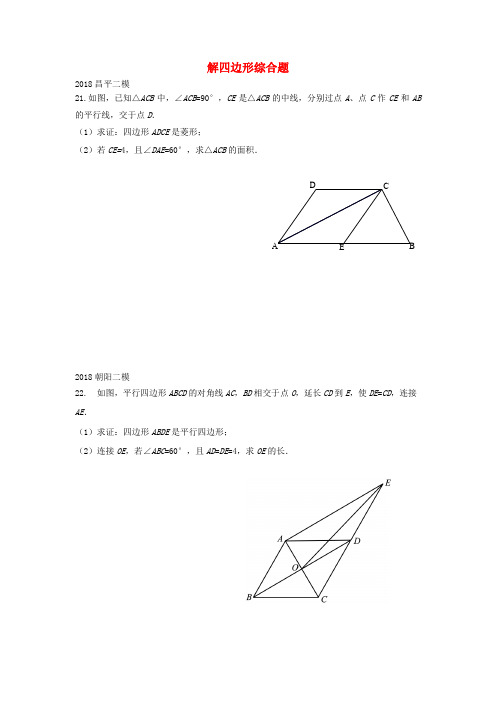
解四边形综合题2018昌平二模21.如图，已知△ACB 中，∠ACB =90°，CE 是△ACB 的中线，分别过点A 、点C 作CE 和AB 的平行线，交于点D ．（1）求证：四边形ADCE 是菱形；（2）若CE=4，且∠DAE =60°，求△ACB 的面积．2018朝阳二模22. 如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，延长CD 到E ，使DE =CD ，连接AE ．（1）求证：四边形ABDE 是平行四边形；（2）连接OE ，若∠ABC =60°，且AD =DE =4，求OE 的长．DECBA2018东城二模21．如图，在菱形ABCD 中，BAD α∠=，点E 在对角线BD 上. 将线段CE 绕点C 顺时针旋转α，得到CF ，连接DF . （1）求证：BE =DF ；（2）连接AC ， 若EB =EC ，求证：AC CF ⊥.2018房山二模21. 已知：如图，四边形ABCD 中，AD ∥BC ，AD =CD ，E 是对角线BD 上一点，且EA =EC ． （1）求证：四边形ABCD 是菱形；（2）如果∠BDC =30°，DE =2，EC =3，求CD 的长．B2018丰台二模21．如图，BD 是△ABC 的角平分线，过点D 作DE ∥BC 交AB 于点E ，DF ∥AB 交BC 于点F ． （1）求证：四边形BEDF 为菱形； （2）如果∠A = 90°，∠C = 30°，BD = 12，求菱形BEDF 的面积．2018海淀二模21．如图，在四边形ABCD 中，ABCD ， BD 交AC 于G ，E 是BD 的中点，连接AE并延长，交CD 于点F ，F 恰好是CD 的中点. （1）求BGGD的值； （2）若CE EB ，求证：四边形ABCF 是矩形.F DEB AEGFABCD2018平谷二模22．如图，已知□ABCD ，延长AB 到E 使BE =AB ，连接BD ，ED ，EC ，若ED =AD ． （1）求证：四边形BECD 是矩形；（2）连接AC ，若AD=4，CD= 2，求AC 的长．2018石景山二模21．如图，在四边形ABCD 中，45A ∠=︒，CD BC =，DE 是AB 边的垂直平分线，连接CE ．（1）求证：DEC BEC ∠=∠；（2）若8AB =，BC =CE 的长．EA2018西城二模21.如图，在Rt △ABC 中，90ACB ∠=︒，CD ⊥AB 于点D ，BE ⊥AB 于点B ，BE=CD ，连接CE ，DE ．（1）求证：四边形CDBE 为矩形； （2）若AC =2，1tan 2ACD ∠=，求DE 的长．2018怀柔二模20.如图，四边形ABCD 是边长为2的菱形，E ，F 分别是AB ，AD 的中点，连接EF ，EC ，将△FAE 绕点F 旋转180°得到△FDM ． (1)补全图形并证明：EF ⊥AC ； (2)若∠B =60°，求△EMC 的面积．A BCDE 2018顺义二模22．如图，四边形ABCD 中，∠C =90°，AD ⊥DB ，点E 为AB 的中点，DE ∥BC ． （1）求证：BD 平分∠ABC ；（2）连接EC ，若∠A =30 ，DC，求EC 的长．2018门头沟二模21．如图，以BC 为底边的等腰△ABC ，点D ，E ，G 分别在BC ，AB ，AC 上，且EG ∥BC ，DE ∥AC ，延长GE 至点F ，使得BF =BE ．（1）求证：四边形BDEF 为平行四边形；（2）当∠C =45°，BD =2时，求D ，F 两点间的距离.。

2023-2024学年北京市平谷区中考二模数学试题一、选择题：本题共8小题，每小题3分，共24分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.据国家能源网消息，截至2023年12月31日，国家能源集团2023年度发电量首次突破万亿千瓦时，其中1200000000000用科学记数法表示为()A. B. C. D.2.下列几何体中，主视图为三角形的是()A. B. C. D.3.一副三角板如图所示摆放，直线，则的度数是()A. B. C. D.4.若，则下列结论不正确的是()A. B. C. D.5.如果正多边形的每个外角都等于，则它的边数为()A.5B.6C.7D.86.布袋中有三个除颜色外其余均相同的小球，小球颜色两红一白，从中随机同时抽取两个小球，则抽到的两个小球颜色恰好相同的概率是()A. B. C. D.7.若关于x的一元二次方程有两个实数根，则k的取值范围为()A. B. C. D.8.如图，正方形ABCD中，点E为CD边上的点点E不与点C、D重合，以CE为边作正方形CEFG，连接AF，设，，，给出下面三个结论：①；②；③；上述结论中，所有正确结论的序号是()A.①②B.①③C.②③D.①②③二、填空题：本题共8小题，每小题3分，共24分。

9.若代数式有意义，则实数x的取值范围是__________.10.分解因式：__________.11.方程的解为__________.12.如图，点A、B分别是反比例函数的图象上两点，分别过点A、B向坐标轴作垂线，四边形ACEG的面积记作，四边形BFDG的面积记作，则__________填>、<或13.某中学共有1000名学生，为了解这1000名学生参加志愿者服务的时长情况，从中随机抽取了100名学生进行访问，获得了他们的志愿者服务时长单位：小时，数据整理如下：志愿者服务时长学生人数102023201512根据以上数据，估计这1000名学生的志愿者服务时长不小于300小时的学生的人数为__________名．14.如图，正方形ABCD的边长为3，点E为AD边的中点，连接、，BD与CE相交于点F，则DF 的长为__________.15.如图，PA，PB分别与相切于A，B两点，C是优弧AB上的一个动点，若，则__________16.某校航模小组的同学正在为即将开始的航模比赛做最后的准备．已知准备工作共有A，B，C，D，E，F，G，H，M，N十项工序，准备工作完成过程需要满足以下要求：只能在A、B、C工序均完成后才能完成；只能在C、D、E工序均完成后才能完成；其余每项工序相互独立，之间没有干扰；一项工序只能由一名学生完成，此工序完成后该学生才能进行其他工序．各项工序所需时间如下表所示：工序A B C DEFGHMN所需时间/分钟1815166758323在不考虑其他因素的前提下，若由若干名学生合作完成准备工作，则至少需要__________分钟才能全部完成；若要在最短的时间内合作完成准备工作，则最少需要__________名学生共同参与．三、解答题：本题共12小题，共96分。

2017年北京市中考数学分类25题圆顺义25．如图，在Rt△ABC中，∠CA B=90 ，以AB为直径的⊙O交BC于点D，点E是AC的中点，连接DE．（1）求证：DE是⊙O的切线；（2）点P是BD上一点，连接AP，DP，若BD:CD=4:1，求sin∠APD的值．EB房山25.如图，△ ABC 中，AC=BC=a，AB=b．以BC为直径作⊙O交AB于点 D，交 AC 于点E，过点D作⊙O的切线MN，交CB的延长线于点M，交 AC 于点N．(1)求证：MN⊥AC；(2)连接BE，写出求BE长的思路．丰台26．如图，AB 为半圆的直径，O 为圆心，C 为圆弧上一点，AD 垂直于过点C 的切线，垂足为点D ，AB 的延长线交切线CD 于点E ．（1）求证：AC 平分∠DAB ；（2）若AB =4，B 为OE 的中点，CF ⊥AB ，垂足为点F ，求CF 的长.平谷25．如图，已知△ABC 内接于⊙O ，AB 是⊙O 的直径，点F 在⊙O 上，且点C 是BF 的中点，过点C 作⊙O 的切线交AB 的延长线于点D ，交AF 的延长线于点E ． （1）求证：AE ⊥DE ；（2）若∠BAF=60°，AF=4，求CE 的长．石景山25．如图，AB为⊙O的直径，弦BC，DE相交于点F，且DE⊥AB于点G，过点C 作⊙O的切线交DE的延长线于点H.（1）求证：HC HF（2）若⊙O的半径为5，点F是BC的中点，tan HCF m∠=，写出求线段BC长的思路.朝阳25．如图，△ABC中，∠A=45°，D是AC边上一点，⊙O过D、A、B三点，OD∥BC．（1）求证：直线BC是⊙O的切线；（2）OD，AB相交于点E，若AB=AC，OD=r，写出求AE长的思路．西城25．如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点B 作⊙O 的切线，与AC 延长线交于点D ，连接BC ，OE ∥BC 交⊙O 于点E ，连接BE 交AC 于点H ． （1）求证：BE 平分∠ABC ；（2）连接OD ，若BH =BD =2，求OD 的长．海淀25．如图，AB 是⊙O 的直径，BC 为弦，D 为AC 的中点，AC ，BD 相交于E 点，过点A 作⊙O 的切线交BD 的延长线于P 点． （1）求证：∠PAC =2∠CBE ；（2）若PD =m ，∠CBE =α，请写出求线段CE 长的思路．东城25.如图，AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D ，CE ⊥AD 交AD 的延长线于点E ．（1）求证：∠BDC =∠A ；（2）若CE =4，DE =2，求AD 的长．通州24.如图，AB 是⊙O 的直径，PC 切⊙O 于点C ，AB 的延长线与PC 交于点P ，PC 的延长线与AD 交于点D ，AC 平分∠DAB .（1）求证：AD ⊥PC ；（2）连接BC ，如果∠ABC ＝60°，BC ＝2，求线段PC 的长．PA昌平25.如图，AB 为⊙O 的直径，点D ，E 为⊙O 上的两个点，延长AD 至C ，使∠CBD=∠BED .（1）求证：BC 是⊙O 的切线；（2）当点E 为弧AD 的中点且∠BED=30°时，⊙O 半径为2，求DF 的长度.BCA怀柔25.如图，AB 是⊙O 的直径，CD 为⊙O 的弦，过点B 作⊙O 的切线，交AD 的延长线于点E ，连接AC 并延长，过点E 作EG ⊥AC 的延长线于点G ，并且∠GCD = ∠GAB . （1）求证：AC BD ；AEE A（2）若AB =10，sin ∠ADC =35，求AG 的长．2017年北京市中考数学二模分类25题圆答案顺义25．（1）证明：连接OD ，AD ，∵AB 为⊙O 的直径，∴∠ADB =90°．∴∠ADC =90°．∵点E 是AC 的中点，∴12DE AC CE ==． ∴∠C =∠1．∵OB =OD ，∴∠B =∠2．在Rt △ABC 中，∵∠CAB =90°，∴∠C +∠B =90°．∴∠1+∠2=90°． ∴∠ODE =180°-（∠1+∠2）=90°．∴OD ⊥DE ． ∴DE 是⊙O 的切线．（2）解：设BD =4x ，CD =x ，则BC =5x ． 由△ABC ∽△DAC ，得AC BCCD AC=．∴55AC x x x ===．∴sin 55AC B BC x ===．∵∠APD=∠B ，∴sin sin 5APD B ∠==．房山25. (1)证明：连接 OD ，CD ．∵BC 是⊙O 的直径，∴∠BDC =90°，即CD ⊥AB321oEDC A∵AC =BC ， ∴D 是AB 的中点又∵BC 是⊙O 的直径，即O 为 BC 的中点 ∴OD ∥AC ，∠MDO =∠MNC ∵MN 是⊙O 的切线，切点为D∴OD ⊥MN 即∠MDO =90°=∠MNC ∴MN ⊥AC (2) 由BC 是⊙O 的直径，可得∠BEC =90°； 由CD ⊥AB ，在 Rt △ACD 中，AD 、AC 的长可知， 用勾股定理可求CD 的长；由AB ⋅CD =2S △ABC =AC ⋅BE ，可得BE 的长 ．丰台26．（1）证明：连接OC ，∵DE 与⊙O 切于点C ，∴OC ⊥DE .∵AD ⊥DE ，∴OC ∥AD ．∴∠2=∠3．∵OA =OC ，∴∠1=∠3．∴∠1=∠2，即AC 平分∠DAB ． （2）解：∵AB =4，B 是OE 的中点，∴OB =BE =2，OC =2．∵CF ⊥OE ，∴∠CFO = 90º，∵∠COF = ∠EOC ，∠OCE = ∠CFO ，∴△OCE ∽△OFC ，∴OEOC OCOF =，∴OF =1．∴CF =3．平谷25．（1）证明：连接OC ．∵DE 切⊙O 于C ，∴OC ⊥DE 于C ．∵点C 是BF 的中点,∴∠BAC =∠EAC ．∵OC=OA ，∴∠BAC =∠OCA ．∴∠EAC =∠OCA∴OC ∥AE ．∴AE ⊥DE 于E ．（2）连接BF ．∵AB 是⊙O 直径，∴∠BFA =∠AEC =∠ECO =90°． ∴四边形CEFG 是矩形．即CO ⊥BF 于G ． ∴BG=GF=CE ．∵∠BAE =60°，AF =4，∴BF =CE =石景山25．（1）证明：连接OC ，如图1．∵CH 是⊙O 的切线， ∴2190∠+∠=°． ∵DE ⊥AB ， ∴3490∠+∠=°．∵OB OC =，∴14∠=∠．∴23∠=∠． 又∵53∠=∠∴25∠=∠． ∴HC HF =． （2）求解思路如下： 思路一：连接OF ，如图2．① OF 过圆心且点F 是BC 的中点，由垂径定理可得2BC CF =，90OFC ∠=°； ② 由6∠与1∠互余，2∠与1∠互余可得62∠=∠，从而可知tan 6m ∠=；图1③ 在Rt OFC △中，由tan 6CF m OF∠==，可设OF x =，CF mx =，由勾股定 理，得222()5x mx +=，可解得x 的值；④ 由22BC CF mx ==，可求BC 的长．思路二：连接AC ，如图3．① 由AB 是⊙O 的直径，可得ACB △是直角三角形，知6∠与4∠互余， 又DE ⊥AB 可知3∠与4∠互余，得63∠=∠；② 由63∠=∠，32∠=∠，可得62∠=∠，从而可知tan 6m ∠=；③ 在Rt ACB △中，由tan 6BCm AC ∠==，可设AC x =，BC mx =，由勾股定理，得222()10x mx +=，可解得x 的值； ④ 由BC mx =，可求BC 的长．朝阳25．（1）证明：连接OB ．∵∠A =45°， ∴∠DOB =90°． ∵OD ∥BC ,∴∠DOB +∠CBO =180°. ∴∠CBO =90°．∴ 直线BC 是⊙O 的切线． （2）求解思路如下：如图,延长BO 交⊙O 于点F ，连接AF .①由AB =AC ，∠BAC =45°，可得∠ABC =67.5°，∠ABF =22.5°； ②在Rt △EOB 中，由OB =r ，可求BE 的长；③由BF 是直径,可得∠FAB =90°，在Rt △FAB 中，由BF =2r ， 可求AB 的长，进而可求AE 的长.西城25（1）∵AB 是⊙O 的直径∴ ∠ACB = 90°∵OE ∥BC ∴ OE ⊥AC ∴ 弧AE =弧EC ．∴ ∠1= ∠2 ．∴BE 平分∠ABC ．H图2 图3（2）BD是⊙O的切线，∴∠ABD = 90°．∵∠ACB = 90°，BH=BD=2，∴∠BDH=∠3．∴∠CBD =∠2．∴∠1= ∠2=∠CBD．∴∠CBD=30°．∠ADB=60°．在Rt△ABD中，∠ADB=90°，∴AB=OB．在Rt△OBD中，222OD OB BD=+，∴OD．海淀25．（1）证明：∵D为AC的中点，∴∠CBA=2∠CBE．∵AB是⊙O的直径，∴∠ACB=90°，∴∠1+∠CBA=90°．∴∠1+2∠CBE =90°．∵AP是⊙O的切线，∴∠PAB=∠1+∠PAC=90°．∴∠PAC =2∠CBE．（2）思路：①连接AD，由D是AC的中点，∠2=∠CBE，由∠ACB=∠PAB=90°，得∠P=∠3=∠4，故AP=AE；②由AB是⊙O的直径，可得∠ADB=90°；由AP=AE，得PE=2PD=2m，∠5=12∠PAC =∠CBE=α③在Rt△PAD中，由PD=m，∠5=α，可求PA的长；④在Rt△PAB中，由PA的长和∠2=α，可求BP的长；由BE PB PE=-可求BE的长；⑤在Rt△BCE中，由BE的长和CBEα∠=，可求CE的长．东城25.（1）证明：连接OD.∵CD是⊙O切线，∴∠ODC=90°.即∠ODB+∠BDC=90°.∵AB为⊙O的直径，∴∠ADB=90°.即∠ODB+∠ADO=90°.∴∠BDC=∠ADO.∵OA=OD，∴∠ADO=∠A.∴∠BDC=∠A.（2）∵CE⊥AE，∴∠E=∠ADB=90°.∴DB∥EC.∴∠DCE=∠BDC.∵∠BD C=∠A，∴∠A=∠DCE.∵∠E=∠E，∴△AEC∽△CED.∴EC2=DE•AE.∴16=2（2+AD）.∴AD=6．通州24.（1）①连接OC，OC//AD②AD⊥PC（2）32昌平25.（1）证明：∵AB为⊙O的直径∴∠ADB=90°∴∠A+∠DBA=90°∵弧BD=弧BD错误！未指定书签。