(2)单位阶跃响应时

实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。

2、研究二阶系统分别工作在ξ=1，0<ξ<1，和ξ> 1三种状态下的单位阶跃响应。

3、分析增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts。

4、研究系统在不同K值时对斜坡输入的稳态跟踪误差。

5、学会使用Matlab软件来仿真二阶系统，并观察结果。

二、实验仪器1、控制理论电子模拟实验箱一台；2、超低频慢扫描数字存储示波器一台；3、数字万用表一只；4、各种长度联接导线。

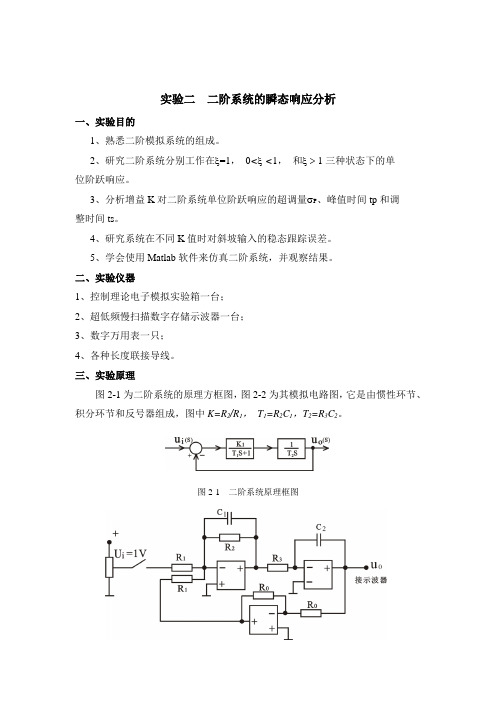
三、实验原理图2-1为二阶系统的原理方框图，图2-2为其模拟电路图，它是由惯性环节、积分环节和反号器组成，图中K=R2/R1，T1=R2C1，T2=R3C2。

图2-1 二阶系统原理框图图2-1 二阶系统的模拟电路由图2-2求得二阶系统的闭环传递函1222122112/() (1)()/O i K TT U S K U S TT S T S K S T S K TT ==++++ :而二阶系统标准传递函数为(1)(2), 对比式和式得n ωξ==12 T 0.2 , T 0.5 , n S S ωξ====若令则。

调节开环增益K 值，不仅能改变系统无阻尼自然振荡频率ωn 和ξ的值，可以得到过阻尼(ξ>1)、临界阻尼（ξ=1）和欠阻尼（ξ<1）三种情况下的阶跃响应曲线。

（1）当K >0.625， 0 < ξ < 1，系统处在欠阻尼状态，它的单位阶跃响应表达式为：图2-3 0 < ξ < 1时的阶跃响应曲线（2）当K =0.625时，ξ=1，系统处在临界阻尼状态，它的单位阶跃响应表达式为：如图2-4为二阶系统工作临界阻尼时的单位响应曲线。

(2) +2+=222nn nS S )S (G ωξωω1()1sin( 2-3n to d d u t t tgξωωωω--=+=式中图为二阶系统在欠阻尼状态下的单位阶跃响应曲线etn o n t t u ωω-+-=)1(1)(图2-4 ξ=1时的阶跃响应曲线（3）当K < 0.625时，ξ> 1，系统工作在过阻尼状态，它的单位阶跃响应曲线和临界阻尼时的单位阶跃响应一样为单调的指数上升曲线，但后者的上升速度比前者缓慢。

控制工程基础练习题（一）一、填空题1、设系统的开环传递函数为2(1)(1)K s s Ts τ++，则其开环幅频特性为 ，相频特性为 。

（；arctan 180arctan T τωω--o (或：2180arctan 1T T τωωτω---+o ) 2、频域性能指标与时域性能指标有着对应关系，开环频域性能指标中的幅值穿越频率c ω对应时域性能指标 ，它们反映了系统动态过程的 。

（调整时间s t ；快速性）3、在经典控制理论中，可采用 、根轨迹法或 等方法判断线性控制系统稳定性。

（劳斯判据(或时域分析法 ；奈奎斯特判据(或频域分析法)4、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+，则该系统的传递函数G(s)为 。

（1050.20.5s s s s+++） 5、控制系统的 称为传递函数。

一阶系统传函标准形式是 ，二阶系统传函标准形式是 。

（输出拉氏变换与输入拉氏变换在零初始条件下的比值；1()1G s Ts =+；222()2n n nG s s s ωζωω=++或：221()21G s T s T s ζ=++）。

6、反馈控制系统开环对数幅频特性三频段的划分是以ωc（截止频率）附近的区段为中频段，该段着重反映系统阶跃响应的稳定性和快速性；而低频段主要表明系统的稳态性能。

7、根轨迹起始于 ，终止于 。

（开环极点；开环零点）1、自动控制系统有两种基本控制方式，当控制装置与受控对象之间只有顺向作用而无反向联系时，称为 ；当控制装置与受控对象之间不但有顺向作用而且还有反向联系时，称为 。

含有测速发电机的电动机速度控制系统，属于 。

（开环控制系统 闭环控制系统 闭环控制系统）2、设系统的开环传递函数为12(1)(1)K s T s T s ++，则其开环幅频特性为 ，相频特性为 。

（()A ω=01112()90()()tg T tg T ϕωωω--=---）3、判断一个闭环线性控制系统是否稳定，可用 、 、等方法。

第3章 系统的时间响应分析在建立系统的数学模型（微分方程或传递函数）之后，就可以采用不同的方法，通过系统的数学模型来分析系统的特性，时间响应分析是重要的方法之一。

第3.1节 时间响应及其组成一、时间响应的概念所谓时间响应指系统在外加激励作用下，其输出量随时间变化的函数关系。

或者说 在输入作用下，系统的输出（响应）在时域的表现形式；在数学上，就是系统的动力学方程在一定初始条件下的解。

自变量为时间t ，因变量为输出()[()]o x t y t二、时间响应的组成分析：第一、二项是由微分方程的初始条件（即系统的初始状态）引起的自由振动，即自由响应。

ω。

应该说第三项的自第三项是由作用力引起的自由振动即自由响应，其振动频率均为nω与作用力频率ω无关，由响应并不完全自由。

因为它的幅值受到F的影响，当然，它的频率n自由即在此。

第四项是由作用力引起的强迫振动即强迫响应，其振动频率即为作用力频率ω。

因此系统的时间响应可从两方面分类：按振动性质可分为自由响应与强迫响应，按振动来源可分为零输入响应（即由“无输入时系统的初态”引起的自由响应）与零状态响应（即在“无输入时的系统初态”为零而仅由输入引起的响应）Array所以我们的研究对象是：零状态响应。

另外还有两个需了解的概念：瞬态响应和稳态响应。

瞬态响应：系统在外加激励作用后，从初始状态到最终状态的响应过程称为瞬态响应。

反映了系统的快、稳特性。

稳态响应：时间趋于无穷大时，系统的输出状态为稳态响应。

反映系统的准确性。

三、系统方程的特征根影响系统自由响应的收敛性和振荡第3.2节 典型的输入信号由于系统的输入具有多样性，所以在分析和设计系统时，需要规定一些典型的输入信号，然后比较各系统对典型信号的时间响应。

不同系统或参数不同的同一系统对同一典型信号的时间响应不同，反映出各种系统动态特性的差异，从而可以定出相应的性能指标，对系统的性能予以评定。

尽管在实际中，输入信号很少是典型信号，但由于系统对典型信号的时间响应和对任意信号的时间响应之间存在一定的关系统，所以知道系统对典型信号的响应就可求出对任意输入的响应。

自动控制原理（上）习 题3-1 设系统的结构如图3-51所示，试分析参数b 对单位阶跃响应过渡过程的影响。

考察一阶系统未知参数对系统动态响应的影响。

解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式：111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时，系统响应速度变慢；当/0T K b -<<时，系统响应速度变快。

3-2 设用11Ts +描述温度计特性。

现用温度计测量盛在容器内的水温，发现1min 可指示96%的实际水温值。

如果容器水温以0.1/min C ︒的速度呈线性变化，试计算温度计的稳态指示误差。

考察一阶系统的稳态性能分析(I 型系统的，斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数，进一步得到时间响应函数为：()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温，由题意得到：600.961Te-=-推出18.64T =，此时求输入为()0.1r t t =⋅时的稳态误差。

由一阶系统时间响应分析可知，单位斜坡响应的稳态误差为T ，所以稳态指示误差为：lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10，并保证总的放大倍数不变，试选择H K 和0K 的值。

解 一阶系统的调节时间s t 与时间常数成正比，则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++）比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-）试求系统的超调量%σ，峰值时间p t ，上升时间r t 和调节时间s t 。

已知阶跃响应求单位脉冲响应引言在信号处理和系统控制的领域中，单位脉冲响应（impulse response）和阶跃响应（step response）是两个常用的概念。

单位脉冲响应是指在系统输入信号为单位脉冲函数时，输出信号的响应。

阶跃响应则是指在系统输入信号为阶跃函数时，输出信号的响应。

本文将详细探讨当已知阶跃响应时，如何求解单位脉冲响应的方法。

1. 单位脉冲响应与阶跃响应的关系单位脉冲响应和阶跃响应之间存在着一种重要的数学关系：单位脉冲函数是阶跃函数的导数。

这使得我们可以通过求解阶跃响应来获取单位脉冲响应。

2. 求解思路为了求解单位脉冲响应，我们可以按照以下步骤进行： 1. 记录系统的阶跃响应。

2. 对阶跃响应进行求导，得到单位脉冲响应。

3. 具体步骤接下来，我们将详细介绍每一步的具体操作。

3.1 记录系统的阶跃响应首先，我们需要记录系统的阶跃响应。

阶跃响应是指在系统输入信号为阶跃函数时，输出信号的响应。

可以通过实验或者数学建模的方式获取系统的阶跃响应。

3.2 对阶跃响应进行求导获得系统的阶跃响应之后，我们需要对其进行求导，以得到单位脉冲响应。

由于单位脉冲函数是阶跃函数的导数，因此我们只需要对阶跃响应进行求导即可。

3.3 求解结果验证在完成对阶跃响应的求导之后，我们可以对结果进行验证。

将求导得到的单位脉冲响应与实际系统中的单位脉冲响应进行比较，以确保求解的正确性。

4. 实例演示为了更好地理解以上方法，我们来看一个具体的例子。

假设有一个线性时不变系统，其阶跃响应为：h(t) = 3e^(-2t)u(t)其中，u(t)表示阶跃函数。

我们可以将阶跃响应进行求导得到单位脉冲响应：h'(t) = -6e^(-2t)u(t) + 3δ(t)其中，δ(t)表示单位脉冲函数。

通过比较求解得到的单位脉冲响应与系统的实际单位脉冲响应进行对比，我们可以验证求解的准确性。

结论通过本文的讨论，我们了解到了如何根据已知的阶跃响应来求解单位脉冲响应。

自动控制理论第五章习题汇总填空题1、系统的频率响应与正弦输入信号之间的关系称为频率响应2、在正弦输入信号的作用下，系统输入的稳态分量称为频率响应简答题：5-2、什么是最小相位系统及非最小相位系统？最小相位系统的主要特点是什么？答在s平面上，开环零、极点均为负实部的系统称为最小相位系统；反之，开环零点或极点中具有正实部的系统称为非最小相位系统。

最小相位系统的主要特点是：相位滞后最小，并且幅频特性与相频特性有惟一的确定关系。

如果知道最小相位系统的幅频特性，可惟一地确定系统的开环传递函数。

5-3、什么是系统的频率响应？什么是幅频特性？什么是相频特性？什么是频率特性？答对于稳定的线性系统，当输入信号为正弦信号时，系统的稳态输出仍为同频率的正弦信号，只是幅值和相位发生了改变，如图5-3所示，称这种过程为系统的频率响应。

图5-3称为系统的幅频特性，它是频率的函数；称为系统的相频特性，它是频率的函数：称为系统的频率特性。

稳定系统的频率特性可通过实验的方法确定。

计算题5-1、设某控制系统的开环传递函数为)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图，并确定剪切频率c ω的值。

解：Bode 图如下所示剪切频率为s rad c /75.0=ω。

5-2、某系统的结构图和Nyquist 图如图(a)和(b)所示，图中2)1(1)(+=s s s G 23)1()(+=s s s H 试判断闭环系统稳定性，并决定闭环特征方程正实部根的个数。

解：由系统方框图求得内环传递函数为：ss s s s s s H s G s G +++++=+23452474)1()()(1)( 内环的特征方程：04742345=++++s s s s s由Routh 稳定判据：1:0310:16:44:171:01234s s s s s由此可知，本系统开环传函在S 平面的右半部无开环极点，即P=0。

自动控制原理试卷A(1)1．（9分）设单位负反馈系统开环零极点分布如图所示，试绘制其一般根轨迹图。

（其中-P 为开环极点,-Z ，试求系统的传递函数及单位脉冲响应。

3.（12分）当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。

K 表示开环增益。

P 表示开环系统极点在右半平面上的数目。

v 表示系统含有的积分环节的个数。

试确定闭环系统稳定的K 值的范围。

4．（12分）已知系统结构图如下，试求系统的传递函数)(,)(s E s C,3==p v （a ）,0==p v （b ）2,0==p v （c ）题4图题2图5．（15分）已知系统结构图如下，试绘制K 由0→+∞变化的根轨迹，并确定系统阶跃响应分别为衰减振荡、单调衰减时K 的取值范围。

6．（15分）某最小相位系统用串联校正，校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所示，试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ，并指出Gc （S ）是什么类型的校正。

7．（15分）离散系统如下图所示，试求当采样周期分别为T=0.1秒和T=0.5秒输入)(1)23()(t t t r ⋅+=时的稳态误差。

8．（12分）非线性系统线性部分的开环频率特性曲线与非线性元件负倒数描述曲线如下图所示，试判断系统稳定性，并指出)(1x N和G （j ω）的交点是否为自振点。

参考答案A(1)1、 根轨迹略，2、 传递函数)9)(4(36)(++=s s s G ；单位脉冲响应)0(2.72.7)(94≥-=--t ee t c tt 。

3、 21,21,21><≠K K K 4、6425316324215313211)()(G G G G G G G G G G G G G G G G G G s R s C ++++= 642531632421653111)()(G G G G G G G G G G G G G G G G G s R s E +++-= 5、 根轨迹略。