当前位置：文档之家 › 三向应力状态简介

三向应力状态简介

  • 格式：ppt
  • 大小：770.00 KB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

应力状态概述二向和三向应力状态的实例二向

应力状态概述二向和三向应力状态的实例二向


2．作应力圆 主应力为 1 , 3 ，并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3．分析 纯剪切应力状态的两个主应力绝对值相等， 但一为拉应力，另一为压应力。由于铸铁抗拉强度较 低，圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy

n

材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系，如下图所 示，（注意选好比例尺） 在坐标系内画出点A( x， xy)和B(y，yx)

x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y （ ） xy 2 2 2
解法2—解析法：分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
应力表示——单元体：
①dx、dy、dz（微小的正六面体） ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力，τ ＝0 A——纯剪切， σ ＝0
D
D——既有 σ ，又有τ
三向应力状态简介

三向应力状态简介


动力应力状态
动力应力状态是指岩体在受 到周期性或非周期性的外力 作用时，其内部应力不断发
生变化的状态。
动力应力状态通常由地震、 车辆振动、机器振动等动态 因素引起，其特点是各向应 力随时间变化，岩体可能发
生动态变形或破坏。
在动力应力状态下，岩体内 部应力的分布和大小均随时 间变化，需要采取相应的减 震、隔震措施以减小岩体的 动态响应。
发展多尺度、跨层次的理论模型
结合微观、细观和宏观尺度，研究三向应力状态下材料在不同尺度上的响应和演化规律。
探索复杂环境因素对三向应力状态的影响
考虑温度、湿度、化学环境等复杂因素，建立更为真实的理论模型，以模拟实际工程中 的复杂应力状态。
实验技术的发展
开发高精度、高分辨率的实验测试技术
发展新型传感器和测量方法，提高对三向应力状态的测量精度和可靠性。
03 三向应力状态的影响因素
地质构造
地质构造是影响三向应力状态的重要 因素之一。地壳中的板块运动、断层 活动、褶皱等地质构造过程会导致岩 层中应力的变化，从而影响三向应力 状态。
不同地区的地质构造特征不同，因此 三向应力状态也会存在差异。例如， 在板块边界、断裂带等地区，岩层中 的应力通常较高，而在盆地、平原等 地区则较低。
03
在地下工程中，三向应力状态可用于分析隧道、地下洞室等结构的稳定性，预 测结构变形和破坏的可能性。
石油工程
石油工程是研究石油和天然气的勘探 、开发和生产的科学，三向应力状态 在石油工程中具有重要应用。在石油 工程中，三向应力状态是指地层中的 岩石在三个方向的应力作用下处于平 衡状态。
在石油工程中，三向应力状态可用于 分析地层的稳定性、预测地层破裂的 可能性以及评估地层压力。例如，在 钻井工程中，三向应力状态可用于分 析井壁的稳定性，预测井壁坍塌的可 能性。
三向应力状态

三向应力状态

2
2
min
例7-1 试求中所示单元体的主应力和最大剪应力。 （1）求主应力
x 10MPa, y 30MPa, x 20MPa max x + y x - y 2 + x 2 2 min
10 + 30 10 - 30 + 202 2 2 + 42.4MPa（ 拉 应 力 ） - 2.4MPa（ 压 应 力 ）
2 2
a 0对应 max
x + y
2
a 0 + 90 对应 min

x + y
2
三、最大和最小剪应力
d a 0 da
2
x - y
2
cos 2a - 2 xy sin 2a 0
x - y tg 2a 2 xy
max
x - y 2 + + xy 2 x - y 2 - 2 + xy
3
a 0 12143'
3
（2）求最大剪应力
1 42.4 2 0 MPa - 2.4 3
1
(a)
max
1 - 3
2
22 .4 MPa
3、 纯剪切应力状态
- 2 x tg 2a 0 - x - y
a0 135
五、不等于零的情况。
二向应力状态：三对主应力中有两对主应力不等
于零的情况。
三向应力状态：三对主应力皆不等于零的情况。
7-2 平面应力状态分析—解析法
一、斜截面上的应力
已知：单元体 x，y，xyyx， a 研究与z轴平行的任一斜截面c e上的应力。 符号规则： q 角：从x轴正方向反时针转至斜截面的 外法线方向为正，反之为负。 正应力：拉为正，压为负。 剪应力：使微元体或其局部产生顺时针方 向转动趋势者为正，反之为负。
三向应力状态简介

三向应力状态简介


例：填空题。
危险点接近于三向均匀受拉的塑性材料，应选用
破坏形式为
。
第一
脆性断裂
强度理论进行计算，因为此时材料的
例：选择题。 纯剪切应力状态下，各向同性材料单元体的体积改变有四种答案：
（A）变大 （B）变小 （C）不变 （D）不确定
123 m
K
例： 圆轴直径为d，材料的弹性模量为E，泊松比为 μ ，为了测得轴端的力偶ｍ之值，但只有一 枚电阻片。 (1) 试设计电阻片粘贴的位置和方向； (2) 若按照你所定的位置和方向，已测得线应
对于二向应力状态：
1 1 E ( 1 2 )
2
1 E
(
2
1)
3 E ( 1 2 )
2 1
CL10TU30
下 面 考 虑 体 积 变 化 ：
V0abc
V 1 a ( 1 1 ) b ( 1 2 ) c ( 1 3 ) 2
a b c ( 1 1 23 )
） ） ）
§10-6 复杂应力状态下的变形比能
拉压变形能：
U1Pl1PPl P2l
2
2 EA 2EA
变形比能：
P
P
l l
uU P2l
2
1
V 2EAAl 2E 2
CL10TU40
变形比能：
u 1
2
u2 1112 1222 133 2
1 3
变形比能：
u21112122 2133
2 1 E 1 2 1 E12 2 13 2 2 （(1 2 2 3 ）23 31 )
强度理论的论述基本一致。
二
例：填空题。
一球体在外表面受均布压力p = 1 MPa作用，则在球心处的主应力 1 =
第九章三向应力状态(6,7,8)

第九章三向应力状态(6,7,8)

1 2 2 2 1 2 2 3 3 1 2 这个理论比第三强度理论更符合已有的一些 平面应力状态下的试验结果，但在工程实践中多 半采用计算较为简便的第三强度理论。




(5) 强度理论的相当应力
上述四个强度理论所建立的强度条件可统一写 作如下形式：
影响材料的脆性和塑性的因素很多，例如低温能提 高脆性，高温一般能提高塑性； 在高速动载荷作用下 脆性提高，在低速静载荷作用下保持塑性。 无论是塑性材料或脆性材料：
在三向拉应力接近相等的情况下，都以断裂的形式破坏， 所以应采用最大拉应力理论；
在三向压应力接近相等的情况下，都可以引起塑性变形， 所以应该采用第三或第四强度理论。
于是，第四强度理论的屈服判据为 vd vdu
1 vd ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 6E


对于由单轴拉伸试验可测定屈服极限s的材料，注 意到试验中1＝ s， 2＝3＝0，而相应的形状改 变能密度的极限值为 1 vdu 2 s2 6E 故屈服判据可写为
1 1 E 1 （ 2 3） 1 2 （ 3 1） 2 E 3 1 3 （ 1 2） E
1 2 2 2 v 1 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 1 2 2 2 1 2 2 3 3 1 2 s2 62 1 2 2 3 3 1 s 2 此式中，1、2、3是构成危险点处的三个主应力， 相应的强度条件则为
§9-7 强度理论及其相当应力
一、强度理论的概念
三向应力

三向应力


z
s z s 30 s 120 ) （

我们应该把X，Y，Z理解 成任意三个垂直的方向
特例（主单元体）
s
2
s3
s1
s
2
s1
1 2 3
1 E 1 E 1 E (s 1 s 2 ) (s s 1 )
s1
1 2 3
1 E 1 E 1 E (s 1 0 )
xy

2 xy

x y
例： 已知一点在某一平面内的 1、 2、 3、方向上的应变 1、
2、 3，三个线应变，求该面内的主应变。
解：由
x cos i y sin i
2 2
i
xy
sin i cos i
i =1,2,3这三个方程求出 x， y， x y；然后在求主应变。
2
co s 2
xy
2
sin 2
x y
2
sin 2
y
xy
2
co s 2
2 s x s t
2
s
s x s

s x s
2
y
cos 2 t xy sin 2
y
sin 2 t xy cos 2
二、应变分析图解法——应变圆（ Strain Circle）
1） x1 方 向 的 线 应 变 ； .沿 2）x1 y 1角 的 剪 应 变 。 .
dx
f ( x , y , z , xy , ) g ( x , y , z , xy , )
y1
y
x1
dy
第九章应力状态(3,4,5)

第九章应力状态(3,4,5)


s
3
e3

1 E
s
3

s 1

s 2
例 9-17
边长a =0.1 m的铜质立方体，置于刚性很大的 钢块中的凹坑内(图a)，钢块与凹坑之间无间隙。 试求当铜块受均匀分布于顶面的竖向荷载F =300 kN时，铜块内的主应力，最大切应力，以及铜块 的体应变。已知铜的弹性模量E =100 GPa，泊松比
1 2
E
sx sy sz
思考: 各向同性材料制成的构件内一点处，
三个主应力为s1＝30 MPa，s2＝10 MPa，s3＝-40
MPa。现从该点处以平行于主应力的截面取出边 长均为a的单元体，试问：(1) 变形后该单元体的 体积有无变化？(2) 变形后该单元体的三个边长之 比有无变化？
弹性,小变形条件下可以
应用叠加原理，故知x方 向的线应变与正应力之
间的关系为
e x

sx
E


sy
E


sz
E


1 E
sx

sy
sz
同理有
e y

1 E
s
y
s x
s z ，e z

1 E
sz

sx
s
最一般表现形式的空间应力状态中有9个应力
分量，但根据切应力互等定理有txy＝tyx，tyz＝tzy ， txz＝tzx，因而独立的应力分量为6个，即sx、sy、sz、 tyx、tzy、tzx。
当空间应力状态的三个主应
力s1、s2、s3已知时(图a)，与
任何一个主平面垂直的那些斜截
面(即平行于该主平面上主应力
第九章三向应力状态(678)PPT课件

第九章三向应力状态(678)PPT课件

1 2112233
v1 2111 2221 233
1
2
3
1
E 1
E 1
E
1 （ 2 3） 2 （ 3 1） 3 （ 1 2）
v 2 1 E1 22 23 2 2(122331 )
变形比能=体积改变比能+形状改变比能
2
v vVvd
m
2 m
1
m
1. 最大拉应力理论（第一强度理论）
假设：无论材料内各点的应力状态如何， 只要有一点的主应力σ1 达到单向拉伸断裂
时的极限应力σu，材料即破坏。
在单向拉伸时，极限应力 σu =σb 失效条件可写为 σ1 ≥ σb
[ ] b
n
第一强度强度条件：1 []
试验证明，这一理论与铸铁、岩石、砼、 陶瓷、玻璃等脆性材料的拉断试验结果相符， 这些材料在轴向拉伸时的断裂破坏发生于拉 应力最大的横截面上。脆性材料的扭转破坏， 也是沿拉应力最大的斜面发生断裂，这些都 与最大拉应力理论相符，但这个理论没有考 虑其它两个主应力的影响。
r [] r 称为相当应力
r1 1
r21(23)
r3 13
r41 2(12)2(23)2(31)2
一般说来，在常温和静载的条件下，脆性材 料多发生脆性断裂，故通常采用第一、第二强度 理论；塑性材料多发生塑性屈服，故应采用第三、 第四强度理论。
影响材料的脆性和塑性的因素很多，例如低 温能提高脆性，高温一般能提高塑性； 在高速动 载荷作用下脆性提高，在低速静载荷作用下保持 塑性。
1 m
3
m
3 m
m
1
2
3
3
3(12)(123)m
E
3
K
v 2 1 E1 22 23 2 2(122331 )
三向应力状态简介4广义胡克定律5

三向应力状态简介4广义胡克定律5

为什么脆性材料扭转时沿45º 螺旋面断开？
三、应力状态的研究方法
取单元体 1、单元体特征 单元体的尺寸无限小，
2
1 3 2
3 1
每个面上应力均匀分布
任意一对平行平面上的应力相等 2、主单元体 各侧面上切应力均为零的单元体
3、主平面 4、主应力 说明:
切应力为零的截面 主平面上的正应力
重要结论：
(1) 同一面上不同点的应力各不相同;
(2) 同一点不同方向面上的应力也是各不相同
一点的应力状态
过一点不同方位面上应力的总和，称为这一点的应力 状态。
二、研究应力状态的目的
1. 解决复杂应力状态下的强度计算问题 2. 有助于理解和解释某些破坏现象 例如
为什么塑性材料拉伸时会出现滑移线？
(2)当x<y 时 ， 0 是x与min之间的夹角
3. 最大切应力

令
x y
2 x y 2

x y
2
cos 2 x sin 2
sin 2 x cos 2
x y d 2[ cos 2 x sin 2 ] 0 d 2
F
t
0
dA ( x dAcos )cos
( x dA cos )sin ( y dA sin )sin ( y dA sin )cos 0
化简以上两个平衡方程最后得

x y
2 x y 2

x y
2
cos 2 x sin 2
sin 2 x cos 2
不难看出
90 x y
即两相互垂直面上的正应力之和保持一个常数
应力状态分析和强度理论

应力状态分析和强度理论


03
弹性极限
材料在弹性范围内所能承受的最大应力状态，当超过这一极限时，材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时，其内部应力状态会发生变化，当达到某一特定应力状态时，材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态，当超过这一极限时，材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服（即非弹性变形）的应力状态，是材料强度分析的重要依据。
根据不同的材料特性，存在多种屈服条件，如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示，用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据，当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时，材料会发生屈服和塑性变形，导致失效。该准则适用于韧性材料的失效分析，尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环，主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线，并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响，因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
第九章三向应力状态(6,7,8)

第九章三向应力状态(6,7,8)

－
1 2
2＋4 2
对于最大剪应力理论（第三强度理论）
r3=1-3= 2＋4 2
对于形状改变比能理论（第四强度理论）
r4=
= 2＋3 2
煤、石料或砼等材料在轴向压缩试验时，
如端部无摩擦，试件将沿垂直于压力的方向 发生断裂，这一方向就是最大伸长线应变的 方向，这与第二强度理论的结果相近。
(3) 最大切应力理论(第三强度理论)： 这个理论 认为引起材料屈服破坏的主要因素是最大切应力，无 论在什么应力状态下，当一点处的最大切应力 max达 到该材料在轴向拉伸试验中屈服时最大切应力的极限 值u时，材料就发生屈服破坏。 第三强度理论的屈服判据为 max u 对于由单轴拉伸试验可测定屈服极限s，从而有u ＝s/2的材料（例如低碳钢），上列屈服判据可写 为 1 3 s 即 1 3 s 2 2
2 m


1 3
m m
3 m
1 m
[9-18]求证 E 2(1 )G 证明： max min

(0, )
max
min

1 , 2 0, 3
E 2(1 )G
(0, )

1 2 1 1 2 2 2 v ( 1 3 2 1 3 ) 2G 2E E
1 1 2 2 2 1 2 2 3 3 1 2 s2 6E 6E


亦即
1 2 2 2 1 2 2 3 3 1 s 2 此式中，1、2、3是构成危险点处的三个主应力， 相应的强度条件则为
r3 1 3 第三强度理论── 第二类强度 最大切应力理论 1 2 { { r4 1 2 理论(塑性 2 第四强度理论── 2 屈服的理论) 2 3 形状改变能密度理论 3 1 2 ]}1 / 2

三向应力状态最大主应力方向计算

三向应力状态最大主应力方向计算（最新版）目录1.引言2.三向应力状态的定义和意义3.最大主应力方向的计算方法4.应用实例5.结论正文【引言】在材料力学中，应力状态是指材料内部各点的应力分布情况。

三向应力状态是指材料在某一点处受到三个大小相等、方向相互垂直的应力作用。

这种应力状态在实际工程中非常常见，如压力容器、桥梁等结构。

对于三向应力状态，最大主应力方向的计算是一个关键问题，它直接影响到结构的强度和稳定性。

本文将介绍三向应力状态的最大主应力方向计算方法。

【三向应力状态的定义和意义】三向应力状态是指材料内部某一点处受到三个大小相等、方向相互垂直的应力作用。

在这种应力状态下，材料内部的应力分布呈现出一种特殊的规律，即最大主应力方向位于三个应力方向的交点处。

三向应力状态在实际工程中具有重要意义，因为它可以反映出材料在复杂应力环境下的强度和稳定性。

【最大主应力方向的计算方法】计算三向应力状态下最大主应力方向的方法有多种，其中较为常用的是莫尔法和屈服准则法。

1.莫尔法莫尔法是一种基于应力圆的概念来计算最大主应力方向的方法。

在三向应力状态下，三个应力方向分别对应三个应力圆。

最大主应力方向位于三个应力圆的交点处，可以通过求解这三个交点来得到最大主应力方向。

2.屈服准则法屈服准则法是一种基于材料屈服特性来计算最大主应力方向的方法。

在三向应力状态下，材料的屈服方向通常是沿着最大主应力方向。

因此，可以通过求解材料的屈服准则来得到最大主应力方向。

【应用实例】假设一个压力容器在顶部受到三个大小相等、方向相互垂直的应力作用，我们需要计算最大主应力方向。

首先，我们可以通过实验或数值模拟得到应力分布情况。

然后，根据莫尔法或屈服准则法，求解最大主应力方向。

最后，根据最大主应力方向，可以判断压力容器在顶部的强度和稳定性。

【结论】对于三向应力状态，最大主应力方向的计算是一个关键问题。

通过莫尔法或屈服准则法，可以有效地计算出最大主应力方向。

应力状态的概述

内压 p 作用
材料力学
pD
2
pD
4
1
pD
2
2
pD
4Leabharlann 3 0材料力学圆杆受扭转和拉伸共同作用
材料力学
FN A
4F πd 2
T
Wt
16 π
Me d3
材料力学
材料力学
材料力学
应力状态的概述
材料力学
材料力学 材料力学
材料力学
主平面 ：切应力为零的平面
主应力：主平面上的正应力 主方向：主平面的法线方向
可以证明：通过受力构件内的任一点，一定存在三个
互相
三个主应力垂用1、直的2、主平3 面。表示, 按代数值大小顺序排
序, 即
1 2 3
材料力学
材料力学
应力状态的分类： 单向应力状态：三个主应力中只有一个不等于零 二向应力状态（平面应力状态）：两个主应力不等于零 三向应力状态（空间应力状态）：三个主应力皆不等于零 单向应力状态也称为简单应力状态 二向和三向应力状态统称为复杂应力状态
材料力学
材料力学
圆筒形薄壁压力容器，平均直径为 D、壁厚为 ，承受

简述应力状态的类型

一、根据主单元体上三个主应力中有几个是非零的数值，可将应力状态分为三类：
1.单向应力状态只有一个主应力不等于零。

2.二向应力状态有两个主应力不等于零。

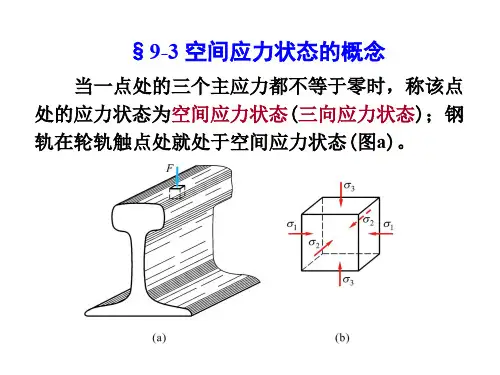
3.三向应力状态三个主应力都不等于零。

单向应力状态又称为简单应力状态，二向和三向应力状态统称为复杂应力状态。

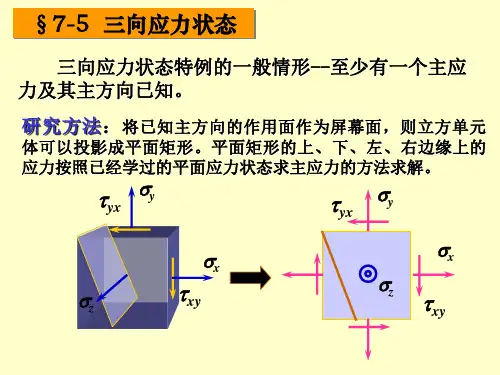
单向及二向应力状态又称为平面应力状态。

二、一点的应力状态：通过受力构件内一点的所有截面上的应力情况称为一点的应力状态。

三、一点的应力状态的表示法—
单元体：围绕所研究的点，截取一个边长为无穷小的正六面体，用各面上的应力分量表示周围材料对其作用。

称为应力单元体。

特点：
1.单元体的尺寸无限小，每个面上的应力为均匀分布。

2.单元体表示一点处的应力，故相互平行截面上的应力相同。

四、主平面、主应力、主单元体：主平面单元体中剪应力等于零的平面。

主应力主平面上的正应力。

可以证明：受力构件内任一点，均存在三个互相垂直的主平面。

三个主应力用σl、σ2和σ3表示，且按代数值排列即σl>σ2>σ3。

主单元体用三对互相垂直的主平面取出的单元体。

三向应力状态简介

例：求图示应力状态的主 应力和最大切应力。 (应力单位为MPa)
材料力学
解： 1 120 40
2
2
120 40 2
302
130 MPa
2
30
3 30 MPa
max
1
3
2
80
MPa
材料力学
材料力学
材料力学
三向应力状态简介 主单元体：六个平面都是主平面
若三个主应力已知，求任意斜截面上的应力:
材料力学
首先分析平行于主应力之一（例3 如 截面上的应力。
）的各斜
材料力学
材料力学
3 对斜截面上的应力没有影响 。 这些斜1 截 面2 上的应力对应于由 主 应力 和 所画的应力圆圆周
材料力学
材料力学
材料力学
至于与三个主方向都不平行的任意斜截面，弹
性力学
n n
中已证明, 其应力 和 可由图中阴影面内某点的
坐标来
表示。
材料力学
材料力学
在三向应力状态下：
max 1
min ax 作用在与 2 平行且 与1 和 3 的方向成45 角的平面上。
材料力学
材料力学
例：求图示应力状态的主 应力和最大切应力 。 (应力单位为MPa)
材料力学
解： 1 30 20
3
2
30
20
2
402
52.2
MPa
2
42.2
2 50 MPa
max
1
3
2
47.2
MPa
材料力学
例：求图示应力状态的主应力和最大切应力。 （应力单位为MPa）
解：1 50 MPa
2 50 MPa
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


变形比能： 1 u 2

2

1 1 1 u 1 1 2 2 3 3 2 2 2
1 3
变形比能： 1 1 1 u 1 1 2 2 3 3 2 2 2
1 2 2 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E 1
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
解： 1 50MPa
2 50MPa 3 50MPa max 1 3
2 50MPa
CL10TU33
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
CL10TU34
解：
120 40 2 2


3(1 2 ) 2 1 2 2 m ( 1 2 3 ) uv 2E 6E
u f u uv
12 2 2 2 m ( 1 2 ) ( 2 3 ) ( 3 1 ) 6E
m
1 2 3
3
3 ( 1 2 ) 1 2 3 m 变形比能 = 体积改变比能 + 形状改变比能 E 3 K u = u + u
v
f CL10TU41
1 2 2 u 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 式中：
E 1 体积弹性模量 K 3 (12 2 ) 2 （ 3 1 ） E 1 2 3 m 1 3 3 （ 1 2 ） 3 E 当 05 . 时， 0
2
3 1
1 3
2

3
2
1
在平行于 σ1 的各个斜截面上，其应力对应 于由主应力 σ2 和 σ3 所画的应力圆圆周上各点 的坐标。
2
3 1
1 3
2

3
2
1
这样，单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力，可由三个应力圆 圆周上各点的坐标来表示。
E
1
（ 2 3 ）
§10-6 复杂应力状态下的变形比能
拉压变形能：
1 1 Pl P l U P l P 2 2 EA 2 EA
2
P P
l l
变形比能：
U P l 1 u V 2 EA Al 2 E 2
2 2



CL10TU40
对于二向应力状态：
1 1 ( 1 2 ) E 1 2 ( 2 1 ) E
2
1
3

E
( 1 2 )
CL10TU30
下面考虑体积变化：
V0 a b c V1 a(1 1 ) b(1 2 ) c(1 3 ) a b c (1 1 2 3 )

3
2
1
至于与三个主方向都不平行的任意斜截面， 弹性力学中已证明，其应力σn和τn可由图中阴 影面内某点的坐标来表示。

3
2
1
• 在三向应力状态情况下：
2
max 1 min 3 1 3 max
2
1 3
• τmax 作用在与σ2平行且与σ1和σ3的方向成45° 角的平面上，以τ1，3表示
1 1引起的应变为 1 E 2 、 3 引起的应变为
2 1 E 3 1 E 当三个主应力同时作用时： 1 1 1 （ 2 3 ） E
2
1 3
CL10TU30
广义胡克定律：
1 （ ） 1 1 2 3 E 1 2 2 （ 3 1 ） E 1 3 3 （ 1 2 ） E
2
单位体积的体积改变为:
V1 V0 1 2 3 V0
b
3 a
c
1
也称为体积应变。
CL10TU30
1 2 1 2 3 ( 1 2 3 ) E 3(1 2 ) 1 2 3 m 3 K E 1
首先分析平行于主应力之一（例如σ3）的 各斜截面上的应力。 σ3 对斜截面上的应力没有影响。这些斜截 面上的应力对应于由主应力 σ1 和 σ2 所画的应 力圆圆周上各点的坐标。
2
3 1 3 1 1 3
2
3
2

3
2
1
同理，在平行于 σ2 的各个斜截面上，其 应力对应于由主应力 σ1 和 σ3 所画的应力圆圆 周上各点的坐标。
1
130 120 40 2 MPa 30 2 30
2
3 30MPa 30MPa
max 1 3
2 80MPa
§10-5 广义胡克定律
纵向应变： E


横向应变：

ECL10TU35来自下面计算沿 1方向的应变：
1 E 1 （ 2 3 ） 1 2 2 （ 3 1 ） E 1 3 3 （ 1 2 ） E


2
1 3
m
m m
2 m
1 m
3 m
CL10TU31
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
CL10TU32
解：
1
52 . 2 30 20 30 20 2 MPa 40 2 2 3 42.2
2
2 50MPa 50MPa
max 1 3
2 47.2MPa