下载文档原格式
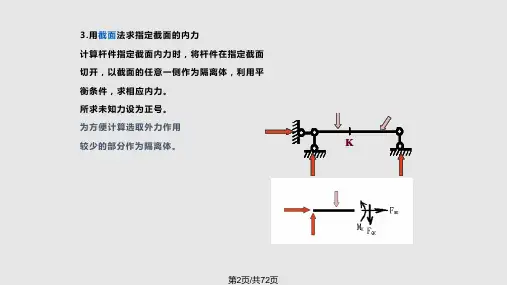
§3-1 单跨静定梁1 反力的求解简支梁伸臂梁悬臂梁 三个支座反力，可由三个平衡方程求解2 截面法求内力轴力（N）—截面一侧所有外力沿杆轴方向投影的代数 和。
以拉为正，压为负。
N+N剪力（Q）—截面一侧所有外力沿垂直杆轴方向投影的 代数和。
使隔离体顺时针转为正，逆时针转为负。
Q+Q弯矩（M）—截面一侧所有外力对截面形心力矩的代数 和。
弯矩图画在杆件的受拉侧！！！截面法—将指定截面切开，取截面任一侧部 分为隔离体，利用平衡条件求得内力。
P1 A由∑X=0 得 HA 由∑MB=0 得 VAP2K由∑Y=0 得 VBBP1HA VA A K QM N步骤：先求反力，再求指定截面的内力。
隔离体与周围约束要全部截断，用相应的约束力代替。
约束力要符合约束力的性质： 链杆： 轴力受弯杆件：轴力、剪力、弯矩 只画隔离体本身所受的荷载与截断约束处的约束力。
未知力假设为正方向，已知外力按实际方向画出。
任 意 截 面{轴力=截面一侧所有轴线方向力的代数和 剪力=截面一侧所有垂直轴线方向力的代数和 弯矩=截面一侧所有力对截面取矩的代数和例：求M、 Q、 N值。
A FP1=10kN C2m 2m FP2=5kNB解：1) 求支反力FxA FP1=10kN FP2=5kN FyBFyA∑Fx=0 ∑MA=0 ∑Fy=0FxA=-5kN （ ） FyB =5kN （ ） FyA =5kN （ ）2）取隔离体，求C左截面内力左部分为隔离体 MCL LA5kN 5kNCNCLQC∑ FX = 0 ∑ FY = 0 ∑MX = 0L N C = 5 KN L Q C = 5 KN L M C = 10 KN ⋅ m3）取隔离体，求C右截面内力 右部分为隔离体 NCRMCRCRB5kNQC∑ FX = 0 ∑ FY = 04）画内力图 M图10kN⋅ mR NC = 0 R Q C = −5 KN R M C = 10 KN ⋅ m∑MX=0Q N5kN5kNAaPb lBPb lPab lPa lq AlBql 2ql 82ql 2a m lm Aa l bBm lb m lm l内力图-表示结构上各 截面内力数值的图形 P 横坐标--截面的位置 A 纵坐标--内力的数值a l bPbB弯矩图—必须绘在 杆件受拉的一侧， 不须标正负号。
