2015-2016学年辽宁省抚顺市六校协作体高一(上)期末数学试卷

辽宁省抚顺市重点高中协作校2014—2015学年度上学期期中考试高一数学试题考试时间：90分钟 试卷总分：100分一、选择题：（本大题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知全集{1,3,5,7}B {2,4,6},A ,6,7},{1,2,3,4,5U ===,则= ( )A.{2,4,6}B.{1,3,5}C.{2,4,5}D.{2,5}2.已知集合A 到B 的映射，那么集合A 中元素2在B 中的象是（ ）A.2B.5C.6D.83．下列函数中，与函数有相同定义域的是（ ）A. B. C. D.4．已知，则的解析式为（ ）A ．B ．C ．D ．5.给定函数①，②，③，④，其中在区间（0，1）上单调递减的函数序号是( )A.①②B.②③C.③④D.①④6.已知函数14)(2---=x x x x f ，在下列区间中，函数不．存在零点的是（ ） A ． B ． C ． D ．7．若偶函数在上是增函数，则下列关系式中成立的是（ ）A ．()()()312f f f -<-<B ．()()()132f f f -<-<C ．()()()231f f f <-<D ．()()()321f f f -<<8．函数的单调增区间是（ ） A ． B ． C ． D ．9.已知⎩⎨⎧<+≥=4)(x )1()4(2)(x f x x f x ，则的值为（ ）A ．24 B. 3 C. 6 D. 1210. 对于实数a 和b ，定义运算“*”：22,*,a ab a b a b b ab a b⎧-≤⎪=⎨->⎪⎩　,设()(21)*(1)f x x x =--，且关于x 的方程恰有三个互不相等的实数根，则实数的取值范围是（ ）A. B. C. D.二、填空题：（本大题共4小题，每小题3分，共12分）11.幂函数2212)22()(m m x m m x f +--=在是减函数，则=12．已知函数的定义域为 13.把243251,5,51-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛这三个数按从小到大的顺序用不等号连接起来是 14.已知函数（为常数）。

2015-2016学年辽宁省抚顺一中高一（上）期末数学试卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5.00分）已知实数集R，集合M={x|0＜x＜2}，集合，则M ∩（∁R N）（）A．{x|0＜x≤1}B．{x|0＜x＜2}C．{x|x＜1}D．∅2．（5.00分）若直线l1：2x+（m+1）y+4=0与直线l2：mx+3y﹣2=0平行，则m 的值为（）A．﹣2 B．﹣3 C．2或﹣3 D．﹣2或﹣33．（5.00分）已知甲商品和乙商品价格相同，甲商品价格先上调10%，后下调10%，乙商品价格先下调10%，再上调10%，则调整后，甲乙两种商品的价格比较情况是（）A．甲商品价格高一些B．乙商品价格高一些C．两种商品价格高一样D．无法确定4．（5.00分）平行六面体ABCD﹣A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为（）A．3 B．4 C．5 D．65．（5.00分）一个圆锥的底面半径为2cm，高为6cm，在其中有一个高为3cm 的内接圆柱，则圆柱的侧面积为（）A．2πcm2B．4πcm2C．6πcm2D．12πcm26．（5.00分）已知集合A=[0，8]，集合B=[0，4]，则下列对应关系中：①，②，③，④f：x→y=x．不能看作从A到B的映射的是（）A．①B．②C．③D．④7．（5.00分）一束光线自点P（﹣1，1，1）发出，被yOz平面反射到达点Q（﹣6，3，3）被吸收，那么光线所走的距离是（）A． B． C． D．8．（5.00分）如图，在半径为3的球面上有A、B、C三点，∠ABC=90°，BA=BC，球心O到平面ABC的距离是，则B、C两点的球面距离是（）A．B．πC．D．2π9．（5.00分）已知平面α⊥平面β，α∩β=l，点A∈α，A∉l，直线AB∥l，直线AC ⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（）A．AB∥m B．AC⊥m C．AB∥βD．AC⊥β10．（5.00分）已知线段PQ两端点的坐标分别为（﹣1，1），（2，2），若直线l：x+my+m=0与线段PQ有交点，则m的范围是（）A． B．C．D．11．（5.00分）已知a=log23，b=20.5，，则a，b，c从大到小的顺序为（）A．c＞b＞a B．b＞c＞a C．a＞b＞c D．c＞a＞b12．（5.00分）函数f（x）=min，其中min，若动直线y=m与函数y=f（x）的图象有三个不同的交点，它们的横坐标分别为x1、x2、x3，则x1+x2+x3的取值范围是（）A．（2，6﹣2）B．（2，+1） C．（4，8﹣2）D．（0，4﹣2）二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5.00分）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是．14．（5.00分）圆x2+y2﹣2x﹣2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为．15．（5.00分）给出下列四个命题：①函数在R上单调递增；②若函数y=x2+2ax+1在（﹣∞，﹣1]上单调递减，则a≤1；③若log0.7（2m）＜log0.7（m﹣1），则m＞﹣1；④若f（x）是定义在R上的奇函数，则f（1﹣x）+f（x﹣1）=0．其中正确的序号是．16．（5.00分）四面体的一条棱长为x，其它各棱长均为1，若把四面体的体积V 表示成关于x的函数V（x），则函数V（x）的单调递减区间是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10.00分）已知△ABC三个定点坐标为A（0，1），B（0，﹣1），C（﹣2，1）．（1）求BC边上的高所在直线l的方程；（2）求AC边中线所在直线方程；（3）求△ABC的外接圆方程．18．（12.00分）正方体ABCD﹣A1B1C1D1中，棱长为2，E、F分别为AB、A1B1中点，现已给出四棱柱EBCD﹣FB1C1D1的左视图．（1）请画出四棱柱EBCD﹣FB1C1D1的主视图和俯视图；（2）请在线段BC上找一点M，使得点M和直线EF所确定的平面（设为α）垂直于面EFD1D，在图中画出α与正方体ABCD﹣A1B1C1D1相交所成的截面，说出BM的长度，并给出证明．19．（12.00分）已知y=f（x）是奇函数，当x＞0时，f（x）=x2﹣4x+8，且当x ∈[﹣5，﹣1]时，n≤f（x）≤m恒成立，求m﹣n的最小值．20．（12.00分）如图，C，D是以AB为直径的圆上的两点，AB=2AD=2，AC=BC，F是AB上的一点，且AF=AB，将圆沿AB折起，使点C在平面ABD的正投影E 在线段BD上，已知CE=，平面EFMN分别交AC、DC于点M、N．（1）求证：AD⊥平面BCE；（2）求证：AD∥MN；（3）求三棱锥A﹣CFD的体积．21．（12.00分）平面内有两个定点A（1，0），B（1，﹣2），设点P到A的距离为d1，到B的距离为d2，且．（1）求点P的轨迹C的方程；（2）点M（0，1）与点N关于直线x﹣y=0对称，问：是否存在过点N的直线l，l与轨迹C相交于E、F两点，且使三角形（O为坐标原点）？若存在，求出直线l的方程；若不存在，请说明理由．22．（12.00分）已知函数是奇函数，且满足g（1）=g（4）．（1）求实数a，b的值；（2）若，当x∈[2，+∞）时，函数f（x）的图象上是否存在不同的两点，使过这两点的直线平行于x轴；（3）对于（2）中的f（x），是否存在实数k同时满足以下两个条件：①不等式对x∈[0，+∞）恒成立，②方程f（x）=k在x∈[﹣8，﹣1）上有解．若存在，求出实数k的取值范围；若不存在，请说明理由．2015-2016学年辽宁省抚顺一中高一（上）期末数学试卷参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5.00分）已知实数集R，集合M={x|0＜x＜2}，集合，则M ∩（∁R N）（）A．{x|0＜x≤1}B．{x|0＜x＜2}C．{x|x＜1}D．∅【解答】解：由x﹣1＞0，得x＞1，所以N={x|x＞1}，C R N={x|x≤1}，∴M∩（C R N）={x|0＜x≤1}故选：A．2．（5.00分）若直线l1：2x+（m+1）y+4=0与直线l2：mx+3y﹣2=0平行，则m 的值为（）A．﹣2 B．﹣3 C．2或﹣3 D．﹣2或﹣3【解答】解：∵直线l1：2x+（m+1）y+4=0与直线l2：mx+3y﹣2=0平行，∴=，解得m=2或﹣3，故选：C．3．（5.00分）已知甲商品和乙商品价格相同，甲商品价格先上调10%，后下调10%，乙商品价格先下调10%，再上调10%，则调整后，甲乙两种商品的价格比较情况是（）A．甲商品价格高一些B．乙商品价格高一些C．两种商品价格高一样D．无法确定【解答】解：设甲乙商品的价格都为1，则调整后甲商品的价格为（1+0.1）（1﹣0.1）=1﹣0.01=0.99；调整后乙商品的价格为（1﹣0.1）（1+0.1）=0.99；∴调整后甲乙两商品价格相同．故选：C．4．（5.00分）平行六面体ABCD﹣A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为（）A．3 B．4 C．5 D．6【解答】解：根据两条平行直线、两条相交直线确定一个平面，可得CD、BC、BB1、AA1、C1D1符合条件．故选：C．5．（5.00分）一个圆锥的底面半径为2cm，高为6cm，在其中有一个高为3cm 的内接圆柱，则圆柱的侧面积为（）A．2πcm2B．4πcm2C．6πcm2D．12πcm2【解答】解：设所求的圆柱的底面半径为r，则有，解得r=1．∴S=2π×1×3=6π（cm2）．圆柱侧故选：C．6．（5.00分）已知集合A=[0，8]，集合B=[0，4]，则下列对应关系中：①，②，③，④f：x→y=x．不能看作从A到B的映射的是（）A．①B．②C．③D．④【解答】解：对于①，当x∈[0，8]时，y∈[0，1]⊆[0，4]，符合映射概念；对于②，当x∈[0，8]时，y∈[0，2]⊆[0，4]，符合映射概念；对于③，当x∈[0，8]时，y∈[0，4]⊆[0，4]，符合映射概念；对于④f：x→y=x，当x∈[0，8]时，y∈[0，8]⊈[0，4]，不符合映射概念．故选：D．7．（5.00分）一束光线自点P（﹣1，1，1）发出，被yOz平面反射到达点Q（﹣6，3，3）被吸收，那么光线所走的距离是（）A． B． C． D．【解答】解：点P（﹣1，1，1）平面xoy的对称点的M坐标（﹣1，1，﹣1），一束光线自点P（﹣1，1，1）发出，遇到平面xoy被反射，到达点Q（﹣6，3，3）被吸收，那么光所走的路程是：=．故选：D．8．（5.00分）如图，在半径为3的球面上有A、B、C三点，∠ABC=90°，BA=BC，球心O到平面ABC的距离是，则B、C两点的球面距离是（）A．B．πC．D．2π【解答】解：∵AC是小圆的直径．所以过球心O作小圆的垂线，垂足O′是AC的中点．O′C=，AC=3，∴BC=3，即BC=OB=OC．∴，则B、C两点的球面距离=．故选：B．9．（5.00分）已知平面α⊥平面β，α∩β=l，点A∈α，A∉l，直线AB∥l，直线AC ⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（）A．AB∥m B．AC⊥m C．AB∥βD．AC⊥β【解答】解：如图所示AB∥l∥m；A对AC⊥l，m∥l⇒AC⊥m；B对AB∥l⇒AB∥β，C对对于D，虽然AC⊥l，但AC不一定在平面α内，故它可以与平面β相交、平行，故不一定垂直；故错．故选：D．10．（5.00分）已知线段PQ两端点的坐标分别为（﹣1，1），（2，2），若直线l：x+my+m=0与线段PQ有交点，则m的范围是（）A． B．C．D．【解答】解：（方法一）直线l：x+my+m=0恒过A（0，﹣1）点，kAP==﹣2，kAQ==，则﹣≥或﹣≤﹣2，∴﹣≤m≤且m≠0，又∵m=0时直线l：x+my+m=0与线段PQ有交点，∴所求m的范围是﹣≤m≤；（方法二）∵P，Q两点在直线的两侧或其中一点在直线l上，∴（﹣1+m+m）•（2+2m+m）≤0解得：﹣≤m≤，∴所求m的范围是﹣≤m≤；故选：B．11．（5.00分）已知a=log23，b=20.5，，则a，b，c从大到小的顺序为（）A．c＞b＞a B．b＞c＞a C．a＞b＞c D．c＞a＞b【解答】解：∵a=log23==＜=c，=＞b=20.5，∴c＞a＞b．故选：D．12．（5.00分）函数f（x）=min，其中min，若动直线y=m与函数y=f（x）的图象有三个不同的交点，它们的横坐标分别为x1、x2、x3，则x1+x2+x3的取值范围是（）A．（2，6﹣2）B．（2，+1） C．（4，8﹣2）D．（0，4﹣2）【解答】解：作出函数f（x）的图象如下图所示：由，解得A（4﹣2，2﹣2），由图象可得，当直线y=m与f（x）图象有三个交点时m的范围为：0＜m＜2﹣2．不妨设0＜x1＜x2＜2＜x3，则由2=m得x 1=，由|x2﹣2|=2﹣x2=m，得x2=2﹣m，由|x3﹣2|=x3﹣2=m，得x3=m+2，且2﹣m＞0，m+2＞0，∴x1+x2+x3=+（2﹣m）+（2+m）=+4，当m=0时，+4有最小值为4，当m=2﹣2时，+4有最大8﹣2，∴x1+x2+x3的取值范围是（4，8﹣2，）故选：C．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5.00分）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是2．【解答】解：由已知作出梯形ABCD是直角梯形，如右图：∵按照斜二测画法画出它的直观图A′B′C′D′，A′D′=2，B′C′=4，A′B′=1，∴直角梯形ABCD中，AB⊥BC，AD=A′D′=2，BC=B′C′=4，AB=2A′B′=2，过D作DE⊥BC，交BC于E，则DE=AB=2，EC=BC﹣AD=4﹣2=2，∴直角梯形DC边的长度为：=2．故答案为：2．14．（5.00分）圆x2+y2﹣2x﹣2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为2．【解答】解：把圆的方程化为标准式方程得：（x﹣1）2+（y﹣1）2=1，所以圆心A（1，1），圆的半径r=1，则圆心A到直线3x+4y+8=0的距离d==3，所以动点Q到直线距离的最小值为3﹣1=2故答案为：215．（5.00分）给出下列四个命题：①函数在R上单调递增；②若函数y=x2+2ax+1在（﹣∞，﹣1]上单调递减，则a≤1；③若log0.7（2m）＜log0.7（m﹣1），则m＞﹣1；④若f（x）是定义在R上的奇函数，则f（1﹣x）+f（x﹣1）=0．其中正确的序号是②④．【解答】解：①函数在R上单调递增是错误的，只能说函数在每一个象限上单调递增，故①错②若函数y=x2+2ax+1在（﹣∞，﹣1]上单调递减只需满足对称轴x=≥﹣1，即a≤1，故②正确③若log0.7（2m）＜log0.7（m﹣1），先注意定义域，再利用对数函数单调性解不等式，2m＞m﹣1，2m＞0，m﹣1＞0三个不等式同时成立，即m＞1，故③错误④若f（x）是定义在R上的奇函数，则f（x）+f（﹣x）=0成立，把x重新看成1﹣x即可，便得到f（1﹣x）+f（x﹣1）=0，故④正确故答案为：②④16．（5.00分）四面体的一条棱长为x，其它各棱长均为1，若把四面体的体积V 表示成关于x的函数V（x），则函数V（x）的单调递减区间是（）．【解答】解：如图，四面体ABCD中，AD=x，其余各棱为1．取AD中点F，BC 中点E在三角形ABC中，∵三角形ABC为正三角形，E点是BC的中点，∴AE⊥BC，同理ED⊥BC，∵AE∩ED=E，∴BC⊥面AED．S△AED=AD•EF，EF==，∴V（x）=•S•BC=，△AED由3﹣x2＞0，得0，∴函数V（x）的定义域为（0，），V′（x）===，由3﹣2x2＜0，得x（舍），或x．∴函数V（x）的单调递减区间是（）．故答案为：（）．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10.00分）已知△ABC三个定点坐标为A（0，1），B（0，﹣1），C（﹣2，1）．（1）求BC边上的高所在直线l的方程；（2）求AC边中线所在直线方程；（3）求△ABC的外接圆方程．【解答】解：（1）由于△ABC三个定点坐标为A（0，1），B（0，﹣1），C（﹣2，1），故BC的斜率为=﹣1，故BC边上的高线的斜率为1，且经过点A，可得BC边上的高所在直线l的方程为y﹣1=x﹣0，即x﹣y+1=0．（2）由于AC的中点为（﹣1，1），B（0，﹣1），故AC边中线所在直线方程为x=﹣1．（3）设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0，则把A、B、C的坐标代入可得，求得，故要求的圆的方程为x2+y2+2x﹣1=0．18．（12.00分）正方体ABCD﹣A1B1C1D1中，棱长为2，E、F分别为AB、A1B1中点，现已给出四棱柱EBCD﹣FB1C1D1的左视图．（1）请画出四棱柱EBCD﹣FB1C1D1的主视图和俯视图；（2）请在线段BC上找一点M，使得点M和直线EF所确定的平面（设为α）垂直于面EFD1D，在图中画出α与正方体ABCD﹣A1B1C1D1相交所成的截面，说出BM的长度，并给出证明．【解答】解：（1）由四棱柱EBCD﹣FB1C1D1的直观图作出主视图和俯视图，如下图：（2）如右图，在线段BC上找一点M，使BM=，则点M和直线EF所确定的平面（设为α）垂直于面EFD1D．证明：∵正方体ABCD﹣A1B1C1D1中，棱长为2，E、F分别为AB、A1B1中点，∴DE==，EM==，DM==，∴DE2+EM2=DM2，∴DE⊥ME，又∵EF⊥面ABCD，EM⊂平面ABCD，∴EF⊥EM，∵EF∩EM=E，∴EM⊥平面EFD1D，∵EM⊂α，∴面EFD1D⊥α．19．（12.00分）已知y=f（x）是奇函数，当x＞0时，f（x）=x2﹣4x+8，且当x∈[﹣5，﹣1]时，n≤f（x）≤m恒成立，求m﹣n的最小值．【解答】解：y=f（x）是奇函数，可得f（﹣x）=﹣f（x），令x＜0，则﹣x＞0，由x＞0时，f（x）=x2﹣4x+8，可得f（﹣x）=x2+4x+8=﹣f（x），即有f（x）=﹣x2﹣4x﹣8，x＜0，当x∈[﹣5，﹣1]时，f（x）=﹣（x+2）2﹣4，当x=﹣2时，f（x）取得最大值﹣4，当x=﹣5时，f（x）取得最小值﹣13．由当x∈[﹣5，﹣1]时，n≤f（x）≤m恒成立，可得n≤﹣13，m≥﹣4，则m﹣n≥﹣4+13=9．可得m﹣n的最小值为9．20．（12.00分）如图，C，D是以AB为直径的圆上的两点，AB=2AD=2，AC=BC，F是AB上的一点，且AF=AB，将圆沿AB折起，使点C在平面ABD的正投影E 在线段BD上，已知CE=，平面EFMN分别交AC、DC于点M、N．（1）求证：AD⊥平面BCE；（2）求证：AD∥MN；（3）求三棱锥A﹣CFD的体积．【解答】（1）证明：依题意，AD⊥BD∵CE⊥平面ABD，∴CE⊥AD，∵BD∩CE=E，∴AD⊥平面BCE；（2）证明：Rt△BCE中，CE=，BC=，∴BE=2，Rt△ABD中，AB=2，AD=，∴BD=3．∴，则AD∥EF，∵AD⊂平面ADC，EF⊄平面ADC，∴EF∥平面ADC．又EF⊂平面EFMN，且平面EFMN∩平面ADC=MN，∴EF∥MN，则AD∥MN；（3）解：由（2）知AD∥EF，AD⊥ED，且ED=BD﹣BE=1，∴F到AD的距离等于E到AD的距离为1．∴S=×．△FAD∵CE⊥平面ABD，∴V A=V C﹣AFD=S△FAD•CE=×=．﹣CFD21．（12.00分）平面内有两个定点A（1，0），B（1，﹣2），设点P到A的距离为d1，到B的距离为d2，且．（1）求点P的轨迹C的方程；（2）点M（0，1）与点N关于直线x﹣y=0对称，问：是否存在过点N的直线l，l与轨迹C相交于E、F两点，且使三角形（O为坐标原点）？若存在，求出直线l的方程；若不存在，请说明理由．【解答】解：（1）设P（x，y），则，d2=，∵，∴=，整理，得：x2+y2﹣2x+8y+9=0．∴点P的轨迹C的方程为x2+y2﹣2x+8y+9=0．（2）不存在过点N的直线l，l与轨迹C相交于E、F两点，且使三角形．理由如下：∵点M（0，1）与点N关于直线x﹣y=0对称，∴N（1，0），当直线l的斜率不存在时，直线l的方程为x=1，联立，得，或，此时S=，成立；△OEF当直线l的斜率成立时，设直线l的方程为y=k（x﹣1），联立，得（1+k2）x2﹣（2k2﹣8k+2）x+k2﹣8k+9=0，△＞0，设E（x1，y1），N（x2，y2），则，，点O到直线y=k（x﹣1）的距离d==，|EF|==，∵，==×=2，∴S△OEF整理，得3k2=﹣1，不成立，综上，存在过点N的直线l：x=1，l与轨迹C相交于E、F两点，且使三角形．22．（12.00分）已知函数是奇函数，且满足g（1）=g（4）．（1）求实数a，b的值；（2）若，当x∈[2，+∞）时，函数f（x）的图象上是否存在不同的两点，使过这两点的直线平行于x轴；（3）对于（2）中的f（x），是否存在实数k同时满足以下两个条件：①不等式对x∈[0，+∞）恒成立，②方程f（x）=k在x∈[﹣8，﹣1）上有解．若存在，求出实数k的取值范围；若不存在，请说明理由．【解答】解：（1）由g（1）=g（4）得=，解得b=4，由是奇函数，g（﹣x）+g（x）=0得2a=0，∴a=0；（5分）（2）由（1）知，f（x）=x+，函数f（x）在区间x∈[2，+∞）单调递增，∴不存在不同的两点，使过这两点的直线平行于x轴；（9分）（3）对于条件①：由（2）可知函数f（x）在x∈（0，+∞）上有最小值f（2）=4 （10分）故若对x∈（0，+∞）恒成立，则需4＞﹣，∴k＞﹣8；（11分）对于条件②：由（2）可知函数f（x）在（﹣∞，﹣2）单调递增，在[﹣2，0）单调递减，∴函数f（x）在[﹣8，﹣2]单调递增，在[﹣2，﹣1]单调递减，（12分）又f（﹣8）=﹣10，f（﹣2）=﹣4，f（﹣1）=﹣5，∴函数f（x）在[﹣8，﹣1]上的值域为[﹣10，﹣4]，（13分）若方程f（x）=k在[﹣8，﹣1]有解，则需﹣10≤k≤﹣4，若同时满足条件①②，则需﹣10≤k≤﹣4．赠送—高中数学知识点【1.3.1】单调性与最大（小）值（1）函数的单调性函数的定义图象判定方法性质函数的单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x ．1．< ．x ．2．时，都有f(x ．．．1．)<f(x ．．．．．2．)．，那么就说f(x)在这个区间上是增函数．．．． x 1x 2y=f(X)xy f(x )1f(x )2o（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图 象上升为增） （4）利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2，当x ．1．< ．x ．2．时，都有f(x ．．．1．)>f(x ．．．．．2．)．，那么就说f(x)在这个区间上是减函数．．．． y=f(X)yx ox x 2f(x )f(x )211（1）利用定义 （2）利用已知函数的单调性（3）利用函数图象（在某个区间图 象下降为减）（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()yf u=为增，()u g x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减． （2）打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数，分别在[,0)a -、]a 上为减函数．（3）最大（小）值定义①一般地，设函数()y f x =的定义域为I ，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．yxo第21页（共21页）【1.3.2】奇偶性（4）函数的奇偶性函数的 性 质定义图象判定方法 函数的奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x ．．．)．,那么函数f(x)叫做奇函数．．．．（1）利用定义（要先判断定义域是否关于原点对称） （2）利用图象（图象关于原点对称）如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称） （2）利用图象（图象关于y 轴对称）②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．故当﹣10≤k ≤﹣4时，条件①②同时满足． （15分）。

抚顺六校联合体2015——2016学年度（下）期末考试高一历史答案一、单项选择题1——5 ADCCA 6——10 DACDD11——15 CBBBA 16——20 BCBDB21——25 BACAB 26——30 ACCDD二、主观题参考答案（其它答案，言之有理，也可给分）31、(20分)【参考答案】（1）特点：①华侨对广州的早期近代化起重要推动作用；②引进西方的技术；③近代化起步较早，是中国近代民族工业的发源地之一。

（任意2条得4分）原因：西方工业文明的冲击（2分）(2)原因：（总）国民政府实行国民经济建设运动。

（分）废除不平等条约；实行币制改革；扶植民间轻工业等（6分,任答3点即可）（3）洋务派兴办企业，标志中国近代工业化起步。

（2分）近代民族资本主义的发展，中国工业化进一步发展。

（2分）新中国成立后，“一五计划”，奠定了工业化的初步基础。

（2分）改革开放，以信息化带动工业化，工业化迅速发展。

（2分）32．(20分)【参考答案】（1）内容：传染病向欧洲以外地区的蔓延；物种的交流；人类移民浪潮的出现。

（6分）（2）特点：资本主义世界市场的形成。

（2分）原因：工业革命促进经济发展；新式交通工具的创制；殖民扩张。

（4分，答两点即可）(3)三大支柱：世界银行、国际货币基金组织；关贸总协定（6分）理由：促进了世界经济的全球化、体系化、制度化（2分）。

高一化学试题参考答案及给分标准一、选择题（每小题3分，共54分）二、非选择题（共46分）19、共11分（1）Ar（1分）；（1分）（2）氯（1分）；第三周期第ⅦA族（1分）（3）SiO2（1分）（4）（2分）（5）NH3（1分）；碱（1分）；Al3++3NH3·H2O == Al(OH)3↓+3NH4+（2分）20、共13分Ⅰ（1）钾（或K）（1分）；铝（或Al）（1分）（2）Cl2+S2- == S↓+2Cl-（2分）Ⅱ（1）变蓝（1分）；防止溶液倒吸（1分）；NaOH（1分，合理即可）（2）有白色沉淀生成（1分）；从B中挥发出的HCl也会和硅酸钠溶液反应生成硅酸（1分，意思对即可）；D（2分）；Na2SiO3+CO2+H2O == H2SiO3↓+Na2CO3（或Na2SiO3+2CO2+2H2O == H2SiO3↓+2NaHCO3）（2分）21、共11分（1）电解池（1分）；石墨（1分）；阳极（1分）（2）4AgNO3+2H2O4Ag+4HNO3+O2↑（2分，无反应条件不给分）（3）CH4-8e-+10OH-== CO32- +7H2O（2分）（4）56（2分）；0.05 mol/L（2分，无单位去1分）22、共11分（1）（2分）（2）-99（2分）；＜（1分）（3）③④（2分，每个1分，有错选零分）（4）3:4（2分）；6.75或27/4（2分）。

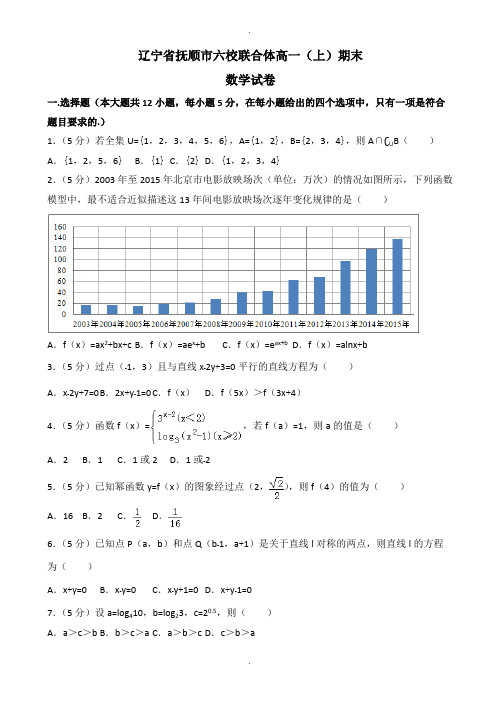
辽宁省抚顺市六校联合体高一（上）期末数学试卷一.选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）若全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，则A∩∁U B（ ）A．{1，2，5，6}B．{1}C．{2}D．{1，2，3，4}2．（5分）2003年至2015年北京市电影放映场次（单位：万次）的情况如图所示，下列函数模型中，最不适合近似描述这13年间电影放映场次逐年变化规律的是（ ）A．f（x）=ax2+bx+c B．f（x）=ae x+b C．f（x）=e ax+b D．f（x）=alnx+b3．（5分）过点（﹣1，3）且与直线x﹣2y+3=0平行的直线方程为（ ）A．x﹣2y+7=0B．2x+y﹣1=0C．f（x）D．f（5x）＞f（3x+4）4．（5分）函数f（x）=，若f（a）=1，则a的值是（ ）A．2B．1C．1或2D．1或﹣25．（5分）已知幂函数y=f（x）的图象经过点（2，），则f（4）的值为（ ）A．16B．2C．D．6．（5分）已知点P（a，b）和点Q（b﹣1，a+1）是关于直线l对称的两点，则直线l的方程为（ ）A．x+y=0B．x﹣y=0C．x﹣y+1=0D．x+y﹣1=07．（5分）设a=log410，b=log23，c=20.5，则（ ）A．a＞c＞b B．b＞c＞a C．a＞b＞c D．c＞b＞a8．（5分）设α，β是两个不同的平面，m，n是两条不同的直线，给出下列四个论断①m∥n；②α∥β③m⊥α；④n⊥β．以其中三个论断作为条件，余下一个论断作为结论，则一共可以写出真命题的个数为（ ）A．1B．2C．3D．49．（5分）一个几何体的三视图如图所示（单位：cm），那么此几何体的表面积（单位：cm2）是（ ）A．102B．128C．144D．18410．（5分）已知函数y=f（x）（x∈R）是奇函数且当x∈（0，+∞）时是减函数，若f（1）=0，则函数y=f（x2﹣2x）的零点共有（ ）A．4个B．6个C．3个D．5个11．（5分）利用“长方体ABCD﹣A1B1C1D1中，四面体A1BC1D”的特点，求得四面体PMNR（其中PM=NR=，PN=MR=，MN=PR=）的外接球的表面积为（ ）A．14πB．16πC．13πD．15π12．（5分）对于函数f（x），若在其定义域内存在两个实数a，b（a＜b），当x∈[a，b]时，f （x）的值域也是[a，b]，则称函数f（x）为“Kobe函数”．若函数f（x）=k+是“Kobe函数”，则实数k的取值范围是（ ）A．[﹣1，0]B．[1，+∞）C．D．二.填空题（本大题共4道小题，每道小题5分，满分20分.）13．（5分）已知集合A={x|x2﹣2x+a＞0}，且1∉A，则实数a的取值范围是 ．14．（5分）在△ABC中，AB=2，BC=1，∠ABC=120°若将△ABC绕直线BC旋转一周，则所形的旋转体的体积是 ．15．（5分）直线和x轴，y轴分别交于点A，B，以线段AB为一边在第一象限内作等边△ABC，则点C的坐标为 ．16．（5分）下列四个命题中，正确的是 （写出所有正确命题的序号）①函数f（x）的定义域为[0，2]，则函数f（2x）的定义域为[0，4]；②设集合A={﹣1，0，1}，B={﹣1，1}，则在A到B的所有映射中，偶函数共有4个；③不存在实数a，使函数的值域为（0，1]④函数在[2，+∞）上是减函数，则﹣4＜a≤4．三.解答题（本大题共6道小题，满分70分，解答应写出文字说明，证明过程或演算步骤.）17．（10分）如图，在平行四边形OABC中，过点C（1，3）做CD⊥AB，垂足为点D，试求CD所在直线的一般式方程．18．（12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过点E，F的平面α与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（保留画图痕迹，不用说明画法和理由）（Ⅱ）求平面α把该长方体分成的两部分中较小部分的体积．19．（12分）已知集合A=（﹣∞，﹣1）∪（3，+∞），B={x|x2﹣4x+a=0，a∈R}．（Ⅰ）若A∩B≠∅，求a的取值范围；（Ⅱ）若A∩B=B，求a的取值范围．20．（12分）为了绿化城市，准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪，其中∠AED=∠EDC=∠DCB=90°，点Q在AB上，且PQ∥CD，QR⊥CD，经测量BC=70m，CD=80m，DE=100m，AE=60m问应如何设计才能使草坪的占地面积最大？并求出最大面积（精确到1m2）．21．（12分）如图，PA垂直于矩形ABCD所在平面，AE⊥PB，垂足为E，EF⊥PC垂足为F．（Ⅰ）设平面AEF∩PD=G，求证：PC⊥AG；（Ⅱ）设PA=，M是线段PC的中点，求证：DM∥平面AEC．22．（12分）已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若m，n∈[﹣1，1]，m+n ≠0时，有＞0．（Ⅰ）证明f（x）在[﹣1，1]上是增函数；（Ⅱ）解不等式f（x2﹣1）+f（3﹣3x）＜0（Ⅲ）若f（x）≤t2﹣2at+1对∀x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数t的取值范围．2016-2017学年辽宁省抚顺市六校联合体高一（上）期末数学试卷参考答案与试题解析一.选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）若全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，则A∩∁U B（ ）A．{1，2，5，6}B．{1}C．{2}D．{1，2，3，4}【解答】解：∵全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，∴C U B={1，5，6}，∴A∩∁U B={1}．故选：B．2．（5分）2003年至2015年北京市电影放映场次（单位：万次）的情况如图所示，下列函数模型中，最不适合近似描述这13年间电影放映场次逐年变化规律的是（ ）A．f（x）=ax2+bx+c B．f（x）=ae x+b C．f（x）=e ax+b D．f（x）=alnx+b【解答】解：由图象可得：这13年间电影放映场次逐年变化规律的是随着x的增大，f（x）逐渐增大，图象逐渐上升．对于A．f（x）=ax2+bx+c，取a＞0，＜0，可得满足条件的函数；对于B．取a＞0，b＞0，可得满足条件的函数；对于C．取a＞0，b＞0，可得满足条件的函数；对于D．a＞0时，为“上凸函数”，不符合图象的特征；a＜0时，为单调递减函数，不符合图象的特征．故选：D．3．（5分）过点（﹣1，3）且与直线x﹣2y+3=0平行的直线方程为（ ）A．x﹣2y+7=0B．2x+y﹣1=0C．f（x）D．f（5x）＞f（3x+4）【解答】解：设过点（﹣1，3）且与直线x﹣2y+3=0平行的直线方程为x﹣2y+m=0，把点（﹣1，3）代入直线方程得﹣1﹣2×3+m=0，m=7，故所求的直线方程为x﹣2y+7=0，故选A．4．（5分）函数f（x）=，若f（a）=1，则a的值是（ ）A．2B．1C．1或2D．1或﹣2【解答】解：若a＜2，则由f（a）=1得，3a﹣2=1，即a﹣2=0，∴a=2．此时不成立．若a≥2，则由f（a）=1得，log=1，得a2﹣1=3，即a2=4，∴a=2，故选：A．5．（5分）已知幂函数y=f（x）的图象经过点（2，），则f（4）的值为（ ）A．16B．2C．D．【解答】解：设幂函数为y=xα，∵幂函数y=f（x）的图象经过点（2，），∴=2α，解得α=．y=x．f（4）==．故选：C．6．（5分）已知点P（a，b）和点Q（b﹣1，a+1）是关于直线l对称的两点，则直线l的方程为（ ）A．x+y=0B．x﹣y=0C．x﹣y+1=0D．x+y﹣1=0【解答】解：∵点P（a，b）与Q（b﹣1，a+1）（a≠b﹣1）关于直线l对称，∴直线l为线段PQ的中垂线，PQ的中点为（，），PQ的斜率为=﹣1，∴直线l的斜率为1，即直线l的方程为y﹣1×（x﹣），化简可得x﹣y+1=0．故选：C．7．（5分）设a=log410，b=log23，c=20.5，则（ ）A．a＞c＞b B．b＞c＞a C．a＞b＞c D．c＞b＞a【解答】解：∵a=log 410=＞b=log23＞=1.5，c=20.5=，∴a＞b＞c．故选：C．8．（5分）设α，β是两个不同的平面，m，n是两条不同的直线，给出下列四个论断①m∥n；②α∥β③m⊥α；④n⊥β．以其中三个论断作为条件，余下一个论断作为结论，则一共可以写出真命题的个数为（ ）A．1B．2C．3D．4【解答】解：同垂直于一个平面的两条直线互相平行，同垂直于两个平行平面的两条直线也互相平行．故②③④⇒①同理，①②③⇒④，①②④⇒③，①③④⇒②为真命题故选D．9．（5分）一个几何体的三视图如图所示（单位：cm），那么此几何体的表面积（单位：cm2）是（ ）A．102B．128C．144D．184【解答】解：由三视图知几何体为正四棱锥，且底面正方形的边长为8，斜高为5，其直观图如图：∴几何体的表面积S=82+4××8×5=144．故选C．10．（5分）已知函数y=f（x）（x∈R）是奇函数且当x∈（0，+∞）时是减函数，若f（1）=0，则函数y=f（x2﹣2x）的零点共有（ ）A．4个B．6个C．3个D．5个【解答】解：根据题意，函数y=f（x）是定义域为R的奇函数，则f（0）=0，当x∈（0，+∞）时是减函数，且f（1）=0，则函数在（0，+∞）上只有一个零点，若函数y=f（x）是奇函数且当x∈（0，+∞）时是减函数，则f（x）在（﹣∞，0）为减函数，又由f（1）=0，则f（﹣1）=﹣f（1）=0，则函数在（﹣∞，0）上只有一个零点，故函数y=f（x）共有3个零点，依次为﹣1、0、1，对于y=f（x2﹣2x），当x2﹣2x=﹣1，解可得x=1，当x2﹣2x=0，解可得x=0或2，当x2﹣2x=1，解可得x=1+或1﹣，故y=f（x2﹣2x）的零点共有5个；故选：D．11．（5分）利用“长方体ABCD﹣A1B1C1D1中，四面体A1BC1D”的特点，求得四面体PMNR（其中PM=NR=，PN=MR=，MN=PR=）的外接球的表面积为（ ）A．14πB．16πC．13πD．15π【解答】解：由题意，构造长方体，使得面上的对角线长分别为，，，则长方体的对角线长等于四面体PMNR外接球的直径．设长方体的棱长分别为x，y，z，则x2+y2=10，y2+z2=13，x2+z2=5，∴x2+y2+z2=14∴三棱锥O﹣ABC外接球的直径为，∴三棱锥S﹣ABC外接球的表面积为π•14=14π，故选A．12．（5分）对于函数f（x），若在其定义域内存在两个实数a，b（a＜b），当x∈[a，b]时，f （x）的值域也是[a，b]，则称函数f（x）为“Kobe函数”．若函数f（x）=k+是“Kobe函数”，则实数k的取值范围是（ ）A．[﹣1，0]B．[1，+∞）C．D．【解答】解：由题意，当x∈[a，b]时，f（x）的值域也是[a，b]，可知函数f（x）是增函数，其图象与y=x有两个不同的交点，可得：x=k+，必有两个不相等的实数根．即：x﹣k=，∵，即x≥1，∴1﹣k≥0，可得k≤1．那么：（x﹣k）2=x﹣1有两个不相等的实数根．其判别式△＞0，即（2k+1）2﹣4k2﹣4＞0，解得：k，∴实数k的取值范围是（，1]．故选D．二.填空题（本大题共4道小题，每道小题5分，满分20分.）13．（5分）已知集合A={x|x2﹣2x+a＞0}，且1∉A，则实数a的取值范围是　（﹣∞，1]　．【解答】解：根据1∉A，可知，集合A在实数集当中没有元素1，又集合A中的元素是由一元二次不等式构成的解集，故问题可转化为一元二次不等式没有实数1．由12﹣2+a≤0解得a≤1．故答案为：（﹣∞，1]．14．（5分）在△ABC中，AB=2，BC=1，∠ABC=120°若将△ABC绕直线BC旋转一周，则所形的旋转体的体积是　π　．【解答】解：依题意可知，旋转体是一个大圆锥去掉一个小圆锥，所以OA=，OB=1，所以旋转体的体积：=π，故答案为：π．15．（5分）直线和x轴，y轴分别交于点A，B，以线段AB为一边在第一象限内作等边△ABC，则点C的坐标为 ．【解答】解：由题意，A（，0），B（0，1），则|AB|=2，AC⊥x轴，∴点C的坐标为．故答案为．16．（5分）下列四个命题中，正确的是　②③④　（写出所有正确命题的序号）①函数f（x）的定义域为[0，2]，则函数f（2x）的定义域为[0，4]；②设集合A={﹣1，0，1}，B={﹣1，1}，则在A到B的所有映射中，偶函数共有4个；③不存在实数a，使函数的值域为（0，1]④函数在[2，+∞）上是减函数，则﹣4＜a≤4．【解答】解：对于①，函数f（x）的定义域为[0，2]，0≤2x≤2，则函数f（2x）的定义域为[0，1]，故错；对于②，依题意可知f（﹣1）=f（1），进而分值域中有1、2个元素进行讨论．当值域中只有一个元素时，此时满足题意的映射有2种，当值域中有两个元素时，此时满足题意的映射有2个，共有4个，故正确；对于③，若存在实数a，使函数的值域为（0，1]时，ax2+2ax+3的值域为（﹣∞，0]，即，a∈∅，故正确；对于④，函数在[2，+∞）上是减函数，则令t=x2﹣ax+3a，则由函数f （x）=g（t）=在区间[2，+∞）上为减函数，可得函数t在区间[2，+∞）上为增函数且t（2）＞0，解得﹣4＜a≤4，故正确．故答案为：②③④三.解答题（本大题共6道小题，满分70分，解答应写出文字说明，证明过程或演算步骤.）17．（10分）如图，在平行四边形OABC中，过点C（1，3）做CD⊥AB，垂足为点D，试求CD所在直线的一般式方程．【解答】解：因为点O（0，0），点C（1，3），所以OC所在直线的斜率为．（2分），在平行四边形OABC中，AB∥OC，因为CD⊥AB，所以CD⊥OC．所以CD所在直线的斜率为．（6分）所以CD所在直线方程为，即x+3y﹣10=0．（10分）18．（12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过点E，F的平面α与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（保留画图痕迹，不用说明画法和理由）（Ⅱ）求平面α把该长方体分成的两部分中较小部分的体积．【解答】解：（Ⅰ）交线围成的正方形EHGF，如图，在面ABCD中做HG平行于BC，连接EH，FG且HB=GC=6，则EF平行且等于HG，所以四边形EFGH是平行四边形，EF平行于A1D1，所以EF垂直面A1AB1B，所以EF垂直于EH，且由题意得EH=FG=10，所以EFGH是正方形．（6分）（Ⅱ）由图形可以看出左半部分体积小…（2分），所以平面α把该长方体分成的两部分中较小部分的体积：…（6分）19．（12分）已知集合A=（﹣∞，﹣1）∪（3，+∞），B={x|x2﹣4x+a=0，a∈R}．（Ⅰ）若A∩B≠∅，求a的取值范围；（Ⅱ）若A∩B=B，求a的取值范围．【解答】解：令f（x）=x2﹣4x+a=（x﹣2）2+a﹣4，则对称轴为x=2，（Ⅰ）由题意得B≠∅，∴△=16﹣4a≥0，解得a≤4…①∵A∩B≠∅，又∵A=（﹣∞，﹣1）∪（3，+∞），∴f（3）＜0，解得a＜3…②，由①②得，实数a的取值范围为（﹣∞，3）．（Ⅱ）∵A∩B=B，∴B⊆A，当△=16﹣4a＜0，即a＞4时，B=∅，这时满足A∩B=B，当△=16﹣4a≥0时，B≠∅，此时a≤4…③，∵B⊆A，∴f（﹣1）＜0，解得a＜﹣5…④，由③④，得a＜﹣5．综上所述，得实数a的取值范围为（﹣∞，﹣5）∪[4，+∞）．20．（12分）为了绿化城市，准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪，其中∠AED=∠EDC=∠DCB=90°，点Q在AB上，且PQ∥CD，QR⊥CD，经测量BC=70m，CD=80m，DE=100m，AE=60m问应如何设计才能使草坪的占地面积最大？并求出最大面积（精确到1m2）．【解答】解：如图，以BC边所在直线为x轴，，以AE边所在直线为y轴建立平面直角坐标系，则A（0，20），B（30，0）．所以直线AB的方程为：+=1，（4分）即设，则矩形PQRD的面积为（0≤x≤30）（8分）化简，得（0≤x≤30）配方，（0≤x≤30）（12分）易得当x=5，y=时，S最大，其最大值为Smax≈6017m2（14分）21．（12分）如图，PA垂直于矩形ABCD所在平面，AE⊥PB，垂足为E，EF⊥PC垂足为F．（Ⅰ）设平面AEF∩PD=G，求证：PC⊥AG；（Ⅱ）设PA=，M是线段PC的中点，求证：DM∥平面AEC．【解答】证明：（Ⅰ）∵PA⊥平面ABCD，BC⊂平面ABCD，∴BC⊥PA；又∵BC⊥AB，PA∩AB=A，∴BC⊥平面ABP；而AE⊂平面ABP，∴AE⊥BC，又∵AE⊥PB，PB∩BC=B，∴AE⊥平面PBC；∵PC⊂平面PBC，∴PC⊥AE，又∵PC⊥EF，EF∩AE=E，∴PC⊥平面AEFG，∵AG⊂平面AEFG，∴PC⊥AG…（6分）（Ⅱ）∵，∴PE=2，BE=1，即PE=2EB，取PE中点N，连结MN，ND，BD，AC，设BD∩AC=O，连结EO，则在△PEC中，PN=NE，PM=MC，∴MN∥EC，同理ND∥EO，∵MN∩ND=N，∴平面MND∥平面AEC，又∵DM⊂平面DMN，∴DM∥平面AEC…（12分）22．（12分）已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若m，n∈[﹣1，1]，m+n ≠0时，有＞0．（Ⅰ）证明f（x）在[﹣1，1]上是增函数；（Ⅱ）解不等式f（x2﹣1）+f（3﹣3x）＜0（Ⅲ）若f（x）≤t2﹣2at+1对∀x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数t的取值范围．【解答】解：（Ⅰ）任取﹣1≤x1＜x2≤1，则，∵﹣1≤x1＜x2≤1，∴x1+（﹣x2）≠0，由已知，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），∴f（x）在[﹣1，1]上是增函数；（Ⅱ）∵f（x）是定义在[﹣1，1]上的奇函数，且在[﹣1，1]上是增函数，∴不等式化为f（x2﹣1）＜f（3x﹣3），∴，解得；（Ⅲ）由（Ⅰ）知f（x）在[﹣1，1]上是增函数，∴f（x）在[﹣1，1]上的最大值为f（1）=1，要使f（x）≤t2﹣2at+1对∀x∈[﹣1，1]恒成立，只要t2﹣2at+1≥1⇒t2﹣2at≥0，设g（a）=t2﹣2at，对∀a∈[﹣1，1]，g（a）≥0恒成立，∴，∴t≥2或t≤﹣2或t=0．。

2015-2016学年辽宁省抚顺市重点高中协作校高二（下）期末数学试卷（文科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）若集合A＝{x|（x﹣1）2＜4}，B＝{x||x|＞1}，则A∩（∁R B）＝（）A．{x|﹣1＜x≤1}B．{x|﹣1≤x＜1}C．{x|﹣1≤x≤1}D．{x|﹣1＜x＜1} 2．（5分）已知函数，则的值是（）A．9B．C．D．﹣93．（5分）已知a＞0且a≠1，函数f（x）＝满足对任意实数x1≠x2，都有＞0成立，则a的取值范围是（）A．（0，1）B．（1，+∞）C．（1，]D．[，2）4．（5分）函数f（x）＝|x|﹣ax﹣1仅有一个负零点，则a的取值范围是（）A．（﹣∞，1）B．（﹣∞，1]C．（1，+∞）D．[1，+∞）5．（5分）已知复数z满足（i是虚数单位），则z的共轭复数为（）A．B．C．D．6．（5分）某商品的销售额y（万元）与广告费用x（万元）之间的关系统计数据如表：由表中数据算出线性回归方程＝x+中的＝9.4，据此估计该商品广告费用为6万元时销售额约为（）万元．A．63.6B．64.2C．65.1D．65.57．（5分）为庆祝冬奥申办成功，随机调查了500名性别不同的大学生是否爱好某项冬季运动，提出假设H：“爱好这项运动与性别无关”，利用2×2列联表计算的K2≈3.918，经查临界值表知P（K2≥3.841）≈0.05．则下列表述中正确的是（）A．有95%的把握认为“爱好这项运动与性别有关”B．有95%的把握认为“爱好这项运动与性别无关”C．在犯错误的概率不超过0.5%的前提下，认为“爱好这项运动与性别有关”D．在犯错误的概率不超过0.5%的前提下，认为“爱好这项运动与性别无关”8．（5分）函数y＝x|x|的图象大致是（）A．B．C．D．9．（5分）“∵四边形ABCD为矩形，∴四边形ABCD的对角线相等”，补充以上推理的大前提为（）A．正方形都是对角线相等的四边形B．矩形都是对角线相等的四边形C．等腰梯形都是对角线相等的四边形D．矩形都是对边平行且相等的四边形10．（5分）已知函数f（x）＝log a x2+a|x|，若f（﹣3）＜f（4），则不等式f（x2﹣2x）≤f（3）的解集为（）A．（﹣1，3）B．[﹣1，3]C．（﹣∞，﹣1）∪（3，+∞）D．[﹣1，0）∪（0，2）∪（2，3] 11．（5分）一批材料可以建成200m长的围墙，现用这些材料在一边靠墙的地方围成一块矩形场，中间隔成3个面积相等的矩形（如图），则围成的矩形最大总面积为（）A．100m2B．10000m2C．2500m2D．6250m212．（5分）若函数f（x）＝log4（mx2+2x+3）的最小值为0，则m的值为（）A．B．C．3D．2二、填空题：本大题共4小题，每小题5分．13．（5分）已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）＝log2x，则f（x）＞0的解集为．14．（5分）设f（x）＝，求：f（0）+f（1）；f（﹣1）+f（2）；f（﹣2）+f（3），由此可以猜想出的一般性结论是．15．（5分）如图所示（算法流程图）的输出值x＝16．（5分）关于函数f（x）＝lg（x≠0），给出下列命题：①其图象关于y轴对称；②当x＞0时，f（x）是增函数；当x＜0时，f（x）是减函数；③f（x）在区间（﹣1，0），（2，+∞）上是增函数；④f（x）的最小值是lg2；⑤f（x）既无最大值，也无最小值．其中正确的序号是．三、解答题17．（12分）已知全集M＝{1，m，3+（m2﹣5m﹣6）i}，集合N＝{x|x2﹣2x﹣3＝0}，若M∩N＝{3}，求M∪N．18．（12分）已知函数f（x）＝x|m﹣x|，且f（4）＝0．（1）求实数m的值；（2）出函数f（x）的单调区间；（3）若方程f（x）＝a只有一个实根，确定a的取值范围．19．（12分）已知定义在（0，+∞）上的函数f（x）对任意正实数x、y恒有①f（2）＝1；②当x＞1时，f（x）＞0；③f（）＝f（x）﹣f（y）．（1）试判断函数f（x）的单调性；（2）若f（t）+f（t﹣3）≤2，试求t的取值范围．20．（12分）某车间为了制定工时定额，需要确定加工零件抽用时间，为此做了四次试验，得到的数据如下：（1）画出散点图；（2）求出回归方程；（3）根据回归方程估计加工10个零件需要多少个小时．（参考公式：＝＝，＝﹣）21．（12分）NBA决赛期间，某高校对学生是否收看直播进行调查，将得到的数据绘成如下的2×2列联表，但部分字迹不清：将表格填写完整，试说明是否收看直播与性别是否有关？附：考生在题（22）（23）（24）中任选一题作答，如果多做，则按所做的第一题计分．做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑．[选修4-1：几何证明选讲] 22．（10分）已知△ABC中，AB＝AC，D是△ABC外接圆劣弧上的点（不与点A，C重合），延长BD至E．（1）求证：AD的延长线平分∠CDE；（2）若∠BAC＝30°，△ABC中BC边上的高为1+，求△ABC外接圆的面积．[选修4-4：坐标系与参数方程]23．已知极坐标的极点在平面直角坐标系的原点O处，极轴与x轴的正半轴重合，且长度单位相同．直线l的极坐标方程为：ρ＝，点P（2cosα，2sinα+2），参数α∈[0，2π]．（1）求点P轨迹的直角坐标方程；（2）求点P到直线l距离的最大值．[选修4-5：不等式选讲]24．已知函数f（x）＝|x+7|+|x﹣1|，对任意实数x，不等式f（x）≥m恒成立．（1）求实数m的取值范围；（2）当m取最大值时，解关于x的不等式：|x﹣3|﹣2x≤2m﹣12．2015-2016学年辽宁省抚顺市重点高中协作校高二（下）期末数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．【解答】解：A＝{x|（x﹣1）2＜4}＝{x|﹣2＜x﹣1＜2}＝{x|﹣1＜x＜3}，B＝{x||x|＞1}＝{x|x＞1或x＜﹣1}，则∁R B＝{x|﹣1≤x≤1}，则A∩（∁R B）＝{x|﹣1＜x≤1}，故选：A．2．【解答】解：＝f（log2）＝f（log22﹣2）＝f（﹣2）＝3﹣2＝，故选：B．3．【解答】解：∵对任意实数x1≠x2，都有＞0成立，∴对任意实数x，函数f（x）＝是增函数，∵a＞0且a≠1，∴，∴1＜a．∴a的取值范围是（1，]．故选：C．4．【解答】解：函数f（x）＝|x|﹣ax﹣1仅有一个负零点，就是方程|x|＝ax+1仅有一个负根，即函数y＝|x|与y＝ax+1只有一个x＜0时的交点．如图：由图象可知a≥1时，函数f（x）＝|x|﹣ax﹣1仅有一个负零点，故选：D．5．【解答】解：∵复数z满足，∴z＝＝＝∴复数的共轭复数是故选：B．6．【解答】解：＝×（4+2+3+5）＝3.5，＝×（49+26+39+54）＝42，∴42＝9.4×3.5+，解得＝9.1．∴回归方程为＝9.4x+9.1．当x＝6时，＝9.4×6+9.1＝65.5．故选：D．7．【解答】解：根据题意，计算的K2≈3.918，经查临界值表知P（K2≥3.841）≈0.05，所以，有0.05的几率说明这两个变量之间的关系是不可信的，即有95%的把握认为“爱好这项运动与性别有关”．故选：A．8．【解答】解：∵f（x）＝x|x|∴f（﹣x）＝﹣x|x|＝﹣f（x）∴函数f（x）＝x|x|为奇函数，排除A，B，当x＞0时，y＝x2，根据y＝x2的图象排除D故选：C．9．【解答】解：用三段论形式推导一个结论成立，大前提应该是结论成立的依据，∵由四边形ABCD为矩形，得到四边形ABCD的对角线相等的结论，∴大前提一定是矩形的对角线相等，故选：B．10．【解答】解：∵函数f（x）＝log a x2+a|x|，∴f（﹣x）＝f（x），故函数为偶函数，当x＞0时，f（x）＝log a x2+a x，由f（﹣3）＝f（3）＜f（4），故a＞1，函数在（0，+∞）上为增函数，若f（x2﹣2x）≤f（3），则﹣3≤x2﹣2x＜0，或0＜x2﹣2x≤3，解得：x∈[﹣1，0）∪（0，2）∪（2，3]，故选：D．11．【解答】解：设每个小矩形的高为am，则长为b＝（200﹣4a）m，记面积为Sm2则S＝3ab＝a•（200﹣4a）＝﹣4a2+200a（0＜a＜50）∴当a＝25时，S max＝2500（m2）∴所围矩形面积的最大值为2500m2故选：C．12．【解答】解：若函数f（x）＝log4（mx2+2x+3）的最小值为0，则函数t＝mx2+2x+3的最小值为1，故，解得：m＝，故选：B．二、填空题：本大题共4小题，每小题5分．13．【解答】解：设x＜0，则﹣x＞0，∵当x∈（0，+∞）时，f（x）＝log2x，∴f（﹣x）＝log2（﹣x），∵f（x）是奇函数，∴f（x）＝﹣f（﹣x）＝﹣log2（﹣x），①当x∈（0，+∞）时，f（x）＞0，即log2x＞0，解得1＜x，②当x∈（﹣∞，0）时，f（x）＞0，即﹣log2（﹣x）＞0，则log2（﹣x）＜0＝log21，解得0＞x＞﹣1，综上，不等式的解集是（1，+∞）∪（﹣1，0）．故答案为：（1，+∞）∪（﹣1，0）．14．【解答】解：f（0）+f（1）＝+＝＝；f（﹣1）+f（2）＝+＝+＝；f（﹣2）+f（3）＝+＝，猜想出的一般性结论是若．故答案为：若．15．【解答】解：模拟执行程序框图，可得x＝1，满足条件x是奇数，x＝2，不满足条件x是奇数，x＝4，不满足条件x＞8，x＝5，满足条件x是奇数，x＝6，不满足条件x是奇数，x＝8，不满足条件x＞8，x＝9，满足条件x是奇数，x＝10，不满足条件x是奇数，x＝12，满足条件x＞8，输出x的值为12．故答案为：12．16．【解答】解：∵函数f（x）＝lg（x≠0），f（﹣x）＝lg＝lg＝f（x），故函数为偶函数，其图象关于y轴对称；故①正确；当x＞0时，f（x）＝lg，在（0，1]上为减函数，在[1，+∞）上是增函数；当x＜0时，f（x）＝lg，在（﹣∞，﹣1]上为减函数，在[﹣1，0）上是增函数；故②错误，③正确；当x＝±1时，函数取最小值lg2，无最大值，故④正确，⑤错误；故答案为：①③④三、解答题17．【解答】解：∵N＝{x|x2﹣2x﹣3＝0}＝{﹣1，3}，（2分）而M∩N＝{3}，∴m≠﹣1且3+（m2﹣5m﹣6）i＝3或m＝3，（6分）∴m＝6或m＝3，（8分）若m＝6，则M＝{1，6，3}，∴M∪N＝{﹣1，1，3，6}，（10分）若m＝3，则M＝{1，3，3﹣12i}，∴M∪N＝{﹣1，1，3，3﹣12i}．（12分）18．【解答】解：（1）函数f（x）＝x|m﹣x|，且f（4）＝0．得4|m﹣4|＝0，解得m＝4；（2）由（1）得f（x）＝x|4﹣x|，当x≥4时，f（x）＝x2﹣4x＝（x﹣2）2﹣4，对称轴x＝2在区间[4，+∞）的左边，f（x）在[4，+∞）递增；当x＜4时，f（x）＝x（4﹣x）＝﹣（x﹣2）2+4，可得f（x）在（﹣∞，2）递增；在（2，4）递减．综上可得f（x）的递增区间为（﹣∞．，2），（4，+∞）；递减区间（2，4）；（3）由f（x）的图象可知，当a＜0或a＞4时，f（x）的图象与直线y＝a只有一个交点，方程f（x）＝a只有一个实根，即a的取值范围是（﹣∞，0）∪（4，+∞）．19．【解答】解：（1）任取x1，x2∈（0，+∞），且x1＜x2则＞1，故f（）＞0，即f（x2）﹣f（x1）＞0 （3分）∴f（x2）＞f（x1）所以f（x）为（0，+∞）上的增函数．（5分）（2）∵f（2）＝f（）＝f（4）﹣f（2）∴f（4）＝2f（2）＝2从而f（t）+f（t﹣3）≤f（4）即f（t）≤f（），∵f（x）为（0，+∞）上的增函数，∴（8分）解得3＜t≤4故t的取值范围是（3，4]（12分）20．【解答】解：（1）作出散点图如下：（4分）（2）由题意，b＝＝0.7a＝3.5﹣0.7×3.5＝1.05于是回归方程y＝0.7x+1.05；（10分）（3）由题意，x＝10时，y＝0.7×10+1.05＝8.05答：根据回归方程，加工能力10个零件，大约需要8.05小时．（12分）21．【解答】解：；（10分）所以有99%的把握认为是否收看直播与性别有关，（12分）考生在题（22）（23）（24）中任选一题作答，如果多做，则按所做的第一题计分．做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑．[选修4-1：几何证明选讲] 22．【解答】（1）证明：如图，设F为AD延长线上一点，A､B､C､D四点共圆．∴∠CDF＝∠ABC，又AB＝AC，∴∠ABC＝∠ACB，且∠ADB＝∠ACB，∴∠ADB＝∠CDF对顶角∠EDF＝∠ADB，故∠EDF＝∠CDF，即AD的延长线平分∠CDE，…（4分）（2）解：设O为外接圆圆心，连接AO比延长交BC于H，交⊙O于点M，连接OC，∵AB＝AC，∴＝，∴AH⊥BC．∴∠OAC＝∠OAB＝∠BAC＝×30°＝15°，∴∠COH＝2∠OAC＝30°，设圆半径为r，则OH＝OC•cos30°＝r，∵△ABC中BC边上的高为1+，∴AH＝OA+OH＝r+r＝1+，解得：r＝1，∴△ABC的外接圆的面积为：π（10分）[选修4-4：坐标系与参数方程]23．【解答】解：（1）设点P（x，y），∵P（2cosα，2sinα+2），∴，且参数α∈[0，2π]，所以点P的轨迹的直角坐标方程为x2+（y﹣2）2＝4．…（3分）（2）∵ρ＝，∴＝5，∴，即．∴直线l的直角坐标方程为．…（6分）由（1）知点P的轨迹方程为x2+（y﹣2）2＝4，是圆心为（0，2），半径为2的圆．圆心到直线的距离d＝＝4，点P所在的圆与直线l相离，…（9分）∴点P到直线l距离的最大值4+2＝6．…（10分）[选修4-5：不等式选讲]24．【解答】解：（1）∵f（x）＝|x+7|+|x﹣1|≥|x+7﹣（x﹣1）|＝8，不等式f（x）≥m恒成立，可得8≥m，即m≤8．（2）由（1）知m的最大值为8，∴原不等式就是|x﹣3|﹣2x≤4，即|x﹣3|≤2x+4．当x＜3时，有3﹣x≤2x+4，解得：x≥﹣，∴﹣≤x＜3；当x≥3时，有x﹣3≤2x+4，解得：x≥﹣7，∴x≥3；所以不等式的解集为{x|x≥﹣}．。

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.如图所示的韦恩图中，A 、B 是非空集合，定义A B *表示阴影部分集合．若,x y R ∈，{|A x y ==，{|3,0}x B y y x ==>，则A B *=（ ）A ．(2,)+∞B ．[0,1)(2,)+∞C ．[0,1](2,)+∞D ．[0,1][2,)+∞【答案】C考点：1、集合的运算；2、新定义问题．2.设集合{,}A a b =，{0,1,2}B =，则从A 到B 的映射的个数有（ ） A ．3 B ．6 C ．8 D ．9 【答案】D 【解析】试题分析：根据映射的定义，必须使A 中的每个元素在集合B 中都有唯一的确定的一个元素与之对应，而A 中的每个元素在集合B 中的像都有3种可能，A 中元素有2个，故从A 到B 的映射的个数有239=，故D 为正确答案． 考点：映射的定义．3.设,αβ是两个不同的平面，l 是一条直线，以下命题正确的是（ ） A ．若,l ααβ⊥⊥，则l β⊂ B ．若,l ααβP P ，则l β⊂ C ．若,l ααβ⊥，则l β⊥ D ．若,l ααβ⊥，则l β⊥【答案】C考点：直线与平面的位置关系．4.若11223420,3420x y x y --=--=，则过1122(,),(,)A x y B x y 两点的直线方程是（ ） A ．4320x y +-= B ．3420x y --= C ．4320x y ++= D ．3420x y -+= 【答案】B 【解析】试题分析：由11223420,3420x y x y --=--=知，直线方程3420x y --=经过1122(,),(,)A x y B x y 两点，故B 为正确答案． 考点：直线方程的一般式． 5.设0.3 1.6211.6,log ,0.89a b c ===，则,,a b c 的大小关系是（ ） A ．a b c << B ．b a c << C ．b c a << D ．c a b << 【答案】C 【解析】试题分析：结合指数函数和对数函数的图象知，1,0,01a b c ><<<，所以b c a <<． 考点：1、指数函数的图象和性质；2、对数函数的图象和性质．6.函数1y x=的定义域是（ ） A ．[4,0)(0,1)- B ．[4,0)(0,1]- C ．(4,0)(0,1)- D ．(,4)[2,)-∞-+∞【答案】A 【解析】考点：定义域的求法．7.某几何体的三视图如图所示，则该几何体的表面积为（ ）A B ． C ．1)π+ D ．2)π 【答案】B 【解析】试题分析：由三视图知，该几何体是上、下部为共底面的圆锥体的组合体，且该圆锥的底面半径为1，高为1，所以该几何体的表面积为21S π=⋅⋅=，故B 为正确答案． 考点：1、空间几何体的三视图；2、表面积的计算．8.若函数()||f x x =(0)a >没有零点，则a 的取值范围是（ ）A ．)+∞B ．(2,)+∞C ．(0,1)(2,)+∞D ．(0,1)(2,)+∞【答案】D 【解析】试题分析：令()||0f x x ==||x =；而y =，圆心在原点的圆的上半部分，||y x =是以(为端点的折线；在同一坐标系中画出它们的图象，如下图：根据图象知，由于两曲线没有公共点，故圆心到折线的距离小于1，所以a 的取值范围是(0,1)(2,)+∞U ，故D 为正确答案． 考点：1、函数零点问题；2、数形结合思想．9.若点00(,)P x y 在圆222:C x y r +=的内部，则直线200xx yy r +=与圆C 的位置关系是（ ） A ．相交 B ．相切 C ．相离 D ．无法确定 【答案】C考点：1、点与圆的位置关系；2、直线与圆的位置关系．10.已知函数()|lg |f x x =，若0a b <<，且()()f a f b =，则4a b +的取值范围是（ ） A ．(4,)+∞ B ．[4,)+∞ C ．(5,)+∞ D ．[5,)+∞ 【答案】C 【解析】试题分析：因为()()f a f b =，所以a b =（舍去），或1b a =，所以44a b a a+=+；又0a b <<，所以01a b <<<，令()4f a a a=+，由对勾函数的性质知函数()f a 在()0,1上为减函数，所以()()41151f a f >=+=，即4a b +的取值范围是(5,)+∞． 考点：1、对数的运算性质；2、对数函数的最值问题．11.已知半径为5的球O 被互相垂直的两个平面所截，得到的两个圆的公共弦长为4，若其中的一圆的半径为4，则另一圆的半径为（ ）A C ． 【答案】D考点：1、球的性质；2、两平面垂直的性质．【技巧点晴】本题主要考查的是球的有关概念以及两平面垂直的性质，属于中档题；可以从三个圆心上找关系，三个圆心以及公共弦的中点围成的四边形为矩形，矩形对角线相等是解决本题的关键；先求出球心到半径为4的圆的距离，再由勾股定理就可以求出另一圆的半径．12.已知函数()f x 的图象如图：则满足2(2)(lg(6120))0xf f x x ⋅-+≤的x 的取值范围是（ ）A ．(,1]-∞B ．[1,)+∞C ．[0,)+∞D ．(,2]-∞ 【答案】A 【解析】试题分析：2(2)(lg(6120))0x f f x x ⋅-+≤等价于2(2)(lg(6120))x f f x x -+和两个函数值一个大于等于0，另一个小于等于0；而220,6120111xx x >-+≥，即()2lg 61202x x -+>，由函数()f x 的图象知，2(2)(lg(6120))0x f f x x ≥-+<0,，即22x ≤，解得1x ≤，故A 为正确答案．考点：1、函数的图象和性质；2、零点问题．【思路点晴】本题主要考查的是函数的图象和性质、函数的零点存在性定理，属于难题；本题的关键是根据2(2)(lg(6120))0xf f x x ⋅-+≤知两函数值异号，或者其中一个为0；直接解不等式是不可取的，应先根据对数函数的图象和性质求出()2lg 61202x x -+>，即2(lg(6120))0f x x -+<；再结合函数()f x 的图象得到22x ≤，解出即可．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13.设(0)()ln (0)x e x f x x x ⎧≤=⎨>⎩，则1[()]2f f -= ．【答案】12-考点：分段函数求值．14.正六棱柱111111ABCDEF A B C D E F -，侧棱长为1，则动点从A 沿表面移到点1D 时的最短的路程是 ．【解析】试题分析：如下图所示，作出正六棱柱111111ABCDEF A B C D E F -的展开图，如果动点从A 经侧面通过11,BB CC 移到点1D 时，=；如果动点从A 经经11A B沿上底面移到点1D 时，根据题目条件，111114BD BB B D =+=+=，=；<考点：1、棱锥的展开图；2、最值问题．15. 若过点(1,1)P -作圆22220x y kx y k ++++=的切线有两条，则实数k 的取值范围是 ．【答案】1k <<-或0k <<考点：1、圆的一般方程；2、点和圆的位置关系．【易错点晴】本题主要考查的是圆的一般方程、点和圆的位置关系，属于中档题；同学一般看完题目就知道点在和圆的位置关系是点(1,1)P -在圆22220x y kx y k ++++=外，解出关于实数k 的取值范围；往往会忽略圆的一般方程的限制条件，方程220x y Dx Ey F ++++=表示圆的条件是2240D E F +->． 16.一个长为8cm ，宽为6cm ，高为10cm 的密封的长方体盒子中放一个半径为1cm 的小球，无论怎样摇动盒子，则小球在盒子中总不能到达的空间的体积为 3cm ． 【答案】58803π- 【解析】试题分析：在长方体的8个顶点处的单位立方体空间内，小球不能到达的空间为：3314481(1)8833ππ⎡⎤-⨯=-⎢⎥⎣⎦；除此之外，在以长方体的棱为一条棱的12个正四棱柱空间内，小球不能到达的空间为2221114118(1)84114(1)44116(1)6444πππ⎡⎤⎡⎤⎡⎤⨯⨯⨯-⨯⨯+⨯⨯⨯-⨯⨯+⨯⨯⨯-⨯⨯⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦7218π=-，故小球不能到达的空间为458(8)72188033πππ-+-=-． 考点：1、球的体积；2、空间想象能力．【思路点晴】本题考查的知识点是球的体积公式、棱柱的体积、分类讨论的数学思想等，属于难题；建立良好的空间想象能力是解答本题的关键，小球在盒子中不能到达的空间要分两种情况，在长方体顶点处的小正方体中，其体积等于小正方体的体积减去球的体积；在棱长处对应的长方体中，其体积等于这些小正四棱柱的体积减去球的半径为底面半径，以长方体的棱长为高的圆柱，其他空间小球均能到达，综合后即可得结果．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分10分）解方程：122log (44)log (23)x x x ++=+- 【答案】2x =．考点：1、对数运算；2、指数运算． 18.（本小题满分12分）设()f x 是定义在[3,3]-上的偶函数，当03x ≤≤时，()f x 单调递减，若(12)()f m f m -<成立，求m 的取值范围．【答案】实数m 的取值范围是11123m m -≤<<≤或． 【解析】试题分析：因为()f x 是定义在[3,3]-上的偶函数，当03x ≤≤时，()f x 单调递减，则当30x -≤≤时，()f x 单调递增；不等式(12)()f m f m -<成立等价于12m m ->，而函数的定义域为[3,3]-，所以3123,33m m -≤-≤-≤≤，联立求解即可．试题解析：解|12|||312333m m m m ->⎧⎪-≤-≤⎨⎪-≤≤⎩……………………………………4分考点：1、函数的性质综合应用；2、不等式的解． 19.（本小题满分12分）如图，四面体ABCD 中，O 是BD 的中点，ABD ∆和BCD ∆均为等边三角形，2AB =，AC =．（Ⅰ）求证：AO ⊥平面BCD ； （Ⅱ）求O 点到平面ACD 的距离．【答案】（Ⅰ）证明过程详见试题解析；（Ⅱ）O 点到平面ACD【解析】试题分析：（Ⅰ）证明：连结OC ，由已知条件得AO BD ⊥；根据2,AB AC ==求出AO CO ==． 由勾股定理的逆定理得AO OC ⊥，所以AO ⊥平面BCD ． （Ⅱ）解：设点O 到平面ACD 的距离为h ． 用等体积转化思想O ACD A OCD V V --=，即可求得点O 到平面ACD 的距离． 试题解析:（Ⅰ）证明：连结OC ．∵ABD ∆为等边三角形，O 为BD 的中点，∴AO BD ⊥． ∵ABD ∆和CBD ∆为等边三角形，O 为BD的中点，2,AB AC ==，ABCD O考点：1、直线与平面垂直的判定定理；2、三棱锥的体积． 20.（本小题满分12分）若已知直线l 在两坐标轴上的截距相等，且(4,3)P 到直线l 的距离为，求直线l 的方程．【答案】直线l 的方程为10x y +-=或130x y +-=或60x y ⎛--= ⎝． 【解析】试题分析：直线l 在两坐标轴上的截距相等，分截距为0和截距不为0两种情况进行讨论；当截距为0时设直线:l y kx =，当截距不为0时设:0l x y a +-=，再结合点(4,3)P 到直线l 的距离为即可求出直线l 的方程．试题解析：（Ⅰ）设:0l x y a +-=113a a =⇒==或……………………5分（Ⅱ）设:l y kx =即0kx y -=，∴6d k ==⇒=-±10分综上，直线方程：10x y +-=或130x y +-=或60x y ⎛-±-= ⎝………………12分. 考点：1、直线方程的求法；2、点到直线的距离公式． 21.（本小题满分12分）已知函数22(1)()714(1)x ax x f x a x a x ⎧-+≤⎪=⎨-+>⎪⎩，若存在12,x x R ∈，且12x x ≠，使得12()()f x f x =． （Ⅰ）求实数a 的取值集合A ；（Ⅱ）若a A ∈，且函数2()lg[(3)4]g x ax a x =+++的值域为R ，求实数a 的取值范围．【答案】（Ⅰ）实数a 的取值集合为{|235}A x x x =<<<或；（Ⅱ）实数a 的取值范围是01a ≤≤．而当1x ≤时：22()()24a a f x x =--+ ①当12a <时满足题意，即2a < ②当12a ≥时，因1x ≤时()1f x a ≤-，而1x >时2()714f x a a >-+ 只需21714a a a ->-+，此时：35a <<综上：{|235}A x x x =<<<或（写成区间亦可(,2)(3,5)A =-∞）…………………………6分（Ⅱ）①当0a =时()lg(34)g x x =+满足题意 ②当20019(3)160a a a a a >⎧⇔<≤≥⎨∆=+-≥⎩或． 则019,a a a A ≤≤≥∈或又．综上01a ≤≤……………………………………………………………………………………12分.考点：1、函数的性质；2、恒成立问题；3、分类讨论的数学思想．【易错点晴】本题主要考查的知识点是函数的性质、恒成立问题、分类讨论等的综合，属于中档题；分类讨论，利用二次函数的单调性，结合存在12,x x R ∈，且12x x ≠，使得12()()f x f x =，即可求出实数a 的取值范围；函数2()lg[(3)4]g x ax a x =+++的值域为R ，即()234y ax a x =+++为一次函数，或二次函数能取遍大于等于0的所有数；本题两问都需要分类讨论，不小心就容易漏算．22.（本小题满分10分）已知⊙O ：221x y +=和定点(2,1)A ，由⊙O 外一点(,)P x y 向⊙O 引切线PQ ，切点为Q ，且满足||2||PQ PA =．（Ⅰ）求动点P 的轨迹方程C ；（Ⅱ）求线段PQ 长的最小值；（Ⅲ）若以⊙P 为圆心所做的⊙P 与⊙O 有公共点，试求P 半径取最小值时的P 点坐标．【答案】（Ⅰ）动点P 的轨迹方程C 为2233168210x y x y +--+=；（Ⅱ）线段PQ 长的最小值是P 点坐标为．试题解析：（Ⅰ）||2||PQ PA =⇒=2233168210x y x y ⇒+--+=…………………………………………………………………4分 （Ⅱ）∵||2||PQ PA = ∴min min ||2||PQ PA =而轨迹C 的方程228417()()339x y -+-=，圆心设为84(,)33C ，半径r =而min ||||PA r AC =-==考点：1、圆的方程；2、圆的切线问题；3、圆与圆的位置关系．【思路点晴】本题主要考查的是圆的标准方程、直线与圆的位置关系、圆与圆的位置关系，属于难题；由题意知点(,)P x y 满足||2||PQ PA =，结合两点间的距离公式即可求出动点P 的轨迹方程C ；根据min ||||PA r AC =-，先求出PA 长的最小值，进而可以求出线段PQ 长的最小值，联立线段OC 与⊙C 的方程即可求出点P 的坐标．：。

某某市协作校2015—2016下学期高一年级期末考试数学试卷注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟．2.第Ⅰ卷选项涂在答题卡上，第Ⅱ卷答在答题纸上．第I 卷（选择题 共60分）一、选择题（本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的） 1.已知tan sin <⋅θθ,那么角θ是( )A.第一或第二象限角B.第二或第三象限角C.第三或第四象限角D.第一或第四象限角 2.点)1,2,3(-M 关于yoz面对称的点的坐标是( )A.)1,2,3(-B.)1,2,3(--C.)1,2,3(-D.)1,2,3(--3.某小组有２名男生和２名女生,从中任选２名同学去参加演讲比赛，在下列选项中,互斥而不对立的两个事件是( )A.“至少有1名女生”与“都是女生”B.“至少有1名女生”与“至多有1名女生”C.“恰有1名女生”与“恰有2名女生”D.“至少有1名男生”与“都是女生” 4.已知角βα,均为锐角,且10103sin ,552cos ==βα,则βα-的值为 ( ) A.3π B.4πC.4π-D.44ππ-或5.如图,在ABC ∆中,点D 是边BC 的中点,点G 在AD 上,且是ABC ∆的重心,则用向量ACAB ,表示BG为( )A.AC AB BG 3132+-= B.AC AB BG 3231+-= C.AC AB BG 3132-= D.AC AB BG 3132+=6.已知回归直线的斜率的估计值为 1.23,样本点的中心为(4,5),则回归直线方程为 ( )A.523.1ˆ+=x yB.423.1ˆ+=x yC.23.108.0ˆ+=x yD.08.023.1ˆ+=x y7.已知圆心)0,0)(,(<<b a b a 在直线12+=x y 上的圆,其圆心到x 轴的距离恰好等于圆的半径,在y 轴上截得的弦长为52,则圆的方程为( )A.25)5()3(22=+++y x B.9)3()2(22=+++y x C.949)37()32(22=-+-y x D.949)37()32(22=+++y x 8.甲、乙两名同学8次数学测验成绩如茎叶图所示,21,x x 分别表示甲、乙两名同学8次数学测验成绩的平均数,21,s s 分别表示甲、乙两名同学8次数学测验成绩的标准差,则有 ( )A.2121,s s x x <>B.2121,s s x x <=C.2121,s s x x ==D.2121,s s x x ><9.如图所示的程序框图,它的输出结果是( ) A.-1B.0C.1D.1610.已知函数)0)(sin()(>+=ωϕωx x f 的部分图象如图所示,下面结论正确的个数是( )①函数)(x f 的最小正周期是π2②函数)(x f 的图象可由函数x x g 2sin )(=的图象向左平移3π个单位长度得到 ③函数)(x f 的图象关于直线12π=x 对称④函数)(x f 在区间⎥⎦⎤⎢⎣⎡6,12ππ上是增函数 A.3 B.2 C.1 D.011.已知10),4,2(),1,(,<==∈AB AC k AB R k 若,则ABC ∆是钝角三角形的概率是( )A.61 B.31 C.32 D.65 12.已知点P 是圆1)22(22=-+y x C ：上的一个动点,点Q 是直线0=-y x l ：上的一个动点,O 为坐标原点,则向量OQ 在向量OP 上的射影的数量的最大值是 ( ) A.3 B.222+ C.32 D.1第II 卷（非选择题 共90分）二、填空题（本大题共4小题,每小题5分,共20分）13.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于70分为合格,则合格人数是.14.已知平面向量a 与b满足4,,2,1π=〉-+〈=-=+b a b a b a b a 且,则=-b a 5.15.若41)6sin(=+πx ，则=++-+-)32cos()3(sin )65sin(2πππx x x .16.关于平面向量，有下列四个命题：①若c a c b b a=⋅=⋅则,.②),,2(),1,1(x b a ==若a b b a 24-+与平行，则2=x .③非零向量b a 和满足b a b a -==，则b a a +与的夹角为060.④点)1,4(),3,1(-B A ，与向量AB 同方向的单位向量为)54,53(-. 其中真命题的序号为.（写出所有真命题的序号）三、解答题（本大题共6小题,共70分,解答题应写出必要的文字说明、证明过程或演算步骤）17.（本小题满分10分）“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响,从而不顾及交通安全.某校对全校学生过马路方式进行调查,在所有参与调查的人中，“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如下表所示：跟从别人闯红灯 从不闯红灯 带头闯红灯男生800450200(I)在所有参与调查的人中,用分层抽样的方法抽取n 人,已知“跟从别人闯红灯”的人中抽取45 人,求n 的值；(II)在“带头闯红灯”的人中,将男生的200人编号为1,2，…，200；将女生的300人编号为201,202，…，500,用系统抽样的方法抽取4人参加“文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均是女生的概率.18.（本小题满分12分）设连续掷两次骰子得到的点数分别为n m 、,令平面向量)3,1(),,(-==b n m a.(I)求使得事件“b a⊥”发生的概率；(II)求使得事件“b a≤”发生的概率；(III)求使得事件“直线x nmy =与圆1)3(22=+-y x 相交”发生的概率. 19.（本小题满分12分）已知)sin ,(sin ),cos ,(sin x x b x x a == ,函数b a x f⋅=)(. (I)求)(x f 的对称轴方程；(II)求使1)(≥x f 成立的x 的取值集合；(III) 若对任意实数,3,6⎥⎦⎤⎢⎣⎡∈ππx 不等式2)(<-m x f 恒成立，某某数m 的取值X 围. 20.（本小题满分12分）已知向量⎥⎦⎤⎢⎣⎡∈-==2,0)2sin ,2(cos ),23sin ,23(cos πx x x b x x a 且 . (I)求b a b a+⋅及；(II)若b a b a x f +-⋅=λ2)(的最小值是23-,某某数λ的值.21．（本小题满分12分）在直角坐标系xoy 中,圆422=+y x O ：与x 轴负半轴交于点A ,过点A 的直线AN AM ,分别与圆O 交于N M ,两点.(I)若21,2-==AN AM k k ,求AMN ∆的面积； (II)过点)5,33(-P 作圆O 的两条切线,切点分别为F 、E ,求PF PE ⋅.22.（本小题满分12分）在平面直角坐标系中,两点),(),,(222111y x P y x P 间的“L -距离”定义为212121y y x x P P -+-=.现将边长为1的正三角形ABC 按如图所示的方式放置,其中顶点A 与坐标原点重合.记边AB 所在直线的斜率为k ,30≤≤k .求：当BC 取最大值时,边AB 所在直线的斜率的值.某某市协作校2015—2016下学期高一年级期末考试数学试卷答案一、选择题（每题5分，共60分）1—5 BDCCA 6—10 DBBAC 11—12 DA 二、填空题（每题5分，共20分）13． 600 14. 10 15.163316. ②④ 三、解答题（共70分，共6题） 17．（本小题满分10分） 解：（I ）由题意得,30015010020045080010080045+++++=+n,100=∴n .…………2分 （II ）由系统抽样得到的分别为100，225，350，475. …………4分 其中100号为男生，设为A ，而225，350，475都为女生，分别设为321,,B B B ， 从这4人中任选取2人所有的基本事件为)(),(),(),(),(),(323121321B B B B B B AB AB AB ，共有6个. …………6分这两人均是女生的基本事件为)(),(),(323121B B B B B B ，共有3个. …………8分 故所求事件的概率为2163==P . …………10分18．（本小题满分12分） 解：（I ）由题意知,{}{}6,5,4,3,2,1,6,5,4,3,2,1∈∈n m , 故),(n m 所有可能的取法有36种. …………3分使得03=-⊥n m b a 即,共有2种(3,1)、(6,2)所以事件b a ⊥发生的概率为181362=. …………6分（II ）10,22≤+≤n m b a 即,共有6种(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1) 所以事件b a ≤发生的概率为61366=. …………9分（III ） 直线x nmy =与圆1)3(22=+-y x 相交，即1322<+=nm m d即228n m <，共有5种(1,3)、(1,4)、(1,5)、(1,6)、(2,6) 所以直线x n m y =与圆1)3(22=+-y x 相交发生的概率为365. …………12分19．（本小题满分12分） 解：（I ）x x x x x b a x f 2sin 2122cos 1cos sin sin )(2+-=⋅+=⋅= …………1分21)42sin(22+-=πx …………2分 令Z k k x ∈+=-,242πππ,解得Z k k x ∈+=,832ππ. )(x f ∴的对称轴方程为Z k k x ∈+=,832ππ. …………4分 （II ） 由1)(≥x f 得121)42sin(22≥+-πx ,即22)42sin(≥-πx …………5分 Z k k x k ∈+≤-≤+∴,2434224πππππ. 故x 的取值集合为⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k x k x ,24|ππππ. …………7分 （III ）1254212,3,6πππππ≤-≤∴⎥⎦⎤⎢⎣⎡∈x x …………8分又⎥⎦⎤⎢⎣⎡=2,0sin π在x y 上是增函数, 125sin)42sin(12sinπππ≤-≤∴x …………9分 又426)46sin(125sin+=+=πππ ⎥⎦⎤⎢⎣⎡∈∴3,6)(ππx x f 在时的最大值是4332142622)(max +=++⨯=x f …10分 2)(<-m x f 恒成立,2)(max ->∴x f m ,即453->m …………11分 ),453(+∞-∴的取值范围是实数m . …………12分20.（本小题满分12分） 解：（I ）x xx x x b a 2cos 2sin 23sin 2cos 23cos =⋅-⋅=⋅ . …………2分22)2sin 23(sin )2cos 23(cos xx x x b a -++=+x x x cos 2cos 22cos 222==+=…………4分x b a x x cos 20cos 2,0=+∴≥∴⎥⎦⎤⎢⎣⎡∈ π. …………5分（II ）22221)(cos 21cos 4cos 2cos 42cos )(λλλλ---=--=-=x x x x x x f1cos 02,0≤≤∴⎥⎦⎤⎢⎣⎡∈x x π …………7分①若0<λ，当且仅当0cos =x 时，)(x f 取得最小值-1，与已知矛盾； ②若10≤≤λ，当且仅当λ=x cos 时，)(x f 取得最小值221λ--， 由23212-=--λ 解得21=λ或21-=λ（舍去）；③若1>λ，当且仅当1cos =x 时，)(x f 取得最小值λ41-， 由2341-=-λ 解得85=λ（舍去）； …………11分综上所述，21=λ. …………12分21.（本小题满分12分） 解：（I ）,21,2),0,2(-==-AN AM k k A 121,42--=+=∴x y AN x y AM 的方程为直线的方程为直线，5545164254=-==∴AM d AM O ，从而的距离到直线圆心.…………2分 55821==∴⊥∴-=⋅d AN AN AM k k AN AM …………4分 5165585542121=⨯⨯=⋅=∴∆AN AM S AMN . …………6分 (II)132)5()33(22=-+=PO344)132(222=-=-=OE PO133213234cos ==∠∴OPE …………8分又13111)1332(21cos 22cos cos 22=-=-∠=∠=∠OPE OPE FPE ………10分135281311)34(cos 2=⨯=∠=⋅∴FPE PF PE . …………12分 22．（本小题满分12分）解：设边AB 所在直线的倾斜角为θ，则⎥⎦⎤⎢⎣⎡∈3,0πθ))3sin(),3(cos(),sin ,(cos πθπθθθ++∴C B …………2分word11 / 11 )3sin(sin )3cos(cos πθθπθθ+-++-=∴BCθθθθcos 23sin 21sin 23cos 21-++= )6cos()6sin(πθπθ+++=…………6分⎥⎦⎤⎢⎣⎡∈+∴⎥⎦⎤⎢⎣⎡∈2,663,0πππθπθ )125sin(2)6cos()6sin(πθπθπθ+=+++=∴BC …………8分 ⎥⎦⎤⎢⎣⎡∈+∴⎥⎦⎤⎢⎣⎡∈43,1251253,0πππθπθ 2BC 12,2125取得最大值时，即当πθππθ==+∴， …………10分 此时12tan 112tan 26tan ,12tan tan 2ππππθ-=== k （或由)64tan(12tan πππ-=求k ） （舍去）或解得3232,12332--=-=-=∴k k k k 32-=∴k . …………12分。

2014-2015学年辽宁省协作校高一（上）期末数学试卷一、选择题（共12小题，每小题5分，满分60分）1．（5.00分）已知全集U={0，1，2，3，5，6，8}，集合A={1，5，8}，B={2}，则集合（∁U A）∪B=（）A．{0，2，3，6}B．{0，3，6}C．{1，2，5，8}D．∅2．（5.00分）已知空间两个点A，B的坐标分别为A（1，2，2），B（2，﹣2，1），则|AB|=（）A．18 B．12 C．D．3．（5.00分）已知直线y=（2a﹣1）x+2的倾斜角为钝角，则实数a的取值范围是（）A．a＜B．a＞C．a≤D．a≥4．（5.00分）一个圆柱的底面直径和高都等于4，则圆柱的表面积为（）A．24πB．16πC．20πD．64π5．（5.00分）已知直线l过圆x2+（y﹣3）2=4的圆心，且与直线x+y+1=0垂直，则l的方程是（）A．x+y﹣2=0 B．x﹣y+2=0 C．x+y﹣3=0 D．x﹣y+3=06．（5.00分）设m、n是两条不同的直线，α，β是两个不同的平面，则（）A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥α7．（5.00分）圆C1：（x﹣6）2+y2=1和圆C2：（x﹣3）2+（y﹣4）2=36的位置关系是（）A．外切B．相交C．内切D．内含8．（5.00分）正三角形ABC的边长为2，△ABC直观图（斜二测画法）的面积是（）A．B．C．D．29．（5.00分）给出下面4个命题①各侧面都是正方形的棱柱一定是正棱柱；②经过球面上不同的两点只能作球的一个大圆；③两条异面直线的平行投影可平行；④过平面外的一条直线，只能作一个平面和这个平面平行；其中正确的个数为（）A．1个 B．2个 C．3个 D．4个10．（5.00分）设f（x）=ah（x）+bg（x）+4，其中h（x），g（x）都是奇函数，a，b是不同时为零的常数，若f[lg（log310）]=5，则f[lg（lg3）]等于（）A．﹣5 B．7 C．3 D．﹣111．（5.00分）正四棱锥的顶点都在同一球面上，若该棱锥的侧棱长为2，底面边长为4，则该球的表面积是（）A．36πB．32πC．18πD．16π12．（5.00分）直线ax+by=1与圆x2+y2=1相交于A，B两点（其中a，b是实数），且∠AOB=120°（O是坐标原点），则点P（a，b）与点（1，1）之间距离的最大值为（）A．B．4 C．D．二、填空题（共4小题，每小题5分，满分20分）13．（5.00分）函数f（x）=e﹣x+x2+2x﹣2的零点个数为．14．（5.00分）如图所示一个几何体的三视图，则该几何体的体积为15．（5.00分）已知函数f（x+1）是偶函数，且当x≥1时，f（x）=，若实数a满足f（2a）＞f（a+1），则a的取值范围是．16．（5.00分）已知圆O：x2+y2=1和点A（﹣2，0），若存在定点B（b，0）（b ≠﹣2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则点P（b，λ）到直线（m+n）x+ny﹣2n﹣m=0距离的最大值为．三、解答题（共6小题，满分70分）17．（10.00分）已知直线l：ax+3y+1=0．（1）若直线l在两坐标轴上的截距相等，求a的值；（2）若直线l与直线x+（a﹣2）y+a=0平行，求a的值．18．（12.00分）在三棱锥S﹣ABC中，平面SAB⊥平面SBC，BC⊥SA，AS=AB，过A作AP⊥SB，垂足为F，点E、G分别是棱SA，SC的中点求证：（1）平面EFG∥平面ABC；（2）AB⊥BC．19．（12.00分）已知f（x）是定义在（0，+∞）上的减函数，满足f（x）+f（y）=f（x•y）．（1）求证：f（x）﹣f（y）=；（2）若f（2）=﹣3，解不等式f（1）﹣f（）≥﹣9．20．（12.00分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB=，BC=1，AA1=AC=2，E、F分别为A1C1、BC的中点．（1）求证：平面ABE⊥平面B1BCC1；（2）求证：C1F∥平面ABE；（3）求多面体A1B1C1﹣ABF的体积．21．（12.00分）已知点P（﹣2，3t﹣），Q（0，2t），（t∈R，t≠0）（1）当t=2时，求圆心在坐标原点且与直线PQ相切的圆的标准方程．（2）是否存在圆心在x轴上的定圆M，对于任意的非零实数t，直线PQ恒与定圆M相切，如果存在，求出圆M的标准方程，如果不存在，请说明理由．22．（12.00分）已知函数f（x）=a X，（a＞0且a≠1），若函数g（x）的图象和函数f（x）的图象关于直线y=x对称，且h（x）=g[（a﹣1）x+2]．（1）求h（x）的定义域；（2）当x∈[3，4]时，h（x）＞0恒成立，求a的取值范围．2014-2015学年辽宁省协作校高一（上）期末数学试卷参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5.00分）已知全集U={0，1，2，3，5，6，8}，集合A={1，5，8}，B={2}，则集合（∁U A）∪B=（）A．{0，2，3，6}B．{0，3，6}C．{1，2，5，8}D．∅【解答】解：∵全集∪={0，1，2，3，5，6，8}，集合A={1，5，8}，B={2}，∴∁U A={0，2，3，6}，则（∁U A）∪B={0，2，3，6}．故选：A．2．（5.00分）已知空间两个点A，B的坐标分别为A（1，2，2），B（2，﹣2，1），则|AB|=（）A．18 B．12 C．D．【解答】解：∵点A，B的坐标分别为A（1，2，2），B（2，﹣2，1），∴|AB|==3．故选：C．3．（5.00分）已知直线y=（2a﹣1）x+2的倾斜角为钝角，则实数a的取值范围是（）A．a＜B．a＞C．a≤D．a≥【解答】解：直线y=（2a﹣1）x+2斜率为2a﹣1，由其倾斜角为钝角，可得2a﹣1＜0，即a＜．故选：A．4．（5.00分）一个圆柱的底面直径和高都等于4，则圆柱的表面积为（）A．24πB．16πC．20πD．64π【解答】解：∵圆柱的底面直径等于4，∴圆柱的底面半径r=2，又∵圆柱的高l=4，∴圆柱的表面积S=2πr（r+l）=24π，故选：A．5．（5.00分）已知直线l过圆x2+（y﹣3）2=4的圆心，且与直线x+y+1=0垂直，则l的方程是（）A．x+y﹣2=0 B．x﹣y+2=0 C．x+y﹣3=0 D．x﹣y+3=0【解答】解：由题意可得所求直线l经过点（0，3），斜率为1，故l的方程是y﹣3=x﹣0，即x﹣y+3=0，故选：D．6．（5.00分）设m、n是两条不同的直线，α，β是两个不同的平面，则（）A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥α【解答】解：A．若m⊥n，n∥α，则m⊥α或m⊂α或m∥α，故A错误．B．若m∥β，β⊥α，则m⊥α或m⊂α或m∥α，故B错误．C．若m⊥β，n⊥β，n⊥α，则m⊥α，正确．D．若m⊥n，n⊥β，β⊥α，则m⊥α或m⊂α或m∥α，故D错误．故选：C．7．（5.00分）圆C1：（x﹣6）2+y2=1和圆C2：（x﹣3）2+（y﹣4）2=36的位置关系是（）A．外切B．相交C．内切D．内含【解答】解：因为圆C1：（x﹣6）2+y2=1的圆心坐标（6，0），半径为1，圆C2：（x﹣3）2+（y﹣4）2=36的圆心坐标（3，4），半径为6，所以圆心距为=5，因为5=6﹣1，所以两个圆的关系是内切．故选：C．8．（5.00分）正三角形ABC的边长为2，△ABC直观图（斜二测画法）的面积是（）A．B．C．D．2【解答】解：∵正△ABC的边长为2，∴正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=×=故选：C．9．（5.00分）给出下面4个命题①各侧面都是正方形的棱柱一定是正棱柱；②经过球面上不同的两点只能作球的一个大圆；③两条异面直线的平行投影可平行；④过平面外的一条直线，只能作一个平面和这个平面平行；其中正确的个数为（）A．1个 B．2个 C．3个 D．4个【解答】解：对于①，各侧面都是正方形的棱柱不一定是正棱柱，因为各相邻侧面并不一定互相垂直．这样的四棱柱就不是正四棱柱，故①错误；对于②，如果这两点是直径的两个端点，则能做无数个球大圆；故②错误；对于③，两条异面直线的平行投影可平行；当两条异面直线处在两个平行的平面中且此两平面都与已知平面垂直时，两直线的投影是两条平行线；对于④，过平面外的一条直线，如果此直线与平面相交时，不可能过此直线作出与已知平面平行的平面，故④错误．故选：A．10．（5.00分）设f（x）=ah（x）+bg（x）+4，其中h（x），g（x）都是奇函数，a，b是不同时为零的常数，若f[lg（log310）]=5，则f[lg（lg3）]等于（）A．﹣5 B．7 C．3 D．﹣1【解答】解：f（x）﹣4=ah（x）+bg（x）；∵h（x），g（x）都是奇函数，a，b不同时为0；∴函数f（x）﹣4是奇函数；而f[lg（log310）]=f[﹣lg（lg3）]=5；∴f[lg（lg3）]﹣4=﹣{f[﹣lg（lg3）]﹣4}=﹣1；∴f[lg（lg3）]=3．故选：C．11．（5.00分）正四棱锥的顶点都在同一球面上，若该棱锥的侧棱长为2，底面边长为4，则该球的表面积是（）A．36πB．32πC．18πD．16π【解答】解：如图所示，设球半径为R，底面中心为O′且球心为O，∵正四棱锥P﹣ABCD中AB=4，PA=2，∴AO′=2，可得PO′=2，OO′=PO′﹣PO=2﹣R∵在Rt△AOO′中，AO2=AO′2+OO′2，∴R2=（2）2+（2﹣R）2，解之得R=3，因此可得外接球的表面积为：4πR2=36π．故选：A．12．（5.00分）直线ax+by=1与圆x2+y2=1相交于A，B两点（其中a，b是实数），且∠AOB=120°（O是坐标原点），则点P（a，b）与点（1，1）之间距离的最大值为（）A．B．4 C．D．【解答】解：∵直线ax+by=1与圆x2+y2=1相交于A，B两点（其中a，b是实数），且∠AOB=120°（O是坐标原点），∴圆心O到直线ax+by=1的距离d=，即a2+b2=4，则点P（a，b）与点C（1，1）之间距离|PC|=，则由图象可知点P（a，b）与点（1，1）之间距离的最大值为|OP|+2=，故选：A．二、填空题（共4小题，每小题5分，满分20分）13．（5.00分）函数f（x）=e﹣x+x2+2x﹣2的零点个数为2．【解答】解：函数f（x）=e﹣x+x2+2x﹣2的零点个数即y=e﹣x与y=﹣x2﹣2x+2的交点的个数，作y=e﹣x与y=﹣x2﹣2x+2的图象如下，共有2个交点，故答案为：2．14．（5.00分）如图所示一个几何体的三视图，则该几何体的体积为【解答】解：由已知的三视图可得：该几何体是一个以俯视图为底面的三棱锥，棱锥的底面面积S=×2×2=2，棱锥的高h=2，故棱锥的体积V==，故答案为：．15．（5.00分）已知函数f（x+1）是偶函数，且当x≥1时，f（x）=，若实数a满足f（2a）＞f（a+1），则a的取值范围是．【解答】解：因为y=f（x+1）是偶函数，所以函数f（x）关于直线x=1对称，当1≤x≤2时，f（x）=﹣（x﹣1）2+1，在[1，2]上是减函数，且f（2）=0；当x＞2时，f（x）=﹣ln（x﹣1）也是减函数，且当x→2时，f（x）→0，故函数在[1，+∞）上为减函数，结合函数的奇偶性可知，f（x）在（﹣∞，1]上增函数，且关于x=1对称，所以由f（2a）＞f（a+1）可得，|2a﹣1|＜|a+1﹣1|，即|2a﹣1|＜|a|，即3a2﹣4a+1＜0，解得（）．故答案为：．16．（5.00分）已知圆O：x2+y2=1和点A（﹣2，0），若存在定点B（b，0）（b ≠﹣2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则点P（b，λ）到直线（m+n）x+ny﹣2n﹣m=0距离的最大值为．【解答】解：设M（x，y），则∵|MB|=λ|MA|，∴（x﹣b）2+y2=λ2（x+2）2+λ2y2，由题意，取（1，0）、（﹣1，0）分别代入可得（1﹣b）2=λ2（1+2）2，（﹣1﹣b）2=λ2（﹣1+2）2，∴b=﹣，λ=．直线（m+n）x+ny﹣2n﹣m=0，即m（x﹣1）+n（x+y﹣2）=0过点（1，1），∴点P（b，λ）到直线（m+n）x+ny﹣2n﹣m=0距离的最大值为=．故答案为：．三、解答题（共6小题，满分70分）17．（10.00分）已知直线l：ax+3y+1=0．（1）若直线l在两坐标轴上的截距相等，求a的值；（2）若直线l与直线x+（a﹣2）y+a=0平行，求a的值．【解答】解：（1）若a=0，直线为：y=﹣，直线在两坐标轴上的截距不等；当a≠0时，由l：ax+3y+1=0，得，则a=3；（2）由直线l：ax+3y+1=0与直线x+（a﹣2）y+a=0平行，得，解得：a=3．18．（12.00分）在三棱锥S﹣ABC中，平面SAB⊥平面SBC，BC⊥SA，AS=AB，过A作AP⊥SB，垂足为F，点E、G分别是棱SA，SC的中点求证：（1）平面EFG∥平面ABC；（2）AB⊥BC．【解答】证明：（1）∵AS=AB，AF⊥SB，∴F是SB的中点，∵E、F分别是SA、SB的中点，∴EF∥AB，又∵EF⊄平面ABC，AB⊆平面ABC，∴EF∥平面ABC，同理：FG∥平面ABC，又∵EF∩FG=F，EF、FG⊆平面ABC，∴平面EFG∥平面ABC．（2）∵平面SAB⊥平面SBC，平面SAB∩平面SBC=SB，AF⊂平面SAB，∴AF⊥SB，∴AF⊥平面SBC，又∵BC⊂平面SBC，∴AF⊥BC，∵BC⊥SA，SA∩AF=A，SA、AF⊂平面SAB，∴BC⊥面SAB，∵AB⊂面SAB，∴BC⊥AB．19．（12.00分）已知f（x）是定义在（0，+∞）上的减函数，满足f（x）+f（y）=f（x•y）．（1）求证：f（x）﹣f（y）=；（2）若f（2）=﹣3，解不等式f（1）﹣f（）≥﹣9．【解答】解：（1）证明：∵f（x）+f（y）=f（xy），将x代换为为，则有f（）+f（y）=f（•y）=f（x）∴f（x）﹣f（y）=f（）；（2）∵f（2）=﹣3，∴f（2）+f（2）=f（4）=﹣6，f（2）+f（4）=f（8）=﹣9而由第（1）问知∴不等式f（1）﹣f（）=f（x﹣8）可化为f（x﹣8）≥f（8）．∵f（x）是定义在（0，+∞）上的减函数，∴x﹣8≤8且x﹣8＞0，∴8＜x≤16故不等式的解集是{x|8＜x≤16}．20．（12.00分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB=，BC=1，AA1=AC=2，E、F分别为A1C1、BC的中点．（1）求证：平面ABE⊥平面B1BCC1；（2）求证：C1F∥平面ABE；（3）求多面体A1B1C1﹣ABF的体积．【解答】（1）证明：在三棱柱ABC﹣A1B1C1中，BB1⊥底面ABC，∴BB1⊥AB，∵AB=，BC=1，AC=2，∴AB⊥BC，∵BC∩BB1=B，∴AB⊥平面B1BCC1，又AB⊂平面ABE，∴平面ABE⊥平面B1BCC1；（2）证明：取AB的中点G，连接EG，FG，∵E，F分别是A1C1，BC的中档，∴FG∥AC，，∵，∴，∴FGEC1为平行四边形，∴C1F∥EG，又EG⊂平面ABE，C1F⊄平面ABE，∴C1F∥平面ABE；（3）解：多面体A 1B1C1﹣ABF的体积V=﹣=．21．（12.00分）已知点P（﹣2，3t﹣），Q（0，2t），（t∈R，t≠0）（1）当t=2时，求圆心在坐标原点且与直线PQ相切的圆的标准方程．（2）是否存在圆心在x轴上的定圆M，对于任意的非零实数t，直线PQ恒与定圆M相切，如果存在，求出圆M的标准方程，如果不存在，请说明理由．【解答】解：（1）当t=2时，直线PQ的方程为3x+4y﹣16=0，圆心（0，0）到直线的距离为，即r=．所以，圆的标准方程为：x2+y2=；（2）假设存在圆心在x轴上的定圆M与直线PQ相切．设圆M的方程为（x﹣x0）2+y2=r2（r＞0），直线PQ方程为：（t2﹣1）x+2ty﹣4t2=0．因为直线PQ和圆相切，则=r，整理得：（t2﹣1）x0﹣4t2=r+rt2①或（t2﹣1）x0﹣4t2=﹣r﹣rt2②．由①可得（x0﹣r﹣4）t2﹣x0﹣r=0对任意t∈R，t≠0恒成立，则有，可解得．所以存在与直线PQ相切的定圆M，方程为：（x﹣2）2+y2=4．22．（12.00分）已知函数f（x）=a X，（a＞0且a≠1），若函数g（x）的图象和函数f（x）的图象关于直线y=x对称，且h（x）=g[（a﹣1）x+2]．（1）求h（x）的定义域；（2）当x∈[3，4]时，h（x）＞0恒成立，求a的取值范围．【解答】解：（1）∵函数f（x）=a X，（a＞0且a≠1），若函数g（x）的图象和函数f（x）的图象关于直线y=x对称∴g（x）=log a x，∵h（x）=g[（a﹣1）x+2]．∴h（x）=log a（（a﹣1）x+2），∵（a﹣1）x+2＞0，∴（a﹣1）x＞﹣2，且a≠1，①当a﹣1＞0，即a＞1时，x，定义域为（，+∞），②当，即0＜a＜1时，x，综上；当a＞1时，定义域为（，+∞），0＜a＜1时，定义域为（﹣∞，）（2）当x∈[3，4]时，f（x）有意义得：，解得：a，①当时，由h（x）＞0恒成立得：（a﹣1）x+2＜1，在x∈[3，4]上恒成立，∴a恒成立，∴a∴，②当a＞1时，由h（x）＞0恒成立得：：（a﹣1）x+2＞1，在x∈[3，4]上恒成立，∴a，∴a＞1，综上：a∈（）∪（1，+∞）．。

绝密★启用前2015-2016学年辽宁省重点高中协作校高一下期末数学试卷（带解析）试卷副标题考试范围：xxx ；考试时间：141分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、已知点P 是圆上的一个动点,点Q 是直线上的一个动点,O 为坐标原点,则向量上的射影的数量的最大值是（ ）A ．3B ．C ．3D ．12、已知,则是钝角三角形的概率是（ ）A ．B ．C ．D ．3、已知函数的部分图象如图所示,下面结论正确的个数是（ ）①函数的最小正周期是②函数的图象可由函数的图象向左平移个单位长度得到③函数的图象关于直线对称④函数在区间上是增函数A ．3B ．2C ．1D ．04、如图所示的程序框图,它的输出结果是（ ）A ．-1B ．0C ．1D ．165、甲、乙两名同学8次数学测验成绩如茎叶图所示,分别表示甲、乙两名同学8次数学测验成绩的平均数,分别表示甲、乙两名同学8次数学测验成绩的标准差,则有（ ）A ．B ．C ．D ．6、已知圆心在直线上的圆,其圆心到轴的距离恰好等于圆的半径,在轴上截得的弦长为,则圆的方程为A ．B ．C ．D ．7、已知回归直线的斜率的估计值为1．23,样本点的中心为（4,5）,则回归直线方程为（ ） A ． B ．C ．D ．8、如图,在中,点是边的中点,点在上,且是的重心,则用向量表示为（ ）B．C．D．9、已知角均为锐角,且,则的值为（）A． B．C． D．10、点关于面对称的点的坐标是（）A． B． C． D．11、已知,那么角是A．第一或第二象限角 B．第二或第三象限角C．第三或第四象限角 D．第一或第四象限角12、某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛，在下列选项中,互斥而不对立的两个事件是（）A．“至少有1名女生”与“都是女生”B．“至少有1名女生”与“至多有1名女生”C．“恰有1名女生”与“恰有2名女生”D．“至少有1名男生”与“都是女生”第II 卷（非选择题）二、填空题（题型注释）13、关于平面向量，有下列四个命题： ①若．②若平行，则． ③非零向量满足，则的夹角为．④点，与向量同方向的单位向量为．其中真命题的序号为 ．（写出所有真命题的序号）14、若，则．15、已知平面向量与满足,则．16、某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于70分为合格,则合格人数是 ．三、解答题（题型注释）17、在平面直角坐标系中,两点间的“-距离”定义为．现将边长为1的正三角形按如图所示的方式放置,其中顶点与坐标原点重合．记边所在直线的斜率为,．求：当取最大值时,边所在直线的斜率的值．18、在直角坐标系中,圆与轴负半轴交于点,过点的直线分别与圆交于两点．（1）若,求的面积；（2）过点作圆的两条切线,切点分别为,求．19、已知向量．（1）求；（2）若的最小值是,求实数的值．20、已知,函数．（1）求的对称轴方程；（2）求使成立的的取值集合；（3）若对任意实数不等式恒成立，求实数的取值范围．21、设连续掷两次骰子得到的点数分别为,令平面向量．（1）求使得事件“”发生的概率； （2）求使得事件“”发生的概率；（3）求使得事件“直线与圆相交”发生的概率．22、 “中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃，即“凑够一撮人就可以走了，和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响，从而不顾及交通安全.某校对全校学生过马路方式进行调查，在所有参与调查的人中，“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示：（Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取n 人，已知“跟从别人闯红灯”的人抽取了45 人，求n 的值；（Ⅱ）在“带头闯红灯”的人中，将男生的200人编号为1，2，…，200；将女生的300人编号为201，202，…，500，用系统抽样的方法抽取4人参加“文明交通”宣传活动，若抽取的第一个人的编号为100，把抽取的4人看成一个总体，从这4人中任选取2人，求这两人均是女生的概率.参考答案1、A2、D3、C4、A5、B6、B7、D8、A9、C10、D11、B12、C13、②④14、15、16、60017、。

2019-2020学年辽宁省抚顺市六校协作体高一上学期期末数学试题一、单选题1．已知集合{}12A x x =-<<，{4B x x =<-或}1x >，则A B =U （ ） A ．{4x x <-或}2x > B ．{4x x <-或}1x > C ．{}2x x << D ．{4x x <-或}1x >-【答案】D【解析】根据集合并集的运算，直接求解. 【详解】{}12A x x =-<<Q ,{4B x x =<-或}1x >, {4A B x x ∴⋃=<-或}1x >-,故选：D. 【点睛】本题主要考查了集合并集的运算，属于容易题. 2．函数ln(1)()2x f x x +=-的定义域是（ ）A ．(1,)-+∞B ．(1,2)(2,)-⋃+∞C ．(1,2)-D ．[1,2)(2,)-+∞U【答案】B【解析】由函数的解析式列出不等式组，求解即可. 【详解】 由题意可得1020x x +>⎧⎨-≠⎩，所以1x >-且2x ≠，即定义域为()()1,22,-⋃+∞，故选B 【点睛】本题主要考查函数的定义域，由已知解析式的函数求其定义域，只需求使解析式有意义的x 的范围，属于基础题型.3．一组数据的平均数为x ，方差为2s ，将这组数据的每个数都乘以()0a a >得到一组新数据，则下列说法正确的是（ ） A ．这组新数据的平均数为x B ．这组新数据的平均数为a x +C ．这组新数据的方差为2asD ．这组新数据的标准差为【答案】D【解析】根据平均数及方差的定义可知，一组数据的每个数都乘以a 得到一组新数据，平均值变为原来a 倍，方差变为原来2a 倍. 【详解】设一组数据1234,,,,,n x x x x x ⋯的平均数为x ，方差为2s , 则平均值为()12341n ax ax ax ax ax ax n++++⋯+=， ()()()()()22222212341n s x x x xx xx xx x n ⎡⎤=-+-+-+-+⋯+-⎢⎥⎣⎦Q ，()()()()()222222212341nax ax axax ax ax ax ax axax a s n ⎡⎤∴-+-+-+-+⋯+-=⋅⎢⎥⎣⎦故选：D. 【点睛】本题主要考查了方差，平均数的概念，灵活运用公式计算是解题关键，属于中档题. 4．下列函数中，满足()()()f xy f x f y =的单调递增函数是（ ） A ．3()f x x = B ．31()f x x=-C ．3()log f x x =D ．()3x f x =【答案】A【解析】根据满足()()()f xy f x f y =即可排除B 、C 、D 【详解】对于B 可知,()()33333311111()y f x f y f xy x x y xy xy ⎛⎫⎛⎫⎛⎫⎛⎫=--==≠-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故排除B ；对于C 可得()()()()3333log log log log =⋅=+≠=f x f y x y x y xy f xy ,故排除C ； 对于D 可得()()()3333xyx yxy f x f y f xy +=⋅=≠=,故排除D ；对于A 可知()()()()333f x f y x y xy f xy =⋅==,且3()f x x =是递增函数,故选A【点睛】本题考查函数的性质,考查指数、对数的运算,属于基础题 5．在同一直角坐标系中，函数()()0af x x x =≥，()log a g x x =-的的图象可能是（ ）A ．B ．C ．D ．【答案】D【解析】就01a <<和1a >分类讨论可得正确的选项. 【详解】解：当01a <<时，函数()()0af x xx =≥为增函数，且图象变化越来越平缓，()log a g x x =-的图象为增函数，当1a >时，函数()()0af x x x =≥为增函数，且图象变化越来越快，()log a g x x=-的图象为减函数， 综上：只有D 符合 故选D ． 【点睛】本题考查指数函数和对数函数的图像性质，属于基础题.6．已知()2132f x x +=-，若a 是函数()4y f x =-的一个零点，则a 的值为（ ） A ．2 B ．5C ．143D ．12-【答案】B【解析】a 是函数()4y f x =-的一个零点可知()4f a =，令()21324f x x +=-=，即可求解. 【详解】因为a 是函数()4y f x =-的一个零点， 所以()4f a =，令()21324f x x +=-=， 解得2x =，所以212215a x =+=⨯+=， 故选：B 【点睛】本题主要考查了函数零点，函数求值，属于中档题.7．设60.60.6066log 6a b c ===．，，，则a b c ，，的大小关系是（ ） A ．a c b << B ．a b c <<C ．c b a <<D ．c a b <<【答案】D【解析】根据指数函数、对数函数的单调性性质利用“1”和“0”比较大小即可.600.600.60.6066log 6log 10a b c ==>=<=．<0.6=1，6=1， 【详解】因为0.6xy =是减函数，所以6006a =<．0.6=1，且0a >，因为6xy =是增函数，所以0.606b =>6=1， 因为0.6log y x =是减函数， 所以0.60.6log 6log 10c =<=， 故c a b <<， 故选：D. 【点睛】本题主要考查了指数函数、对数函数的单调性，属于中档题. 8．已知0a b >>,下列不等式中正确的是( ) A ．c c a b> B ．2ab b < C ．2a ab -<-D ．1111a b <-- 【答案】C【解析】利用作差法证明，或举出反例推翻选项. 【详解】A 选项：当0c =时，选项不成立；B 选项：()20ab b b a b -=->，所以选项不正确；C 选项：()()20a ab a a b ---=--<，所以2a ab -<-，该选项正确；D 选项：当12,2a b ==时，111,211a b ==---，选项不正确. 故选：C 【点睛】此题考查不等式的性质的应用，常用作差法比较大小，或举出反例推翻命题.9．某射击运动员射击一次命中目标的概率为p ，已知他独立地连续射击三次，至少有一次命中的概率3764，则p 为（ ）A ．14 B ．34C ．8D ．8【答案】A【解析】三次都未命中的概率为3(1)p -，连续射击三次，至少有一次命中的对立事件为三次都未射中，即可求解. 【详解】因为射击一次命中目标的概率为p ， 所以射击一次未命中目标的概率为1p -， 因为每次射击结果相互独立，所以三次都未命中的概率为3(1)p -，因为连续射击三次，至少有一次命中的对立事件为三次都未射中， 所以连续射击三次，至少有一次命中的概率31(1)3764p --=， 解得14p =. 故选：A 【点睛】本题主要考查了n 次独立重复试验，对立事件，属于中档题.10．定义在R 上的偶函数()f x 在[)0+∞，上单调递增，若()12f -=，且()22f x -≤，则x 的取值范围是（ ）A ．[]13， B ．()13， C ．[)1+∞， D ．[)3+∞，【答案】A【解析】定义在R 上的偶函数()f x 在[)0+∞，上单调递增, ()22(1)f x f -≤=-可等价转化为|2||1|x -≤-，即可求解. 【详解】因为()f x 是定义在R 上的偶函数，且()12f -= 所以()()|2|21f x f-≤=-，又()f x 在[)0+∞，上单调递增， 所以|2||1|1x -≤-=， 即121x -≤-≤， 解得13x ≤≤. 故选：A 【点睛】本题主要考查了函数的奇偶性应用，函数的单调性应用，属于中档题.二、多选题11．若“x M x x ∀∈>，”为真命题，“3x M x ∃∈>，”为假命题，则集合M 可以是（ ）A ．()5-∞-，B ．(]31--，C ．()3+∞，D ．[]03，【答案】AB【解析】根据假命题的否定为真命题可知3x M x ∀∈≤，，又x M x x ∀∈>，，求出命题成立的条件，求交集即可知M 满足的条件. 【详解】Q 3x M x ∃∈>，为假命题,3x M x ∴∀∈≤，为真命题，可得(,3]M ⊆-∞，又x M x x ∀∈>，为真命题，可得(,0)M ⊆-∞， 所以(,0)M ⊆-∞， 故选：AB 【点睛】本题主要考查了含量词命题的真假，集合的包含关系，属于中档题. 12．下列结论中正确的是（ ）A ．已知函数()f x 的定义域为R ，且()f x 在任何区间内的平均变化率均比()2g x =在同一区间内的平均变化率小，则函数()f x 在R 上是减函数；B ．已知总体的各个个体的值由小到大依次为2，3，3，7，10，11，12，a ，18，20，且总体的平均数为10，则这组数的75%分位数为13；C ．方程()()255log 21log 2x x +=-的解集为{}13-，；D ．一次函数()0y kx b k =+≠一定存在反函数． 【答案】AD【解析】A 选项可利用任何区间内平均变化率的大小判断增减性；B 选项根据平均数计算a ,可判断75%分位数；C 选项要注意真数大于0；D 选项一次函数是单调函数，即可判断反函数存在. 【详解】A 中，由题意知()f x 在任何区间内的平均变化率都小于0，从而函数()f x 在R 上是减函数正确；B 中，由2，3，3，7，10，11，12，a ，18，20的平均数为10，可求得14a =，根据75%分位数概念计算可知312(1412)13.54+⨯-=，故不正确，C 中，1x =-时，()()255log 21,log 2x x +-无意义，显然错误；D 中，一次函数()0y kx b k =+≠具有单调性，反解()x g y =可以构成函数，故存在反函数，正确.故选：AD 【点睛】本题主要考查了平均变化率，75%分位数，对数方程，反函数的概念，属于中档题.三、填空题13．已知对于不同的0a >且1a ≠，函数()243x f x a-=+必过一个定点A ，则A 的坐标是_________．【答案】()24，【解析】根据指数函数性质可知当240x -=时，即可求出A 。