当前位置：文档之家 › 自动控制理论第7章非线性系统的分析

自动控制理论第7章非线性系统的分析

  • 格式：ppt
  • 大小：1.20 MB
  • 文档页数：62

下载文档原格式

  / 62

合集下载

自动控制原理非线性分析知识点总结

自动控制原理非线性分析知识点总结

自动控制原理非线性分析知识点总结自动控制原理是工程领域中的一门重要学科，它研究的是如何通过设备和技术手段，使得系统的运行能够自动控制并满足特定的性能要求。

非线性分析则是探讨系统在非线性条件下的行为特性。

在这篇文章中，我们将对自动控制原理中的非线性分析知识点进行总结。

一、非线性系统的定义与特点非线性系统是指系统的输出与输入之间的关系不是简单的比例关系，而是呈现出非线性的特征。

与线性系统相比，非线性系统具有以下几个特点：1. 非线性叠加性：系统的输出并不是输入信号的简单叠加，而是受到系统自身状态和非线性特性的影响。

2. 非线性失稳性：非线性系统可能会出现失稳现象，即系统的输出会趋向于无穷大或无穷小。

3. 非线性动态行为：非线性系统在输入信号发生变化时，其输出信号的变化可能是不连续的，出现跳跃、震荡等现象。

二、非线性系统的分析方法1. 相平面分析法：通过绘制相平面图，可以直观地了解系统的非线性行为。

相平面图可以显示出系统的轨迹、奇点等信息，帮助我们分析系统的稳定性和动态特性。

2. 频域分析法：利用频域分析方法，我们可以对非线性系统进行频谱分析，找出系统的频率响应和频率特性。

通过分析系统的幅频特性和相频特性，我们可以判断系统的稳定性和动态性能。

3. 时域响应分析法：时域分析是对系统的输入信号与输出响应进行时间上的观察和分析。

通过观察和分析系统的阶跃响应、脉冲响应、频率响应等，可以推断出系统的稳定性和动态特性。

4. 广义函数法：广义函数是处理非线性系统时常用的一种数学方法。

通过引入广义函数，我们可以简化非线性系统的数学描述，方便进行分析与计算。

5. 数值模拟方法：对于复杂的非线性系统，我们可以利用计算机进行仿真和数值模拟，通过对系统的模拟实验，得到系统的动态行为和性能参数。

三、非线性系统的稳定性分析1. 稳定性概念：稳定性是衡量系统响应的一种重要指标。

对于非线性系统，我们通常关注的是渐近稳定性和有界稳定性。

自动控制原理__(13)

自动控制原理__(13)

x0 e t , 其中x0 x(0) t 1 x0 x 0 e
江南大学物联网工程学院——自动控制原理
（2）会产生自激振荡 非线性系统即使无外界作用，往往也会产生具有一定振幅 和频率的稳定性振荡，称为自激（自持）振荡。在有的非线性 系统中，还可能产生不止一种振幅和频率的自激振荡。自激振 荡是非线性系统一种特有的运动形式，其振幅和频率由系统本 身特性决定。 说明：
江南大学物联网工程学院——自动控制原理
2. 典型的非线性特性
常见的非线性特性有饱和、死区、间隙（回环）、继电等。 (1)饱和特性 特点：当输入信号超过某一范围后，输出信号不再随输 入信号而变化，将保持某一常数值不变。可将饱和非线性元 件看作为一个变增益的比例环节。
x2 f ( x1 ) tan , x1 ＜s 如图： x2 f ( x1 ) K x1 x1 0, x1 ＞s
作用：饱和特性将使系 统等效增益减小，因此可用 来改善系统的稳定性，但会 降低稳态精度。在有些系统 中利用饱和特性起信号限幅 作用。
（a）理想饱和特性
（b）实际饱和特性
图7-2 理想与实际饱和特性
江南大学物联网工程学院——自动控制原理
（2）死区（不灵敏区）特性 特点：是当输入信号在零值附近的某一小范围之内变化 时，没有相应的输出信号，只有当输入信号大于此范围时， 才有信号输出。 常见于测量、放大、变换元件中，执行机构中静摩擦的 影响往往也可用死区来表示。 影响：控制系统中死区特性的存 在，将导致系统稳态误差增大，而测 量元件死区的影响尤为显著。摩擦死 区会造成系统低速运动的不均匀，导 致随动系统不能准确地跟踪目标。
3. 非线性系统的分析方法
目前，对于非线性系统的分析与设计，工程上常用的近似方法有：小 偏差线性化法、分段线性化法、反馈线性化法、描述函数法、相平面法及 计算机仿真等。本章将重点介绍应用较多的相平面法和描述函数法。 （1） 相平面法 相平面法是基于时域的图解分析方法。特点是保留非线性特性，将高 阶的线性部分近似地化为二阶，利用二阶系统的状态方程，绘制由状态变 量所构成的的相轨迹图。可用来分析系统的稳定性及运动特性。 只适用于一、二阶的简单非线性系统分析。
自动控制原理课件 第7章 非线性控制系统

自动控制原理课件 第7章 非线性控制系统

描述函数法是基于频率域的等效线性化方法。该法不受系统 阶次的限制，但系统必须满足一定的假设条件，且只能提供系 统稳定性和自激振荡的信息。 3. 波波夫法
波波夫法是一个关于系统渐近稳定充分条件的频率域判据。 它可以应用于高阶系统，并且是一个准确判定稳定性的方法。
2020年11月17日
EXIT
第7章第16页
4．可以用频率特性的概念来研究和分析线性系统的固 有特性。不能用频率特性、传递函数等线性系统常用的 方法来研究非线性系统。
2020年11月17日
EXIT
第7章第15页
7.1.4 非线性系统的分析和设计方法
1. 相平面法 相平面法是求解一阶或二阶非线性系统的图解法。这种方法
既能提供的稳定性信息，又能提供时间响应信息。其缺点是只 限于一阶和二阶系统。 2. 描述函数法
齿轮传动的齿隙特性，液压传动的的油隙特性等均属于 这类特性。
当系统中有间隙特性存在时，将使系统输出信号在相位 上产生滞后，从而使系统的稳定裕度减少，动态特性变坏。
间隙的存在常常是系统产生自持振荡的主要原因。
2020年11月17日
EXIT
第7章第9页
4.继电器特性
0 y(t) b0sgn e(t)
在控制系统中若存在饱和特性，将使系统在大信号
作用下的等效放大倍数降低，从而引起瞬态过程时间 的延长和稳态误差的增加。对于条件稳定系统，甚至 可能出现小信号时稳定，而大信号时不稳定的情况。
2020年11月17日
EXIT
第7章第7页
2.死区（不灵敏区）特性
y (t )
0
k
e(t)
a sgn
e(t)
e(t) a e(t) a
2. 线性系统的稳定性与输入响应的性质只由系统本身的 结构及参量决定，而与系统的初始状态无关。而非线性 系统的稳定性及零输入响应的性质不仅取决于系统本身 的结构和参量，而且还与系统的初始状态有关。
自动控制原理第7章_非线性控制系统

自动控制原理第7章_非线性控制系统


7.2 相平面法
1. 基本概念 2. 相平面图的绘制 3. 线性系统的相轨迹 4. 非线性系统的相平面分析
7.2 相平面法
1. 基本概念 相平面法是一种求解二阶常微分方程的图解方法。 1) 相平面图 f ( x, x ) 0 x 二阶系统的数学描述 ，得下列一阶微分方程组 设x1=x，x2= x

非线性系统一般理解为非线性微分方程所描述的
系统。 线性系统的本质特征是叠加原理，因此非线性系 统也可以理解为不满足叠加原理的系统。

7.1 概述
2. 典型的非线性特性
1) 饱和特性
2) 死区特性
3) 间隙特性(滞环特性)
4) 变放大系数特性
5) 继电器特性
7.1 概述
1) 饱和特性
x(t) k 0 a e(t)
数学表达式
ke(t ) x(t ) ka signe(t )
1 signe(t ) 1 不定
e(t ) a e(t ) a
-a
符号函数(开关函数)
e(t ) 0 e(t ) 0 e(t ) 0
图 7.2 饱和特性
a – 线性域宽度 k – 线性域斜率
(d)半稳定极限环
(a) 可通过实验观察到。设计时应尽量减少极限环 的大小，以满足系统的稳态误差要求。
(b) 不能通过实验观察到。设计时应尽量增大极限 环的大小，以扩大系统的稳定域。
(c)、(d)不能通过实验观察到。(c)不稳定。(d)稳 定，但过渡过程时间将由于极限环的存在而增加。
7.2 相平面法
单输入-单输出的线性定常系 统
现代控制理论（20世纪50 年代后）
可以是比较复杂的系统
自动控制原理第七章非线性控制系统的分析

自动控制原理第七章非线性控制系统的分析

X X
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e
王建辉《自动控制原理》(名校考研真题 非线性系统分析)【圣才出品】

王建辉《自动控制原理》(名校考研真题 非线性系统分析)【圣才出品】

第7章　非线性系统分析一、选择题1．非线性系统的无穷多条相轨迹相交的点称为（）。

[华中科技大学研]A．奇点B．会合点C．分离点D．终点【答案】A2．输出信号的一次谐波分量和输入信号的复数比定义为非线性环节的（）。

[华中科技大学研]A．传递函数B．描述函数C．谐波函数D．频率特性【答案】B二、解答题1．已知非线性系统如图7-1所示，其中，T＞0，K＞0，现要求系统输入量c（t）的ωc＝10，试确定参数T和K的数值。

（非线性环节自振振幅X c＝0.1，角频率为）[上海交通大学研]图7-1解：由已知ωc ＝10，线性部分传递函数为即又由于ωc ＝10，自振振幅X c ＝0.1得因此有2．已知某非线性系统结构如图所示，试用描述函数法分析K （K ＞0）值对系统稳定性的影响。

[南京航空航天大学2006研]图7-2 非线性系统结构图解：该饱和特性的描述函数为负倒描述函数当A ＝1时，，当A→＋∞时，，因此位于负实轴上的－1~－∞区段。

线性部分频率特性为令ImG （j ω）＝0，得G （j ω）与负实轴交点的频率为，且在复平面上绘制G （j ω）曲线以及曲线如下图所示。

由图可见，当时，即0＜K ＜6系统稳定；当时，即K ＞6系统产生自振。

自振频率，振幅A 由求得。

图7-33．某单位负反馈非线性系统如图所示，非线性环节的描述函数为，线性部分的传递函数如图所示。

试分析：（1）系统是否存在自振。

（2）若产生自振，计算自振频率及振幅，并讨论极限环的稳定性。

[浙江大学2008研]图7-4 非线性系统结构图解：非线性环节负倒描述函数为线性部分频率特性为且在复平面上绘制G（jω）曲线以及曲线如下图所示，相交于B点，有解得即系统存在自振的频率为1.155，振幅为11.246。

图7-54．已知非线性控制系统的结构图如图7-6所示。

为了使系统不产生自持振荡，试采用描述函数法确定图中非线性环节的特性参数a和b的数值。

[长安大学研][南京理工大学研][华中科技大学研]图7-6解：由题知非线性环节为死区继电器特性，则图形如图7-8所示。

自动控制原理 第七章 非线性系统

自动控制原理 第七章 非线性系统


实质上是应用谐波线性化的方法，将非线性特性线性化， 然后用频域法的结论来研究非线性系统，它是线性理论 中的频率法在非线性系统中的推广，不受系统阶次的限 制。
（2）相平面法（本质非线性）：图解法。通过在相平 面上绘制相轨迹，可以求出微分方程在任何初始条件下 的解。是一种时域分析法，仅适用于一阶和二阶系统。
1
ωt
y1 (t ) B1 sint
由式（7-15）可得饱和特性的描述函数为
B1 2k a a a 2 N ( A) arcsin 1 ( ) A A A A

M sin td ( t )
yMFra bibliotek0 π2π
ωt
所以基波分量为：
y1 ( t )
4M

sin t
故理想继电器特性的描述函数为
Y1 4M N ( A) 1 A A
2.饱和特性
请牢记！
即 N(A)的相位角为零度,幅值是输入正弦信号A的函数.
当输入为x(t)＝Asinωt，且A大于线性区宽度a 时， 饱和特性的输出波形如图7-10所示。
7.1.3
非线性系统的分析方法
非线性的数学模型为非线性微分方程，大多数尚无
法直接求解。到目前为止，非线性系统的研究还不成熟， 结论不能像线性系统那样具有普遍意义，一般要针对系 统的结构，输入及初始条件等具体情况进行分析。工程 上常用的方法有以下几种：
（1）描述函数法（本质非线性）：是一种频域分析法，
r(t)=0 x
N
y
G(s)
c(t)
图7-8 非线性系统典型结构图
（2）非线性环节的输入输出静特性曲线是奇对称的，即 y(x)=-y(-x)，以保证非线性元件在正弦信号作用下的输出不 包含直流分量。 （3）系统的线性部分具有良好的低通滤波特性。能较好的滤 除非线性环节在正弦输入下输出中的高次谐波，于是可以认 为在闭环通道中只有基波分量在流通，此时应用描述函数法 所得的分析结果才是比较准确的。实际系统基本都能满足。
自动控制原理第七章非线性系统ppt课件

自动控制原理第七章非线性系统ppt课件


7.1.3 非线性系统的分析方法
非线性的数学模型为非线性微分方程，大多数尚无 法直接求解。到目前为止，非线性系统的研究还不成熟， 结论不能像线性系统那样具有普遍意义，一般要针对系 统的结构，输入及初始条件等具体情况进行分析。工程 上常用的方法有以下几种：
（1）描述函数法（本质非线性）：是一种频域分析法，
实质上是应用谐波线性化的方法，将非线性特性线性化， 然后用频域法的结论来研究非线性系统，它是线性理论 中的频率法在非线性系统中的推广，不受系统阶次的限 制。
（2）相平面法（本质非线性）：图解法。通过在相平 面上绘制相轨迹，可以求出微分方程在任何初始条件下 的解。是一种时域分析法，仅适用于一阶和二阶系统。
4M
sin t
故理想继电器特性的描述函数为
N ( A)
Y1 A
1
4M
A
请牢记！
即 N(A)的相位角为零度,幅值是输入正弦信号A的函数.
2.饱和特性
当输入为x(t)＝Asinωt，且A大于线性区宽度a 时，
饱和特性的输出波形如图7-10所示。
y
x
N
M
k 0a
x
yy
0 ψ1
π
2π
ωt
0 x
ψ1
π
A sin 1
x(t) Asint
则其输出一般为周期性的非正弦信号，可以展成傅氏级 数：
y(t ) A0 ( An cos nt Bn sin nt ) n1
若系统满足上述第二个条件，则有A0=0
An
1
2 y(t ) cos ntd t
0
Bn
1
2 y(t ) sin ntd t
0
由于在傅氏级数中n越大,谐波分量的频率越高，An，Bn
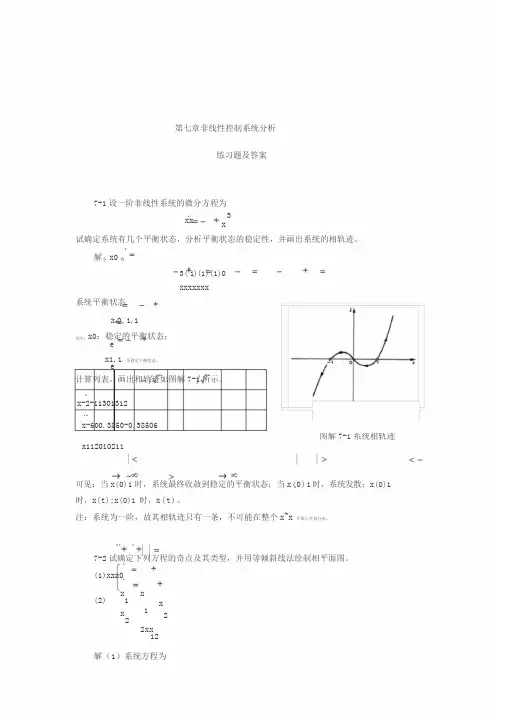
自动控制原理考试试题第七章习题与答案

自动控制原理考试试题第七章习题与答案

第七章非线性控制系统分析练习题及答案7-1设一阶非线性系统的微分方程为xx3 x试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解令x0得3(21)(1)(1)0xxxxxxx系统平衡状态x e0,1,1其中：x0：稳定的平衡状态；ex1,1：不稳定平衡状态。

e计算列表，画出相轨迹如图解7-1所示。

x-2-11301312x-600.3850-0.38506x112010211图解7-1系统相轨迹可见：当x(0)1时，系统最终收敛到稳定的平衡状态；当x(0)1时，系统发散；x(0)1 时，x(t);x(0)1时，x(t)。

注：系统为一阶，故其相轨迹只有一条，不可能在整个x~x平面上任意分布。

7-2试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1)xxx0(2) x1x2xx122xx12解（1）系统方程为1:xxx0(x0):xxx0(x0)令xx0，得平衡点：x e0。

系统特征方程及特征根：132:ss10,sj(稳定的焦点)1,2222:ss10,s1.618,0.618(鞍点)1,2xf(x,x)xx, d xdxxxxdx dx 1xx,1xxx11I:1(x0)1II:1(x0)计算列表-∞-3-1-1/301/313∞x0:11-1-2/302-∞-4-2-4/3-1x0:11-1-4/3-2-4∞20-2/3-1用等倾斜线法绘制系统相平面图如图解7-2（a）所示。

2图解7-2（a）系统相平面图（2）xxx112①x22xx②12由式①：x2x1x1③式③代入②：(x1x1)2x1(x1x1)即x12x1x10④令x1x10得平衡点：x e0由式④得特征方程及特征根为2.4142ss2101,2（鞍点）0.414画相轨迹，由④式xx 11 d x1dxx12x1x1x 1 x1 2计算列表322.53∞11.52=1/(-2)∞210-1-2∞用等倾斜线法绘制系统相平面图如图解7-2（b）所示。

自动控制原理第七章

自动控制原理第七章

基本思想 相轨迹的特点 相轨迹的绘制方法 线性系统的相平面图 非线性系统的相平面图
基本思想
ɺ x
x
相平面分析法是分析非线性系统性能的一种图 示方法。 示方法。而相轨迹和相平面图的绘制为该分析方法的前提 条件。 条件。
x 1 (t), 2 (t) x
相平面定义：由两个线性无关的状态变量 作为坐标的平面称 为相平面。通常采用位移和位移的变化率作为状态变量用于描述一、二 阶系统的运动特性。
ɺɺ = -f(x, x ) ɺ x ⇒ ɺ ɺɺ = d x x = − f(x, x ) ɺ ɺ x dx ⇒ ɺ ɺ dx f(x, x ) = − ɺ dx x
ɺ x
x
相轨迹的绘制方法
解析法
消除变量法 直接积分法
等倾线法绘制相轨迹思 ɺɺ + f(x,ɺ ) = 0 x x 令： ⇒ 路： ɺ dx f(x,ɺ ) x =− ɺ x dx
E 0
Im
∞
Re
死区继电器的负倒描述函数曲线
Im
N(E) N(E)
4M = πE = 0
Δ2 1− E 2 (E ≤ Δ )
(E
≥ Δ)
∆ ∞
E Re
−
1 N(E)
= − 4M
πE
Δ2 1− E 2
(E
≥ Δ)
拐点参数：
E = 2 Δ 1 − N(E) E =
Y ϕ 非线性环节的描述函数 ：N = 1 e j 1 = E
2 2 − A 1 + B 1 jtg 1 B 1 B A = 1+j 1 e E E E
A1
描述函数的自变量为输入正弦信号的幅值
求取描述函数应用举例
自动控制原理非线性系统知识点总结

自动控制原理非线性系统知识点总结

自动控制原理非线性系统知识点总结自动控制原理是现代控制领域中的核心学科，广泛应用于各个工程领域。

在自动控制原理课程中，非线性系统是一个重要的研究对象。

非线性系统具有较复杂的动态行为，与线性系统相比，其稳定性和性能分析更为困难。

在本文中，我们将对非线性系统的知识点进行总结。

1. 静态非线性系统静态非线性系统是最简单的非线性系统，其输出仅与输入的幅值相关。

常见的静态非线性函数有幂函数、指数函数、对数函数等。

分析静态非线性系统时，通常采用泰勒级数展开或者离散化的方法。

2. 动态非线性系统动态非线性系统是具有时间相关性的非线性系统。

其中最基本的形式是非线性微分方程。

在动态非线性系统中，常见的动力学行为有极值、周期、混沌等。

在分析动态非线性系统时，可以采用相位平面分析、Lyapunov稳定性分析等方法。

3. 线性化由于非线性系统分析的困难性，常常采用线性化的方法来近似描述非线性系统的行为。

线性化方法可以将非线性系统在某一操作点上进行线性近似，从而得到一个线性系统。

采用线性化方法时，需要注意选取适当的操作点，以保证线性化模型的准确性。

4. 系统稳定性非线性系统的稳定性是研究非线性系统的重点之一。

与线性系统相比，非线性系统的稳定性分析更为困难。

常用的方法有Lyapunov稳定性分析、输入输出稳定性分析等。

在稳定性分析时，需要考虑非线性系统的各种动力学行为，比如局部极大值点、周期分岔点、混沌行为等。

5. 非线性反馈控制非线性反馈控制是应用最广泛的非线性控制方法之一。

非线性反馈控制利用非线性函数对系统的输出进行修正，以实现系统的稳定性和性能要求。

其中，常见的非线性反馈控制方法有滑模控制、自适应控制、模糊控制等。

6. 非线性系统的鲁棒性鲁棒性是研究非线性系统控制的重要性能指标之一。

鲁棒控制能够保证系统在存在不确定性或者干扰的情况下，仍然保持稳定性和性能要求。

常见的鲁棒控制方法有H∞控制、鲁棒自适应控制等。

7. 非线性系统的最优控制最优控制是针对非线性系统的性能指标进行优化设计的方法。

自动控制原理-第七章 非线性系统分析


p p p ( x1 , x 2 ) ( x1 x 10 ) ( x 2 x 20 ) x1 x 2 Q ( x , x ) Q ( x x ) Q ( x x ) 1 2 1 10 2 20 x1 x 2
p ( x1 , x 2 ) a ( x1 x10 ) b( x 2 x 20 ) Q( x1 , x 2 ) c( x1 x10 ) d ( x 2 x 20 )

c 区域： a Tc c k m
c k m c 1 （k m c) T T ct 0 由奇点定义： k m c 0 c 常数 c k m 1 k m c dc T dc c 区域： c 常数 奇线： c k m
§7-4
奇点及极限环
dx 0 奇点概念：相轨迹上满足 dx 0 不定式的特殊点，称为奇点。
在奇点处有多条相轨迹穿过或趋于该奇点，相当于系统处于 平衡状态 一 奇点分类：(线性系统)
2 2 n x n x 0 x 2 2 n x n x x dx 2 x dx 2 n x n x dt (*) 相轨迹方程 dx x dx x dt
介绍：典型非线性特性、相平面法、描述 函数法
§7-1引言
稳定性 1．线性系统与非线性系统区别： 输出曲线 等幅振荡 稳态输出
2．非线性特性（典型） 1）死区
0 x a y k ( x a ) x a k ( x a ) x a
0 = k ( x aSignx)
x1 a ( x1 x 10 ) b( x 2 x 20 ) x 2 c( x1 x10 ) d ( x 2 x 20 )

自动控制原理(第三版)第7章非线性控制系统(1)

大连民族学院机电信息工程学院
自动控制原理
4）当非线性输入的信号为正弦作用时，由 于非线性其输出将不再是正弦信号，而包 含有各种谐波分量，发生非线性畸变。
大连民族学院机电信息工程学院
自动控制原理
5）混沌
大连民族学院机电信息工程学院
自动控制原理
非线性系统运动的特殊性
• 不满足叠加原理 — 线性系统理论原则上不能运用 (区别） • 稳定性问题 — 不仅与自身结构参数，且与输入， 初条件有关，平衡点可能不惟一，可以稳定且可以 在多个平衡点稳定，可能不稳定—发散、衰减等 nonlinear • 自振运动— 非线性系统特有的运动形式，产生自 持振荡 • 发生频率激变—频率响应的复杂性 — 跳频响应， 倍/分频响应，组合振荡
大连民族学院机电信息工程学院
自动控制原理
3、滞环（非单值特性）
) x 0 , 且y 0 k ( x a sgn x y ＝0 y x2 m sgn x
滞环特性会 使系统的相 角裕度减小, 动态性能恶 化,甚至产生 自持振荡。
x2
x2m
x2
x2m
a
0
x1
a
x2m
7.3 描述函数法 7.4 相平面法
7.5 Matlab 在本章中的应用
大连民族学院机电信息工程学院
自动控制原理
7.1 非线性控制系统概述
如果一个控制系统包含一个或一个以上具有非 线性特性的元件或环节,则此系统即为非线性系统。
• 前面研究的线性系统满足叠加性和齐次性； • 严格地说，由于控制元件或多或少地带有非线性特 性，所以实际的自动控制系统都是非线性系统； • 一些系统作为线性系统来分析： ①系统的非线性 不明显，可近似为线性系统。②某些系统的非线性 特性虽然较明显，但在某些条件下，可进行线性化 处理； • 但当系统的非线性特征明显且不能进行线性化处理 时，就必须采用非线性系统理论来分析。这类非线 大连民族学院机电信息工程学院 性称为本质非线性。

自动控制原理第七章非线性系统分析


02
非线性系统的分析方法
相平面法
相平面法是一种通过绘制系统的 相图来分析非线性系统的动态行
为的方法。
它通过将系统的状态变量绘制在 二维平面上，显示系统的平衡状 态、周期运动和混沌运动等不同
状态。
相平面法可以用于分析非线性系 统的稳定性、分岔和混沌等现象。
描述函数法
描述函数法是一种通过引入描 述函数来分析非线性系统的频 率特性的方法。
滑模控制是一种变结构控制方法，通过设计滑模面和滑模控制器，使 得系统状态在滑模面上滑动，以达到控制系统的目的。
非线性系统的设计方法
相平面法
通过分析非线性系统的相轨迹，了解系统的动态行为，并 设计适当的控制器来控制系统状态。
描述函数法
通过分析非线性系统的频率特性，了解系统的动态行为， 并设计适当的控制器来控制系统状态。
它通过将非线性系统近似为线 性系统，并利用频率响应函数 来描述系统的频率特性。
描述函数法可以用于分析非线 性系统的谐振、倍周期分岔等 现象。
逆系统法
逆系统法是一种通过构建逆系统来补偿非线性系 统的非线性特性的方法。
它通过设计一个逆系统来抵消原系统的非线性， 从而将非线性系统转化为线性系统进行处理。
根轨迹法
根轨迹法是通过绘制系统的根轨迹图来分析系统的稳定性，根轨迹是指系统的极点随参数变化而变化 的轨迹。
劳斯稳定判据
劳斯稳定判据是判断线性系统稳定性的重要方法之一，其基本思想是通过 计算系统的极点，判断极点是否位于复平面的左半部分。
劳斯稳定判据的优点是简单易行，适用于多变量系统，可以同时考虑系统 的所有极点。
03
非线性系统的稳定性分析
定义与特点
定义
非线性系统的稳定性是指系统在受到 扰动后，能否恢复到原来的平衡状态 。

夏德钤《自动控制原理》(第4版)章节题库-第7章 非线性系统的分析【圣才出品】

第7章　非线性系统的分析1．试计算并绘制下列各微分方程的相平面图。

解：（1）求得运用积分法解得相轨迹方程为其相轨迹如图7-1所示。

（2）求得运用积分法解得相轨迹方程为其相轨迹如图7-2所示。

图7-1 系统的相轨迹 图7-2 系统的相轨迹（3）求得令切线斜率，则可得等倾线方程为，即可见等倾线为一簇水平线。

①当α＝0时，，则该等倾线亦为一条相轨迹，因相轨迹互不相交，故其他相轨迹均以此线为渐近线。

②当α→∞时，，表明相轨迹垂直穿过x轴。

③当α→－1/T时，，说明相平面上下无穷远处的相轨迹斜率为－1/T。

最后根据等倾线作图法可得其概略相轨迹如图7-3所示。

图7-3 系统的概略相轨迹（4）求得令切线斜率，则可得等倾线方程为，即可见等倾线为一簇水平线。

①当α＝0时，x＝M，则该等倾线亦为一条相轨迹，因相轨迹互不相交，故其他相轨迹均以此线为渐近线。

②当α→∞时，，表明相轨迹垂直穿过x轴。

③当α→－1/T时，，说明相平面上下无穷远处的相轨迹斜率为－1/T。

最后根据等倾线作图法可得其概略相轨迹，如图7-4所示。

图7-4 系统的概略相轨迹（5）求得运用积分法可解得相轨迹方程为为一抛物线，其概略相轨迹如图7-5所示。

图7-5 系统的概略相轨迹（6）运用积分法可解得相轨迹方程为其中c为一常数，其相轨迹如图7-6所示。

图7-6 系统的相轨迹２．非线性控制系统结构图如图7-7所示，M ＝1。

要使系统产生振幅A＝4，频率ω＝1的自振运动，试确定参数K ，τ的值。

图7-7 系统结构图解：画出和G （jω）曲线如图8．7所示，当K 改变时，只影响自振振幅A ，不改变自振频率ω；而当τ≠0时，会使自振频率降低，幅值增加。

因此可以调节K ，τ大小实现要求的自振运动。

由自振条件N （A ）G （jω）＝-1即将ω＝1代入上式可解得K ＝9.93，τ＝0.322图7-8 和G （jω）曲线3．设继电型控制系统结构如图7-9所示，输入r （t ）＝R·1（t ），c （0）＝0。

自动控制原理课件第七章4

2
极点分布 奇点 相迹图
稳定的 焦点 0 1
稳定的 节点 1
中心点 0
极点分布 奇点 相迹图
不稳定 的焦点 1 0
不稳定 的节点 1
鞍点 正反馈 且 0
3
极限环
相平面图上孤立的封闭相轨迹，而其附近的 相轨迹都趋向或发散于这个封闭的相轨迹
各
类
极
稳定的极限环
限
环
不稳定的极限环
半稳定的极限环
r (t )
e(t )
M
x(t )
K
c(t )
s(Ts 1)
e0
解：系统的微分方程为
Tc c Kx
c r e
饱和非线性输入输出关系为
e
x
M
M
e e0 e e0 e e0
2021/9/16
7
根据系统方程
Tc c Kx
c r e
以 e 为变量的运动方程为
Te e Kx Tr r
e 0
和Ⅱ区分界线上，是个虚奇点。
e •
A (R,0)
Te e K (e e0 ) 0 xee0 Tx x Kx 0
由于 T , K 0 ，因此奇点类型为稳定焦点或稳定节点。
14
（3）Ⅲ区： e e0 此时 x e e0 ，相应微分方程为 Te e K (e e0 ) 0
1
2、二阶线性系统中奇点的类型
r=1(t) E(S)
n2
C(S)
－ s(s 2n )
e 2ne n2e 0
斜率： de = - 2ζωne + ωn2e
de
e
奇点：
e 0
2n
e
n2e
0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

k
0
a
x1
此处： x1 输入
x2m
x2 输出
k 比例系数
饱和非线性对系统的影响：
• 饱和非线性使系统在大信号作用下的等 效增益下降，严重的可以使系统丧失闭 环控制作用。
2、死区
x2 k(x10signx1x1)x1
1 si gn1 x1
3）非线性系统的数学模型是非线性微分方 程；但至今为止非线性微分方程没有成 熟的解法；
4）描述函数法、相平面法和李亚谱诺夫第 二方法是分析非线性系统的三种方法。
7-2 典型非线性环节
1、饱和非线性
kx1 x2 kax2m kax2m
x1 a
x2
x1 a
x2m
x1 a a
• 前面研究的线性系统满足叠加性和齐次性； • 严格地说，由于控制元件或多或少地带有非线性特
性，所以实际的自动控制系统都是非线性系统； • 一些系统作为线性系统来分析： ①系统的非线性
不明显，可近似为线性系统。②某些系统的非线性 特性虽然较明显，但在某些条件下，可进行线性化 处理； • 但当系统的非线性特征明显且不能进行线性化处理 时，就必须采用非线性系统理论来分析。这类非线 性称为本质非线性。
第7章 非线性系统的分析
7-1 非线性特性对系统的影响 7-2 典型非线性环节 7-3 描述函数的基本概念 7-4 典型非线性环节的描述函数 7-5 用描述函数研究非线性系统 7-6 相平面的基本概念 7-7 线性控制系统的相平面分析
7-1 非线性特性对系统的影响
如果一个控制系统包含一个或一个以上具有非 线性特性的元件或环节,则此系统即为非线性系统。
• 线性系统只有两种工作模式：要么发散， 要么收敛；
• 非线性系统有收敛、发散和自持振荡三 种状态。
4）当非线性输入的信号为正弦作用时，由 于非线性其输出将不再是正弦信号，而包 含有各种谐波分量，发生非线性畸变。
5）混沌
• 非线性系统分析方法：
1）非线性系统的运动比线性系统复杂得 多；
2）分析线性系统的分析方法不能用于分析 非线性系统；
7-3 描述函数的基本概念
描述函数的基本概念
R
G 1 x1 非 线 性x2 G 2
Y

当非线性元件输入一个正弦信号 eXsi nt
输出是一个含有高次谐波的周期函数：
y A 0 A 1 st i B 1 c n t o A 2 s 2 s t i B 2 c n t o
输出的信号；
y 1 A 1 si t n B 1 ct o Y 1 s si t n 1 )(
Y1
A12
B12,1
arctBg1 A1
A1120ysintdt,B1
12yc
0
ostd(t)
• 这个过程实际上是一个线性化过程，经
过线性化输出的信号与输入信号同频率，
• 线性系统系统的稳定性只取决于系统结构 和参数，与输入信号及初始条件无关。
但非线性系统的稳 定性不仅与系统的 结构和参数有关， 还与输入信号及初 始条件有关。即可 能在某个初始条件 下稳定，而在另一 个初始条件下系统 可能不稳定。
3）非线性系统可以产生自持振荡：
在没有外作用时,有可能产生频率和振幅 一定的稳定周期性响应。该周期响应过 程物理上可实现并可保持,通常将其称为 自持振荡或自振荡；
如果满足下列条件： • 系统的输入为0，非线性元件的输入为
正弦信号：eXsi nt
• 非线性元件的静特性不是时间t的函数, 即为非储能元件；
• 非线性元件的特性是奇对称的，即有 f(e)f(e) ——直流分量为0；
• 系统的线性部分具有较好的低通滤波特 性——滤去高次谐波。
• 满足上面条件,可以用基波信号代替整个
只是在幅值和相位上有差异；
• 经过线性化之后的输入输出关系
N (x)Y X 1 1A 1 2B 1 2 X arB c 1A 1 tg
• N (x) 被称为非线性特性的描述函数。
• 一般情况下，描述函数 N (x) 为入幅值 X 的函数，而与频率无关。当非线性特 性为单值时，相应的描述函数为一实 数，表示输入与输出是同相的。
7-4 典型非线性环节的描述函数
1 饱和非线性：
x2
x2
x2(t)KAsint
(Aa)
a
0
a
x1

0
t
KAsint 0t
x2(t)Ka,
t (Aa)
KAsint, t
• 本质非线性系统有以下特点： 1）初始条件与输入量对非线性系统的影响
非线性系统可能 会出现某一初始 条件下的响应过 程为单调衰减， 而在另一初始条 件下则为衰减振 荡，如图所示。
线性系统如果某系统在某初始条件下的响应过程 为衰减振荡，则其在任何输入信号及初始条件下 该系统的暂态响应均为衰减振荡形式。
x1 0 x1 0
在实际系统中死区可由众多原因引起，它对系统可产生不同 的影响：一方面它使系统不稳定或者产生自振荡；另一方面 有时人们又人为的引入死区特性，使系统具有抗干扰能力。
3、滞环（非单值特性）
x2 k x2 (m x1 s gn ax s1 gnx1)xx 2 ＝ 1 00,且 x20
滞环特性会 使系统的相 角裕度减小, 动态性能恶 化,甚至产生 自持振荡。
x2 x2m
a
x1
0a
x2m c)
x2 x2m
b a
x1
0
ab
x2m d)
4、继电器特性
x2

x2m


x2m
x2 x2m
x1 0
x2m
x2
x1 0
a)
b)
x2
x1 0
c)
继电器非线性会使系统产生自持振荡，甚至 会导致系统不稳定，并且使稳态误差加大。
初始条件不同时非线性系统不同的响应特性
2）系统的稳定性也与输入信号的大小、初 始条件有关
x& (1x)x0
（1）当初始条件xo＜1时,1－xo＞0,上式具有负 的特征根,其暂态过程按指数规律衰减,该系统稳 定。
（2）当xo=1时,1-xo=0,上式的特征根为零,其暂 态过程为一常量。
（3）当xo＞1时,1-xo＜0,上式的特征根为正值, 系统暂态过程指数规律发散,系统不稳定。