概率论与数理统计期末复习资料(学生)

概率论与数理统计总复习知识点归纳1.概率论的基础概念-随机事件、样本空间和事件的关系。

-频率和概率的关系，概率的基本性质。

-古典概型和几何概型的概念。

-条件概率和乘法定理。

-全概率公式和贝叶斯公式。

-随机变量和概率分布函数的概念。

-离散型随机变量和连续型随机变量的定义、概率质量函数和概率密度函数的性质。

2.随机变量的数字特征-随机变量的数学期望、方差、标准差和切比雪夫不等式。

-协方差、相关系数和线性变换的数学期望和方差公式。

-两个随机变量的和、差、积的数学期望和方差公式。

3.大数定律和中心极限定理-大数定律的概念和三级强大数定律。

-中心极限定理的概念和中心极限定理的两种形式。

4.数理统计的基本概念和方法-总体、样本和抽样方法的概念。

-样本统计量和抽样分布的概念。

-点估计和区间估计的概念。

-假设检验的基本思想和步骤。

-正态总体的参数的假设检验和区间估计。

5.参数估计和假设检验的方法和推广-极大似然估计的原理和方法。

-矩估计的原理和方法。

-最小二乘估计的原理和方法。

-一般参数的假设检验和区间估计。

6.相关分析和回归分析-相关系数和线性相关的概念和性质。

-回归分析的一般原理。

-简单线性回归的估计和检验。

7.非参数统计方法-秩和检验和符号检验的基本思想和应用。

-秩相关系数的计算和检验。

8.分布拟合检验和贝叶斯统计-卡方拟合检验的原理和方法。

-正态总体参数的拟合优度检验。

-贝叶斯估计的基本思想和方法。

9.时间序列分析和质量控制-时间序列的基本性质和分析方法。

-时间序列预测的方法和模型。

-质量控制的基本概念和控制图的应用。

以上是概率论与数理统计总复习知识点的归纳，希望对你的复习有所帮助。

概率统计期末知识点复习一、概率计算⒈事件的关系和运算⑴ 子事件(事件的包含)B A ⊂：若A 发生，则B 必然发生； ⑵ 相等事件A B =：B A ⊂且A B ⊃； ⑶ 并事件B A ：“,A B 中至少发生一个”； ⑷ 交（积）事件AB ：“,A B 都发生”； ⑸ 互不相容（互斥）事件:AB =∅； ⑹ 对立事件：若AB =Ω，且AB =∅，称B 为A 的对立事件，记为A B =．⑺ 差事件B A -：“A 发生，而B 不发生”． ⑻ 事件的运算律 ①交换律：A B B A =，AB BA =；②结合律：()()A B C A B C =，()()AB C A BC =； ③分配律：()A B C ACBC =，()()()AB C A C B C =；④摩根律：AB A B =，AB A B =．⒉概率计算的基本公式⑴非负性：设A 为任一随机事件，则0()1P A ≤≤． ⑵规范性：()1P Ω=，()0P ∅=． ⑶并事件概率计算公式：()()()()P AB P A P B P AB =+-；()()()()()()()()P A B C P A P B P C P AB P AC P BC P ABC =++---+．如果事件12,n A A A ,,两两互不相容，则1212()()()()n n P A A A P A P A P A =+++．⑷差事件概率计算公式：()()()()()P A B P AB P A AB P A P AB -==-=-； 若B A ⊂，则①()()()P A B P A P B -=-； ②()()P B P A ≤． ⑸对立事件概率计算公式：()1()P A P A =-．1A 2A 3A nA 21(|)P A A 1()P A 312(|)P A A A11(|)nnP A AA -B2A ∙1A nA 1()P A 2()P A ()n P A 1()P B A 2()P B A ()n P B A ⒊条件概率公式、乘法公式 ⑴条件概率：()P B A ．①公式法：()(),()0()P AB P B A P A P A =>；②代入法：改变样本空间直接计算．⑵乘法公式：()0P A >，有()()()P AB P A P B A =． 设12()0n P A A A >，2n ≥，则12()n P A A A 12131211()(|)(|)(|)-=n n P A P A A P A A A P A A A ．适用范围：链式结构⒋全概公式、逆概公式 ⑴全概率公式：1,,n A A 为一完备事件组，则1()()()ni i i P B P A P B A ==∑．适用范围：并列结构⑵贝叶斯公式(逆概公式):1()()()()()i i i nkkk P A P B A P A B P A P B A ==∑．⒌古典概型、几何概型、贝努里概型 ⑴古典概型：()A P A =事件所含样本点的个数所有样本点的个数．掌握简单的排列组合．⑵几何概型：()A P A =Ω的几何测度的几何测度，其中几何测度分别为长度或面积．对比均匀分布．⑶贝努里概型：在n 重贝努里试验中事件A 恰好发生k 次的概率为(1)kkn kn C p p --，其中0,1,2,,k n =，()p P A =，01p <<．对比二项分布．⒍事件的独立性⑴事件A 和B 相互独立的直观理解为事件A 和B 各自发生与否没有任何关系．并会根据实际问题判断事件A 和B 的独立性．⑵事件,A B 相互独立()()()P AB P A P B ⇔=(|)()(()0)P B A P B P A ⇔=>.⑶,,A B C 两两独立⇔()()(),()()(),()()().P AB P A P B P AC P A P C P BC P B P C =⎧⎪=⎨⎪=⎩⑷,,A B C 相互独立⇔,,()()()().A B C P ABC P A P B P C ⎧⎨=⎩两两独立,⑸独立性的有关结论：①设()0P B >，则事件A 和B 相互独立的充要条件为()()P A B P A =．②设,A B 为两个随机事件，如果A 和B 相互独立，则A 和B 相互独立；A 和B 相互独立； A 和B 也相互独立．③设,A B 为两个随机事件，且0()1P B <<，则A 和B 相互独立的充要条件为()()P A B P A B =．④如果随机事件12,,,n A A A 相互独立，则12,,,n A A A 的任一部分事件（至少两个事件）也相互独立．⑤如果随机事件12,,,n A A A 相互独立，则分别将i A 不变或换成i A 后所得事件仍相互独立．例如12,,,n A A A ，12,,,n A A A 等也分别相互独立．⑥如果随机事件1212,,,,,,,m n A A A B B B 相互独立，则由12,,,m A A A 组成的随机事件与由12,,,n B B B 组成的随机事件相互独立．⒎切比雪夫不等式（估计概率） 设μ=EX，2σ=DX ，则对任意的0ε>，有22{}1P X σμεε-<≥- 或22{}P X σμεε-≥≤．⒏利用分布计算概率⑴利用分布函数计算概率：①{}()()P a X b F b F a <≤=-，000{}()(0)P X x F x F x ==--等等． ②1212{,}<≤<≤P x X x y Y y 22211211(,)(,)(,)(,)F x y F x y F x y F x y =--+． ⑵利用分布律计算概率：①{}P X L ∈=i ix Lp ∈∑． ②(,){(,)}i j ij x y DP X Y D p ∈∈=∑．⑶利用密度函数计算概率：①{}{}P a X b P a X b <≤=≤≤{}P a X b =≤<{}P a X b =<<()b af x dx =⎰．②{(,)}(,)DP X Y D f x y dxdy ∈=⎰⎰．③00{}()X Y LP X L Y y f x y dx ∈==⎰；00{}()Y X LP Y L X x f y x dy ∈==⎰．二、随机变量的分布⒈分布函数及性质⑴一维随机变量的分布函数：(){},F x P X x x =≤-∞<<+∞． ⑵一维随机变量分布函数的性质：①0()1F x ≤≤； ②()0F -∞=，()1F +∞=； ③()F x 处处单调不减； ④()F x 处处右连续． ⑶二维随机变量的分布函数：(,){,}=≤≤F x y P X x Y y ，2(,)x y R ∈． ⑷二维随机变量分布函数的性质： ①0(,)1F x y ≤≤，其中2(,)x y R ∈；②(,)1,(,)(,)(,)0F F x F y F +∞+∞=-∞=-∞=-∞-∞=； ③(,)F x y 分别为关于变量x 和y 单调不减的函数； ④(,)F x y 分别关于变量x 和y 处处右连续． ⒉分布律及性质⑴一维离散型随机变量的分布律：{}i i P X x p ==，1,2,i =；或1212~i ix x x X p p p ⎛⎫⎪⎝⎭． ⑵一维离散型随机变量分布律的性质：①0i p ≥，1,2,i =； ②1iip=∑．⑶二维离散型随机变量的分布律：{,}i j ij P X x Y y p ===，1,2,,1,2,i j ==；或2j y121j p⑷二维离散型随机变量分布律的性质： ①0ij p ≥，1,2,,1,2,i j ==； ②1ijijp=∑∑．⒊密度函数及性质⑴一维连续型随机变量的密度()f x ：()f x 满足()()x F x f t dt -∞=⎰，x -∞<<+∞．⑵一维连续型随机变量密度函数的性质： ①()0,(,)f x x ≥∈-∞+∞； ②()1f x dx +∞-∞=⎰．⑶二维连续型随机变量的密度(,)f x y ：(,)f x y 满足(,)(,)x yF x y f u v dudv -∞-∞=⎰⎰，2(,)x y R ∈．⑷二维连续型随机变量密度函数的性质： ①(,)0≥f x y ，2(,)x y R ∈； ②(,)1f x y dxdy +∞+∞-∞-∞=⎰⎰．⒋常见分布及其数字特征⑴01-分布~(1,)X B p ：1{}(1)k k P X k p p -==-，0,1;,k EX p DX pq ===． ⑵二项分布(,)B n p ：{}(1),0,1,2,,,01kkn kn P X k C p p k n p -==-=<<；,EX np DX npq ==．应用背景．．：记X 为n 重贝努利试验中A 发生的次数．．,则(,)X B n p .⑶泊松分布()P λ：{},0,0,1,2,!kP X k e k k λλλ-==>=，EX DX λ==.⑷均匀分布~[,]X U a b ：1,,()0,a x b f x b a ⎧<<⎪=-⎨⎪⎩其它.()2,212b a a b EX DX -+==. ⑸指数分布()E λ：,0,()00,0.x e x f x x λλλ-⎧>=>⎨≤⎩,211,EX DX λλ==.⑹正态分布X ~),(2σμN：22()2()x f x μσ--=，x -∞<<+∞；2,EX DX μσ==.5．常见分布的性质⑴（了解）设随机变量12,,,n X X X 相互独立，且~(,),1,2,,i i X B n p i n =，则11~(,)nnii i i XB n p ==∑∑．特别地，设随机变量12,,,n X X X 相互独立，且~(1,),1,2,,i X B p i n =，则1~(,)nii XB n p =∑．反之，服从二项分布(,)B n p 的随机变量X 可以分解为n 个相互独立，且均服从(1,)B p 的随机变量12,,n X X X 之和．⑵（了解）设随机变量12,,,n X X X 相互独立，且~(),1,2,,i i X P i n λ=，则11~()nnii i i XP λ==∑∑．⑶（了解）设随机变量12,,,n X X X 相互独立，且~(),1,2,,i i X E i n λ=，则121min{,,,}~()nn i i X X X E λ=∑．⑷（了解）设随机变量12~[,]X U θθ，则12~[,](0)aX b U a b a b a θθ+++>；21~[,](0)aX b U a b a b a θθ+++<．⑸（了解）设二维随机变量(,)X Y 服从均匀分布，,,U aX bY V cX dY =+⎧⎨=+⎩且0ad bc -≠，则(,)U V 也服从均匀分布．⑹设随机变量2~(,)X N μσ，则22~(,)Y aX b N a b a μσ=++，其中0a ≠．特别地，~(0,1)X N μσ-．⑺设随机变量12,,,n X X X 相互独立，且2~(,),1,2,,i i i X N i n μσ=，12,,,n a a a 是不全为零的常数，则22111~(,)n n ni i i i i i i i i a X N a a μσ===∑∑∑．特别地，设随机变量12,,,n X X X 相互独立，且2~(,),1,2,,i X N i n μσ=，则211~(,)n i i X N n nσμ=∑． ⑻设二维随机变量(,)X Y 服从二维正态分布，,,U aX bY V cX dY =+⎧⎨=+⎩且0ad bc -≠，则(,)U V 也服从二维正态分布．⑼设二维随机变量221212(,)~(,,,,)X Y N μμσσρ，则X 和Y 相互独立⇔0ρ=．⒌边缘分布 ⑴离散型{}i ij jP X x p ==∑，1,2,i =；{}j ijiP Y y p==∑，1,2,j =．关于X 的边缘分布律可对表中的i j p 进行纵向求和即得；关于Y 的边缘分布律可对表中的i j p 进行横向求和即得．⑵连续型()(,)X f x f x y dy +∞-∞=⎰,x -∞<<+∞；()(,)Y f y f x y dx +∞-∞=⎰,y -∞<<+∞．()X f x 可通过在给定点x 处，),(y x f 的纵向积分（对y 从-∞到+∞积分）求得，()Y f y 可通过在给定点y 处，),(y x f 的横向积分（对x 从-∞到+∞积分）求得．⒍条件分布 ⑴离散型1212()~i jj ij j jjjx x x p p p X Y y p pp⎛⎫⎪= ⎪ ⎪⎝⎭；1212()~j ij i i i iiiy y y p Y X x p p p p p ⎛⎫⎪= ⎪ ⎪⎝⎭． ⑵连续型(,)()()X Y Y f x y f x y f y =，x -∞<<+∞；(,)()()Y X X f x y f y x f x =，y -∞<<+∞．⒎随机变量的独立性⑴随机变量X 和Y 相互独立的直观意义是指X 和Y 的各自取值情况没有任何关系． ⑵利用分布函数：(,)()()X Y F x y F x F y =． ⑶利用分布律：ij i j p p p =，1,2,,1,2,i j ==．⑷利用密度函数：(,)()()X Y f x y f x f y =． ⑸随机变量独立性的有关结论①设随机变量X 与Y 相互独立，则对任意实数集合12,L L ，有1212{,}{}{}P X L Y L P X L P Y L ∈∈=∈∈．②如果随机变量12(,,,)m X X X 和12(,,,)n Y Y Y 相互独立，,g h 分别为m 元连续函数和n 元连续函数，则随机变量12(,,,)m g X X X 与12(,,,)n h Y Y Y 也相互独立．特别地，设随机变量X 与Y 相互独立，(),()g x h y 是连续函数，则随机变量()g X 与()h Y 也相互独立．⒏随机变量函数的分布⑴离散型随机变量函数的分布可直接列表求得． ⑵连续型随机变量函数分布采用分布函数法①()Y g X =：先求()(){}{()}()Y X g x yF y P Y y P g X y f x dx ≤=≤=≤=⎰,②(,)Z g X Y =：先求(,)(){}{(,)}(,)Z g x y zF z P Z z P g X Y z f x y dxdy ≤=≤=≤=⎰⎰，然后对y 或z 进行讨论然后求导数.⑶熟记1max i i nM X ≤≤=和1min i i nN X ≤≤=的分布函数和密度函数公式.①若随机变量12,,,n X X X 相互独立，i X 的密度函数为()i f x ，分布函数为()i F x ，1,2,,i n =，则M 和N 的分布函数(),()M N F x F x 和密度函数(),()M N f x f x 分别为12(){}()()()M n F x P M x F x F x F x =≤=，()()M Mf x F x '=； ()()()12(){}1[1][1][1]N n F x P N x F x F x F x =≤=----，()()N Nf x F x '=． ②当12,,,n X X X 独立同分布时，()()i f x f x =，()()i F x F x =，1,2,,i n =，则 ()[()]n M F x F x =，1()[()]()n M f x n F x f x -=；()1[1()]n N F x F x =--，1()[1()]()n N f x n F x f x -=-．⒐数字特征计算⑴数学期望(均值)：①一维随机变量函数的数学期望：1(),(())()().i i i g x p E g X g x f x dx ∞=+∞-∞⎧⎪=⎨⎪⎩∑⎰注: 2,()EX E X 为其特例．②二维随机变量函数的数学期望：11(,),((,))(,)(,).i j i j i j g x y p E g X Y g x y f x y dxdy ∞∞==+∞+∞-∞-∞⎧⎪⎪=⎨⎪⎪⎩∑∑⎰⎰注: 22,(),,(),()EX E X EY E Y E XY 为其特例．⑵方差：222()()()DX E X EX E X EX =-=-．⑶协方差：ov(,)[()()]()C X Y E X EX Y EY E XY EXEY =--=-．⑷相关系数：XY ρ=．⑸数字特征的性质（见教材）． ⑹不相关：①若0XY ρ=，称X 与Y 不相关；X 与Y 不相关的直观意义指X 与Y 没有线性关系． ②X 与Y 不相关ov(,)0C X Y ⇔=()D X Y DX DY ⇔±=+()E XY EXEY ⇔=．③设221212(,)~(,,,,)X Y N μμσσρ，则X 与Y 的相关系数XY ρρ=．④设221212(,)~(,,,,)X Y N μμσσρ，则X 和Y 相互独立⇔0ρ=⇔X 与Y 不相关．⑤如果X 与Y 相互独立，且X 与Y 的相关系数XY ρ存在，则X 与Y 不相关．反之未必．⒑中心极限定理的应用 ⑴设12,,n X X X 独立同分布，且2,0i i EX DX μσ==≠(1,2,)i =，则当n 充分大（30n ≥）时，有21~(,)nii XN n n μσ=∑近似．⑵设~(,)X B n p ，则当n 充分大（30n ≥）时，~(,(1))X N np np p -近似．三、计算过程中需要分段讨论的几种类型与方法⒈已知X 的分布律，求X 的分布函数()F x ．三个特征： ⑴分1n +段；⑵每段上，将概率逐次累加（初始值为0，终值为1）； ⑶每个区间为左闭右开． ⒉已知X 的密度函数()f x （分段函数），求X 的分布函数()F x ． ⑴分1n +段；⑵每段上，将()f x 在(,]x -∞上积分；⑶由于()F x 为连续函数，故每个区间为开闭均可．⒊已知(,)X Y 的密度函数(,)f x y （分段函数），求X 的分布函数(,)F x y ． ⑴结合(,)F x y 的原理图和(,)f x y 特征图，将全平面分若干块； ⑵每块上，将(,)f x y 在区域(,](,]x y D -∞⨯-∞上积分．⒋连续型随机变量函数的分布⑴一维连续型随机变量函数()Y g X =的分布函数()Y F y ：①先确定()Y g X =取值范围；例如m Y M ≤≤，其中,m M 为实数，则采用三段式讨论．②当y m <时，()0Y F y =．③当m y M <≤时，利用定积分()()()Y X g x yF y f x dx ≤=⎰计算．④当y M ≥时，()1Y F y =．⑤当m =-∞或M =+∞或其它情况时，还可能采用两段式或四段式讨论等． ⑥若Y 为连续型随机变量，则Y 的密度函数()()Y Y f y F y '=． ⑵二维连续型随机变量函数(,)Z g X Y =的分布函数()Z F z ：①确定(,)Z g X Y =的取值范围；例如m Z M ≤≤，其中,m M 为实数，则采用三段式讨论．②当z m <时，()0Z F z =．③当m z M <≤时，利用二重积分(,)()(,)Z g x y zF z f x y dxdy ≤=⎰⎰计算．④当z M ≥时，()1Z F z =．⑤当m =-∞或M =+∞或其它情况时，还可能采用两段式或四段式讨论等． ⑥若Z 为连续型随机变量，则Z 的密度函数()()Z Z f z F z '=． ⒌二维连续型随机变量(,)X Y 的边缘密度 ⑴()(,)X f x f x y dy +∞-∞=⎰，x -∞<<+∞．①作出),(y x f 的特征图．②用垂直直线x m =和x M =将D 夹住． ③当x m <或x M >时，()0X f x =． ④当m x M ≤≤时，()(,)X f x f x y dy +∞-∞=⎰．⑤当m =-∞或M =+∞或其它情况时，也可能采用其它方式讨论． ⑵()(,)Y f y f x y dx +∞-∞=⎰,y -∞<<+∞．①作出),(y x f 的特征图．②用水平直线y m =和y M =将D 夹住． ③当y m <或y M >时，()0Y f y =． ④当m y M ≤≤时，()(,)Y f y f x y dx +∞-∞=⎰．⑤当m =-∞或M =+∞或其它情况时，也可能采用其它方式讨论．四、数理统计的基础知识⒈总体X ，样本12(,,,)n X X X 和观察值的概念．关注简单随机样本的独立性和代表性．⒉常用统计量：样本均值∑==n i i X n X 11，样本方差2211()1n i i S X X n ==--∑， 顺序统计量*11min i i nX X ≤≤=，*1max n i i nX X ≤≤=．⒊常见分布⑴正态分布：见概率论中的内容． ⑵2χ分布：设12(,,,)n X X X 为来自总体~(0,1)X N 的一个样本，就称统计量22222121ni ni X X X X ===+++∑χ服从自由度为n 的2χ分布，记作)(~22n χχ． ①设)(~22n χχ，则2()E n =χ，2()2D n =χ． ②设~(0,1)X N ，则22~(1)X χ．③设22~()i i n χχ，1,2i =，且2212,χχ相互独立，则2221212~()n n ++χχχ．⑶ t 分布：设随机变量~(0,1)X N ，2~()Y n χ，且X 与Y 相互独立，就称T =服从自由度为n 的t 分布，记作)(~n t T ．⑷F 分布：设随机变量)(~12n X χ，)(~22n Y χ，且X 与Y 相互独立，就称21n Y n X F =服从第一自由度为1n ，第二自由度为2n 的F 分布，记作),(~21n n F F ． ①如果~()T t n ，则2~(1,)T F n ． ②如果12~(,)F F n n ，则211~(,)F n n F． ⒋上侧分位点p x ：{},{}1p p P X x p P X x p ≥≥≤≥-． 如U α，2()t n α，21()n αχ-，2121(,)Fn n α-等等（下标为该点处右侧的面积）． 注意：1U U αα-=-，1()()t n t n αα-=-，112211(,)(,)F n n F n n αα-=．⒌单正态总体2~(,)X N μσ中X 和2S 的分布（其中12(,,,)n X X X 为样本）： ⑴2~(,)X N nσμ，或nX /σμ-~)1,0(N ；⑵nS X /μ-～)1(-n t ；⑶2212()()nii Xn μχσ=-∑；⑷222122()(1)(1)nii XX n Sn χσσ=--=-∑,且X 与2S 相互独立．五、参数估计⒈点估计 ⑴矩估计：①原理：用样本矩估计理论矩．②方法：建立方程（组）11()n rr i i X E X n ==∑，1,2,r =，解出θ，得θ的矩估计θ．⑵最大似然估计：①原理：概率最大的事件最有可能出现． ②方法：构造似然函数)(L θ=12)(,,,;n L x x x θ（似然函数体现了样本12(,,,)n X X X 出现的概率大小），求似然函数L 的最大值点，即为θ的极大使然估计θ． ③步骤：第一步：写出似然函数)(L θ．如果连续型总体X 的密度函数为(;)f x θ，则1()(;)n i i L f x θθ==∏．如果离散型总体X 的分布律为(;)p x θ，则1()(;)ni i L p x θθ==∏． 第二步：取对数ln )(L θ，并令ln 0)(d d L θθ=，或ln 0)(i L θθ∂=∂，1,2,,i k =，建立方程(组)．如果从中解得惟一驻点θˆ，则θˆ即为θ的最大似然估计； 第三步：如果上述方程无解，则通过单调性的讨论，在某边界点处，求出θ的最大似然估计量θˆ． ⒉估计量的评价标准⑴无偏性：如果E θθ=，就称θ为θ的无偏估计．主要结论有：①如果总体X 的数学期望EX 存在，则X 是μ的无偏估计，即E X μ=． ②如果总体X 的方差DX 存在，则2S 是2σ的无偏估计，即22()E S σ=．③设估计量12ˆˆˆ,,m θθθ均为θ的无偏估计，12,,,m c c c 为常数，且11mi i c ==∑，则1ˆmi i i c θ=∑仍为θ的无偏估计．注意：即使ˆθ为θ的无偏估计，而ˆ()g θ未必为．．．()g θ的无偏估计． ⑵（较）有效性：设21ˆ,ˆθθ均为θ的无偏估计，如果12ˆˆD D θθ<，就称1ˆθ比2ˆθ有效．⑶一致性（相合性）：设ˆθ为θ的估计量，如果对任意的0ε>，均有ˆl i m {}1n P θθε→∞-<=，就称θˆ为θ的一致估计量或相合估计量． ⒊单正态总体2(,)N μσ中2,σμ的区间估计⑴2σ已知，μ的置信度1α-的置信区间为22X u X u αα⎛⎫-+ ⎝． ⑵2σ未知，求μ的置信度为1α-的置信区间为2(X t n α⎛⎫±- ⎝． ⑶2σ的置信度为1α-的置信区间为2222122(1)(1),(1)(1)n Sn S n n ααχχ-⎛⎫-- ⎪ ⎪-- ⎪⎝⎭． 六、假设检验⒈假设检验的有关概念了解假设检验的背景，假设的提法，假设检验中的反证法思想，假设检验的基本原理，显著性检验，双侧检验和单侧检验等相关内容．⒉假设检验的两类错误⒊假设检验的四个步骤⑴根据给定的问题，建立假设检验问题01(,)H H ． ⑵根据检验问题01(,)H H 及条件，选择检验统计量12(,,,)n g X X X ．当0H 为成立时，确定该统计量12(,,,)n g X X X 的分布．⑶根据显著性水平α，确定临界值和原假设0H 的拒绝域W ． ⑷通过样本值12(,,,)n x x x ，计算统计量12(,,,)n g X X X 的值12(,,,)n g x x x ．若12(,,,)n g x x x W ∈，则拒绝0H ，否则接受0H ．⒋单正态总体中均值和方差的假设检验。

概率论与数理统计复习资料要点总结--学⽣《概率论与数理统计》复习资料⼀、复习提纲注：以下是考试的参考内容，不作为实际考试范围，仅作为复习参考之⽤。

考试内容以教学⼤纲和实施计划为准；注明“了解”的内容⼀般不考。

1、会事件关系的运算，了解概率的古典定义2、能较熟练地求解古典概率；了解概率的公理化定义3、掌握概率的基本性质和应⽤这些性质进⾏概率计算；理解条件概率的概念；掌握加法公式与乘法公式4、能准确地选择和运⽤全概率公式与贝叶斯公式解题；掌握事件独⽴性的概念及性质。

5、理解随机变量的概念，掌握离散性随机变量分布率的性质及求法,掌握(0—1)分布、⼆项分布、泊松分布的分布律。

6、理解分布函数的概念及性质，理解并掌握连续型随机变量的概率密度及性质。

7、掌握指数分布(参数λ)、均匀分布、正态分布8、会求特殊的⼀维随机变量函数分布的分布律或概率密度。

9、会求分布中的待定参数。

会求区间的概率.10、会求边缘分布律、边缘密度函数，会判别随机变量的独⽴性。

11、掌握⼆维连续型随机变量未知参数的计算,落在区域概率的计算。

12、理解⼆维随机变量的概念，理解⼆维随机变量的联合分布函数及其性质，掌握⼆维离散型随机变量的联合分布律及其性质，掌握⼆维连续型随机变量的联合概率密度及其性质，并会⽤它们计算有关事件的概率。

13、会求⼆维离散型随机变量函数的分布率.14、掌握数学期望和⽅差的定义及性质,会熟练地求随机变量及其函数的数学期望和⽅差。

会熟练地默写出⼏种重要随机变量的数学期望及⽅差。

15、较熟练地求协⽅差与相关系数.16、会⽤独⽴正态随机变量线性组合性质解题。

17、理解总体、样本、简单随机样本、统计量及抽样分布概念，样本均值与样本⽅差及样本矩概念，掌握χ2分布(及性质)、t 分布、F 分布及其分位点概念。

18、理解正态总体样本均值与样本⽅差的抽样分布定理；会⽤矩估计⽅法来估计未知参数。

19、掌握极⼤似然估计法，⽆偏性与有效性的判断⽅法。

《概率论与数理统计（A ）》期末复习资料一、选择题：1.设A ，B 为两个任意事件，那么与事件B A B A B A ++相等的事件是（）．(A) AB (B) B A + (C) A (D) B2.设B A ,为两个随机事件，若0)(=AB P ，则( ).(A)A 和B 两事件互不相容(互斥)； (B)AB 是不可能事件； (C)AB 未必是不可能事件； (D)0)(=A P 或0)(=B P . 3.如果0)(=AB P ，则( ).(A))()(A P B A P =-； (B)A 与B 不相容； (C)A 与B 不相容； (D))()()(B P A P B A P -=-. 4.如果1)()(=+B P A P ，则( ).(A)1)(=⋃B A P ； (B)0)(=⋂B A P ； (C))()(B A P B A P ⋂=⋂； (D))()(B A P B A P ⋃=⋂. 5.设A 和B 相互独立，则下列结论错误的是( ).(A)B ,A 独立； (B)B ,A 独立； (C))()()(B P A P B A P =； (D)φ=AB .6.设B A ⊂且相互独立，则( ).(A)0)(=A P ； (B)1)(0)(==B P A P 或； (C)1)(=A P ； (D)上述都不对. 7.设随机变量~(2,)X B p ，若()159X P ≥=，则p =( ). (A)32； (B)21； (C)31； (D)2719.8.设随机变量X 概率分布为,,2,1)1()( =+==k k k ak X P ，则a 为( ).(A)0； (B)1； (C)2； (D)3.9.设随机变量X 服从泊松分布，且(1)(2)P X P X ===，则λ=( ). (A)2； (B)1； (C)4； (D)0.5.10.若)(x f 与)(x F 分别为连续型随机变量X 的密度函数与分布函数,则等式（ ）成立．(A) X a P <(≤⎰∞+∞-=x x F b d )() (B) X a P <(≤⎰=bax x F b d )()(C) X a P <(≤⎰=b ax x f b d )() (D) X a P <(≤⎰∞+∞-=x x f b d )()11.设随机变量),(~2σμN X ，且022=++X x x 无实根的概率为0.5，=μ( ). (A)-1； (B)0； (C)1； (D)2.12.随机变量),(Y X 的联合概率密度为⎩⎨⎧<<<<=其他,0,20,20,),(y x cx y x f ，则c 为( ).(A)0.25； (B)1； (C)2； (D)4.13.设随机变量Y X ,相互独立，它们的密度函数分别为⎩⎨⎧≤>=-000x ,;x ,e )x (f x X ，⎩⎨⎧≤>=-00022y ,;y ,e )y (f y Y ，则=>)Y X (P ( ).(A)31； (B)21； (C)32； (D)43.14.设X ～)4,2(N 且b aX +～)1,0(N ，则( ). (A)22-==b a ，； (B)12-=-=b a ，； (C)121==b a ，； (D)121-==b a ，.15.设)1(~P X ,)2(~P Y ,且X 与Y 相互独立,则~Y X +( ). (A) (1,2)b (B) (3)P (C) (1.5)P(D) (2,1)b16.设随机变量)6.0,20(~b X ,)6.0,10(~b Y ,且X 与Y 相互独立,则~Y X +( ). (A) (10,0.6)b (B) (20,0.6)b (C) b(30,0.6) (D) (18)P17.设),(~p n b X 且6 3.6EX DX ==，,则有()(A) 100.6n p ==， (B) 200.3n p ==，(C) 150.4n p ==， (D) 120.5n p ==， 18.设12,,n X X X 是取自正态总体X ～)1,0(N 的样本，2,S X 分别是样本均值和样本方差，则下列结论正确的是( ).(A)X ～)1,0(N ； (B)X n ～)1,0(N ； (C)S X /～)1(-n t ； (D)∑=ni i X 12～)(2n χ.19.设n X X X 21,是取自正态总体X ～),(2σμN 的样本（2>n ）, 2,S X 分别是样本均值和样本方差，则下列结论正确的是( ).(A)1--n SX μ～)1(-n t ； (B)22)(S X n μ-～)1,1(-n F ； (C)22σS ～)1(2-n χ； (D)122X X -～),(2σμN .20.设12,,,n X X X 为来自正态总体2(,)N μσ的一个样本，2211(())1ni i S X X n ==--∑ X 分别为样本方差和样本均值，则下面结论中不正确的是( ). (A)2~(,)X N n σμ ；(B)22()E S σ=； (C)22()1nE S n σ=-； (D)222(1)/~(1)n S n σχ--. 21.已知随机变量X 与Y 相互独立,且2~(40)X χ,2~(80)Y χ,则~/2Y X ().(A)2(40)χ (B) (20,40)F (C) (40,80)F (D) 2(80)χ22.设n X X X ,,,21 是来自正态总体N (,)μσ2的样本，则（ ）是μ无偏估计．(A) 321X X X ++ (B) 321525252X X X ++ (C) 321515151X X X ++ (D) 321535151X X X ++23.对正态总体),(2σμN 的假设检验问题中,Z 检验解决的问题是（ ）． (A) 已知方差,检验均值 (B) 未知方差,检验均值(C) 已知均值,检验方差 (D) 未知均值,检验方差24.对来自正态总体X N ~(,)μσ2（μ未知）的一个样本X X X 123,,,则下列各式中（ ）不是统计量．(A)1X (B) μ+X(C)221σX (D)1X μ25.设n X X X ,,,21 是正态总体),(~2σμN X （2σ已知）的一个样本,按给定的显著性水平α检验0H ：0μμ=（已知）；1H ：0μμ≠时,判断是否接受0H 与（ ）有关.(A) 样本值,显著水平α (B) 样本值,样本容量(C) 样本容量n ,显著水平α (D) 样本值,样本容量n ,显著水平α 26.在对单正态总体N (,)μσ2的假设检验问题中,T 检验法解决的问题是（ ）． (A) 已知方差,检验均值 (B) 未知方差,检验均值 (C) 已知均值,检验方差 (D) 未知均值,检验方差 27.假设检验时,若增大样本容量,则犯两类错误的概率（ ）． (A) 有可能都增大 (B) 有可能都减小(C) 有可能都不变 (D) 一定一个增大,一个减小二、填空题：1.设B A ,是两个事件，且=)(B A P 1，则=-)(A B P .2.设()0.7P A =，()0.3P A B -=，则()AB P = ，()B A P = .3.设事件B A ,和B A ⋃的概率分别为0.2，0.3和0.4，则=)(A B P _______.4.设B A ,是两个随机事件，()0.4()0.3P A P B ==，，若B A ,相互独立，则()P A B ⋃= ，则()P B A = .5.三个人独立地向一架飞机射击，每个人击中飞机的概率都是0.4，则飞机被击中的概率为 .6.设甲、乙两人投篮命中率分别为0.7和0.8，每人投篮3次，则有人投中的概率为 .7.从0,1,2,,9这10个数字中任意选出3个不同的数字，则3个数字中不含0或5的概率为 .8.某工厂一个班组共有男工9人，女工5人，现在要选出3个代表，则选的3 个代表中至少有1个女工的概率为 .9.设随机变量X 服从参数为λ的泊松分布，且()2D X =，则(1)p X ==________. 10.设随机变量),(N ~X 42，则~X Y 22-=. 11.设随机变量Y 在]5,0[上服从均匀分布，则关于x 的一元二次方程02442=+++Y xY x 有实根的概率为 .12.设)(1x F 与)(2x F 分别是任意两个随机变量分布函数，令=)(x F)()(21x bF x aF +，则下列各组数中使)(x F 为某随机变量的分布函数的有 =a ， =b .13.已知连续随机变量X 的分布函数为1,0()0,0x e x F x x λ--≥=<⎧⎨⎩，0λ>，则其密度函数为 ，(2)P x ≤= ；已知随机变量X 的密度函数⎩⎨⎧≤≤=其它 , 010,2)(x x x f 则:)5.15.0(<<X p = .14.设随机变量X 分布律为令,12+=X Y 则随机变量X 分布律为 ;=)(Y E _________.15.若二维随机变量(,)X Y 具有分布律：则(21)P Y X ===________. 16.设随机变量X 分布列如下表则E (X )=________，D (X )=________.17.两独立随机变量X Y 和都服从正态分布，且()()~3,4~2,9X N Y N ，，则()D X Y +=________;又两个相互独立的随机变量~(3),V ~P(2)U E ,则(22)D U V ++=________.18.设X 服从[-1，2]上的均匀分布，令⎩⎨⎧<-≥=,01,01X X Y ，，则=)(Y E ，=)(Y D .19.设相互独立的随机变量X ,Y 均服从参数为5的指数分布，则当0,0x y >>时，(,)X Y 的概率密度(,)f x y =________.20.设总体)1,0(~N X ,1210,,,X X X 是来自总体X 的样本，则~X .21.设总体2~(0,)X N σ，921,X X X 为总体的一个样本，则)(9196521X X X X X X ++++++= 分布为 .22.设),(21n X X X 是取自参数为λ泊松分布的样本，则统计量i ni X Y ∑==1服从分布.23.设12n X X X ,,,为来自总体X 的样本，且~(0,1)X N ，则统计量21~nii X=∑ .24.设12,,,n X X X 是来自总体)1,0(~N X 的简单随机样本，则21()ni i X X =-∑服从的分布为 .25.设n X X X 21,是来自正态总体X ～N (μ，2σ)的样本，即它们是独立同分布，则~X ，~)1(22σS n - .26.在单边假设检验中,原假设为0H ：μ≤0μ,则其备择假设为1H ：_______________.27.设总体X 服从正态分布2(,)N μσ,其中2σ未知,12,,n X X X 为其样本.若假设检验问题为0010:,:,H H μμμμ=≠则采用的检验统计量表达式应为_______________.三、计算题1.一个袋内装有大小相同的7个球，其中4个是白球，3个是黑球，从中一次抽取3个，计算至少有两个是白球的概率.2.有甲、乙两批种子，发芽率分别为0.8和0.7，在两批种子中各随机取一粒，求： (1)两粒都发芽的概率；(2)至少有一粒发芽的概率；(3)恰有一粒发芽的概率.3.某地某天下雪的概率为0.3，下雨的概率为0.5，既下雪又下雨的概率为0.1,求： (1)在下雨条件下下雪的概率；(2)这天下雨或下雪的概率.4.已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率（假设男人和女人各占人数的一半）.5.某工厂生产的产品中96%是合格品,检查产品时,一个合格品被误认为是次品的概率为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.6.甲、乙、丙三人独立地向同一飞机射击，设击中的概率分别是0.4,0.5,0.7，若只有一人击中，则飞机被击落的概率为0.2；若有两人击中，则飞机被击落的概率为0.6；若三人都击中，则飞机一定被击落，求：飞机被击落的概率.7.有一繁忙的汽车站,每天有大量汽车通过,设每辆车在一天的某时段出事故的概率为0.0001,在某天的该时段内有1000辆汽车通过,问出事故的次数不小于2的概率是多少（利用泊松定理）？8.有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险.在一年中每个人死亡的概率为0.002，每个参加保险的人在1月1日须交12元保险费，而在死亡时家属可从保险公司领取2000元赔偿金.求： (1)保险公司亏本的概率；(2)保险公司获利分别不少于10000元、20000元的概率.9.设某种仪器内装有三只同样的电子管，电子管使用寿命X 的密度函数为f (x )=⎪⎩⎪⎨⎧<≥.100,0,100,1002x x x求：(1)在开始150小时内没有电子管损坏的概率；(2)在这段时间内有一只电子管损坏的概率； (3)F (x ).10.某教科书出版了2000册,因装订等原因造成错误的概率为0.001,试求在这2000册书中恰有5册错误的概率.11.由某机器生产的螺栓长度（cm ）~(10.05,0.062)X N ,规定长度在10.050.12±内为合格品,求一螺栓为不合格品的概率..12.设一工厂生产的电子管寿命X （小时）服从正态分布),160(2δN ,若要求{}8.0200120≥≤<X P ,允许δ最大不超过多少？13.设X ~N （3，22），(1)求P {2<X ≤5}，P {4<X ≤10}，P {｜X ｜＞2}，P {X ＞3}; (2)确定c 使P {X ＞c }=P {X ≤c }.14.将一硬币抛掷三次，以X 表示在三次中出现正面的次数，以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律.（2）求（X ，Y ）的边缘分布律； （3）求W =X +Y 的分布律.16.设随机变量(X ，Y )的概率密度为()⎩⎨⎧<<<<--=.,0,42,20),6(,其他y x y x k y x f (1)确定常数k ；(2)求P {X ＜1，Y ＜3}； (3)求P {X <1.5}； (4)求P {X +Y ≤4}.17.设二维随机变量（X ，Y ）的联合分布函数为()⎩⎨⎧>>--=--.,0,0,0),e 1)(e 1(,24其他y x y x F y x求(X ，Y )的联合分布密度.18.设随机变量X 的概率密度为()⎪⎩⎪⎨⎧≤≤-<≤-+=.,0,10 ,1,01 ,1其他x x x x x f求)()(X D X E ，.19.设随机变量X 的概率密度为()⎪⎩⎪⎨⎧≤≤-<≤=.,0,21,2,10,其他x x x x x f求)()(X D X E ，.20.设随机变量(X ，Y )的概率密度为()⎩⎨⎧<<<<=.,0,0,10,,其他x y x k y x f 试确定常数k ，并求)(XY E .21.设X ，Y 是相互独立的随机变量，其概率密度分别为()⎩⎨⎧≤≤=;,0,10,2其他x x x f X ()(5)e ,5,0,.y Y y f y --⎧>=⎨⎩其他 求E (XY ).22.设总体X 服从二项分布b (n ，p )，n 已知，X 1，X 2，…，X n 为来自X 的样本，求参数p 的矩估计.23.设总体X 的密度函数()2(x )2,,f x e x R μμ--=∈X 1，X 2，…，X n 为其样本，试求参数μ的矩估计. 24.设12,,,n x x x 为来自正态总体2~N(,)X μδ的一个样本的X1，X2， (X)观测值，试求总体未知参数2,μδ的极大似然估计.25.设总体X 的密度函数为⎩⎨⎧<<=-.,0,10,),(1其他x x x f θθθn X X X 21,为其样本，求θ 的极大似然估计.26.某车间生产的螺钉，其直径2~N(,)X μδ，由过去的经验知道2δ=0.06,今随机抽取6枚，测得其长度（单位mm ）如下：14.7 15.0 14.8 14.9 15.1 15.2 求μ的置信概率为0.95的置信区间.27.来自正态总体2~N(,)X μδ的一个样本为X 1，X 2，…，X n ，并且2μδ未知，已知，求μ的置信概率为1α-的置信区间.28.在正常状态下，某种牌子的香烟一支平均1.1克，若从这种香烟堆中任取36支作为样本；测得样本均值为1.008（克），样本方差2s =0.1(2g ).问这堆香烟是否处于正常状态.已知香烟（支）的重量（克）近似服从正态分布（取α=0.05）.。

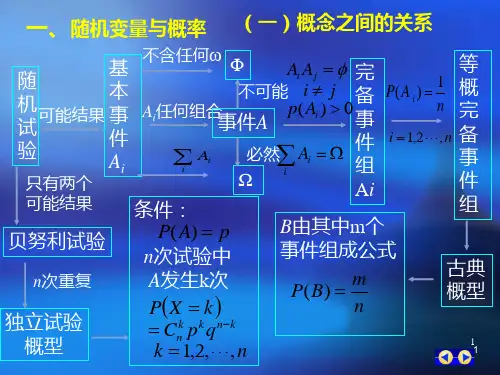
概率论与数理统计总复习本课件仅供用作《概率论与与数理统计》课程复习1一、随机事件与概率主要问题: 事件间的关系与运算, 条件概率，乘法公式, 全概率公式, 贝叶斯公式,事件的独立性, Bernoulli概型.常见考点: 全概率公式和Bayes 公式; 加法公式与乘法公式.2同则结合异则分配34由因说果执果溯因5•若P(AB)=0，则P(ABC)=0？P ABC=P C AB P(AB)•Bernoulli概型（n重Bernoulli试验）随机试验只有两个可能结果A,A，记P A=p,P A=q，把该随机试验独立地重复n次记B 为“在n重Bernoulli试验中事件A恰好发生k次”，则P B k=C n k p k q1 k,0≤k≤n6P AB=P A −B =P(A −AB)•对立和互斥之间的关系：除A⋂B =∅外，互斥还要求A⋃A =ΩΩABA ΩA BA −BA −B78910二、随机变量及其概率分布求密度函数f(x); 求分布函数F xf(x),F(x) 的性质：F x =P X ≤x F x = f(t)xdtf x dx=1P x 1<X ≤x 2=F x 2−F x 1= f x dxx 2x 1做完一定要验算：F′(x)=f(x)！11121314已知连续型随机变量X的概率密度f x 求随机变量Y=g(X) 的概率密度f (y)• 分布函数微分法*• 积分转化法f xϕxdx=f(ϕ(x))ϕ′(x)更一般地1516积分转化法（容易推广到多维随机变量情形）设随机变量X 的概率密度为fx ，g(x)是连续或单调函数，Y =g(X)。

如果对任何有界连续函数ℎ(x)，成立ℎg x f x dx= ℎ(y)p y dy其中，−∞≤α<β≤∞，则Y =g(X)的概率密度为f y =p y ,α<y <β0, 其他换元、交换积分次序等变换17181920六种重要分布（三种离散型+三种连续型）1、如果随机试验只有两个结果：A 与A ，则称该试验为Bernoulli 试验。

概率论与数理统计复习资料### 概率论与数理统计复习资料#### 第一章：概率论基础1. 概率的定义与性质- 事件的概率定义- 概率的公理化体系- 概率的加法和乘法规则2. 条件概率与事件独立性- 条件概率的计算- 事件独立性的定义与性质- 贝叶斯定理3. 随机变量及其分布- 离散型随机变量及其分布律- 连续型随机变量及其概率密度函数- 随机变量的期望值与方差4. 多维随机变量及其分布- 联合分布函数- 边缘分布函数- 协方差与相关系数5. 大数定律与中心极限定理- 切比雪夫不等式- 伯努利大数定律- 中心极限定理的应用#### 第二章：数理统计基础1. 样本与统计量- 样本均值、方差与标准差- 样本矩- 顺序统计量2. 参数估计- 点估计与区间估计- 估计量的优良性准则- 极大似然估计3. 假设检验- 假设检验的基本原理- 单样本假设检验- 双样本假设检验4. 方差分析- 单因素方差分析- 双因素方差分析- 方差分析的计算步骤5. 回归分析- 一元线性回归- 多元线性回归- 回归模型的诊断#### 第三章：概率分布与随机过程1. 常见概率分布- 二项分布- 泊松分布- 正态分布2. 随机过程的基本概念- 随机过程的定义- 马尔可夫链- 泊松过程3. 随机过程的参数估计- 随机过程的均值与方差估计- 随机过程的回归分析4. 随机过程的模拟- 蒙特卡洛方法- 随机模拟的应用5. 随机过程的统计推断- 随机过程的假设检验- 随机过程的参数估计#### 第四章：统计决策与贝叶斯统计1. 统计决策理论- 损失函数- 风险函数- 决策规则2. 贝叶斯统计- 贝叶斯后验概率- 贝叶斯估计- 贝叶斯决策3. 贝叶斯网络- 贝叶斯网络的结构- 贝叶斯网络的推理- 贝叶斯网络的应用4. 统计推断的贝叶斯方法- 贝叶斯假设检验- 贝叶斯参数估计5. 贝叶斯模型选择- 贝叶斯信息准则- 交叉验证通过以上内容的复习，可以对概率论与数理统计的基本概念、理论及其应用有一个系统的理解。

概率论与数理统计第一章期末复习(一)随机事件1.随机现象定义1在一定的条件下，并不总是出现相同结果的现象称为随机现象．定义2只有一个结果的现象称为确定性现象．2.样本空间定义3一个试验如果满足下述条件：(1)试验可以在相同的情形下重复进行；(2)试验的所有可能结果是明确可知的，并且不止一个；(3)每次试验总是恰好出现这些可能结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果．就称这样的试验是一个随机试验，记作E．定义4随机试验E的所有可能结果组成的集合称为E的样本空间，记作Ω．样本空间的元素，即E的每个结果，称为样本点，记作ω．3.随机事件定义5随机试验的某些样本点的集合称为随机事件，简称事件，常用大写英文字母A，B，C，…表示．定义6由样本空间Ω中的单个元素组成的子集称为基本事件．而样本空间Ω的最大子集(即Ω本身)称为必然事件，样本空间Ω的最小子集(即空集∅)称为不可能事件．4.事件的关系与运算下面的讨论总是假设在同一个样本空间Ω中进行．1)包含关系⊂如果属于A的样本点必属于B，则称A包含于B或称B包含A，记作A B ⊃．用概率的语言说：事件A发生必然导致事件B发生．或B A对任一事件A，必有∅Ω⊂A．⊂2)相等关系如果属于A的样本点必属于B，且属于B的样本点必属于A，即BA⊂且=．AB⊂，则称事件A与B相等，记作A B3)互不相容(互斥)如果A 与B 没有相同的样本点，则称A 与B 互不相容(互斥)．即事件A 与事件B 不可能同时发生．4)两事件的和事件“事件A 与B 中至少有一个发生”，这样的一个事件称作事件A 与B 的和(或并)，记作B A ．5)两事件的积事件“事件A 与B 同时发生”，这样的一个事件称作事件A 与B 的积(或交)，记作B A (或AB )．6)两事件的差事件“事件A 发生而B 不发生”，这样的事件称为事件A 对B 的差，记作A B -．7)对立事件或逆事件若=AB ∅且Ω=B A ，则称A 与B 为对立事件或互为逆事件，事件A 的对立事件记作A ．【例1】设A 、B 、C 是Ω中的随机事件，则(1)事件{A 发生且B 与C 至少有一个发生}可表示为：)(C B A ；(2)事件{A 与B 发生而C 不发生}可表示为：C AB ；(3)事件{A 、B 、C 中至少有两个发生}可表示为：BC AC AB ；(4)事件{A 、B 、C 中至多有两个发生}可表示为：ABC ；(5)事件{A 、B 、C 中不多于一个发生}可表示为：AB BC AC ；(6)事件{A 、B 、C 中恰有一个发生}可表示为：ABC ABC ABC ．【例2】关系()成立，则事件A 与B 为对立事件．A ．=AB ∅B ．Ω=B AC ．=AB ∅，Ω=B AD ．=AB ∅，Ω≠B A 【解析】由对立事件的概念可知选项C 正确．【例3】甲、乙两人谈判，设事件A ，B 分别表示甲、乙无诚意，则B A 表示()A ．两人都无诚意B ．两人都有诚意C ．两人至少有一人无诚意D ．两人至少有一人有诚意【解析】由题可知A 与B 分别表示甲、乙有诚意，则B A 表示甲、乙两人至少有一人有诚意，故选项D 正确．5.事件的运算性质(1)交换律：A B B A =，BA AB =；(2)结合律：C B A C B A )()(=，)()(BC A C AB =；(3)分配律：()()()A B C AB AC = ，()()()A B C A C B C = ；(4)对偶律：B A B A = ，B A AB =．一些有用的等式：A A A = ，A Ω=Ω ，A A ∅= AA A =，A A Ω=，A ∅=∅A B A AB AB -=-=，A B A B A =【例4】化简下列各式：(1)))((B A B A ；(2)))((C B B A ；(3)))((B A B A B A ．【解】(1) A B B A B A B A ==)())((ØA =；(2)AC B C A B C B B A ==)())((；(3)))(())((B A B B A B A B A B A =AB AB A A B A A === )(．(二)随机事件的概率1.概率的公理化定义定义1设E 是随机试验，Ω是它的样本空间．对于E 的每一事件A 赋予一个实数，记为)(A P ，称为事件A 的概率，如果集合函数)(⋅P 满足下列条件：(1)非负性0)(≥A P ，对Ω∈A ；(2)规范性()1P Ω=；(3)可列可加性若=j i A A ∅，j i ≠， ,2,1,=j i ，有∑+∞=+∞==11)()(i i i i A P A P ．2.概率的性质性质1不可能事件的概率为0，即()0P ∅=．性质2概率具有有限可加性，即若=j i A A ∅(n j i ≤<≤1)，则∑===ni i n i i A P A P 11)()( ．性质3对任一随机事件A ，有()1()P A P A =-．性质4若A B ⊂，则)()()(B P A P B A P -=-．推论若A B ⊂，则)()(B P A P ≥．性质5对任意的两个事件A ，B ，有)()()(AB P A P B A P -=-．性质6对任意的两个事件A ，B ，有()()()()P A B P A P B P AB =+- ．对任意三个事件A ，B ，C ，有)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= ．推论对任意的两个事件A ，B ，有)()()(B P A P B A P +≤ ．【例1】设A 与B 互不相容，且0)(>A P ，0)(>B P ，则下列结论正确的是()A ．A 与B 为对立事件B ．A 与B 互不相容C ．)()()(B P A P B A P -=-D ．)()(A P B A P =-【解析】因为A 与B 互不相容，所以AB =∅，0)(=AB P ，故选项A ：互不相容不一定对立，故选项A 错误；选项B ：互不相容不一定对立，故B A 不一定等于Ω，所以B A B A =不一定等于∅，即A 与B 不一定互不相容，故选项B 错误；选项C ：)()()()(A P AB P A P B A P =-=-，故选项C 错误，进而选项D 正确．【例2】已知B A ⊂，3.0)(=A P ，5.0)(=B P ，求(A P ，)(AB P ，)(B A P 和)(B A P ．【解】(1)7.0)(1)(=-=A P A P ；(2)∵B A ⊂，∴A AB =，则3.0)()(==A P AB P ；(3)2.0)()()()(=-=-=AB P B P A B P B A P ；(4))(1()(B A P B A P B A P -==5.0)]()()([1=-+-=AB P B P A P ．【注】事件的概率的计算常常需要结合对偶律，应用性质3．【例3】已知事件A ，B ，B A 的概率分别是0.4，0.3，0.6，求(B A P ．【解】)()()()(AB P B P A P B A P -+= )(3.04.06.0AB P -+=所以1.0)(=AB P ，则3.0)()()((=-=-=AB P A P B A P B A P ．【例4】已知41)()()(===C P B P A P ，0)(=AB P ，161)()(==BC P AC P ．求：(1)A ，B ，C 中至少发生一个的概率；(2)A ，B ，C 都不发生的概率．【解】(1)因为0)(=AB P ，且AB ABC ⊂，所以由概率的单调性知0)(=ABC P ；再由加法公式，得A ，B ，C 中至少发生一个的概率为)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= 8516243=-=．(2)因为{A ，B ，C 都不发生}的对立事件为{A ，B ，C 中至少发生一个}，所以A ，B ，C 都不发生的概率为83851(=-=C B A P ．3.古典概型定义2若随机试验E 具有下述特征：(1)样本空间的元素(即样本点)只有有限个，不妨设为n 个，并记它们为12,,,n ωωω ．(2)每个样本点出现的可能性相等(等可能性)，即有12()()()n P P P ωωω=== ．则称这种等可能性的概率模型为古典概型．对任意一个随机事件Ω∈A ，有nk A A P =Ω=中所有样本点的个数所含有样本点的个数事件)(．【例5】袋中有大小相同的4个白球，3个黑球，从中任取3个至少有2个白球的概率为．【解析】袋中共有7个球，从中任取3个，共有37C 中取法，即样本空间Ω中共有37C 个样本点．取出的3个球中至少有2个白球，分为2个白球1个黑球和3个白球两种情况．当取出的3个球中有2个白球1个黑球时，共有1324C C 中取法；当取出的3个球中有3个白球时，共有0334C C 中取法．记=A {从中任取3个至少有2个白球}，则事件A 中共有03341324C C C C +个样本点．因此3522)(3703341324=+=C C C C C A P ．(三)条件概率1.条件概率定义1设A 与B 是样本空间Ω中的两个事件，若0)(>B P ，则称)()()(B P AB P B A P =为“在事件B 发生条件下事件A 发生的条件概率”，简称条件概率．【例1】已知31)()(==B P A P ，61)(=B A P ，求(B A P ．【解】∵61)()()(==B P AB P B A P ，∴181)(=AB P ，)(1)()()()(B P B A P B P B A P B A P -== )(1)]()()([1B P AB P B P A P --+-=127=．【注】条件概率的计算通常与概率的性质结合使用．【技巧】在计算过程中，只要有概率的性质可以用，就一直用概率的性质计算，直到没有概率的性质可用时，对得到的式子进行化简整理，代入已知数据计算．2.乘法公式定理1(乘法公式)(1)若0)(>B P ，则)()()(B A P B P AB P =．(2)若0)(121>-n A A A P ，则)()()()()(12121312121-=n n n A A A A P A A A P A A P A P A A A P ．【例2】一批零件共100个，次品率为10%，每次从其中任取一个零件，取出的零件不再放回，求第三次才取得合格品的概率．【解】设=i A {第i 次取得合格品}，3,2,1=i ．由题意知，所求概率为)(321A A A P ，易知10010)(1=A P ，999)(12=A A P ，9890)(213=A A A P ．由此得)()()()(213121321A A A P A A P A P A A A P =0083.0989099910010≈⋅⋅=．3.全概率公式定义2设Ω为试验E 的样本空间，1B ，2B ，…，n B 为E 的一组事件．如果=j i B B ∅，j i ≠，n j i ,,2,1, =且Ω=n B B B 21，则称1B ，2B ，…，n B 为样本空间Ω的一个划分．定理2(全概率公式)设1B ，2B ，…，n B 为样本空间Ω的一个划分，若0)(>i B P ，n i ,,2,1 =，则对任一事件A 有)()()(1i ni i B A P B P A P ∑==．4.贝叶斯公式定理3(贝叶斯公式)设1B ，2B ，…，n B 为样本空间Ω的一个划分，若0)(>A P ，0)(>i B P ，n i ,,2,1 =，则∑==n i j j i i i B A P B P B A P B P A B P 1)()()()()(，n i ,,2,1 =．【例3】一批同型号的零件由编号为Ⅰ、Ⅱ、Ⅲ的三台机器共同生产，各台机器生产的零件占这批零件的比例分别为35%、40%和25%，各台机器生产的零件的次品率分别为3%、2%和1%．(1)求该批零件的次品率；(2)现从该批零件中抽到一颗次品，试问这颗零件由Ⅰ号机器生产的概率是多少？【解】设=A {零件是次品}，=1B {零件由Ⅰ号机器生产}，=2B {零件由Ⅱ号机器生产}，=3B {零件由Ⅲ号机器生产}，则由题设知35.0)(1=B P ，4.0)(2=B P ，25.0)(3=B P ，03.0)(1=B A P ，02.0)(2=B A P ，01.0)(3=B A P ．(1)题目要求的是)(A P ，由全概率公式，得∑==31)()()(i i i B A P B P A P 021.0=．(2)题目要求的是)(1A B P ，由贝叶斯公式，得21)|()()|()()(31111==∑=i i i B A P B P B A P B P A B P ．【例4】有甲、乙、丙三厂同时生产某种产品．甲、乙、丙三厂的产量之比为1：1：3，次品率分别为4%，3%，2%．(1)若从一批产品中随机抽出一件，求这件产品为次品的概率．(2)若产品的售后部门接到一名顾客投诉，说其购买的产品为次品，请问哪个厂最该为此事负责，为什么？【解】设=A {产品为次品}，=1B {产品由甲厂生产}，=2B {产品由乙厂生产}，=3B {产品由丙厂生产}，则由题设知，2.0)(1=B P ，2.0)(2=B P ，6.0)(3=B P ，04.0)(1=B A P ，03.0)(2=B A P ，02.0)(3=B A P ．(1)题目要求的是)(A P ，由全概率公式，得∑==31)()()(i i i B A P B P A P 026.0=．(2)由贝叶斯公式，得134)|()()|()()(31111==∑=i i i B A P B P B A P B P A B P ，133)|()()|()()(31222==∑=i i i B A P B P B A P B P A B P ，136)|()()|()()(31333==∑=i i i B A P B P B A P B P A B P ．所以在产品为次品的情况下，产品来自丙厂的可能性最大，丙厂最该负责．【注】全概率公式与贝叶斯公式通常一起考试．(四)独立性1.两个事件的独立性定义1若)()()(B P A P AB P =成立，则称事件A 与事件B 相互独立，简称A 与B 独立．否则称A 与B 不独立或相依．定理1若事件A 与B 独立，则A 与B 独立；A 与B 独立；A 与B 独立．【例1】甲、乙两人彼此独立的向同一个目标射击，甲击中目标的概率为0.9，乙击中目标的概率为0.8，求目标被击中的概率．【解】设=A {甲击中目标}，=B {乙击中目标}，则=B A {目标被击中}．则)()()()(AB P B P A P B A P -+= )()()()(B P A P B P A P -+=98.0=．【例2】若事件A 与B 相互独立，8.0)(=A P ，6.0)(=B P ，求：)(B A P 和)|(B A A P ．【解】∵A 与B 相互独立，∴)()()()(AB P B P A P B A P -+= )()()()(B P A P B P A P -+=92.0=．)())(()|(B A P B A A P B A A P =)()()()()(B A P B P A P B A P B A P ==13.0=．【例3】设)()(B A P B A P =，证明：A 与B 相互独立．【证】因为)()(B A P B A P =，所以有)(1)()()(1)()()()()(B P AB P A P B P B A P B P B A P B P AB P --=--==，即有)]()()[()](1)[(AB P A P B P B P AB P -=-，整理得)()()(B P A P AB P =，所以A 与B 相互独立．2.多个事件的相互独立性定义2设A ，B ，C 是三个事件，若有⎪⎩⎪⎨⎧===)()()()()()()()()(C P B P BC P C P A P AC P B P A P AB P (1)第11页共11页则称A ，B ，C 两两独立．若还有)()()()(C P B P A P ABC P =，(2)则称A ，B ，C 相互独立．注意：只有(1)式与(2)式同时成立，事件A ，B ，C 才相互独立．(1)式成立不能保证(2)式成立；反过来，(2)式成立也不能保证(1)式成立．定义3设有n 个事件1A ，2A ，…，n A ，对任意的n k j i ≤<<<≤ 1，若以下等式均成立⎪⎪⎩⎪⎪⎨⎧===)()()()()()()()()()()(2121n n k j i k j i j i j i A P A P A P A A A P A P A P A P A A A P A P A P A A P 则称此n 个事件1A ，2A ，…，n A 相互独立．定理2如果n (2≥n )个事件1A ，2A ，…，n A 相互独立，则其中任何m (n m ≤≤1)个事件换成相应的对立事件，形成的n 个新的事件仍相互独立．【例4】三人独立地去破译一份密码，已知各人能译出的概率分别为51，31，41，问三人中至少有一人能将此密码译出的概率是多少？【解】设A ，B ，C 分别表示三人独立译出密码，则51)(=A P ，31)(=B P ，41)(=C P ，且A ，B ，C 相互独立，有方法1：)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= )()()()()()()()()()()()(C P B P A P C P B P C P A P B P A P C P B P A P +---++=6.0=．方法2：)(1)(C B A P C B A P -=(1C B A P -=()()(1C P B P A P -=53411)(311)(511(1=----=．。

概率论与数理统计期末复习题一一、填空题（每空2分，共20分）1、设X 为连续型随机变量，则P{X=1}=( 0 ).2、袋中有50个球,其编号从01到50,从中任取一球,其编号中有数字4的概率为(14/50 或7/25 ).3、若随机变量X 的分布律为P{X=k}=C(2/3)k,k=1,2,3,4,则C=( 81/130 ). 4、设X 服从N （1，4）分布，Y 服从P(1)分布，且X 与Y 独立，则 E （XY+1-Y ）=（ 1 ） ，D （2Y-X+1）=（ 17 ）.5、已知随机变量X ～N(μ,σ2),(X-5)/4服从N(0,1),则μ=( 5 );σ=( 4 ). 6且X 与Y 相互独立。

则A=( 0.35 ),B=( 0.35 ).7、设X 1,X 2,…,X n 是取自均匀分布U[0,θ]的一个样本，其中θ>0,n x x x ,...,,21是一组观察值，则θ的极大似然估计量为( X (n) ).二、计算题（每题12分，共48分）1、钥匙掉了,落在宿舍中的概率为40%,这种情况下找到的概率为0.9; 落在教室里的概率为35%,这种情况下找到的概率为0.3; 落在路上的概率为25%,这种情况下找到的概率为0.1,求(1)找到钥匙的概率;(2)若钥匙已经找到,则该钥匙落在教室里的概率.解：(1)以A 1,A 2,A 3分别记钥匙落在宿舍中、落在教室里、落在路上，以B 记找到钥匙.则 P(A 1)=0.4,P(A 2)=0.35,P(A 3)=0.25, P(B| A 1)=0.9 ,P(B| A 2)=0.3,P(B| A 3)=0.1 所以,49.01.025.03.035.09.04.0)|()()(31=⨯+⨯+⨯==∑=ii iA B P A P B P(2)21.049.0/)3.035.0()|(2=⨯=B A P 2、已知随机变量X 的概率密度为其中λ>0为已知参数.(1)求常数A; (2)求P{-1＜X ＜1/λ)}; (3)F(1).⎪⎩⎪⎨⎧<≥=-000)(2x x e A x f x λλ解：（1）由归一性：λλλλλλ/1,|)(102==-===∞+--+∞+∞∞-⎰⎰A A e A dx e A dx x f x x 所以（2）⎰=-==<<--λλλλ/1036.0/11}/11{e dx e X P x（3）⎰---==11)1(λλλe dx eF x3、设随机变量X 的分布律为且X X Y 22+=，求(1)()E X ; (2)()E Y ; (3))(X D . 解：（1）14.023.012.001.01)(=⨯+⨯+⨯+⨯-=X E （2）24.043.012.001.01)(2=⨯+⨯+⨯+⨯=X E422)(2)()2()(22=+=+=+=X E X E X X E Y E（3）112)]([)()(22=-=-=X E X E X D4、若X ～N(μ,σ2),求μ, σ2的矩估计.解：（1）E(X)=μ 令μ=-X 所以μ的矩估计为-Λ=X μ（2）D(X)=E(X 2)-[E(X)]2又E(X 2)=∑=n i i X n 121D(X)= ∑=n i i X n 121--X =212)(1σ=-∑=-n i i X X n所以σ2的矩估计为∑=-Λ-=ni i X X n 122)(1σ三、解答题（12分）设某次考试的考生的成绩X 服从正态分布，从中随机地抽取36位考生的成绩，算得平均成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为在这次考试中全体考生的平均成绩为70分? 解：提出假设检验问题：H 0: μ=70, H 1 ：μ≠70,nS X t /70-=-～t(n-1),其中n=36,-x =66.5,s=15,α=0.05,t α/2(n-1)=t 0.025(35)=2.03 (6)03.24.136/15|705.66|||<=-=t所以,接受H 0,在显著性水平0.05下,可认为在这次考试中全体考生的平均成绩为70分四、综合题（每小题4分，共20分） 设二维随机变量),(Y X 的联合密度函数为：32,01,01(,)0,x ce y x y f x y ⎧≤≤≤≤=⎨⎩其它试求: )1( 常数C ；)2(()X f x , )(y f Y ；)3( X 与Y 是否相互独立？)4( )(X E ,)(Y E ,)(XY E ； )5( )(X D ,)(Y D . 附：Φ（1.96）=0.975； Φ（1）=0.84； Φ（2）=0.9772t 0.05(9)= 1.8331 ; t 0.025(9)=2.262 ; 8595.1)8(05.0=t ， 306.2)8(025.0=t t 0.05(36)= 1.6883 ; t 0.025(36)=2.0281 ; 0.05(35) 1.6896t =， 0.025(35) 2.0301t = 解：(1))1(9|31|3113103103101010102323-=⋅⋅=⋅==⎰⎰⎰⎰e c y e c dy y dx e c dxdy y ce x x x 所以,c=9/(e 3-1)(2)0)(1319)(,103323103=-=-=≤≤⎰x f x e e dy y e e x f x X xx X 为其它情况时，当当所以,333,01()10,xX e x f x e ⎧≤≤⎪=-⎨⎪⎩其它同理, 23,01()0,Y y y f y ⎧≤≤=⎨⎩其它(3)因为: 32333,01,01()()(,)10,x X Y e y x y f x f y f x y e ⎧⋅≤≤≤≤⎪==-⎨⎪⎩其它所以,X 与Y 相互独立. (4)113333013130303331111(|)1213(1)x xx x EX x e dx xde e e y e e dx e e e =⋅=--=⋅--+=-⎰⎰⎰124100333|44EY y y dx y =⋅==⎰ 3321()4(1)e E XY EX EY e +=⋅=- (5) 22()DX EX EX =-11223231303300133130303331|21112(|)13529(1)x x xx x EX x e dy x e e xdx e e e xe e dx e e e ⎡⎤=⋅=⋅-⋅⎢⎥⎣⎦--⎡⎤=--⎢⎥-⎣⎦-=-⎰⎰⎰ ∴3323326332521(21)9(1)9(1)1119(1)e DX e e e e e e -=-+---+=-22()DY EY EY =- 12225010333|55EY y y dy y =⋅==⎰ ∴ 2333()5480DY =-=概率论与数理统计期末复习题二一、计算题（每题10分，共70分）1、设P （A ）=1/3，P （B ）=1/4，P （A ∪B ）=1/2.求P （AB ）、P （A-B ）.解：P （AB ）= P （A ）+P （B ）- P （A ∪B ）=1/12P （A-B ）= P （A ）-P （AB ）=1/42、设有甲乙两袋，甲袋中装有3只白球、2只红球，乙袋中装有2只白球、3只红球.今从甲袋中任取一球放入乙袋，再从乙袋中任取两球，问两球都为白球的概率是多少？解：用A 表示“从甲袋中任取一球为红球”， B 表示“从乙袋中任取两球都为白球”。

概率论与数理统计期末复习20题及解答【第一章】 随机事件与概率1、甲袋中有4个白球3个黑球，乙袋中有2个白球3个黑球，先从甲袋中任取一球放入乙袋, 再从乙袋中任取一球返还甲袋. 求经此换球过程后甲袋中黑球数增加的概率.2、某人忘记了电话号码的最后一个数字，因而他随意地拨号，求此人拨号不超过两次而接通所需电话的概率．3、已知将1,0两字符之一输入信道时输出的也是字符0或1，且输出结果为原字符的概率为)10(<<αα. 假设该信道传输各字符时是独立工作的. 现以等概率从“101”，“010”这两个字符串中任取一个输入信道.求输出结果恰为“000”的概率.4、试卷中的一道选择题有4个答案可供选择，其中只有1个答案是正确的．某考生如果会做这道题，则一定能选出正确答案；若该考生不会做这道题，则不妨随机选取一个答案．设该考生会做这道题的概率为85.0．（1）求该考生选出此题正确答案的概率；（2）已知该考生做对了此题，求该考生确实会做这道题的概率．【第二章】 随机变量及其分布5、设连续随机变量X 的分布函数为+∞<<∞-+=x x B A x F ,arctan )(．（1）求系数A 及B ；（2）求X 落在区间)1,1(-内的概率；（3）求X 的概率密度．6、设随机变量X 的概率密度为⎩⎨⎧≤≤=其它,0,10,)(x ax x f ，求：（1）常数a ；（2）)5.15.0(<<X P ；（3）X 的分布函数)(x F ．7、设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<+=.,0;1,1),1(),(其它y x xy A y x f 求：（1）系数A ；（2）X 的边缘概率密度)(x f X ；（3）概率)(2X Y P ≤．8、设二维随机变量),(Y X 的概率密度为⎩⎨⎧<<<<=.,0;20,10,1),(其它x y x y x f求：（1）),(Y X 的边缘概率密度)(x f X ，)(y f Y ；（2）概率)1,21(≤≤Y X P ；（3）判断X ,Y 是否相互独立.9、设X 和Y 是两个相互独立的随机变量，]2.0,0[~U X ，Y 的概率密度函数为⎩⎨⎧≤>=-.0,0,0,5)(5y y e y f y Y（1）求X 和Y 的联合概率密度),(y x f ；（2）求概率)(X Y P ≤．【第三章】数字特征10、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤<-≤≤+-=,,0,21,)2(,10,)()(其它x x a x b x b a x f ，已知21)(=X E ，求：（1）b a ,的值；（2）)32(+X E ．11、设随机变量X 的概率密度为⎩⎨⎧≤>=-.0,0,0,)(2x x Ae x f x 求：（1）常数A ；（2）)(X E 和)(X D ．12、设),(Y X 的联合概率分布如下：XY1104/14/12/10（1）求Y X ,的数学期望)(X E ,)(Y E ，方差)(X D ，)(Y D ．（2）求Y X ,的协方差),cov(Y X 与相关系数),(Y X R ．【第四章】正态分布13、假设某大学学生在一次概率论与数理统计统考中的考试成绩X （百分制）近似服从正态分布，已知满分为100分平均成绩为75分，95分以上的人数占考生总数的2.3%.（1）试估计本次考试的不及格率（低于60分为不及格）；（2）试估计本次考试成绩在65分至85分之间的考生人数占考生总数的比例. [已知9332.0)5.1(,8413.0)1(≈≈ΦΦ，9772.0)2(=Φ]14、两台机床分别加工生产轴与轴衬．设随机变量X （单位：mm ）表示轴的直径，随机变量Y （单位：mm ）表示轴衬的内径，已知)3.0,50(~2N X ，)4.0,52(~2N Y ，显然X 与Y 是独立的．如果轴 衬的内径与轴的直径之差在3~1mm 之间，则轴与轴衬可以配套使用．求任取一轴与一轴衬可以配套使用的概率．[已知9772.0)2(≈Φ]【第五章】 数理统计基本知识15、设总体)1,0(~N X ，521,,,X X X 是来自该总体的简单随机样本，求常数0>k 使)3(~)2(25242321t XX X X X k T +++=．16、设总体)5 ,40(~2N X ，从该总体中抽取容量为64的样本，求概率)1|40(|<-X P ．【第六章】参数估计17、设总体X 的概率密度为⎩⎨⎧≥=--,,0,2,);()2(其它x e x f x λλλ其中参数0>λ．设n X X X ,,,21 是取自该总体的一组简单随机样本，n x x x ,,,21 为样本观测值.（1）求参数λ的矩估计量．（2）求参数λ的最大似然估计量．18、设总体X 的概率密度为⎪⎩⎪⎨⎧≤>=-,0,0;0,e 1);(2x x x xf x λλλ 其中参数0>λ．设n X X X ,,,21 是取自该总体的一组简单随机样本, n x x x ,,,21 为样本观测值.（1）求参数λ的最大似然估计量.（2）你得到的估计量是不是参数λ的无偏估计，请说明理由.【第七章】假设检验19、矩形的宽与长之比为618.0（黄金分割）时将给人们视觉上的和谐美感. 某工艺品厂生产矩形裱画专用框架. 根据该厂制定的技术标准，一批合格产品的宽与长之比必须服从均值为618.00=μ的正态分布. 现从该厂某日生产的一批产品中随机抽取25个样品，测得其宽与长之比的平均值为,646.0=x 样本标准差为093.0=s . 试问在显著性水平05.0=α水平上能否认为这批产品是合格品？20、已知某种口服药存在使服用者收缩压(高压)增高的副作用. 临床统计表明，在服用此药的人群中收缩压的增高值服从均值为220=μ（单位:mmHg ,毫米汞柱）的正态分布. 现在研制了一种新的替代药品，并对一批志愿者进行了临床试验. 现从该批志愿者中随机抽取16人测量收缩压增高值，计算得到样本均值)mmHg (5.19=x ，样本标准差)mmHg (2.5=s . 试问这组临床试验的样本数据能否支持“新的替代药品比原药品副作用小”这一结论 （取显著性水平05.0=α）.解答部分【第一章】 随机事件与概率1、甲袋中有4个白球3个黑球，乙袋中有2个白球3个黑球，先从甲袋中任取一球放入乙袋, 再从乙袋中任取一球返还甲袋. 求经此换球过程后甲袋中黑球数增加的概率.【解】设A 表示“从甲袋移往乙袋的是白球”，B 表示“从乙袋返还甲袋的是黑球”，C 表示“经此换球过程后甲袋中黑球数增加”，则AB C =， 又2163)(,74)(===A B P A P ，于是由概率乘法定理得所求概率为 )()(AB P C P =)()(A B P A P ==722174=⋅.2、某人忘记了电话号码的最后一个数字，因而他随意地拨号，求此人拨号不超过两次而接通所需电话的概率．【解】 设i A 表示“此人第i 次拨号能拨通所需电话” )2,1(=i ，A 表示“此人拨号不超过两次而接通所需电话”，则211A A A A +=，由概率加法定理与乘法定理得所求概率为)()()()(211211A A P A P A A A P A P +=+=)()()(1211A A P A P A P +=2.091109101=⋅+=.3、已知将1,0两字符之一输入信道时输出的也是字符0或1，且输出结果为原字符的概率为)10(<<αα. 假设该信道传输各字符时是独立工作的. 现以等概率从“101”，“010”这两个字符串中任取一个输入信道.求输出结果恰为“000”的概率.【解】设:1A 输入的是“101”，:2A 输入的是“010”，:B 输出的是“000”，则2/1)(1=A P ，2/1)(2=A P ，αα21)1()(-=A B P ，)1()(22αα-=A B P ，从而由全概率公式得)()()()()(2211A B P A P A B P A P B P +=)1(21)1(2122αααα-+-=)1(21αα-=.4、试卷中的一道选择题有4个答案可供选择，其中只有1个答案是正确的．某考生如果会做这道题，则一定能选出正确答案；若该考生不会做这道题，则不妨随机选取一个答案．设该考生会做这道题的概率为85.0．（1）求该考生选出此题正确答案的概率；（2）已知该考生做对了此题，求该考生确实会做这道题的概率．【解】设A 表示“该考生会解这道题”，B 表示“该考生选出正确答案”，则85.0)(=A P ，2.0)(=A P ，1)(=A B P ，25.0)(=A B P ．（1）由全概率公式得)()()()()(A B P A P A B P A P B P +=25.02.0185.0⨯+⨯=9.0=．（2）由贝叶斯公式得944.018179.0185.0)()()()(≈=⨯==B P A B P A P B A P ．【第二章】 随机变量及其分布5、设连续随机变量X 的分布函数为+∞<<∞-+=x x B A x F ,arctan )(．（1）求系数A 及B ；（2）求X 落在区间)1,1(-内的概率；（3）求X 的概率密度．【解】（1）由分布函数的性质可知0)2()(lim )(=-⋅+==-∞-∞→πB A x F F x ，12)(lim )(=⋅+==+∞+∞→πB A x F F x ，由此解得 π1,21==B A ． （2）X 的分布函数为)(arctan 121)(+∞<<-∞+=x x x F π， 于是所求概率为21))1arctan(121()1arctan 121()1()1()11(=-+-+=--=<<-ππF F X P ．（3）X 的概率密度为)1(1)()(2x x F x f +='=π．6、设随机变量X 的概率密度为⎩⎨⎧≤≤=其它,0,10,)(x ax x f ，求：（1）常数a ；（2）)5.15.0(<<X P ；（3）X 的分布函数)(x F ．【解】（1）由概率密度的性质可知⎰∞+∞-dx x f )(121===⎰aaxdx ， 由此得2=a ．（2） )5.15.0(<<X P 75.000212/122/3112/1=+=+=⎰⎰x dx xdx .（3）当0<x 时，有00)(==⎰∞-xdx x F ；当10<≤x 时，有20020)(x xdx dx x F x=+=⎰⎰∞-；当1≥x 时，有1020)(1100=++=⎰⎰⎰∞-xdx xdx dx x F .所以，X 的分布函数为⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(2x x x x x F7、设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<+=.,0;1,1),1(),(其它y x xy A y x f 求：（1）系数A ；（2）X 的边缘概率密度)(x f X ；（3）概率)(2X Y P ≤．【解】（1）由联合概率密度的性质可知=⎰⎰+∞∞-+∞∞-dxdy y x f ),(14)1(1111==+⎰⎰--A dy xy A dx ，由此得41=A ． （2）当11<<-x 时，有=)(x f X =⎰+∞∞-dy y x f ),(214111=+⎰-dy xy ； 当1-≤x 或1≥x 时，显然有0)(=x f X ．所以X 的边缘概率密度⎩⎨⎧<<-=.,0;11,2/1)(其它x x f X（3）)(2X Y P ≤⎰⎰≤=2),(x y dxdy y x f dy xy dx x ⎰⎰--+=211141dx x x x )1221(412511+-+=⎰-32=．8、设二维随机变量),(Y X 的概率密度为⎩⎨⎧<<<<=.,0;20,10,1),(其它x y x y x f求：（1）),(Y X 的边缘概率密度)(x f X ，)(y f Y ；（2）概率)1,21(≤≤Y X P ；（3）判断X ,Y 是否相互独立.【解】（1）当10<<x 时，有x dy dy y x f x f xX 2),()(20⎰⎰===+∞∞-；当0≤x 或1≥x 时，显然有0)(=x f X .于是X 的边缘概率密度为⎩⎨⎧<<=.,0;10,2)(其它x x x f X 当20<<y 时，有⎰⎰-===+∞∞-1221),()(y Y ydx dx y x f y f ； 当0≤y 或2≥y 时，显然有0)(=y f Y .于是Y 的边缘概率密度为⎪⎩⎪⎨⎧<<-=.,0;20,21)(其它y y y f Y（2）⎰⎰⎰⎰===≤≤∞-∞2/12/102/11-41),()}1,21{(y dx dy dx y x f dy Y X P .（3）容易验证)()(),(y f x f y x f Y X ≠,故X 与Y 不独立.9、设X 和Y 是两个相互独立的随机变量，]2.0,0[~U X ，Y 的概率密度函数为⎩⎨⎧≤>=-.0,0,0,5)(5y y e y f y Y（2）求X 和Y 的联合概率密度),(y x f ；（2）求概率)(X Y P ≤．【解】（1）由题意知，X 的概率密度函数为⎩⎨⎧<<=.,0;2.00,5)(其它x x f X因为X 和Y 相互独立，故X 和Y 的联合概率密度⎩⎨⎧><<==-.,0;0,2.00,25)()(),(5其它y x e y f x f y x f y Y X（2）12.005052.00)1(525),()(---≤=-===≤⎰⎰⎰⎰⎰e dx e dy e dx dxdy y x f X Y P x x y xy ．【第三章】数字特征10、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤<-≤≤+-=,,0,21,)2(,10,)()(其它x x a x b x b a x f ，已知21)(=X E ，求：（1）b a ,的值；（2）)32(+X E ． 【解】（1）由概率密度的性质可知=⎰∞+∞-dx x f )(12)2(])[(2110=+=-++-⎰⎰ba dx x a dxb x b a ； 又dx x xf X E ⎰∞+∞-=)()(.216)2(])[(2110=+=-++-=⎰⎰b a dx x x a xdx b x b a联立方程组⎪⎩⎪⎨⎧=+=+,216,12b a b a 解得41=a ，23=b ． （2） 由数学期望的性质，有432123)(2)32(=+⋅=+=+X E X E ． 11、设随机变量X 的概率密度为⎩⎨⎧≤>=-.0,0,0,)(2x x Ae x f x求：（1）常数A ；（2）)(X E 和)(X D ．【解】（1）由概率密度的性质可知=⎰∞+∞-dx x f )(122==⎰∞+-Adx Ae x ， 由此得2=A ．（2）由数学期望公式得⎰⎰∞++∞-=-=⋅=0022212)(dt te dx ex X E t tx x21)2(Γ21==. 由于⎰∞+-⋅=02222)(dx ex X E xdt e t t tx ⎰+∞-==0224121!241)3(Γ41=⋅==，故利用方差计算公式得41)21(21)]([)()(222=-=-=X E X E X D .12、设),(Y X 的联合概率分布如下：XY1104/14/12/10（1）求Y X ,的数学期望)(X E ,)(Y E ，方差)(X D ，)(Y D ．（2）求Y X ,的协方差),cov(Y X 与相 关系数),(Y X R ．【解】 由),(Y X 的联合概率分布知Y X ,服从"10"-分布：4/1)0(==X P ，4/3)1(==X P ， 2/1)0(==Y P ，2/1)1(==Y P ，由"10"-分布的期望与方差公式得16/3)4/11(4/3)(,4/3)(=-⨯==X D X E ， 4/1)2/11(2/1)(,2/1)(=-⨯==Y D Y E ，由),(Y X 的联合概率分布知2/14/1114/1010104/100)(=⨯⨯+⨯⨯+⨯⨯+⨯⨯=XY E ,从而8/12/14/32/1)()()(),cov(=⨯-=-=Y E X E XY E Y X ，=),(Y X R 334/116/38/1)()(),cov(==Y D X D Y X ．【第四章】正态分布13、假设某大学学生在一次概率论与数理统计统考中的考试成绩X （百分制）近似服从正态分布，已知满分为100分平均成绩为75分，95分以上的人数占考生总数的2.3%.（1）试估计本次考试的不及格率（低于60分为不及格）；（2）试估计本次考试成绩在65分至85分之间的考生人数占考生总数的比例. [已知9332.0)5.1(,8413.0)1(≈≈ΦΦ，9772.0)2(=Φ]【解】 由题意，可设X 近似服从正态分布),75(2σN .已知%3.2)95(=≥X P ，即%3.2)20(1)7595(1)95(1)95(=-=--=<-=≥σΦσΦX P X P ，由此得977.0)20(=σΦ，于是220≈σ，10≈σ，从而近似有)10,75(~2N X .（1）0668.09332.01)5.1(1)5.1()107560()60(=-≈-=-=-=<ΦΦΦX P ， 由此可知，本次考试的不及格率约为%68.6.（2）)107565()107585()8565(---=≤≤ΦΦX P 6826.018413.021)1(2)1()1(=-⨯≈-=--=ΦΦΦ，由此可知，成绩在65分至85分之间的考生人数约占考生总数的%26.68.14、两台机床分别加工生产轴与轴衬．设随机变量X （单位：mm ）表示轴的直径，随机变量Y （单位：mm ）表示轴衬的内径，已知)3.0,50(~2N X ，)4.0,52(~2N Y ，显然X 与Y 是独立的．如果轴 衬的内径与轴的直径之差在3~1mm 之间，则轴与轴衬可以配套使用．求任取一轴与一轴衬可以配套使用的概率．[已知9772.0)2(≈Φ]【解】 设X Y Z -=，由X 与Y 的独立性及独立正态变量的线性组合的性质可知，)4.03.0,5052(~22+--=N X Y Z ， 即)5.0,2(~2N Z ．于是所求概率为)2()2()5.021()5.023()31(--=---=≤≤ΦΦΦΦZ P .9544.019772.021)2(2=-⨯≈-=Φ【第五章】 数理统计基本知识15、设总体)1,0(~N X ，521,,,X X X 是来自该总体的简单随机样本，求常数0>k 使)3(~)2(25242321t X X X X X k T +++=．【解】 由)1,0(~N X 知)5,0(~221N X X +，于是)1,0(~5221N X X +，又由2χ分布的定义知)3(~2252423χX X X ++，所以)3(~2533/)(5/)2(2524232125242321t X X X X X X X X X X T +++⋅=+++=，比较可得53=k ．16、设总体)5 ,40(~2N X ，从该总体中抽取容量为64的样本，求概率)1|40(|<-X P ． 【解】 由题设40=μ，5=σ，64=n ，于是)1,0(~8540N X nX u -=-=σμ从而)58|8/540(|)1|40(|<-=<-X P X P .8904.019452.021)6.1(2)58|(|=-⨯≈-=<=Φu P【第六章】参数估计17、设总体X 的概率密度为⎩⎨⎧≥=--,,0,2,);()2(其它x e x f x λλλ其中参数0>λ．设n X X X ,,,21 是取自该总体的一组简单随机样本，n x x x ,,,21 为样本观测值.（1）求参数λ的矩估计量．（2）求参数λ的最大似然估计量． 【解】（1）21)2(),()(02)2(2+=+===-+∞=---+∞+∞∞-⎰⎰⎰λλλλλλdt e t dx ex dx x xf X E t tx x ，令)(X E X =，即21+=λX ，解得参数λ的矩估计量为21-=∧X λ． （2）样本似然函数为∑====--=--=∏∏ni i i n x nni x n i i eex f L 1)2(1)2(1),()(λλλλλλ，上式两边取对数得∑--==ni i n X n L 1)2(ln )(ln λλλ，上式两边对λ求导并令导数为零得=λλd L d )(ln 0)2(1=∑--=n i i n x nλ， 解得2121-=∑-==x nx nni i λ，从而参数λ的最大似然估计量为 21-=∧X λ． 18、设总体X 的概率密度为⎪⎩⎪⎨⎧≤>=-,0,0;0,e 1);(2x x x xf x λλλ 其中参数0>λ．设n X X X ,,,21 是取自该总体的一组简单随机样本, n x x x ,,,21 为样本观测值. （1）求参数λ的最大似然估计量.（2）你得到的估计量是不是参数λ的无偏估计，请说明理由. 【解】（1）样本似然函数为,e1e1),()(1121211∏∏∏=-=-=∑⋅====n i x inni x i n i i ni iixx x f L λλλλλλ上式两边取对数得∑∑==-+-=ni i ni i x x n L 111ln ln 2)(ln λλλ， 求导数得∑=+-=ni i x n L d d 1212)(ln λλλλ， 令0)(ln =λλL d d解得2211x x n n i i==∑=λ，于是参数λ的极大似然估计量为 221ˆ1X X n n i i ==∑=λ. （2）dx x X E x λλ/202e 1)(-+∞⎰=dx x x λλ/20e )(-+∞⎰=dx t t t x -∞+=⎰=e 02λλλΓλ2)3(==， λλλ=⋅====221)(21)(21)2()ˆ(X E X E X E E ， 于是221ˆ1X X n ni i ==∑=λ是λ的无偏估计.【第七章】假设检验19、矩形的宽与长之比为618.0（黄金分割）时将给人们视觉上的和谐美感. 某工艺品厂生产矩形裱画专用框架. 根据该厂制定的技术标准，一批合格产品的宽与长之比必须服从均值为618.00=μ的正态分布. 现从该厂某日生产的一批产品中随机抽取25个样品，测得其宽与长之比的平均值为,646.0=x 样本标准差为093.0=s . 试问在显著性水平05.0=α水平上能否认为这批产品是合格品？【解】由题意，待检验的假设为0H ： 618.00==μμ； 1H ： 618.0≠μ．因为σ未知，所以检验统计量为)24(~)618.0(525/618.0/0t S X S X n S X t -=-=-=μ， 关于0H 的拒绝域为 06.2)24()1(||025.02/==->t n t t α． 现在646.0=x ，093.0=s ，所以统计量t 的观测值为505.1093.0)618.0646.0(5=-=t ． 因为)24(06.2505.1||025.0t t =<=，即t 的观测值不在拒绝域内，从而接受．．原假设，即可以认为这批产品是合格品．20、已知某种口服药存在使服用者收缩压(高压)增高的副作用. 临床统计表明，在服用此药的人群中收缩压的增高值服从均值为220=μ（单位:mmHg ,毫米汞柱）的正态分布. 现在研制了一种新的替代药品，并对一批志愿者进行了临床试验. 现从该批志愿者中随机抽取16人测量收缩压增高值，计算得到样本均值)mmHg (5.19=x ，样本标准差)mmHg (2.5=s . 试问这组临床试验的样本数据能否支持“新的替代药品比原药品副作用小”这一结论 （取显著性水平05.0=α）.【解】由题意，待检验的假设为0H ： 220==μμ； 1H ： 22<μ．因为σ未知，所以取统计量)15(~)22(4/0t S X nS X t -=-=μ， 且关于0H 的拒绝域为 753.1)15()1(05.0-=-=--<t n t t α. 现在5.19=x ，2.5=s ，所以统计量t 的观测值为923.12.5)225.19(4-≈-=t ． 因为)15(753.1923.105.0t t -=-<-≈，即t 的观测值在拒绝域内，从而拒绝．．原假设，即认为这次试验支持“新的替代药品比原药品副作用小”这一结论.。

概率论与数理统计复习资料概率论与数理统计复习资料概率论与数理统计是数学中的重要分支，广泛应用于各个领域。

无论是在自然科学、社会科学还是工程技术领域，概率论与数理统计都扮演着重要的角色。

为了更好地理解和应用这门学科，我们需要进行系统的复习和总结。

本文将为大家提供一些有关概率论与数理统计的复习资料，帮助大家更好地掌握这门学科。

一、概率论概率论是研究随机事件发生的可能性的数学学科。

它以概率为基础，通过建立数学模型来描述随机事件的规律性。

在概率论的学习中，我们需要掌握以下几个重要概念：1. 随机事件：随机事件是指在一定条件下可能发生也可能不发生的事件。

例如，掷硬币的结果、骰子点数的出现等都属于随机事件。

2. 概率：概率是描述随机事件发生可能性的数值。

它的取值范围在0到1之间，0表示不可能发生，1表示必然发生。

3. 随机变量：随机变量是指随机事件的结果所对应的数值。

它可以是离散型的，也可以是连续型的。

离散型随机变量的取值是有限或可数的，例如掷骰子的点数；连续型随机变量的取值是无限的，例如身高、体重等。

4. 概率分布：概率分布是随机变量所有可能取值及其对应的概率的分布规律。

离散型随机变量的概率分布可以用概率质量函数来描述，连续型随机变量的概率分布可以用概率密度函数来描述。

5. 期望：期望是随机变量取值的平均值，反映了随机变量的平均水平。

对于离散型随机变量，期望可以通过加权平均的方式计算；对于连续型随机变量，期望可以通过积分的方式计算。

二、数理统计数理统计是研究如何从样本中获取总体信息的学科。

它通过对样本数据进行分析和推断，来对总体进行估计和推断。

在数理统计的学习中，我们需要掌握以下几个重要概念：1. 总体与样本：总体是指研究对象的全体，样本是从总体中抽取的一部分个体。

样本是对总体的一种观察和研究。

2. 统计量：统计量是样本数据的函数，用于对总体参数进行估计。

例如，样本均值、样本方差等都是统计量。

3. 抽样分布：抽样分布是指统计量的分布规律。

非常全面的《概率论与数理统计》复习材料一、基本概念1、随机事件随机事件是指在一定条件下，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件。

例如，掷一枚骰子，出现点数为 6就是一个随机事件。

2、样本空间样本空间是指随机试验的所有可能结果组成的集合。

例如，掷一枚骰子的样本空间就是｛1, 2, 3, 4, 5, 6}。

3、概率概率是用来衡量随机事件发生可能性大小的数值。

概率的取值范围在 0 到 1 之间，0 表示不可能事件，1 表示必然事件。

4、条件概率条件概率是指在已知某一事件发生的条件下，另一事件发生的概率。

二、随机变量1、离散型随机变量离散型随机变量是指其取值可以一一列举的随机变量。

例如，掷一枚骰子出现的点数就是一个离散型随机变量。

2、连续型随机变量连续型随机变量是指其取值充满某个区间的随机变量。

例如，某地区一天的气温就是一个连续型随机变量。

3、随机变量的分布函数分布函数是描述随机变量取值概率分布的函数。

4、常见的离散型分布（1）二项分布：描述 n 次独立重复试验中成功的次数。

（2）泊松分布：常用于描述在一定时间或空间内稀有事件发生的次数。

5、常见的连续型分布（1）正态分布：在自然界和社会现象中广泛存在，具有重要的地位。

（2）均匀分布：在某个区间内取值的概率相等。

三、数字特征1、数学期望数学期望反映了随机变量取值的平均水平。

2、方差方差衡量了随机变量取值的离散程度。

3、协方差和相关系数用于描述两个随机变量之间的线性关系程度。

四、大数定律和中心极限定理1、大数定律表明随着试验次数的增加，样本均值趋近于总体均值。

2、中心极限定理指出大量独立随机变量的和近似服从正态分布。

五、抽样分布1、样本均值和样本方差的分布了解样本均值和样本方差在不同条件下的分布规律。

2、 t 分布、F 分布和χ²分布这三种分布在假设检验和参数估计中经常用到。

六、参数估计1、点估计通过样本数据估计总体参数的值。

《概率论与数理统计》复习提要第一章随机事件与概率1．事件的关系φφ=Ω-⋃⊂AB A B A AB B A B A 2．运算规则（1）BAAB A B B A =⋃=⋃ （2）)()( )()(BC A C AB C B A C B A =⋃⋃=⋃⋃（3）))(()( )()()(C B C A C AB BC AC C B A ⋃⋃=⋃⋃=⋃（4）BA AB B A B A ⋃==⋃ 3．概率)(A P 满足的三条公理及性质：（1）1)(0≤≤A P （2）1)(=ΩP （3）对互不相容的事件n A A A ,,,21 ，有∑===nk kn k kA P A P 11)()( （n 可以取∞）（4）0)(=φP （5）)(1)(A P A P -=（6）)()()(AB P A P B A P -=-，若B A ⊂，则)()()(A P B P A B P -=-，)()(B P A P ≤（7）)()()()(AB P B P A P B A P -+=⋃（8）)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++=⋃⋃4．古典概型：基本事件有限且等可能5．几何概率6．条件概率（1）定义：若0)(>B P ，则)()()|(B P AB P B A P =（2）乘法公式：)|()()(B A P B P AB P =若n B B B ,,21为完备事件组，0)(>i B P ，则有（3）全概率公式：∑==ni iiB A P B P A P 1)|()()(（4）Bayes 公式：∑==ni iik k k B A P B P B A P B P A B P 1)|()()|()()|(7．事件的独立性：B A ,独立)()()(B P A P AB P =⇔（注意独立性的应用）第二章随机变量与概率分布1．离散随机变量：取有限或可列个值，i i p x X P ==)(满足（1）0≥i p ，（2）∑iip=1（3）对任意R D ⊂，∑∈=∈Dx i ii pD X P :)(2．连续随机变量：具有概率密度函数)(x f ，满足（1）1)(,0)(-=≥⎰+∞∞dx x f x f ；（2）⎰=≤≤badx x f b X a P )()(；（3）对任意R a ∈，0)(==a X P 3．几个常用随机变量名称与记号分布列或密度数学期望方差两点分布),1(p B p X P ==)1(，pq X P -===1)0(p pq 二项式分布),(p n B n k q p C k X P kn k k n ,2,1,0,)(===-，npnpqPoisson 分布)(λP,2,1,0,!)(===-k k e k X P kλλλλ几何分布)(p G,2,1 ,)(1===-k p qk X P k p 12p q 均匀分布),(b a U b x a a b x f ≤≤-= ,1)(，2b a +12)(2a b -指数分布)(λE 0,)(≥=-x e x f x λλλ121λ正态分布),(2σμN 222)(21)(σμσπ--=x ex f μ2σ4．分布函数)()(x X P x F ≤=，具有以下性质（1）1)( ,0)(=+∞=-∞F F ；（2）单调非降；（3）右连续；（4）)()()(a F b F b X a P -=≤<，特别)(1)(a F a X P -=>；（5）对离散随机变量，∑≤=xx i ii px F :)(；（6）对连续随机变量，⎰∞-=xdt t f x F )()(为连续函数，且在)(x f 连续点上，)()('x f x F =5．正态分布的概率计算以)(x Φ记标准正态分布)1,0(N 的分布函数，则有（1）5.0)0(=Φ；（2）)(1)(x x Φ-=-Φ；（3）若),(~2σμN X ，则()(σμ-Φ=x x F ；（4）以αu 记标准正态分布)1,0(N 的上侧α分位数，则)(1)(αααu u X P Φ-==>6．随机变量的函数)(X g Y =（1）离散时，求Y 的值，将相同的概率相加；（2）X 连续，)(x g 在X 的取值范围内严格单调，且有一阶连续导数，则|))((|))(()('11y g y g f y f X Y --=，若不单调，先求分布函数，再求导。