分块矩阵的各种运算
- 格式：doc
- 大小：15.00 KB
- 文档页数：1
下载文档原格式
合集下载
2-3分块矩阵及其运算
λ A11 L λ A1 r M . λA = M λA L λ Asr s1
(3 ) 设 A 为 m × l矩阵 , B 为 l × n 矩阵 , 分块成
A11 A= M A s1 L L A1 t M A st , B 11 B = M B t1 L L B1 r M B tr ,
0 1 −1 2 B= 1 0 −1 −1
1 0 0 1 , 4 1 2 0
1 解 把 A, B 分块成 0 A = −1 1
0 1
0 0 0 0 2 1 0 1 0 1
E O = , 1 A E
0 1 −1 2 B= 1 0 −1 −1
第三节、 第三节、分块矩阵及运算
一、矩阵的分块 二、分块矩阵的运算规则
一、矩阵的分块
对于行数和列数较高的矩阵A，为了 简化运算，经常采用分块法 分块法， 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算. 具体做法是： 运算化成小矩阵的运算. 具体做法是：将 矩阵A用若干条纵线和横线分成许多个小 矩阵， 子块， 矩阵，每一个小矩阵称为A的子块，以子 分块矩阵. 块为元素的形式上的矩阵称为分块矩阵 块为元素的形式上的矩阵称为分块矩阵.
例
a 0 A= 1 0
1 a 0 1
0 0 b 1
0 A1 0 = A2 , 1 A3 b
即
A
A 1 = A2 A3
A = (a 1 0 0) 1
0 a 0 0 A2= 0 1 1 b
其中 Ai (i = 1,2, L s )
A1 都是方阵 , 那末称 A 为 O A2 分块对角矩阵 . A= , O O A = diag A1 , A2 ,L , As . As
(3 ) 设 A 为 m × l矩阵 , B 为 l × n 矩阵 , 分块成
A11 A= M A s1 L L A1 t M A st , B 11 B = M B t1 L L B1 r M B tr ,
0 1 −1 2 B= 1 0 −1 −1
1 0 0 1 , 4 1 2 0
1 解 把 A, B 分块成 0 A = −1 1
0 1
0 0 0 0 2 1 0 1 0 1
E O = , 1 A E
0 1 −1 2 B= 1 0 −1 −1
第三节、 第三节、分块矩阵及运算
一、矩阵的分块 二、分块矩阵的运算规则
一、矩阵的分块
对于行数和列数较高的矩阵A，为了 简化运算，经常采用分块法 分块法， 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算. 具体做法是： 运算化成小矩阵的运算. 具体做法是：将 矩阵A用若干条纵线和横线分成许多个小 矩阵， 子块， 矩阵，每一个小矩阵称为A的子块，以子 分块矩阵. 块为元素的形式上的矩阵称为分块矩阵 块为元素的形式上的矩阵称为分块矩阵.
例
a 0 A= 1 0
1 a 0 1
0 0 b 1
0 A1 0 = A2 , 1 A3 b
即
A
A 1 = A2 A3
A = (a 1 0 0) 1
0 a 0 0 A2= 0 1 1 b
其中 Ai (i = 1,2, L s )
A1 都是方阵 , 那末称 A 为 O A2 分块对角矩阵 . A= , O O A = diag A1 , A2 ,L , As . As
§4 矩阵的分块运算
下页
返回
3. 乘法 设A为m × l矩阵 , B为l × n矩阵 , 分块成 A11 L A1t B11 L B1r A= M M , B = M M , A L A B L B st s1 tr t1 其中 Ai1 , Ai 2 , L , Ait 的列数分别等于 B1 j , B2 j , L , Btj的行数 , 那么
o
上页
下页
返回
1 3 例1 设 A = 0 0 0
2 5 0 0 0
0 0 0 0 1 2 0 −1 0 0
解 把A进行分块得 1 2 , 其中A1 = 3 5 1 2 3 A2 = 0 − 1 4 . 0 0 1
且A1−1
0 0 3 , 求A−1 . 4 1 1 3 A = 0 0 0
B −1 − B −1 DC −1 . 因此 A −1 = O C −1
O A = O B−1 另外 A−1 O B O
−1
上页
下页
返回
1 0 例3 设 A = 0 0
ቤተ መጻሕፍቲ ባይዱ
解
4 3 ; 求 A −1 2 1 1 2 3 利用分块法 A = 0 1 2 0 0 1 0 0 0 2 1 0 0 3 2 1 0
B3 = [0 1 1 b].
上页 下页 返回
一、分块矩阵
总体思想：对于行数和列数较高的矩阵 中 总体思想：对于行数和列数较高的矩阵A中，为了简化 运算，在矩阵A中 用横、竖虚线， 运算，在矩阵 中，用横、竖虚线，将A分成若干 分成若干 小块，视每一块为一元素进行相应的运算， 小块，视每一块为一元素进行相应的运算，然后再 对每一小块进行相应的运算，降阶运算， 对每一小块进行相应的运算，降阶运算，此法称为 矩阵分块法。 矩阵分块法。 具体做法是：将矩阵 用若干条纵 用若干条纵、 具体做法是：将矩阵A用若干条纵、横虚线分成许多个 小矩阵，每一个小矩阵称为矩阵A的子块， 小矩阵，每一个小矩阵称为矩阵 的子块，以子块 为元素的形式上的矩阵称为分块矩阵 分块矩阵. 为元素的形式上的矩阵称为分块矩阵 其中C1 = [a 1], 又如 C 2 = [0 0], a 1 0 0 0 a 0 0 C 1 C 2 A= 0 a 0 0 = C C 1 0 b 1 3 4 C 3 = 1 0 , C 4 = b 1 . 0 1 0 1 1 b 1 b
4 矩阵的分块运算
A2 B2 0
它们还是准对角阵.
10
返回
准对角阵的行列式具有如下性质:
A A1 A2 As . 由此可知,若 Ai 0 ( i 1,2, , s), 则 A 0, 从而A可逆, 且有
A11 1 0 A 0 0 A2
1
0
11
0 0 0 . 1 0 As 0
2
返回
例如，把A分成若干子块
a11 a A 21 a31 a12 a22 a32 a13 a23 a33 a14 A11 a24 A 21 a34 A12 A22 A13 . A14
当然，还有其它分块法. 比如：
a11 a A 21 a31 a12 a22 a32 a13 a23 a33
A11 A1 s B11 B1t , B . A Ar 1 Ars Bs 1 Bst C11 C1t , 于是有 AB C r 1 C rt 其中 C ij Ai 1 B1 j Ai 2 B2 j Ais Bsj
其中子块Aij与Bij的行数相同, 列数也相同, 则有
4
返回
A11 B11 A B 21 21 A B Ar 1 Br 1
A12 B12 A22 B22 Ar 2 Br 2
A1 s B1 s A2 s B2 s . Ars Brs
( i 1,2,, r; j 1,2,, t ).
6
返回
注意: 在分块矩阵的乘积中,左矩阵列的分 法必须与右矩阵行的分法一样.
分块矩阵及其运算
第二章
矩阵及其 运算
1
第二章 矩阵概念及其运算
第三节 分块矩阵(Block matrix) 及其运算
分块矩阵的概念 分块矩阵的运算 问题与思考
2
一、分块矩阵的概念
将矩阵A用若干条纵线和横线分成许多小矩阵,每个小 矩阵称为A的一个子块.以这些子块为元素的形式上的矩阵 称为分块矩阵.
例如矩阵:
a11 a12 a13 a14
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
1 0 1 0
B
1 1
2 0
0 4
1 1
B
1 1
2 0
Байду номын сангаас
0 1 4 1
1 1 2 0
1 1 2 0
1 0 1 0
B
A a21 a31
a22 a32
a23 a33
a24
a34
记为 A11
A21
其中
A11
a11 a21
a12 a22
a13 a23
;
A12
a14 a24
;
A12
A22
A21 a31 a32 a33 ;
A22 a34
3
注: 任一矩阵A有多种分块方法,较特殊的分块有:
1)将矩阵A视为一个子块的分块矩阵; A
k 1
7
3.分块矩阵的转置
设矩阵A分块如下:
A11
矩阵及其 运算
1
第二章 矩阵概念及其运算
第三节 分块矩阵(Block matrix) 及其运算
分块矩阵的概念 分块矩阵的运算 问题与思考
2
一、分块矩阵的概念
将矩阵A用若干条纵线和横线分成许多小矩阵,每个小 矩阵称为A的一个子块.以这些子块为元素的形式上的矩阵 称为分块矩阵.
例如矩阵:
a11 a12 a13 a14
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
1 0 1 0
B
1 1
2 0
0 4
1 1
B
1 1
2 0
Байду номын сангаас
0 1 4 1
1 1 2 0
1 1 2 0
1 0 1 0
B
A a21 a31
a22 a32
a23 a33
a24
a34
记为 A11
A21
其中
A11
a11 a21
a12 a22
a13 a23
;
A12
a14 a24
;
A12
A22
A21 a31 a32 a33 ;
A22 a34
3
注: 任一矩阵A有多种分块方法,较特殊的分块有:
1)将矩阵A视为一个子块的分块矩阵; A
k 1
7
3.分块矩阵的转置
设矩阵A分块如下:
A11
矩阵分块法
As1
A1r Asr
A11 A
As1
A1r
Asr
其运算律与数乘矩阵相同.
λ为数，那末
3.分块矩阵的乘法.
设A为 m×l 矩阵，B为l×n矩阵，分块成
A11 A12
A
Ai1
Ai2
As1
As 2
A1t
B11 B1 j B1r
Ait
§4. 矩阵分块法
一、分块矩阵的定义
把一个阶数较高的矩阵,用若干条横线和竖 线分成若干小块 , 每一小块都叫做矩阵的子块 , 以子块为元素的矩阵称为分块矩阵.
例如：将3×4矩阵
A
a11 a21
a12 a22
a13 a23
a14 a24
a31 a32 a33 a34
分块形式如下：
A22 A12
a11 a12
1
a21
a22
a31 a32
A21 A11
a13 a23
a14 a24
2
a11 a21
a12 a13 a22 a23
a14 a24
a33 a34
a31
a32 a33
a34
A11 A21
A12 A22
A13 A23
3
a11 a21
a12 a22
a13 a23
0 0 1 1
6.分块矩阵的应用
设A为m×n矩阵，将A按行分块，得
1
A
2
m
其中 i (i 1,2, , m) 是A的第 i 行.
将A按列分块,得
A =（ β1， β2，…， βn ）.
其中 βj ( j = 1, 2, … ,n ). 是 A 的第 j 列. 对于线性方程组
A1r Asr
A11 A
As1
A1r
Asr
其运算律与数乘矩阵相同.
λ为数，那末
3.分块矩阵的乘法.
设A为 m×l 矩阵，B为l×n矩阵，分块成
A11 A12
A
Ai1
Ai2
As1
As 2
A1t
B11 B1 j B1r
Ait
§4. 矩阵分块法
一、分块矩阵的定义
把一个阶数较高的矩阵,用若干条横线和竖 线分成若干小块 , 每一小块都叫做矩阵的子块 , 以子块为元素的矩阵称为分块矩阵.
例如：将3×4矩阵
A
a11 a21
a12 a22
a13 a23
a14 a24
a31 a32 a33 a34
分块形式如下：
A22 A12
a11 a12
1
a21
a22
a31 a32
A21 A11
a13 a23
a14 a24
2
a11 a21
a12 a13 a22 a23
a14 a24
a33 a34
a31
a32 a33
a34
A11 A21
A12 A22
A13 A23
3
a11 a21
a12 a22
a13 a23
0 0 1 1
6.分块矩阵的应用
设A为m×n矩阵，将A按行分块，得
1
A
2
m
其中 i (i 1,2, , m) 是A的第 i 行.
将A按列分块,得
A =（ β1， β2，…， βn ）.
其中 βj ( j = 1, 2, … ,n ). 是 A 的第 j 列. 对于线性方程组
2.5 分块矩阵的运算
求A
1
解
2 3 A 0 0 0
3 0 0 0 6 0 0 0 0 4 0 0 0 0 3 2 0 0 7 5
则
2 3 A1 3 6
A2 4
3 2 A3 7 5
A1 A
其中Aij与Bij的行数相同,
列数相同, 则
A11 B11 A1r B1r A B A B A B sr sr s1 s1
A11 A1r 2 设 A A A sr s1 为数, 则
A11 A 0
A11 0
1
A11 A12 A22 1 A22
1 1
1
A12 A11 A22 0
A11 A12 A22 1 A22
1 1
A11 A11 0
1
A11 A11 A12 A22 A12 A22 1 A22 A22
2.5 分块矩阵的运算 一、矩阵的分块 对于行数和列数较高的矩阵为了 简化运算，常采用分块法， 使大矩阵运算化成小矩阵的运算 具体做法是： 将矩阵A用若干条纵线和横线分成 许多个小矩阵，每个小矩阵称为
A的子块， 以子块为元素的形式上的矩阵 称为分块矩阵. a 1 0 0 例
0 a 0 0 A 1 0 b 1 0 1 1 b
0 0 1 b
A1 A2 A3 A4
二、分块矩阵的运算法则
1 设A与B的行数相同, 列数相同,
采用相同的分块法, 有
A11 A A s1 B11 B B s1
A1r Asr B1r Bsr
分块矩阵及其运算
1 2 4 8 8 4 因A11 B22 2, A22 B22 3 4 6 2 12 16 2 0 0 所以AB 0 8 4 0 12 16
0 B22 性
代
线
数
= =
A C 1 矩阵D 也可逆, 并求D的逆阵D 0 B
线 性
则 XA I1 X A1 ,
WA 0 W 0, XC+ZB 0, 数
1
将X A1代入, 有ZB A1C , Z A1CB 1 , WC+YB I 2 , 将W 0代入 Y B , 所以
= =
1.4 分块矩阵及其运算
一般地, 若A1 , A2 , 则 X Ar X 1 1 A1
, Ar 均为可逆方阵(阶数不一定相同) A2 A1 为可逆阵, 且其逆阵为 1 Ar
7 1 14 2 AB 6 3 0 2
3k 2 2 4k 2 1 , A B 6 3 0 k 0 2 1 3 2 4 1 0 0 1
1 3 2 4 0 0 0 0
= =
1.4 分块矩阵及其运算
又如矩阵按列分块
a11 a A 21 am1 其中 j a12 a22 am 2 a1n a2 n 1 amn
线 性
2
n
代 数
a1 j a 2j , j 1, 2, amj
= =
1.4 分块矩阵及其运算
a11 a12 a1n b1 j b a a a 21 22 2n 2 j a m1 a m 2 a mn bmj A j
0 B22 性
代
线
数
= =
A C 1 矩阵D 也可逆, 并求D的逆阵D 0 B
线 性
则 XA I1 X A1 ,
WA 0 W 0, XC+ZB 0, 数
1
将X A1代入, 有ZB A1C , Z A1CB 1 , WC+YB I 2 , 将W 0代入 Y B , 所以
= =
1.4 分块矩阵及其运算
一般地, 若A1 , A2 , 则 X Ar X 1 1 A1
, Ar 均为可逆方阵(阶数不一定相同) A2 A1 为可逆阵, 且其逆阵为 1 Ar
7 1 14 2 AB 6 3 0 2
3k 2 2 4k 2 1 , A B 6 3 0 k 0 2 1 3 2 4 1 0 0 1
1 3 2 4 0 0 0 0
= =
1.4 分块矩阵及其运算
又如矩阵按列分块
a11 a A 21 am1 其中 j a12 a22 am 2 a1n a2 n 1 amn
线 性
2
n
代 数
a1 j a 2j , j 1, 2, amj
= =
1.4 分块矩阵及其运算
a11 a12 a1n b1 j b a a a 21 22 2n 2 j a m1 a m 2 a mn bmj A j
分块矩阵
引言为了研究行数、列数较高的矩阵，常常对矩阵采用分块的方法。
类似于集合的划分，是把矩阵完全地分成一些互不相交的子矩阵，使得原矩阵的每一个元落到一个分快的子矩阵中。
以这些子块为元素的矩阵就称为分块矩阵。
线形代数以其独特的理论体系和解题技巧而引人入胜。
在线性代数中,分块矩阵是一个十分重要的概念,它可以使矩阵的表示简单明了,使矩阵的运算得以简化.而且还可以利用分块矩阵解决某些行列式的计算问题.而事实上,利用分块矩阵方法计算行列式,时常会使行列式的计算变得简单,并能收到意想不到的效果.而且利用分快矩阵还可以求出某些矩阵的逆矩阵，证明矩阵的秩等。
第一章 矩阵的分块和分块矩阵的定义设A 是数域K 上的m n ⨯矩阵，B 是K 上n k ⨯矩阵，将A 的行分割r 段，每段分别包含12r m m m 个行，又将A 的列分割为s 段，每段包含12s n n n 个列。
A=111212122212s s r r rs A A A A A A A A A ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭于是A 可用小块矩阵表示如下：，其中ij A 是i j m n ⨯矩阵。
对B 做类似的分割，只是要求它的行的分割法和A 的列的分割法一样。
于是B 可以表示为B= 111212122212s s r r rs B B B B B B B B B ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭其中ij B 是i j n k ⨯的矩阵。
这种分割法称为矩阵的分块。
二．分块矩阵加法和乘法运算设()ij m n A a ⨯=()ij m n B b ⨯=为同型矩阵（行和列数分别相等）。
若采用相同的分块法。
A=111212122212s s r r rs A A A A A A A A A ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭B= 111212122212s s r r rs B B B B B B B B B ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭则可以直接相加 乘法:设，则C 有如下分块形式：C=111212122212s s r r rs C C C C C C C C C ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭ ，其中ij C 是i j m k ⨯矩阵，且 1nij ij ij i C A B ==∑定义 称数域K 上的分块形式的n 阶方阵A=12S A A A ⎛⎫⎪⎪ ⎪ ⎪⎝⎭为准对角矩阵，其中为阶方阵（），其余位置全是小块零矩阵。
分块矩阵的概念
As
i 1,2,L , s.
a1 j
按列分块 A
A1, A2 ,L
, An ，其中
Aj
a2 j M
,
j 1,2,L ,n. anj
一、分块矩阵的运算
1、加法 设 A, B 是两个 m n 矩阵，对它们
用同样的分法分块:
A11 A
As1
A1r
B11
, B
A1t
A2t L
Ast
例1 设
1 0 0 0
A
0 1
1 2
0 1
00 ,
1 1 0 1
求 AB.
1 0 1 0
B
1 1
2 0
0 4
1 1
,
1 1 2 0
解 把A, B分块成
1 0
A
0
1
1 0
0 1
E
E
,
1 0 1 0
B
1 1
2 0
0 4
1 1
1 1 2 0
,
O
Bs
A1 B1
则 A B
A2 B2
O
，
O
O
As
BS
A1B1
AB
A2 B2
O
O
.
O
As BS
(2) 准对角矩阵
A1
A
A2
O O
O
As
可逆
Ai 0，i 1,L , s Ai可逆，i 1,L , s
且
A11
A1
A21
O
O
O
As1
5 0 0
AB
Cs1 Csr
分块矩阵的概念及运算
19
2.3.3 分块初等阵
分块单位阵 一次初等变换 分块初等阵
Em
En
(1)
0 Em
En 0
或
0 En
Em 0
换法:
倍法:
(2)
P 0
0 En
或
Em 0
0 P
消法:
(3)
Em K
0 En
或
Em 0
K En
20
对分块矩阵进行一次初等行(列)变换, 相当于给它左(右)乘以一个相应的分 块初等矩阵：
30
例5
1 x1 y1
计算 x2 y1
x1 y2 1 x2 y2
x1 yn x2 yn
解
1 x1 y1 x1 y2 x2 y1 1 x2 y2
xn y1 xn y2
xn y1
xn y2
x1 yn
x1 y1
x2 yn
En
x2
y1
1 xn yn
xn
y1
1 xn yn
x1 y2
x1 yn
1.
3A AB
0 5B
3A 5B
33 A (5)3 B 234 53
2.
0 AB
3A 5B
(1)33
3A 5B
0 AB
(1)33
3A
AB
33 A (1)3 A B 235
14
尤其要注意 AmpBpn 0 时的特殊情况:
*例4
AB A(B1, B2 , , Bn ) A为一子块
(AB1, AB2, , ABn)
A21
A12
A22
a31 a32 a33 a34
特殊 A ——视为一个子块
分块矩阵
高等代数
2. 按行分块
对于 m n 矩阵 A 可以进行如下分块：
a11 a12 a1n 1T T a a a 21 22 2n 2 A . a T a a mn m m1 m 2
A1 A A2 , As
其中 Ai ( i = 1, 2, … , s ) 都是方阵,那么称 A 为分块 对角矩阵.
高等代数
分块对角矩阵的性质:
1)
2)
|A| = |A1| |A2| … |As| ;
若 |Ai| 0 ( i = 1, 2, … , s) , 则 |A| 0, 且
(1)
Ax = b .
1T 1T x b1 , b1 T T 2 2 x b2 , b2 x 或 T b T m m m x bm ,
其中 Ai1 , Ai2 , …, Ait 的列数分别等于 B1j , B2j , …, Btj 的行数,那么
高等代数
C11 AB C s1
t
C1r , C sr
其中
Cij Aik Bkj i 1, ,s; j 1, ,r .
k 1
高等代数
例1 设
1 0 A 1 1
求 AB.
0 0 0 0 1 1 0 0 1 2 ,B 2 1 0 1 0 1 1 1 0 1
1 0 0 1 , 4 1 2 0
高等代数
4.分块矩阵的转置
T 1 1 T 2 1
T 1 2 T 2 2
分块矩阵及其运算共21页
则
AB
A11 0
0 B11
A22
0
0 B22
A11 B11
0
0
A2
2
B
2
2
因 A11 B22
2,
A22 B22
1 3
2 4
4
6
8
2
8 1 2
4
16
2 0 0
所以AB
0
8
4
0 12 16
线
0
B
22
性
代
数
= =
1.4 分块矩阵及其运算
▪乘法
线
Amn, Bnp,设对A关于列的分法与对B关于行的分法
相同,分别得分块矩阵
性
A11 A12 L A A21 A22 L
A1t
B11 B12 L
Байду номын сангаасA2t
,
B
B21
B22
L
B1s
B2s
代
M M
M
Ar1
Ar2
L
Art
M M
M
Bt1
Bt2
L
Bts
数
=
即Ai1, Ai2,L , Ait的列数等于B1j,B2j,L ,Btj的行数
i1,L,r; j 1,L,s
1,L
,s)
性
A
s
s
代
A 1 11
都 可 逆 ,则 A -1=
A 1 22
O
数
=
A
1 ss
=
1.4 分块矩阵及其运算
1 2 0 0 0
2 3 0
0
0
线
分块矩阵的13个公式
分块矩阵的13个公式分块矩阵是线性代数中的一个重要概念，它可以让我们更简洁、高效地处理复杂的矩阵运算。
下面就来给大家讲讲分块矩阵的13 个公式。
咱们先来说说分块矩阵的加法公式。
假设我们有两个分块矩阵 A 和B ，它们的分块方式相同，那么对应块相加就得到了A + B 。
比如说，A 中有个块是[1 2; 3 4]，B 中对应的块是[5 6; 7 8]，那相加之后这个块就变成了[6 8; 10 12]。
再来看分块矩阵的数乘公式。
如果有一个数 k ，乘以分块矩阵 A ，那么就是每个块都乘以这个数 k 。
就像你有一堆水果，每个水果的价格都乘以一个倍数，总价也就相应地变化啦。
接着说分块矩阵的乘法公式。
这可有点复杂，但别怕，咱们慢慢捋。
分块矩阵相乘时，要保证左边矩阵的列的分块方式和右边矩阵行的分块方式一致。
比如说 A 是 m×n 的矩阵，分块成 A11、A12 等，B 是n×p 的矩阵，分块成 B11、B12 等。
那么 A 乘以 B 时，就是 A11B11 +A12B21 等等这样的运算。
给大家讲个我曾经遇到的事儿吧。
有一次我给学生们讲分块矩阵的乘法，有个学生怎么都理解不了。
我就拿教室座位打比方，把每个座位看成矩阵的元素，不同的排和列看成分块。
经过这样形象的解释，他终于恍然大悟，那种成就感真的很棒！分块矩阵的转置公式也很重要。
就是把每个块都转置，然后调整一下位置。
这个就像是把书架上的书换个方向摆放，位置也变一变。
还有分块对角矩阵的乘法公式。
如果是分块对角矩阵相乘，那就简单多了，对应对角线上的块相乘就行。
分块矩阵的逆公式也有讲究。
如果一个分块矩阵可逆，那么它的逆矩阵也是分块矩阵，而且每个块的逆也有特定的规律。
分块矩阵求行列式的公式也不能忘。
这需要根据具体的分块情况来计算，有时候可以通过分块简化行列式的计算。
再说说分块矩阵的秩的公式。
通过分块，可以更方便地判断矩阵的秩。
分块矩阵的伴随矩阵公式也有它的特点。
分块矩阵及其运算
1 2 4 8 8 4 因A11 B22 = 2, A22 B22 = 6 2 = 12 16 3 4 2 0 0 所以AB = 0 8 4 0 12 16
线
0 B22 性
代 数
= =
1.4 分块矩阵及其运算
乘法
线 性
Am×n , Bn× p , 设对A关于列的分法与对B关于行的分法 相同, 分别得分块矩阵 A11 A 21 A= Ar1 A12 A22 Ar 2 A1t B11 B A2t , B = 21 Art Bt1 B12 B1s B22 B2 s Bt 2 Bts
A22
A11 = Amm
n n
ij
A22
n
n Amm
ij
线 性 代 数
其中A (I=1,2,…,m) ,m)均为方阵 其中Aii(I=1,2,…,m)均为方阵
例 1 . 13 . 设 A = ( a 则 Ab 的第 j 列为 )
m × n
, B = (b
线 性 代 数
k 0 kA = 0 0
0
k
k 2k 0 k 0 0
7 1 14 2 AB = 6 3 0 2
3k 2 2 2 1 4k , A+ B = 6 3 0 k 0 2 1 3 2 4 1 0 0 1
1 3 2 4 0 0 0 0
= =
1.4 分块矩阵及其运算
1 1 2
线 性 代 数
= =
1.4 分块矩阵及其运算
例
设A,C分别为n阶和m阶可逆方阵，试证明：
0 矩阵X = C A 0 C 1 也可逆, 且X 1 = 1 0 0 A
线
B1 1 解： X = 设 B 3
B2 AB3 1 , XX = CB B4 1
线
0 B22 性
代 数
= =
1.4 分块矩阵及其运算
乘法
线 性
Am×n , Bn× p , 设对A关于列的分法与对B关于行的分法 相同, 分别得分块矩阵 A11 A 21 A= Ar1 A12 A22 Ar 2 A1t B11 B A2t , B = 21 Art Bt1 B12 B1s B22 B2 s Bt 2 Bts
A22
A11 = Amm
n n
ij
A22
n
n Amm
ij
线 性 代 数
其中A (I=1,2,…,m) ,m)均为方阵 其中Aii(I=1,2,…,m)均为方阵
例 1 . 13 . 设 A = ( a 则 Ab 的第 j 列为 )
m × n
, B = (b
线 性 代 数
k 0 kA = 0 0
0
k
k 2k 0 k 0 0
7 1 14 2 AB = 6 3 0 2
3k 2 2 2 1 4k , A+ B = 6 3 0 k 0 2 1 3 2 4 1 0 0 1
1 3 2 4 0 0 0 0
= =
1.4 分块矩阵及其运算
1 1 2
线 性 代 数
= =
1.4 分块矩阵及其运算
例
设A,C分别为n阶和m阶可逆方阵，试证明：
0 矩阵X = C A 0 C 1 也可逆, 且X 1 = 1 0 0 A
线
B1 1 解： X = 设 B 3
B2 AB3 1 , XX = CB B4 1
分块矩阵及其运算
1 2 1 0 1 0 A1 B11 B21 1 1 1 2 1 1 0 2 4 3 4 1 , 0 2 1 1 1 1 1 2 4 1 3 3 A1 B22 , 1 1 2 0 3 1
1 2
第 二 章 矩 阵
1 A 1 1 A O
O 1 A2
1 0 0 5 0 1 1. 0 2 3
杨建新
第四节 分块矩阵及其运算
第 二 章 矩 阵
有问题可通过Email询问:
mathgaoshu@
1 1
第 二 章 矩 阵
解
O , A2 3 1 A2 , 2 1
1 A1 5, A ; 5 1 1 1 A2 ; 2 3
杨建新
第四节 分块矩阵及其运算
1 A ; 5
1 1
1 1 A ; 2 3
1 解 把A, B分块成 0 A 1 1
杨建新
0 0 1 0 0 2 1 0 1 0 1
E O , A 1 E
第四节 分块矩阵及其运算
第 二 章 矩 阵
0 1 1 2 B 1 0 1 1
1 0 0 1 B E 11 4 1 B21B22 2 0
杨建新
1 0 a a 0 0 1 0 A2 b b 1 b2 0 a 1 0 1 0 A3b ,a 其中 3A 1 4 4 4 1 3 0 1 b 1 b 0
第四节 分块矩阵及其运算
二、分块矩阵的运算规则
1 设矩阵A与B的行数相同 , 列数相同 , 采用
2-3--分块矩阵及其运算
A21
As
As1
类似地有：
As
A2
A11
A11
A1 s1
As1
说明2）：做个笔记
A O
C B
AB
特别的：
A O
O B
A
B
2021/6/7
13
5 2 0 0
例2 设
A
2
1
0
0
,
0 0 1 2
0
0
1
1
求 A1和 A
5 2 0 0
解
(1)
A
2
0
0
1 0 0
1)将矩阵A视为一个子块的分块矩阵; A
2)将矩阵A每一元素视为一个子块的分块矩阵;
A(A ij)m n;A ijaij
3)将矩阵A每一行视为子块的分块矩阵,记为:
A
T 1
T 1
行的记法可看作是列的转置
iT ( a i1 ,a i2 , ,a in ) ,i 1 ,2 , ,m
4)将 矩1 T阵 A每一列视为子块的分块矩阵,记为:
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 1 0
B
1 1
2 0
0 1 4 1
1 1 2 0
满足条件的B的分法 共有八种.
2021/6/7
10
1 0 1 0
取B分块如下
B
1 1
2 0
0 1 4 1
1 1 2 0
1 0 0 0 1 01 0
分 块 矩 阵
Ar1
Ar2
A1s
A2
s
Ars
2. 分块矩阵的加法
将m×n 矩阵A 与B 按相同的分块法分别分成r×s的分块矩阵
A11 A12
A
A21
A22
Ar1
Ar 2
A1s
B11 B12
A2 s
,
B
B21B22
Ars
Br1
Br 2
B1s
B2s
Brs
则
A11 B11 A12 B12
3 1
4
0
0
1
在利用分块矩阵的乘法讨论AB 时，下面的特殊情形值得注意。 设A 为m ×l 矩阵，B 为l×n 矩阵，将右矩阵B 按列分块:
B= b11 b12 bn
则
AB= Ab11 Ab12 Abn
若AB=O，则 Ab11 Ab12 Abn O (OO O) ，从而
线性代数
分块矩阵
1
2
3
分块矩阵 的概念
分块矩阵 的运算
分块对角矩阵
1.1 分块矩阵的概念
定义1
用若干条横线与若干条纵线将矩阵分成若干小块，每个小块 称为矩阵的子块;以子块为元素的形式上的矩阵称为分块矩阵。
a b 0 0
例如
A
c
d
0
0
0 0 p q
0
0
r
s
按下述分法分块
a b 0 0
A
Abj O( j 1,2, n)
即 bj ( j 1, 2, n) 是矩阵方程 Aml Xl1 Om1 的解，也就是说 B 的列是 Aml Xl1 Om1 的解。
4. 分块矩阵的转置
将m×n 矩阵A 分成r×s的分块矩阵
矩阵分块法
反证法
作业 1.利用逆矩阵解线性方程组:
2.设
3.设n阶矩阵A和s阶矩阵B都可逆,求
例如：将3×4矩阵 分块形式如下：
二、分块矩阵的运算
1、分块矩阵的加法： 同型矩阵,分法相同,对应子块相加. 设 A 和 B 均为 m×n矩阵,分法下:
其运算律与矩阵的加法相同.
2.分块矩阵的数乘 设分块矩阵
λ为数，那末
其运算律与数乘矩阵相同.
3.分块矩阵的乘法. 设A为 m×l 矩阵，B为l×n矩阵，分块成
Ax = b
按行分块矩阵, Ax = b又可写成:
b1
b2
,
M
bm
即 αi Tx = bi ( i = 1, 2, … , m ) .
按列分块矩阵, Ax = b又可写成
1 ,2 ,L n
b
即 x1β1+ x2 β2 + … + xn βn = b
矩阵 主 要 知 识网 络图
概 念
其中 βj ( j = 1, 2, … ,n ). 对于线性方程组
是 A 的第 j 列.
记
A=
x=
b=
B=
其中 A 称为系数矩阵, x 称为未知向量 , b 称为常数项向量 , B称为增广矩 阵, 记为:
或 B = ( A,b ) = ( β1, β2,… , β n , b )
利用矩阵的乘法,此方程可记为:
A1n A2n L
An1
An2
L
Ann
概
如果AB=BA=E,则A可逆，
念
B是A的逆矩阵.
用定义
逆矩 阵
求法
用伴随矩阵
A1 1 A A
分块对角 矩阵
作业 1.利用逆矩阵解线性方程组:
2.设
3.设n阶矩阵A和s阶矩阵B都可逆,求
例如：将3×4矩阵 分块形式如下：
二、分块矩阵的运算
1、分块矩阵的加法： 同型矩阵,分法相同,对应子块相加. 设 A 和 B 均为 m×n矩阵,分法下:
其运算律与矩阵的加法相同.
2.分块矩阵的数乘 设分块矩阵
λ为数，那末
其运算律与数乘矩阵相同.
3.分块矩阵的乘法. 设A为 m×l 矩阵，B为l×n矩阵，分块成
Ax = b
按行分块矩阵, Ax = b又可写成:
b1
b2
,
M
bm
即 αi Tx = bi ( i = 1, 2, … , m ) .
按列分块矩阵, Ax = b又可写成
1 ,2 ,L n
b
即 x1β1+ x2 β2 + … + xn βn = b
矩阵 主 要 知 识网 络图
概 念
其中 βj ( j = 1, 2, … ,n ). 对于线性方程组
是 A 的第 j 列.
记
A=
x=
b=
B=
其中 A 称为系数矩阵, x 称为未知向量 , b 称为常数项向量 , B称为增广矩 阵, 记为:
或 B = ( A,b ) = ( β1, β2,… , β n , b )
利用矩阵的乘法,此方程可记为:
A1n A2n L
An1
An2
L
Ann
概
如果AB=BA=E,则A可逆，
念
B是A的逆矩阵.
用定义
逆矩 阵
求法
用伴随矩阵
A1 1 A A
分块对角 矩阵
分块矩阵的计算方法
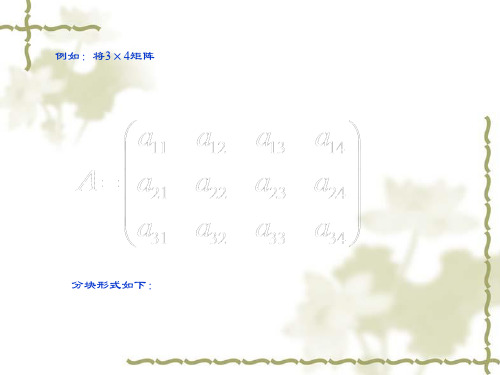
分块矩阵的计算方法
分块矩阵的计算方法可以分为以下几个步骤：
1. 将分块矩阵拆分成多个子矩阵，每个子矩阵是一个小的矩阵块。
2. 对每个子矩阵进行独立的计算，可以使用通常的矩阵计算方法，如矩阵乘法、矩阵加法、矩阵转置等。
3. 将计算得到的结果重新组合成原始的分块矩阵格式。
需要注意的是，在实际计算过程中，可能需要进行一些优化和调整，以提高计算效率和降低存储开销。
比如，在矩阵乘法时，可以采用分块矩阵乘法算法，将大的矩阵块分解成多个小的矩阵块进行计算。
在存储分块矩阵时，也可以采用压缩存储等方法，以减少存储空间的占用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
分块矩阵是一种将矩阵分割成若干个子矩阵的特殊矩阵。
通过对分块矩阵进行运算，我们可以更方便地处理一些大规模的矩阵问题。
以下是分块矩阵的几种常见运算：
分块矩阵的加法
分块矩阵的加法是指将两个同型分块矩阵的对应子矩阵分别相加，得到一个新的分块矩阵。
具体地，设两个同型的分块矩阵 A 和 B，其分块形式相同，则新的分块矩阵 C 可以表示为 C=(A1+B1,A2+B2,...,An+Bn)，其中 Ai 和 Bi 是 A 和 B 的对应子矩阵。
分块矩阵的减法
分块矩阵的减法是指将两个同型分块矩阵的对应子矩阵分别相减，得到一个新的分块矩阵。
具体地，设两个同型的分块矩阵 A 和 B，其分块形式相同，则新的分块矩阵 C 可以表示为 C=(A1-B1,A2-B2,...,An-Bn)，其中 Ai 和 Bi 是 A 和 B 的对应子矩阵。
分块矩阵的乘法
分块矩阵的乘法是指将两个同型分块矩阵的对应子矩阵分别相乘，得到一个新的分块矩阵。
具体地，设两个同型的分块矩阵 A 和 B，其分块形式相同，则新的分块矩阵 C 可以表示为 C=(A1B1,A2B2,...,An*Bn)，其中 Ai 和 Bi 是 A 和 B 的对应子矩阵。
分块矩阵的转置
分块矩阵的转置是指将分块矩阵的子矩阵分别进行转置，得到一个新的分块矩阵。
具体地，设一个分块矩阵 A，其分块形式为 (A1,A2,...,An)，则 A 的转置矩阵 AT 可以表示为(A1T,A2T,...,AnT)。
通过对分块矩阵进行以上几种运算，我们可以更好地处理大规模的矩阵问题。
同时，这些运算也具有很好的递推性质，可以通过递归的方式进行计算，进一步降低了计算的复杂度。