徐闻县2010—2011学年度第一学期期中联合调研测试八年级数学试卷

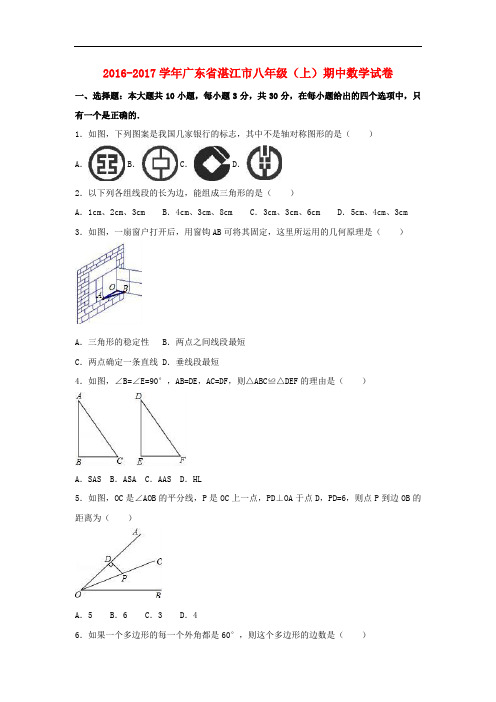
2016-2017学年广东省湛江市八年级（上）期中数学试卷一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是正确的．1．如图，下列图案是我国几家银行的标志，其中不是轴对称图形的是（）A．B．C．D．2．以下列各组线段的长为边，能组成三角形的是（）A．1cm、2cm、3cm B．4cm、3cm、8cm C．3cm、3cm、6cm D．5cm、4cm、3cm 3．如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）A．三角形的稳定性B．两点之间线段最短C．两点确定一条直线 D．垂线段最短4．如图，∠B=∠E=90°，AB=DE，AC=DF，则△ABC≌△DEF的理由是（）A．SAS B．ASA C．AAS D．HL5．如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（）A．5 B．6 C．3 D．46．如果一个多边形的每一个外角都是60°，则这个多边形的边数是（）A．3 B．4 C．5 D．67．如图，△ABC≌△DEF，BE=4，AE=1，则DE的长是（）A．5 B．4 C．3 D．28．如图，在△ABC和△FED中，AC=FD，BC=ED，要利用“SSS”来判定△ABC和△FED全等时，下面的4个条件中：①AE=FB；②AB=FE；③AE=BE；④BF=BE，可利用的是（）A．①或②B．②或③C．①或③D．①或④9．如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35°，则∠BAC的度数为（）A．45° B．40° C．60° D．70°10．如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC 于点D，CD=3，则BC的长为（）A．6 B．6 C．9 D．3二、填空题：本大题共6小题，每小题4分，共24分．11．在平面直角坐标系中，点（﹣3，2）关于y轴的对称点的坐标是．12．已知一个等腰三角形的顶角为30°，则它的一个底角等于．13．如图，AB、CD相交于点O，AC⊥CD于点C，若∠BOD=38°，则∠A= ．14．如图所示，D是BC的中点，E是AC的中点，若S△ADE=1，则S△ABC= ．15．若等腰三角形的两条边长分别为7cm和14cm，则它的周长为cm．16．如图，在△ABC中，∠BAC=90°，AB=3，AC=4，BC=5，EF垂直平分BC，点P为直线EF 上的任一点，则△ABP周长的最小值是．三、解答题（一）：本大题3小题，每小题6分，共18分．17．求出图中的x的值．18．若点M（1，a）与点N（b﹣5，2）关于x轴对称，求a+b的值．19．如图，在△ABC中，∠A=36°，∠C=72°，BD平分∠ABC，求∠DBC的度数．四、解答题（二）：本大题3小题，每小题7分，共21分．20．如图，在△ABC中，点D是AB上的一点，且AD=DC=DB，∠B=30°．求证：△ADC是等边三角形．21．如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE．（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明．22．在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，﹣1）．（1）将△ABC沿y轴正方向平移3个单位得到△A1B1C1，画出△A1B1C1，并写出点B1坐标；（2）画出△A1B1C1关于y轴对称的△A2B2C2，并写出点C2的坐标．五、解答题（三）：本大题3小题，每小题9分，共27分．23．如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1．（1）求点D到AB的距离；（2）求BD的长度．24．如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于点Q，PQ=3，PE=1．（1）求证：AD=BE；（2）求AD的长．25．已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（s）．（1）当动点P、Q同时运动2s时，则BP= cm，BQ= cm．（2）当动点P、Q同时运动t（s）时，分别用含有t的式子表示；BP= cm，BQ= cm．（3）当t为何值时，△PBQ是直角三角形？2016-2017学年广东省湛江市徐闻县八年级（上）期中数学试卷参考答案与试题解析一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是正确的．1．如图，下列图案是我国几家银行的标志，其中不是轴对称图形的是（）A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形的概念求解．【解答】解：A、B、D都是轴对称图形；C、不是轴对称图形．故选：C．2．以下列各组线段的长为边，能组成三角形的是（）A．1cm、2cm、3cm B．4cm、3cm、8cm C．3cm、3cm、6cm D．5cm、4cm、3cm 【考点】三角形三边关系．【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”进行分析．【解答】解：根据三角形的三边关系，A、1+2=3，不能组成三角形；B、4+3＜8，不能够组成三角形；C、3+3=6，不能组成三角形；D、4+3＞5，能组成三角形．故选D．3．如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）A．三角形的稳定性B．两点之间线段最短C．两点确定一条直线 D．垂线段最短【考点】三角形的稳定性．【分析】根据加上窗钩，可以构成三角形的形状，故可用三角形的稳定性解释．【解答】解：构成△AOB，这里所运用的几何原理是三角形的稳定性．故选：A．4．如图，∠B=∠E=90°，AB=DE，AC=DF，则△ABC≌△DEF的理由是（）A．SAS B．ASA C．AAS D．HL【考点】直角三角形全等的判定；全等三角形的判定．【分析】根据直角三角形的判定定理进行选择．【解答】解：∵在Rt△ABC与Rt△DEF中，，∴Rt△ABC≌Rt△DEF（HL）．故选：D．5．如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（）A．5 B．6 C．3 D．4【考点】角平分线的性质．【分析】过点P作PE⊥OB于E，根据角平分线上的点到角的两边距离相等可得PE=PD，再根据点到线段的距离的定义解答．【解答】解：如图，过点P作PE⊥OB于E，∵OC是∠AOB的平分线，PD⊥OA，∴PE=PD=6，∴点P到边OB的距离为6．故选B．6．如果一个多边形的每一个外角都是60°，则这个多边形的边数是（）A．3 B．4 C．5 D．6【考点】多边形内角与外角．【分析】由一个多边形的每一个外角都等于60°，且多边形的外角和等于360°，即可求得这个多边形的边数．【解答】解：∵一个多边形的每一个外角都等于60°，且多边形的外角和等于360°，∴这个多边形的边数是：360÷60=6．故选：D．7．如图，△ABC≌△DEF，BE=4，AE=1，则DE的长是（）A．5 B．4 C．3 D．2【考点】全等三角形的性质．【分析】根据全等三角形对应边相等，DE=AB，而AB=AE+BE，代入数据计算即可．【解答】解：∵△ABC≌△DEF∴DE=AB∵BE=4，AE=1∴DE=AB=BE+AE=4+1=5故选A．8．如图，在△ABC和△FED中，AC=FD，BC=ED，要利用“SSS”来判定△ABC和△FED全等时，下面的4个条件中：①AE=FB；②AB=FE；③AE=BE；④BF=BE，可利用的是（）A．①或②B．②或③C．①或③D．①或④【考点】全等三角形的判定．【分析】要利用SSS进行△ABC和△FED全等的判定，还需要条件AB=FE，结合题意给出的条件即可作出判断．【解答】解：由题意可得，要用SSS进行△ABC和△FED全等的判定，需要AB=FE，若添加①AE=FB，则可得AE+BE=FB+BE，即AB=FE，故①可以；若添加AB=FE，则可直接证明两三角形的全等，故②可以．若添加AE=BE，或BF=BE，均不能得出AB=FE，不可以利用SSS进行全等的证明，故③④不可以．故选A．9．如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35°，则∠BAC的度数为（）A．45° B．40° C．60° D．70°【考点】等腰三角形的性质；平行线的性质．【分析】首先由AE∥BD，根据平行线的性质，求得∠DBC的度数，然后由BD平分∠ABC，求得∠ABC的度数，再由AB=AC，利用等边对等角的性质，求得∠C的度数，继而求得答案．【解答】解：∵AE∥BD，∴∠DBC=∠E=35°，∵BD平分∠ABC，∴∠ABC=2∠DBC=70°，∵AB=AC，∴∠C=∠ABC=70°，∴∠BAC=180°﹣∠ABC﹣∠C=40°．故选B．10．如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC 于点D，CD=3，则BC的长为（）A．6 B．6 C．9 D．3【考点】含30度角的直角三角形；线段垂直平分线的性质．【分析】根据线段垂直平分线上的点到线段两端距离相等可得AD=BD，可得∠DAE=30°，易得∠ADC=60°，∠CAD=30°，则AD为∠BAC的角平分线，由角平分线的性质得DE=CD=3，再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2DE，得结果．【解答】解：∵DE是AB的垂直平分线，∴AD=BD，∴∠DAE=∠B=30°，∴∠ADC=60°，∴∠CAD=30°，∴AD为∠BAC的角平分线，∵∠C=90°，DE⊥AB，∴DE=CD=3，∵∠B=30°，∴BD=2DE=6，∴BC=9，故选C．二、填空题：本大题共6小题，每小题4分，共24分．11．在平面直角坐标系中，点（﹣3，2）关于y轴的对称点的坐标是（3，2）．【考点】关于x轴、y轴对称的点的坐标．【分析】根据关于y轴对称的点，纵坐标相同，横坐标互为相反数，可得答案．【解答】解：在平面直角坐标系中，点（﹣3，2）关于y轴的对称点的坐标是（3，2），故答案为：（3，2）．12．已知一个等腰三角形的顶角为30°，则它的一个底角等于75°．【考点】等腰三角形的性质．【分析】已知明确给出等腰三角形的顶角是30°，根据等腰三角形的性质及三角形的内角和定理易求得底角的度数．【解答】解：∵等腰三角形的顶角是30°，∴这个等腰三角形的一个底角==75°．故答案为75°．13．如图，AB、CD相交于点O，AC⊥CD于点C，若∠BOD=38°，则∠A= 52°．【考点】直角三角形的性质；对顶角、邻补角．【分析】利用对顶角相等得到∠AOC的度数，然后利用直角三角形两锐角互余求得角A即可．【解答】解：∵∠BOD=38°，∴∠AOC=38°，∵AC⊥CD于点C，∴∠A=90°﹣∠AOC=90°﹣38°=52°．故答案为52°．14．如图所示，D是BC的中点，E是AC的中点，若S△ADE=1，则S△ABC= 4 ．【考点】三角形的面积；三角形的角平分线、中线和高．【分析】先根据D是BC的中点，E是AC的中点，得出△ADE的面积等于△ABC的面积的四分之一，再根据S△ADE=1，得到S△ABC=4．【解答】解：∵D是BC的中点，E是AC的中点，∴△ADC的面积等于△ABC的面积的一半，△ADE的面积等于△ACD的面积的一半，∴△ADE的面积等于△ABC的面积的四分之一，又∵S△ADE=1，∴S△ABC=4．故答案为：4．15．若等腰三角形的两条边长分别为7cm和14cm，则它的周长为35 cm．【考点】等腰三角形的性质；三角形三边关系．【分析】题目给出等腰三角形有两条边长为7cm和14cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：①14cm为腰，7cm为底，此时周长为14+14+7=35cm；②14cm为底，7cm为腰，则两边和等于第三边无法构成三角形，故舍去．故其周长是35cm．故答案为：35．16．如图，在△ABC中，∠BAC=90°，AB=3，AC=4，BC=5，EF垂直平分BC，点P为直线EF 上的任一点，则△ABP周长的最小值是7 ．【考点】轴对称-最短路线问题；线段垂直平分线的性质．【分析】根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可得到结论．【解答】解：∵EF垂直平分BC，∴B、C关于EF对称，连接AC交EF于D，∴当P和D重合时，AP+BP的值最小，最小值等于AC的长，∴△ABP周长的最小值是4+3=7．故答案为：7．三、解答题（一）：本大题3小题，每小题6分，共18分．17．求出图中的x的值．【考点】三角形的外角性质．【分析】根据三角形的外角等于不相邻的两个内角的和列方程求解．【解答】解：由图知：x+80=x+x+20．解得x=60．∴x的值是60．18．若点M（1，a）与点N（b﹣5，2）关于x轴对称，求a+b的值．【考点】关于x轴、y轴对称的点的坐标．【分析】根据关于x轴对称的点的横坐标相等，纵坐标互为相反数，可得答案．【解答】解：∵M（1，a）与点（b﹣5，2）关于x轴对称∴b﹣5=1，a=﹣2，解得：b=6，a=﹣2，∴a+b=6+（﹣2）=4，即：a+b的值为4．19．如图，在△ABC中，∠A=36°，∠C=72°，BD平分∠ABC，求∠DBC的度数．【考点】三角形内角和定理．【分析】首先根据三角形的内角和定理求得∠ABC的度数，然后利用角的平分线的定义求解．【解答】解：∵∠A=36°，∠C=72°，∴∠ABC=180°﹣∠A﹣∠C=180°﹣36°﹣72°=72°，∵BD平分∠ABC，∴∠DBC=∠ABC=×72°=36°．即：∠DBC的度数为36°．四、解答题（二）：本大题3小题，每小题7分，共21分．20．如图，在△ABC中，点D是AB上的一点，且AD=DC=DB，∠B=30°．求证：△ADC是等边三角形．【考点】等边三角形的判定．【分析】由等腰三角形的性质得到∠DCB=∠B=30°，求得∠ADC=60°，即可得到结论．【解答】证明：∵DC=DB，∠B=30°∴∠DCB=∠B=30°，∴∠ADC=∠DCB+∠B=60°，又∵AD=DC，∴△ADC是等边三角形．21．如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE．（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明．【考点】全等三角形的判定．【分析】（1）根据题目所给条件可分析出△ABE≌△CDF，△AFD≌△CEB；（2）根据AB∥CD可得∠1=∠2，根据AF=CE可得AE=FC，然后再证明△ABE≌△CDF即可．【解答】解：（1）△ABE≌△CDF，△AFD≌△CEB；（2）∵AB∥CD，∴∠1=∠2，∵AF=CE，∴AF+EF=CE+EF，即AE=FC，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS）．22．在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，﹣1）．（1）将△ABC沿y轴正方向平移3个单位得到△A1B1C1，画出△A1B1C1，并写出点B1坐标；（2）画出△A1B1C1关于y轴对称的△A2B2C2，并写出点C2的坐标．【考点】作图-轴对称变换；作图-平移变换．【分析】（1）直接利用平移的性质得出平移后对应点位置进而得出答案；（2）利用轴对称图形的性质得出对应点位置进而得出答案．【解答】解：（1）如图所示：△A1B1C1，即为所求；点B1坐标为：（﹣2，﹣1）；（2）如图所示：△A2B2C2，即为所求，点C2的坐标为：（1，1）．五、解答题（三）：本大题3小题，每小题9分，共27分．23．如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1．（1）求点D到AB的距离；（2）求BD的长度．【考点】含30度角的直角三角形．【分析】（1）根据角平分线的性质定理解答；（2）根据三角形内角和定理求出∠BAC=60°，根据角平分线的定义求出∠DAB，根据直角三角形的性质和等腰三角形的性质计算即可．【解答】解：（1）过点D作DE⊥AB于点E，∵AD平分∠CAB，∠C=90°，DE⊥AB，∴DE=CD=1，即：点D到AB的距离为1；（2）∵∠C=90°，∠B=30°，∴∠BAC=90°﹣30°=60°，∵AD平分∠CAB，CD=1．∴∠BAD=∠CAD=30°，即：BD=AD=2CD=2，∴BD的长度是2．24．如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于点Q，PQ=3，PE=1．（1）求证：AD=BE；（2）求AD的长．【考点】等边三角形的性质；全等三角形的判定与性质；含30度角的直角三角形．【分析】（1）根据等边三角形的三条边都相等可得AB=CA，每一个角都是60°可得，∠BAE=∠ACD=60°，然后利用“边角边”证明△ABE和△CAD全等，根据全等三角形对应边相等证明即可；（2）根据全等三角形对应角相等可得∠CAD=∠ABE，然后求出∠BPQ=60°，再根据直角三角形两锐角互余求出∠PBQ=30°，然后根据直角三角形30°角所对的直角边等于斜边的一半求出BP=2PQ，再根据AD=BE=BP+PE代入数据进行计算即可得解．【解答】（1）证明：∵△ABC为等边三角形，∴AB=CA=BC，∠BAE=∠ACD=60°；在△ABE和△CAD中，，∴△ABE≌△CAD（SAS），∴AD=BE；（2）解：∵△ABE≌△CAD，∴∠CAD=∠ABE，∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°；∵BQ⊥AD，∴∠AQB=90°，∴∠PBQ=90°﹣60°=30°，∵PQ=3，∴在Rt△BPQ中，BP=2PQ=6，又∵PE=1，∴AD=BE=BP+PE=6+1=7．25．已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（s）．（1）当动点P、Q同时运动2s时，则BP= 1 cm，BQ= 2 cm．（2）当动点P、Q同时运动t（s）时，分别用含有t的式子表示；BP= （3﹣t）cm，BQ= t cm．（3）当t为何值时，△PBQ是直角三角形？【考点】等边三角形的性质．【分析】（1）根据路程=速度×时间即可求得；（2）根据路程=速度×时间即可求得；（3）根据等边三角形的性质可以知道这个直角三角形∠B=60°，所以就可以表示出BQ与PB的关系，要分情况进行讨论：①∠BPQ=90°；②∠BQP=90°．然后在直角三角形BQP中根据BP，BQ的表达式和∠B的度数进行求解即可．【解答】解：（1）BQ=1×2=2（cm），BP=3﹣2=1（cm），故答案为1，2；（2）BP=（3﹣t） cm，BQ=tcm，故答案为（3﹣t），t；（3）根据题意，得AP=t cm，BQ=t cm．在△ABC中，AB=BC=3 cm，∠B=60°，∴BP=（3﹣t）cm．在△PBQ中，BP=（3﹣t）cm．，BQ=tcm，若△PBQ是直角三角形，则只有∠BQP=90°或∠BPQ=90°①当∠BQP=90°时，BQ=BP，即t=（3﹣t），解得t=1；②当∠BPQ=90°时，BP=BQ，即3﹣t=t．解得t=2．答：当t=1s或t=2s时，△PBQ是直角三角形．。

2013-2014学年度第一学期八年级期中考试数学试卷学校：班级：座号：姓名：分数：说明：1．本试卷满分100分，考试时间90分钟．2．本试卷共4页，共3大题．注意：在答题卡上作图必须用蓝、黑色字迹的钢笔或签字笔.一、选择题：本大题12小题，每小题3分，共36分.只有一项是正确．题号 1 2 3 4 5 6 7 8 9 10 11 12答案1．若等腰三角形的底角为54°，则顶角为A．108° B．72° C．54°D．36°2．已知一个多边形的内角和是540 ，则这个多边形是A．四边形 B．五边形 C．六边形 D．七边形3．下列说法正确的是A．轴对称图形的对称轴只有一条B．角的对称轴是角的平分线C．成轴对称的两条线段必在对称轴同侧 D．等边三角形是轴对称图形4．如图，CD是AB的垂直平分线，AC＝1.6cm，BD＝2.3cm，则四边形ACBD的周长为A．3.9cm B．8.8cm C．7.8cm D．无法计算5．如图，给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E，BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；④AB＝DE，AC＝DF，∠B＝∠E．其中，能使△ABC≌△DEF的条件共有A．1组 B．2组 C． 3组 D．4组6．下列四幅图案中，不是轴对称图形的是7．已知一个等腰三角形的两边长是3cm和7cm，则它的周长为A．13 cm B．17cm C．13cm或17cm D．10cm或13cm8．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是A． B． C． D．9．如图△ABD和△ACE都等边，则△ADC≌△ABE的根据是A．SSS B．SAS C．ASA D．AAS10．如图△ABC 中AB ＝AC ，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，则下列四个结论① AB 上一点与AC 上一点到D 的距离相等；②AD 上任意一点到AB 、AC 的距离相等；③∠BDE ＝∠CDF ；④BD =CD ，AD ⊥BC 。

广东省徐闻县梅溪中学2010-2011学年八年级上学期期末调研测试数学试题北师大版一、精心选一选（本大题15个小题，共30分．每小题给出的4个选项中只有一个符合题意，请将正确选项的代号填入下面答案卡相应的位置．） 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 选项1.下列判断中，你认为正确的是 A ．0的绝对值是0 B ．31是无理数 C ．4的平方根是2 D ．1的倒数是1- 2.169的平方根是±43，用数学式子表示为 A.169=±43 B.169=43 C.±169=±43D.±169=43 3. 如图所示的尺规作图是作A ．线段的垂直平分线B ．一个半径为定值的圆C ．一条直线的平行线D ．一个角等于已知角4. 已知△ABC 中，∠B =60o，AB=AC ，BC =3，则△ABC 的周长为A ．9B ．8C ．6D ．12 5. 如图,一次函数b kx y +=的图象经过点A 、B ，则它的解析式是 A ．23y x =+ B. 23y x =-+ C. 332y x =-+ D. 233y x =-+ 6. 把正比例函数y=2x 图象向上平移3个单位，得到图象解析式是A ．y=2x-3 B.y=2x+3 C.y=3x-2 D.y=3x+2 7．直线y=2x+6与y 轴交点的坐标是 A ．（0，-3）B ．（0，6）C ．（6，0） D.（-3,0） 8. 如图，给出下列四组条件：①AB DE BC EF AC DF ===，，；②AB DE B E BC EF =∠=∠=，，； ③B E BC EF C F ∠=∠=∠=∠，，； ④AB DE AC DF B E ==∠=∠，，． 其中，能使ABC DEF △≌△的条件共有 A ．1组 B ．2组 C ．3组 D ．4组 9. 一次函数21y x =-+的图象经过A ．一、二、三象限B ．一、二、四象限C ．一、三、四象限D ．二、三、四象限 10. 下面是某学生在一次测试中的计算摘录，正确的是 A ．236(2)8x x = B ．22523a b a b -=C ．623x x x ÷=D ．222()a b a b -=-第8题图第5题AB 第3题11. 化简：22(1)(1)a a +--=A ．2B ．4C ．4aD ．222a +12. 已知一次函数(2)y a x b =-+的图像如图，那么a 的取值范围是A.2a <B.2a >C.0a <D.0a >13．已知四条直线y ＝kx －3，y ＝－1，y ＝3和x ＝1所围成的四边形的面积是12，则k 的值为A ．1或－2B ．2或－1C ．3D ．414. 如图，已知 函数x y =1，34312+=x y ．当21y y >时， x 的范围是A. x ＜-1 B ．-1＜x ＜2 C ．x ＜-1或x ＞2 D ．x ＞215. 已知a ≠0，12S a =，212S S =，322S S =，…，201020092S S =，…，则2010S 用含a 的代数式表示为A.2aB.aC.2aD.1a二、细心填一填（本大题共5个小题，共15分．请将正确答案填写在相应的位置） 16．分解因式：3312a a -= ． 17．计算：34x x x -÷()= ． 18．点(21)P -，关于x 轴的对称点的坐标为 ．19. 对于函数1y x =-，若函数值y 满足条件10y -<<，则x 的取值范围是 ． 20. 观察算式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…， ……．通过观察，用你所发现的规律确定的22011的末位数字是 。

2010～2011学年度第二学期期末联合调研测试八 年 级 数 学（时间90分钟，满分100分）一、精心选一选：（本大题12个小题，共24分）（每小题给出的4个选项中只有一个符合题意，请将正确选项的代号填入下面答案卡相应的位置．）1. 计算13-的结果是 A .13 B .13- C .3 D .－3 2. 反比例函数图象经过点(2,3)M ，则下列各点在该函数图象上的是 A .(1,6)- B .2(9,)3 C .(6,1)- D .2(9,)3- 3. 在□ABCD 中，50A ∠=，则C ∠为A.40°B. 50°C.130°D.无法确定 4. 数据 1，2，4，6，6，9 的众数是A .6B .5.5C .5D .45. 一组数据共4个数，其平均数为5，极差是6，则下列满足条件的一组数据是A ．0 8 6 6B ．1 5 5 7C ．1 7 6 6D ．3 5 6 66. 已知□ABCD 的周长为32，4AB =，则BC =A .7B .12C .14D .24 7. 矩形具备而菱形不具有的性质是A ．对角线相等B ．邻角互补C ．对角线互相平分D ．对角相等8. 甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是2=0.58S 甲，2=0.56S 乙，2=0.48S 丙，2=0.38S 丁，则射箭成绩最稳定的是 A .甲 B .乙 C .丙 D .丁 9. 用两个边长为5cm 的等边三角形纸片拼成的四边形是A .正方形B .矩形C .菱形D .等腰梯形10. 化简22++a b a b a b-的结果是 A .a b + B .a b - C .22a b - D .1 11. 一个样本的各数据都减少9，则该组数据的学校 班别 姓名 学号………………………………………密………………………封………………………线……………………………………………A B C D A .平均数减少9，方差不变 B .平均数减少9，方差减少3 C .平均数与极差都不变 D .平均数减少9，方差减少9 12. 矩形的面积为2k cm ，矩形的长ycm 与宽xcm 之间的函数关系的图象大致是二、细心填一填：（本大题共8个小题,每小题3分，其中17~20小题每空1.5分，共24分．） 13. 反比例函数32y x =-自变量x 的取值范围是 . 14. 在平行四边形ABCD 中，若100A C ∠+∠=︒，则______B ∠=.15. 某校管乐队年龄情况统计如图所示，则该队学生年龄数据的平均数为 岁. 16. 如图，矩形内有两个相邻的正方形，边长．．分别为4和2，那么阴影部分的面积是 .17. 等边三角形的边长为1，则等边三角形的高是 ，面积是 .18. 菱形的周长为20cm ，一条对角线的长为8cm ，则另一条对角线的长为 ，面积为 .19. □ABCD 中，若10,6,60DC AD A ==∠=︒，那么面积为 ，BC 边上的高为 . 20. 如图，已知等腰梯形的一个底角是60︒，它的两底分别是6,16cm cm ，则等腰梯形的周长是 ，面积是 . 三、专心解一解：（本大题共8个小题，共52分. ） 21.（本小题5分） 解分式方程：02311=-+-x x .第16题图 第15题图第20题图22.（本小题5分）如图所示，某人欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达地点B 相距50米，结果他在水中实际游的路程比河的宽度多10米，求该河的宽度AB .23.（本小题6分）在质量不变的情况下，某物体的密度3(/)kg m ρ与体积3()V m 成反比例，其函数如图所示，解答下列问题：（1）求ρ与V 之间的函数关系式；（2分） （2）当310V m =时，物体的密度是多少？（2分） 并写出该物体的密度ρ与体积V 的变化规律. （2分）24.（本小题6分）如图，在□ABCD 中，,E F 是对角线AC 上两点，,AE CF = 求证:.EBF FDE ∠=∠第24题25.（本小题7分）我县某中学对学校倡导的“压岁钱捐款活动”进行抽样调查，得到一组学生捐款的数据， 下图是根据这组数据绘制的统计图，图中从左到右长方形的高度之比为2:4:5:8:6.又知此次调查中捐款20元和25元的学生一共28人. （1）他们一共调查了多少学生？（2分） （2）写出这组数据的中位数、众数；（2分）（3）若该校共有2000名学生，估计全校学生大约捐款多少元？（3分）26.（本小题7分）某次射击练习，甲、乙两个学生各射靶5次,射中的环数如下表所示:已算得甲射中环数的平均数甲-x =7,方差8.02=甲S .求乙射中环数的平均数与方差,并指出哪个学生射击的成绩比较稳定.27.（本小题8分）已知正方形ABCD，GE⊥BD于B，AG⊥GE于G ，AE=AC，AE交BC于F，求证：（1）四边形AGBO是矩形；（3分）（2）求∠CFE的度数.（5分）O G F ED CB A第23题第27题图28.（本小题8分）如图, 已知一次函数b kx y +=（k 、b 为常数）的图象与反比例函数xmy =（m 为常数， 0≠m ）的图象相交于点 A （1，3）、 B （n ，-1）两点. （1）求上述两个函数的解析式；(4分)（2）如果M 为x 轴正半轴上一点，N 为y 轴负半轴上一点， 以点A ，B ，N ，M 为顶点的四边形是平行四边形，求直线MN 的函数解析式．（4分）一、选择题1~6: ABBACB ；7~12: ADCBAD ﹒二、填空题13.2x ≠ ；14. 130︒ ；15.14.6；16.4;；18.6cm ，224cm;19.; 20.42cm,2. 三、解答题21、解：方程两边都乘以(1)(2)x x --得：（1分）0)1(32=-+-x x （2分）解这个整式方程，得45=x （4分） 检验：把45=x 代入0)2)(1(≠--x x∴45=x 是原方程的解。

2010—2011学年度第一学期期中联合调研测试八 年 级 数 学 试 卷（时间90分钟, 满分100分）一、精心选一选（本大题15个小题，共30分．每小题给出的4个选项中只有一个符合题意，请将正确答案填写在相应的位置．） 1. 下列所给的数中，是无理数的是（ ）．Ａ.2 ＢＣ.12Ｄ.0.1 2.）．A ．3B ．3-C ．3±D3. 8-的立方根是（ ）．A．-B ．2-C．-D4. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是 （ ）．5. 给出四个数0，2,一21，0.3其中最小的是( ) ． A ．0 B ．2 C ．一21D ．0.36. Rt Rt ABC DEF △≌△，则E ∠的度数为（ ）. A ．30B ．45C ．60D ．907. 下列判断中，你认为正确的是（ ）. A ．0的绝对值是0 B ．31是无理数 C ．4的平方根是2 D ．1的倒数是1- 8. 在ABC △和DEF △中，,,AB DE AC DF A D ==∠=∠，如果ABC △的周长是16，面积是12，那么DEF △的周长、面积依次为（ ）．A ．8，3B ．8，6C ．16，12D ．４，6ADCBE第6题图9. 实数a 、b 在数轴上的位置如图所示，则a 与b 的大小关系是（ ）．A ．a > bB ． a = bC ． a < bD ． 不能判断10. 如图，AB AC ，要说明△ADC ≌△AEB ，需添加的条件不能．．是（ ) ． A ．∠B ＝∠CB. AD = AE C ．∠ADC ＝∠AEBD. DC = BE11. 如图，BD 是△ABC 的角平分线，∠ABD ＝36°，∠C ＝72°，则图中的等腰三角形有（ ）．A.0个B.1个C.2个D.3个 12. 如图，在ΔABC 中，AC =DC =DB ，∠ACD =100°，则∠B 等于（ ）．A ．50°B ．40°C ．25°D ．20°13. 下列式子中，正确的是（ ）.A.10＜127＜11B. 11＜127＜12C. 12＜127＜13D. 13＜127＜14 14. 下图是小华画的正方形风筝图案，他以图中的对角线AB 为对称轴，在对角线的下方再画一个三角形，使得新的风筝图案成为轴对称图形，若下列有一图形为轴对称图形，则此图为( ) ．BA B DC 第14题图AB第9题图CB第4题图DA第12题图 ABCD第11题图15.如图所示的正方形网格中，网格线的交点称为格点．已知A 、B 是两格点，如果C 也是图中的格点，且使得ABC ∆为等腰三角形．．．．．， 则点C 的个数是（ ）． A ．6B ．7C ．8D ．9二、细心填一填（本大题共5个小题，共15分．请将正确答案填写在相应的位置） 16．写出一个比1-小的实数 ．17．等腰三角形的一个角是110︒，则它的底角是 ． 18．如图，BAC ABD ∠=∠，请你添加一个条件： ，使OC OD = （只添一个即可）．19. 如图，ABC ∆中，∠C=90°，∠ABC =60°，BD 平分∠ABC ，若AD=6，则CD= ．20. 观察下列正三角形的三个顶点所标的数字规律，那么2010这个数在第___ ___个三角形的_ _顶点处（第二空填：上、左下、右下）．第4个三角形第3个三角形第2个三角形第1个三角形……121110987654321三、专心解一解（本大题共8个小题，共55分. 请认真读题，冷静思考．解答题应写出文字说明、证明过程或演算步骤，请将答案写在答题卷相应题号的位置） 21.（本题满分5分）+第19题图DO CBA第18题图第15题图求下列各式中的x 的值：（1）225x = （2） 3(1)8x +=-23.（本题满分6分）已知：如图，∠A ＝∠DCF ，F 是AC 的中点． 求证：△AEF ≌△CDF ．24.（本题满分6分）如图，AB AD =，AC AE =，12∠=∠， 求证：BC DE =BE第24题图第23题图如图，点B 、D 、C 、F 在一条直线上，且BC = FD ，AB = EF. （1）请你只添加一个条件（不再加辅助线），使△ABC ≌△EFD ，你添加的条件是 ；(2分) （2）添加了条件后，证明△ABC ≌△EFD.（6分）26.（本题满分8分）如图，在平面直角坐标系xoy 中，(15)A -，， (10)B -，，(43)C -，． （1）求ABC △的面积．（2分）（2）在图中作出ABC △关于y 轴的对称图形111A B C △．（3分） （3）写出点111A B C ，，的坐标．（3分）第26题图FABCDE 第25题图27.（本题满分8分）如图，在等腰ABC △中，AB AC =，CD AB ⊥于点D ,BE AC ⊥ 于点E ，BE 与CD交于点F ．试写出图中所有全等的三角形，并选其中一对加以证明．28.（本题满分8分）如图，在等边ABC ∆的AC 边上取中点D ,BC 的延长线上取一点E ，使CE CD = ． 求证：BD DE =．第27题图第28题图。

2010—2011学年度第一学期期中考试（人教）八年级数学试卷题号 一二三四五六总分得分试卷满分100分，考试时间100分钟一、选择题：（本题满分30分，每小题3分）在下列各题的四个备选答案中，只有一个是正确的，请把你认为正确的答案的字母代号填在题后的括号内。

．．．．．．．．．1．下列图案是轴对称图形的有（）。

A.（1）（2）B.（1）（3）C.（1）（4）D.（2）（3）(1)(2)(3)(4)2.下列几种说法：①全等三角形的对应边相等；②面积相等的两个三角形全等；③周长相等的两个三角形全等；④全等的两个三角形一定重合。

其中正确的是（）。

A.①②B.②③C.③④D.①④3．已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为（）。

A.2㎝B.4㎝C.6㎝D.8㎝4．点M （1，2）关于x 轴对称的点的坐标为（）。

A.（—1，2）B.（－1，－2）C.（1，－2）D.（2，－1） 5.等腰三角形的底角与顶角的度数之比为2∶1，则顶角为()。

A.72°B.36°C.36°或72°D.18° 6．如图，∠B=∠D=90°，CB=CD ，∠1=40°，则∠2=（）。

A ．40°B.45°C.50°D.60°7.如图，△ABC 中，AD ⊥BC ，D 为BC 的中点，以下结论：（1）△ABD ≌△ACD ；（2）AB=AC ；（3）∠B=∠C ；（4）AD 是△ABC 的角平分线。

其中正确的有（）。

A ．1个B.2个C.3个D.4个 8.下列说法错误的是（）。

A.1的平方根是1B.–1的立方根是－1C.2是2的平方根D.0是0的平方根9．在下列实数21,π,4,31,5中，无理数有()。

A ．1个B ．2个C ．3个D ．4个第6题AB CD第7题学校班级姓名考号AC B D10．如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,有下列结论：①AB∥CD②AB=CD③AB⊥BC④AO=OC其中正确的有（）。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（）A．5 B.6 C.11 D.16试题2:下列图形中具有稳定性的有 ( )A.正方形B.长方形C.梯形D.直角三角形试题3:若一个多边形的外角和与它的内角和相等,则这个多边形是 ( )A.三角形B.四边形C.五边形D.六边形试题4:等腰三角形的周长为13cm，其中一边长为3,则该等腰三角形的底边长为( )A.7B.3C.9D.5试题5:如图所示，分别表示△ABC的三边长，则下面与△一定全等的三角形是（）A B C D试题6:下列由数字组成的图形中，是轴对称图形的是( )．试题7:如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A. SSSB. SASC. AASD. ASA试题8:若一个三角形三个内角度数的比为2：7：1，那么这个三角形是A．钝角三角形B．直角三角形C．锐角三角形D．等边三角形试题9:如图，Rt△ABC中，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm,AC=6cm,则BE的长度为（）A．10cm B．6cm C．4cm D．2cm试题10:在△ABC和△中,AB=,∠B=∠,补充条件后仍不一定能保证△ABC≌△,则补充的这个条件是( )A．BC= B．∠A=∠ C．AC= D．∠C=∠试题11:已知：如图所示，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）A．∠A与∠D互为余角 B．∠A=∠2 C．△ABC≌△CED D．∠1=∠2试题12:如图是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔．如果一个球按图中所示的方向被击出(球可以经过多次反射)，那么该球最后将落入的球袋是( )．A．1号袋 B．2号袋C．3号袋 D．4号袋试题13:若一个多边形的内角和是外角和的2倍，则这个多边形边数是。

初中数学试卷桑水出品湛江市徐闻县2015~2016学年度第一学期期中质量检测八年级数学试卷说明：1、考试时间：100分钟；2、满分：120分。

一、单项选择题（本大题10小题，每小题3分，共30分）1、如图，下列图案中，是轴对称图形的是（）2、以下面各组线段的长为边，能组成三角形的是（）A、1，2，3B、3，4，8C、5，6，11D、2，3，43、下列图形中具有不稳定性的是（）A、长方形B、等腰三角形C、直角三角形D、锐角三角形4、如图，AC平分∠BAD，∠B=∠D，AB=8cm，则AD=（）A、6cmB、8cmC、10cmD、4cm5、已知直角三角形中30°角所对的直角边为2cm，则斜边的长度为（）A、2cmB、4cmC、6cmD、8cm6、一个三角形三个内角的度数之比为1:2:3，则这个三角形一定是（）A、等腰三角形B、锐角三角形C、直角三角形D、钝角三角形7、点P（1，2）关于x轴对称点的坐标是（）A、（－1，2）B、（1，－2）C、（1，2）D、（－1，－2）8、等腰三角形有两条边长分别为5和10，则这个等腰三角形的周长为（）A、15B、20C、25或20D、259、下列条件中，不能判定两个直角三角形全等的是（）A、两锐角对应相等B、斜边和一条直角边对应相等C、两直角边对应相等D、一个锐角和斜边对应相等10、如图，△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，则∠BDC的度数为（）A、72°B、36°C、60°D、82°二、填空题（本大题6小题，每小题4分，共24分）11、正十二边形的内角和是。

12、已知点A（m+2，－3），B（－2，n－4）关于y轴对称，则m= ,n= 。

13、△ABC和△A′B′C′，已知AB=A′B′，BC=B′C′，则增加条件后，△ABC≌△A′B′C′。

（填写一个即可）14、如图，在等边△ABC中，AD⊥BC，AB=5cm，则DC的长为。

徐闻第一中学2010—2011学年第一学期初二数学期末考试试题一、选择题（每小题3分，共45分） 1、9的算术平方根等于( )A.±3B.－3C.3D.81 2、下列图形中，是轴对称图形的是（ ）3、下列计算正确的是 （ ）A 、a·a 2＝a 2B 、(a 2)2＝a 4C 、C.3a +2a =5a 2D 、(a 2b)3＝a 2·b 34、 在may x xy x x ,3,3,21,21,12++π中，分式的个数是（ ） A 2 B 3 C 4 D 55、点M （3，－4）关于x 轴的对称点的坐标是 （ ）A.（3， 4）B.（－3，－4）C.（－3， 4）D.（－4，3） 6、下列各点中，在函数xy 2-=的图像上的是（ ） A 、（2，1） B 、（-2，1） C 、（2，-2） D 、（1，2） 7、 把分式方程12121=----xxx ，的两边同时乘以x-2，约去分母，得（ ） A 1-(1-x) =1 B 1+(1-x)=1 c 1-(1-x)=x-2 D 1+(1-x)=x-2 8、反比例函数y=2x的图象位于（ ） A 、第一、二象限 B 、第一、三象限 C 、第二、三象限 D 、第二、四象限 9、函数y=2x+1的图象经过（ ） A ．(2 , 0)B ．(0 , 1) C. (1 , 0) D ．(12, 0) 10、将多项式m 2－4进行因式分解，结论正确的为( )A.(m ＋2)(m －2)B.(m ＋4)(m －4)C.(m －2)2D.(m ＋2)211、函数y =-x+2的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限12、若52-=m xy 为反比例函数，则m= ( )A. -4B. -5C. 4D. 513、小明和小张两人练习电脑打字，小明每分钟比小张少打6个字，小明打120个字所用的时间和小张打180个字所用的时间相等。