特殊角的三角函数

【基础知识回顾】一、锐角三角函数定义：1.在Rt △ABC 中，∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ，则∠A 的正弦可表示为： sinA= ，∠A 的余弦可表示为cosA= ∠A 的正切：tanA= ， 它们统称为∠A 的锐角三角函数二、特殊角的三角函数值：2、正弦和正切值随着角度的增大而 余弦值随着角度的增大而3、几个特殊关系：⑴sin 2A+cos 2A= , tanA =sin A （ ） ⑵若∠A+∠B=900，则sinA= ，tanA.tanB =三、解直角三角形：1、定义：由直角三角形中除直角外的 个已知元素，求出另外 个未知元素的过程叫解直角三角形。

2、解直角三角形的依据：Rt ∠ABC 中，∠C=900 三边分别为a 、b 、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA cosA tanAsinB cosB tanB3、解直角三角形应用中的有关概念 ⑴仰角和俯角：如图：在图上标上仰角和俯角⑵坡度坡角：如图： 斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度，用i 表示，即i= 坡面与水平面得夹角为 用字母α表示，则i=tanα=h l。

经典例题1.如图，将∠AOB 放置在5×5的正方形网格中，则tan ∠AOB 的值是（ ）A ．23B ．32C ．21313D ．313132.计算6tan45°-2cos60°的结果是（ ）A ．43B ．4C ．53D ．5αsinα cosα tanα 300450600铅直水平线 视线3.如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，∠BOC=120°，则四边形ABCD的面积为．（结果保留根号）4.河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：3，则AB的长为（）A．12 B．43米C．53米D．63米5.一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（）A．103海里/小时B．30海里/小时C．203海里/小时D．303海里/小时6.某校研究性学习小组测量学校旗杆AB的高度，如图在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼三楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知每层楼的高度为3米，则旗杆AB的高度为米．7.如图，某海监船向正西方向航行，在A处望见一艘正在作业渔船D在南偏西45°方向，海监船航行到B处时望见渔船D在南偏东45°方向，又航行了半小时到达C处，望见渔船D在南偏东60°方向，若海监船的速度为50海里/小时，则A，B之间的距离为（取3≈1.7，结果精确到0.1海里）．D8.如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之。

（1）特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0.866025404 二分之根号3cos45=0.707106781 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.577350269 三分之根号3tan45=1tan60=1.732050808 根号3tan90=无cot0=无cot30=1.732050808 根号3cot45=1cot60=0.577350269 三分之根号3cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（见下）（3）锐角三角函数值的变化情况（i）锐角三角函数值都是正值（ii）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时，tanα>0, cotα>0.“锐角三角函数”属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。

从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。

在义务教育第三学段，主要研究锐角三角函数和解直角三角形的内容，本套教科书安排了一章的内容，就是本章“锐角三角函数”。

在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。

无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。

三角函数特殊角三角函数是数学中的一大分支，主要研究角与三角比的关系。

在三角函数中，有一组特殊的角度，被称为特殊角。

这些特殊角的数值与三角函数的值具有简单的关系，方便计算和使用。

本文将详细介绍这些特殊角及其性质，帮助读者更好地理解和运用三角函数。

首先，我们来介绍最常见的两个特殊角：0度和90度。

0度角是一条射线与x轴正方向重合的角，符号表示为0°。

它的正弦值、余弦值和正切值都为零，即sin0°=0，cos0°=1，tan0°=0。

90度角是一条射线与y轴正方向重合的角，符号表示为90°。

它的正弦值为1，余弦值为0，正切值为无穷大，即sin90°=1，cos90°=0，tan90°=∞。

接下来，我们介绍30度角和60度角。

30度角是一条射线与x轴正方向夹角为30度的角，符号表示为30°。

它的正弦值等于其对边与斜边的比值，即sin30°=1/2，余弦值等于其邻边与斜边的比值，即cos30°=√3/2，正切值等于其对边与邻边的比值，即tan30°=1/√3。

60度角是一条射线与x轴正方向夹角为60度的角，符号表示为60°。

它的正弦值等于其对边与斜边的比值，即sin60°=√3/2，余弦值等于其邻边与斜边的比值，即cos60°=1/2，正切值等于其对边与邻边的比值，即tan60°=√3。

接下来，我们介绍45度角。

45度角是一条射线与x轴正方向夹角为45度的角，符号表示为45°。

它的正弦值等于其对边与斜边的比值，即sin45°=√2/2，余弦值等于其邻边与斜边的比值，即cos45°=√2/2，正切值等于1，即tan45°=1。

特殊角的性质不仅可以通过直角三角形来理解，还可以通过单位圆来表示。

单位圆是以原点为圆心、半径为1的圆。

高中特殊角的三角函数值口诀
在高中数学学习过程中，三角函数是一个非常重要的概念，而特殊角的三角函数值更是需要我们牢记于心。

为了帮助同学们更好地记忆高中特殊角的三角函数值，下面我整理了一些口诀，希望对大家有所帮助。

正玄口诀
1.零秒一
2.一根二
3.根二二
4.根三三
5.根二四
6.根一六
7.根零七
8.一根八
9.零
根据这个口诀，我们可以轻松地记忆出0°、30°、45°、60°、90°五个特殊角的正弦值。

余玄口诀
1.根零一
2.一根二
3.根三二
4.根二三
5.根一二
通过这个口诀，我们可以记住0°、30°、45°、60°、90°五
个特殊角的余弦值。

正旋口诀
1.根零
2.根一二
3.根三二
4.根二三
5.根一二
6.根零
这个口诀帮助我们记忆了0°、30°、45°、60°、90°五个特殊角的正切值。

余旋口诀
1.零
2.根三
3.根三
4.根三
5.根一
最后这个口诀则帮我们牢记了0°、30°、45°、60°、90°五个特殊角的余切值。

以上就是针对高中特殊角的三角函数值的口诀总结。

希望大家能够通过这些口诀轻松记忆特殊角的三角函数值，在数学学习中取得更好的成绩。

三角函数特殊角引言在学习三角函数的过程中，我们经常会遇到一些特殊角。

这些特殊角具有一些特殊的性质和计算方法，对于求解三角函数的值以及解题起到了重要作用。

本文将介绍三角函数的特殊角，包括零度角、30度角、45度角、60度角和90度角，以及它们的性质与计算方法。

一、零度角（0°）零度角是最简单的特殊角之一，即角度为0°。

在三角函数中，零度角的正弦、余弦、正切和余切的值具有特殊的计算方法和性质：•正弦值（sin）：零度角的正弦值为0，即sin(0°) = 0；•余弦值（cos）：零度角的余弦值为1，即cos(0°) = 1；•正切值（tan）：由于正切是正弦与余弦的比值，因此零度角的正切值为0，即tan(0°) = 0；•余切值（cot）：由于余切是余弦与正弦的比值，零度角的余切值不存在。

二、三十度角（30°）三十度角是一个重要的特殊角，它的角度为30°。

在三角函数中，三十度角的正弦、余弦、正切和余切的值也具有特殊的计算方法和性质：•余弦值（cos）：三十度角的余弦值为√3/2，即c os(30°) = √3/2；•正切值（tan）：三十度角的正切值为√3/3，即tan(30°) = √3/3；•余切值（cot）：三十度角的余切值为√3，即cot(30°) = √3。

三十度角在三角函数中的值是非常常见且重要的，它在几何图形的计算、物理学等领域中都有广泛的应用。

三、四十五度角（45°）四十五度角也是一个特殊角，它的角度为45°。

在三角函数中，四十五度角的正弦、余弦、正切和余切的值同样具有特殊的计算方法和性质：•正弦值（sin）：四十五度角的正弦值为√2/2，即sin(45°) = √2/2；•余弦值（cos）：四十五度角的余弦值为√2/2，即cos(45°) = √2/2；•正切值（tan）：四十五度角的正切值为1，即tan(45°) = 1；•余切值（cot）：四十五度角的余切值为1，即cot(45°) = 1。

28.1.3 特殊角的三角函数值教学目标1．知识与技能（1）通过实例认识直角三角形的边角关系，即锐角三角函数（sinA，cosA，tanA），知道30°，45°，60°角的三角函数值．（2）记住30°，45°，60°锐角的三角函数值，从而达到知道特殊角能求三角函数和知道特殊三角函数值来求锐角的效果。

（3）运用特殊角三角函数值解决直角三角形有关的简单的实际问题．（4）能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题．2．过程与方法经历探索30°，45°，60°角的三角函数值的过程，发展学生观察、分析，•解决问题的能力．贯彻在实践活动中发现问题，提出问题，再探究问题的过程中找出规律。

3．情感、态度与价值观通过用30°，45°，60°角的特殊三角函数值的应用过程，发展学生观察、分析，•解决问题的能力．培养学生数形结合的思想．重点与难点1．重点运用三角函数的知识，自主探索，推导出30°、45°、60°角的三角函数值.2．难点熟记三个特殊锐角的三角函数值，并能准确地加以运用.复习引入如图在Rt △ABC 中，∠C=900AB BCA sinA =∠=斜边的对边AB ACA cosA =∠=斜边的邻边ACBCA A tanA =∠∠=的邻边的对边1. 对于sin α与tan α，角度越大，函数值越 ； 对于cos α，角度越大，函数值越 .2. 互余的两角之间的三角函数关系：若∠A+∠B=90°，则sinA cosB ，cosA sinB ， tanA · tanB = .在学生回答了这个问题后，教师再复述一遍，提出新问题：两块三角尺中有几个不同的锐角？是多少度？分别求出这几个锐角的正弦值、余弦值和正切值．提醒学生：在300,600,900为角三角板时可以设300角所对的边长为a ，•利用勾股定理和三角函数的定义可以求出这些三角函数值．在450,450,900为角三角板时可以设450角所对的边长为a ，•利用勾股定理和三角函数的定义可以求出这些三角函数值． 探究新知（一）特殊值的三角函数学生在求完这些角的正弦值、余弦值和正切值后教师加以总结． 30°、45°、60°的正弦值、余弦值和正切值如下表：∠A的邻边b∠A的对边a 斜边c CBA通过上表，让学生观察上表中数字变化的规律并加以总结：对于正弦值，分母都是22，．对于正切，60•，即是下一个角的正切值． 要求学生记住上述特殊角的三角函数值．教师强调：（sin60°）2用sin 260°表示，即为（sin60°）·（sin60°）． （二）特殊角三角函数的应用1．师生共同完成课本第114页（盲文课本第314页）例3：求下列各式的值．（1）cos 260°+sin 260°． （2）cos 45sin 45︒︒-tan45°．教师以提问方式一步一步解上面两题．学生回答，教师板书．解：（1）cos 260°+sin 260°=（12）2+（2）2=1（2）cos 45sin 45︒︒-tan45°=2÷2-1=0巩固练习 一、选择题．1．已知：Rt △ABC 中，∠C=90°，∠A=600，则sinA 是（ ）．A ．21 B ．22 C ．23D ．1 2．已知：Rt △ABC 中，∠C=90°，tanB=33，则∠A 是（ ）． A ．300 B ．450 C ．600 D ．900二、计算：(1) sin30°+ cos45°； (2) sin 230°+ cos 230°－tan45° 解：原式 =2212221+=+解：原式 =01232122=-+）（）（2．师生共同完成课本第115页（盲文课本第315页）例4：教师解答题意：（1）如课本图28．1-9（1），在Rt △ABC 中，∠C=90，AB=6，BC=3，求∠A 的度数．（2）如课本图28．1-9（2），已知圆锥的高AO 等于圆锥的底面半径OB 的3倍，求a ．教师分析解题方法：要求一个直角三角形中一个锐角的度数，可以先求它的某一个三角函数的值，如果这个值是一个特殊解，那么我们就可以求出这个角的度数．解：（1）在课本图28．1-9（1）中，∵sinA=BC AB =， ∴∠A=45°．（2）在课本图28．1-9（2）中，∵tana=AO OB OB=∴a=60°． 当堂练习1.tan α＝1，锐角 α 的度数应是 ( )A ．40°B ．30°C ．20°D ．10°2. 已知sinA =21，则下列正确的是 ( )A. cosA =22B. cosA =23C. tanA = 1D. tanA =33. tan (α+10°)，锐角 α 的度数应是 ( ) A ．60° B ．50° C ．40° D ．30° . 4. 求下列各式的值：(1) 1－2 sin30°cos30°；(2) 3tan30°－tan45°+2sin60°；课时总结 学生要牢记下表：对于sina 与tana，角度越大函数值也越大；对于cosa ，角度越大函数值越小． 拓展延伸1. 已知：| tanB －| ＋ (2 sinA － )2 ＝0， 求∠A ，∠B 的度数.解：∵ | tanB － | ＋ (2 sinA － )2 ＝0， ∴ tanB － =0 ，2 sinA ＝0， ∴ tanB ＝ ，sinA＝2∴ ∠B ＝60°，∠A ＝60°.2.已知 △ABC 中的 ∠A 与 ∠B满足 (1－tanA)2 ＋|sinB － 2|＝0，试判断 △ABC 的形状．解：∵ (1－tanA)2 ＋ | sinB －2|＝0， ∴ 1－tanA=0 ， sinB － =0 ∴ tanA ＝1，sinB ∴ ∠A ＝45°，∠B ＝60°， ∠C ＝180°－45°－60°＝75°，∴ △ABC 是锐角三角形． 课堂小结特殊角的三角函数值⎪⎩⎪⎨⎧三角函数值角函数通角的三角函数值60、45、30000过作业设计 课本练习做课本第114页习题28．1复习巩固第3题． 1．下列各式中不正确的是（ ）．A ．sin 260°+cos 260°=1B ．sin30°+cos30°=1C ．sin35°=cos55°D ．tan45°>sin45° 2．计算2sin30°-2cos60°+tan45°的结果是（ ）． A ．2 BCD ．1 3．已知∠A 为锐角，且cosA ≤12，那么（ ） A ．0°<∠A ≤60° B ．60°≤∠A<90° C ．0°<∠A ≤30° D ．30°≤∠A<90° 4．在△ABC 中，∠A 、∠B 都是锐角，且sinA=12，ABC 的形状是（ ）A ．直角三角形B ．钝角三角形C ．锐角三角形D ．不能确定5．如图Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，BC=3，AC=4，设∠BCD=a ，则tana•的值为（ ）．A ．34 B ．43 C ．35 D ．456．当锐角a>60°时，cosa 的值（ ）． A ．小于12 B ．大于12CD ．大于17．在△ABC 中，三边之比为a ：b ：c=1：2，则sinA+tanA 等于（ ）．A1.2B C D + 8．sin 272°+sin 218°的值是（ ）． A ．1 B ．0 C ．12D9）2+││=0，则△ABC （ ）． A ．是直角三角形 B ．是等边三角形C ．是含有60°的任意三角形D ．是顶角为钝角的等腰三角形 二、填空题．10．设α、β均为锐角，且sin α-cos β=0，则α+β=_______． 11．cos 45sin 301cos 60tan 452︒-︒︒+︒的值是_______．12．已知，等腰△ABC•的腰长为，•底为30•°，•则底边上的高为______，•周长为______．13．在Rt △ABC 中，∠C=90°，已知cosA=________． 三、解答题．14．求下列各式的值．（1）sin30°·cos45°+cos60°;（2）2sin60°-2cos30°·sin45°（3）2cos602sin 302︒︒-; （4）sin 45cos3032cos 60︒+︒-︒-sin60°（1-sin30°）．（5）tan45°·sin60°-4sin30°·cos45°·tan30°（6）sin 45tan 30tan 60︒︒-︒+cos45°·cos30°15．若方程2x 2+（4sin θ）x+1=0（0<θ<90°）有两个相等的实数根，求θ的值．班主任经验介绍班主任是份繁琐的工作，我于2008年参加教师工作以来，一直在乡镇学校任教并且一直当班主任，整整十二年了，在这十二年里我想我付出了很多也得到了很多，谈谈以下几点：1.首先，作为班主任要明确自己的身份和责任，以自身来讲，要不断的学习，提高自身的业务水平，特别是勤于参加各种培训学习，如国培，外出跟班学习，参加名校，名师的学习，理论知识的学习等。

特殊角的三角函数特殊角的三角函数是指在单位圆上的某些特殊角度上，正弦、余弦和正切等三角函数的取值具有特殊的简化形式。

这些特殊角常见于三角函数的计算中，对于解决各种数学和物理问题非常有用。

本文将介绍几个常见的特殊角，并讨论它们的定义、性质以及在实际问题中的应用。

一、零度角与一百八十度角零度角和一百八十度角是特殊角中最简单的两个角度。

根据定义，在单位圆上，零度角对应于圆的正方向，也就是x轴正半轴上的点(1, 0)。

而一百八十度角则是对角线的方向，也就是x轴负半轴上的点(-1, 0)。

由于这两个角是相等的，因此它们的三角函数值也是相等的，即sin(0°) =sin(180°) = 0，cos(0°) = cos(180°) = -1，tan(0°) = tan(180°) = 0。

零度角和一百八十度角在解三角方程和证明三角恒等式等问题中经常使用。

另外，在物理学中，当物体在水平方向上做匀速直线运动时，其位移和速度在t=0时的数值都是零。

二、三十度角与一百五十度角三十度角也是一个常见的特殊角，它对应于单位圆上的点(√3/2, 1/2)。

根据定义，sin(30°) = 1/2，cos(30°) = √3/2，tan(30°) = 1/√3。

一百五十度角对应于圆的上半部分，即点(-√3/2, -1/2)。

根据定义，sin(150°) = -1/2，cos(150°) = -√3/2，tan(150°) = -1/√3。

这两个角度常用于计算等边三角形的面积、证明三角恒等式以及解决与等边三角形相关的几何问题。

三、四十五度角与一百三十五度角四十五度角对应于单位圆上的点(√2/2, √2/2)。

根据定义，sin(45°) = cos(45°) = √2/2，tan(45°) = 1。

特殊角的三角函数特殊角的三角函数第一篇：常用特殊角的三角函数在三角函数中，我们常常会遇到一些特殊角，它们具有特殊的性质和数值。

这些特殊角的三角函数在数学和物理中经常被用到，因此熟悉并掌握它们的性质和计算方法是非常重要的。

本文将介绍一些常用特殊角的三角函数，并详细解释它们的定义和性质。

1. 0度和180度的三角函数0度是一个非常特殊的角，它的正弦、余弦和正切的值均为0。

因为0度代表了一条水平线，而水平线的斜率为0，所以三角函数的值全都为0。

正弦和余弦的值是指角度的正弦和余弦值，而正切的值是指正弦和余弦的比值。

180度是另一个特殊的角，它的正弦值为0，余弦值为-1，正切值则不存在。

180度代表了一条直线的反方向，因此正弦值为0，余弦值为-1。

正切值不存在是因为正切的定义是正弦除以余弦，而在180度时，余弦为0，所以无法计算正切的值。

2. 30度和150度的三角函数30度是一个非常重要的特殊角，它的正弦值为1/2，余弦值为√3/2，正切值为1/√3。

正弦值为1/2表明在一个30度的角度下，对边与斜边的比值为1:2。

余弦值为√3/2说明在一个30度的角度下，邻边与斜边的比值为√3:2。

正切值为1/√3则表示在一个30度的角度下，对边与邻边的比值为1:√3。

150度是30度的补角，它的正弦值和正切值与30度相等，余弦值为-√3/2。

由于余弦值为负，说明在一个150度的角度下，邻边与斜边的比值为-√3:2。

3. 45度和135度的三角函数45度是一个非常特殊的角，它的正弦值和余弦值均为√2/2，正切值为1。

正弦值为√2/2表示在一个45度的角度下，对边与斜边的比值为√2:2。

余弦值同样也为√2/2，说明在一个45度的角度下，邻边与斜边的比值也是√2:2。

正切值为1表示在一个45度的角度下，对边与邻边的比值为1:1。

135度是45度的补角，它的正弦值和余弦值与45度相同，正切值为-1。

正弦值和余弦值同样也为√2/2，正切值为-1表示在一个135度的角度下，对边与邻边的比值为-1:1。

三角形特殊角的函数值特殊角是指在三角函数中具有特殊取值的角度，例如30度、45度、60度等。

这些角度在三角函数中有着特殊的函数值，对于解决各类数学问题具有重要的作用。

下面我将以人类的视角，为您描述一些特殊角的函数值和它们的应用。

一、30度角30度角是一个相对较小的角度，它的正弦值、余弦值和正切值都可以用简单的分数表示。

正弦30度等于1/2，余弦30度等于√3/2，而正切30度则等于1/√3。

这些简单的函数值使得30度角在三角函数的计算中十分常见。

例如，在直角三角形中，当一个角为30度时，可以利用正弦函数求解对边与斜边的比值。

当我们已知一个角为30度，且斜边长度为2时，可以通过正弦函数求解对边的长度：sin(30°) = 对边/斜边，即1/2 = 对边/2，解得对边长度为1。

这样，我们就可以利用30度角的函数值，求解三角形中各边的长度。

二、45度角45度角是一个非常特殊的角度，它的正弦值和余弦值相等，均为√2/2。

这个特殊的函数值使得45度角在许多几何问题中十分方便。

例如，在等腰直角三角形中，当两个锐角均为45度时，利用45度角的函数值可以轻松求解等腰直角三角形的各边长度。

根据勾股定理，我们知道等腰直角三角形的两条直角边的长度相等，假设为a，斜边长度为c，则根据余弦函数可得：cos(45°) = a/c，即√2/2 = a/c，解得a = c/√2。

这样，我们就可以利用45度角的函数值，求解等腰直角三角形中各边的长度。

三、60度角60度角是一个较大的角度，它的正弦值、余弦值和正切值也可以用简单的分数表示。

正弦60度等于√3/2，余弦60度等于1/2，而正切60度则等于√3。

这些简单的函数值使得60度角在三角函数的计算中也十分常见。

例如，在等边三角形中，每个内角都为60度。

根据正弦函数，我们可以求解等边三角形的边长。

假设等边三角形的边长为a，则sin(60°) = (边长的一半)/边长，即√3/2 = a/2a，解得 a = √3。

特殊三角函数值记忆口诀
三角函数在数学中占有重要的地位，而特殊角的三角函数值是我们在解题中经常需要用到的。

为了便于记忆和应用，我们可以使用口诀来帮助我们记忆这些特殊角的三角函数值。

下面就为大家整理了一些特殊角的三角函数值记忆口诀：
正弦值口诀
•正弦30度，约根儿2除4；
•正弦45度，根儿2除2；
•正弦60度，根儿3除2。

余弦值口诀
•余弦30度，根儿3除2；
•余弦45度，根儿2除2；
•余弦60度，约根儿2除4。

正切值口诀
•正切30度，约1除根儿3；
•正切45度，1；
•正切60度，根儿3。

余切值口诀
•余切30度，根儿3；
•余切45度，1；
•余切60度，约1除根儿3。

这些口诀可以帮助我们在需要用到特殊角的三角函数值时快速记忆，提高我们解题的效率和准确性。

希望大家能多加练习，牢记这些口诀，更加熟练地运用特殊三角函数值在数学问题中。

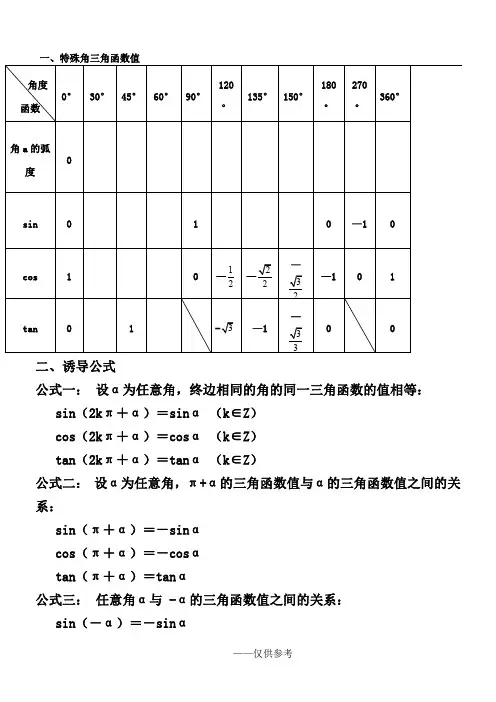
一、特殊角三角函数值二、诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinα（k∈Z）cos（2kπ＋α）＝cosα（k∈Z）tan（2kπ＋α）＝tanα（k∈Z）公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαsin（π/2－α）＝cos αcos（π/2＋α）＝－sinαcos（π/2－α）＝sin αtan（π/2＋α）＝－cotαtan（π/2－α）＝cotαsin（3π/2＋α）＝－cosαsin（3π/2－α）＝－cosαcos（3π/2＋α）＝sinαcos（3π/2－α）＝－sinαtan（3π/2＋α）＝－cotαtan（3π/2－α）＝cotα（以上k∈Z）THANKS !!!致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求欢迎您的下载，资料仅供参考。