生猪价格的预测模型

我国生猪周期理论与模式评估及价格预测分析近年来，我国养猪产业受到了生猪周期的影响，生猪价格的波动使得养殖户面临着巨大的经济压力。

为了有效应对这种周期性的特点，研究人员提出了我国生猪周期理论与模式评估及价格预测分析。

本文将对这一理论进行介绍并进行评估与预测。

我国生猪周期理论认为，生猪市场具有一定的周期性，其价格会在一定的时间内发生波动。

这种周期性主要受到供需关系、种猪库存、政策调控等多种因素的影响。

周期性的发生使得生猪价格的波动性增大，给养殖户带来了较大的风险和不确定性。

为了更好地评估生猪周期理论的准确性，研究人员通过实证分析了过去几年生猪市场的价格数据。

他们发现，生猪价格确实存在周期波动，且周期长度约为2至3年。

同时，种猪产能、进口环境以及政策调控等因素在周期性波动中扮演重要角色。

通过对这些因素的综合分析，可以较为准确地预测未来生猪价格的变动趋势。

基于以上分析，研究人员提出了一种生猪价格预测的模型。

该模型基于时间序列分析和经济数据分析，通过考虑种猪养殖规模、屠宰企业库存、国内外市场需求等因素，对未来生猪价格进行预测。

研究人员利用历史数据对模型进行验证，并取得了一定的预测准确率。

这种模型的应用使得养殖户能够提前调整生产策略，降低经济风险。

综上所述，我国生猪周期理论与模式评估及价格预测分析为养殖户提供了有效应对生猪价格波动的方法。

通过该理论和模型，养殖户能够更好地应对市场风险，并进行合理经营决策，从而减少经济损失。

这一理论的应用和发展对于稳定我国生猪市场，促进养猪产业的可持续发展具有重要意义。

随着我国经济的快速发展和人民生活水平的提高，对猪肉的需求不断增长。

然而，由于生猪周期的存在，生猪价格的波动性较大，给养殖户带来了一定的风险和不确定性。

为了更好地应对这一问题，研究人员开始关注生猪周期的理论与模式评估，并通过价格预测分析来提前进行经营决策。

生猪周期是指生猪价格在一定时间内发生周期性波动的现象。

这种周期性主要受到供需关系、种猪库存、政策调控等多种因素的影响。

猪肉价格的统计模型摘要本文就猪肉价格预测的问题，根据题目中的条件和要求，在合理的假设下，建立三个模型。

模型一为简单的直线方程模型；模型二是在采用灰色关联度建立猪肉价格与其影响因素的关系模型后，利用关联度返算，建立猪肉价格预测模型；模型三是建立养猪场盈亏平衡点等式模型。

通过求解这三个模型，很好的解决了问题。

在问题一中，利用半数平均法，建立猪肉价格预测模型。

首先通过对2000年1月至2009年6月我国猪肉价格数据的分析，得出猪肉价格在短期内呈线性增长趋势，然后用直线方程拟合该时间序列（猪肉价格随时间变化的序列），在完全确定直线方程模型后，通过该方程求出时间序列的各趋势值，接着运用EXCEL 软件作出二者的曲线并进行比较，证明该直线方程模型的可行性，最后在此基础上，预测出2009年下半年猪肉价格的趋势值。

在问题二中，确定影响猪肉价格的因素，采用灰色关联法，建立猪肉价格与其影响因素的关系模型。

首先使用季节平均法得出猪肉价格的季节指数（1234'1,'0.98,' 1.08,' 1.13S S S S ====），其次对猪肉价格与玉米价格时间序列图进行观察比较，易知两者变化呈正相关，然后利用灰色关联法，以往年的猪肉价格作为参考序列，以往年的玉米价格和季节指数作为比较序列，求出玉米价格和猪肉价格和季节指数与猪肉价格的关联度分别为0.755和0.972。

最后，利用关联度返算，推导得出猪肉价格的预测公式： 2.92109.26'i X G S =++.在问题三中，首先根据猪的不同重量，将猪分为三个成长阶段：1Kg ～15Kg 为幼年期；15Kg ～90Kg 为成长期；90Kg ～100Kg 为成年期。

由于猪的体重从5到100公斤呈正态分布，可以算出三个阶段的猪的数量分别为5，990，5。

然后根据猪场收入与成本建立猪场盈亏平衡点等式模型，可以得到猪粮比为6.5：1，即该养猪场的盈亏平衡点。

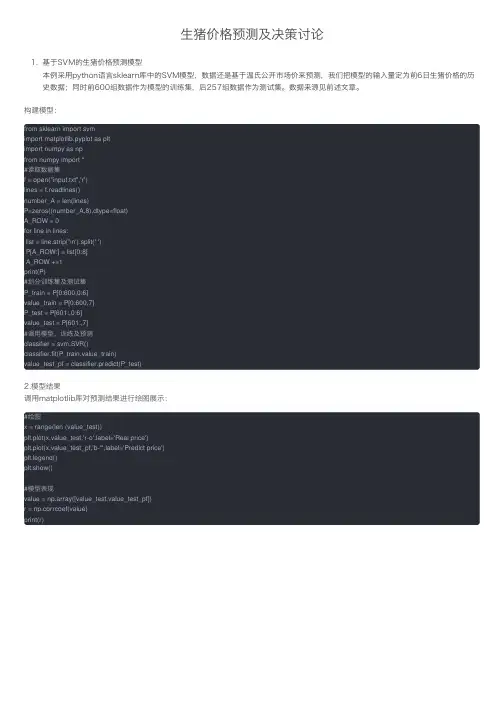
⽣猪价格预测及决策讨论1. 基于SVM的⽣猪价格预测模型本例采⽤python语⾔sklearn库中的SVM模型，数据还是基于温⽒公开市场价来预测，我们把模型的输⼊量定为前6⽇⽣猪价格的历史数据；同时前600组数据作为模型的训练集，后257组数据作为测试集。

数据来源见前述⽂章。

构建模型：from sklearn import svmimport matplotlib.pyplot as pltimport numpy as npfrom numpy import *#读取数据集f = open("input.txt",'r')lines = f.readlines()number_A = len(lines)P=zeros((number_A,8),dtype=float)A_ROW = 0for line in lines:list = line.strip('\n').split(' ')P[A_ROW:] = list[0:8]A_ROW +=1print(P)#划分训练集及测试集P_train = P[0:600,0:6]value_train = P[0:600,7]P_test = P[601:,0:6]value_test = P[601:,7]#调⽤模型、训练及预测classifier = svm.SVR()classifier.fit(P_train,value_train)value_test_pf = classifier.predict(P_test)2.模型结果调⽤matplotlib库对预测结果进⾏绘图展⽰：#绘图x = range(len (value_test))plt.plot(x,value_test,'r-o',label='Real price')plt.plot(x,value_test_pf,'b-*',label='Predict price')plt.legend()plt.show()#模型表现value = np.array([value_test,value_test_pf])r = np.corrcoef(value)print(r)下图即为本次模型测试的结果：结果讨论：svm模型的表现相⽐于GA-BP模型较差⼀点，相关性分析只有97.07%;相对于GA-BP模型，SVM没有出现⽋拟合的现象，⽣猪价格出现暴涨暴跌的情况；当前模型的输⼊量为前6⽇⽣猪价格的历史数据，从散点图的对⽐可以看出svm模型的预测值依然出现了滞后的情况；从两次模型的表现来看，想要破除模型滞后的情况，应该从输⼊数据⼊⼿，加⼊诸如母猪存栏量、屠宰量、消费量等数据。

§2 生猪的出售时机模型［问题的提出］ 一饲养场每天投入4元资金用于饲料、设备、人力，估计可使一头80公斤重的生猪每天增加2公斤．目前生猪出售的市场价格为每公斤8元，但是预测每天会降低0．1元，问该场应该什么时候出售这样的生猪．如果上面的估计和预测有出入，对结果有多大影响．[问题分析及符号约定] 投入资金可使生猪体重随时间增长，但售价(单价)随时间减少，应该存在一个最佳的出售时机，使获得利润最大．这是一个优化问题，根据给出的条件，可作如下的简化假设．每天投入4元资金使生猪体重每天增加常数 (=2公斤)；生猪出售的市场价格每r 天降低常数g(=0．1元)．[模型的建立] 给出以下记号：～时间(天)．～生猪体重(公斤)；单价 (元／t w ~p 公斤)；R-出售的收入(元)；C-t 天投入的资金(元)；Q-纯利润(元)．按照假设，．又知道，再)1.0(8),2(80=-==+=g gt p r rt w t C pw R 4,==考虑到纯利润应扣掉以当前价格(8元／公斤)出售80公斤生猪的收入，有 ，得到目标函数(纯利润)为808⨯--=C R Q其中．求使最大．1.0,2==g r )0(≥t )(t Q [模型的求解] 这是求二次函数最大值问题，用代数或微分法容易得到当时，，即10天后出售，可得最大纯利润20元．1.0,2==g r 20)10(,10==Q t [敏感性分析] 由于模型假设中的参数(生猪每天体重的增加和价格的降低g)是r 估计和预测的，所以应该研究它们有所变化时对模型结果的影响．1．设每天生猪价格的降低元不变，研究变化的影口向，由(2)式可得1.0 g r是的增函数，表1和图3给出它们的关系．t r 2．设每天生猪体重的增加=2公斤不变，研究g 变化的影响，由(2)式可得r是的减函数，表2和图4给出它们的关系． t r可以用相对改变量衡量结果对参数的敏感程度．对的敏感度记作，定义为t r ).(r t S由(3)式，当=2时可算出r 即生猪每天体重增加1％，出售时间推迟3％．r 类似地定义对g 的敏感度，由(4)式，当g=0．1时可算出t ).(g t S即生猪价格每天的降低g 增加1％，出售时间提前3％。

基于分类模型的生猪价格预测吕逸鹏，林旭东*（华南农业大学数学与信息学院，广东广州 510642）摘 要：本文旨在通过研究中国南方某养殖企业2000年7月—2015年11月生猪价格的涨跌规律，建立一个可以预测未来每月生猪价格和趋势的模型，为企业的调整和布局提供参考。

本文先使用支持向量机（SVM）、反向传播神经网络（BPNN）和Xgboost模型对样本进行涨跌分类，再根据分类结果使用不同参数的多元回归模型进行生猪价格预测。

结果显示：使用BPNN_Xgboost的组合模型在涨跌分类中的正确率达到94.59%，先分类再预测方法的平均绝对百分比误差为2.64%。

先分类再预测方法与直接预测方法相比可以降低预测的误差。

关键词：涨跌分类；BP神经网络；生猪价格预测；组合模型中图分类号：F326.3 文献标识码：A DOI编号：10.19556/j.0258-7033.20191120-03猪肉是我国居民餐桌上的主要肉食来源，2006年我国猪肉产量已达5 197.2万t[1]。

受“非洲猪瘟”影响，2019年12月我国猪肉月均价格相比于2019年1月上涨了172.42%。

据学者统计，不仅玉米价格、仔猪价格、“猪周期”、存栏量等因素会影响生猪价格[2-5]，疫情也会长期影响生猪价格[6]。

如果可以预测未来生猪价格，那么企业可以在未来价格过低时减少生猪存栏量，降低亏损，在未来价格处于较高区间时提前扩大生产，创造更多盈利。

目前众多学者常采用价格分解、经验模态分解、反向传播神经网络（BPNN）、支持向量机（SVM）、灰度模型、ARIMA模型和向量自回归模型等深度学习和机器学习算法进行生猪价格预测、风险预警、走势分析和波动分析等研究[7-14]。

较为典型的方法是使用经验模态分解将价格序列分解成不同频率，再逐个使用SVM或神经网络算法分别进行预测[15]。

另一种是使用多元回归的方法，研究影响猪肉价格的因素，再用BP神经网络进行预测[16]。

生猪价格预测及控制模型摘要本题目的在于建立描述饲料商、养猪户和消费者之间的生猪价格定价策略的数学模型, 给出调整养殖结构的方法和原则，并讨论政府调控手段对生猪市场价格的作用。

该题实际上是一个预测模型，在已知的条件和合理假设下，首先建立GM(1,1)模型,用以预测各主要因素（玉米价格（代表饲料商），猪肉价格（代表消费者），仔猪价格（代表养殖户））的价格趋势；接着在采用灰色关联度建立生猪价格与其影响因素的关系模型后，利用关联度返算，建立生猪价格预测模型并得出其表达式。

最后是建立养猪场盈亏平衡点等式模型。

把这三个问题解决了题目的主要意图也就达到了。

1.，建立GM（1，1）各主要因素的价格预测模型。

首先通过对2010年3月21日至2010年5月25日我国玉米，猪肉，仔猪价格数据的分析，得出各主要因素价格在短期内的趋势，然后GM（1，1）中方程拟合该时间序列（猪肉价格随时间变化的序列），在完全确定方程模型后，通过该方程求出时间序列的各趋势值，接着运用MATALAB作出各主要因素曲线并进行与真实值比较，可得到该方程模型的可行性，接下来就可以预测出2010年5月25日后的个主要因素价格的趋势值。

2.确定影响生猪价格的因素，采用灰色关联法，建立生猪价格与其影响因素的关系模型。

以所得的数据中生猪价格作为参考序列，以玉米价格，猪肉价格，仔猪价格作为比较序列，求出玉米价格，猪肉价格，仔猪价格与生猪价格的关联度分别为γ2，γ3，γ1。

最后，利用关联度返算，推导得出生猪价格的预测公式3.首先根据猪的不同重量，将猪分为三个成长阶段：1Kg～15Kg为幼年期；15Kg～90Kg为成长期；90Kg～100Kg为成年期。

由于猪的体重从5到100公斤呈正态分布，可以算出三个阶段的猪的数量分别为5，990，5。

然后根据猪场收入与成本建立猪场盈亏平衡点等式模型，可以得到猪粮比为6.5：1，即该养猪场的盈亏平衡点。

4.从最终得结果来看，使我们不但了解一些主要因素在影响生猪价格的作用，还会联想到其他一些因素对生猪价格的影响。

收稿日期：2019-09-17基金项目：辽宁省社会科学规划基金项目（L19DJY001）第一作者：孙若愚（1984-），男，沈阳农业大学讲师，博士，从事畜牧业经济与管理研究。

通讯作者：李大兵（1975-），男，沈阳农业大学副教授，博士，从事畜牧业经济与管理研究。

生猪产品价格预测模型分析孙若愚a ，闫大波b ，高靖羽a ，李大兵a（沈阳农业大学a.经济管理学院；b.财务处，辽宁沈阳110161）摘要:本研究通过自回归分布滞后模型（ADL ），利用2000年1月至2019年4月的仔猪、活猪和猪肉的价格及相关数据，对生猪产品价格进行了模拟分析和价格预测评价。

研究发现，从长期来看仔猪、活猪和玉米等价格存在稳定的变动关系；活鸡、玉米价格，以外生性变量显著作用于生猪产品的价格；仔猪、活猪和猪肉的价格呈现Granger 因果关系，各变量具有内生性特点。

同时，生猪产品价格波动受到季节和时间惯性影响；自回归分布滞后模型（ADL ）能够较好地模拟生猪产品价格的影响因素，且模型对于价格预测精度准确。

可通过稳定生猪产品生产，加强动物疾病防控；促进上游产业发展，稳定饲养原料供应；加强生猪价格监测预警系统，完善市场价格异常波动应急机制等促进生猪产品价格稳定。

关键词:生猪；产品价格；模拟分析；预测中图分类号:F326.3;F323.7文献标识码:A文章编号:1008-9713（2019）06-0651-06俗话说“国以民为本，民以食为天，猪粮安天下”，可见猪粮的作用十分重要。

根据“猪价格网”数据，现阶段我国居民仍以猪肉作为最主要的肉类消费品，而生猪产品的价格波动问题，对经济社会发展和居民消费造成了一定影响。

因此，以生猪产品价格波动以及合理预测作为研究内容，对于指导生猪生产，进而满足消费者对生猪产品的需求有较强的现实意义。

国内学者十分关注生猪产品价格方面的问题，研究成果多集中在以下几个方面：第一，关于猪肉价格波动周期的研究。

严斌剑等分析了某一时间段内我国生猪市场价格波动的周期性特征，并对国家实施的生猪调控政策效果进行了评价，得出加强生猪生产的调控性对策建议[1]。