实验三内容
- 格式:wps
- 大小:103.00 KB
- 文档页数:3

实验三:高锰酸钾法测定软锰矿氧化力一、实验内容(实验书P302 ~ 304)1. 0.02 mol/L KMnO 4标准溶液的配制与标定2. 软锰矿氧化力的测定二、实验目的1. 了解KMnO 4标准溶液的配制及标定原理与方法2. 掌握自身指示剂的应用及终点判断3. 熟悉采用返滴定法测定软锰矿氧化力的原理及方法三、实验原理1. KMnO 4标准溶液浓度的标定原理由于Na 2C 2O 4易于提纯,稳定,不含结晶水,在105 – 110 ℃干燥2小时即可使用,故用Na 2C 2O 4基准物标定KMnO 4溶液,反应式如下:5C 2O 42- + 2MnO 4- + 16H + == 10CO 2 + 2Mn 2+ + 8H 2O2. 软锰矿氧化力的测定原理软锰矿的主要成分MnO 2是一种氧化剂,软锰矿中除了含MnO 2外,还有少量锰的低价氧化物和氧化铁,测定软锰矿中MnO 2含量实际上是测定软锰矿的氧化能力。
测定时,常在酸性溶液中使之与过量的还原剂Na 2C 2O 4作用,剩余的Na 2C 2O 4用KMnO 4标准溶液返滴定。
处理: MnO 2 + C 2O 42- + 4H + = Mn 2+ + 2CO 2↑+ 2H 2O滴定 5C 2O 42- + 2MnO 4 + 16H + = 10CO 2 + 2Mn 2+ +8H 2O四、实验步骤1. 0.02 mol/L KMnO 4溶液的配制 500 mL 烧杯中500mL 棕色试剂瓶备用过滤(玻璃漏斗,玻璃棉) 放置1周 贴上标签 冷却 并随时补充挥发的水分 加热并保持微沸1h 盖上表面皿 加H 2O 500mL 在台秤上称取1.6g KMnO 42. 0.02 mol/L KMnO 4溶液的标定 250mL 锥形瓶中溶解 微红色,半分钟不褪色3. 软锰矿氧化力的测定250mL 烧杯中不再冒大气泡为止 微红色,半分钟不褪色五、思考题1. 配500 mL 0.02 mol/L KMnO 4溶液,应称固体试剂多少?为何称取量比理论值大些?2. 配制KMnO 4标准溶液,为何要把KMnO 4水溶液煮沸一段时间?为何放置一周后再标定?为何要过滤?过滤时能否用滤纸?3. 在用Na 2C 2O 4基准物标定KMnO 4溶液的实验中,1)溶液酸度为何要在1 mol/L 左右?若酸度较低有何影响?为何要在H 2SO 4介质中,而不能在HCl 介质中进行滴定?2)为何必须用KMnO 4滴定Na 2C 2O 4,而不能用Na 2C 2O 4滴定KMnO 4?3)为何要在加热条件下进行,且开始必须慢滴?4. 装KMnO 4的器皿放置较久时,其壁上的棕色沉淀是什么?应如何洗涤?5. 测定软锰矿氧化力的原理及测定条件是什么?6. 软锰矿经Na 2C 2O 4分解后,能否用HCl 或HNO 3调节酸度?7. 软锰矿溶解、还原完毕,为何要用沸水稀释至100 mL ?沸水稀释后为何要立即滴定?8. 写出KMnO 4标准溶液浓度及 MnO2%计算公式。

一、实验内容:实验三 利用欧拉法、梯形数法和二阶显式Adams 法对RLC 串联电路的仿真1前向欧拉法状态方程:Du CX y Bu AX X m +=+=+•1 然后根据前向欧拉法(其中h 为步长)•++=m m m hX X X 1即可得到系统的差分方程2后向欧拉法根据前向欧拉法得到的系统状态方程,结合后向欧拉法(其中h 为步长)•+++=11m m m hX X X 即可得到系统的差分方程3梯形法由前面的系统状态方程,结合梯形法)(211+••+++=m m m m X X h X X 即可得到系统的差分方程4二阶显式Adams 方法由前面的状态方程,结合二阶显式Adams 方法)51623(12211--++-+=m m m m m F F F h X X 即可得到系统的差分方程但是二阶显式Adams 法不能自起步,要使方程起步,需要知道开始的三个值,但是我们只知道第一个值。
经过分析后,二阶显式Adams 方法精度是二阶的,而梯形法精度也是二阶的,因此我们可以先借助梯形法得到输出的前三个值,以达到起步的目的,然后借助上面得到的差分方程对其进行求解。
二、实验波形:下图为前向欧拉法、后向欧拉法、梯形法、二阶显式Adams 方法的系统差分方程得到相应的输出波形:图1 h=410 时四种方法的输出波形图2 h=56-⨯时四种方法的输出波形10图3 h=510-时四种方法的输出波形图4 h=610-时四种方法的输出波形三、实验分析:由输出波形可以看到各种方法的特点(在图中蓝色线均表示连续系统模型的实际输出波形,红色线表示在对应方法下系统的输出波形。
):1前向欧拉法和二阶显式Adams方法对步长的要求很强。
步长太大,最后的到的结果不是绝对收敛,而是发散。
在小步长下才显得收敛,这也从另一方面验证,步长越小,截断误差越小;2步长不能太小,太小的步长相应的舍入误差和累积误差也会增大;3前向欧拉法也可称为显式欧拉法,后向欧拉法也可称为隐式欧拉法,可以看到,后向欧拉法的稳定域要比前向欧拉法大,计算精度也要高一些。

实验3生产管理本次实验根据LRP工单的要求安排生产,经由工艺管理子系统,适时监控和调整原材料投入生产、在制品转移、成品入库等各项作业信息,保证生产顺利进行,并在此过程中提高生产效率。
一、实验目的1.了解企业生产的基本流程;2.理解ERP系统中生产管理(车间管理)信息流程及单据特征;3.初步了解主要的基础数据含义及其设置方法;4.掌握生产管理(车间管理)中操作流程及单据处理的基本方法。
本实验包括四个部分:1.审核工单及录入工单工艺2.录入投产单及领料单3.录入转移单4.录入入库单二、实验内容与步骤(要求:针对实验案例的每项工作,完成实验,并分别撰写实验步骤)一、实验内容1. 完成生产管理的基本流程;2. 单据包括:工单、工单工艺、投料单、领料单、转移单、入库单等。
二、实验步骤1 、生产管理的基本流程如下:(1 )查询并审核LRP 工单。
登录系统,修改时间;选择“生产管理” ——“:工单/ 委外子系统” ——“录入工单”模块,进入“录入工半日”界面,查询工单。
最后关闭窗口。
(2 )录入工单工艺。
选择“生产管理” ——“工艺管理子系统” ——录入工艺工单“模块,进入”录入工艺工单“界面。
查询并修改信息,选择”产品工艺路线信息品号“。
保存单据,最后关闭窗口。
(3 )录入投产单。
选择“生产管理”——“ 工艺管理子系统”——“ 录入投产单” 模块进入“录入投产单”界面。
新增一张投产单,选择“投资单别——生产投产单”,移出仓库为—— YCLC (原材料仓),移入地为—— BGYJGZX (办公椅加工中心),投产单来源的“工单单别” ——保存并查询单据。
最后关闭窗口。
(4 )从投产单自动生成领料单。
选择“生产管理” ——“工艺管理子系统” ——“从投产自动生成领料单”模块,进入“从投产单自动生成领料单”界面,选择“投产单号起” ——办公椅,开窗口选择“工单单号止”,“选择工厂” ——BGJJGC (办公家具工厂),“工艺” —— 001 打磨,“领料单别” —— LL 厂内领料单,单击“直接处理”,处理完成后,单击“ OK ”,最后关闭界面。


实验三数据库中的数据查询及视图操作实验报告实验三数据库中的数据查询及视图操作实验报告一、实验目的本实验的主要目的是熟悉数据库中的数据查询和视图操作。
通过本实验,我们可以掌握使用SQL语句进行数据查询和创建视图的方法,进一步提高对数据库的操作能力。
二、实验环境本实验使用MySQL数据库管理系统,并在Windows操作系统下进行实验。
三、实验内容本实验主要包括以下内容:1. 数据查询:使用SELECT语句查询数据库中的数据,并进行排序、过滤和聚合操作。
2. 视图操作:创建和删除视图,以及对视图进行查询和更新操作。
四、实验步骤与结果1. 数据查询首先,我们需要连接到数据库,并选择要查询的表。
假设我们选择的表名为"students",包含以下字段:学号、姓名、性别、年龄、班级。
a. 查询所有学生的信息:```sqlSELECT * FROM students;```执行以上SQL语句后,我们可以得到所有学生的信息,包括学号、姓名、性别、年龄和班级。
b. 查询男生的信息:```sqlSELECT * FROM students WHERE 性别 = '男';```执行以上SQL语句后,我们可以得到所有性别为男的学生的信息。
c. 查询年龄小于20岁的学生的姓名和班级:```sqlSELECT 姓名, 班级 FROM students WHERE 年龄 < 20;```执行以上SQL语句后,我们可以得到年龄小于20岁的学生的姓名和班级。
d. 查询学生按照年龄降序排列的结果:```sqlSELECT * FROM students ORDER BY 年龄 DESC;```执行以上SQL语句后,我们可以得到按照年龄降序排列的学生信息。
e. 查询学生按照班级分组,并统计每个班级的人数:```sqlSELECT 班级, COUNT(*) AS 人数 FROM students GROUP BY 班级;```执行以上SQL语句后,我们可以得到每个班级的人数统计结果。
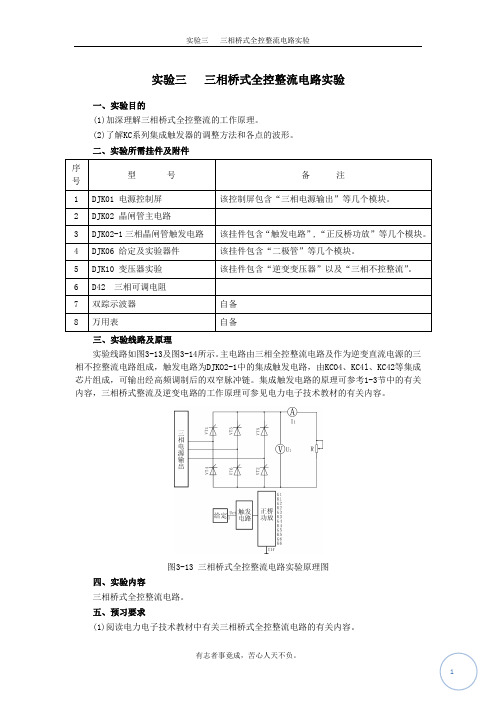
实验三三相桥式全控整流电路实验一、实验目的(1)加深理解三相桥式全控整流的工作原理。
(2)了解KC系列集成触发器的调整方法和各点的波形。
二、实验所需挂件及附件三、实验线路及原理实验线路如图3-13及图3-14所示。
主电路由三相全控整流电路及作为逆变直流电源的三相不控整流电路组成,触发电路为DJKO2-1中的集成触发电路,由KCO4、KC4l、KC42等集成芯片组成,可输出经高频调制后的双窄脉冲链。
集成触发电路的原理可参考1-3节中的有关内容,三相桥式整流及逆变电路的工作原理可参见电力电子技术教材的有关内容。
图3-13 三相桥式全控整流电路实验原理图四、实验内容三相桥式全控整流电路。
五、预习要求(1)阅读电力电子技术教材中有关三相桥式全控整流电路的有关内容。
(2))学习本教材中有关集成触发电路的内容,掌握该触发电路的工作原理。
六、思考题(1)如何解决主电路和触发电路的同步问题?在本实验中主电路三相电源的相序可任意设定吗?答:①采用宽脉冲触发或双脉冲触发发式。
在本实验中使脉冲宽度大于1/6个周期。
②在除法某个晶闸管的同时,前一个晶闸管补发脉冲,即用两个窄脉冲替代宽脉冲。
(2)在本实验的整流时,对α角有什么要求?为什么?答:在本实验的整流时,移相角度α角度为0-90度,这是因为移相角度α超过90度就会进入逆变状态。
七、实验方法(1)三相桥式全控整流电路按图3-13接线,将DJK06上的 “给定”输出调到零(逆时针旋到底),使电阻器放在最大阻值处,按下“启动”按钮,调节给定电位器,增加移相电压,使α角在30°~150°范围内调节,用示波器观察并记录α=30°、60°及90°时的整流电压U d 和晶闸管两端电压U vt 的波形,并记录相应的U d 数值于下表中。
计算公式:U d =2.34U 2cosα (0~60O) U d =2.34U 2[1+cos(a+3)] (60o ~120o) 描绘α=300、600时Ud 、Uvt 的波形。
实验三 典型环节(或系统)的频率特性测量一.实验目的1.学习和掌握测量典型环节(或系统)频率特性曲线的方法和技能。
2.学习根据实验所得频率特性曲线求取传递函数的方法。
二.实验内容1.用实验方法完成一阶惯性环节的频率特性曲线测试。
2.用实验方法完成典型二阶系统开环频率特性曲线的测试。
3.用软件仿真方法求取一阶惯性环节频率特性和典型二阶系统开环频率特性,并与实验所得结果比较。
三、实验原理及说明1.实验用一阶惯性环节传递函数参数、电路设计及其幅相频率特性曲线:对于1)(+=Ts Ks G 的一阶惯性环节,其幅相频率特性曲线是一个半圆,见图3.1。
取ωj s =代入,得)()(1)(ωϕωωωj e r T j Kj G =+=(3-2-1)在实验所得特性曲线上,从半园的直径(0)r ,可得到环节的放大倍数K ,K =(0)r 。
在特性曲线上取一点k ω,可以确定环节的时间常数T ,kk tg T ωωϕ)(-=。
(3-2-2)实验用一阶惯性环节传递函数为12.01)(+=s s G ,其中参数为R 0=200K Ω,R 1=200K Ω,C=1uF ,参数根据实验要求可以自行搭配,其模拟电路设计参阅下图3.2。
在进行实验连线之前,先将U13单元输入端的100K 可调电阻顺时针旋转到底(即调至最大),使输入电阻R 0的总阻值为200K;其中,R1、C1在U13单元模块上。
U8单元为反相器单元,将U8单元输入端的10K 可调电阻逆时针旋转到底(即调至最小),使输入电阻R 的总值为10K;注明:所有运放单元的+端所接的100K 、10K 电阻均已经内部接好,实验时不需外接。
图3.22.实验用典型二阶系统开环传递函数参数、电路设计及其幅相频率特性曲线:对于由两个惯性环节组成的二阶系统,其开环传递函数为12)1)(1()(2221++=++=Ts s T Ks T s T K s G ξ )1(≥ξ 令上式中 s j ω=,可以得到对应的频率特性 )(22)(12)(ωϕωωξωωj e r T j T Kj G =++-=二阶系统开环传递函数的幅相频率特性曲线,如图所示。
实验三直流并励电动机一、实验目的:掌握直流并励电动机的调速方法二、实验内容:测取调速特性(1)改变电枢电压调速保持U=U N、I f=I fN=常数、T2=常数(即I F=常数),测取n=f(Ea) (2)改变励磁电流调速保持U=U N、T2=常数(即I F=常数),测取n=f(I f)三、实验设备:DD03 导轨、测速发电机及转速表1台DJ23 校正直流测功机1台DJ15 直流并励电动机1台D31 直流电压、毫安、安培表2件D42 三相可调电阻器1件D44 可调电阻器、电容器1件D51 波形测试及开关板1件四、实验线路:R1——D44上180ΩR f1——D44上1800Ω加上D41上360ΩR2——D42上2个900Ω串联电阻加上2个900Ω并联电阻共2250ΩR f2——D42上1800Ω五、实验说明:1、改变电枢端电压调速:(!)调节电阻,电动机起动。
(2)将R1调至0,电枢电源电压调至220V,调节R f2使I f2=100mA,再调节R2和R f1,使电动机达到额定值:U=U N,I=I N(A3为1.1A),n=n N,此时I f即为I fN。
(3)调R2、R f1使U=U N,I=0.5I N(Ia=0.5A),I f=I fN,记下此时MG的I F(4)保持I F(即T2)不变,I f=I fN,将R1从零逐渐调至最大值,在这个过程中测取Ea、n和Ia,取5~6组数据记入表一中。
2、改变励磁电流的调速(1)M运行后,将R1、R f1调至零,保持I f2=100mA,再调R2,使U=U N,I=0.5I N(即Ia=0.5A),记下此时的I F值。
(2)保持I F和U N不变,缓慢增加R f1,分别测取n、I f、Ia,直至n=1.3n N,在这个过程中共取5~6组数据记入表二中。
六、实验记录:(表一)I f=I fN= mA(表二)七、思考题:1、当M的T2和If不变时,减小Ua,为什么会引起n的下降?2、当M的T2和电枢两端电压不变时,减小If,为什么会引起n的上升?。
实验3 随机过程的特征估计
1、实验目的
了解随机过程特征估计的基本概念和方法,学会运用Matlab 函数对随机过程进行特征 估计,并且通过实验了解不同估计方法所估计出来结果之间的差异。
2、实验原理
设随机序列 X(n)、Y(n)为各态历经过程,样本分别为x(n)、y(n)(n=0,1,....N-1)。
1、均值的估计
^
x m =N
1∑-=1
N n n
x
(1)
2、方差的估计
方差估计有两种情况,如果均值 m x 已知,则
^
2
x
σ=N
12
1
)(x N n n
m x
-∑-= (2)
如果均值未知,那么
^
2x
σ =1
1-N 2
^
1
)(x N n n
m x
-∑-= (3)
3、相关函数估计
)(^
m R x =m
N -1n m N n n
m x x
∑--=+1
(4)
4、功率谱估计
功率谱的估计有几种方法, (1)自相关法
先求相关函数的估计,
)(^
m R x =m N -1
n m N n n
m x x
∑--=+1
(5)
然后对估计的相关函数做傅立叶变换,
)(^
ωx G =ω
jm N N m x
e
m R
-+--=∑)(1
)
1( (6)
(2)周期图法
先对序列 x(n)做傅立叶变换,
)(ωX =ωjn N m e n x --=∑1
)( (7)
则功率谱估计为
)(^
ωx G =
2
)(1ωX N
(8)
周期图法是一种非参数谱估计方法,另外还有一种修正的周期图方法,也叫Welch 法, MA TLAB 有周期图和Welch 法的谱估计函数。
(3)现代谱估计技术
现代谱估计主要有参数谱估计和子空间谱估计。
参数谱估计法是假定待估计功率谱的信 号是白噪声驱动线性系统的输出,常用的方法有基于最大墒估计的伯格算法和Y uler-Walk 自回归(AR)方法,这些方法是估计线性系统的参数,通常会得到比经典谱估计方法更好的估计。
子空间法也称为高分辨率谱估计或超分辨率谱估计,常用的方法有MUSIC 法和特征矢量法,这些方法是根据相关矩阵的特征分析或特征分解得到对信号的频率分量的估计,特别适合于线谱(即正弦信号)的估计,是低信噪比环境下检测正弦信号的有效方法。
MATLAB 有许多估计数字特征的统计函数: (1)均值与方差
mean(A),返回序列的均值,序列用矢量A 表示。
V AR(X),返回序列X 的方差。
(2)互相关函数估计xcorr 用法: c = xcorr(x,y) c = xcorr(x) c = xcorr(x,y ,'option')
c = xcorr(x,'option')
xcorr(x,y)计算X 与Y 的互相关,矢量X 表示序列x(n),矢量Y 表示序列y(n)。
xcorr(x) 计算X 的自相关。
option 选项是: 'biased':有偏估计
)(^
m R x =n m N n m
n x x
N
∑--=+1
1
'unbiased'::无偏估计
)(^
m R x =
n m N n m
n x x
m
N ∑--=+-1
1
'coeff':m=0 的相关函数值归一化为1。
'none':不作归一化处理。
(3)功率谱估计
MA TLAB 提供了许多功率铺估计的函数: 函数名
用法
功能
periodogram [Pxx,w] = periodogram(x)
[Pxx,w]=periodogram(x,window) 返回序列x 用周期图法的功率谱估计加参
数 window 是采用修正的周期图法,window 指定窗的系数。
pyulear Pxx = pyulear(x,p)
使用Y uler-walker 方法的功率谱估计,p 表示AR 模型的阶数 pburg Pxx = pburg(x,p)
使用Burg 算法谱估计,p 是估计功率谱时指定的信号的自回归模型阶数
3、实验内容
1、产生一组均值为1,方差为4 的正态分布的随机序列(1000 个样本),估计该序列的均值与方差。
2、按如下模型产生一组随机序列:
x(n)=0.8x(n-1)+w(n)
其中w(n)为均值为1,方差为4 的正态分布白噪声序列。
估计过程的自相关函数与功率谱。
3、设信号为x(n)=sin(2πf1n)+2cos(2πf2n)+w(n),n=1,2,....,N,其中f1=0.05,f2=0.12,w(n)为正态白噪声,试在N=356 和1024 点时,分别产生随机序列x(n)、画出x(n)的波形并估计x(n) 的相关函数和功率谱。
4、实验要求
(1) 用MA TLAB 编写程序;
(2) 写出详细试验报告。