【精品】2014-2015年广东省广州七中八年级(上)期中数学试卷带答案

2014-2015学年广东省广州市天河区八年级（上）期中数学试卷一、选择题．1．（3分）下列图形中，不是轴对称图形的是（）A．B．C．D．2．（3分）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，43．（3分）七边形外角和为（）A．180°B．360°C．900° D．1260°4．（3分）已知等腰△ABC的边长为3、5，则腰AC的长可能为（）A．5 B．5或3 C．3 D．25．（3分）如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）A．AB=AD B．AC平分∠BCD C．AB=BD D．△BEC≌△DEC6．（3分）如图，△ABC中，AB=AC，∠B=70°，则∠A的度数是（）A．70°B．55°C．50°D．40°7．（3分）如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A．∠A=∠C B．AD=CB C．BE=DF D．AD∥BC8．（3分）如图，AB与CD交于点O，OA=OC，OD=OB，∠A=50°，∠B=30°，则∠D的度数为（）A．50°B．30°C．80°D．100°9．（3分）四边形的内角和为（）A．180°B．360°C．540° D．720°10．（3分）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt △ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°二、填空题（本大题共6小题，每小题3分，满分18分）11．（3分）已知点P在线段AB的垂直平分线上，PA=6，则PB=．12．（3分）点P（3，2）关于x轴对称的点的坐标为．13．（3分）如图，在△ABC中，∠C=20°，CA=CB，则△ABC的外角∠ABD=°．14．（3分）如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是．15．（3分）在△ABC中，三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B，则∠B=度．16．（3分）一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为．三、解答题（本大题共9小题，满分102分，解答应写出文字说明，证明过程货演算步骤）17．（9分）如图，在边长为1个单位长度的小正方形所组成的网格中，△ABC 的顶点均在格点上．画出△ABC关于直线l对称的△A1B1C1（A与A1，B与B1，C 与C1相对应），连接AA1，BB1，并计算梯形AA1B1B的面积．18．（9分）如图，∠B=∠D，∠BAC=∠DAC．求证：AB=AD．19．（10分）如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）20．（10分）如图，E、F分别是等边三角形ABC的边AB，AC上的点，且BE=AF，CE、BF交于点P．（1）求证：CE=BF；（2）求∠BPC的度数．21．（10分）如图，BA⊥AD，∠ADB=∠ABD=∠DAO，∠DBC=60°，∠DCO=∠BCO．（1）求证：BD⊥AC；（2）求∠DCO的度数；（3）求证：BC=DC．22．（12分）如图，△ABC中，AB=AC，∠A=36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC）（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是度和度；（2）在图2中画2条线段，使图中有4个等腰三角形；（3）继续按以上操作发现：在△ABC中画n条线段，则图中有个等腰三角形，其中有个黄金等腰三角形．23．（12分）如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC 的中点．（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）；①作∠DAC的平分线AM；②连接BE并延长交AM于点F；（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．24．（14分）如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上．（1）作点B关于y轴的对称点B′，并写出点B′的坐标．（2）当△ABC的周长最小时，求点C的坐标．25．（16分）在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C 重合），M在BC的延长线上．（1）如图1，△ABC和△APE均为正三角形，连接CE．①求证：△ABP≌△ACE．②∠ECM的度数为°．（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM 的度数为°．②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM 的度数为°．（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．2014-2015学年广东省广州市天河区八年级（上）期中数学试卷参考答案与试题解析一、选择题．1．（3分）下列图形中，不是轴对称图形的是（）A．B．C．D．【解答】解：A、不是轴对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误．故选：A．2．（3分）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，4【解答】解：A、1+2＜6，不能组成三角形，故此选项错误；B、2+2=4，不能组成三角形，故此选项错误；C、1+2=3，不能组成三角形，故此选项错误；D、2+3＞4，能组成三角形，故此选项正确；故选：D．3．（3分）七边形外角和为（）A．180°B．360°C．900° D．1260°【解答】解：七边形的外角和为360°．故选：B．4．（3分）已知等腰△ABC的边长为3、5，则腰AC的长可能为（）A．5 B．5或3 C．3 D．2【解答】解：当腰长为3时，三角形的三边为3、3、5，满足三角形的三边关系，则另一腰长为3，当腰长为5时，三角形的三边为5、5、3，满足三角形的三边关系，则另一腰长为5，综上可知腰AC可能为3或5，故选：B．5．（3分）如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）A．AB=AD B．AC平分∠BCD C．AB=BD D．△BEC≌△DEC【解答】解：∵AC垂直平分BD，∴AB=AD，BC=CD，∴AC平分∠BCD，EB=DE，∴∠BCE=∠DCE，在Rt△BCE和Rt△DCE中，，∴Rt△BCE≌Rt△DCE（HL），故选：C．6．（3分）如图，△ABC中，AB=AC，∠B=70°，则∠A的度数是（）A．70°B．55°C．50°D．40°【解答】解：∵AB=AC，∠B=70°，∴∠A=180°﹣2∠B=180°﹣2×70°=40°．故选：D．7．（3分）如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A．∠A=∠C B．AD=CB C．BE=DF D．AD∥BC【解答】解：∵AE=CF，∴AE+EF=CF+EF，∴AF=CE，A、∵在△ADF和△CBE中∴△ADF≌△CBE（ASA），正确，故本选项错误；B、根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；C、∵在△ADF和△CBE中∴△ADF≌△CBE（SAS），正确，故本选项错误；D、∵AD∥BC，∴∠A=∠C，∵在△ADF和△CBE中∴△ADF≌△CBE（ASA），正确，故本选项错误；故选：B．8．（3分）如图，AB与CD交于点O，OA=OC，OD=OB，∠A=50°，∠B=30°，则∠D的度数为（）A．50°B．30°C．80°D．100°【解答】解：∵OA=OC，OD=OB，∠AOD=∠COB，∴△AOD≌△COB（SAS），∴∠D=∠B=30°．故选：B．9．（3分）四边形的内角和为（）A．180°B．360°C．540° D．720°【解答】解：四边形的内角和=（4﹣2）•180°=360°．故选：B．10．（3分）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt △ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°【解答】解：∵在Rt△ACB中，∠ACB=90°，∠A=25°，∴∠B=90°﹣25°=65°，∵△CDB′由△CDB反折而成，∴∠CB′D=∠B=65°，∵∠CB′D是△AB′D的外角，∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°．故选：D．二、填空题（本大题共6小题，每小题3分，满分18分）11．（3分）已知点P在线段AB的垂直平分线上，PA=6，则PB=6．【解答】解：∵点P在线段AB的垂直平分线上，PA=6，∴PB=PA=6．故答案为：6．12．（3分）点P（3，2）关于x轴对称的点的坐标为（3，﹣2）．【解答】解：根据轴对称的性质，得点P（3，2）关于y轴对称的点的坐标为（3，﹣2）．故答案为：（3，﹣2）．13．（3分）如图，在△ABC中，∠C=20°，CA=CB，则△ABC的外角∠ABD=100°．【解答】解：∵CA=CB，∠C=20°，∴∠A=∠ABC==80°，∴∠ABD=180°﹣∠ABC=180°﹣80°=100°，故答案为：100．14．（3分）如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是15．【解答】解：过D作DE⊥BC于E，∵∠A=90°，∴DA⊥AB，∵BD平分∠ABC，∴AD=DE=3，∴△BDC的面积是×DE×BC=×10×3=15，故答案为：15．15．（3分）在△ABC中，三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B，则∠B=60度．【解答】解：∵∠B﹣∠A=∠C﹣∠B，∴∠A+∠C=2∠B，又∵∠A+∠C+∠B=180°，∴3∠B=180°，∴∠B=60°．故答案为：60．16．（3分）一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为80海里．【解答】解：如图∠NPM=180°﹣70°﹣40°=70°，∵向北的方向线是平行的，∴∠M=70°，∴∠NPM=∠M，∴NP=MN=40海里×2=80海里，故答案为：80海里．三、解答题（本大题共9小题，满分102分，解答应写出文字说明，证明过程货演算步骤）17．（9分）如图，在边长为1个单位长度的小正方形所组成的网格中，△ABC 的顶点均在格点上．画出△ABC关于直线l对称的△A1B1C1（A与A1，B与B1，C 与C1相对应），连接AA1，BB1，并计算梯形AA1B1B的面积．【解答】解：△A1B1C1如图所示，梯形AA1B1B的面积=×（2+8）×4=20．18．（9分）如图，∠B=∠D，∠BAC=∠DAC．求证：AB=AD．【解答】证明：在△BAC和△DAC中，，∴△BAC≌△DAC（AAS），∴AB=AD．19．（10分）如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）【解答】AC=DF．证明：∵BF=EC，∴BF﹣CF=EC﹣CF，∴BC=EF，在△ABC和△DEF中∴△ABC≌△DEF（SAS）．20．（10分）如图，E、F分别是等边三角形ABC的边AB，AC上的点，且BE=AF，CE、BF交于点P．（1）求证：CE=BF；（2）求∠BPC的度数．【解答】（1）证明：如图，∵△ABC是等边三角形，∴BC=AB，∠A=∠EBC=60°，∴在△BCE与△ABF中，，∴△BCE≌△ABF（SAS），∴CE=BF；（2）解：∵由（1）知△BCE≌△ABF，∴∠BCE=∠ABF，∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°，即∠PBC+∠PCB=60°，∴∠BPC=180°﹣60°=120°．即：∠BPC=120°．21．（10分）如图，BA⊥AD，∠ADB=∠ABD=∠DAO，∠DBC=60°，∠DCO=∠BCO．（1）求证：BD⊥AC；（2）求∠DCO的度数；（3）求证：BC=DC．【解答】（1）证明：∵BA⊥AD，∴∠BAD=90°，∴∠ABD=∠ADB=45°，∴∠DAO=45°，∴∠AOD=90°，∴BD⊥AC；（2）解：∵∠DCO=∠BCO，且∠DBC=60°，∴∠DCO=∠BCO=30°；（3）证明：由（1）可知O为BD中点，且AC⊥BD，∴AC垂直平分BD，∴BC=DC．22．（12分）如图，△ABC中，AB=AC，∠A=36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC）（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是108度和36度；（2）在图2中画2条线段，使图中有4个等腰三角形；（3）继续按以上操作发现：在△ABC中画n条线段，则图中有2n个等腰三角形，其中有n个黄金等腰三角形．【解答】解：（1）如图1所示：∵AB=AC，∠A=36°，∴当AE=BE，则∠A=∠ABE=36°，则∠AEB=108°，则∠EBC=36°，∴这2个等腰三角形的顶角度数分别是108度和36度；故答案为：108，36；（2）如图2所示：（3）如图3所示：当1条直线可得到2个等腰三角形；当2条直线可得到4个等腰三角形；当3条直线可得到6个等腰三角形；…∴在△ABC中画n条线段，则图中有2n个等腰三角形，其中有n个黄金等腰三角形．故答案为：2n，n．23．（12分）如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC 的中点．（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）；①作∠DAC的平分线AM；②连接BE并延长交AM于点F；（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．【解答】解：（1）如图所示；（2）AF∥BC，且AF=BC，理由如下：∵AB=AC，∴∠ABC=∠C，∴∠DAC=∠ABC+∠C=2∠C，由作图可得∠DAC=2∠FAC，∴∠C=∠FAC，∴AF∥BC，∵E为AC中点，∴AE=EC，在△AEF和△CEB中，∴△AEF≌△CEB（ASA）．∴AF=BC．24．（14分）如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上．（1）作点B关于y轴的对称点B′，并写出点B′的坐标．（2）当△ABC的周长最小时，求点C的坐标．【解答】解：（1）点B′的坐标为（﹣3，0）；（2）连接AB′，由轴对称确定最短路线问题，交点即为△ABC的周长最小的点C的位置，设直线AB′的解析式为y=kx+b，则，解得，所以，直线AB′的解析式为y=x+3，令x=0，则y=3，所以，点C的坐标为（0，3）．25．（16分）在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C 重合），M在BC的延长线上．（1）如图1，△ABC和△APE均为正三角形，连接CE．①求证：△ABP≌△ACE．②∠ECM的度数为60°．（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM 的度数为45°．②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM 的度数为36°．（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．【解答】解：（1）①证明：如图1，∵△ABC与△APE均为正三角形，∴AB=AC，AP=AE，∠BAC=∠PAE=60°，∴∠BAC﹣∠PAC=∠PAE﹣∠PAC即∠BAP=∠CAE，在△ABP和△ACE中，，∴△ABP≌△ACE （SAS）．②∵△ABP≌△ACE，∴∠ACE=∠B=60°，∵∠ACB=60°，∠ECM=180°﹣60°﹣60°=60°．故答案为：60．（2）①如图2，作EN⊥BN，交BM于点N∵四边形ABCD和APEF均为正方形，∴AP=PE，∠B=∠ENP=90°，∴∠BAP+∠APB=∠EPM+∠APB=90°，即∠BAP=∠NPE，在△ABP和△PNE中，，∴△ABP≌△ANE （AAS）．∴AB=PN，BP=EN，∵BP+PC=PC+CN=AB，∴BP=CN，∴CN=EN，∴∠ECM=∠CEN=45°②如图3，作EN∥CD交BM于点N，∵五边形ABCDF和APEGH均为正五边方形，∴AP=PE，∠B=∠BCD，∵EN∥CD，∴∠PNE=∠BCD，∴∠B=∠PNE∵∠BAP+∠APB=∠EPM+∠APB=180°﹣∠B，即∠BAP=∠NPE，在△ABP和△PNE中，，∴△ABP≌△PNE （AAS）．∴AB=PN，BP=EN，∵BP+PC=PC+CN=AB，∴BP=CN，∴CN=EN，∴∠NCE=∠NEC，∵∠CNE=∠BCD=108°，∴∠ECM=∠CEN=（180°﹣∠CNE）=×（180°﹣108°）=36°．故答案为：45，36．（3）如图4中，过E作EK∥CD，交BM于点K，∵n边形ABC…和n边形APE…为正n边形，∴AB=BC AP=PE∠ABC=∠BCD=∠APE=∵∠APK=∠ABC+∠BAP，∠APK=∠APE+∠EPK∴∠BAP=∠KPE∵EK∥CD，∴∠BCD=∠PKE∴∠ABP=∠PKE，在△ABP和△PKE中，，∴△ABP≌△PKE（AAS）∴BP=EK，AB=PK，∴BC=PK，∴BC﹣PC=PK﹣PC，∴BP=CK，∴CK=KE，∴∠KCE=∠KEC，∵∠CKE=∠BCD=∴∠ECK=．。

广州2014年八年级上数学期中测试模拟卷说明：满分120分，测试时间120分钟；请把选择题答案写进答题卡。

第一部分（选择题 共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1、下列长度的三条线段，不能组成三角形的是（ ）A ．3、8、4B ．4、9、6C ．15、20、8D ．9、15、82、小华在电话中问小明：“已知一个三角形三边长分别是4、9、12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解”。

小华根据小明的提示作出的图形正确的是（ ）A. B ． C ． D ． 3、三角形内有一点到三角形三边的距离都相等，则这点一定是（ ）A ．三边垂直平分线的交点B ．三条中线的交点C ． 三条高线的交点D ．三内角平分线的交点4、等腰三角形的周长为13cm ，其中一边长为3cm ，则该等腰三角形的底边长是（ ）A ．7cmB ．3cmC ．9cmD ．5cm5、等腰三角形ABC 在直角坐标系中，底边的两端点是()()2,0,6,0-，则其顶点的坐标能确定 的是（ ）A ．横坐标B ．纵坐标C ．横坐标及纵坐标D ．横坐标或纵坐标6、如图，点P 在OC 上，PD ⊥OA ，PE ⊥OB ，垂足分别为D 、E ，PD =PE ，则些列结论中错误的是（ ）A ． DOP EOP ∠=∠B ．OD OE =C ．DPO EPO ∠=∠D ．PD OD =7、尺规作图作AOB ∠的平分线方法如下：以O 为圆心，任意长为半径画弧交OA 、OB 于C 、 D ，再分别以点C 、D 为圆心，以大于12CD 长为半径画弧，两弧交于点P ，作射线OP ， 由作法得OCP ∆≌ODP ∆的根据是（ ）A ．SASB ．ASAC ．AASD ．SSS8、如图，六边形ABCFED 是轴对称图形，CD 所在的直线是它的对称轴，若∠AFC +∠BCF =130°，则∠E +∠D 的大小是（ ）A ． 130°B ．220°C ． 260°D ．230°9、如图，ABC ∆中，AB AC =，AD AE =，20BAD ∠=︒，则EDC ∠=（ ）A ．18︒B ．15︒C ．10︒D ．8︒10、如图，已知：∠MON =30°，点1234A A A A ⋯、、、在射线ON 上，点123B B B ⋯、、在射线OM 上，112223334A B A A B A A B A ⋯、、均为等边三角形，若16671OA A B A =，则的边长为（ ）A ．6B ．12C ．32D ．64第二部分 非选择题（共90分）二、 填空题（每小题3分，共计18分） 11、 在Rt ABC ∆，C 90︒∠=，A 30︒∠=，AB +BC=12cm ，则AB = cm ．12、 等腰三角形一腰上的高与另一腰的夹角为60︒，则这个等腰三角形的顶角为 ．13、 如图，CD 与BE 互相垂直平分，AD ⊥DB ，∠BDE =70°，则∠CAD =_________．14、如图，AD BC ∥，ABC ∠的角平分线BP 与BAD ∠的角平分线AP 相交于点E ，作P E A B ⊥于点E 。

广州市第一一三中学2013学年第一学期期中考试初二年级 数学试卷命题时间：2014 年 10 月 命题人：唐黎莎 审稿人：刘永红本试卷分第I 卷和第II 卷两部分，共150分。

考试时间120分钟。

Ⅰ卷（共100分）一、选一选（本题有10个小题, 每小题3分, 满分30分 ,下面每小题给出的四个选项中, 只有一个是正确的. ）1、如图，下列图案是我国几家银行的标志，其中轴对称图形有（ ）A 、1个B 、2个C 、3个D 、4个2. 将下列长度的三条线段首尾顺次相接，能组成三角形的是（ ）。

A ．1cm ，2 cm ，3 cm B ．2 cm ，3 cm ，5 cm C ．5cm ，6 cm ，10 cm D ．25cm ，12 cm ，11 cm 3．下列图形中，正确画出AC 边上的高的是（ ）。

4、下列计算正确的是 ( )A.43)(a =7aB.2a ·4a =8aC.(23a )2 =46aD.1266a a a =+ 5．在平面直角坐标系内，点A （-2，3）关于x 轴的对称点A′的坐标是（ ）. A ．（-2，-3） B ．（2，3） C ．（-3，-2） D ．（2，-3）6.等腰三角形的周长为13cm 、其中一边长为3cm,则该等腰三角形的底边长为 ( )A ．7cmB ．3cmC ．3cm 或5cmD ．3cm 或7cm初 年级 班 考号： 姓名： 试室号：密 封 线7．如图，OP 平分∠AOB ，PA ⊥OA ，PB ⊥OB ， 垂足分别为A 、B ．下列结论中不一定成立的是（ ）. A ．PA=PB B ．AB 垂直平分OPC ．OA=OBD ．PO 平分∠APB8．如图所示，已知∠1＝∠2，若添加一个条件使△ABC ≌△ADC ，则添加错误的是（ ）.A ．AB=ADB ．∠B=∠DC ．∠BCA=∠DCAD ．BC=DC 9．如图，△ABC 是等腰三角形，AB=AC ，AD 是∠BAC 的角平分线，下面结论中不一定成立的是（ ）.A ．∠BAD= ∠DACB ．BD=DC C ．∠ADC=90°D ．∠B= ∠BAD10．如图，MN 是正方形ABCD 的一条对称轴，点P 是直线MN 上的一个动点，当PC+PD 最小时，∠PCD 是（ ）．A ． 30°B ．45°C ．60°D ．90° 二、耐心填一填（本题有6个小题，每小题3分, 满分18分） 11．计算：32)2(b a =_____________.12．如果x a =3，y a =5，则y x a 2=___________.13．如图，两个三角形全等，根据图中所给条件，可得∠α= °. 14．如果等腰三角形一个角为80°，则其底角为 .15．如图，△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 交EF 于F ， 若BF=AC ，则∠ABC 等于 °.16. 如图：点P 为∠AOB 内一点，分别作出P 点关于OA 、OB 的对称点P 1，P 2，连接P 1P 2交OA 于M ，交OB 于N ，P 1P 2=15，则△PMN 的周长为 ．第7题第8题第9题第10题DAMNBCPP 2P 1N MO PBA三、用心答一答（本大题有9小题, 共102分，解答要写出文字说明, 证明过程或计算步骤）17. （本题满分10分）（1）2)3(-x －23)(x ÷4x （2）)2()1)(1(+--+x x x x 18．（本题满分10分）如图，在平面直角坐标系中，A(2,3)，B(3,1)， C(-2，-2)．（1）在图中作出△ABC 关于y 轴的对称 图形△A 1B 1C 1．（2）写出点A 1、B 1、C 1的坐标（直接写答案）． A 1 _______；B 1 _______ ； C 1 _______.19. （本题满分10分）如图，已知点E C ，在线段BF 上，BE=CF ，AB ∥DE ，∠ACB =∠F ． 求证：△ABC ≌△DEF ．20.如图， DE 是BC 的垂直平分线.AC=9，△ABD 的周长为15，求AB 的长.（本题满分10分）第20题21.如图，四边形ABCD 中，AD ∥BC ，∠ABD =30o ，AB=AD ，DC ⊥BC 于点C ，若BD =6，求CD 的长. （本题满分12分）Ⅱ卷（共50分）22.如图：在ABC ∆中，AB=AC, D 、E 分别在AC ，AB 上，BD=BC ，AD=DE=BE ， 求∠A 的度数。

2014 年中考真题秘密★启用前广州市 2014 年初中毕业生学业考试数学本试卷分选择题和非选择题两部分，共三大题25 小题，满分150 分．考试时间120 分钟．注意事项：1．答卷前，考生务必在答题卡第 1 面、第 3 面、第 5 面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、座位号，再用2B 铅笔把对应这两个号码的标号涂黑．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题同的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分选择题（共30 分）一、选择题（本大题共10 小题，每小题 3 分，满分30 分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（）的相反数是（）．（ A ）（B）（C）（D）【考点】相反数的概念【分析】任何一个数的相反数为．【答案】 A2．下列图形是中心对称图形的是（）．（ A ）（B）（C）（D）【考点】轴对称图形和中心对称图形．2014 年中考真题【分析】旋转180°后能与完全重合的图形为中心对称图形．【答案】 D3．如图 1，在边长为 1 的小正方形组成的网格中，的三个顶点均在格点上，则（）．（ A ）（B）（C）（D）【考点】正切的定义．【分析】．【答案】D4．下列运算正确的是（）．（ A）（B）（C）（D）【考点】整式的加减乘除运算．【分析】， A 错误；，B错误；，C 正确；，D错误．【答案】 C5．已知和的半径分别为2cm 和 3cm，若，则和的位置关系是（）．（A ）外离（B）外切（C）内切（D）相交【考点】圆与圆的位置关系．【分析】两圆圆心距大于两半径之和，两圆外离．【答案】 A6．计算，结果是（）．（ A）（B）（C）（D）【考点】分式、因式分解【分析】【答案】 B7．在一次科技作品制作比赛中，某小组八件作品的成绩（单位：分）分别是：7， 10， 9， 8， 7， 9， 9，8．对这组数据，下列说法正确的是（）．（ A）中位数是8（B）众数是9（C）平均数是8（D）极差是7【考点】数据【分析】中位数是8.5；众数是9；平均数是8.375；极差是3．【答案】 B8．将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，（）．（ A）（B）2（C）（D）图 2-①图2-②【考点】正方形、有内角的菱形的对角线与边长的关系【分析】由正方形的对角线长为 2 可知正方形和菱形的边长为，当=60°时，菱形较短的对角线等于边长，故答案为．【答案】 A9．已知正比例函数（）的图象上两点（，）、（，），且，则下列不等式中恒成立的是（）．（ A）（B）（C）（D）【考点】反比例函数的增减性【分析】反比例函数中，所以在每一象限内随的增大而减小，且当时，，时，∴当时，，故答案为【答案】 C10．如图 3，四边形、都是正方形，点在线段上，连接，和相交于点．设，（）．下列结论：①；②；③；④．其中结论正确的个数是（）．（A ） 4 个（B）3个（C）2个（D）1个【考点】三角形全等、相似三角形【分析】①由可证，故①正确；②延长 BG交 DE于点 H，由①可得，（对顶角）∴=90°，故②正确；③由可得，故③不正确；④，等于相似比的平方，即，∴，故④正确．【答案】 B第二部分非选择题（共120 分）二、填空题（共 6 小题，每小题 3 分，满分 18分）11．中，已知，，则的外角的度数是 _____．【考点】三角形外角【分析】本题主要考察三角形外角的计算，，则的外角为【答案】12．已知是∠ AOB的平分线，点 P 在 OC上， PD⊥ OA，PE⊥OB，垂足分别为点，，则 PE 的长度为 _____．【考点】角平线的性质【分析】角平分线上的点到角的两边距离相等．【答案】 1013．代数式有意义时，应满足的条件为______．【考点】分式成立的意义，绝对值的考察【分析】由题意知分母不能为0，即，则【答案】14．一个几何体的三视图如图4，根据图示的数据计算该几何体的全面积为_______（结果保留）．【考点】三视图的考察、圆锥体全面积的计算方法【分析】从三视图得到该几何体为圆锥体，全面积=侧面积+ 底面积，底面积为圆的面积为：，侧面积为扇形的面积，首先应该先求出扇形的半径R，由勾股定理得，，则侧面积，全面积．【答案】15．已知命题：“如果两个三角形全等，那么这两个三角形的面积相等．”写出它的逆命题：_________，该逆命题是 _____命题（填“真”或“假”）．【考点】命题的考察以及全等三角形的判定【分析】本题主要考察命题与逆命题的转换，以及命题真假性的判断【答案】如果两个三角形的面积相等，那么这两个三角形全等．假命题．16．若关于的方程有两个实数根、，则的最小值为___.【考点】一元二次方程根与系数的关系，最值的求法【分析】该题主要是考察方程思想与函数思想的结合，由根与系数的关系得到：，，原式化简．因为方程有实数根，∴，．当时，最小值为．【答案】三、解答题（本大题共9 小题，满分102 分，解答应写出文字说明、证明过程或演算步骤）．17．（本小题满分分）解不等式：，并在数轴上表示解集.【考点】不等式解法【分析】利用不等式的基本性质，将两边不等式同时减去，再同时加上，再除以，不等号的方向不变 .注意在数轴上表示时，此题是小于等于号，应是实心点且方向向左.【答案】解：移项得，，合并同类项得，，系数化为 1 得，，在数轴上表示为：18．（本小题满分分）如图 5，平行四边形的对角线相交于点，过点且与、分别交于点，求证：．图 5【考点】全等三角形的性质与判定、平行四边形的性质【分析】根据平行四边形的性质可知，，，又根据对顶角相等可知，，再根据全等三角形判定法则，，得证.【答案】证明：∵平行四边形的对角线相交于点∴，∴在和中，∴19．（本小题满分10 分）已知多项式.（1）化简多项式；（2）若，求的值 .【考点】（1）整式乘除（ 2）开方,正负平方根【分析】（1）没有公因式,直接去括号,合并同类型化简（ 2）由第一问答案,对照第二问条件,只需求出，注意开方后有正负【答案】解 :（ 1）（ 2）,则20．（本小题满分10 分）某校初三（ 1）班 50 名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：自选项目人数频率立定跳远90.18三级蛙跳12一分钟跳绳80.16投掷实心球0.32推铅球50.10合计501（1）求，的值；（2）若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；2014 年中考真题（ 3）在选报“推铅球”的学生中，有 3 名男生， 2 名女生，为了了解学生的训练效果，从这机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多．．有一名女生的概率．5 名学生中随【考点】（【分析】（1）频率（ 2）①频率与圆心角；②树状图，概率1）各项人数之和等于总人数50 ; 各项频率之和为1（2）所占圆心角=频率 *360（3）画出列表图，至多有一名女生包括有一个女生和一个女生都没有两种情况．【答案】（ 1）（2）“一分钟跳绳”所占圆心角 =（ 3）至多有一名女生包括两种情况有 1 个或者 0 个女生列表图：男 A男 B男 C女 D女 E男 A（ A ， B）（ A ， C）（ A ， D）（ A ， E）男 B（ B ， A）（B ， C）（ B ， D）（ B ， E）男 C（ C， A）（ C， B）（ C，D）（ C， E）女 D（ D ， A ）（ D ， B）（ D ， C）（ D ， E）女 E（ E， A ）（ E， B）（ E， C）（ E， D）有1 个女生的情况： 12 种有0 个女生的情况： 6 种至多有一名女生包括两种情况18 种至多有一名女生包括两种情况 == =0.90已知一次函数的图像与反比例函数的图像交于两点，点的横坐标为2．（1）求的值和点的坐标；（2）判断点的象限，并说明理由．【考点】 1 一次函数； 2 反比例函数； 3 函数图象求交点坐标【分析】第（ 1）问根据点是两个图象的交点，将代入联立之后的方程可求出，再将点的横坐标代入函数表达式求出纵坐标；第（2）问根据一次函数与反比例函数的解析式分析两图像经过的象限，得出两图像交点所在象限. 此题主要考查反比例函数与一次函数的性质【答案】解：（1）将与联立得：1点是两个函数图象交点，将解得故一次函数解析式为将代入得，带入 1 式得：，反比例函数解析式为的坐标为（2）点在第四象限，理由如下：一次函数经过第一、三、四象限，反比例函数经过第二、四象限，因此它们的交点都是在第四象限.从广州某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400 千米，普通列车的行驶路程是高铁的行驶路程的 1.3 倍．（1）求普通列车的行驶路程；（ 2）若高铁的平均速度（千米/时）是普通列车平均速度（千米/时）的 2.5 倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短 3 小时，求高铁的平均速度．【考点】行程问题的应用【分析】路程 =速度×时间，分式方程的实际应用考察【解析】（1）依题意可得，普通列车的行驶路程为400×1.3=520（千米）千米 / 时．（2）设普通列车的平均速度为千米/时，则高铁平均速度为依题意有：可得：答：高铁平均速度为 2.5 ×120=300 千米 /时．23、（本小题满分12 分）如图 6，中，，．（1）动手操作：利用尺规作以为直径的，并标出与的交点，与的交点（保留作图痕迹，不写作法）：（2）综合应用：在你所作的圆中，①求证：；②求点到的距离．【考点】（ 1）尺规作图；（ 2）①圆周角、圆心角定理；②勾股定理，等面积法【分析】（ 1）先做出中点，再以为圆心，为半径画圆 .（ 2）①要求，根据圆心角定理，同圆中圆心角相等所对的弧也相等，只需证出即可，再根据等腰三角形中的边角关系转化.②首先根据已知条件可求出，依题意作出高，求高则用勾股定理或面积法，注意到为直径，所以想到连接，构造直角三角形，进而用勾股定理可求出，的长度，那么在中，求其高，就只需用面积法即可求出高.【答案】（1）如图所示，圆为所求（ 2）①如图连接，设,又则②连接,过作于,过作于cosC=, 又,又为直径设，则，在和中，有即解得：即又即24．（本小题满分14 分）已知平面直角坐标系中两定点A（-1，0）， B（4，0），抛物线（）过点A、B，顶点为 C．点 P（ m，n）（ n<0）为抛物线上一点．（1）求抛物线的解析式与顶点C的坐标．（2）当∠APB为钝角时，求m的取值范围．（ 3）若，当∠为直角时，将该抛物线向左或向右平移t （）个单位，点、C移动后对APB P 应的点分别记为、，是否存在 t ，使得首尾依次连接A、 B、、所构成的多边形的周长最短？若存在，求t 值并说明抛物线平移的方向；若不存在，请说明理由．【考点】动点问题.(1)二次函数待定系数法;(2)存在性问题 , 相似三角形 ;(3)最终问题 , 轴对称 , 两点之间线段最短【答案】 (1) 解: 依题意把的坐标代入得:;解得 :抛物线解析式为顶点横坐标,将代入抛物线得(2) 如图 ,当时,设,则过作直线轴,(注意用整体代入法)2014 年中考真题解得,当在之间时，或时，为钝角.(3) 依题意，且设移动（向右，向左）连接则又的长度不变四边形周长最小，只需最小即可将沿轴向右平移 5 各单位到处沿轴对称为∴当且仅当、 B 、三点共线时，最小，且最小为，此时，设过的直线为，代入∴即将代入，得：，解得：∴当， P、 C 向左移动单位时，此时四边形ABP’C’周长最小。

2014广州七中八年级上学期期中考试二．语言知识及运用第一节单项选择11. The air in Guangzhou is getting much __________.A. cleanB. the cleanestC. cleanerD. more clean12. The necklace is made __________ gold.A. ofB. up ofC. byD. in13. When I saw her dance for __________ time, I was amazed.A. oneB. the firstC. a firstD. once14. —Oh, this coffee is wonderful. Would you like __________?--Thanks, but I don’t feel like drinking __________ now.A. some, somethingB. any, anythingC. some, anythingD. any, something15. —Jim, do you enjoy playing __________ piano?--No, I like playing__________ chess.A. the,/B. /,theC. the, theD. /,/16. Mother bought a big bottle of milk for me. I only drank half of it just now. The __________ of it __________ in the fridge now.A. others, areB. other, isC. rest, areD. rest, it17. He _______ to Guangzhou in 2007. Since then, he ______ as a manager in the company.A. comes, worksB. came, workedC. came, has workedD. has come, worked18. I am better than Ben __________ English, but he does better than me __________ Chinese.A. at, atB. in, inC. at, inD. in, at19. You should tell __________ possible to support your idea.A. as many facts asB. many as facts asC. much as fact asD. as much facts as20. We __________ the whole holiday __________ in Shanghai. It was really a great holiday.A. spent, to stayB. took, stayingC. took, stayD. spent, staying第二节语法选择We don’t have electrical accidents very often. But when they happen, you should know 21 to do. It can make a 22 of “being alive or dead”. Maybe you won’t be in a fire all 23 life, you can still tell the people around you how to save themselves. So it is very important for everyone 24 something about them.Sometimes electrical accidents can lead to fire. Electrical fires are different 25 other fires. Water conducts electricity. So 26 water in an electrical fire can only make the fire 27 .Here is what you should keep in mind:1. Never use water in an electrical fire;2. Turn 28 the power in the house;3. If the fire is not a large one, tell an adult 29 it out properly. If the fire is a very large one, leave the house and take everyone with you;4. Call 119 and tell the police about the electrical fire. 30 , leave the fire address you're your name.21. A. that B. how C. when D. what22. A. differ B. difference C. differences D. different23. A. yourself B. you C. your D. yours24. A. to learn B. learn C. learning D. learnt25. A. at B. from C. of D. with26. A. throwing B. to throwing C. threw D. throw27. A. strong B. more strong C. stronger D. the s trongest28. A. on B. out C. off D. down29. A. put B. putting C. to put D. puts30. A. In addition B. As well C. For example D. At the same time三．完形填空Many people think the horse is an ordinary (普通的) animal.B ut I don’t think so. Why? When it 31 to this world it begins to stand and never lies down until it dies. Even it goes to 32 , it also stands well.There are other 33 for me to love the horse. First, it runs fast. It runs 34 than any other animal that I have ever seen with my own eyes. Next, it works 35 all day. It uses most of its time to eat at night but sleeps for a short time. And then, it goes on working for people.Besides, the horse can also be our good friends. I 36 this when I was a soldier in theSecond World War. That afternoon I was working with a cart (马车) driver, a (n) 37 man of over sixty. Our horse fell down on the way because one of its 38 was broken by a bomb (炸弹). But the horse got up from the 39 and went on running with three legs. At last we were 40 but the horse fell onto the ground again and never got up.31. A. chooses B. takes C. goes D. comes32. A. sit B. sleep C. run D. stand33. A. reasons B. questions C. problems D. answers34. A. harder B. better C. faster D. sooner35. A. hard B. hardly C. easily D. slowly36. A. discussed B. knew C. studied D. looked37. A. rich B. young C. small D. old38. A. nose B. mouth C. arms D. legs39. A. driver B. ground C. world D. house40. A. fine B. dangerous C. clean D. happy四．阅读理解(A)It is very important to keep yourself in good health.When you are sick, you will neither be able to study nor enjoy yourself. One of the factors(因素) leading to good health is to have a balanced diet. Remember: “you are what you eat.”You should eat more fruits and vegetables which contain（包含）a lot of fibre（纤维）.Try to eat less fried food and choose foods that are boiled, steamed, baked or sewed. You should also cut down on oily, fatty and sugared foods and eat more food with carbohydrates（碳水化合物）such as rice, bread and cereals for energy, especially if you have a most active lifestyle.The basic rule to remember is to include something from every food group at each meal using the suggested proportions.(比例)41. What is the underlined word “balanced” mean? It means _____.A. 美味的B. 健康的C. 均衡的D. 清淡的42. According to the Pyramid Diet, we should eat more ____.A. fish and chickenB. meat and vegetablesC. butter and breadD. bread and fruits43. Carbohydrates provide our bodies with _____.A. fibreB. energyC. oilD. water44. _____ food should be eaten less.A. FriedB. BoiledC. BakedD. Stewed45. To keep a balanced diet, we should eat _____.A. everything we likeB. everything from the food groupC. as much as we canD. right amount of food from every food group(B)Many people believe that before 2100 we will live on Mars.火星。

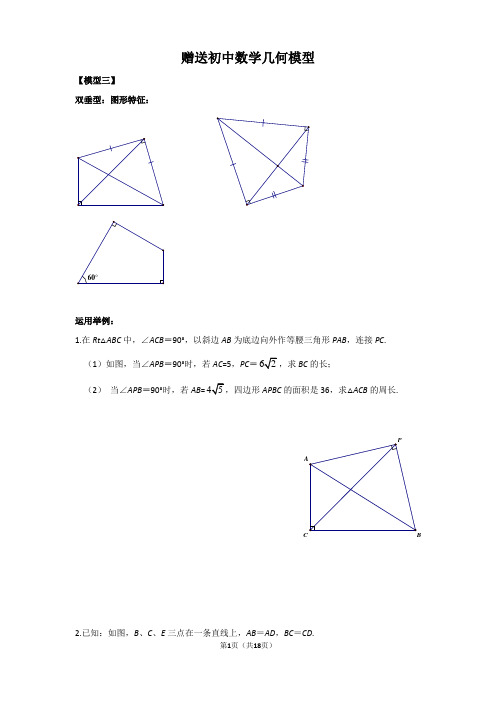
赠送初中数学几何模型【模型三】双垂型：图形特征：60°运用举例：1.在Rt△ABC中，∠ACB＝90°，以斜边AB为底边向外作等腰三角形PAB，连接PC. （1）如图，当∠APB＝90°时，若AC=5，PC＝62，求BC的长；（2）当∠APB＝90°时，若AB=45APBC的面积是36，求△ACB的周长.P 2.已知：如图，B、C、E三点在一条直线上，AB＝AD，BC＝CD.（1）若∠B＝90°，AB＝6，BC＝23，求∠A的值；（2）若∠BAD＋∠BCD＝180°，cos∠DCE＝35，求ABBC的值.3.如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，（1）若AB=3，BC+CD=5，求四边形ABCD的面积（2）若p= BC+CD，四边形ABCD的面积为S，试探究S与p之间的关系。

DBC2014-2015学年广东省广州市增城区新塘中学八年级（上）期中数学试卷一、填空题（每题3分，共24分）1．（3分）下列平面图形中，不是轴对称图形的是（）A． B． C．D．2．（3分）以下列各组线段为边，能组成三角形的是（）A．2cm，3cm，5cm B．3cm，3cm，6cm C．5cm，8cm，2cm D．4cm，5cm，6cm3．（3分）如果等腰三角形两边长是6cm和3cm，那么它的周长是（）A．9 cm B．12 cm C．15 cm或12 cm D．15 cm4．（3分）等腰三角形的一个角为40°，则它的底角为（）A．100°B．40°C．70°D．70°或40°5．（3分）两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（）A．两角和一边B．两边及夹角C．三个角D．三条边6．（3分）如图所示，AB⊥BC，CD⊥BC，垂足分别为B、C，AB=BC，E为BC的中点，且AE⊥BD于F，若CD=4cm，则AB的长度为（）A．4cm B．8cm C．9cm D．10cm7．（3分）如图，在△ABC中，AB=AC=20cm，DE垂直平分AB，垂足为E，交AC 于D，若△DBC的周长为35cm，则BC的长为（）A．5cm B．10cm C．15cm D．17.5cm8．（3分）如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么下列说法不正确的是（）A．△EBD是等腰三角形，EB=EDB．折叠后∠ABE和∠CBD一定相等C．折叠后得到的图形是轴对称图形D．△EBA和△EDC′一定是全等二、填空题（每题3分，共21分）9．（3分）点A（2，﹣1）关于x轴对称的点的坐标是．10．（3分）某三角形的两边之和是12，它们之差为5．那么该三角形第三边a 的取值为．11．（3分）正十边形的内角和为，外角和为，每个内角为．12．（3分）如图所示，在四边形ABCD中，∠A=20°．直线l与边AB、AD分别相交于点M、N，则∠1+∠2=．13．（3分）如图所示，已知∠MOS=∠NOS，PA⊥OM，垂足是A，如果AP=5cm，那么点P到ON的距离等于cm．14．（3分）如图，∠1=∠2，要使△ABE≌△ACE，还需添加一个条件是（填上你认为适当的一个条件即可）．15．（3分）如图，△ABC中，点D、E分别在边AB、AC的中点，将△ADE沿过DE折叠，使点A落在BC上F处，若∠B=50°，则∠BDF=度．三、解答题（共55分）16．（6分）如图已知，AB∥DC，AB=DC，AE=CF．求证：△ABF≌△CDE．17．（6分）如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．18．（6分）如图，AD=BC，AE=CF，AE⊥BD于E，CF⊥BD于F．求证：BE=DF．19．（8分）△ABC在平面直角坐标系中的位置如图所示．（1）作出△ABC关于y轴对称的三角形△A1B1C1．（2）将△ABC向下平移3个单位长度，画出平移后的△A2B2C2（3）写出点A1和A2的坐标．20．（9分）在等腰△ABC中，AB=AC．求证：BC边上的高线，中线，∠A的角平分线互相重合．（提示：作BC边上的高AD）21．（10分）如图，△ABC中，∠C=90°，AC=BC，AD是∠CAB的平分线，DE⊥AB于E．已知AB=6cm，求△DEB的周长．22．（10分）如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明．①AB=DE，②AC=DF，③∠ABC=∠DEF，④BE=CF．解：我写的真命题是：在△ABC和△DEF中，如果，那么．（不能只填序号）证明如下：2014-2015学年广东省广州市增城区新塘中学八年级（上）期中数学试卷参考答案与试题解析一、填空题（每题3分，共24分）1．（3分）下列平面图形中，不是轴对称图形的是（）A． B． C．D．【解答】解：：A、不是轴对称图形，本选项正确；B、是轴对称图形，本选项错误；C、是轴对称图形，本选项错误；D、是轴对称图形，本选项错误．故选：A．2．（3分）以下列各组线段为边，能组成三角形的是（）A．2cm，3cm，5cm B．3cm，3cm，6cm C．5cm，8cm，2cm D．4cm，5cm，6cm【解答】解：根据三角形的三边关系，知A、2+3=5，不能组成三角形；B、3+3=6，不能够组成三角形；C、2+5=7＜8，不能组成三角形；D、4+5＞6，能组成三角形．故选：D．3．（3分）如果等腰三角形两边长是6cm和3cm，那么它的周长是（）A．9 cm B．12 cm C．15 cm或12 cm D．15 cm【解答】解：当腰为3cm时，3+3=6，不能构成三角形，因此这种情况不成立．当腰为6cm时，6﹣3＜6＜6+3，能构成三角形；此时等腰三角形的周长为6+6+3=15cm．故选：D．4．（3分）等腰三角形的一个角为40°，则它的底角为（）A．100°B．40°C．70°D．70°或40°【解答】解：当40°为顶角时，底角为：（180°﹣40°）÷2=70°．40°也可以为底角．故选：D．5．（3分）两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（）A．两角和一边B．两边及夹角C．三个角D．三条边【解答】解：判定两三角形全等，就必须有边的参与，因此C选项是错误的．A选项，运用的是全等三角形判定定理中的AAS或ASA，因此结论正确；B选项，运用的是全等三角形判定定理中的SAS，因此结论正确；D选项，运用的是全等三角形判定定理中的SSS，因此结论正确；故选：C．6．（3分）如图所示，AB⊥BC，CD⊥BC，垂足分别为B、C，AB=BC，E为BC的中点，且AE⊥BD于F，若CD=4cm，则AB的长度为（）A．4cm B．8cm C．9cm D．10cm【解答】解：∵AB⊥BC，CD⊥BC，∴∠ABC=∠ACD=90°∴∠AEB+∠A=90°∵AE⊥BD∴∠BFE=90°∴∠AEB+∠FBE=90°∴∠A=∠FBE，又∵AB=BC，∴△ABE≌△BCD，∴BE=CD=4cm，AB=BC∵E为BC的中点∴AB=BC=2BE=8cm．故选：B．7．（3分）如图，在△ABC中，AB=AC=20cm，DE垂直平分AB，垂足为E，交AC 于D，若△DBC的周长为35cm，则BC的长为（）A．5cm B．10cm C．15cm D．17.5cm【解答】解：∵△DBC的周长=BC+BD+CD=35cm（已知）又∵DE垂直平分AB∴AD=BD（线段垂直平分线的性质）故BC+AD+CD=35cm∵AC=AD+DC=20（已知）∴BC=35﹣20=15cm．故选：C．8．（3分）如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么下列说法不正确的是（）A．△EBD是等腰三角形，EB=EDB．折叠后∠ABE和∠CBD一定相等C．折叠后得到的图形是轴对称图形D．△EBA和△EDC′一定是全等【解答】解：∵四边形ABCD是矩形，∴AB=CD，AD=BC，∠A=C=90°，AD∥BC，∴∠ADB=∠CBD．∵△DBC与△DBC′关于BD对称，∴△DBC≌△DBC′，∴DC=DC′，BC′=BC，∠DBC=∠DBC′，∠C=∠C′．∴AB=C′D，∠A=∠C′．∠EBD=∠EDB，∴BE=DE，∴△EBD是等腰三角形．故A正确．在△AEB和△C′ED中，，∴△AEB≌△C′ED（AAS），故D正确，∴折叠后得到的图形是轴对称图形．∵∠DBC=∠DBC′，∴∠ABE和∠CBD不一定相等．故B错误．故选：B．二、填空题（每题3分，共21分）9．（3分）点A（2，﹣1）关于x轴对称的点的坐标是（2，1）．【解答】解：点A（2，﹣1）关于x轴对称的点的坐标是（2，1），故答案为：（2，1）．10．（3分）某三角形的两边之和是12，它们之差为5．那么该三角形第三边a 的取值为5＜x＜12．【解答】解：设这个三角形的两边长分别为：x、y，由题意得，，解得：，则x﹣y＜a＜x+y，即5＜x＜12．故答案为：5＜x＜12．11．（3分）正十边形的内角和为1440°，外角和为360°，每个内角为144°．【解答】解；正十边形的内角和为1440°，外角和为360°，每个内角为144°，故答案为：1440°，360°，144°．12．（3分）如图所示，在四边形ABCD中，∠A=20°．直线l与边AB、AD分别相交于点M、N，则∠1+∠2=200°．【解答】解：四边形的内角和是（4﹣2）×180°=360°，（∠B+∠C+∠D）=360°﹣∠A=360°﹣20°=340°．五边形内角和是（5﹣2）×180°=540°，∠1+∠2=540°﹣（∠B+∠C+∠D）=540°﹣340°=200°，故答案为：200°．13．（3分）如图所示，已知∠MOS=∠NOS，PA⊥OM，垂足是A，如果AP=5cm，那么点P到ON的距离等于5cm．【解答】解：如图，过点P作PB⊥ON于B，∵∠MOS=∠NOS，PA⊥OM，∴BP=AP=5cm．故答案为：5．14．（3分）如图，∠1=∠2，要使△ABE≌△ACE，还需添加一个条件是∠B=∠C（填上你认为适当的一个条件即可）．【解答】解：∵∠1=∠2，∴∠AEB=∠AEC，又AE公共，∴当∠B=∠C时，△ABE≌△ACE（AAS）；或BE=CE时，△ABE≌△ACE（SAS）；或∠BAE=∠CAE时，△ABE≌△ACE（ASA）．15．（3分）如图，△ABC中，点D、E分别在边AB、AC的中点，将△ADE沿过DE折叠，使点A落在BC上F处，若∠B=50°，则∠BDF=80度．【解答】解：∵点D、E分别在边AB、AC的中点，∴DE是△ABC的中位线，∴DE∥BC，∴∠ADE=∠B．∵△ADE与△FDE关于DE对称，∴△ADE≌△FDE，∴∠ADE=∠FDE．∵∠B=50°，∴∠ADE=50°，∴∠FDE=50°．∵∠BDF+∠ADF=180°，∴∠BDF=80°．故答案为：80．三、解答题（共55分）16．（6分）如图已知，AB∥DC，AB=DC，AE=CF．求证：△ABF≌△CDE．【解答】解：∵AB∥DC，∴∠C=∠A，∵AE=CF，∴AE+EF=CF+EF，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS）．17．（6分）如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．【解答】解：∵∠AFE=90°，∴∠AEF=90°﹣∠A=90°﹣35°=55°，∴∠CED=∠AEF=55°，∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°．答：∠ACD的度数为83°．18．（6分）如图，AD=BC，AE=CF，AE⊥BD于E，CF⊥BD于F．求证：BE=DF．【解答】证明：∵AE⊥AD交BD于点E，CF⊥BC交BD于点F，∴∠EAD=∠FCB=90°，在Rt△ADE和Rt△CBF中，，∴Rt△ADE≌Rt△CBF（HL），∴DE=BF，∴BE=DF．19．（8分）△ABC在平面直角坐标系中的位置如图所示．（1）作出△ABC关于y轴对称的三角形△A1B1C1．（2）将△ABC向下平移3个单位长度，画出平移后的△A2B2C2（3）写出点A1和A2的坐标．【解答】解：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求；（3）如图所示：A1（2，3），A2（﹣2，0）．20．（9分）在等腰△ABC中，AB=AC．求证：BC边上的高线，中线，∠A的角平分线互相重合．（提示：作BC边上的高AD）【解答】证明：如图，过点A作AD⊥BC于D，在Rt△ABD和Rt△ACD中，，∴Rt△ABD≌Rt△ACD（HL），∴BD=CD，∠BAD=∠CAD，故BC边上的高线，中线，∠A的角平分线互相重合．21．（10分）如图，△ABC中，∠C=90°，AC=BC，AD是∠CAB的平分线，DE⊥AB于E．已知AB=6cm，求△DEB的周长．【解答】解：∵AD是∠CAB的平分线，DE⊥AB，∠C=90°，∴CD=ED，∵在Rt△ACD和Rt△AED中，，∴Rt△ACD≌Rt△AED（HL），∴AC=AE，又∵AC=BC，∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB，∵AB=6cm，∴△DEB的周长=6cm．22．（10分）如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明．①AB=DE，②AC=DF，③∠ABC=∠DEF，④BE=CF．解：我写的真命题是：在△ABC和△DEF中，如果AB=DE，AC=DF，BE=CF，那么∠ABC=∠DEF．（不能只填序号）证明如下：【解答】解：如图，在△ABC和△DEF中，点B、E、C、F在同一条直线上，如果AB=DE，AC=DF，BE=CF．那么∠ABC=∠DEF．证明：∵BE=CF，∴BE+EC=CF+EC，即BC=EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SSS），∴∠ABC=∠DEF；故答案是：AB=DE，AC=DF，BE=CF；∠ABC=∠DEF．。

广东实验中学2014-2015学年（上）中段质量检测初二级 数学试题一、选择题（每题3分，共30分） 1．下列图形中具有稳定性有（ ）DC B A2．芝麻作为食品和药物，均广泛使用．经测算，一粒芝麻约有0.000 002 01kg ，用科学记数法表示为（ ） A ．-72.0110kg ⨯B ．-50.20110kg ⨯C ．-720.110kg ⨯D ．-62.0110kg ⨯3．下列正多边形中，不能铺满地面的是（ ）A ．正方形B ．正六边形C ．长方形D ．正五边形4．分式22x x -+的值为0，则（ ） A ．2x =- B ．2x =± C ．2x = D ．0x = 5．下列计算正确的是（ ） A ．4416a a a ⋅= B ．()325a a = C ．623a a a ÷= D ．34a a a ⋅=6．如()x m +与()3x +的乘积中不含x 的一次项，则m 的值为（ ）A ．3-B ．3C ．0D ．17．如图，将一副直角三角板如图所示放置，使含30︒角的三角板的一条直角边和含45︒角的三角板的一条直角边重合，则1∠的度数为（ ）A ．55︒B ．65︒C ．75︒D ．85︒8．已知1112a b -=，则aba b-的值是（ ） A ．12 B ．12- C ．2 D ．2-9．某乡镇决定对一段长6 000米的公路进行修建改造．根据需要，该工程在实际施工时增中了施工人员，每天修建的公路比原计划增加了50%，结果提前4天完成任务．设原计划每天修建x 米，那么下面所列方程中正确的是（ ）A ．()600060004150%x x +=+B ．()600060004150%x x=--C ．()600060004150%x x-=+ D ．()600060004150%x x=+- 10．如图所示，在ABC △中，CD 、BE 分别是AB 、AC 边上的高，并且CD 、BE 交于点P ，若50A ∠=︒，则BPC ∠等于（ ）EDCB AA ．90︒B ．130︒C ．270︒D ．315︒ 二、填空题（每题3分，共18分）11．因式分解：（1）23a a +=______；（2）222x xy y -+-=___________； （3）3a a -=____________________．12．等腰三角形的两条边长为5，10，则等腰三角形的周长为______．13．2m a =，3n a =则2m n a -=______．14．如图，在ABC △中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且4cm BC =，则BD =______，24cm ABC S =△，则=S 阴影______．15．已知24a b +=，1ab =，则224a b +=______．16．如图，设k =甲图中阴影部分面积乙图中阴影部分面积()0a b >>，则k 的取值范围为______．乙甲三、解答题（72分） 17．（6分）在ABC △中，2A B ∠=∠，100C B ∠=∠+︒，求ABC △的三个内角度数． 18．计算（每题4分，共20分）（1）()222193a a a ⎛⎫--⋅- ⎪⎝⎭（2）()()()2322y z y z z y --+-+ （3）()()322323a b ab --⋅（4）2231366x x x x x+-⋅-+ （5）2221648x x y x y --- 19．（6分）在ABC △中，AD BC ⊥，AE 平分BAD ∠（1）80BAC ∠=︒，60C ∠=︒，求AED ∠（2）作出ACD △中AC 边上的高DF ，且已知4AD =，3CD =，5AC =，求DF 的长度．ED CBA20．解方程（每题4分，共8分）（1）2153x x =+ （2）28124x x x -=-- 21．（6分）先化简，再求值：222222322a b b b a a ab b a b a b -+⎛⎫+÷ ⎪-+--⎝⎭，其中5a =，2b =-． 22．（6分）一个大正方形和四个全等的小正方形按图①、②两种方式摆放．（1）设小正方的边长为x ，求x ．（用a 、b 的代数式表示）． （2）求图②中阴影部分面积（用a 、b 的代数式表示）．②①23．（8分）一项绿化工程由甲、乙两工程队承担，已知甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成． （1）求乙工程队单独完成这项工作需要多少天？（2）因工期的需要，将此项工程分成两部分，甲做其中一部分用了x 天完成，乙做另一部分用了y 天完成，其中x 、y 均为正整数，且46x <，52y <，求甲、乙两队各做了多少天？ 24．（12分）在平面直角坐标系中，B 为x 轴负半轴上一点，A 为第二象限内的点． （1）如图（1），PB 、PO 分别平分ABO ∠、AOB ∠，若70A ∠=︒，则BPO ∠=______；若A a ∠=,BPO ∠=_______（用a 表示）． （2）如图（2），将ABO △沿x 轴向右平移后可得COD △，PB 、PD 分别平分ABO ∠、CDO ∠．A a ∠=，求BPD ∠． （3）如图（3），直线OA 与直线ED 交于C ，MA 、MB 分别平分OAB ∠、OBA ∠，NC 、ND 分别平分OCD ∠、ODE ∠，试确定AM B ∠与CND ∠有何数量关系，并说明理由． （4）如图（4），若OAB ∠、OBA ∠的n 等分线依次相交于1M ，2M ，…，1n M -，若OCD∠和ODE ∠二角的角平分线的交点记为1N ，1N CD ∠和1N DE ∠二角的角平分线的交点记为2N ，依次类推，1n N CD -∠和1n N DE -∠二角的角平分线的交点记为n N ，则1n A M B -∠与n CN D∠的关系为____________________________．（用n 表示）(4)(3)(2)(1)。

2014-2015学年广东省广州市越秀区八年级（上）期末数学试卷一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中有几个选项符合题意，选错、不选、多选或涂改不清的均不给分）1．（3分）在下列四个轴对称图形中，对称轴的条数最多的是（）A．等腰三角形B．等边三角形C．圆D．正方形2．（3分）下面有4个汽车标志图案，其中不是轴对称图形的是（）A．B．C．D．3．（3分）若分式的值为零，则x的值为（）A．±1B．﹣1C．1D．不存在4．（3分）下列运算错误的是（）A．x2•x4=x6B．（﹣b）2•（﹣b）4=﹣b6C．x•x3•x5=x9D．（a+1）2（a+1）3=（a+1）55．（3分）下列各因式分解中，结论正确的是（）A．x2﹣5x﹣6=（x﹣2）（x﹣3）B．x2+x﹣6=（x+2）（x﹣3）C．ax+ay+1=a（x+y）+1D．ma2b+mab2+ab=ab（ma+mb+1）6．（3分）如图，在△ABC中，若AB=AC，∠A=30°，DE垂直平分AC，则∠BCD 的度数是（）A．45°B．40°C．35°D．30°7．（3分）到三角形三条边的距离都相等的点是这个三角形的（）A．三条中线的交点B．三条高的交点C．三条边的垂直平分线的交点D．三条角平分线的交点8．（3分）若等腰三角形的两条边的长分别为3cm和7cm，则它的周长是（）A．10cm B．13cm C．17cm D．13cm或17cm9．（3分）如图，若AB=AC，BE=CF，CF⊥AB，BE⊥AC，则图中全等的三角形共有（）对．A．5对B．4对C．3对D．2对10．（3分）如图是屋架设计图的一部分，点D是斜梁AB的AB的中点，立柱BC、DE垂直于横梁AF．已知AB=12m，∠ADE=60°，则DE等于（）A．3m B．2m C．1m D．4m二、填空题（本题共有6小题，每小题3分，共18分）11．（3分）要使分式有意义，那么x必须满足．12．（3分）已知一个n边形的内角和是其外角和的5倍，则n=．13．（3分）如图，已知△ABC≌△AFE，若∠ACB=65°，则∠EAC等于度．14．（3分）如图，若AB=AC，BD=CD，∠B=20°，∠BDC=120°，则∠A等于度．15．（3分）如图，已知BD是∠ABC的角平分线，DE⊥AB于E点，AB=6cm，BC=4cm，S△ABC=10cm2，则DE=cm．16．（3分）如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号．①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．三、解答题（本题共有7小题，共72分）17．（10分）完成下列运算（1）计算：7a2•（﹣2a）2+a•（﹣3a）3（2）计算：（a+b+1）（a﹣b+1）+b2﹣2a．18．（14分）完成下列运算（1）先化简，再求值：（2x﹣y）（y+2x）﹣（2y+x）（2y﹣x），其中x=1，y=2（2）先化简，再求值：，其中x=1，y=3．19．（9分）如图，在△ABC中，AC=BC，AD平分∠BAC，∠ADC=60°，求∠C的度数．20．（9分）如图，已知AB=AC，D是BC边的中点，DE和DF分别平分∠ADB和∠ADC，求证：DE=DF．21．（10分）客车和货车同时分别从甲乙两城沿同一公路相向而行，相遇时客车比货车多行驶了180千米，相遇后，客车再经过4小时到达乙城，货车再经过9小时到达甲城，求客车、货车的速度和甲乙两城间的路程．22．（10分）如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，求证：AB=AC+BD．23．（10分）在等腰直角三角形AOB中，已知AO⊥OB，点P、D分别在AB、OB 上，（1）如图1中，若PO=PD，∠OPD=45°，证明△BOP是等腰三角形．（2）如图2中，若AB=10，点P在AB上移动，且满足PO=PD，DE⊥AB于点E，试问：此时PE的长度是否变化？若变化，说明理由；若不变，请予以证明．2014-2015学年广东省广州市越秀区八年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中有几个选项符合题意，选错、不选、多选或涂改不清的均不给分）1．（3分）在下列四个轴对称图形中，对称轴的条数最多的是（）A．等腰三角形B．等边三角形C．圆D．正方形【解答】解：A、有1条对称轴；B、有3条对称轴；C、有无数条对称轴；D、有4条对称轴．故选：C．2．（3分）下面有4个汽车标志图案，其中不是轴对称图形的是（）A．B．C．D．【解答】解：A、是轴对称图形，故错误；B、是轴对称图形，故错误；C、是轴对称图形，故错误；D、不是轴对称图形，故正确．故选：D．3．（3分）若分式的值为零，则x的值为（）A．±1B．﹣1C．1D．不存在【解答】解：由分式的值为零的条件得，|x|﹣1=0，且x﹣1≠0，解得x=﹣1．故选：B．4．（3分）下列运算错误的是（）A．x2•x4=x6B．（﹣b）2•（﹣b）4=﹣b6C．x•x3•x5=x9D．（a+1）2（a+1）3=（a+1）5【解答】解：A、底数不变指数相加，故A正确；B、底数不变指数相加，故B错误；C、底数不变指数相加，故C正确；D、底数不变指数相加，故D正确；故选：B．5．（3分）下列各因式分解中，结论正确的是（）A．x2﹣5x﹣6=（x﹣2）（x﹣3）B．x2+x﹣6=（x+2）（x﹣3）C．ax+ay+1=a（x+y）+1D．ma2b+mab2+ab=ab（ma+mb+1）【解答】解：A、原式=（x﹣6）（x+1），错误；B、原式=（x﹣2）（x+3），错误；C、原式不能分解，错误；D、原式=ab（ma+mb+1），正确，故选：D．6．（3分）如图，在△ABC中，若AB=AC，∠A=30°，DE垂直平分AC，则∠BCD 的度数是（）A．45°B．40°C．35°D．30°【解答】解：∵AB=AC，∠A=30°，∴∠ABC=∠ACB=75°．∵DE垂直平分AC，∴AD=CD，∴∠A=∠ACD=30°∴∠BCD=∠ACB﹣∠ACD=45°．故选：A．7．（3分）到三角形三条边的距离都相等的点是这个三角形的（）A．三条中线的交点B．三条高的交点C．三条边的垂直平分线的交点D．三条角平分线的交点【解答】解：∵角的平分线上的点到角的两边的距离相等，∴到三角形的三边的距离相等的点是三条角平分线的交点．故选：D．8．（3分）若等腰三角形的两条边的长分别为3cm和7cm，则它的周长是（）A．10cm B．13cm C．17cm D．13cm或17cm【解答】解：①当腰是3cm，底边是7cm时：不满足三角形的三边关系，因此舍去．②当底边是3cm，腰长是7cm时，能构成三角形，则其周长=3+7+7=17（cm）．故选：C．9．（3分）如图，若AB=AC，BE=CF，CF⊥AB，BE⊥AC，则图中全等的三角形共有（）对．A．5对B．4对C．3对D．2对【解答】解：由题意可得出：△ABE≌△ACF（HL），△ADF≌△ADE（HL），△ABD ≌△ACD（SAS），△BFD≌△CED（ASA）．故选：B．10．（3分）如图是屋架设计图的一部分，点D是斜梁AB的AB的中点，立柱BC、DE垂直于横梁AF．已知AB=12m，∠ADE=60°，则DE等于（）A．3m B．2m C．1m D．4m【解答】解：如右图所示，∵立柱BC、DE垂直于横梁AC，∴BC∥DE，∵D是AB中点，∴AD=BD，∴AE：CE=AD：BD，∴AE=CE，∴DE是△ABC的中位线，∴DE=BC，在Rt△ABC中，∵∠ADE=60°，∴∠A=30°，∴BC=AB=6m，∴DE=3m．故选：A．二、填空题（本题共有6小题，每小题3分，共18分）11．（3分）要使分式有意义，那么x必须满足x≠2．【解答】解：由题意得，x﹣2≠0，解得x≠2．故答案为：x≠2．12．（3分）已知一个n边形的内角和是其外角和的5倍，则n=12．【解答】解：多边形的外角和是360°，根据题意得：180°•（n﹣2）=360°×5，解得n=12．故答案为：12．13．（3分）如图，已知△ABC≌△AFE，若∠ACB=65°，则∠EAC等于50度．【解答】解：∵△ABC≌△AFE，∴∠ACB=∠AEF=65°，∴∠EAC=180°﹣∠ACB﹣∠AEF=50°．故答案为50．14．（3分）如图，若AB=AC，BD=CD，∠B=20°，∠BDC=120°，则∠A等于80度．【解答】解：过D作射线AF，在△BAD和△CAD中，，∴△BAD≌△CAD（SSS），∴∠BAD=∠CAD，∠B=∠C=20°，∵∠BDF=∠B+∠BAD，∠CDF=∠C+∠CAD，∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD，∴∠BDC=∠B+∠C+∠BAC，∵∠C=∠B=20°，∠BDC=120°，∴∠BAC=80°．故答案为：80．15．（3分）如图，已知BD是∠ABC的角平分线，DE⊥AB于E点，AB=6cm，BC=4cm，S△ABC=10cm2，则DE=2cm．【解答】解：过D作DF⊥BC于F，∵BD是∠ABC的角平分线，DE⊥AB，∴DF=DE，=10cm2，AB=6cm，BC=4cm，∵S△ABC∴×BC×DF+×AB×DE=10，∴×4×DE+×6×DE=10，∴DE=2，故答案为：2．16．（3分）如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号①②④．①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．【解答】解：∵射线OC上的任意一点到∠AOB的两边的距离都相等，∴OC平分∠AOB．①若①∠ODE=∠ODF，根据ASA定理可求出△ODE≌△ODF，由三角形全等的性质可知OE=OF．正确；②若∠OED=∠OFD，根据AAS定理可得△ODE≌△ODF，由三角形全等的性质可知OE=OF．正确；③若ED=FD条件不能得出．错误；④若EF⊥OC，根据ASA定理可求出△OGE≌△OGF，由三角形全等的性质可知OE=OF．正确．故答案为①②④．三、解答题（本题共有7小题，共72分）17．（10分）完成下列运算（1）计算：7a2•（﹣2a）2+a•（﹣3a）3（2）计算：（a+b+1）（a﹣b+1）+b2﹣2a．【解答】解：（1）原式=7a2•4a2+a•（﹣27a3）=28a4﹣27a4=a4；（2）原式=（a+1）2﹣b2+b2﹣2a=a2+2a+1﹣2a=a2+1．18．（14分）完成下列运算（1）先化简，再求值：（2x﹣y）（y+2x）﹣（2y+x）（2y﹣x），其中x=1，y=2（2）先化简，再求值：，其中x=1，y=3．【解答】解：（1）原式=4x2﹣y2﹣4y2+x2=5（x2﹣y2），当x=1，y=2时，原式=5×（1﹣4）=﹣15；（2）原式=﹣•=+===，当x=1，y=3，∴原式=3．19．（9分）如图，在△ABC中，AC=BC，AD平分∠BAC，∠ADC=60°，求∠C的度数．【解答】解：设∠BAD=x．∵AD平分∠BAC，∴∠CAD=∠BAD=x，∠BAC=2∠BAD=2x．∵AC=BC，∴∠B=∠BAC=2x．∵∠ADC=∠B+∠BAD=60°，∴2x+x=60°，∴x=20°，∴∠B=∠BAC=40°．在△ABC中，∵∠BAC+∠B+∠C=180°，∴∠C=180°﹣∠B﹣∠BAC=100°．20．（9分）如图，已知AB=AC，D是BC边的中点，DE和DF分别平分∠ADB和∠ADC，求证：DE=DF．【解答】证明：∵AB=AC，D是BC边的中点，∴AD⊥BC，∠EAD=∠FAD．又∵DE和DF分别平分∠ADB和∠ADC，∴∠EDA=∠FDA=45°．在△AED与△AFD中，，∴△AED≌△AFD（ASA），∴DE=DF．21．（10分）客车和货车同时分别从甲乙两城沿同一公路相向而行，相遇时客车比货车多行驶了180千米，相遇后，客车再经过4小时到达乙城，货车再经过9小时到达甲城，求客车、货车的速度和甲乙两城间的路程．【解答】解：设客车的速度是x千米/小时，则货车的速度是千米/小时，依题意有=，解得x1=90，x2=﹣18（不合题意舍去），经检验，x=90是原方程的解，==60，90×4+60×9=360+540=900（千米）．答：客车的速度是90千米/小时，则货车的速度是60千米/小时，甲乙两城间的路程是900千米．22．（10分）如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，求证：AB=AC+BD．【解答】证明：在AB上取一点F，使AF=AC，连结EF．∵EA、EB分别平分∠CAB和∠DBA，∴∠CAE=∠FAE，∠EBF=∠EBD．∵AC∥BD，∴∠C+∠D=180°．在△ACE和△AFE中，，∴△ACE≌△AFE（SAS），∴∠C=∠AFE．∵∠AFE+∠EFB=180°，∴∠EFB=∠D．在△BEF和△BED中，，∴△BEF≌△BED（AAS），∴BF=BD．∵AB=AF+BF，∴AB=AC+BD．23．（10分）在等腰直角三角形AOB中，已知AO⊥OB，点P、D分别在AB、OB 上，（1）如图1中，若PO=PD，∠OPD=45°，证明△BOP是等腰三角形．（2）如图2中，若AB=10，点P在AB上移动，且满足PO=PD，DE⊥AB于点E，试问：此时PE的长度是否变化？若变化，说明理由；若不变，请予以证明．【解答】（1）证明：∵PO=PD，∠OPD=45°，∴∠POD=∠PDO==67.5°，∵等腰直角三角形AOB中，AO⊥OB，∴∠B=45°，∴∠OPB=180°﹣∠POB﹣∠B=67.5°，∴∠POD=∠OPB，∴BP=BO，即△BOP是等腰三角形；（2）解：PE的值不变，为PE=5，证明如下：如图，过点O作OC⊥AB于C，∵∠AOB=90°，AO=BO，∴△BOC是等腰直角三角形，∠COB=∠B=45°，点C为AB的中点，∴OC=AB=5，∵PO=PD，∴∠POD=∠PDO，又∵∠POD=∠COD+∠POC=45°+∠POC，∠PDO=∠B+∠DPE=45°+∠DPE，∴∠POC=∠DPE，在△POC和△DPE中，，∴△POC≌△DPE（AAS），∴OC=PE=5，∴PE的值不变，为5．附赠：初中数学易错题填空专题一、填空题1、如果一个数的绝对值等于它的相反数，那么这个数一定是____ _____。

2014-2015学年广东省广州市八年级（上）期末数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列四个图案中，是轴对称图形的是（）A．B．C．D．2．（3分）等腰三角形一边长等于5，一边长等于9，则它的周长是（）A．14B．23C．19D．19或23 3．（3分）下列从左到右的变形中是因式分解的有（）①x2﹣y2﹣1=（x+y）（x﹣y）﹣1；②x3+x=x（x2+1）；③（x﹣y）2=x2﹣2xy+y2；④x2﹣9y2=（x+3y）（x﹣3y）．A．1个B．2个C．3个D．4个4．（3分）三角形内有一点到三角形三顶点的距离相等，则这点一定是三角形的（）A．三条中线的交点B．三边垂直平分线的交点C．三条高的交点D．三条角平分线的交点5．（3分）已知（a+b）2=m，（a﹣b）2=n，则ab等于（）A．B．C．D．6．（3分）如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（）A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE 7．（3分）下列各式中，正确的是（）A．B．C．D．8．（3分）如图，将三角形纸片ABC沿直线DE折叠后，使得点B与点A重合，折痕分别交BC，AB于点D，E．如果AC=5cm，△ADC的周长为17cm，那么BC 的长为（）A．7cm B．10cm C．12cm D．22cm9．（3分）某园林公司增加了人力进行园林绿化，现在平均每天比原计划多植树50棵，现在植树600棵所需的时间与原计划植树450棵所需的时间相同，如果设原计划平均每天植树x棵，那么下面所列方程中，正确的是（）A．B．C．D．10．（3分）如果，那么的值为（）A．B．C．D．二、填空题（共6小题，每小题3分，满分18分）11．（3分）如图，已知AC=DB，要使△ABC≌△DCB，只需增加的一个条件是．12．（3分）因式分解：3a2﹣27b2=．13．（3分）当x=时，分式的值为零．14．（3分）等腰三角形的一个角是70°，则它的另外两个角的度数是．15．（3分）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的高，AB=8，则BD=．16．（3分）已知，求的值为．三、解答题（共9小题，满分102分）17．（10分）（1）因式分解：a3﹣6a2﹣a（2）解方程：．18．（10分）先化简代数式，然后选取一个使原式有意义的x 值代入求值．19．（10分）如图，电信部门要在公路m，n之间的S区域修建一座电视信号发射塔P．按照设计要求，发射塔P到区域S内的两个城镇A，B的距离必须相等，到两条公路m，n的距离也必须相等．发射塔P建在什么位置？在图中用尺规作图的方法作出它的位置并标出（不写作法但保留作图痕迹）．20．（10分）已知：如图，∠1=∠2，∠3=∠4，求证：△ABE≌△ADE．21．（10分）随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的2.5倍，求私家车的速度是多少．22．（10分）如图，在Rt△ABC中，AB=AC，AD⊥BC，垂足为D．E、F分别是CD、AD上的点，且CE=AF．如果∠AED=62°，求∠DBF的度数．23．（14分）先阅读，然后回答问题．若，求的值．解：因为，所以a=﹣2b（第一步）所以===（第二步）（1）回答问题：①第一步运用了的基本性质；②第二步的解题过程运用了的方法，由得，是对分式进行了．（2）模仿运用，已知，求的值．24．（14分）如图1，点A是线段BC上一点，△ABD，△AEC都是等边三角形，BE交AD于点M，CD交AE于N．（1）求证：BE=DC；（2）求证：△AMN是等边三角形；（3）将△ACE绕点A按顺时针方向旋转90°，其它条件不变，在图2中补出符合要求的图形，并判断（1）、（2）两小题结论是否仍然成立，并加以证明．25．（14分）已知，△ABC为等边三角形，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．（1）如图1，当点D在边BC上时，①求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB+∠DAC是否成立；（2）如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB+∠DAC是否成立？请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；（3）如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系．2014-2015学年广东省广州市八年级（上）期末数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列四个图案中，是轴对称图形的是（）A．B．C．D．【解答】解：A、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意；B、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意；C、是轴对称图形，符合题意；D、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意．故选：C．2．（3分）等腰三角形一边长等于5，一边长等于9，则它的周长是（）A．14B．23C．19D．19或23【解答】解：当腰长为5时，则三角形的三边分别为5、5、9，满足三角形的三边关系，其周长为19；当腰长为9时，则三角形的三边分别为9、9、5，满足三角形的三边关系，其周长为23；综上可知三角形的周长为19或23，故选：D．3．（3分）下列从左到右的变形中是因式分解的有（）①x2﹣y2﹣1=（x+y）（x﹣y）﹣1；②x3+x=x（x2+1）；③（x﹣y）2=x2﹣2xy+y2；④x2﹣9y2=（x+3y）（x﹣3y）．A．1个B．2个C．3个D．4个【解答】解：①没把一个多项式转化成几个整式积的形式，故①不是因式分解；②把一个多项式转化成几个整式积的形式，故②是因式分解；③整式的乘法，故③不是因式分解；④把一个多项式转化成几个整式积的形式，故④是因式分解；故选：B．4．（3分）三角形内有一点到三角形三顶点的距离相等，则这点一定是三角形的（）A．三条中线的交点B．三边垂直平分线的交点C．三条高的交点D．三条角平分线的交点【解答】解：三角形内有一点到三角形三顶点的距离相等，则这点一定是三角形的三边垂直平分线的交点，故选：B．5．（3分）已知（a+b）2=m，（a﹣b）2=n，则ab等于（）A．B．C．D．【解答】解：已知两式相减得：（a+b）2﹣（a﹣b）2=m﹣n，即（a+b+a﹣b）（a+b﹣a+b）=4ab=m﹣n，则ab=（m﹣n），故选：C．6．（3分）如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（）A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE【解答】解：A、添加DE=AB与原条件满足SSA，不能证明△ABC≌△DEF，故A 选项正确．B、添加DF∥AC，可得∠DFE=∠ACB，根据AAS能证明△ABC≌△DEF，故B选项错误．C、添加∠E=∠ABC，根据AAS能证明△ABC≌△DEF，故C选项错误．D、添加AB∥DE，可得∠E=∠ABC，根据AAS能证明△ABC≌△DEF，故D选项错误．故选：A．7．（3分）下列各式中，正确的是（）A．B．C．D．【解答】解：A 分母中的a没除以b，故A错误；B 异分母分式不能直接相加，故B错误；C 分式的分子分母没同乘或除以同一个不为零整式，故C错误；D 分式的分子分母都乘以（a﹣2），故D正确；故选：D．8．（3分）如图，将三角形纸片ABC沿直线DE折叠后，使得点B与点A重合，折痕分别交BC，AB于点D，E．如果AC=5cm，△ADC的周长为17cm，那么BC 的长为（）A．7cm B．10cm C．12cm D．22cm【解答】解：∵将△ABC沿直线DE折叠后，使得点B与点A重合，∴AD=BD，∵AC=5cm，△ADC的周长为17cm，∴AD+CD=BC=17﹣5=12（cm）．故选：C．9．（3分）某园林公司增加了人力进行园林绿化，现在平均每天比原计划多植树50棵，现在植树600棵所需的时间与原计划植树450棵所需的时间相同，如果设原计划平均每天植树x棵，那么下面所列方程中，正确的是（）A．B．C．D．【解答】解：设原计划平均每天植树棵x棵，现在每天植树（x+50）棵，依题意得，=．故选：B．10．（3分）如果，那么的值为（）A．B．C．D．【解答】解：=，2x+2y=3x，x=2y，==，故选：A．二、填空题（共6小题，每小题3分，满分18分）11．（3分）如图，已知AC=DB，要使△ABC≌△DCB，只需增加的一个条件是AB=DC．【解答】解：∵AC=BD，BC=BC，∴可添加AB=DC利用SSS判定△ABC≌△DCB．故填：AB=DC．12．（3分）因式分解：3a2﹣27b2=3（a+3b）（a﹣3b）．【解答】解：3a2﹣27b2，=3（a2﹣9b2），=3（a+3b）（a﹣3b）．13．（3分）当x=2时，分式的值为零．【解答】解：由题意得：（x+2）（x﹣2）=0，且x2﹣x﹣6≠0，解得：x=2，故答案为：2．14．（3分）等腰三角形的一个角是70°，则它的另外两个角的度数是55°、55°或70°、40°．【解答】解：（1）当顶角为70°时，则它的另外两个角的度数是55°，55°；（2）当底角70°时，则它的另外两个角的度数是70°，40°；所以另外两个角是55°，55°或70°，40°．故答案为：55°，55°或70°，40°．15．（3分）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的高，AB=8，则BD=2．【解答】解：Rt△ABC中，∵∠ACB=90°，∠A=30°，AB=8，∴BC=AB=4，在Rt△BCD中，∵∠B=90°﹣∠A=90°﹣30°=60°，∴∠BCD=90°﹣∠B=30°，∴BD=BC=2．故答案为：2．16．（3分）已知，求的值为2．【解答】解：由﹣=﹣=3，得到x﹣y=﹣3xy，则原式===2．故答案为：2三、解答题（共9小题，满分102分）17．（10分）（1）因式分解：a3﹣6a2﹣a（2）解方程：．【解答】解：（1）原式=a（a2﹣6a﹣1）；（2）去分母得：x﹣3+2（x+3）=12，去括号得：x﹣3+2x+6=12，移项合并得：3x=9，解得：x=3，经检验x=3是增根，分式方程无解．18．（10分）先化简代数式，然后选取一个使原式有意义的x 值代入求值．【解答】解：原式=﹣==，当x=0时，原式=﹣4．19．（10分）如图，电信部门要在公路m，n之间的S区域修建一座电视信号发射塔P．按照设计要求，发射塔P到区域S内的两个城镇A，B的距离必须相等，到两条公路m，n的距离也必须相等．发射塔P建在什么位置？在图中用尺规作图的方法作出它的位置并标出（不写作法但保留作图痕迹）．【解答】解：如图所示．20．（10分）已知：如图，∠1=∠2，∠3=∠4，求证：△ABE≌△ADE．【解答】证明：在△DEC和△BEC中∵，∴△DEC≌△BEC（ASA）．∴DE=BE．∵∠3=∠4，∴∠DEA=∠BEA．∵DE=BE，AE=AE，在△ABE和△ADE中∵，∴△ABE≌△ADE（SAS）．21．（10分）随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的2.5倍，求私家车的速度是多少．【解答】解：设公交车的速度是x千米/分钟，则私家车的速度是2.5x千米/分钟，由题意得，﹣=15，解得：x=0.32，经检验，x=0.32是原分式方程的解，且符合题意，则2.5x=2.5×0.32=0.8．答：私家车的速度是0.8千米/分钟．22．（10分）如图，在Rt△ABC中，AB=AC，AD⊥BC，垂足为D．E、F分别是CD、AD上的点，且CE=AF．如果∠AED=62°，求∠DBF的度数．【解答】解：∵AB=AC，AD⊥BC，∴BD=CD．又∵∠BAC=90°，∴BD=AD=CD．又∵CE=AF，∴DF=DE．∴Rt△BDF≌Rt△ADE（SAS）．∴∠DBF=∠DAE=90°﹣∠AED=90°﹣62°=28°．23．（14分）先阅读，然后回答问题．若，求的值．解：因为，所以a=﹣2b（第一步）所以===（第二步）（1）回答问题：①第一步运用了等式的基本性质；②第二步的解题过程运用了代入的方法，由得，是对分式进行了约分．（2）模仿运用，已知，求的值．【解答】解：（1）①第一步运用了等式的基本性质；②第二步的解题过程运用了代入的方法，由得，是对分式进行了约分．故答案为：等式，代入，约分；（2）∵==≠0，∴令===k，则x=3k，y=4k，z=6k，∴原式===．24．（14分）如图1，点A是线段BC上一点，△ABD，△AEC都是等边三角形，BE交AD于点M，CD交AE于N．（1）求证：BE=DC；（2）求证：△AMN是等边三角形；（3）将△ACE绕点A按顺时针方向旋转90°，其它条件不变，在图2中补出符合要求的图形，并判断（1）、（2）两小题结论是否仍然成立，并加以证明．【解答】证明：（1）∵△ABD，△AEC都是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=60°，∴∠DAC=∠BAE，在△ABE和△ADC中，，∴△ABE≌△ADC（SAS），∴BE=DC；（2）由（1）证得：△ABE≌△ADC，∴∠ABE=∠ADC．在△ABM和△ADN中，，∴△ABM≌△ADN（ASA），∴AM=AN．∵∠DAE=60°，∴△AMN是等边三角形；（3）∵△ABD，△AEC都是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=60°，∴∠DAC=∠BAE，在△ABE和△ADC中，，∴△ABE≌△ADC（SAS），∴BE=DC，∠ABE=∠ADC，∵∠BAC=90°∴∠MAN＞90°，∵∠MAN≠60°，∴△AMN不是等边三角形，∴（1）的结论成立，（2）的结论不成立．25．（14分）已知，△ABC为等边三角形，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．（1）如图1，当点D在边BC上时，①求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB+∠DAC是否成立；（2）如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB+∠DAC是否成立？请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；（3）如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系．【解答】解：（1）①证明：∵△ABC为等边三角形，∴AB=AC，∠BAC=60°，∵∠DAF=60°，∴∠BAC=∠DAF，∴∠BAD=∠CAF，∵四边形ADEF是菱形，∴AD=AF，在△ABD和△ACF中AB=AC，∠BAD=∠CAF，AD=AF，∴△ABD≌△ACF，∴∠ADB=∠AFC，②结论：∠AFC=∠ACB+∠DAC成立．（2）结论∠AFC=∠ACB+∠DAC不成立．∠AFC、∠ACB、∠DAC之间的等量关系是∠AFC=∠ACB﹣∠DAC．证明：∵△ABC为等边三角形，∴AB=AC，∠BAC=60°，∵∠BAC=∠DAF，∴∠BAD=∠CAF，∵四边形ADEF是菱形，∴AD=AF．在△ABD和△ACF中AB=AC，∠BAD=∠CAF，AD=AF，∴△ABD≌△ACF．∴∠ADB=∠AFC．又∵∠ACB=∠ADC+∠DAC，∴∠AFC=∠ACB﹣∠DAC．（3）补全图形如下图：∠AFC、∠ACB、∠DAC之间的等量关系是：∠AFC=2∠ACB﹣∠DAC （或∠AFC+∠DAC+∠ACB=180°以及这两个等式的正确变式）．。

2014-2015学年广东省广州广大附八年级（上）期中数学试卷一．选择题（共10小题）1．（2014秋•越秀区校级期中）下列运算中正确的是（）A ．x3•x3=2x6B．（﹣x3）2=﹣x6C．x5+x=x6D．（5x）3=125x32．（2009春•广东校级期末）等腰三角形两边长分别为3，7，则它的周长为（）A ．13 B．17 C．13或17 D．不能确定3．（2014秋•花垣县期末）下列多项式相乘，不能用平方差公式计算的是（）A ．（x﹣2y）（2y+x）B．（﹣2y﹣x）（x+2y）C．（x﹣2y）（﹣x﹣2y）D．（2y﹣x）（﹣x﹣2y）4．（2012•无锡）若一个多边形的内角和为1080°，则这个多边形的边数为（）A ．6 B．7 C．8 D．95．（2014秋•越秀区校级期中）如图，AB∥CD，∠A=35°，∠C=75°，则∠E的度数为（）A ．35°B．40°C．45°D．75°6．（2011秋•衡水期末）下列各命题中，假命题的个数为（）①面积相等的两个三角形是全等三角形；②三个角对应相等的两个三角形是全等三角形；③全等三角形的周长相等；④有两边及其中一边的对角对应相等的两个三角形是全等三角形．A ．1 B．2 C．3 D．47．（2014秋•肥西县期末）如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（）A ．1：1：1 B．1：2：3 C．2：3：4 D．3：4：58．（2009•临沂）如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（）A ．PA=PB B．PO平分∠APBC．OA=OB D．AB垂直平分OP9．（2014秋•越秀区校级期中）如果ab=﹣1，n=2012，那么a n•b n的值为（）A ．﹣2012 B．2012 C．1 D．﹣110．（2011•呼伦贝尔）如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（）A20°B30°C35°D40°第5题第7题第8题第10题二．填空题（共6小题）11．（2014秋•越秀区校级期中）三角形三个内角度数之比是1﹕2﹕3，则此三角形是三角形．12．（2014秋•越秀区校级期中）2a2（3a2﹣5b）=．13．（2014秋•越秀区校级期中）如图，已知AD=BC，根据“SSS”，还需要一个条件，可证明△ABC≌△BAD；根据“要SAS”，还需要一个条件，可证明△ABC≌△BAD．14．（2014秋•越秀区校级期中）一个三角形两边长分别为2和9，则第三边长x的取值范围．15．（2014秋•越秀区校级期中）如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC 于F，△ABC的面积是27cm2，AB=10cm，AC=8cm，则DE的长为cm．16．（2014秋•越秀区校级期中）如图，在△ABC中，AB=AC，∠BAD=∠CAD，则下列结论：①△ABD≌△ACD；②∠B=∠C；③BD=CD，④AD⊥BC．其中正确的有（填写编号）第13题第15题第16题三．解答题（共7小题）17．（2014秋•越秀区校级期中）计算下列各式（1）2ab•（﹣3a2）3 （2）（3x﹣2y）（x+y）（3）﹣2a3•a4+3a2•5a5（4）（15x3y5﹣10x4y4﹣20x3y2）÷（﹣5x3y2）18．（2014秋•越秀区校级期中）先化简，再求值：（x+2）2﹣（x+1）（x﹣1），其中x=﹣．19．（2014秋•孟津县期中）已知：a+b=3，ab=2，求a2+b2的值．20．（2014秋•越秀区校级期中）已知：如图，AB⊥BC，AD⊥DC，且AD=AB．求证：BC=DC．21．（2014秋•越秀区校级期中）已知△ABC中，∠C=90°，点D在AC上，DE⊥AB于点E，且DC=DE，∠A=40°，求∠CBD的度数．22．（2011•内江）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点．将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE23．（2014秋•越秀区校级期中）附加题：（此题分数加入总分，但总分超过100分就计100分）如图，已知在△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点，点P在线段BC上由B点向C 点运动，同时，点Q在线段CA上由点C向点A运动．（1）如果点P、Q的速度均为3厘米/秒，经过1秒后，△BPD与△CQP是否全等？请说明理由；（2）若点P的运动速度为2厘米/秒，点Q的运动速度为2.5厘米/秒，是否存在某一个时刻，使得△BPD 与△CQP全等？如果存在请求出这一时刻并证明；如果不存在，请说明理由．2014-2015学年广东省广州二十一中八年级（上）期中数学试卷参考答案与试题解析一．选择题（共10小题）1．（2014秋•越秀区校级期中）下列运算中正确的是（）A ．x3•x3=2x6B．（﹣x3）2=﹣x6C．x5+x=x6D．（5x）3=125x3考点：幂的乘方与积的乘方；合并同类项；同底数幂的乘法．分析：根据同底数幂的乘法、幂的乘方、合并同类项、积的乘方进行解答．解答：解：A、x3•x3=x3+3=x6，故本选项错误；B、（﹣x3）2=x3×2=x6，故本选项错误；C、x5+x≠x6，故本选项错误；D、（5x）3=53x3=125x3，故本选项正确．故选D．点评：本题考查了幂的乘方与积的乘方、合并同类项、同底数幂的乘法，要根据不同形式，选择合适的方法解答．2．（2009春•广东校级期末）等腰三角形两边长分别为3，7，则它的周长为（）A ．13 B．17 C．13或17 D．不能确定考点：等腰三角形的性质；三角形三边关系．专题：计算题．分析：分情况考虑：当相等的两边是3时或当相等的两边是7时．然后根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，判断能否构成三角形，最后再进一步计算其周长．解答：解：当相等的两边是3时，3+3＜7，不能组成三角形，应舍去；当相等的两边是7时，能够组成三角形，此时周长是7+7+3=17．故选B．点评：本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．3．（2014秋•花垣县期末）下列多项式相乘，不能用平方差公式计算的是（）A ．（x﹣2y）（2y+x）B．（﹣2y﹣x）（x+2y）C．（x﹣2y）（﹣x﹣2y）D．（2y﹣x）（﹣x﹣2y）考点：平方差公式．分析：把A得到（x﹣2y）（x+2y），把C变形得到﹣（x﹣2y）（x+2y），把D变形得到（x﹣2y）（x+2y），它们都可以用平方差公式进行计算；而把B变形得到﹣（x+2y）2，用完全平方公式计算．解答：解：A、（x﹣2y）（2y+x）=（x﹣2y）（x+2y）=x2﹣4y2，所以A选项不正确；B、（﹣2y﹣x）（x+2y）=﹣（x+2y）2，用完全平方公式计算，所以B选项正确；C、（x﹣2y）（﹣x﹣2y）=﹣（x﹣2y）（x+2y）=﹣x2+4y2，所以C选项不正确；D、（2y﹣x）（﹣x﹣2y）=（x﹣2y）（x+2y）=x2﹣4y2，所以D选项不正确．故选B．点评：本题考查了平方差公式：（a+b）（a﹣b）=a2﹣b2．也考查了完全平方公式．4．（2012•无锡）若一个多边形的内角和为1080°，则这个多边形的边数为（）A ．6 B．7 C．8 D．9考点：多边形内角与外角．分析：首先设这个多边形的边数为n，由n边形的内角和等于180°（n﹣2），即可得方程180（n ﹣2）=1080，解此方程即可求得答案．解答：解：设这个多边形的边数为n，根据题意得：180（n﹣2）=1080，解得：n=8．故选C．点评：此题考查了多边形的内角和公式．此题比较简单，注意熟记公式是准确求解此题的关键，注意方程思想的应用．5．（2014秋•越秀区校级期中）如图，AB∥CD，∠A=35°，∠C=75°，则∠E的度数为（）A ．35°B．40°C．45°D．75°考点：平行线的性质．分析：首先根据两直线平行，同位角相等可得∠C=∠EFB=75°，再根据三角形内角与外角的性质可得∠E 的度数．解答：解：∵AB∥CD，∴∠C=∠EFB=75°，∵∠A=35°，∴∠E=75°﹣35°=40°，故选：B．点评：此题主要考查了平行线的性质，关键是掌握两直线平行，同位角相等．①面积相等的两个三角形是全等三角形；②三个角对应相等的两个三角形是全等三角形；③全等三角形的周长相等；④有两边及其中一边的对角对应相等的两个三角形是全等三角形．A ．1 B．2 C．3 D．4考点：命题与定理．分析：根据全等三角形全等的性质可判断③的正误，据全等三角形全等的判定方法可判断①②④的正误，即可得解．解答：解：①面积相等的两个三角形不一定重合，所以不一定全等，故此选项是假命题；②角应相等的两个三角形，边不一定相等，两三角形也不一定全等；故此选项是假命题；③全等三角形的周长相等，根据全等三角形性质是正确的，故此选项正确，是真命题；④有两边及其中一边的对角对应相等的两个三角形，满足SSA时不能证明三角形全等的，故此选项是假命题，故假命题有3个，故选：C．点评：本题考查三角形全等的判定及性质，熟练掌握全等三角形的性质和判定方法是解题的关键．7．（2014秋•肥西县期末）如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（）A ．1：1：1 B．1：2：3 C．2：3：4 D．3：4：5考点：角平分线的性质．专题：数形结合．分析：利用角平分线上的一点到角两边的距离相等的性质，可知三个三角形高相等，底分别是20，30，40，所以面积之比就是2：3：4．解答：解：利用同高不同底的三角形的面积之比就是底之比可知选C．故选C．点评：本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式．做题时应用了三个三角形的高时相等的，这点式非常重要的．8．（2009•临沂）如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（）A ．PA=PB B．PO平分∠APBC．OA=OB D．AB垂直平分OP考点：角平分线的性质．分析：本题要从已知条件OP平分∠AOB入手，利用角平分线的性质，对各选项逐个验证，选项D是错误的，虽然垂直，但不一定平分OP．解答：解：∵OP平分∠AOB，PA⊥OA，PB⊥OB ∴PA=PB∴△OPA≌△OPB∴∠APO=∠BPO，OA=OB∴A、B、C项正确设PO与AB相交于E∵OA=OB，∠AOP=∠BOP，OE=OE∴△AOE≌△BOE∴∠AEO=∠BEO=90°∴OP垂直AB而不能得到AB平分OP故D不成立故选D．点评：本题主要考查平分线的性质，由已知能够注意到△OPA≌△OPB，进而求得△AOE≌△BOE是解决的关键．9．（2014秋•越秀区校级期中）如果ab=﹣1，n=2012，那么a n•b n的值为（）A ．﹣2012 B．2012 C．1 D．﹣1考点：幂的乘方与积的乘方．分析：将原式转化为a n•b n=（ab）n，然后代入求值．解答：解：a n•b n=（ab）n=（﹣1）2012=1，故选C．点评：本题考查了幂的乘方和积的乘方，要根据不同形式选择合适的方法．10．（2011•呼伦贝尔）如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（）A ．20°B．30°C．35°D．40°考点：全等三角形的性质．专题：计算题．分析：本题根据全等三角形的性质并找清全等三角形的对应角即可．解答：解：∵△ACB≌△A′CB′，∴∠ACB=∠A′CB′，即∠ACA′+∠A′CB=∠B′CB+∠A′CB，∴∠ACA′=∠B′CB，又∠B′CB=30°∴∠ACA′=30°．故选：B．点评：本题考查了全等三角形的判定及全等三角形性质的应用，利用全等三角形的性质求解．二．填空题（共6小题）11．（2014秋•越秀区校级期中）三角形三个内角度数之比是1﹕2﹕3，则此三角形是直角三角形．考点：三角形内角和定理．分析：根据比例设三角形的三个内角分别为k、2k、3k，然后根据三角形的内角和等于180°列出方程求出k，再求出最大的角的度数，即可得解．解答：解：设三角形的三个内角分别为k、2k、3k，由题意得，k+2k+3k=180°，解得k=30°，∴3k=3×30°=90°，∴此三角形是直角三角形．故答案为：直角．点评：本题考查了三角形的内角和定理，利用设k法求解更简便．12．（2014秋•越秀区校级期中）2a2（3a2﹣5b）=6a4﹣10a2b．考点：单项式乘多项式．分直接利用单项式乘以多项式运算法则求出即可．答：故答案为：6a4﹣10a2b．点评：此题主要考查了单项式乘以多项式，正确把握运算法则是解题关键．13．（2014秋•越秀区校级期中）如图，已知AD=BC，根据“SSS”，还需要一个条件BD=AC，可证明△ABC≌△BAD；根据“要SAS”，还需要一个条件∠DAB=∠CBA，可证明△ABC≌△BAD．考点：全等三角形的判定．专题：证明题．分析：图形中隐含条件BC=BC，找出第三边BD和AC即可，找出∠DAB和∠CBA即可．解答：解：BD=AC，∠DAB=∠CBA，理由是：在△ABC和△BAD中，∴△ABC≌△BAD（SSS），在△ABC和△BAD中，∴△ABC≌△BAD（SAS）．故答案为：BD=AC，∠DAB=∠CBA．点评：本题考查了全等三角形的判定的应用，关键是考查学生是否理解SSS和SAS的含义，题目比较典型，主要考查了学生运用定理进行推理的能力．14．（2014秋•越秀区校级期中）一个三角形两边长分别为2和9，则第三边长x的取值范围7＜x＜11．考点：三角形三边关系．分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边即可得出第三边取值范围．解答：解：设第三边长为x，根据三角形三边关系，∴9﹣2＜x＜2+9，即7＜x＜11，故答案为：7＜x＜11．点评：本题主要考查了三角形的三边关系，牢记三边关系式解答本题的关键．15．（2014秋•越秀区校级期中）如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC 于F，△ABC的面积是27cm2，AB=10cm，AC=8cm，则DE的长为3cm．考点：角平分线的性质．分析：根据角平分线上的点到角的两边距离相等可得DE=DF，然后利用△ABC的面积列方程求解即可．解答：解：∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，∴DE=DF，∵△ABC的面积是27cm2，AB=10cm，AC=8cm，∴×10•DE+×8•DF=27，解得DE=3cm．故答案为：3．点评：本题考查了角平分线上的点到角的两边距离相等的性质，三角形的面积，熟记性质并根据三角形的面积列出方程是解题的关键．16．（2014秋•越秀区校级期中）如图，在△ABC中，AB=AC，∠BAD=∠CAD，则下列结论：①△ABD≌△ACD；②∠B=∠C；③BD=CD，④AD⊥BC．其中正确的有①②③④（填写编号）考点：全等三角形的判定与性质；等腰三角形的性质．分析：由于AB=AC，∠BAD=∠CAD，利用等边对等角，等腰三角形三线合一定理，可知AD⊥BD，BD=CD，∠B=∠C，从而易证△ABD≌△ACD．解答：解：∵在△ABC中，AB=AC，∠BAD=∠CAD，∴AD⊥BD，BD=CD，∠B=∠C，∴△ABD≌△ACD（SSS）．故答案为①②③④．点评：本题考查了等腰三角形的性质、三角形全等的判定．等腰三角形的角平分线、底边上的中线、底边上的高互相重合．三．解答题（共7小题）17．（2014秋•越秀区校级期中）计算下列各式（1）2ab•（﹣3a2）3（2）（3x﹣2y）（x+y）（3）﹣2a3•a4+3a2•5a5（4）（15x3y5﹣10x4y4﹣20x3y2）÷（﹣5x3y2）考点：整式的混合运算．分析：（1）先算乘方，再算乘法；（2）根据多项式乘以多项式法则求出即可；（3）先算乘法，再合并同类项即可；（4）根据多项式除以单项式法则求出即可．解答：解：（1）原式=2ab•（﹣27a6）=﹣54a7b；（2）原式=3x2+3xy﹣2xy﹣2y2=3x2+xy﹣2y2；（3）原式=﹣2a7+15a7=13a7；（4）（15x3y5﹣10x4y4﹣20x3y2）÷（﹣5x3y2）=﹣3y3+2xy2+4．点评：本题考查了整式的混合运算的应用，主要考查学生的计算能力和化简能力，题目比较好，难度适中．18．（2014秋•越秀区校级期中）先化简，再求值：（x+2）2﹣（x+1）（x﹣1），其中x=﹣．考点：整式的混合运算—化简求值．分析：先算乘法，再合并同类项，最后代入求出即可．解答：解：（x+2）2﹣（x+1）（x﹣1）=x2+4x+4﹣x2+1=4x+5，当x=﹣时，原式=4×（﹣）+5=3．点评：本题考查了整式的混合运算的应用，主要考查学生的计算能力和化简能力，题目比较好，难度适中．19．（2014秋•孟津县期中）已知：a+b=3，ab=2，求a2+b2的值．考点：完全平方公式．专题：常规题型．分析：把a+b=3两边平方，再利用完全平方公式展开，再把ab=2代入进行计算即可得解．解答：解：∵a+b=3，∴（a+b）2=9，即a2+2ab+b2=9，∵ab=2，∴a2+b2=9﹣2ab=9﹣2×2=5．故答案为：5．点评：本题考查了完全平方公式，熟记公式的几个变形公式对解题大有帮助．20．（2014秋•越秀区校级期中）已知：如图，AB⊥BC，AD⊥DC，且AD=AB．求证：BC=DC．考点：全等三角形的判定与性质．专题：证明题．分析：连接AC，然后利用“HL”证明Rt△ABC和Rt△ADC全等，根据全等三角形对应边相等证明即可．解答：证明：连接AC，∵AB⊥BC，AD⊥DC，∴∠B=∠D=90°，在Rt△ABC和Rt△ADC中，，∴Rt△ABC≌Rt△ADC（HL），∴BC=BD．点评：本题考查了全等三角形的判定与性质，作辅助线，构造出全等三角形是解题的关键，也是本题的难点．21．（2014秋•越秀区校级期中）已知△ABC中，∠C=90°，点D在AC上，DE⊥AB于点E，且DC=DE，∠A=40°，求∠CBD的度数．考点：角平分线的性质．分析：首先利用角平分线的判定方法得到BD为∠ABC的平分线，然后利用直角三角形的性质求得∠ABC的度数，从而求得结论．解答：解：∵DE⊥AB于点E，DC=DE，∴∠CBD=∠EBD，∵∠A=40°，∴∠CBA=50°，∴∠BCD=∠CBA=×50°=25°．点评：本题考查了角平分线的性质，解题的关键是根据已知条件得到BD为∠ABC的平分线，难度不大．22．（2011•内江）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点．将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE 和EC的数量及位置关系，并证明你的猜想．考点：全等三角形的判定与性质．分析：数量关系为：BE=EC，位置关系是：BE⊥EC；利用直角三角形斜边上的中线等于斜边的一半，以及等腰直角三角形的性质，即可证得：△EAB≌△EDC即可证明．解答：数量关系为：BE=EC，位置关系是：BE⊥EC．证明：∵△AED是直角三角形，∠AED=90°，且有一个锐角是45°，∴∠EAD=∠EDA=45°，∴AE=DE，∵∠BAC=90°，∴∠EAB=∠EAD+∠BAC=45°+90°=135°，∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°，∴∠EAB=∠EDC，∵D是AC的中点，∴AD=CD=AC，∵AC=2AB，∴AB=AD=DC，∵在△EAB和△EDC中，∴△EAB≌△EDC（SAS），∴EB=EC，且∠AEB=∠DEC，∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°，∴BE⊥EC．点评：本题主要考查了全等三角形的判定与应用，证明线段相等的问题一般的解决方法是转化为证明三角形全等．23．（2014秋•越秀区校级期中）附加题：（此题分数加入总分，但总分超过100分就计100分）如图，已知在△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点，点P在线段BC上由B点向C 点运动，同时，点Q在线段CA上由点C向点A运动．（1）如果点P、Q的速度均为3厘米/秒，经过1秒后，△BPD与△CQP是否全等？请说明理由；（2）若点P的运动速度为2厘米/秒，点Q的运动速度为2.5厘米/秒，是否存在某一个时刻，使得△BPD 与△CQP全等？如果存在请求出这一时刻并证明；如果不存在，请说明理由．考点：全等三角形的判定与性质；等腰三角形的性质．专题：动点型．分析：（1）求出BP=CQ，CP=BD，∠B=∠C，根据SAS证出两三角形全等即可；（2）假设存在时刻t，根据全等三角形的性质得出方程组，求出t后，看看是否符合题意，再根据全等三角形的判定推出即可．解答：（1）解：△BPD与△CQP是全等，理由是：当t=1秒时BP=CQ=3，CP=8﹣3=5，∵D为AB中点，∴BD=AC=5=CP，∵AB=AC，∴∠B=∠C，在△BDP和△CPQ中∵，∴△BDP≌△CPQ（SAS）．（2）解：假设存在时间t秒，使△BDP和△CPQ全等，则BP=2t，BD=5，CP=8﹣2t，CQ=2.5t，∵△BDP和△CPQ全等，∠B=∠C，∴或（此方程组无解），解得：t=2，∴存在时刻t=2秒时，△BDP和△CPQ全等，此时BP=4，BD=5，CP=8﹣4=4=BP，CQ=5=BD，在△BDP和△CQP中∵，∴△BDP≌△CQP（SAS）．点评：本题考查了全等三角形的性质和判定，主要考查学生的推理能力，题目比较好，但是有一定的难度．。