单纯形法完全c语言程序

/*单纯形法程序*//*p46--5(2)*/#include "stdio.h"main(){int i,j,r,k,l,jj[4],m=4,n=7,maxjj,mini,count=0;floata[4][7]={{0,2,-1,1,0,0,0},{60,3,1,1,1,0,0,},{10,1,-1,2,0,1,0},{20,1, 1,-1,0,0,1}};floatb[4][4],e[4][4],t[4][4],y[4],maxcj,tb[4],tp[4],cb[4],cj[7],theta,lk,z; jj[1]=4;jj[2]=5;jj[3]=6;for(i=0;i<m;i++)for(j=0;j<m;j++)b[i][j]=0.0;for(i=1;i<m;i++) b[i][i]=1.0;printf("*********************************\n");for(i=0;i<m;i++){ for(j=0;j<n;j++)printf("%6.1f",a[i][j]);printf("\n");}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d\n",k); while(maxcj>0){ count++;for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }for(i=1;i<m;i++){ tp[i]=0.0;for(r=1;r<m;r++)tp[i]+=b[i][r]*a[r][k]; }/*for(i=1;i<m;i++)printf("%6.1f",tb[i]);for(i=1;i<m;i++)printf("%6.1f",tp[i]);printf("tb--tp\n"); */theta=1000.0;for(j=1;j<m;j++){ if(tp[j]>0)if (theta>tb[j]/tp[j]){ theta=tb[j]/tp[j]; mini=j;}}/* printf("LLL=%d Theta=%f\n",mini,theta); */l=mini;lk=tp[l];jj[l]=k;printf("*********************************\n");for(i=0;i<m;i++)for(j=0;j<m;j++)e[i][j]=0.0;for(i=1;i<m;i++) e[i][i]=1.0;for(i=1;i<m;i++)e[i][l]=(-1)*tp[i]/lk;e[l][l]=1.0/lk;for(i=1;i<m;i++){ for(j=1;j<m;j++)printf("%6.1f",e[i][j]);printf("\n"); } /* for(j=1;j<m;j++)printf("%6.1f",tp[j]); printf("\n");*/ for(i=1;i<m;i++)for(j=1;j<m;j++){ t[i][j]=0.0;for(r=1;r<m;r++)t[i][j]+=e[i][r]*b[r][j];}for(i=1;i<m;i++){ for(j=1;j<m;j++){ b[i][j]=t[i][j];printf("%6.1f",b[i][j]);}printf(" x%d\n",jj[i]);}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d\n",k);}for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }z=0.0;for(i=1;i<m;i++){ cb[i]=a[0][jj[i]];printf(" x%d=%6.1f\n",jj[i],tb[i]);z+=tb[i]*cb[i];}printf(" Max_z=%5.1f THE_count=%d\n",z,count);}/*p37--li1-13*/#include "math.h"#include "stdio.h"main(){int i,j,r,k,l,jj[4],m,n,maxjj,mini,count=0;floatb[4][4],e[4][4],t[4][4],y[4],maxcj,tb[4],tp[4],cb[4],cj[7],theta,lk,z; floata[4][6]={{0,700,1200,0,0,0},{360,9,4,1,0,0,},{200,4,5,0,1,0},{300, 3,10,0,0,1}};m=4;n=6;jj[1]=3;jj[2]=4;jj[3]=5;for(j=0;j<m;j++)b[i][j]=0.0;for(i=1;i<m;i++) b[i][i]=1.0;printf("*********************************\n");for(i=0;i<m;i++){ for(j=0;j<n;j++)printf("%6.1f",a[i][j]);printf("\n");}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d\n",k);while(maxcj>0.0001){ count++;for(i=1;i<m;i++){ tb[i]=0.0;for(i=1;i<m;i++){ tp[i]=0.0;for(r=1;r<m;r++)tp[i]+=b[i][r]*a[r][k]; }/*for(i=1;i<m;i++)printf("%6.1f",tb[i]);for(i=1;i<m;i++)printf("%6.1f",tp[i]);printf("tb--tp\n"); */theta=1000.0;for(j=1;j<m;j++){ if(tp[j]>0)if (theta>tb[j]/tp[j]){ theta=tb[j]/tp[j]; mini=j;}}/* printf("LLL=%d Theta=%f\n",mini,theta); */l=mini;lk=tp[l];jj[l]=k;printf("*********************************\n");for(i=0;i<m;i++)for(j=0;j<m;j++)e[i][j]=0.0;for(i=1;i<m;i++) e[i][i]=1.0;for(i=1;i<m;i++)e[i][l]=(-1)*tp[i]/lk;e[l][l]=1.0/lk;for(i=1;i<m;i++){ for(j=1;j<m;j++)printf("%6.1f",e[i][j]);printf("\n"); } /* for(j=1;j<m;j++)printf("%6.1f",tp[j]); printf("\n");*/ for(i=1;i<m;i++)for(j=1;j<m;j++){ t[i][j]=0.0;for(i=1;i<m;i++){ for(j=1;j<m;j++){ b[i][j]=t[i][j];printf("%6.1f",b[i][j]);}printf(" x%d\n",jj[i]);}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d MAXcj=%f\n",k,maxcj);} /*while--end*/for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }z=0.0;for(i=1;i<m;i++){ cb[i]=a[0][jj[i]];printf(" x%d=%6.1f\n",jj[i],tb[i]);z+=tb[i]*cb[i];}printf(" Max_z=%5.1f THE_count=%d\n",z,count);}/*p47--6(5)*/#include "math.h"#include "stdio.h"main(){int i,j,r,k,l,jj[4],m,n,maxjj,mini,count=0,ok=0;floatb[4][4],e[4][4],t[4][4],y[4],maxcj,tb[4],tp[4],cb[4],cj[8],theta,lk,z; floata[4][8]={{0,-1,-1,3,0,0,-1000,-1000},{11,1,-2,1,1,0,0,0},{3,2,1,-4,0 ,-1,1,0},{1,1,0,-2,0,0,0,1}};m=4;n=8;jj[1]=4;jj[2]=6;jj[3]=7;for(i=0;i<m;i++)for(j=0;j<m;j++)b[i][j]=0.0;for(i=1;i<m;i++) b[i][i]=1.0;printf("*********************************\n");for(i=0;i<m;i++){ for(j=0;j<n;j++)printf("%6.1f",a[i][j]);printf("\n");}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d\n",k);while(maxcj>0.001&&count<5){ count++;for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }for(i=1;i<m;i++){ tp[i]=0.0;for(r=1;r<m;r++)tp[i]+=b[i][r]*a[r][k]; }/*for(i=1;i<m;i++)printf("%6.1f",tb[i]);for(i=1;i<m;i++)printf("%6.1f",tp[i]);for(i=1;i<m;i++)if(tp[i]<=0)ok=-1;if (ok==-1){ printf("*** z\030 \354 ***\n");return;} */theta=1000.0;for(j=1;j<m;j++){ if(tp[j]>0.01)if (theta>tb[j]/tp[j]){ theta=tb[j]/tp[j]; mini=j;}}/* printf("LLL=%d Theta=%f\n",mini,theta); */l=mini;lk=tp[l];jj[l]=k;printf("*********************************\n"); /* getchar();*/for(i=0;i<m;i++)for(j=0;j<m;j++)e[i][j]=0.0;for(i=1;i<m;i++) e[i][i]=1.0;for(i=1;i<m;i++)e[i][l]=(-1)*tp[i]/lk;e[l][l]=1.0/lk;for(i=1;i<m;i++){ for(j=1;j<m;j++)printf("%6.1f",e[i][j]);printf("\n"); }/* for(j=1;j<m;j++)printf("%6.1f",tp[j]); printf("\n");*/for(i=1;i<m;i++)for(j=1;j<m;j++){ t[i][j]=0.0;for(r=1;r<m;r++)t[i][j]+=e[i][r]*b[r][j];}for(i=1;i<m;i++){ for(j=1;j<m;j++){ b[i][j]=t[i][j];printf("%6.1f",b[i][j]);}printf(" x%d\n",jj[i]);}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d MAXcj=%f\n",k,maxcj);} /*while--end*/for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }z=0.0;for(i=1;i<m;i++){ cb[i]=a[0][jj[i]];printf(" x%d=%6.1f\n",jj[i],tb[i]);z+=tb[i]*cb[i];}printf(" Max_z=%5.1f THE_count=%d\n",z,count);}/*p47---6(3)*/#include "math.h"#include "stdio.h"main(){int i,j,r,k,l,jj[4],m,n,maxjj,mini,count=0;floatb[4][4],e[4][4],t[4][4],y[4],maxcj,tb[4],tp[4],cb[4],cj[8],theta,lk,z; floata[4][7]={{0,-4,-1,0,0,-1000,-1000},{3,3,1,0,0,1,0},{6,4,3,-1,0,0,1}, {4,1,2,0,1,0,0}};m=4;n=7;jj[1]=5;jj[2]=6;jj[3]=4;for(i=0;i<m;i++)for(j=0;j<m;j++)b[i][j]=0.0;for(i=1;i<m;i++) b[i][i]=1.0;printf("*********************************\n");for(i=0;i<m;i++){ for(j=0;j<n;j++)printf("%6.1f",a[i][j]);printf("\n");}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d\n",k);while(maxcj>0.001){ count++;for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }for(i=1;i<m;i++){ tp[i]=0.0;for(r=1;r<m;r++)tp[i]+=b[i][r]*a[r][k]; }/*for(i=1;i<m;i++)printf("%6.1f",tb[i]);for(i=1;i<m;i++)printf("%6.1f",tp[i]);printf("tb--tp\n"); */theta=1000.0;for(j=1;j<m;j++){ if(tp[j]>0.01)if (theta>tb[j]/tp[j]){ theta=tb[j]/tp[j]; mini=j;}}/* printf("LLL=%d Theta=%f\n",mini,theta); */l=mini;lk=tp[l];jj[l]=k;printf("*********************************\n"); /* getchar();*/for(i=0;i<m;i++)for(j=0;j<m;j++)e[i][j]=0.0;for(i=1;i<m;i++) e[i][i]=1.0;for(i=1;i<m;i++)e[i][l]=(-1)*tp[i]/lk;e[l][l]=1.0/lk;for(i=1;i<m;i++){ for(j=1;j<m;j++)printf("%6.1f",e[i][j]);printf("\n"); }/* for(j=1;j<m;j++)printf("%6.1f",tp[j]); printf("\n");*/for(i=1;i<m;i++)for(j=1;j<m;j++){ t[i][j]=0.0;for(r=1;r<m;r++)t[i][j]+=e[i][r]*b[r][j];}for(i=1;i<m;i++){ for(j=1;j<m;j++){ b[i][j]=t[i][j];printf("%6.1f",b[i][j]);}printf(" x%d\n",jj[i]);}for(i=1;i<m;i++) cb[i]=a[0][jj[i]];for(j=1;j<m;j++){ y[j]=0.0;for(i=1;i<m;i++) y[j]+=cb[i]*b[i][j]; }for(j=1;j<n;j++){for(r=1;r<m;r++)if(jj[r]==j){cj[j]=0.0;break; }cj[j]=a[0][j];for(i=1;i<m;i++) cj[j]=cj[j]-y[i]*a[i][j];}maxcj=cj[1]; maxjj=1;for(j=2;j<n;j++)if(maxcj<cj[j]){ maxcj=cj[j]; maxjj=j;}k=maxjj;for(j=1;j<n;j++)printf("%6.1f",cj[j]);printf(" k=%d MAXcj=%f\n",k,maxcj);} /*while--end*/for(i=1;i<m;i++){ tb[i]=0.0;for(r=1;r<m;r++)tb[i]+=b[i][r]*a[r][0]; }z=0.0;for(i=1;i<m;i++){ cb[i]=a[0][jj[i]];printf(" x%d=%6.1f\n",jj[i],tb[i]);z+=tb[i]*cb[i];}printf(" Max_z=%5.1f THE_count=%d\n",z,count);}。

完全数 C 语言程序
什么是完全数
完全数（Perfect Number），也称为完美数或完备数，是指一个数等于其因子（不包括自己）之和，例如6就是完全数，因为6的因子为1、2、3，而
1+2+3=6。

目前已知的完全数只有以下几个：6、28、496、8128、33550336等等。

程序设计
为了判断一个数是否为完全数，我们需要先求出这个数的因数，然后将其因数相加，最后判断相加的和是否等于这个数本身。

所以，我们的程序需要完成以下几个步骤：
1.输入目标整数n。

2.使用循环结构求出这个数n的因数，并存储在一个数组中。

3.对数组中存储的因数进行求和操作。

4.判断相加的和是否等于目标整数n本身。

5.输出结果。

代码如下：
```c #include <stdio.h>
int main(void) { int n, sum = 0, i, j, factors[100], count = 0;
// 输入目标整数
printf(\。

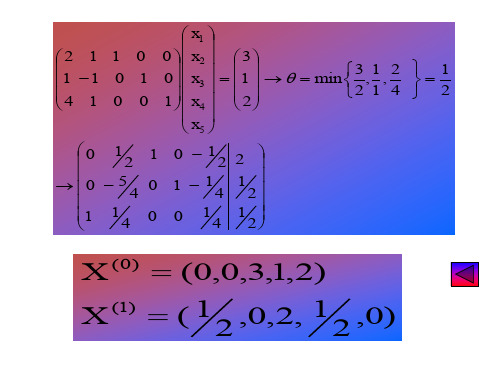
//单纯形法程序（C语言）#include<stdio.h>#include<math.h>#define m 4 /*定义约束条件方程组的个数*/#define n 6 /*定义未知量的个数*/float M=1000000.0;float A[m][n]; /*用于记录方程组的数目和系数;*/float C[n]; /*用于存储目标函数中各个变量的系数*/float b[m]; /*用于存储常约束条件中的常数*/float CB[m]; /*用于存储基变量的系数*/float seta[m]; /*存放出基与入基的变化情况*/float delta[n]; /*存储检验数矩阵*/float x[n]; /*存储决策变量*/int num[m]; /*用于存放出基与进基变量的情况*/float ZB=0; /*记录目标函数值*/void input();void print();int danchunxing1();int danchunxing2(int a);void danchunxing3(int a,int b);int danchunxing1() //把void改为int{int i,k=0;int flag=0;float max=0; //把min改为max，因为这里是求目标函数最大值for(i=0;i<n;i++)if(delta[i]<=0)flag=1;else {flag=0;break;}if(flag==1)return -1;for(i=0;i<n;i++){if(max<delta[i]) //把min>改为max<{max=delta[i];k=i;}}return k; //找到检验数最小的一列i}int danchunxing2(int a){int i,k,j;int flag=0;float min;k=a;for(i=0;i<m;i++)if(A[i][k]<=0)flag=1; //加上分号else {flag=0;break;}if(flag==1){printf("\n该线性规划无最优解!\n"); return -1;} for(i=0;i<m;i++){if(A[i][k]>0)seta[i]=b[i]/A[i][k];else seta[i]=M;}min=M;for(i=0;i<m;i++){if(min>=seta[i]){min=seta[i];j=i;}}num[j]=k+1;CB[j]=C[k];return j;}void danchunxing3(int p,int q){int i,j,c,l;float temp1,temp2,temp3;c=p;/*行号*/l=q;/*列号*/temp1=A[c][l];b[c]=b[c]/temp1;for(j=0;j<n;j++)A[c][j]=A[c][j]/temp1;for(i=0;i<m;i++){if(i!=c)if(A[i][l]!=0){temp2=A[i][l];b[i]=b[i]-b[c]*temp2;for(j=0;j<n;j++)A[i][j]=A[i][j]-A[c][j]*temp2;}}temp3=delta[l];for(i=0;i<n;i++)delta[i]=delta[i]-A[c][i]*temp3;}void print() //用于输出，每个数长度至少为8位且保留2位小数{int i,j=0;printf("\n--------------------------------------------------------------------------\n");for(i=0;i<m;i++){printf("%8.2f\tX(%d) %8.2f ",CB[i],num[i],b[i]);for(j=0;j<n;j++)printf("%8.2f ",A[i][j]);printf("\n");}printf("\n--------------------------------------------------------------------------\n");printf("\t\t\t");for(i=0;i<n;i++)printf(" %8.2f",delta[i]);printf("\n--------------------------------------------------------------------------\n");}void input() //用于输入线性规划问题，分为约束方程组的系数矩阵A[i][j]、初始基变量的数字代码num矩阵、方程组右端的常数矩阵b[i]、目标函数的系矩阵C[i]{ //加上花括号int i,j; /*循环变量*/int k;printf("请输入方程组的系数矩阵A(%d行%d列):\n",m,n);for(i=0;i<m;i++)for(j=0;j<n;j++)scanf("%f",&A[i][j]);printf("\n请输入初始基变量的数字代码num矩阵:\n");for(i=0;i<m;i++)scanf("%d",&num[i]);printf("\n请输入方程组右边的值矩阵b:\n");for(i=0;i<m;i++)scanf("%f",&b[i]);printf("\n请输入目标函数各个变量的系数所构成的系数阵C:\n");for(i=0;i<n;i++)scanf("%f",&C[i]);for(i=0;i<n;i++)delta[i]=C[i];for(i=0;i<m;i++){k=num[i]-1;CB[i]=C[k];}}main() //程序运行的起点{int i,j=0;int p,q,temp;input();printf("\n--------------------------------------------------------------------------\n"); printf(" \tCB\tXB\tb\t");for(i=0;i<n;i++)printf(" X(%d)\t",i+1);for(i=0;i<n;i++)x[i]=0;printf("\n");while(1){q=danchunxing1();if(q==-1){print();printf("\n所得解已经是最优解!\n");printf("\n最优解为:\n");for(j=0;j<m;j++){temp=num[j]-1;x[temp]=b[j];}for(i=0;i<n;i++){printf("x%d=%.2f ",i+1,x[i]); //输出最优解ZB=ZB+x[i]*C[i]; //计算最优解对应的目标函数值}printf("ZB=%.2f",ZB); //输出目标函数最大值ZB，保留两位小数break;}print();p=danchunxing2(q);printf("\np=%d,q=%d",p,q);if(q==-1) break;danchunxing3(p,q);}}。

完全数C语言程序1. 什么是完全数完全数是一个非常有趣的数学概念。

在数论中，一个数如果等于其他所有因子（包括1但不包括自身）之和，那么我们称它为完全数。

例如，6是一个完全数，因为它的因子是1、2、3，而1+2+3=6。

另一个例子是28，它的因子是1、2、4、7、14，而1+2+4+7+14=28。

2. 完全数的历史完全数的概念可以追溯到古代。

在中国，完全数被称为“完美数”，在希腊和罗马文化中被称为“完全数”。

早在公元前300年，欧几里得就在他的著作《几何原本》中提到了完全数的概念。

数学家们对完全数的研究一直延续至今，尽管如今我们已经发现的完全数非常有限。

3. 完全数的特性完全数具有一些非常有趣的特性，我们在下面的内容中将逐一介绍。

3.1 完全数的因子如前所述，完全数的因子是它本身之外的所有正因子（即能整除它的正整数）。

以6为例，它的因子是1、2、3，这三个数之和正好等于6。

找出完全数的因子是判断一个数是否是完全数的第一步。

3.2 完全数的奇偶性经过观察可以发现，所有已知的完全数都是偶数。

这是因为如果一个数是完全数，那么它的因子必定是成对出现的。

例如，如果2是一个完全数的因子，那么n2也是该完全数的因子。

假设这些因子按照从小到大的顺序排列，那么第一个因子和最后一个因子的乘积一定等于该完全数。

因此，完全数的因子必定可以配对，而配对的因子一定是一个奇数乘以一个偶数，因此完全数必定是偶数。

3.3 完全数的稀少性迄今为止，我们只知道很少的完全数。

根据目前已知的情况，前几个完全数是6、28、496、8128和33550336。

然而，数学家们认为完全数的数量非常有限，可能只有有限多个。

目前还没有找到一个奇完全数（一个奇数作为完全数），也还没有找到一个大于33550336的完全数。

寻找新的完全数一直是数学界的一个挑战。

4. 用C语言编写完全数的程序既然我们已经了解了完全数的一些基本概念和特性，现在让我们看看如何用C语言编写一个程序来找到完全数。

单纯形法C++实现使⽤单纯型法来求解线性规划，输⼊单纯型法的松弛形式，是⼀个⼤矩阵，第⼀⾏为⽬标函数的系数，且最后⼀个数字为当前轴值下的 z 值。

下⾯每⼀⾏代表⼀个约束，数字代表系数每⾏最后⼀个数字代表 b 值。

算法和使⽤单纯性表求解线性规划相同。

对于线性规划问题：Max x1 + 14* x2 + 6*x3s . t . x1 + x2 + x3 <= 4 x1<= 2 x3 <= 3 3*x2 + x3 <= 6 x1,x2,x3 >= 0我们可以得到其松弛形式：Max x1 + 14*x2 + 6*x3s.t. x1 + x2 + x3 + x4 = 4 x1 + x5 = 2 x3 + x6 = 3 3*x2 + x3 + x7 = 6 x1 , x2 , x3 , x4 , x5 , x6 , x7 ≥ 0我们可以构造单纯性表，其中最后⼀⾏打星的列为轴值。

单纯性表x1x2x3x4x5x6x7bc1=1c2=14c3=6c4=0c5=0c6=0c7=0-z=011110004100010020010010303100016****在单纯性表中，我们发现⾮轴值的x上的系数⼤于零，因此可以通过增加这些个x的值，来使⽬标函数增加。

我们可以贪⼼的选择最⼤的c，再上⾯的例⼦中我们选择c2作为新的轴，加⼊轴集合中，那么谁该出轴呢？其实我们由于每个x都⼤于零，对于x2它的增加是有所限制的，如果x2过⼤，由于其他的限制条件，就会使得其他的x⼩于零，于是我们应该让x2⼀直增⼤，直到有⼀个其他的x刚好等于0为⽌，那么这个x就被换出轴。

我们可以发现，对于约束⽅程1，即第⼀⾏约束，x2最⼤可以为4（4/1），对于约束⽅程4，x2最⼤可以为3(6/3），因此x2最⼤只能为他们之间最⼩的那个，这样才能保证每个x都⼤于零。

因此使⽤第4⾏，来对各⾏进⾏⾼斯⾏变换，使得⼆列第四⾏中的每个x都变成零，也包括c2。

线性规划问题的单纯形法程序程序设计人员 ：闫 保 （20010674010）专业 ：应用数学数学模型 ： max z = ∑=nj jj x c 1St. ⎪⎩⎪⎨⎧≥≤∑=01jnj i ij x b a (i=1,..,m) (j=1,….,n) 标准形： max z = si m i n j j j x x c ∑∑==+110=∑+=mn j j j x c 1 St. ⎪⎩⎪⎨⎧≥=+∑=01j i si nj j ij x b x x a (i=1,…..,m) (j=1,…..,n+m)使用说明： 本程序只适用于求解上面的模型。

输入数据时输入化为标准型后的参数。

程序（除start()函数外）是针对所有的约束情形（≤,=,,≥）b i 设计的。

在start()函数中，由于初始基可行解时没对人工变量加以标注的代码段（声明A ）。

程序不适用于求解需用大M 法解的规划问题（=,,≥）b i 。

若要求解带有人工变量的线性规划问题还有待修改。

程序应用实例：max z= 2x 1+x 2S.T ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,524261552121212x x x x x x xn=5 m=3 c[n]={2,1,0,0,0} b[m]={15,24,5}a[m][n]={{0,5,1,0,0},{6,2,0,1,0},{1,1,0,0,1}, }程序流程图：（单纯形法计算步骤的框图）程序#include<string.h>#include<stdio.h>#define N 10 /*定义最大列维数* /#define M 10 /*定义最大行维数*/typedef struct Xappearance{int base; /*base=-1：代表变量x不是基。

Base=0,1...m-1：代表变量x是基，且第base 个分量是1*/int man; /*变量x是否是人工变量。

// 彻底终结单纯形法.cpp : Defines the entry point for the console application.#include "stdafx.h"#include<math.h>#include<iostream>using namespace std;float fcsz[100][100],d[100][100],x[100]; /* 记录总方程的数组,存放B-1矩阵，解的数组*/ int a[100],q=1; /* 记录基础、非基础的解的情况：0为非基础；1为基础，q为条件判断*/float bb[100]; /* 存放资源数量bi*/int m,n,s,type; /* 方程变量,约束数,所有变量个数之和，求最大最小值的类型：0为最小；1为最大*/int sybl,scbl,rgbl; /* 剩余变量,松弛变量,人工变量*/void Jckxj() /* 基础可行解*/{int i,j;for(i=0;i<n;i++)for(j=0;j<s;j++)if(fcsz[i][j]==1&&a[j]==1){x[j]=fcsz[i][s];j=s;}for(i=0;i<s;i++)if(a[i]==0) x[i]=0;}int Rj() /*判断是否为基础的解的情况：0为非基础；1为基础*/ {int i;for(i=0;i<s;i++)if(fabs(fcsz[n][i])>=0.000001)if(fcsz[n][i]<0)return 0;return 1;}int Min() /*寻找入基变量*/{int i,temp=0;float min=fcsz[n][0];for(i=1;i<s;i++)if(min>fcsz[n][i]){min=fcsz[n][i];temp=i;}return temp;}void JustArtificial() /*判断人工变量*/{int i;for(i=m+sybl+scbl;i<s;i++)if(fabs(x[i])>=0.000001){printf("无可行解\n");return;}}int Check(int in) /* 判断无界情况*/{int i;float max1=-1;for(i=0;i<n;i++)if(fabs(fcsz[i][in])>=0.000001&&max1<fcsz[i][s]/fcsz[i][in])max1=fcsz[i][s]/fcsz[i][in];if(max1<0)return 1;return 0;}int SearchOut(int *temp,int in) /*寻找出基变量*/{int i;float min=10000;for(i=0;i<n;i++)if(fabs(fcsz[i][in])>=0.000001&&(fcsz[i][s]/fcsz[i][in]>=0)&&min>fcsz[i][s]/fcsz[i][in]){min=fcsz[i][s]/fcsz[i][in];*temp=i;}for(i=0;i<s;i++)if(a[i]==1&&fcsz[*temp][i]==1)return i;}void Mto(int in,int temp) /* 主元化1 */{int i;for(i=0;i<=s;i++)if(i!=in)fcsz[temp][i]=fcsz[temp][i]/fcsz[temp][in];fcsz[temp][in]=1;}void Be(int temp,int in) /* 初等变换*/ {int i,j;float c;for(i=0;i<=n;i++){c=fcsz[i][in]/fcsz[temp][in];if(i!=temp)for(j=0;j<=s;j++)fcsz[i][j]=fcsz[i][j]-fcsz[temp][j]*c;}}void Achange(int in,int out) /* 改变a[]的值*/ {int temp=a[in];a[in]=a[out];a[out]=temp;}void Print() /* 打印*/{int i,j,k,temp=0;for(i=0;i<n;i++){for(k=temp;k<s;k++)if(a[k]==1){printf("X%d ",k+1);temp=k+1;k=s;}for(j=0;j<=s;j++)printf("%8.2f",fcsz[i][j]);printf("\n");}printf("检");for(j=0;j<=s;j++)printf("%8.2f",-fcsz[n][j]);printf("\n");}void cshprint() /* 初始化打印*/{int i;printf("XB");for(i=0;i<s;i++)printf(" X%d",i+1);printf(" b\n");Print();printf("\n");}void Result() /*打印每次变化后的单纯形表*/ {int i;printf("X=(");for(i=0;i<s;i++)printf("%8.2f",x[i]);printf(" )");if(type==1)printf(" Zmax=%f\n\n",fcsz[n][s]);elseprintf(" Zmin=%f\n\n",fcsz[n][s]);}void PrintResult() /* 打印最后结果*/ {int i,j;for(j=0;j<=s;j++){if(a[j]==0 && -fcsz[n][j]==0){printf("有无穷多最优解\n");q=5;break;}}if(q!=5){printf("有唯一最优解\n");}printf("最优解为(");for(i=0;i<s;i++)printf("%8.2f",x[i]);printf(" )\n");if(type==0)printf("最优值为%f\n",-fcsz[n][s]);elseprintf("最优值为%f\n",fcsz[n][s]);for(i=0;i<n;i++) /*求B-1矩阵并打印*/{for(j=s-n+1;j<=s;j++)d[i][j+n-s-1]=fcsz[i][j-1];}printf("矩阵B-1为\n");for(i=0;i<n;i++){for(j=0;j<n;j++)printf("%8.2f",d[i][j]);printf("\n");}}void Merge(float sy[][100],float sc[][100],float rg[][100],float b[]) /* 合并*/ {int i,j;for(i=0;i<n;i++){for(j=m;j<m+sybl;j++)if(sy[i][j-m]!=-1)fcsz[i][j]=0;elsefcsz[i][j]=-1;for(j=m+sybl;j<m+sybl+scbl;j++)if(sc[i][j-m-sybl]!=1)fcsz[i][j]=0;elsefcsz[i][j]=1;for(j=m+sybl+scbl;j<s;j++)if(rg[i][j-m-sybl-scbl]!=1)fcsz[i][j]=0;elsefcsz[i][j]=1;fcsz[i][s]=b[i];}for(i=m;i<m+sybl+scbl;i++)fcsz[n][i]=0;for(i=m+sybl+scbl;i<s;i++)fcsz[n][i]=100;fcsz[n][s]=0;}void ProcessA() /* 初始化a[] */{int i;for(i=0;i<m+sybl;i++)a[i]=0;for(i=m+sybl;i<s;i++)a[i]=1;}void Input(float b[],int code[]){int i=0,j=0;printf("输入变量个数和约束条件个数\n"); /* 输入变量个数和约束数*/cin>>m>>n;for(i=0;i<n;i++){printf("输入第%d约束条件右边的值和约束类型（0为<= ；1为= ；2为>=）\n",i+1); /* 输入约束条件右边的值,code的值*/cin>>b[i]>>code[i];bb[i]=b[i];printf("输入第%d约束条件系数\n",i+1);for(j=0;j<m;j++)cin>>fcsz[i][j]; /* 输入约束条件*/}printf("输入求最大值还是最小值（0为Min ；1为Max ）\n"); /* 输入求最大值还是最小值*/do{cin>>type;if(type!=0&&type!=1)printf("输入错误\n");}while(type!=0&&type!=1);printf("输入Z的各个系数\n"); /* 输入z*/for(i=0;i<m;i++)cin>>fcsz[n][i];if(type==1)for(i=0;i<m;i++)fcsz[n][i]=-fcsz[n][i];}void Xartificial() /* 消去人工变量*/{int i,j,k;if(rgbl!=0){for(i=m+sybl+scbl;i<s;i++){for(j=0;j<n;j++)if(fcsz[j][i]==1){for(k=0;k<=s;k++)fcsz[n][k]=fcsz[n][k]-fcsz[j][k]*100;j=n;}}}}void Process(float c[][100],int row,int vol) /* 初始化c[][100] */ {int i;for(i=0;i<n;i++)if(i!=row)c[i][vol]=0;}void standardize(float b[],int code[]) /* 化标准型*/{int i;float sy[100][100],sc[100][100],rg[100][100]; /* 剩余变量数组,松弛变量数组,人工变量数组*/sybl=scbl=rgbl=0;for(i=0;i<n;i++){if(code[i]==0){sc[i][scbl++]=1; Process(sc,i,scbl-1);}if(code[i]==1){rg[i][rgbl++]=1; Process(rg,i,rgbl-1);}if(code[i]==2){rg[i][rgbl++]=1;sy[i][sybl++]=-1;Process(rg,i,rgbl-1);Process(sy,i,sybl-1);}}s=sybl+scbl+rgbl+m;Merge(sy,sc,rg,b); /* 合并*/ProcessA(); /* 初始化a[] */cshprint(); /* 初始化打印*/Xartificial(); /* 消去人工变量*/}void simple() /* 单纯型算法*/{int in,out,temp=0;while(1){Jckxj(); /* 基础可行解*/Print(); /* 打印*/Result(); /* 打印结果*/if(!Rj())in=Min(); /* 求换入基*/else{if(rgbl!=0) JustArtificial(); /* 判断人工变量*/PrintResult(); /* 打印最后结果*/return;}if(Check(in)){ /* 判断无界情况*/printf("无界解\n");return;}out=SearchOut(&temp,in); /* 求换出基*/Mto(in,temp); /* 主元化1 */Be(temp,in); /* 初等变换*/Achange(in,out); /* 改变a[]的值*/ }}void lmdfx(){float c[100][100];int i,j;for(i=0;i<n;i++){for(j=0;j<n;j++)c[i][j]=(fcsz[j][s]-d[j][i]*bb[i])/d[j][i];}printf("资源数量bi的变化范围:如有#不考虑此数\n");for(i=0;i<n;i++){printf("b%d",i+1);{for(j=0;j<n;j++)if(d[j][i]>=0){printf(">=%f",-c[i][j]);printf("\n");}else{printf("<=%f",-c[i][j]);printf("\n");}}}}void main(){int code[100]; /* 输入符号标记*/ float b[100]; /* 方程右值*/Input(b,code); /* 初始化*/standardize(b,code); /* 化标准型*/simple(); /* 单纯型算法*/lmdfx(); /*灵敏度分析*/}。