2018年北师大版九年级数学 《反比例函数的图象》同步练习

6.2《反比例函数的图象与性质》同步练习卷一．选择题1．若反比例函数的图象经过（2，﹣2），（m，1），则m＝（）A．1B．﹣1C．4D．﹣42．已知点A（1，2）在反比例函数y＝的图象上，则该反比例函数的解析式是（）A．y＝B．y＝C．y＝D．y＝2x3．反比例函数y＝（k为常数）的图象位于（）A．第一、二象限B．第一、三象限C．第二、四象限D．第三、四象限4．关于反比例函数y＝﹣，下列说法正确的是（）A．图象过（1，2）点B．图象在第一、三象限C．当x＞0时，y随x的增大而减小D．当x＜0时，y随x的增大而增大5．函数y＝ax﹣a与y＝（a≠0）在同一直角坐标系中的图象可能是（）A．B．C．D．6．若点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y＝﹣图象上的点，并且y1＜0＜y2＜y3，则下列各式中正确的是（）A．x1＜x2＜x3B．x1＜x3＜x2C．x2＜x1＜x3D．x2＜x3＜x1 7．如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝（k≠0，x＞0）的图象同时经过顶点C，D．若点C的横坐标为5，BE＝3DE，则k的值为（）A．B．3C．D．58．如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数的图象上．若点A的坐标为（﹣2，﹣2），则k的值为（）A．1B．﹣3C．4D．1或﹣39．如图，正比例函数y1＝k1x的图象与反比例函数y2＝的图象相交于A，B两点，其中点A的横坐标为2，当y1＜y2时，x的取值范围是（）A．x＜﹣2或x＞2B．x＜﹣2或0＜x＜2C．﹣2＜x＜0或0＜x＜2D．﹣2＜x＜0或x＞210．已知反比例函数y＝﹣，下列结论：①图象必经过（﹣2，4）；②图象在二，四象限内；③y随x的增大而增大；④当x＞﹣1时，则y＞8．其中错误的结论有（）个A．3B．2C．1D．011．如图，反比例函数的图象经过点A（2，1），若y≤1，则x的范围为（）A．x≥1B．x≥2C．x＜0或0＜x≤1D．x＜0或x≥2 12．如图，过点A（4，5）分别作x轴、y轴的平行线，交直线y＝﹣x+6于B、C两点，若函数y＝（x＞0）的图象△ABC的边有公共点，则k的取值范围是（）A．5≤k≤20B．8≤k≤20C．5≤k≤8D．9≤k≤20二．填空题13．若反比例函数的图象经过第一、三象限，则k的取值范围是．14．已知反比例函数y＝，当x＞0时，y随x增大而减小，则m的取值范围是．15．如图，一次函数y1＝﹣x﹣1与反比例函数y2＝﹣的图象交于点A（﹣2，1），B（1，﹣2），则使y1＞y2的x的取值范围是．16．如图，在平面直角坐标系中，函数y＝（k＞0，x＞0）的图象与等边三角形OAB的边OA，AB分别交于点M，N，且OM＝2MA，若AB＝3，那么点N的横坐标为．17．如图，在平面直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数y＝（k≠0，x＞0）的图象过点B，E．若AB＝2，则k的值为．18．如图，直线y1＝﹣x与双曲线y＝交于A，B两点，点C在x轴上，连接AC，BC．若∠ACB＝90°，△ABC的面积为10，则k的值是．19．如图，曲线AB是抛物线y＝﹣4x2+8x+1的一部分（其中A是抛物线与y轴的交点，B 是顶点），曲线BC是双曲线y＝（k≠0）的一部分．曲线AB与BC组成图形W．由点C开始不断重复图形W形成一组“波浪线”．若点P（2020，m），Q（x，n），在该“波浪线”上，则m的值为，n的最大值为．三．解答题20．下表给出了两个变量x，y的部分对应值．x…0.51 1.523468…y…126432 1.510.75…（1）以表中x的值为横坐标，对应的y的值为纵坐标，在给出的平面直角坐标系中描点；（2）选用一个你学过的函数来描述两个变量x，y之间的关系，并确定其函数表达式．21．如图，一次函数y＝k1x+b的图象与反比例函数y＝的图象相交于A、B两点，其中点A的坐标为（﹣1，4），点B的坐标为（4，n）．（1）根据图象，直接写出满足k1x+b＞的x的取值范围；（2）求这两个函数的表达式；（3）点P在线段AB上，且S△AOP：S△BOP＝1：2，求点P的坐标．22．已知反比例函数y＝，（k为常数，k≠1）．（1）若点A（1，2）在这个函数的图象上，求k的值；（2）若在这个函数图象的每一分支上，y随x的增大而增大，求k的取值范围；（3）若k＝13，试判断点B（3，4），C（2，5）是否在这个函数的图象上，并说明理由．23．如图，在△ABC中，AC＝BC，AB⊥x轴，垂足为A．反比例函数y＝（x＞0）的图象经过点C，交AB于点D．已知AB＝4，BC＝．（1）若OA＝4，求k的值；（2）连接OC，若BD＝BC，求OC的长．24．如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO＝90°，∠AOB＝30°，OB＝2，反比例函数y＝（x＞0）的图象经过OA的中点C，交AB于点D．（1）求反比例函数的关系式；（2）连接CD，求四边形CDBO的面积．参考答案一．选择题1．解：设反比例函数解析式y＝，将（2，﹣2）代入得﹣2＝，∴k＝﹣4，即函数解析式为y＝﹣，将（m，1）代入解析式得1＝﹣，∴m＝﹣4．故选：D．2．解：∵点A（1，2）在反比例函数y＝的图象上，∴2＝，∴k＝2，则这个反比例函数的解析式是y＝．故选：C．3．解：∵k2+1≥1＞0，∴反比例函数y＝（k为常数）的图象位于第一、三象限．故选：B．4．解：∵k＝﹣2＜0，所以函数图象位于二四象限，在每一象限内y随x的增大而增大，图象是轴对称图象，故A、B、C错误．故选：D．5．解：A、从反比例函数图象得a＞0，则对应的一次函数y＝ax﹣a图象经过第一、三、四象限，所以A选项错误；B、从反比例函数图象得a＞0，则对应的一次函数y＝ax﹣a图象经过第一、三、四象限，所以B选项错误；C、从反比例函数图象得a＜0，则对应的一次函数y＝ax﹣a图象经过第一、二、四象限，所以C选项错误；D、从反比例函数图象得a＜0，则对应的一次函数y＝ax﹣a图象经过第一、二、四象限，所以D选项正确．故选：D．6．解：∵反比例函数y＝﹣中k＝﹣1＜0，∴此函数的图象在二、四象限，且在每一象限内y随x的增大而增大，∵y1＜0＜y2＜y3，∴点（x1，y1）在第四象限，（x2，y2）、（x3，y3）两点均在第二象限，∴x2＜x3＜x1．故选：D．7．解：过点D做DF⊥BC于F由已知，BC＝5∵四边形ABCD是菱形∴DC＝5∵BE＝3DE∴设DE＝x，则BE＝3x∴DF＝3x，BF＝x，FC＝5﹣x在Rt△DFC中，DF2+FC2＝DC2∴（3x）2+（5﹣x）2＝52∴解得x＝1∴DE＝1，FD＝3设OB＝a则点D坐标为（1，a+3），点C坐标为（5，a）∵点D、C在双曲线上∴1×（a+3）＝5a∴a＝∴点C坐标为（5，）∴k＝故选：C．8．解：设C（x，y）．∵四边形ABCD是矩形，点A的坐标为（﹣2，﹣2），∴B（﹣2，y）、D（x，﹣2）；∵矩形ABCD的对角线BD经过坐标原点，∴设直线BD的函数关系式为：y＝kx，∵B（﹣2，y）、D（x，﹣2），∴k＝，k＝，∴＝，即xy＝4；①又∵点C在反比例函数的图象上，∴xy＝k2+2k+1，②由①②，得k2+2k﹣3＝0，即（k﹣1）（k+3）＝0，∴k＝1或k＝﹣3，故选：D．9．解：∵正比例函数y1＝k1x的图象与反比例函数y2＝的图象相交于A、B两点，∴A，B两点坐标关于原点对称，∵点A的横坐标为2，∴B点的横坐标为﹣2，∵y1＜y2∴在第一和第三象限，正比例函数y1＝k1x的图象在反比例函数y2＝的图象的下方，∴x＜﹣2或0＜x＜2，故选：B．10．解：①当x＝﹣2时，y＝4，即图象必经过点（﹣2，4），正确；②k＝﹣8＜0，图象在第二、四象限内，正确；③k＝﹣8＜0，每一象限内，y随x的增大而增大，错误；④k＝﹣8＜0，每一象限内，y随x的增大而增大，若0＞x＞﹣1，y＞8，x＞0时，y＜8，故④错误，故选：B．11．解：在第一象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为x≥2；在第三象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为x＜0．故选：D．12．解：∵过点A（4，5）分别作x轴、y轴的平行线，交直线y＝﹣x+6于B、C两点，∴点B的纵坐标为5，点C的横坐标为4，将y＝5代入y＝﹣x+6，得x＝1；将x＝4代入y＝﹣x+6得，y＝2，∴点B的坐标为（1，5），点C的坐标为（4，2），∵函数y＝（x＞0）的图象与△ABC的边有公共点，点A（4，5），点B（1，5），∴1×5≤k≤4×5即5≤k≤20，故选：A．二．填空题13．解：∵反比例函数的图象经过第一、三象限，∴1﹣3k≥0，解得k＜．故答案为：k＜．14．解：∵反比例函数y＝，当x＞0时，y随x增大而减小，∴m﹣2＞0，解得：m＞2．故答案为：m＞2．15．解：使y1＞y2的x的取值范围是点A左侧和点B的左侧到y轴之间部分，所以x＜﹣2或0＜x＜1．故答案为：x＜﹣2或0＜x＜1．16．解：过点N、M分别作NC⊥OB，MD⊥OB，垂足为C、D，∵△AOB是等边三角形，∴AB＝OA＝OB＝3，∠AOB＝60°∵又OM＝2MA，∴OM＝2，MA＝1，在Rt△MOD中，OD＝OM＝1，MD＝，∴M（1，）；∴反比例函数的关系式为：y＝，设OC＝a，则BC＝3﹣a，NC＝，在Rt△BCN中，NC＝BC，∴＝（3﹣a），解得：x＝，x＝（舍去）故答案为：，17．解：设E（x，x），∴B（2，x+2），∵反比例函数y＝（k≠0，x＞0）的图象过点B、E．∴x2＝2（x+2），解得x1＝1+，x2＝1﹣（舍去），∴k＝x2＝6+2，故答案为6+2．18．解：设点A为（a，﹣a），则OA＝＝﹣a，∵点C为x轴上一点，∠ACB＝90°，且△ACB的面积为10，∴OA＝OB＝OC＝﹣a，∴S△ACB＝×OC×（A y+|B y|）＝×（﹣a）×（﹣a）＝10，解得，a＝﹣或（舍弃），∴点A为（﹣，2），∴k＝﹣×2＝﹣6，故答案为﹣6．19．解：∵y＝﹣4x2+8x+1＝﹣4（x﹣1）2+5，∴当x＝0时，y＝1，∴点A的坐标为（0，1），点B的坐标为（1，5），∵点B（1，5）在y＝的图象上，∴k＝5，∵点C在y＝的图象上，点C的横坐标为5，∴点C的纵坐标是1，∴点C的坐标为（5，1），∵2020÷5＝404，∴P（2020，m）在抛物线y＝﹣4x2+8x+1的图象上，m＝﹣4×0+8×0+1＝1，∵点Q（x，n）在该“波浪线”上，∴n的最大值是5，故答案为：1，5．三．解答题20．解：（1）如右图所示；（2）观察这些点的排列规律，可用反比例函数描述两个变量x、y之间的关系，设y＝，∵当x＝1时，y＝6，∴6＝，得k＝6，∴函数表达式为y＝．21．解：（1）∵点A的坐标为（﹣1，4），点B的坐标为（4，n）．由图象可得：k1x+b＞的x的取值范围是x＜﹣1或0＜x＜4；（2）∵反比例函数y＝的图象过点A（﹣1，4），B（4，n）∴k2＝﹣1×4＝﹣4，k2＝4n∴n＝﹣1∴B（4，﹣1）∵一次函数y＝k1x+b的图象过点A，点B∴，解得：k1＝﹣1，b＝3∴直线解析式y＝﹣x+3，反比例函数的解析式为y＝﹣；（3）设直线AB与y轴的交点为C，∴C（0，3），∵S△AOC＝×3×1＝，∴S△AOB＝S△AOC+S△BOC＝×3×1+×4＝，∵S△AOP：S△BOP＝1：2，∴S△AOP＝×＝，∴S△COP＝﹣＝1，∴×3•x P＝1，∴x P＝，∵点P在线段AB上，∴y＝﹣+3＝，∴P（，）．22．解：（1）∵点A（1，2）在这个函数的图象上，∴k﹣1＝1×2，解得k＝3；（2）∵在函数y＝图象的每一支上，y随x的增大而增大，∴k﹣1＜0，解得k＜1；（3）∵k＝13，有k﹣1＝12，∴反比例函数的解析式为y＝．将点B的坐标代入y＝，可知点B的坐标满足函数关系式，∴点B在函数y＝的图象上，将点C的坐标代入y＝，由5≠，可知点C的坐标不满足函数关系式，∴点C不在函数y＝的图象上．23．解：（1）作CE⊥AB，垂足为E，∵AC＝BC，AB＝4，∴AE＝BE＝2．在Rt△BCE中，BC＝，BE＝2，∴CE＝，∵OA＝4，∴C点的坐标为：（，2），∵点C在的图象上，∴k＝5，（2）设A点的坐标为（m，0），∵BD＝BC＝，∴AD＝，∴D，C两点的坐标分别为：（m，），（m﹣，2）．∵点C，D都在的图象上，∴m＝2（m﹣），∴m＝6，∴C点的坐标为：（，2），作CF⊥x轴，垂足为F，∴OF＝，CF＝2，在Rt△OFC中，OC2＝OF2+CF2，∴OC＝．24．解：（1）∵∠ABO＝90°，∠AOB＝30°，OB＝2，∴AB＝OB＝2，作CE⊥OB于E，∵∠ABO＝90°，∴CE∥AB，∴OC＝AC，∴OE＝BE＝OB＝，CE＝AB＝1，∴C（，1），∵反比例函数y＝（x＞0）的图象经过OA的中点C，∴1＝，∴k＝，∴反比例函数的关系式为y＝；（2）∵OB＝2，∴D的横坐标为2，代入y＝得，y＝，∴D（2，），∴BD＝，∵AB＝2，∴AD＝，∴S△ACD＝AD•BE＝××＝，∴S四边形CDBO＝S△AOB﹣S△ACD＝OB•AB﹣＝×2×2﹣＝．。

反比例函数的图象和性质同步练习一、选择题1、 函数x k y =的图象经过点（－4，6），则下列各点中在xk y =图象上的是（ ） A ．（3，8） B ．（3，－8） C ．（－8，－3） D ．（－4，－6） 2若直线y ＝kx ＋b 经过第一、二、四象限，则函数x kb y =的图象在（ ） （A ）第一、三象限 （B ）第二、四象限（C ）第三、四象限 （D ）第一、二象限3、反比例函数xy 1=的图象上有两点),(11y x A 、),(22y x B 且021<<x x ，那么1y 与2y 之间的大小关系为（ ）A 、21y y <B 、 21y y >C 、 21y y =D 、不能确定4、若点（－2，1y ）、（－1，2y ）、（2，3y ）在反比例函数xy 100-=的图象上，则（ ） A 、1y >2y >3y B 、2y >1y >3y C 、3y >1y >2y D 、3y >2y >1y5．下列图象中，是反比例函数的图象的是 （ ）6．在反比例函数y=k x（k<0）的图象上有两点A （x 1，y 1），B （x 2，y 2），且x 1>x 2>0，则y 1-y 2的值为 （ ）（A ）正数 （B ）负数 （C ）非正数 （D ）非负数 二、填空题7、函数4y x=的图象的两个分支在第 象限；在每个象限y 都随x 的增大而 . 8、函数4y x=-的图象的两个分支在第 象限；在每个象限y 都随x 的增大而 . 9、在反比例函xk y -=1的图象的每一条曲线上，y 都随x 的增大而增大，则k 的值是 10、设反比例函数y=3m x -的图象上有两点A （x 1，y 1）和B （x 2，y 2），且当x 1<0<x 2时，有y 1<y 2，则m 的取值范围是 ．11、已知反比例函数y=kx的图象如图所示，则k 0，在图象的每一支上， y值随x的增大而．12．已知反比例函数y=2kx-的图象在第一、三象限内，则k的值可是________（写出满足条件的一个k值即可）．13．在直角坐标系中，若一点的横坐标与纵坐标互为倒数，•则这点一定在函数图象上（填函数关系式）三、解答题14如图，已知正比例函数y=3x的图象与反比例函数kyx=的图象交于点A（1，m）和点B．求m的值和反比例函数的解析式．BA246---4- 2 6 --0 xy。

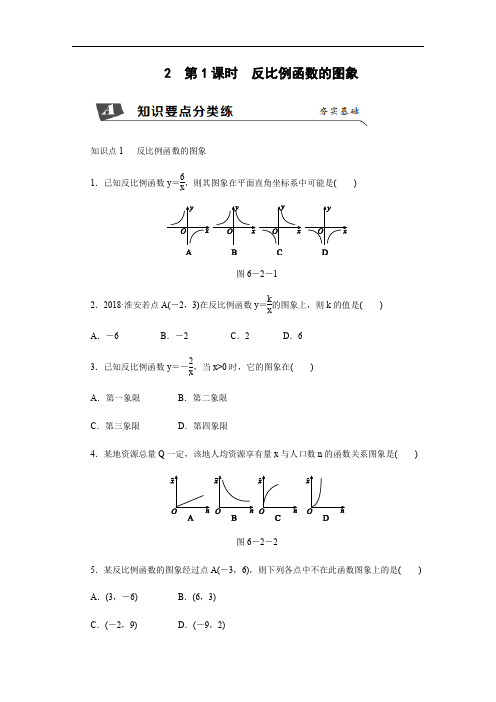
2 第1课时 反比例函数的图象知识点1 反比例函数的图象1．已知反比例函数y ＝6x，则其图象在平面直角坐标系中可能是( )图6－2－12．2018·淮安若点A(－2，3)在反比例函数y ＝kx 的图象上，则k 的值是( )A ．－6B ．－2C ．2D ．63．已知反比例函数y ＝－2x ，当x>0时，它的图象在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．某地资源总量Q 一定，该地人均资源享有量x 与人口数n 的函数关系图象是( )图6－2－25．某反比例函数的图象经过点A(－3，6)，则下列各点中不在此函数图象上的是( ) A ．(3，－6) B ．(6，3) C ．(－2，9)D ．(－9，2)6．2018·齐齐哈尔已知反比例函数y＝2－kx的图象在第一、三象限内，则k的值可以是________．(写出满足条件的一个k的值即可)7．在同一平面直角坐标系中，分别画出函数y＝3x与y＝－3x的图象．知识点2反比例函数图象的对称性8．如图6－2－3，边长为4的正方形ABCD的对称中心是坐标原点O，AB∥x轴，BC∥y轴，反比例函数y＝2x与y＝－2x的图象均与正方形ABCD的边相交，则图中阴影部分的面积是()图6－2－3A．2 B．4 C．6 D．89．2018·湖州如图6－2－4，已知直线y＝k1x(k1≠0)与反比例函数y＝k2x(k2≠0)的图象交于M，N两点．若点M的坐标是(1，2)，则点N的坐标是()图6－2－4 A．(－1，－2) B．(－1，2)C．(1，－2) D．(－2，－1)10．2018·怀化函数y＝kx－3与y＝kx(k≠0)在同一坐标系内的图象可能是()图6－2－511．2018·无锡已知点P(a，m)，Q(b，n)都在反比例函数y＝－2x的图象上，且a＜0＜b，则下列结论一定正确的是()A．m＋n＜0 B．m＋n＞0C．m＜n D．m＞n12．如图6－2－6，已知OA＝6，∠AOB＝30°，则经过点A的反比例函数的表达式为________．图6－2－613．如图6－2－7是三个反比例函数y＝k1x，y＝k2x，y＝k3x在x轴上方的图象，由此观察得到k1，k2，k3的大小关系为____________(用“<”连接)．图6－2－714．已知一个函数的图象与反比例函数y＝6x的图象关于x轴成轴对称，则该函数的表达式为________．15．已知一次函数y＝x＋1的图象与反比例函数y＝kx的图象都经过点A(a，2)．(1)求a的值及反比例函数的表达式；(2)判断点B(2 2，22)是否在该反比例函数的图象上，并说明理由．16．2018·柳州如图6－2－8，一次函数y ＝mx ＋b 的图象与反比例函数y ＝kx 的图象交于A(3，1)，B ⎝⎛⎭⎫－12，n 两点． (1)求该反比例函数的表达式； (2)求n 的值及该一次函数的表达式．图6－2－817．如图6－2－9，一次函数y＝kx＋b与反比例函数y＝mx的图象相交于A(1，4)，B(4，n)两点．(1)求反比例函数的表达式；(2)求一次函数的表达式；(3)P是x轴上的一个动点，求PA＋PB的值最小时点P的坐标．图6－2－9教师详解详析1．C2．A [解析] 将A (－2，3)代入反比例函数y ＝kx ，得k ＝－2×3＝－6，故选A.3．D [解析] ∵k ＝－2＜0， ∴其图象位于第二、四象限， ∴当x >0时，它的图象位于第四象限． 故选D. 4．B5．B [解析] k ＝－3×6＝－18.A ．3×(－6)＝－18，点(3，－6)在反比例函数图象上，不符合题意；B ．3×6＝18，点(6，3)不在反比例函数图象上，符合题意；C ．－2×9＝－18，点(－2，9)在反比例函数图象上，不符合题意；D ．－9×2＝－18，点(－9，2)在反比例函数图象上，不符合题意．故选B.6．1(答案不唯一，满足k <2即可) [解析] 因为反比例函数y ＝2－k x 的图象在第一、三象限内，所以2－k ＞0，故k ＜2，则满足条件的k 值可以为1.7．略 8．D9．A [解析] ∵直线y ＝k 1x (k 1≠0)与反比例函数y ＝k 2x (k 2≠0)的图象交于M ，N 两点，∴M ，N 两点关于原点对称．∵点M 的坐标是(1，2)，∴点N 的坐标是(－1，－2)．故选A.10．B [解析] ∵当k ＞0时，函数y ＝kx －3的图象经过第一、三、四象限，函数y ＝kx 的图象位于第一、三象限；当k ＜0时，函数y ＝kx －3的图象经过第二、三、四象限，函数y ＝kx 的图象位于第二、四象限，∴B 正确．11．D [解析] y ＝－2x 的k ＝－2＜0，图象位于第二、四象限．∵a ＜0，∴P (a ，m )在第二象限，∴m ＞0.∵b ＞0，∴Q (b ，n )在第四象限，∴n ＜0，∴n ＜0＜m ，即m ＞n ，故D 正确．12.y ＝9 3x [解析] 如图，过点A 作AC ⊥x 轴于点C .∵∠AOB ＝30°，∴AC ＝12OA .∵OA＝6，∴AC ＝3.在Rt △ACO 中，OC 2＝AO 2－AC 2，∴OC ＝3 3，∴点A 的坐标是(3 3，3)．设反比例函数的表达式为y ＝kx (k ≠0)．∵反比例函数的图象经过点A ，∴k ＝3×3 3＝9 3，∴反比例函数的表达式为y ＝9 3x.13．k 1＜k 2＜k 314．y ＝－6x [解析] 关于x 轴对称，横坐标不变，纵坐标互为相反数，即－y ＝6x ，则y＝－6x .故答案为：y ＝－6x.15．解：(1)∵一次函数y ＝x ＋1的图象经过点A (a ，2)， ∴2＝a ＋1，解得a ＝1.又∵反比例函数y ＝kx 的图象经过点A (1，2)，∴2＝k 1，∴k ＝2，∴y ＝2x.即a 的值为1，反比例函数的表达式为y ＝2x.(2)点B ⎝⎛⎭⎫2 2，22在该反比例函数的图象上． 理由：∵2 2×22＝2＝k ，∴点B ⎝⎛⎭⎫2 2，22在该反比例函数的图象上． 16．解：(1)∵反比例函数y ＝kx 的图象经过点A (3，1)，∴k ＝3×1＝3，∴反比例函数的表达式为y ＝3x.(2)把B ⎝⎛⎭⎫－12，n 代入反比例函数表达式，可得－12n ＝3，解得n ＝－6，∴B ⎝⎛⎭⎫－12，－6. 把A (3，1)，B ⎝⎛⎭⎫－12，－6代入一次函数y ＝mx ＋b ，可得⎩⎪⎨⎪⎧1＝3m ＋b ，－6＝－12m ＋b ，解得⎩⎪⎨⎪⎧m ＝2，b ＝－5，∴一次函数的表达式为y ＝2x －5.17．解：(1)∵点A (1，4)在反比例函数y ＝mx 的图象上，∴m ＝xy ＝4，∴反比例函数的表达式为y ＝4x .(2)把B (4，n )代入y ＝4x ，得n ＝44＝1，∴B (4，1)．∵一次函数y ＝kx ＋b 的图象经过点A (1，4)，B (4，1)，∴⎩⎪⎨⎪⎧4＝k ＋b ，1＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1，b ＝5. ∴一次函数的表达式为y ＝－x ＋5.(3)作点B 关于x 轴的对称点B ′，连接AB ′与x 轴交于点P ，此时P A ＋PB 的值最小． 点B 关于x 轴的对称点B ′的坐标为(4，－1)，设直线AB ′的函数表达式为y ＝ax ＋c ， 由⎩⎪⎨⎪⎧4＝a ＋c ，－1＝4a ＋c ，解得⎩⎨⎧a ＝－53，c ＝173.∴直线AB ′的函数表达式为y ＝－53x ＋173.令y ＝0，得x ＝175，∴当点P 的坐标为(175，0)时，P A ＋PB 的值最小．。

《反比例函数的图像及其性质》同步测试1. 当x >0时，函数y =－的图象在（）A.第四象限 B.第三象限 C.第二象限 D.第一象限2. 设点A （x 1,y 1）和B （x 2,y 2）是反比例函数y =图象上的两个点，当x 1＜x 2＜0时，y 1＜y 2，则一次函数y =-2x +k 的图象不经过的象限是（ ）A.第一象限B.第二象限C.第三象限D.第四象限3. 在同一直角坐标系中，函数和的图象大致是（ ）4. 已知反比例函数y =，当1<x <3时，y 的取值范围是()A.0<y <1 B.1<y <2 C.2<y <6 D.y >65. 若点A (a ,b )在反比例函数y =的图象上，则代数式ab -4的值为（ ）A.0B.-2C.2D.-66. 若反比例函数y=的图象位于第二、四象限，则k 的取值可能是( )A.0 B.2 C.3 D.47. 一个反比例函数图象过点A (2,3)，则这个反比例函数的表达式是________。

8．如果一个正比例函数的图象与反比例函数y =的图象交于A （x 1,y 1）、B （x 2,y 2）两点，那么（x 2-x 1）（y 2-y 1）的值为。

9. 如图，一次函数（为常数，且）的图象与反比例函数的图象交于，两点。

（1）求一次函数的表达式；（2）若将直线向下平移个单位长度后与反比例函数的图象有且只有一个公共点，求的值。

10. 如图，直线y=mx与双曲线相交于A，B两点，A点的坐标为（1，2）。

（1）求反比例函数的表达式；（2）根据图象直接写出当mx＞时，x的取值范围；（3）计算线段AB的长。

答案与解析1. A解析：因为函数y =－中k =-5＜0,所以其图象位于第二、四象限，当x ＞0时，其图象位于第四象限。

2. A解析：对于反比例函数，∵ x 1＜x 2＜0时，y 1＜y 2，说明在同一个象限内，y 随x 的增大而增大，∴ k ＜0，∴ 一次函数y =-2x +k 的图象与y 轴交于负半轴，其图象经过第二、三、四象限，不经过第一象限。

北师大版九年级数学上册《6.2.2反比例函数的图形与性质》同步练习题带答案学校:___________班级：___________姓名：___________考号：___________考试时间:60分钟满分100分一、单选题（本大题共8小题，总分24分）1．若反比例函数y=k−1x在每个象限内的函数值y随x的增大而减小，则（）A．k＜0B．k＞0C．k＞1D．k＜12．反比例函数y=kx的图象经过点（﹣2，1），则下列说法错误的是（）A．k＝﹣2B．当x＜0时，y随x的增大而减小C．当x＞0时，y随x的增大而增大D．函数图象分布在第二、四象限3．若点A（﹣1，y1），B（1，y2），C（5，y3）都在反比例函数y=5x的图象上，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y3＜y1D．y1＜y3＜y24．如图，点A是反比例函数y=6x(x＞0)的图象上一点，过点A作AB⊥x轴于点B，连接OA，则△ABO的面积为（）A．12B．6C．3D．25．如图，直线l⊥x轴于点P，且与反比例函数y1=k1x（x＞0）及y2=k2x（x＞0）的图象分别交于点A，B，连接OA，OB，已知k1﹣k2的值为8，则△OAB的面积为（）A ．2B ．3C ．4D ．﹣4 6．如图，▱ABCD 的顶点分别在坐标轴和反比例函数y =k x (x ＞0)的图象上，并且▱ABCD 的面积为6，则k 的值为（ ）A ．6B ．﹣6C ．3D ．﹣37．如图所示在平面直角坐标系xOy 中，矩形ABCD ，A （6，3），B ，D 在坐标轴上，CD ＝5，若反比例函数过点C 则反比例函数解析式为（ ）A ．y =32xB ．y =−32xC ．y =−18xD ．y =18x 8．如图，OABC 是平行四边形，对角线OB 在y 轴正半轴上，位于第一象限的点A 和第二象限的点C 分别在双曲线y =k 1x 和y =k 2x的一个分支上，分别过点A 、C 作x 轴的垂线段，垂足分别为点M 和点N ，先给出如下四个结论：①AM CN =|k 1k 2|；②阴影部分的面积是12(k 1+k 2)；③当∠AOC ＝90°时，|k 1|＝|k 2|；④若OABC是菱形，则k1+k2＝0以上结论正确的是（）A．①③B．①②③C．②③④D．①④二、填空题（本大题共6小题，总分24分）9．当x＞0时，反比例函数y＝mx2m2+3m﹣6随x的减小而增大，则m的值为，图象在第象限．10．对于反比例函数y=kx(k＞0)，当x1＜0＜x2＜x3时，其对应的值y1、y2、y3的大小关系是．（用“＜”连接）11．如图，在平面直角坐标系中，点A，B的坐标分别为（5，0），（2，6），过点B作BC∥x轴交y轴于点C，点D为线段AB上的一点，且BD＝2AD，反比例函数y=kx（x＞0）的图象经过点D交线段BC于点E，则四边形ODBE的面积是．12．如图，正方形ABCD的顶点A，B在y轴上，反比例函数y=kx的图象经过点C和AD的中点E，若AB＝4，则k的值是．13．如图，点P，Q，R在反比例函数y=kx(x＞0)的图象上，分别过这三个点作x轴、y轴的平行线．图中所构成的阴影部分面积从左到右依次为S1，S3，S3．若OE＝ED＝DC，S2+S3＝20，则k＝．14．如图，已知在平面直角坐标系xOy中，点P是▱ABCO对角线OB的中点，反比例函数y=kx(x≠0)的图象经过点A，点P．若▱ABCO的面积为30，且y轴将▱ABCO的面积分为1：3，则k的值为．三、解答题（本大题共6小题，总分52分）15．已知反比例函数y=kx图象经过A（1，1）．（1）求反比例函数解析式；（2）若点（2，y1），（4，y2）是反比例函数图象上两点，试比较y1，y2大小．16．如图，一次函数y＝kx+b与反比例函数y=mx的图象交于A（n，3），B（﹣3，﹣2）两点．（1）求反比例函数与一次函数的解析式；（2）过点A作AC⊥y轴，垂足为C，求△ABC的面积S△ABC．17．如图，在平面直角坐标系中，一次函数y＝kx+b与反比例函数y=−6x的图象交于A（﹣1，m），B（n，﹣3）两点，一次函数y＝kx+b的图象与y轴交于点C．（1）求一次函数的解析式；（2）根据函数的图象，直接写出不等式kx+b≤−6x的解集；（3）点P是x轴上一点，且△BOP的面积等于△AOB面积的2倍，求点P的坐标．18．如图，一次函数y1＝kx+b（k≠0）的图象与反比例函数y2=mx（m≠0）的图象交于A（﹣1，n），B（3，﹣2）两点．（1）求一次函数和反比例函数的解析式；（2）结合函数图象，直接写出kx+b−mx＞0时x的取值范围；（3）点P在x轴上，且满足△ABP的面积等于4，请直接写出点P的坐标．19．如图，正比例函数y＝﹣3x与反比例函数y=kx(k≠0)的图象交于A，B（1，m）两点，点C在x轴负半轴上，∠ACO＝45°．（1）m＝，k＝，点A的坐标为，点C的坐标为；（2）点P在x轴上，若以B，O，P为顶点的三角形与△AOC相似，求点P的坐标．20．阅读与思考阅读以下材料，并按要求完成相应的任务：反比例函数是初中函数学习的重要组成部分，它与物理、化学等密切相关，函数本身又是一个重要的数学思想，利用函数的思想和方法可以加深对一些代数问题的理解，现从反比例函数系数k的几何意义出发来探究反比例函数的一些规律．逐梦学习小组在熟练掌握k的几何意义基础之上又进行了深入的探究后发现：如图1，以矩形OCBA的顶点O为坐标原点，射线OA为x轴正半轴、射线OC为y轴的正半轴建立平面直角坐标系，若反比例函数y=kx(x＞0)的图象交BC于点E，交AB于点F，当CE＝BE时，则AF＝BF，在老师指导下逐梦学习小组进行了如下推理，证明了这一结论是正确的．证明：在图1中，过点E作EG⊥x轴，垂足为G，过点F作FH⊥y轴，垂足为H 根据k的几何意义，易知S矩形OCEG＝S矩形OHF A＝|k|∵CE＝BE∴S矩形OCEG =S矩形GEBA=12S矩形OCBA∴S矩形OHFA =12S矩形OCBA∴AF=12AB，即AF＝BF．任务：（1）在图1中，已知CE＝BE，若反比例函数y=kx(x＞0)的系数k＝1，则矩形OCBA的面积＝；（2）逐梦学习小组继续探究后发现，如图2，若反比例函数y=kx(x＞0)的图象交BC于点E，交AB于点F，若CE=12BE，则AF=12BF，请帮助逐梦学习小组完成证明；（3）如图3，反比例函数y=1x(x＞0)的图象交BC于点E，交AB于点F，若CE=13BE，则图中阴影部分（即四边形OEBF）的面积＝．参考答案一、单选题（本大题共8小题，总分24分）1-8．CBDCCABD．二、填空题（本大题共6小题，总分24分）9．1；一、三．10．y1＜y3＜y2．11．12．12．16．13．30．14．4．三、解答题（本大题共6小题，总分52分）15．解：（1）将点A（1，1）代入y=kx，得k＝1∴反比例函数解析式为：y=1 x（2）∵点（2，y1），（4，y2）是反比例函数图象上两点∴当x＝2时，y1=12，当x＝4时，y2=14∴y1＞y2．16．解：（1）将点B（﹣3，﹣2）代入y=mx∴m＝6∴y=6 x∴n＝2∴A（2，3）将A（2，3），B（﹣3，﹣2）代入y＝kx+b{3=2k+b−2=−3k+b∴{k =1b =1∴y ＝x +1；（2）y ＝x +1与x 轴交点坐标D （0，1）过点A 作AE ⊥x 轴∴S =12×CD ×（BC +AE ）=12×2×（3+2）＝5．17．解：（1）∵反比例函数y =−6x的图象经过点A （﹣1，m ），B （n ，﹣3） ∴﹣1×m ＝﹣6，﹣3n ＝﹣6解得m ＝6，n ＝2∴A （﹣1，6），B （2，﹣3）把A 、B 的坐标代入y ＝kx +b 得{−k +b =62k +b =−3解得{k =−3b =3∴一次函数的解析式为y ＝﹣3x +3．（2）观察图象，不等式kx +b ≤−6x 的解集为：﹣1≤x ＜0或x ≥2．（3）连接OA ，OB ，由题意C （0，3）S △AOB ＝S △AOC +S △BOC =12×3×1+12×3×2=92设P （m ，0）由题意12•|m |•3=92×2 解得m ＝±6∴P （6，0）或（﹣6，0）．18．解：（1）由题意可得：点B （3，﹣2）在反比例函数y 2=m x 图象上 ∴−2=m 3，则m ＝﹣6 ∴反比例函数的解析式为y 2=−6x 将A （﹣1，n ）代入y 2=−6x 得：n =−6−1=6，即A （﹣1，6） 将A ，B 代入一次函数解析式中，得{−2=3k +b 6=−k +b 解得：{k =−2b =4∴一次函数解析式为y 1＝﹣2x +4；（2）由图可得：x ＜﹣1或0＜x ＜3时，kx +b −m x ＞0； （2）∵点P 在x 轴上设点P 的坐标为（a ，0）∵一次函数解析式为y 1＝﹣2x +4，令y ＝0，则x ＝2 ∴直线AB 与x 轴交于点（2，0）由△ABP 的面积为4，可得：12×(y A −y B )×|a ﹣2|＝4，即12×8×|a ﹣2|＝4解得：a ＝1或a ＝3∴点P 的坐标为（1，0）或（3，0）．19．解：（1）将B （1，m ）代入y ＝﹣3x ，得m ＝﹣3×1＝﹣3 ∴B （1，﹣3）．将B （1，﹣3）代入y =k x ，得−3=k 1∴k ＝﹣3．如图，过点A 作AD ⊥x 轴于点D ，则∠ADC ＝90°．∵点A ，B 关于原点O 对称∴A （﹣1，3）∴OD ＝1，AD ＝3．又∵∠ACO ＝45°∴CD ＝AD ＝3∴OC ＝OD +CD ＝1+3＝4∴C （﹣4，0）．（2）由（1）可知，B （1，﹣3），A （﹣1，3）． 当点P 在x 轴的负半轴上时，∠BOP ＞90° ∴∠BOP ＞∠AOC ．又∵∠BOP ＞∠ACO ，∠BOP ＞∠CAO∴△BOP 与△AOC 不可能相似．当点P 在x 轴的正半轴上时，∠AOC ＝∠BOP ． ①若△AOC ∽△BOP ，则OA OB =OC OP ∵OA ＝OB∴OP ＝OC ＝4∴P （4，0）；②若△AOC ∽△POB ，则OA OP =OC OB又∵OA =√(−1)2+32=√10，OB =√12+(−3)2=√10，OC ＝4 ∴OP =52 ∴P(52，0)．综上所述，点P 的坐标为（4，0）或(52，0)．20．（1）解：由题意知，S 矩形OCEG ＝1∵CE ＝BE∴S 矩形OCEG =12S 矩形OCBA =1解得，S 矩形OCBA ＝2故答案为：2；（2）证明：如图2，作EG ⊥OA 于G ，FH ⊥OC 于H根据k 的几何意义，易知S 矩形OCEG ＝S 矩形OHFA ＝|k | ∵CE =12BE∴S 矩形OCEG =12S 矩形GEBA =13S 矩形OCBA∴S 矩形OHFA =13S 矩形OCBA∴AF =13AB∴AF=12 BF．（3）解：如图3，作EG⊥OA于G，FH⊥OC于H 根据k的几何意义，易知S矩形OCEG＝S矩形OHFA＝1∵CE=13 BE∴S矩形OCEG =13S矩形GEBA=14S矩形OCBA解得，S矩形OCBA＝4∴S△AOF=12S矩形OHFA =12，S△COE=12S矩形OCEG=12∴S阴影＝S矩形OCBA﹣S△COE﹣S△AOF＝3。

2反比例函数的图象与性质一、选择题1．下列不是反比例函数图像的特点的是（ ）A ．图像是由两部分构成B ．图像与坐标轴无交点C ．图像要么总向右上方，要么总向右下方D ．图像在坐标轴相交而成的一对对顶角内2．若点（3，6）在反比例函数y =x k (k ≠0)的图像上，那么下列各点在此图像上的是（ ）A ．（－3，6）B ．（2，9）C ．（2，－9）D ．（3，－6）3．当x ＜0时，下列图像中表示函数y =－x1的图像是（ ）4．如果x 与y 满足xy +1=0，则y 是x 的（ ）A ．正比例函数B ．反比例函数C ．一次函数D ．二次函数5．已知反比例函数的图像过（2，－2）和（－1，n ），则n 等于（ ）A ．3B ．4C ．6D ．12二、填空题1．反比例函数y =xk (k ≠0)的图像是__________，当k ＞0时，图像的两个分支分别在第__________、__________象限内，在每个象限内，y 随x 的增大而__________；当k ＜0时，图像的两个分支分别在第__________、__________象限内，在每个象限内，y 随x 的增大而__________．2．已知函数y =－x41，当x ＜0时，y __________0，此时，其图像的相应部分在第__________象限．3．当k =__________时，双曲线y =xk 过点（3，23）． 4．若A （x 1,y 1）,B (x 2，y 2)，C （x 3,y 3）都是反比例函数y =－x 1的图像上的点，且x 1＜0＜x 2＜x 3，则y 1,y 2,y 3由小到大的顺序是__________．5．已知y 与x 成正比例，z 与y 成反比例，则z 与x 成__________关系，当x =1时，y =2；当y =2时，z =－2，则当x =－2时，z =__________．三、解答题1．已知反比例函数y =x k 4,分别根据下列条件求k 的取值范围，并画出草图．（1）函数图像位于第一、三象限．（2）函数图像的一个分支向右上方延伸．2．已知y 与x 的部分取值满足下表：（1）试猜想y 与x 的函数关系可能是你们学过的哪类函数，并写出这个函数的解析式．（不要求写x 的取值范围）（2）简要叙述该函数的性质．参考答案一、1．C 2．B 3．C 4．B 5．B二、1．双曲线 一 三 减小 二 四 增大2．＞ 二3．64．y 2＜y 3＜y 15．反比例 1三、1．（1）k ＜4 图略（2）k ＞4 图略2．（1）反比例函数，y =x6 ． （2）该函数性质如下：①图像与x 轴、y 轴无交点；②图像是双曲线，两分支分别位于第二、四象限；③图像在每一个分支都朝右上方延伸，当x ＜0时，y 随x 的增大而增大，当x ＞0时，y 随x 的增大而增大．。

北师大版九年级数学上册《6.2 反比例函数的图象和性质》同步练习题-附答案学校:___________班级：___________姓名：___________考号：___________一、单选题1．反比例函数()0k y k x=≠图象经过点()21，，则下列说法错误的是（ ） A ．函数图象始终经过点()12--，B ．函数图象分布在第一、三象限C ．当0x >时，y 随x 的增大而减小D ．当0x >时，y 随x 的增大而增大 2．以下各点在反比例函数y=5x -图象上的是（） A ．（5，1） B ．（1，5） C ．（5，-1） D ．1,15⎛⎫ ⎪⎝⎭3．若点()11,A x y ，()22,B x y 在反比例函数12k y x -=的图象上，且当120x x <<时12y y <，则k 的取值范围是（ ）A ．12k >- B ．12k <- C ．12k > D ．12k < 4．如图，正比例函数11y k x =和反比例函数22k y x=的图象交于1212A B --（，），（，）两点，若12y y ＜，则x 的取值范围是（ ）A ．x ＜-1或x ＞1B ．x ＜-1或0＜x ＜1C ．-1＜x ＜0或0＜x ＜1D ．-1＜x ＜0或x ＞1 5．如图，点A 是函数2y x =图像上的任意一点，点B 、C 在反比例函数k y x=的图像上．若AB x ∥轴，AC y ∥轴，阴影部分的面积为4，则k 的值是（ ）A ．2B ．3C ．4D ．6 6．探究函数132y x =+-的图像发现，可以由1y x =的图像先向右平移2个单位，再向上平移3个单位得到．根据以上信息判断，下列直线中与函数131y x =--的图像没有公共点的是（ ） A ．经过点(0,3)且平行于x 轴的直线 B ．经过点(0,3)-且平行于x 轴的直线C ．经过点(1,0)-且平行于y 轴的直线D ．经过点(3,0)且平行于y 轴的直线7．已知三个点()12,y -，()21,y 和()32,y 在反比例函数()0k y k x =<的图象上，下列结论正确的是（ ） A ．123y y y << B ．213y y y << C ．231y y y << D ．321y y y <<8．如图，在平面直角坐标系中，P 为正方形的对称中心，A 、B 分别在x 轴和y 轴上，双曲线()60y x x =>经过C 、P 两点，则正方形ABCD 的面积为（ ）A ．13B ．14C ．15D ．209．如图，下列解析式能表示图中变量x y ，之间关系的是（ ）A ．1||y x =B ．1||y x =C ．1||y x =-D ．1||y x=- 10．已知在一、三或二、四象限内，正比例函数(0)y kx k =≠和反比例函数(0)b y b x=≠的函数值都随x 的增大而增大，则这两个函数在同一坐标系中的大致图象是（ ）A ．B ．C ．D ．二、填空题11．已知点()11,A y ，()23,B y 在反比例函数()0m y m x=>上，则1y 2y （填“>，＜，=”） 12．如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l∥y 轴，且直线l 分别与反比例函数y=8x （x ＞0）和y=k x（x ＞0）的图象交于P 、Q 两点，若S △POQ =14，则k 的值为 ．13．点A （3，﹣2）关于y 轴的对称点B 在反比例函数y ＝k x的图象上，则B 点的坐标为 ；k ＝ ． 14．若点()1,A a -，点()2,B b 均在反比例函数k y x=（k 为常数）的图象上，若a b <，则k 的取值范围是 ． 15．如图，已知双曲线y ＝k x（k ＞0）经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若∥OBC 的面积为3，则k ＝ ．16．已知反比例函数y=k x(k≠0) 的图象过点（-1，2），则当x>0时，y 随x 的增大而 ． 17．如图，过原点的直线与反比例函数()0k y k x =>的图象交于,A B 两点，点A 在第一象限．点C 在x 轴正半轴上，连结AC 交反比例函数图象于点D ．AE 为BAC ∠的平分线，过点B 作AE 的垂线，垂足为E ，连结DE ．若3AC DC =，ADE ∆的面积为6，则k 的值为 ．18．如图，在直角坐标系中，O 为坐标原点，函数6y x =与2y x =在第一象限的图象分别为曲线12,l l ，点P为曲线1l 上的任意一点，过点P 作y 轴的垂线交2l 于点A ，交y 轴于点M ，作x 轴的垂线交2l 于点B ，则AOB 的面积是 ．19．反比例函数()0k y k x=>在第一象限内的图象如图，点M 是图象上一点，MP 垂直x 轴于点P ，如果MOP ∆的面积为4，那么k 的值是 ．20．反比例函数y=2m x-的图象是双曲线，在每一个象限内，y 随x 的增大而减小，若点A （–3，y 1），B （–1，y 2），C （2，y 3）都在该双曲线上，则y 1、y 2、y 3的大小关系为 ．（用“<”连接）三、解答题21．探究函数性质时，我们经历了列表、描点、连线画函数图像，观察其图像特征，概括函数性质的过程，以下是我们研究函数22y x m =-+性质及其应用的部分过程，请按要求完成下列各小题． x ．．． 3- 2-1- 0 1 2 3 4 5 ．．． y ．．． 3 a 1- 3- 5- 3- b 13(1)写出函数关系式中m 及表格中a ，b 的值；(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图像，并根据图像写出该函数的一条性质：(3)已知函数4y x =的图像如图所示，结合你所画的函数图像，直接写出不等式422x m x<-+的解集．22．【阅读材料】： 解方程：2(1)12x x ⎛⎫+-=- ⎪⎝⎭时，先两边同乘以x ，得(1)(2)2x x x +-=-，解之得12x =- 21x =，经检验无增根，所以原方程的解为12x =- 21x =．【模仿练习】（1）解方程6(3)36x x ⎛⎫-+= ⎪⎝⎭； 【拓展应用】（2）如图1，等腰直角ABC 的直角顶点A 的坐标为(3,0)，B ，C 两点在反比例函数6y x=的图象上，点B 的坐标是6,n n ⎛⎫ ⎪⎝⎭，且0n >，求n 的值；（3）如图2在双曲线(0)k y k x =>有(,)M m a ，(,)N n b 两点，如果MN OM =，90OMN ∠=︒那么n m m n +是否为定值，若存在请求出，不存在请说明理由．23．【教材再现】：北师大版九年级上册数学教材第122页第21题：“怎样把一块三角形的木板加工成一个面积最大的正方形桌面？”某小组同学对此展开了思考．（1）若木板的形状是如图（甲）所示的直角三角形21.5m ABC S =△， 1.5m AB =根据“相似三角形对应的高的比等于相似比”可以求得此时正方形DEFG 的边长是________．【问题解决】：若木板是面积仍然为21.5m 的锐角三角形ABC ，按照如图（乙）所示的方式加工，记所得的正方形DEFG 的面积为S ，如何求S 的最大值呢？某学习小组做了如下思考：设DE x =，AC=a ，AC 边上的高BH h =，则12ABC Sah =，3h a ∴=由BDE BAC ∽△△得：BM DE BH AC =，从而可以求得2S x a h=+，若要内接正方形面积S 最大，即就是求x 的最大值，因为 1.5S =为定值，因此只需要分母最小即可．（2）小组同学借鉴研究函数的经验，令23(0)S y a h a a a a a=+=+=+>．探索函数3y a a =+的图象和性质： ∥下表列出了y 与a 的几组对应值，其中m =________． a … 14 13 12 1 32 2 3 4 …y … 1124 193m 4 132 132 4 344 … ∥在如图（丙）所示的平面直角坐标系中画出该函数的大致图象；∥结合表格观察函数3y a a=+图象，以下说法正确的是 A ．当1a >时，y 随a 的增大而增大．B ．该函数的图象可能与坐标轴相交．C ．该函数图象关于直线y a =对称．D ．当该函数取最小值时，所对应的自变量a 的取值范围在1~2之间．24．某商贩出售一批进价为l 元的钥匙扣，在销售过程中发现钥匙扣的日销售单价x （元）与日销售量y （个）之间有如下关系：（1）根据表中数据在平面直角坐标系中，描出实数对（x ，y ）对应的点；（2）猜想并确定y 与x 的关系式，并在直角坐标系中画出x>0时的图像；（3）设销售钥匙扣的利润为T 元，试求出T 与x 之间的函数关系式：若商贩在钥匙扣售价不超过8元的前提下要获得最大利润，试求销售价x 和最大利润T ．25．如图，在平面直角坐标系中，等腰三角形ABC 的底边BC 在x 轴的正半轴上，点A 在反比例函数(0)k y x x=>的图象上，延长AB 交y 轴于点D ，若5OC OB =，BOD 的面积为12，求k 的值．参考答案1．D2．C3．C4．B5．D6．B7．C8．C9．B10．C11．>12．-2013． （﹣3，﹣2）， 6． 14．0k ＞15．216．增大17．9218．8319．820．y 2＜y 1＜y 3．21．(1)5m =- 1a = 1b(2)作图略，函数最小值为5-(3)0x <或>4x22．（1）13x =-22x =；（2）2；（3）是定值 3+=n m m n 23．（1）30m 37；（2）∥162；∥略；∥D 24．（1）略；（2）24y x=，略；（3）()241T x x =-，x=8，max 21T =（元） 25．K=6。

6.2 反比例函数的图象与性质一．选择题1．下列不是反比例函数图象的特点的是 （ ） （A ）图象是由两部分构成 （B ）图象与坐标轴无交点（C ）图象要么总向右上方，要么总向右下方（D ）图象在坐标轴相交而成的一对对顶角内2．若点（3，6）在反比例函数x ky = (k ≠0)的图象上，那么下列各点在此图象上的是（ ）（A ） （3-，6） （B ） （2，9） （C ） （2，9-） （D ） （3，6-）3．当0<x 时，下列图象中表示函数xy 1-=的图象是 （ ）4．如果x 与y 满足01=+xy ，则y 是x 的 （ ） （A ） 正比例函数 （B ） 反比例函数 （C ） 一次函数 （D ） 二次函数 5．已知反比例函数的图象过（2，－2）和（－1，n ），则n 等于 （ ） （A ） 3 （B ） 4（C ） 6（D ） 126．已知某县的粮食产量为a (a 为常数)吨，设该县平均每人粮食产量为y 吨，人口数为x ，则y 与x 之间的函数关系的图象可能是下图中的 （ ）（A ） （B ） （C ） （D ）7．若ab ＜0,则函数ax y =与x by =在同一坐标系内的图象大致可能是下图中的 （ ）（A ） （B ） （C ） （D ）二．填空题： 8．反比例函数xky =(k ≠0)的图象是__________，当k ＞0时，图象的两个分支分别在第__________、__________象限内，在每个象限内，y 随x 的增大而__________；当k ＜0时，图象的两个分支分别在第__________、__________象限内，在每个象限内，y 随x 的增大而__________；9．已知函数xy 41-=，当x ＜0时，y _______0，此时，其图象的相应部分在第_______象限； 10．当_____=k 时，双曲线y =xk过点（3，23）；11．已知xky = (k ≠0)的图象的一部分如图（1），则0______k ；12．如图（2），若反比例函数xky =的图象过点A ， 则该函数的解析式为__________；13．若A （x 1，y 1）,B (x 2，y 2)，C （x 3，y 3）都是反比例函数xy 1-=的图象上的点，且x 1＜0＜x 2＜x 3，则y 1，y 2，y 3由小到大的顺序是 ；14．已知y 与x 成正比例，z 与y 成反比例，则z 与x 成__________关系，当1=x 时，2=y ；当2=y 时，2-=z ，则当2-=x 时，______=z ； 三．解答题15．已知反比例函数xky -=4,分别根据下列条件求k 的取值范围，并画出草图. （1）函数图象位于第一、三象限. （2）函数图象的一个分支向右上方延伸.x －6 －5 －4 －3 －2 －1 2 3 4 5 6 …… y11.2 1.5 236－3 －2－1.5－1.2－1……（1）试猜想y 与x 的函数关系可能是你们学过的哪类函数，并写出这个函数的解析式.（不要求写x 的取值范围） （2）简要叙述该函数的性质.参考答案一、1.C 2.B 3.C 4.B 5.B 6A 7B 二、8.双曲线 一 三 减小 二 四 增大 9.＞ 二10.6 11 ＞ 12 y =x2113.y 2＜y 3＜y 1 14.反比例 1三、15.（1）k ＜4 图略 （2）k ＞4 图略 16.（1）反比例函数，y =x6 . （2）该函数性质如下： ①图象与x 轴、y 轴无交点；②图象是双曲线，两分支分别位于第二、四象限；③图象在每一个分支都朝右上方延伸，当x ＜0时，y 随x 的增大而增大，当x ＞0时，y 随x 的增大而增大.掌握的三个数学答题方法 树枝答题法关注数学题的解题过程2014年上海市中考状元徐瑜卿认为,数学是一门思维学科,并不是平时做题多就一定会拿高分。

6.2反比例函数的图像和性质同步练习一．选择题（共10小题）1．已知Rt△ABC在平面直角坐标系中如图放置，∠ACB＝90°，且y轴是BC边的中垂线．已知S△ABC＝6，反比例函数y＝（k≠0）图象刚好经过A点，则k的值为（）A．6B．﹣6C．3D．﹣32．下列各点中，在反比例函数y＝﹣图象上的是（）A．（﹣2，﹣6）B．（﹣2，6）C．（3，4）D．（﹣4，﹣3）3．如图，反比例函数y1＝经过矩形ABCD的顶点D，反比例函数y2＝经过矩形ABCD 的顶点C．矩形ABCD的顶点A在x轴的负半轴上运动，矩形ABCD的顶点B在x轴的正半轴运动上，如果矩形ABCD的面积为定值，下列哪个值不变（）A．a+b B．a﹣b C．D．ab4．如图所示为反比例函数的部分图象，AB⊥OA，AB交反比例函数的图象于点D，且AD：BD＝1：3，若S△AOB＝8，则k的值为（）A．4B．﹣4C．2D．﹣25．关于反比例函数，下列说法错误的是（）A．图象经过点（1，﹣3）B．y随x的增大而增大C．图象关于原点对称D．图象与坐标轴没有交点6．已知点A（x1，y1），B（x2，y2）在反比例函数y＝﹣的图象上，若y1＜y2＜0，则下列结论正确的是（）A．x1＜x2＜0B．x2＜x1＜0C．0＜x1＜x2D．0＜x2＜x17．如图，点A在反比例函数y＝（x＞0）的图象上，过点A作AB⊥x轴，垂足为点B，点C在y轴上，则△ABC的面积为（）A．3B．2C．1.5D．18．如图，面积为2的Rt△OAB的斜边OB在x轴上，∠ABO＝30°，反比例函数y＝图象恰好经过点A，则k的值为（）A．﹣2B．2C．D．﹣9．已知函数y＝x与y＝在同一平面直角坐标系内的图象如图所示，由图象可知，x取什么值时，x＞（）A．x＜﹣1或x＞1B．x＜﹣1或0＜x＜1C．﹣1＜x＜0或x＞1D．﹣1＜x＜0或0＜x＜110．如图，平面直角坐标系中，过点A（1，2）作AB⊥x轴于点B，连接OA，将△ABO绕点A逆时针旋转90°，O、B两点的对应点分别为C、D．当双曲线y＝（x＞0）与△ACD有公共点时，k的取值范围是（）A．2≤k≤3B．3≤k≤6C．2≤k≤6D．3≤k≤4二．填空题（共5小题）11．若点（﹣1，y1），（2，y2），（3，y3）在反比例函数y＝（k＜0）的图象上，则y1，y2，y3的大小关系是．12．若点P（n，1），Q（n+6，3）在反比例函数图象上，请写出反比例函数的解析式．13．如图，点A是反比例函数y＝图象上一点，过点A作AB⊥y轴于点B，点C、D在x 轴上，且BC∥AD，四边形ABCD的面积为4，则k＝．14．如图，矩形ABCD 的两边AD ，AB 的长分别为3、8，E 是DC 的中点，反比例函数的图象经过点E ，与AB 交于点F ．若AF ﹣AE ＝2，则反比例函数的表达式为 ．15．如图，直线y ＝x 与双曲线y ＝（k ＞0）交于A ，B 两点，BC ⊥AB 交该双曲线于点C ，则ACBC 的值是 ．三．解答题（共2小题）16．如图，一次函数y ＝2x ﹣b 的图象与反比例函数（x ＞0）的图象交于点A （m ，2），与x 轴交于点B ，与y 轴交于点C （0，﹣2）．（1）求一次函数和反比例函数的表达式；（2）当x ＞0时，求关于x 的不等式＞2x 的解集．17．如图，直线y＝﹣x+4与x轴、y轴分别交于A、B两点，与双曲线y＝（x＞0）交于M、N两点，且BM＝．（1）求k的值；（2）求△BNO的面积．参考答案1．解：作AD⊥y轴于D，设AB与y轴的交点为E，则四边形ACOD是矩形，∴AD＝OC，∵y轴是BC边的中垂线．∴OC＝OB，∴AD＝OB，在△ADE和△BOE中，，∴△ADE≌△BOE（AAS），∴S矩形ACOD＝S△ABC＝6，∵k＜0，∴k＝﹣6，故选：B．2．解：∵﹣2×（﹣6）＝12，﹣2×6＝﹣12，3×4＝12，﹣4×（﹣3）＝12，∴点（﹣2，6）在反比例函数y＝﹣图象上．故选：B．3．解：∵四边形ABCD是矩形，矩形ABCD的面积为定值，∴|a|+|b|为定值，∵a＜0，b＞0，∴﹣a+b是定值，∴a﹣b与﹣a+b是互为相反数，∴a﹣b是定值，故选：B．4．解：连接OD，如图，∵BA⊥x轴于点A，AD：BD＝1：3，∴S△AOD＝S△AOB＝2，而S△AOC＝|k|＝2，又∵k＜0，∴k＝﹣4．故选：B．5．解：A、反比例函数，当x＝1时y＝﹣3，说法正确，故本选项不符合题意；B、反比例函数中k＝﹣3＜0，则该函数图象经过第二、四象限，在每个象限象限内y随x的增大而增大，说法错误，故本选项符合题意；C、反比例函数的图象关于原点对称，说法正确，故本选项不符合题意；D、图象与坐标轴没有交点，说法正确，故本选项不符合题意．故选：B．6．解：∵﹣3＜0，∴图象位于第二、四象限，在每一个象限内，y随x的增大而增大，又∵y1＜y2＜0，∴图象在第四象限，∴0＜x1＜x2，故选：C．7．解：连结OA，如图，∵AB⊥x轴，∴OC∥AB，∴S△OAB＝S△CAB，而S△OAB＝|k|＝2，∴S△CAB＝2，故选：B．8．解：作AD⊥OB于D，∵Rt△OAB中，∠ABO＝30°，∴OA＝OB，∵∠ADO＝∠OAB＝90°，∠AOD＝∠BOA，∴△AOD∽△BOA，∴＝（）2＝，∴S△AOD＝S△BOA＝×2＝，∵S△AOD＝|k|，∴|k|＝，∵反比例函数y＝图象在二、四象限，∴k＝﹣，故选：D．9．解：根据图象得，y＝x的图象在反比例函数的图象的上边，x比大，即当﹣1＜x＜0或x＞1时，x＞，故选：C．10．解：∵点A（1，2），∴AB＝2，BO＝1，∵∵将△ABO绕点A逆时针旋转90°，∴AD＝AB＝2，OB＝CD＝1，∴点D（3，2），点C（3，1），当点A在双曲线y＝（x＞0）的图象上时，k＝1×2＝2，当点C在双曲线y＝（x＞0）的图象上时，k＝3×1＝3，当点D在双曲线y＝（x＞0）的图象上时，k＝3×2＝6，∴当2≤k≤6时，双曲线y＝（x＞0）与△ACD有公共点，故选：C．11．解：∵k＜0，∴在每个象限内，y随x值的增大而增大，∴当x＝﹣1时，y1＞0，∵2＜3，∴y2＜y3＜0，∴y2＜y3＜y1，故答案为：y2＜y3＜y1．12．解：设反比例函数解析式为y＝，由题意得，k＝n＝3（n+6），解得n＝﹣9，k＝﹣9，∴反比例函数的解析式为y＝﹣，故答案为y＝﹣．13．解：连接OA，∵AB⊥y，BC∥AD，∴四边形ABCD是平行四边形，又∵平行四边形ABCD的面积为4，即，AB•OB＝4，∴S△AOB＝AB•OB＝2＝|k|，∴k＝﹣4或k＝4（舍去）故答案为：﹣4．14．解：∵矩形ABCD的两边AD、AB的长分别为3、8，∴AE＝＝＝5，∵AF﹣AE＝2，∴AF＝7，设B（t，0），则F（t，1），C（t+3，0），E（t+3，4），∵E是DC的中点，∴E（t+3，4），F（t，1），∵E（t+3，4），F（t，1）在反比例函数y＝的图象上，∴t×1＝4（t+3），解得t＝﹣4，∴F（﹣4，1），∴m＝﹣4×1＝﹣4，∴反比例函数的表达式是y＝﹣．故答案为y＝﹣．15．解：∵与交于A、B两点，∴联立方程组，解得，，∴， ∴AB 的长为，设直线BC 的解析式为y ＝mx +b ，∵BC ⊥AB ，∴m ＝﹣2，∴b ＝﹣， ∴， 联立，解得，，∴BC ＝， 由勾股定理得，AC ＝， ∴ACBC =． 故答案为：．16．解：（1）把C （0，﹣2）代入y ＝2x ﹣b 中得：﹣2＝﹣b ，解得b ＝2，∴一次函数的表达式为y ＝2x ﹣2，把A （m ，2）代入y ＝2x ﹣2中，得m ＝2，∴A （2，2），把A （2，2）代入中，得k ＝4，∴反比例函数的表达式是；（2）∵+b＞2x，∴＞2x﹣b，根据图象可知，当x＞0时，不等式＞2x﹣b的解集为0＜x＜2．17．解：作ME⊥x轴于E，MF⊥y轴于F，ND⊥x轴于D，如图所示，∵直线y＝﹣x+4与x轴、y轴分别交于A、B两点，∴A（4，0），B（0，4），∴OA＝OB，∴∠OAB＝∠OBA＝45°，∵MF∥OA，∴∠BMF＝∠BAO＝45°，∴△BMF，△DNA都是等腰直角三角形，∵BM＝，根据对称性可知，NA＝BM＝，∴BF＝MF＝1，DN＝DA＝1，∴M（1，3），N（3，1），∵双曲线y＝（x＞0）经过M、N两点，∴k＝1×3＝3；（2）S△BON＝S△AOB﹣S△AON＝﹣＝6．。

6.2 反比例函数的图象与性质一、单项选择题1．已知反比例函数y ＝－kx 图象在一、三象限内，则一次函数y ＝kx－4的图象经过的象限是( ) A ．第一、二、三象限 B ．第一、二、四象限 C ．第二、三、四象限D ．第一、三、四象限2．若反比例函数y ＝kx (k≠0)的图象经过点P(－2,3)，则该函数的图象不经过的点是( )A ．(3，－2)B ．(1，－6)C ．(－1,6)D ．(－1，－6)3. 对于函数y ＝4x ，下列说法错误的是( )A.这个函数的图象位于第一、三象限B.这个函数的图象既是轴对称图形又是中心对称图形C.当x ＞0时，y 随x 的增大而增大D.当x ＜0时，y 随x 的增大而减小4. 若A(x 1，y 1)、B(x 2，y 2)都在函数y ＝2020x 的图象上，且x 1＜0＜x 2，则( )A.y 1＜y 2B.y 1＝y 2C.y 1＞y 2D.y 1＝－y 25. 关于反比例函数y ＝2x 的图象，下列说法正确的是( )A ．图象经过点(1,1)B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．当x ＜0时，y 随x 的增大而减小6. 如图，矩形AOBC 的面积为4，反比例函数y ＝kx 的图象的一支经过矩形对角线的交点P ，则该反比例函数的表达式是( )A ．y ＝4xB ．y ＝2xC ．y ＝1xD ．y ＝12x7. 反比例函数y ＝1－6t x 的图象与直线y ＝－x ＋2有两个交点，且两交点横坐标的积为负数，则t 的取值范围是( ) A ．t ＜16 B ．t ＞16 C ．t≤16 D ．t≥168. 若点A(－5，y 1)、B(－3，y 2)、C(2，y 3)在反比例函数y ＝3x 的图象上，则y 1、y 2、y 3的大小关系是( )A ．y 1＜y 3＜y 2B ．y 1＜y 2＜y 3C ．y 3＜y 2＜y 1D ．y 2＜y 1＜y 3二、填空题9. 正比例函数y ＝6x 的图象与反比例函数y ＝6x的图象的交点位于第 、 象限.10. 若反比例函数y ＝kx 的图象经过点(－1，－2)，则k 的值为 .11. 已知P 1(x 1，y 1)、P 2(x 2，y 2)两点都在反比例函数y ＝2x 的图象上，且x 1＜x 2＜0，则y 1 y 2(填“＞”或“＜”).12. 如图，直线y ＝kx 与反比例函数y ＝2x (x ＞0)交于点A(1，a)，则k ＝ .13. 如图，菱形OABC 的顶点C 的坐标为(3,4)，顶点A 在x 轴的正半轴上，反比例函数y ＝kx(x ＞0)的图象经过顶点B ，则k 的值为 .14. 如图，A 、B 两点在反比例函数y ＝4x 图象上，分别过A 、B 两点向x 轴、y 轴作垂线段，已知S 阴影＝1，则S 1＋S 2＝ .15．反比例函数y ＝3x 关于y 轴对称的函数的解析式为 .16. 如图，在平面直角坐标系xOy 中，正方形OABC 的边长为2，写出一个函数y ＝kx (k≠0)，使它的图象与正方形OABC 有公共点，这个函数的表达式为 .三、解答题17. (1)在同一平面直角坐标系中作出反比例函数y 1＝4x 与一次函数y 2＝2x －2的图象，并根据图象求出交点坐标． (2)观察图象，当x 取任何值时，y 1＞y 2?18. 已知：如图，在平面直角坐标系xOy 中，直线AB 与x 轴交于点A(－2,0)，与反比例函数在第一象限内的图象交于点B(2，n)，连结BO ，若S △AOB ＝4.(1)求该反比例函数的解析式和直线AB 的解析式；(2)若直线AB 与y 轴的交点为C ，求△OCB 的面积．19. 如图，一次函数y 1＝x ＋1的图象与反比例函数y 2＝kx (x ＞0)的图象交于点M ，作MN ⊥x 轴，N 为垂足，且ON ＝1.(1)在第一象限内，当x 取何值时，y 1＞y 2？(根据图象直接写出结果)(2)求反比例函数的表达式.20. 如图，点A 、B 分别在x 轴、y 轴上，点D 在第一象限内，DC ⊥x 轴于C ，AO ＝CD ＝2，AB ＝DA ＝5，反比例函数y ＝kx (k ＞0)的图象过CD 的中点E.(1)求证：△AOB ≌△DCA ； (2)求k 的值；(3)△BFG 和△DCA 关于某点成中心对称，其中点F 在y 轴上，试判断点G 是否在反比例函数的图象上，并说明理由．21. 如图，在平面直角坐标xOy 中，正比例函数y ＝kx 的图象与反比例函数y ＝mx的图象都经过点A(2，－2)．(1)分别求这两个函数的表达式；(2)将直线OA 向上平移3个单位长度后与y 轴交于点B ，与反比例函数图象在第四象限内的交点为C ，连接AB 、AC ，求点C 的坐标及△ABC 的面积．22. 已知反比例函数y ＝m －7x的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限，并求m 的取值范围； (2)如图，O 为坐标原点，点A 在该反比例函数位于第一象限的图象上，点B 与点A 关于x 轴对称，若△OAB 的面积为6，求m 的值.答案： 一、1-8 CDCAD CBD 二、9. 一 三 10. 2 11. ＞ 12. 2 13. 32 14. 615. y ＝－3x16. y ＝4x三、17. 解：(1)画图象如下：由图象可得：交点坐标(－1，－4)，(2,2)；(2)由两交点坐标并结合函数图象可知：当x ＜－1或0＜x ＜2时，y 1＞y 2.解：(1) 由A(－2,0)，得OA ＝2.∵点B(2，n)在第一象限内，S △AOB ＝4，∴12OA×n＝4，∴n ＝4.∴点B 的坐标为(2,4)，设反比例函数的解析式为y ＝a x (a≠0)，将点B 的坐标代入，得4＝a2，∴a ＝8，∴反比例函数的解析式为y ＝8x，设直线AB 的解析式为y ＝kx ＋b(k≠0)，将点A 、B 的坐标分别代入，得⎩⎪⎨⎪⎧－2k ＋b ＝02k ＋b ＝4，解得⎩⎪⎨⎪⎧k ＝1b ＝2，∴直线AB 的解析式为y ＝x ＋2；(2) 在y ＝x ＋2中，令x ＝0，得y ＝2，∴点C 的坐标是(0,2)，∴OC ＝2.∴S △OCB ＝12OC·x B ＝12×2×2＝2.19. 解：(1)x ＞1；(2)∵ON＝1，MN⊥x 轴，∴M 点的横坐标为x ＝1，把x ＝1代入y 1＝x ＋1得y 1＝1＋1＝2，∴M 点的坐标为(1,2)，把M 点的坐标(1,2)代入y 2＝k x ，得k ＝2，∴反比例函数的表达式y 2＝2x.20. 解: (1)∵点A 、B 分别在x 轴、y 轴上，点D 在第一象限内，DC ⊥x 轴，∴∠AOB ＝∠DCA ＝90°.在Rt △AOB 和Rt △DCA 中，⎩⎪⎨⎪⎧AO ＝DC AB ＝DA，∴Rt △AOB ≌Rt △DCA ；(2)在Rt △ACD 中，CD ＝2，AD ＝5，∴AC ＝AD 2－CD 2＝1，∴OC ＝OA ＋AC ＝2＋1＝3，∴D 点坐标为(3,2)，∵点E 为CD 的中点，∴点E 的坐标为(3,1)，∴k ＝3×1＝3；(3)点G 在反比例函数的图象上．理由如下：∵△BFG 和△DCA 关于某点成中心对称，∴△BFG ≌△DCA ，∴FG ＝CA ＝1，BF ＝DC ＝2，∠BFG ＝∠DCA ＝90°.又OB ＝AC ＝1，∴OF ＝OB ＋BF ＝1＋2＝3，∴G 点坐标为(1,3)，∵1×3＝3，∴G(1,3)在反比例函数y ＝3x的图象上．21. 解：(1)y ＝－x ，y ＝－4x；(2)直线OA ：y ＝－x 向上平移3个单位后解析式为y ＝－x ＋3，则点B的坐标为(0,3)，联立两函数解析式⎩⎪⎨⎪⎧y ＝－x ＋3，y ＝－4x ，解得⎩⎪⎨⎪⎧x ＝－1，y ＝4，或⎩⎪⎨⎪⎧x ＝4y ＝－1，∴第四象限内的交点C 的坐标为(4，－1)，连接OC ，∵OA ∥BC ，∴S △ABC ＝S △OBC ＝12×3×4＝622. 解：(1)该函数图象的另一支在第三象限，∴m－7＞0，∴m＞7； (2)设点A 的坐标为(x ，y)，∵点B 与点A 关于x 轴对称，∴点B 的坐标为(x ，－y).∵S △OAB ＝6，∴12×2y×x＝6，∴xy＝6.∵点A 在反比例函数y ＝m －7x的图象上，∴xy＝m －7，∴m－7＝6，∴m＝13.。