图像相似度

相似度阈值
相似度阈值是指在进行相似度比较时所设定的最小阈值。

在许多应用中，需要对文本、图像等进行相似度比较，以判断它们之间的相似程度。

相似度阈值的设定直接影响到相似度比较的结果，因此需要根据具体应用场景进行合理的设置。

在文本相似度比较中，相似度阈值通常设定为0.8-0.9之间。

当两个文本的相似度超过设定的阈值时，就可以认为它们相似。

在图像相似度比较中，相似度阈值的设定要根据具体的应用场景来确定，例如在人脸识别中，相似度阈值可以设定为0.6-0.7，表示当两张图像的相似度超过该阈值时，可以认为它们是同一张人脸。

相似度阈值的设定需要考虑到误判率和漏报率的平衡。

过高的相似度阈值容易导致漏报，即将相似的文本或图像误判为不相似；而过低的相似度阈值则容易导致误判，即将不相似的文本或图像误判为相似。

因此，在设定相似度阈值时，需要综合考虑误判率和漏报率的平衡，根据具体应用场景进行调整，以达到最优的识别效果。

- 1 -。

人脸识别算法欧氏距离余弦相似度一、人脸识别算法的基本原理人脸识别算法是一种利用人脸特征信息进行身份识别的技术。

它主要通过采集图像或视频中的人脸信息，然后提取特征并对比库中已存在的人脸信息，最终确定身份的一种技术手段。

在人脸识别算法中，欧氏距离和余弦相似度是两种常用的相似度计算方法。

在我们深入讨论这两种方法之前，我们需要先了解一下它们的基本原理。

欧氏距离是一种用于度量向量之间的距离的方法，其计算公式为：d(x, y) = √((x1 - y1)² + (x2 - y2)² + ... + (xn - yn)²) 。

在人脸识别算法中，常用欧氏距离来度量两张人脸图像之间的相似度，即通过比较特征向量之间的欧氏距离来识别身份。

与欧氏距离相似，余弦相似度也是一种用于度量向量之间的相似度的方法，其计算公式为：sim(x, y) = (x·y) / (‖x‖·‖y‖)，其中x和y分别为两个向量。

在人脸识别算法中，余弦相似度常用于比较两个特征向量之间的夹角，来度量它们之间的相似度。

二、人脸识别算法中的欧氏距离应用在人脸识别算法中，欧氏距离常被用于度量两张人脸图像之间的相似度。

通过将人脸图像转化为特征向量，并使用欧氏距离来比较这些向量之间的距离，来确定是否为同一人。

举例来说，当系统需要识别一个人脸时，它首先会将该人脸图像提取特征并转化为特征向量，然后与存储在数据库中的特征向量进行比较。

通过计算欧氏距离，系统可以得出两个特征向量之间的距离，从而确定该人脸是否为已知身份。

三、人脸识别算法中的余弦相似度应用除了欧氏距离外，余弦相似度在人脸识别算法中也有着广泛的应用。

与欧氏距离不同，余弦相似度更侧重于计算两个向量之间的夹角，而非距离。

在人脸识别算法中，余弦相似度被用来比较两个特征向量之间的夹角，通过夹角的大小来确定它们之间的相似度。

这种方法能够更好地捕捉到特征向量之间的方向性信息，从而提高识别的准确性。

Opencvpython图像处理-图像相似度计算⼀、相关概念1. ⼀般我们⼈区分谁是谁，给物品分类，都是通过各种特征去辨别的，⽐如⿊长直、⼤⽩腿、樱桃唇、⽠⼦脸。

王⿇⼦脸上有⿇⼦，隔壁⽼王和⼉⼦很像，但是⼉⼦下巴涨了⼀颗痣和他妈⼀模⼀样，让你确定这是你⼉⼦。

还有其他物品、什么桌⼦带腿、镜⼦反光能在⾥⾯倒影出东西，各种各样的特征，我们通过学习、归纳，⾃然⽽然能够很快识别分类出新物品。

⽽没有学习训练过的机器就没办法了。

2. 但是图像是⼀个个像素点组成的，我们就可以通过不同图像之间这些差异性就判断两个图的相似度了。

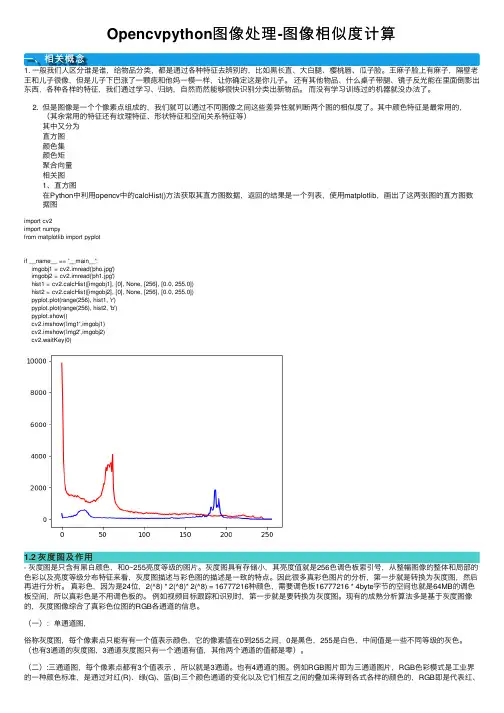
其中颜⾊特征是最常⽤的，（其余常⽤的特征还有纹理特征、形状特征和空间关系特征等）其中⼜分为直⽅图颜⾊集颜⾊矩聚合向量相关图1、直⽅图在Python中利⽤opencv中的calcHist()⽅法获取其直⽅图数据，返回的结果是⼀个列表，使⽤matplotlib，画出了这两张图的直⽅图数据图import cv2import numpyfrom matplotlib import pyplotif __name__ == '__main__':imgobj1 = cv2.imread('pho.jpg')imgobj2 = cv2.imread('ph1.jpg')hist1 = cv2.calcHist([imgobj1], [0], None, [256], [0.0, 255.0])hist2 = cv2.calcHist([imgobj2], [0], None, [256], [0.0, 255.0])pyplot.plot(range(256), hist1, 'r')pyplot.plot(range(256), hist2, 'b')pyplot.show()cv2.imshow('img1',imgobj1)cv2.imshow('img2',imgobj2)cv2.waitKey(0)1.2 灰度图及作⽤- 灰度图是只含有⿊⽩颜⾊，和0~255亮度等级的图⽚。

基于深度学习的图片相似度分析技术方案一、引言随着数字图像数量的爆炸性增长，图片相似度分析成为了信息检索、电子商务、社交网络和数字版权管理等众多领域的关键技术。

传统的图片相似度分析方法主要基于像素级别的比较，对于光照、尺度、旋转等变化鲁棒性较差。

近年来，深度学习技术的发展为图片相似度分析提供了新的解决方案。

二、技术方案概述本技术方案提出了一种基于深度学习的图片相似度分析方法。

该方法采用卷积神经网络（CNN）提取图像特征，并使用余弦相似度度量图像之间的相似度。

具体而言，本技术方案包括以下步骤：1.数据预处理：对原始图像进行缩放、裁剪等操作，使其符合CNN模型的输入要求。

2.特征提取：使用预训练的CNN模型提取图像特征，得到一个固定长度的特征向量。

3.相似度计算：计算两个特征向量之间的余弦相似度，作为图像之间的相似度得分。

4.阈值判定：根据业务需求设定相似度阈值，判断两张图片是否相似。

三、技术方案细节1.数据预处理数据预处理阶段主要包括图像缩放、裁剪等操作，以便符合CNN 模型的输入要求。

具体而言，我们可以将原始图像缩放到统一大小（如256x256），然后进行中心裁剪或随机裁剪，得到一个固定大小的输入图像。

2.特征提取特征提取阶段使用预训练的CNN模型，如VGG16、ResNet50等，提取图像的特征。

这些预训练模型在大量图像数据集上进行过训练，具有较强的泛化能力。

我们可以使用这些模型的全连接层输出作为图像的特征向量。

为了提高特征提取的效率，我们可以采用模型剪枝、知识蒸馏等技术对预训练模型进行压缩。

3.相似度计算相似度计算阶段采用余弦相似度作为度量标准。

余弦相似度通过计算两个特征向量之间的夹角余弦值来衡量它们之间的相似度。

具体公式如下：similarity = cos(θ) = A · B / (||A|| ||B||)其中，A和B是两个特征向量，·表示点积，||A||和||B||表示向量的模长。

相似图像的检测方法一、哈希算法哈希算法可对每张图像生成一个“指纹”(fingerprint)字符串，然后比较不同图像的指纹。

结果越接近，就说明图像越相似。

常用的哈希算法有三种：1．均值哈希算法(ahash)均值哈希算法就是利用图片的低频信息。

将图片缩小至8*8，总共64个像素。

这一步的作用是去除图片的细节，只保留结构、明暗等基本信息，摒弃不同尺寸、比例带来的图片差异。

将缩小后的图片，转为64级灰度。

计算所有64个像素的灰度平均值，将每个像素的灰度，与平均值进行比较。

大于或等于平均值，记为1；小于平均值，记为0。

将上一步的比较结果，组合在一起，就构成了一个64位的整数，这就是这张图片的指纹。

均值哈希算法计算速度快，不受图片尺寸大小的影响，但是缺点就是对均值敏感，例如对图像进行伽马校正或直方图均衡就会影响均值，从而影响最终的hash值。

2．感知哈希算法(phash)感知哈希算法是一种比均值哈希算法更为健壮的算法，与均值哈希算法的区别在于感知哈希算法是通过DCT（离散余弦变换）来获取图片的低频信息。

先将图像缩小至32*32，并转化成灰度图像来简化DCT的计算量。

通过DCT变换，得到32*32的DCT系数矩阵，保留左上角的8*8的低频矩阵（这部分呈现了图片中的最低频率）。

再计算8*8矩阵的DCT的均值，然后将低频矩阵中大于等于DCT均值的设为”1”，小于DCT均值的设为“0”，组合在一起，就构成了一个64位的整数，组成了图像的指纹。

感知哈希算法能够避免伽马校正或颜色直方图被调整带来的影响。

对于变形程度在25%以内的图片也能精准识别。

3．差异值哈希算法(dhash)差异值哈希算法将图像收缩小至8*9，共72的像素点，然后把缩放后的图片转化为256阶的灰度图。

通过计算每行中相邻像素之间的差异，若左边的像素比右边的更亮，则记录为1，否则为0，共形成64个差异值，组成了图像的指纹。

相对于pHash，dHash的速度要快的多，相比aHash，dHash在效率几乎相同的情况下的效果要更好，它是基于渐变实现的。

计算机视觉中的图像匹配技术在当今快速发展的数字化时代，计算机视觉技术的应用越来越广泛。

其中，图像匹配技术作为计算机视觉领域的核心技术之一，具有重要的研究和应用价值。

本文将介绍图像匹配的概念、方法和应用，以及其在计算机视觉领域中的重要性。

一、图像匹配的概念和意义图像匹配是指通过计算机程序，在两幅或多幅图像中找到相似或相同的目标的过程。

在实际应用中，图像匹配技术可以用于目标识别、图像检索、三维重建等方面。

图像匹配的意义在于帮助计算机理解和处理复杂的视觉信息。

通过图像匹配技术，计算机可以实现自动的目标识别和定位，从而为人们提供更加便捷和智能的应用和服务。

二、图像匹配的方法1. 特征提取：图像匹配的第一步是提取图像中的特征。

常用的特征包括角点、边缘、纹理等。

通过提取图像的特征，可以将图像转化为计算机可识别的数字特征，为后续的图像匹配提供基础。

2. 特征描述：特征提取后，需要对提取到的特征进行描述。

常用的特征描述方法包括尺度不变特征变换（SIFT）、加速稳健特征（SURF）和方向梯度直方图（HOG）等。

这些方法可以将提取到的特征转化为具有一定描述性的向量表示。

3. 相似度计算：在图像匹配中，需要计算图像之间的相似度。

常用的相似度计算方法包括欧氏距离、汉明距离和余弦相似度等。

这些方法可以度量不同图像之间的相似程度，并为后续的目标匹配提供依据。

4. 匹配策略：根据相似度计算的结果，需要选取合适的匹配策略进行目标匹配。

常用的匹配策略包括最近邻匹配、几何一致性匹配和基于模型的匹配等。

这些策略可以通过对特征点的匹配关系进行分析和推理，找到最符合要求的目标匹配结果。

三、图像匹配的应用领域1. 目标识别与跟踪：图像匹配技术可以用于目标识别与跟踪。

通过对目标图片和实时图像进行匹配，可以实现自动目标识别和跟踪，为安防监控、智能交通等领域提供重要的技术支持。

2. 图像检索：图像匹配技术可以用于图像检索。

通过对用户提供的查询图像与数据库中的图像进行匹配，可以快速找到相似的图像。

qdrant 相似度查询算法一、qdrant相似度查询算法的原理qdrant相似度查询算法是一种基于向量空间模型的相似度计算方法。

该算法通过将待查询的向量与已有的向量集合进行相似度比较，从而找到与之最相似的向量。

在qdrant相似度查询算法中，首先需要将待查询的向量和已有的向量进行向量化，通常使用词袋模型或者词向量模型进行表示。

然后，通过计算两个向量之间的余弦相似度来衡量它们之间的相似程度。

余弦相似度是通过计算两个向量的内积除以它们的模长得到的，值域在[-1, 1]之间，值越接近1表示两个向量越相似。

二、qdrant相似度查询算法的应用场景1. 文本相似度查询：qdrant相似度查询算法可以用于文本相似度查询，通过将文本向量化，并计算文本之间的相似度，可以实现文本的快速检索和推荐。

2. 图像相似度查询：qdrant相似度查询算法也可以用于图像相似度查询，通过将图像向量化，并计算图像之间的相似度，可以实现图像的快速搜索和匹配。

3. 推荐系统：qdrant相似度查询算法可以用于推荐系统中的用户相似度计算和物品相似度计算，通过计算用户之间或物品之间的相似度，可以为用户提供个性化的推荐结果。

三、qdrant相似度查询算法的优势1. 高效性：qdrant相似度查询算法利用向量空间模型进行相似度计算，避免了传统的遍历搜索方法，因此具有较高的查询效率。

2. 精确性：qdrant相似度查询算法使用余弦相似度作为相似度度量，可以较准确地衡量向量之间的相似程度。

3. 可扩展性：qdrant相似度查询算法可以处理大规模的向量集合，支持高并发的查询请求，具有良好的可扩展性。

4. 应用广泛：qdrant相似度查询算法可以应用于文本、图像等多种类型的数据，适用于各种不同的应用场景。

qdrant相似度查询算法是一种基于向量空间模型的相似度计算方法，可以用于文本相似度查询、图像相似度查询以及推荐系统等应用中。

该算法具有高效性、精确性、可扩展性和广泛的应用范围，对于提高数据检索和推荐的效率和准确性具有重要意义。

直⽅图对⽐（两个直⽅图的相似性如何度量）本⽂档尝试解答如下问题:如何使⽤OpenCV函数产⽣⼀个表达两个直⽅图的相似度的数值。

如何使⽤不同的对⽐标准来对直⽅图进⾏⽐较。

原理要⽐较两个直⽅图( and ), ⾸先必须要选择⼀个衡量直⽅图相似度的对⽐标准 () 。

OpenCV 函数执⾏了具体的直⽅图对⽐的任务。

该函数提供了4种对⽐标准来计算相似度：1. Correlation ( CV_COMP_CORREL )其中是直⽅图中bin的数⽬。

2. Chi-Square ( CV_COMP_CHISQR )3. Intersection ( CV_COMP_INTERSECT )4. Bhattacharyya 距离( CV_COMP_BHATTACHARYYA )源码本程序做什么?装载⼀张基准图像和两张测试图像进⾏对⽐。

产⽣⼀张取⾃基准图像下半部的图像。

将图像转换到HSV格式。

计算所有图像的H-S直⽅图，并归⼀化以便对⽐。

将基准图像直⽅图与两张测试图像直⽅图，基准图像半⾝像直⽅图，以及基准图像本⾝的直⽅图分别作对⽐。

显⽰计算所得的直⽅图相似度数值。

下载代码: 点击代码⼀瞥:#include "opencv2/highgui/highgui.hpp"#include "opencv2/imgproc/imgproc.hpp"#include <iostream>#include <stdio.h>using namespace std;using namespace cv;/** @函数 main */int main( int argc, char** argv ){Mat src_base, hsv_base;Mat src_test1, hsv_test1;Mat src_test2, hsv_test2;Mat hsv_half_down;/// 装载三张背景环境不同的图像if( argc < 4 ){ printf("** Error. Usage: ./compareHist_Demo <image_settings0> <image_setting1> <image_settings2>\n");return -1;}src_base = imread( argv[1], 1 );src_test1 = imread( argv[2], 1 );src_test2 = imread( argv[3], 1 );/// 转换到 HSVcvtColor( src_base, hsv_base, CV_BGR2HSV );cvtColor( src_test1, hsv_test1, CV_BGR2HSV );cvtColor( src_test2, hsv_test2, CV_BGR2HSV );hsv_half_down = hsv_base( Range( hsv_base.rows/2, hsv_base.rows - 1 ), Range( 0, hsv_base.cols - 1 ) );/// 对hue通道使⽤30个bin,对saturatoin通道使⽤32个binint h_bins = 50; int s_bins = 60;int histSize[] = { h_bins, s_bins };// hue的取值范围从0到256, saturation取值范围从0到180float h_ranges[] = { 0, 256 };float s_ranges[] = { 0, 180 };const float* ranges[] = { h_ranges, s_ranges };// 使⽤第0和第1通道int channels[] = { 0, 1 };/// 直⽅图MatND hist_base;MatND hist_half_down;MatND hist_test1;MatND hist_test2;/// 计算HSV图像的直⽅图calcHist( &hsv_base, 1, channels, Mat(), hist_base, 2, histSize, ranges, true, false );normalize( hist_base, hist_base, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_half_down, 1, channels, Mat(), hist_half_down, 2, histSize, ranges, true, false );normalize( hist_half_down, hist_half_down, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_test1, 1, channels, Mat(), hist_test1, 2, histSize, ranges, true, false );normalize( hist_test1, hist_test1, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_test2, 1, channels, Mat(), hist_test2, 2, histSize, ranges, true, false );normalize( hist_test2, hist_test2, 0, 1, NORM_MINMAX, -1, Mat() );///应⽤不同的直⽅图对⽐⽅法for( int i = 0; i < 4; i++ ){ int compare_method = i;double base_base = compareHist( hist_base, hist_base, compare_method );double base_half = compareHist( hist_base, hist_half_down, compare_method );double base_test1 = compareHist( hist_base, hist_test1, compare_method );double base_test2 = compareHist( hist_base, hist_test2, compare_method );printf( " Method [%d] Perfect, Base-Half, Base-Test(1), Base-Test(2) : %f, %f, %f, %f \n", i, base_base, base_half , base_test1, base_test2 ); }printf( "Done \n" );return 0;}解释1. 声明储存基准图像和另外两张对⽐图像的矩阵( RGB 和 HSV )Mat src_base, hsv_base;Mat src_test1, hsv_test1;Mat src_test2, hsv_test2;Mat hsv_half_down;2. 装载基准图像(src_base) 和两张测试图像:if( argc < 4 ){ printf("** Error. Usage: ./compareHist_Demo <image_settings0> <image_setting1> <image_settings2>\n");return -1;}src_base = imread( argv[1], 1 );src_test1 = imread( argv[2], 1 );src_test2 = imread( argv[3], 1 );3. 将图像转化到HSV格式:cvtColor( src_base, hsv_base, CV_BGR2HSV );cvtColor( src_test1, hsv_test1, CV_BGR2HSV );cvtColor( src_test2, hsv_test2, CV_BGR2HSV );4. 同时创建包含基准图像下半部的半⾝图像(HSV格式):hsv_half_down = hsv_base( Range( hsv_base.rows/2, hsv_base.rows - 1 ), Range( 0, hsv_base.cols - 1 ) );5. 初始化计算直⽅图需要的实参(bins, 范围，通道 H 和 S ).int h_bins = 50; int s_bins = 32;int histSize[] = { h_bins, s_bins };float h_ranges[] = { 0, 256 };float s_ranges[] = { 0, 180 };const float* ranges[] = { h_ranges, s_ranges };int channels[] = { 0, 1 };6. 创建储存直⽅图的 MatND 实例:MatND hist_base;MatND hist_half_down;MatND hist_test1;MatND hist_test2;7. 计算基准图像，两张测试图像，半⾝基准图像的直⽅图:calcHist( &hsv_base, 1, channels, Mat(), hist_base, 2, histSize, ranges, true, false );normalize( hist_base, hist_base, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_half_down, 1, channels, Mat(), hist_half_down, 2, histSize, ranges, true, false );normalize( hist_half_down, hist_half_down, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_test1, 1, channels, Mat(), hist_test1, 2, histSize, ranges, true, false );normalize( hist_test1, hist_test1, 0, 1, NORM_MINMAX, -1, Mat() );calcHist( &hsv_test2, 1, channels, Mat(), hist_test2, 2, histSize, ranges, true, false );normalize( hist_test2, hist_test2, 0, 1, NORM_MINMAX, -1, Mat() );8. 按顺序使⽤4种对⽐标准将基准图像(hist_base)的直⽅图与其余各直⽅图进⾏对⽐:for( int i = 0; i < 4; i++ ){ int compare_method = i;double base_base = compareHist( hist_base, hist_base, compare_method );double base_half = compareHist( hist_base, hist_half_down, compare_method );double base_test1 = compareHist( hist_base, hist_test1, compare_method );double base_test2 = compareHist( hist_base, hist_test2, compare_method );printf( " Method [%d] Perfect, Base-Half, Base-Test(1), Base-Test(2) : %f, %f, %f, %f \n", i, base_base, base_half , base_test1, base_test2 );}结果1. 使⽤下列输⼊图像:第⼀张为基准图像，其余两张为测试图像。

结构相似性
SSIM(Structural Similarity)，结构相似性，是一种衡量两幅图像相似度的指标。

该指标首先由德州大学奥斯丁分校的图像和视频工程实验室(Laboratory for Image and Video Engineering)提出。

SSIM使用的两张图像中，一张为未经压缩的无失真图像，另一张为失真后的图像。

结构相似性，是一种衡量两幅图像相似度的指标，通常用作图像质量评估，在图像重建、压缩领域，可以计算输出图像与原图的差距。

MSE有很多算法可以计算输出图像与原图的差距，其中最常用的一种是Mean Square Error loss（MSE）。

它的计算公式很简单：
M S E = 1 n ∑[ I i − K i ] 2 MSE=\frac{1}{n} \sum [I_i-K_i]^{2} MSE=n1∑[Ii−Ki]2
就是计算重建图像与输入图像的像素差的平方，然后在全图上求平均。

有时候两张图片只是亮度不同，但是之间的MSE loss 相差很大。

而一幅很模糊与另一幅很清晰的图，它们的MSE loss 可能反而相差很小。

作为结构相似性理论的实现，结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度的，反映场
景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合。

用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。

医学图像配准中的图像处理方法随着医学科技的不断发展，人们对医学图像的要求也越来越高。

而在医学图像处理中，图像配准（image registration）是最为重要和基础的一步，旨在将两张或多张医学图像按照一定的标准进行对齐、平移和旋转等操作，以实现医学图像的融合。

医学图像配准需要借助计算机来完成，而在图像处理的过程中，数字图像处理（digital image processing）技术起到了至关重要的作用。

下面，我们将介绍一些在医学图像配准中常用的数字图像处理方法。

1. 线性配准线性配准（linear registration）是一种非常基础和简单的医学图像配准方法。

它主要是基于线性变换的原理进行的，通过线性变换对医学图像进行平移、旋转和缩放等操作，以实现图像的对齐。

在线性配准方法中，最为常用的是刚体变换（rigid transform），可以实现医学图像的旋转和平移。

当然，在实际操作中，由于人体器官的变形和图像的拍摄角度等原因，线性配准往往难以完全实现图像对齐，需要使用更加复杂的非线性配准方法。

2. 相似性度量在医学图像配准中，为了衡量图像之间的相似度，常用的指标是相似性度量（similarity measurement）。

相似性度量是一种量化医学图像相似度的方法，通常采用像素级别的比较。

在相似性度量中，最为常用的是均方根误差（root mean square error，RMSE）和皮尔逊相关系数（Pearson correlation coefficient，PCC）。

RMSE可以量化两幅医学图像之间的差异程度，而PCC则可以反映两幅医学图像的相似度。

3. 非线性配准由于医学图像的复杂性和变形，线性配准方法在实际操作中往往难以完全实现图像对齐。

因此，在医学图像配准中，非线性配准（nonlinear registration）方法应运而生。

非线性配准通过使用更为复杂的变换模型（如弹性变换、位似变换、光流估计等），可以更为准确地对医学图像进行仿射、变形和对齐等操作。