三角形网格下二维浅水方程的 高分辨率格式

二维浅水波方程
二维浅水波方程（2D shallow water wave equation）是描述水波在水平平面上传播和演化的方程。

其数学表达形式为：
∂h/∂t + ∂(hu)/∂x + ∂(hv)/∂y = 0，
∂(hu)/∂t + ∂(hu^2)/∂x + ∂(huv)/∂y + gh(∂h/∂x) + fhv = 0，
∂(hv)/∂t + ∂(huv)/∂x + ∂(hv^2)/∂y + gh(∂h/∂y) + fhu = 0。

其中，h是水深，u和v分别是水平和垂直方向的水速，t是时间，x和y是水平和垂直方向的空间坐标，g是重力加速度，f是科氏力参数（因地球自转而引起的离心力）。

这个方程组描述了水深变化、水平和垂直速度的变化以及重力和离心力对水波运动的影响。

这些方程在海洋动力学和水工学等领域中被广泛应用，用来模拟洋流、风浪和海啸等现象。

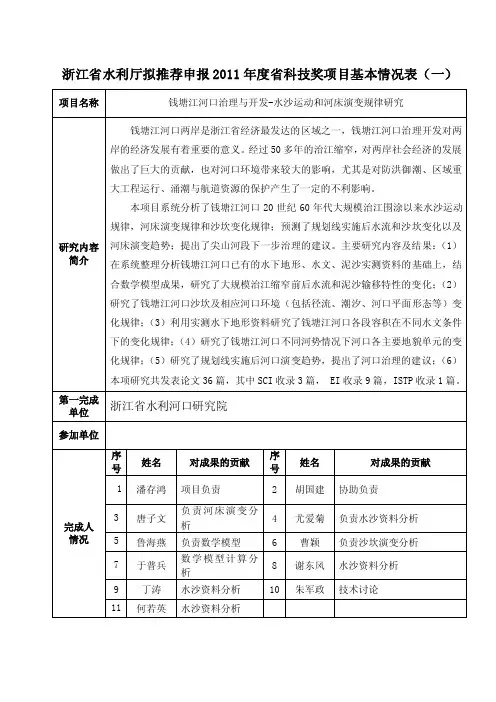
松虎航道整治工程水流数学模型的建立与应用简秋敏;刘轶;李子龙;邹振华;肖潇【摘要】为研究松虎航道整治工程对河道水位、流场等水流条件的影响，基于浅水方程，利用有限体积法进行离散，采用非结构三角形网格，建立了二维水流数学模型。

根据实测的水文和地形资料，对模型进行水面线和流速相关验证。

验证结果表明，所建立的模型能够较好反映松虎航道水流运动规律。

同时，计算分析的流速分布等水流特性也可证明松虎航道整治工程治理措施的有效性。

【期刊名称】《水利水电快报》【年(卷),期】2016(037)007【总页数】6页(P27-31,43)【关键词】航道整治;水面线;流速;数学模型;模型验证;松虎航道【作者】简秋敏;刘轶;李子龙;邹振华;肖潇【作者单位】长江水利委员会水文局长江中游水文水资源勘测局，湖北武汉430012;杭州市千岛湖原水股份有限公司，浙江杭州 311799;长江水利委员会水文局长江中游水文水资源勘测局，湖北武汉 430012;长江水利委员会水文局长江中游水文水资源勘测局，湖北武汉 430012;长江水利委员会水文局长江中游水文水资源勘测局，湖北武汉 430012【正文语种】中文【中图分类】U617.6河道演变松虎航道是松滋河东支与虎渡河汇合后的合称，是洞庭湖区重要的水运通道之一。

松虎航道始于新开口经小河口于肖家湾汇入澧水洪道，承接部分长江洪水进入洞庭湖，其分流与调蓄作用对长江中游地区防洪起着十分重要的作用。

但是，松虎航道地形复杂，河道形态变化多样，浅滩、分汊河段交错，为了能使松虎航道等级提升到1 000 t级航道标准，应保持航道路线及航槽的位置不变。

因分汊河段的通航汊道稳定，整治工程主要利用疏浚和切滩对航道进行扩建。

本文针对该工程情况，利用二维水流数学模型[1-5]进行模拟研究，探索整治工程的合理性。

河段位置示意见图1。

1.1 基本控制方程采用基于水深平均的平面二维数学模型来描述水流运动，直角坐标系下水流运动的控制方程如下。

大连理工大学硕士学位论文浅水间断流动数值模拟及其在溃坝水流问题中的应用姓名:刘刚申请学位级别:硕士专业:水力学及河流动力学指导教师:金生20090625大连理工大学硕士学位论文摘要现代浅水流动数值模拟的一个主要方向是利用齐次浅水方程和方程在数学形式上的相似性,借用计算气体动力学的高性能算法,并结合浅水流动的特殊性建立适合与模拟溃坝、涌潮等有间断或弱间断纯在的流动数值模拟。

本文在前人研究的基础上,采用高性能格式有限体积方法,建立了一套基于非结构化网格三角形的二维浅水流动数值模拟。

在模型的空间离散过程中,本文应用迎风有限体积方法,建立了二维带源项浅水的高精度、高分辨率非结构化网格模型,并成功应用于复杂地形下间断流和溃坝波的数值模拟。

采用非结构化网格技术,以格式的近似解为基础,建立了二维带源项浅水方程的通量平衡求解格式。

提出了特征分解和迎风处理源项的方法,平衡了非平底时界面通量,保证了非平底坡浅水方程计算的和谐性、增加了格式的稳定性。

方程中通量梯度项与源项的平衡,使模型可以适合复杂地形下浅水流动问题和间断问题的求解,并最终建立了和谐的.格式的有限体积模型。

动边界是浅水模拟中一个关键性难题。

本文提出了一种处理带有干湿界面的非恒定浅水流动的无质量误差方法。

采用适当的干湿界面处理技术以满足静水问题,同时对有干湿界面的复杂地形的非恒定流达到无质量误差。

将本文建立的非结构网格迎风格式的有限体积模型对间断水流中一些经典的或有解析解的算例,比如问题、二维局部溃坝问题、倾斜水跃问题、二维非平底溃坝问题以及有激波混合流问题等,进行数值模拟。

所有计算结果符合其物理意义,与解析解吻合较好,在间断附近陡峭,不含非物理的伪振荡,验证了本文模型的正确性与适用性。

模型也成功应用于实际水流、溃坝的数值模拟中,验证了该格式具有相容性好、物理意义更为清晰,编程易于实现等优点。

所有研究成果表明,本文建立的数学模型具有较好的水流模拟性能,具有广泛的应用前景。

二维浅水方程
二维浅水方程是一类描述水波传播的偏微分方程，也可用于模拟洪水、海啸等自然灾害。

该方程的基本形式为：
$$begin{aligned}
frac{partial h}{partial t}+
abla cdot left(hboldsymbol{u}right)=0,
frac{partial boldsymbol{u}}{partial t}+boldsymbol{u}cdot abla boldsymbol{u}+g
abla h=0,
end{aligned}$$
其中$h$为水深，$boldsymbol{u}$为水平速度，$g$为重力加速度。

这两个方程可以看作是质量守恒和动量守恒的表述，描述了水体在流动过程中的行为。

二维浅水方程的求解是一个复杂的数值计算问题，需要运用数值方法和计算机模拟技术。

常用的求解方法包括有限差分法、有限体积法、有限元法等。

这些方法都需要根据具体问题的特点来选取适当的离散格式，以保证数值解的精度和稳定性。

二维浅水方程在自然灾害预测、海洋工程、水资源管理等领域有广泛的应用。

许多研究者也在不断地改进和完善求解方法，以适应更加复杂的实际问题。

- 1 -。

基于无结构化网格浅水方程的隐式解法唐岳灏【摘要】In order to improve the numerical stability of shallow water equation calculated by Finite Volume Method, by emplo-ying Roe's approximate Riemann solution to calculate the interface flux and TVD-MUSCL Format to reconstruct the conservation variable, a high efficient implicit computation scheme is derived. On the basis of the unstructured grids, this format improves the computation accuracy to grade 2. It computes the velocity gradient by the area weight and satisfies the stationary hydraulic pres-sure equilibrium by handling the bed slope term. In order to use the implicit scheme for the time integration, the full resolution form of Jacobian matrix is analytically derived, which was solved by Newton-Raphson algorithm iteratively. By the comparison with various numerical studies on dam-breaking cases, this computation method is proved to be stable, compatible and efficient with the capability of accurately capturing the shock wave in dam-breaking problems.%为提高有限体积法计算浅水方程的数值稳定性，采用Roe方法近似Riemann解计算界面通量，利用TVD-MUSCL格式对守恒变量进行重构，推导并建立了高效的隐式计算格式。

基于Roe格式黎曼近似解的二维FVM模型汪梅华;张铭;柳杨;乌景秀【摘要】提出一种基于黎曼近似解Godunov格式的二维FVM模型求解口门区二维通航水力特性,并采用Roe格式计算界面通量.采用水面坡度代表源项中压力项的作用,有利于复杂地形条件计算的稳定性;通过对斜底单元干湿特性的合理划分,确保计算单元的水量和动量平衡及数值计算精度.利用该模型计算分析了衢江梯级塔底枢纽上下游口门区及引航段发电及泄洪条件下的通航水力特性,结果表明Roe格式的有限体积方法计算复杂地形条件下的水流流场稳定性好、计算精度高,为合理制定衢江梯级枢纽调度规则提供数据支持.【期刊名称】《水利水运工程学报》【年(卷),期】2016(000)003【总页数】8页(P27-34)【关键词】山溪型航道;有限体积法;Roe格式;二维水力计算模型【作者】汪梅华;张铭;柳杨;乌景秀【作者单位】衢州市港航管理局,浙江衢州324002;南京水利科学研究院,江苏南京210029;南京水利科学研究院,江苏南京210029;南京水利科学研究院,江苏南京210029【正文语种】中文【中图分类】TV135.4金沙江、乌江、西江、衢江等为我国重要通航水运要道，一大批通航枢纽已陆续建成并投入运行[1-3]。

西部航道具有显著的山溪型航道特征，河道地形复杂，水力特性敏感，电站调峰或大坝泄洪对航运的影响十分突出，枢纽瞬时下泄流量的快速改变恶化枢纽附近口门区、上下游引航道、连接段及下游航道通航水力学条件[4-6]，对枢纽下游航运带来安全隐患。

本文提出一种基于黎曼近似解Godunov格式的二维FVM模型求解口门区二维通航水力特性，并采用Roe格式计算界面通量。

该模型源项中采用水面坡度代表压力项的作用，避免了对底坡项的复杂处理，有利于复杂地形条件下计算的稳定性；通过对斜底单元干湿特性的合理划分，实现水位和水深合理转换；基于物理通量严格守恒，确保计算单元的水量和动量平衡及数值计算精度[9-11]。

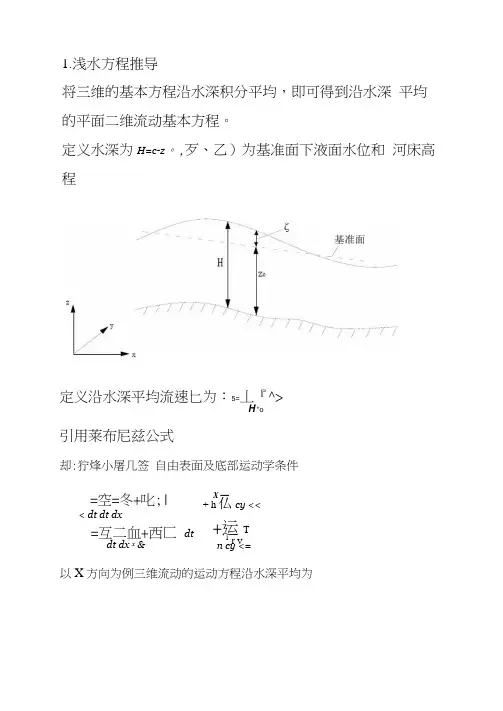
1.浅水方程推导将三维的基本方程沿水深积分平均，即可得到沿水深 平均的平面二维流动基本方程。

定义水深为H=c-z 。

,歹、乙）为基准面下液面水位和 河床高程定义沿水深平均流速匕为：5=丄『^>H "o引用莱布尼兹公式却:狞烽小屠几签 自由表面及底部运动学条件=空=冬+叱;|< dt dt dx=互二血+西匚 dtdt dx x &以X 方向为例三维流动的运动方程沿水深平均为X —+ h 仏 cy <<+运T1r v n cy <=类似，可以得到代如竹6HU x Uy祐—一L z - 一鬲一_§你比j d2u v d2U~d （-- 、 d ,---- 、d （-- 、1 dp ^d2u x-・・、. v 叫、丿n八施W"）坛曲”别沁“万乔5龙+肩+廿）比" 非恒定项积分£敎冷帥-知0HU x朗一=——一—你dt dt对流项积分首先将时均流速分解为兀=式中s为垂线平均流速，A坷为时均流速匚与垂线平均流速S的差值。

+聪匚dx x xu x u s dz, = P (t/v + Aw v)(t/v + Aw v)dz=[(S匕+ △匚瓯+ 2U庖⑷J®二叫S+J* 4：^x dz = P xx HUp x「Aw v Aw v tZz式中，久i+皂― ，是由于流速沿垂线分布不均匀而引入的HU X U X修正系数，类似于水力学中的动量修正系数，其数值一般在1.02-1.05,可以近似取1.0,因此^du x u x^_dHU x U x & Jdz = ------ -^-u.u rdx dx dx x xL如—=c^~dy UxUy上几式相加，并利用底部及自由表面运动学条件可得§ ___ 6 ______ e +去U 叫）+咅他竹）+王（叫M z ）战 dHU v dHUU v dHU x U xdtdx压力项积分将万二Qg （孑-Z ）代入上式后化简得:=PgH g + pgH J = pgH 二ox oxex扩散项积分M （勢+襄+襄）心气（学+摯比 dr 0）厂 dz ：汰勿-H上式右边后两项分别为由底部创而阻力和表而风阻力引起的阻力项。

防洪保护区水动力一二维精细化模拟模型及应用张庆梓;刘小龙;陈俊鸿;彭思韦【摘要】为准确合理地进行洪水演进模拟,完成防洪保护区的洪水风险图编制工作,本文建立了能够对防洪保护区溃堤洪水进行模拟的一、二维耦合水动力学模型.一维水动力学模型采用有限差分法求解,二维水动力学模型采用二维有限体积法求解浅水流方程组.模拟结果表明,与传统方法相比该模型能有效提高复杂区域内模型计算效率,所得信息可为防洪决策部门提供参考依据.【期刊名称】《治淮》【年(卷),期】2016(000)009【总页数】3页(P19-21)【关键词】水动力学;一、二维耦合模型;洪水风险分析;药湖联圩【作者】张庆梓;刘小龙;陈俊鸿;彭思韦【作者单位】河海大学南京 210098;南京水利科学研究院水文水资源与水利工程科学国家重点实验室南京 210029;河海大学南京 210098;河海大学南京 210098【正文语种】中文水动力数值模拟技术可以广泛地应用于灾害预警、避险转移、洪水影响评价、洪泛区管理等方面，为相关部门提供有力的决策支撑。

目前，一维动力学模型主要用于长河段的洪水演进预报，主要优点是可以快速、准确地模拟复杂河网的水位、流量过程，同时在处理河道上的一些建筑物（如闸门、泵站等）时非常灵活方便。

但溃堤后的洪水具有明显的二维特性，对于防洪保护区，水流运动复杂，人工建筑物（如房屋、道路等）常常改变水流流向，二维动力学模型更适宜进行此类复杂的水流运动模拟。

相对于一维水动力学模型而言，二维水动力学模型能够提供更加丰富的计算信息，如洪水到达时间、淹没范围、淹没水深、淹没历时等。

但二维水动力学模型也存在计算时间较长、对地形资料要求较高、在洪水风险图系统中数据调用效率较低等问题。

对于解决具有多空间尺度的实际问题（如河道溃堤及溃堤水流演进问题），针对不同的研究区域，运用不同的数学模型，充分发挥模型各自的优势，满足实际需要与提高模型计算效率很有必要。

本文运用地理信息系统，整合防洪保护区地形、道路及建筑物等空间信息，建立基于防洪保护区一维河网模型与二维保护区模型一、二维水动力耦合模型，对道路进行抽稀处理后，将道路和堤防作为保护区内的挡水建筑物处理。

A辑第22卷第3期水动力学研究与进展Ser.A,Vol.22,No.32007年5月JOURNAL OF H YDRODYN AMICS May,2007文章编号:100024874(2007)0320305206二维浅水方程的高阶松弛格式求解*陈建忠1,史忠科2,胡彦梅2(1.西北工业大学,西安710072;2.长安大学理学院,西安710064)摘要:利用松弛方法,将二维浅水方程转化为松弛方程组,并用逐维五阶WENO重构和显隐式Runge2Kutta方法对松弛方程组的空间和时间方向进行离散,建立了求解二维浅水方程的五阶松弛格式。

WENO重构方法的引入既提高了格式的精度,又可保证格式是无振荡的。

应用该格式对圆柱溃坝等问题进行了数值模拟,计算结果与用其它方法所得结果吻合,表明了方法的有效性。

关键词:二维浅水方程;松弛格式;WENO重构;逐维方法中图分类号:T V131.4文献标识码:ANumerical solution of the two2dimensional shallowwater equations by high order relaxation schemeCH EN Jian2zhong1,SH I Zhong2ke1,H U Yan2mei2(1.N orthwestern Polytechnical U niversity,Xi.an710072,China;2.College of Science,Chang.an U niversity,Xi.an710064,China)Abstr act:A fifth2order relaxation scheme for the two2dimensional shallow water equations is proposed in this pa per.The scheme is based on replacing t wo2dimensional shallow water equations by t he r elaxation syst em.The spatial discr etization and time integration of the relaxation system a re implemented by a fifth2order weighted essentia lly non2oscillatory(WENO)recon2 str uction and the implicit2explicit Runge2Kutt a method,respect ively.The WENO reconstruction is chosen to improve the accu2 r acy and guar antee the non2oscillatory behavior of the pr esent scheme.T he resulting method is applied to simulat ing several tests,in par ticular,cir cular dam2br eak problem.The results show in good agr eement with numerical results obtained by other met hods.The simulated r esults also demonst rate that the pr esented met hod is stable and eff icient.Key words:two2dimensional shallow water equations;relaxation scheme;WENO reconstruction; dimension2by2dimension approach*收稿日期:2006212201(2007201230修改稿)作者简介:陈建忠(1976)),男,宁夏盐池人,讲师,博士。

基于自适应网格的二维水动力模型
于汪洋;马建明;尹岳明;喻海军;吴滨滨;穆杰
【期刊名称】《中国防汛抗旱》
【年(卷),期】2022(32)3
【摘要】为准确地模拟流域洪水传播和淹没情况,基于自适应网格技术,以有限体积法为离散格式构建数值模型。

模型以二维浅水方程为控制方程,采用HLL格式近似黎曼解计算界面通量,采用WAF格式对计算的通量进行加权修正,保证时间和空间上的二阶精度,并使其满足TVD条件,减小数值振荡。

底坡源项采用水深差分重构,摩阻源项采用半隐式格式,保证数值计算的和谐性和稳定性。

自适应网格形式为四叉树网格,在水位梯度较大的区域进行网格细化。

算例验证表明:自适应网格技术可以自动识别参数梯度较大的区域以及干湿边界,自行调整网格尺寸,准确模拟水流传播的动态变化,可应用于实际的洪水模拟。

【总页数】7页(P66-72)
【作者】于汪洋;马建明;尹岳明;喻海军;吴滨滨;穆杰
【作者单位】中国水利水电科学研究院防洪减灾研究所;水利部防洪抗旱减灾工程技术研究中心;国家自然灾害防治研究院;四川省水利规划研究院
【正文语种】中文
【中图分类】TV131;TV877
【相关文献】
1.黄浦江二维曲线网格水动力与物质输运数学模型及其应用
2.基于滑移网格与RNG湍流模型的螺旋桨水动力性能研究
3.基于HEC-RAS和二维水动力模型的斜交桥梁壅水计算优化
4.基于二维水动力模型的应急水源地引调水方案优化设计
5.基于一二维水动力模型的山丘区小流域洪水模拟与淹没分析
因版权原因，仅展示原文概要，查看原文内容请购买。

基于二维水流数学模型的壅水分析计算段璆【摘要】长沙市湘江巴溪洲综合整治利用工程建成后,使上下游河段水流形态发生变化,上游河段水位有不同程度的壅高,为了较精确地计算巴溪洲工程建设对湘江河道防洪的影响,采用河道平面二维水流数学模型进行工程对河道行洪水位和流场影响的计算,并对工程前后工程河段水位和流速等的变化进行分析.【期刊名称】《湖南水利水电》【年(卷),期】2016(000)002【总页数】4页(P42-45)【关键词】壅高;二维水流数学模型;水位;流速【作者】段璆【作者单位】长沙市水利水电勘测设计院长沙市410015【正文语种】中文（长沙市水利水电勘测设计院长沙市410015）巴溪洲综合整治利用工程位于湘江干流长沙河段南部，湘江黑石铺大桥以南约3 km位置，隶属长沙市岳麓区。

巴溪洲与湘江东岸（长沙市天心区暮云开发区）隔水相距不到1 km，与湘江西岸（坪塘集镇）相隔不到300 m。

巴溪洲长约3 450 m，平均宽度约300 m，最大宽度约400 m，总体地形为北高南低，洲面高程主要在（30～34）m之间，最高洲面高程为36.4 m。

该河段平均河宽约1 100 m，最大河宽约1 230 m。

巴溪洲位于湘江河道左侧，将湘江分为左右两汊，左汊河宽（180～260）m；右汊为主航道，河宽（600～820）m。

由于巴溪洲是由河道泥沙淤积形成的天然沙洲，洲滩地质条件较差，目前岸坡崩塌、失稳现象比较普遍，巴溪洲综合整治工程的建设会加大洲滩边坡的冲刷，势必会对巴溪洲的建设造成较大的不利影响。

加上湘江长沙综合枢纽下闸蓄水后，水位抬升更加容易引起巴溪洲岸坡崩塌、失稳等。

2.1 工程阻水要素分析根据工程设计方案，选取断面k3+650、k3+400、k2+650、k1+800、K1+000、k0+200为控制断面。

根据巴溪洲河段河道地形以及实测大断面，确定工程建设前各频率设计洪水位下过水面积及水面宽；根据巴溪洲综合整治工程可研方案，计算工程建设后各频率设计洪水位过水面积。

第34卷第3期 2011年9月中 国 航 海N AV IG AT ION O F CH IN AVol.34No.3 S ep.2011收稿日期:2011-05-16作者简介:石爱国(1956-),男,吉林德惠人,教授,从事舰船操纵性研究。

E -mail:AGShi56@.文章编号:1000-4653(2011)03-0069-05船舶浅水水动力导数的数值计算石爱国, 闻 虎, 李 理, 刘 可, 刘 博(海军大连舰艇学院,辽宁大连116018)摘 要:船舶浅水水动力导数对研究浅水中船舶操纵性有重要的意义。

以/M ariner 0船模为研究对象,采用Realiz -ablek-E 湍流模型来封闭RA N S 方程,运用SIM PL E 算法,对两种水深的浅水定漂角、定舵角、纯艏摇试验进行了数值模拟。

实现了浅水水动力导数的求取,并将计算结果与模型试验结果进行对比,验证了方法的有效性。

关键词:船舶,舰船工程;操纵性;计算流体力学;浅水水动力导数;数值模拟;模型试验中图分类号:U 661.1 文献标志码:AComputation of Hydrodynamic Derivatives for Ships in Shallow WaterShi A ig uo , Wen H u , L i L i, L iu K e, L iu Bo (Dalian N av al Academ y,Dalian 116018,China)Abstract:H ydro dy namic deriv atives of ships in shallow w ater ar e essential for study ing ship maneuv erability in sha-l lo w w ater.T aking t he ship model "M a riner"as the study ing object,this pa per carr ies o ut a series of numerical sim -ulatio n under stat ic dr ift,st atic rudder and pure y aw in tw o differ ent w ater depths by so lving the Reynolds -aver age N -S equations w ith Realizable turbulence model using SIM PL E algo rithm.T he numerical results are compared w ith ex per iment al results and calculated results published in literature to pro ve t he effect iveness of the numer ical method.Key words:ship,nav al engineer ing ;maneuv erability ;CFD;hy dr odynamic der ivatives f or shallow water ;numer ical simulation;mo del ex periment操纵性是船舶的重要航海性能,与航行的安全性和营运的经济性密切相关。