八年级数学上册各章主要知识数学思想方法框架图素材(新版)北师大版

各章主要知识数学思想方法框架图
方程思想
综合运用
寻求不变量
方案优选第二章实数
点重绝对值恒等变形
二次根式的定义二立估平次程序化思想方方根算最简二次根式式根根
比较大小法估算有限与无限
夹逼法
一次函数第四章．
二元一次方程组五章第
现实情
境消元法
一次方程有关概念
程序化思想主要一次方程
三元一次方程组对应思想二元一次方程组
数形结合
念二方与方殊三念三化归与转化元）元元一程一程一一
次次组次次
方组方方函的程
程程
变化思想（平组的两数组组的的种的的解应有有法关解关关（用系法概概特待定系数法
法列表
象图法
数据的分析第六章
均中众中中数
与获取、处理信
加位位位权
平
均
数数数数数处理问题方法
第七章平行线的证明
定义、命题的含义
定义与基本事实法例反公理、定理、证明的含义
同平三论三法反证角行角角形线等形的角的内三对性角边质顶多样化思考问和关与角的系的判定的定证理证明及明
推。

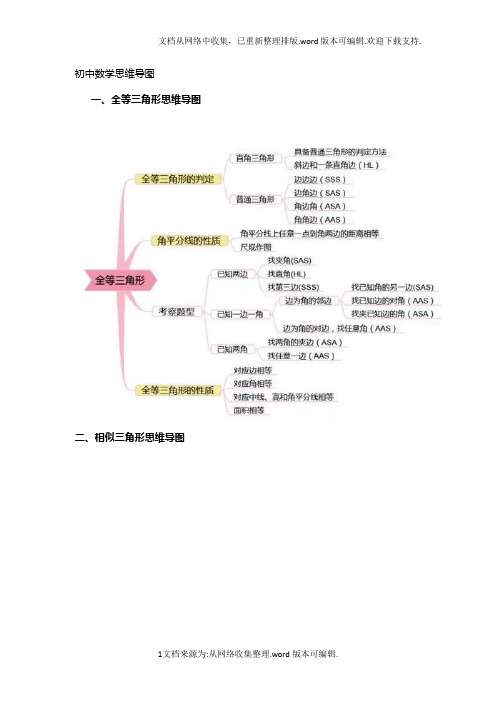
八年级各章知识点思维导图厚积薄发，学习的过程离不开知识点的积累。

在学习新知识的同时，我们也需要对已经学过的知识点进行整理和回顾。

在这里，为大家提供八年级各章知识点思维导图，旨在帮助同学们回顾所学知识，加深记忆，提高成绩。

一、数学第一章有理数- 有理数的概念- 有理数的比较大小- 有理数的加减法- 有理数的乘法- 有理数的除法第二章整式与分式- 整式的概念- 分式的概念- 分式的化简与运算- 多项式的运算第三章一次函数及其图象- 一次函数的概念- 一次函数的表示方法及其性质- 一次函数的图象及其特征- 一次函数的应用第四章等比数列- 等比数列的概念- 等比数列的通项公式- 等比数列的前n项和- 等比数列的应用二、英语第一章数字和时间- 数字的读法及运用- 时间的读法及运用第二章班级活动和照片介绍- 班级活动的常用表达- 照片的描述方法- 班级活动和照片的介绍第三章询问地址和指路- 询问地址的表达方式- 指路的表达方式- 询问地址和指路的实际运用第四章常见交通工具及其介绍- 常见交通工具的表达方式- 交通工具的介绍方法- 交通工具的选择与使用三、语文第一章古诗词鉴赏- 古诗词的基本概念- 古诗词的分类- 古诗词的鉴赏方法第二章作文- 作文的基本要素- 作文的分类- 作文的写作技巧第三章阅读理解- 阅读理解的基本技能- 阅读理解的常用题型- 阅读理解的解题技巧第四章修辞手法- 修辞手法的基本概念- 修辞手法的分类- 修辞手法的应用及效果思维导图是一种有效的学习工具，其能够帮助我们整理、归纳知识，帮助我们记忆和应用所学知识。

希望同学们能够运用这些思维导图进行学习，取得更好的成绩。

让我们一起加油！。

初中数学八年级上册思维导图一、数的开方1. 平方根：如果一个正数x的平方等于a，那么x是a的平方根，记作x=√a。

正数a的平方根有两个，它们互为相反数，分别记作+√a 和√a。

0的平方根是0，负数没有平方根。

2. 立方根：如果一个数x的立方等于a，那么x是a的立方根，记作x=³√a。

每个实数都有唯一的立方根。

3. 开方运算：开方运算是求一个数的平方根或立方根的运算。

对于正数a，开方运算可以表示为√a或³√a。

二、实数1. 实数的概念：实数包括有理数和无理数。

有理数是可以表示为两个整数比的数，无理数是不能表示为两个整数比的数。

2. 实数的分类：实数可以分为正实数、负实数和0。

正实数是大于0的实数，负实数是小于0的实数，0既不是正实数也不是负实数。

3. 实数的运算：实数可以进行加法、减法、乘法和除法运算。

在运算过程中，需要遵循实数的运算规律，如交换律、结合律和分配律。

三、勾股定理1. 勾股定理的内容：勾股定理指出，在一个直角三角形中，直角边的平方和等于斜边的平方。

即a²+b²=c²，其中a、b是直角边，c是斜边。

2. 勾股定理的应用：勾股定理可以用来解决直角三角形中的边长问题，也可以用来解决一些与直角三角形相关的实际问题。

3. 勾股定理的证明：勾股定理的证明有多种方法，其中一种常见的证明方法是使用几何图形的面积关系。

四、一次函数1. 一次函数的概念：一次函数是指函数的图像是一条直线，其一般形式为y=kx+b，其中k是斜率，b是截距。

2. 一次函数的性质：一次函数的图像是一条直线，斜率k表示直线的倾斜程度，截距b表示直线与y轴的交点。

3. 一次函数的应用：一次函数可以用来描述一些线性关系，如物体的速度与时间的关系、正比例关系等。

五、不等式1. 不等式的概念：不等式是表示两个数之间大小关系的数学表达式，如a>b、a<b、a≥b、a≤b等。

2. 不等式的性质：不等式可以进行加减、乘除运算，但在乘除运算中需要注意符号的变化。

《数学》（八年级上册）知识点总结第一章 勾股定理1、勾股定理 直角三角形两直角边 a ，b 的平方和等于斜边 c 的平方，即 a 2 b 2 c 22、勾股定理的逆定理 如果三角形的三边长 a ，b ，c 有关系 a 2 b 2 c 2，那么这个三角形是直角三角形。

3、勾股数 ：满足 a 2 b 2 c 2的三个正整数，称为勾 股数。

常用勾股数组及几种通式 （3 、4、5） （5 、12、13） （7 、24、 25） 第二章 实数 、实数的概念及分类1、实数的分类正有理数 零 负有理数 正无理数无限不循环小数负无理数2、无理数： 无限不循环小数叫做无理数。

在理解无理数时，要抓住“无限不循环” ，归纳起来有四类：（1）开方开不尽的数，如 7,32 等；（ 2）有特定意义的数，如圆周率 π，或化简后含有 π的数，如 π+8 等； （ 3）有特定结构的数，如 0.1010010001⋯等； （4）某些三角函数值，如 sin60o等 二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零） ，从数轴上看，互为相反 数的两个数所对应的点关于原点对称，如果 a 与 b 互为相反数，则有 a+b=0， a= -b ，反之亦成立。

2、绝对值在数轴上，一个数所对应的点与原点的距离，叫做该数的绝对值。

（ |a|≥0）。

零的绝对值是它本身，也可看成它的相反数，若 |a|=a ，则 a ≥0；若 |a|= -a ，则 a ≤0。

3、倒数如果 a 与 b 互为倒数，则有 ab=1，反之亦成立。

倒数等于本身的数是 1 和-1。

零没有倒数。

4、数轴规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可） 三、平方根、算数平方根和立方根1、算术平方根：一般地，如果一个正数 x 的平方等于 a ，即 x 2=a ，那么这个正数 x 就叫做 a 的算术平方根。

初中数学八年级上册思维导图一、数的开方1. 平方根：如果一个正数x的平方等于a，那么x是a的平方根，记作x=√a。

正数a的平方根有两个，它们互为相反数，分别记作√a和√a。

0的平方根是0。

2. 立方根：如果一个数x的立方等于a，那么x是a的立方根，记作x=³√a。

立方根只有一个。

3. 算术平方根：正数a的正的平方根，记作√a，称为a的算术平方根。

4. 立方根的性质：①正数的立方根是正数；②负数的立方根是负数；③0的立方根是0。

二、实数1. 实数的概念：实数包括有理数和无理数。

有理数是可以表示为两个整数比的数，无理数是不能表示为两个整数比的数。

2. 实数的分类：①正实数；②负实数；③零。

3. 实数的运算：实数的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

三、二次根式1. 二次根式的概念：形如√a的式子，其中a≥0，称为二次根式。

2. 二次根式的性质：①√a²=a（a≥0）；②（√a）²=a（a≥0）；③√ab=√a√b（a≥0，b≥0）；④√a²+b²=√a²+√b²（a≥0，b≥0）。

3. 二次根式的运算：二次根式的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

四、一元二次方程1. 一元二次方程的概念：形如ax²+bx+c=0（a≠0）的方程，称为一元二次方程。

2. 一元二次方程的解法：①配方法；②求根公式法；③因式分解法。

3. 一元二次方程的根的判别式：判别式△=b²4ac，当△>0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△<0时，方程没有实数根。

五、不等式1. 不等式的概念：表示不相等关系的式子称为不等式。

2. 不等式的性质：①两边同时加上或减去同一个数，不等号方向不变；②两边同时乘以或除以同一个正数，不等号方向不变；③两边同时乘以或除以同一个负数，不等号方向改变。