离散小波变换去噪Matlab源程序
- 格式:pdf
- 大小:176.36 KB
- 文档页数:3

matlab小波去噪源码以下是一个简单的Matlab小波去噪的示例源码:matlab.% 加载待去噪的信号。
load('noisy_signal.mat'); % 假设信号保存为noisy_signal.mat文件中的一个变量。
% 设置小波去噪的参数。
wavelet = 'db4'; % 选择小波基函数,这里使用Daubechies 4小波。
level = 5; % 小波分解的层数。
threshold_rule = 'sqtwolog'; % 阈值选取规则,这里使用sqtwolog规则。
% 对信号进行小波分解。
[c, l] = wavedec(noisy_signal, level, wavelet);% 估计噪声水平。
sigma = median(abs(c)) / 0.6745;% 计算阈值。
threshold = sigma sqrt(2 log(length(noisy_signal))); % 应用软阈值。
c_denoised = wthresh(c, threshold_rule, threshold);% 重构去噪后的信号。
denoised_signal = waverec(c_denoised, l, wavelet);% 可视化结果。
subplot(2,1,1);plot(noisy_signal);title('原始信号');subplot(2,1,2);plot(denoised_signal);title('去噪后的信号');这段代码首先加载待去噪的信号,然后设置小波去噪的参数,包括选择小波基函数、小波分解的层数和阈值选取规则。
接下来,代码对信号进行小波分解,并估计噪声水平。
然后,计算阈值,并应用软阈值函数对小波系数进行去噪处理。
最后,通过小波重构得到去噪后的信号,并将原始信号和去噪后的信号进行可视化比较。


基于小波变换的信号降噪研究摘要:本文分析了通信系统信号处理中噪声的小波分析特性,用一维小波对含有噪声的信号进行了分析和研究,提出了基于小波分析理论对于高频信号和高频噪声干扰相混叠的信号中小波变换用于对含有噪声信号进行的小波分解仿真实验。
利用小波变换对含噪信号进行小波分解,实现了信号的降噪处理。
关键词:小波分析 降噪 MATLAB1 引言在这个科技飞速发展,信息传递日益方便快捷的时代。
信息资源中的信号应用日益广泛,信号的结构越来越复杂,为了更加清楚的分析和研究实际工程中信号的有用信息,对信号进行消噪处理是至关重要的,而且在现实生活和工作中,噪声无处不在,在许多领域中,如天文、医学图像和计算机视觉方面收集到的数据常常是含有噪声的。
噪声可能来自获取数据的过程,也可能来自环境影响。
在工程实际测试得到的信号中,由于种种原因,总会存在噪声,噪声的存在往往会掩盖信号本身所要表现的信息,所以在根据测试信号对设备进行故障诊断时,一般首先要对信号进行消噪处理,消噪的主要基础就是噪声和信号的频率特征不同。
小波分析是近年来发展起来的一种新的信号处理工具,这种方法源于傅立叶分析,小波(wavelet ),即小区域的波,仅仅在非常有限的一段区间有非零值,而不是像正弦波和余弦波那样无始无终[4]。
小波可以沿时间轴前后平移,也可按比例伸展和压缩以获取低频和高频小波,构造好的小波函数可以用于滤波或压缩信号,从而可以提取出已含噪声信号中的有用信号。
2 小波分析基本理论设Ψ(t)∈L 2( R) ( L 2( R) 表示平方可积的实数空间,即能量有限的信号空间) , 其傅立叶变换为Ψ(t)。
当Ψ(t)满足条件[4,7]:2()R t dw w C ψψ=<∞⎰ (1)时,我们称Ψ(t)为一个基本小波或母小波,将母小波函数Ψ(t)经伸缩和平移后,就可以得到一个小波序列:,()()a b t b t aψ-= ,,0a b R a ∈≠ (2) 其中a 为伸缩因子,b 为平移因子。

完整版)小波变换图像去噪MATLAB实现本论文旨在研究数字图像的滤波去噪问题,以提高图像质量。
数字图像处理(Digital Image Processing。
DIP)是指用计算机辅助技术对图像信号进行处理的过程。
DIP技术在医疗、艺术、军事、航天等图像处理领域都有着十分广泛的应用。
然而,图像的采集、获取、编码和传输的过程中,都存在不同程度被各种噪声所“污染”的现象。
如果图像被污染得比较严重,噪声会变成可见的颗粒形状,导致图像质量的严重下降。
因此,通过一些卓有成效的噪声处理技术后,尽可能地去除图像噪声,有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。
小波变换处理应用于图像去噪外,在其他图像处理领域都有着十分广泛的应用。
小波定义为对给定函数局部化的新领域,小波可由一个定义在有限区域的函数Ψ(x)来构造,Ψ(x)称为母小波,或者叫做基本小波。
一组小波基函数,{Ψa,b(x)},可以通过缩放和平移基本小波来生成。
当a=2j和b=ia的情况下,一维小波基函数序列定义为Ψi,j(x)=2-j2Ψ2-jx-1.函数f(x)以小波Ψ(x)为基的连续小波变换定义为函数f(x)和Ψa,b(x)的内积。
在频域上有Ψa,b(x)=ae-jωΨ(aω)。
因此,本论文以小波变换作为分析工具处理图像噪声,研究数字图像的滤波去噪问题,以提高图像质量。
当绝对值|a|减小时,小波函数在时域的宽度会减小,但在频域的宽度会增大,同时窗口中心会向|ω|增大的方向移动。
这说明连续小波的局部变化是不同的,高频时分辨率高,低频时分辨率低,这是小波变换相对于___变换的优势之一。
总的来说,小波变换具有更好的时频窗口特性。
噪声是指妨碍人或相关传感器理解或分析图像信息的各种因素。
噪声通常是不可预测的随机信号。
由于噪声在图像输入、采集、处理和输出的各个环节中都会影响,特别是在输入和采集中,噪声会影响整个图像处理过程,因此抑制噪声已成为图像处理中非常重要的一步。

【引言】1. 背景介绍:在实际工程和科研中,数据经常受到各种噪声的干扰,因此需要对数据进行降噪处理。
2. 目的和意义:降噪处理可以使得数据更加真实可靠,有利于后续的分析和应用。
【matlab 曲线降噪的方法】3. 小波变换简介:小波变换是一种时频分析的方法,可以将信号分解为不同尺度的成分,对于曲线降噪具有很好的效果。
4. matlab中的小波变换函数:matlab提供了丰富的小波变换函数,包括连续小波变换和离散小波变换,用户可以根据具体需求选择合适的函数进行数据处理。
【matlab 曲线降噪的实现步骤】5. 数据准备:首先需要准备需要处理的数据,可以是实验采集的曲线数据,也可以是从其他渠道获取的曲线信息。
6. 选择小波函数:根据数据的特点和需求,选择合适的小波函数进行变换,常用的小波函数包括Daubechies小波、Haar小波等。
7. 对数据进行小波变换:利用matlab提供的小波变换函数,对数据进行小波分解,得到不同尺度的小波系数。
8. 降噪处理:根据小波系数的大小和分布,可以采用阈值处理、软硬阈值处理等方法对小波系数进行滤波,实现曲线的降噪处理。
9. 重构数据:经过降噪处理后,需要利用小波系数重构原始数据,得到降噪后的曲线信息。
【matlab 曲线降噪的应用实例】10. 实验数据:以某地震波形数据为例,介绍如何利用matlab的小波变换函数进行曲线降噪处理。
11. 数据分析:对比降噪前后的波形数据,分析降噪处理的效果和优势。
12. 结果展示:通过图表展示降噪前后的数据对比,直观地展现曲线降噪的效果。
【matlab 曲线降噪的注意事项】13. 参数选择:在进行小波变换和降噪处理时,需要合理选择小波函数和参数,以及阈值处理的方式和大小。
14. 原理理解:对小波变换的原理和数据特点有一定的理解,有利于选择合适的方法和优化参数。
15. 实时调试:在实际应用中,可以通过反复调试和对比分析来确定最佳的处理方案,实现最佳的降噪效果。


%自动小波阈值选择去噪(scale-dependent),lambda=m/0.6745*sqrt(2*ln(n))%参考文献:% Ma X, Zhou C, Kemp I J. Automated wavelet selection and thresholding for PD detection[J]. Electrical Insulation Magazine IEEE, 2002, 18(2):37-45.%主要函数:wavedec,detcoef,wrcoeffunction y_denoised=DWTdenoising_automaticthreshold(noisydata,wavebase,nlevel,thresholdtype,threshold)% y_denoised--去噪后信号% noisydata--含噪信号-待去噪信号% wavebase--母小波、小波基函数% nlevel--分解层数% thresholdtype--去噪方法(hard-硬阈值,soft-软阈值)% threshold--去噪时使用的阈值策略Scale: median(C)/0.6745*sqrt(2*ln(nj)); Robust: median(C)/0.6745*sqrt(2*ln(N)); Sqtwolog: sqrt(2*ln(N))% 读程序之前先了解[C,L]=wavedec得到的结果N=length(noisydata); %数据长度if size(noisydata,1)>size(noisydata,2) %处理行向量,列向量转置noisydata=noisydata';endif nargin==1 %查看输入的参数个数(nargin),比如只输入了noisydata,后面的wavebase等参数均为输入wavebase='db1'; %小波基nlevel=1; %分解层数thresholdtype='hard'; %阈值方法threshold='Scale';elseif nargin==2nlevel=1; %分解层数thresholdtype='hard'; %阈值方法threshold='Scale';elseif nargin==3thresholdtype='hard';threshold='Scale';elseif nargin==4threshold='Scale';endendendend[C,L]=wavedec(noisydata,nlevel,wavebase);L1=fliplr(L(1:nlevel+1));switch thresholdtypecase 'hard' %硬阈值去噪for j=1:nlevelCD=detcoef(C,L,j);if strcmp(threshold,'Robust')lambda=median(abs(CD))/0.6745*sqrt(2*log(N));elseif strcmp(threshold,'Sqtwolog')lambda=sqrt(2*log(N));elselambda=median(abs(CD))/0.6745*sqrt(2*log(L1(j))); %scale-dependent threshold endendfor k=1:L1(j)if abs(CD(k))<=lambdaCD(k)=0;endendC(sum(L1(j+1:end))+1:sum(L1(j+1:end))+L1(j))=CD;endcase 'soft' %软阈值去噪for j=1:nlevelCD=detcoef(C,L,j);if strcmp(threshold,'Robust')lambda=median(abs(CD))/0.6745*sqrt(2*log(N));elseif strcmp(threshold,'Sqtwolog')lambda=sqrt(2*log(N));elselambda=median(abs(CD))/0.6745*sqrt(2*log(L1(j))); %scale-dependent threshold endendfor k=1:L1(j)if abs(CD(k))<=lambdaCD(k)=0;elseif CD(k)>lambdaCD(k)=CD(k)-lambda;elseif CD(k)<-lambdaCD(k)=CD(k)+lambda;endendendendC(sum(L1(j+1:end))+1:sum(L1(j+1:end))+L1(j))=CD;endotherwiseprintf('Wrong Input Parameters!\n');endy_denoised=zeros(size(noisydata));for j=1:nlevely_denoised=y_denoised+wrcoef('d',C,L,wavebase,j); %逐层恢复细节系数endy_denoised=y_denoised+wrcoef('a',C,L,wavebase,nlevel); %恢复近似系数。

小波去噪是信号处理中常用的一种方法,在MATLAB中也有相应的函数可以实现小波去噪。
下面我们将介绍MATLAB中对1维数据进行小波去噪的具体过程。
1. 准备原始数据我们需要准备一维的原始数据,可以是来自传感器采集的数据,也可以是从文件中读取的数据。
在MATLAB中,可以使用load函数或者从其它数据源导入数据。
2. 选择小波基和分解层数在进行小波去噪之前,需要选择适合的小波基和分解层数。
MATLAB 中提供了丰富的小波基选择,包括Daubechies小波、Symlet小波、Coiflet小波等。
根据信号的特点和需要去除的噪声类型,选择合适的小波基和分解层数。
3. 进行小波分解使用MATLAB中的wavedec函数对原始数据进行小波分解。
该函数的调用形式为[C, L] = wavedec(X, N, wname),其中X为原始数据,N为分解层数,wname为小波基名称。
函数返回小波系数C和长度向量L。
4. 去除小波系数中的噪声根据小波分解得到的小波系数,可以利用MATLAB中的过滤函数对小波系数进行去噪。
常用的去噪方法包括阈值去噪、软硬阈值去噪等。
这些方法可以有效地去除信号中的噪声成分,得到干净的信号。
5. 重构信号经过去噪处理后,可以使用MATLAB中的waverec函数对去噪后的小波系数进行重构,得到去噪后的信号。
该函数的调用形式为X = waverec(C, L, wname),其中C为去噪后的小波系数,L为长度向量,wname为小波基名称。
6. 可视化和分析可以利用MATLAB中丰富的绘图函数对去噪前后的信号进行可视化比较,以及对去噪效果进行分析。
通过比较原始信号和去噪后的信号,可以直观地了解去噪效果,并进行进一步的分析和处理。
通过以上步骤,我们可以在MATLAB中对一维数据进行小波去噪处理,去除信号中的噪声成分,得到干净的信号。
小波去噪是一种简单而有效的信号处理方法,在实际应用中具有广泛的应用前景。

小波变换matlab程序小波变换是一种信号处理技术,它可以将信号分解成不同频率的成分,并且可以在不同时间尺度上进行分析。
在Matlab中,可以使用内置的小波变换函数来实现这一技术。
下面是一个简单的小波变换Matlab程序示例:matlab.% 生成一个示例信号。
t = 0:0.001:1; % 时间范围。
f1 = 10; % 信号频率。
f2 = 50; % 信号频率。
y = sin(2pif1t) + sin(2pif2t); % 信号。
% 进行小波变换。
[c, l] = wavedec(y, 3, 'db1'); % 进行3层小波分解,使用db1小波基函数。
% 重构信号。
yrec = waverec(c, l, 'db1'); % 使用小波系数和长度进行信号重构。
% 绘制原始信号和重构信号。
subplot(2,1,1);plot(t, y);title('原始信号');subplot(2,1,2);plot(t, yrec);title('重构信号');这个程序首先生成了一个包含两个频率成分的示例信号,然后使用`wavedec`函数对信号进行小波分解,得到小波系数和长度。
接着使用`waverec`函数对小波系数和长度进行信号重构,最后绘制了原始信号和重构信号的对比图。
小波变换在信号处理、图像处理等领域有着广泛的应用,可以用于信号去噪、特征提取、压缩等方面。
通过Matlab中的小波变换函数,我们可以方便地进行小波分析和处理,从而更好地理解和利用信号的特性。

小波变换去噪matlab源码小波变换是一种广泛应用于信号处理和图像处理的技术。
它通过将信号分解成不同频率的子信号,从而提供了一种有效的降噪方法。
要在MATLAB中进行小波变换去噪,您可以使用MATLAB的信号处理工具箱中提供的函数。
下面是一个示例的MATLAB源代码,用于实现小波变换去噪:```MATLAB% 加载待处理的信号signal = load('input_signal.mat');% 设置小波函数和分解层数wavelet = 'db4'; % 使用 Daubechies 4 小波函数level = 5; % 设置分解层数% 执行小波变换[coefficients, levels] = wavedec(signal, level, wavelet);% 通过阈值处理降噪threshold = wthrmngr('dw2ddenoLVL', coefficients, levels);cleaned_coefficients = wthresh(coefficients, 'h', threshold);denoised_signal = waverec(cleaned_coefficients, levels, wavelet);% 显示和保存降噪后的信号plot(denoised_signal);save('denoised_signal.mat', 'denoised_signal');```这段代码首先加载了待处理的信号,然后定义了所使用的小波函数和分解层数。
接下来,它执行了小波变换,并通过阈值处理来降噪信号。
最后,代码显示了降噪后的信号,并将其保存到文件中。
值得注意的是,该示例中使用了默认的阈值选取方式(dw2ddenoLVL),您可以根据具体的应用场景选择适合的阈值选取方法。
以上是关于在MATLAB中使用小波变换进行信号去噪的简单示例代码。
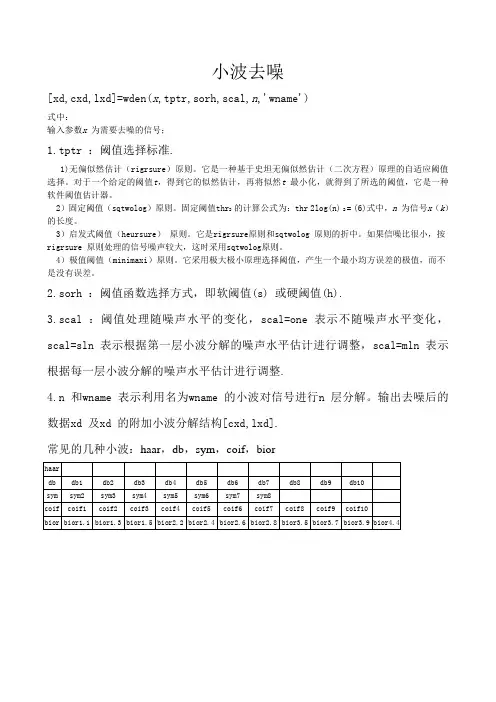
小波去噪[xd,cxd,lxd]=wden(x,tptr,sorh,scal,n,'wname')式中:输入参数x 为需要去噪的信号;1.tptr :阈值选择标准.1)无偏似然估计(rigrsure)原则。
它是一种基于史坦无偏似然估计(二次方程)原理的自适应阈值选择。
对于一个给定的阈值t,得到它的似然估计,再将似然t 最小化,就得到了所选的阈值,它是一种软件阈值估计器。
2)固定阈值(sqtwolog)原则。
固定阈值thr2 的计算公式为:thr 2log(n) 2 = (6)式中,n 为信号x(k)的长度。
3)启发式阈值(heursure)原则。
它是rigrsure原则和sqtwolog 原则的折中。
如果信噪比很小,按rigrsure 原则处理的信号噪声较大,这时采用sqtwolog原则。
4)极值阈值(minimaxi)原则。
它采用极大极小原理选择阈值,产生一个最小均方误差的极值,而不是没有误差。
2.sorh :阈值函数选择方式,即软阈值(s) 或硬阈值(h).3.scal :阈值处理随噪声水平的变化,scal=one 表示不随噪声水平变化,scal=sln 表示根据第一层小波分解的噪声水平估计进行调整,scal=mln 表示根据每一层小波分解的噪声水平估计进行调整.4.n 和wname 表示利用名为wname 的小波对信号进行n 层分解。
输出去噪后的数据xd 及xd 的附加小波分解结构[cxd,lxd].常见的几种小波:haar,db,sym,coif,bior用MATLAB对一语音信号进行小波分解,分别用强阈值,软阈值,默认阈植进行消噪处理。
复制内容到剪贴板代码:%装载采集的信号leleccum.matload leleccum;%=============================%将信号中第2000到第3450个采样点赋给sindx=2000:3450;s=leleccum(indx);%=============================%画出原始信号subplot(2,2,1);plot(s);title('原始信号');%=============================%用db1小波对原始信号进行3层分解并提取系数[c,l]=wavedec(s,3,'db1');a3=appcoef(c,l,'db1',3);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);%=============================%对信号进行强制性消噪处理并图示结果dd3=zeros(1,length(d3));dd2=zeros(1,length(d2));dd1=zeros(1,length(d1));c1=[a3 dd3 dd2 dd1];s1=waverec(c1,l,'db1');subplot(2,2,2);plot(s1);grid;title('强制消噪后的信号');%=============================%用默认阈值对信号进行消噪处理并图示结果%用ddencmp函数获得信号的默认阈值[thr,sorh,keepapp]=ddencmp('den','wv',s);s2=wdencmp('gbl',c,l,'db1',3,thr,sorh,keepapp); subplot(2,2,3);plot(s2);grid;title('默认阈值消噪后的信号');%=============================%用给定的软阈值进行消噪处理sosoftd2=wthresh(d2,'s',1.823);softd3=wthresh(d3,'s',2.768);c2=[a3 softd3 softd2 softd1];s3=waverec(c2,l,'db1');subplot(2,2,4);plot(s3);grid;title('给定软阈值消噪后的信号');ftd1=wthresh(d1,'s',1.465);。
小波变换图像降噪的matlab代码求小波变换图像降噪的matlab代码load wbarb; % 装载原始图像subplot(221); % 新建窗口image(X); % 显示图像colormap(map); % 设置色彩索引图title('原始图像'); % 设置图像标题axis square; % 设置显示比例,生成含噪图像并图示init=2055615866; % 初始值randn('seed',init); % 随机值XX=X+8*randn(size(X)); % 添加随机噪声subplot(222); % 新建窗口image(XX); % 显示图像colormap(map); % 设置色彩索引图title('含噪图像'); % 设置图像标题axis square; %用小波函数coif2 对图像XX 进行2 层分解[c,l]=wavedec2(XX,2,'coif2'); % 分解n=[1,2]; % 设置尺度向量p=[10.28,24.08]; % 设置阈值向量,对高频小波系数进行阈值处理%nc=wthcoef2('h',c,l,n,p,'s');%nc=wthcoef2('v',c,l,n,p,'s');nc=wthcoef2('d',c,l,n,p,'s');X1=waverec2(nc,l,'coif2'); % 图像的二维小波重构subplot(223); % 新建窗口image(X1); % 显示图像colormap(map); %设置色彩索引图title('第一次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例,再次对高频小波系数进行阈值处理%mc=wthcoef2('h',nc,l,n,p,'s');mc=wthcoef2('v',nc,l,n,p,'s');mc=wthcoef2('d',nc,l,n,p,'s');X2=waverec2(mc,l,'coif2'); % 图像的二维小波重构subplot(224); % 新建窗口image(X2); % 显示图像colormap(map); % 设置色彩索引图title('第二次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例。
基于小波空域相关法去噪MATLAB源程序close all;clc;clear;snr=5;init=2055615866;[xref,x]=wnoise(1,10,snr,init);signal=x;points=1024; level=5; wf='bior 1.5'; %sym8,bior 1.5[Lo_D,Hi_D,Lo_R,Hi_R]=wfilters(wf);[swa,swd] = swt(signal,level,Lo_D,Hi_D);%swd是细节系数,swa是近似系数Swd_n=swd;swd_org=swd;mask_n=zeros(size(Swd_n)); %先把系数处理矩阵设置为全0。
for j=1:(level-1)%在1:(level-1)分解层次上对高频系数处理,最后一层无法求相关系数,所以不作处理。
Noise_d1=swd_org(j,:);Noise_d1=Noise_d1(1:80);Noise_var=var(Noise_d1); %以信号的前80个只含有噪声的点估计噪声在各层的方差。
Pw_var=var(swd_org(j,:));Corr=swd_org(j,:).*swd_org(j+1,:); %定义相关系数为相邻两层的乘积。
cc=1.7; %_______用以设定停止迭代的噪声能量阈值,需要根据情况调节。
________%while Pw_var>cc*Noise_varPw=sum(abs(swd(j,:)).^2); %计算小波能量Pcorr=sum(abs(Corr).^2); %计算相关系数能量Corr_new=Corr.*((Pw/Pcorr)^0.5); %归一化corr_mod=abs(Corr_new);w_mod=abs(swd(j,:));swd_n=swd(j,:).*(corr_mod>w_mod);%(corr_mod>w_mod)返回0或者1swd_n1=(swd_n~=0);mask_n(j,:)=mask_n(j,:)+swd_n1; %将选出的点赋给系数处理矩阵相应位置。
%自动小波阈值选择去噪(scale-dependent),lambda=m/0.6745*sqrt(2*ln(n))
%参考文献:
% Ma X, Zhou C, Kemp I J. Automated wavelet selection and thresholding for PD detection[J]. Electrical Insulation Magazine IEEE, 2002, 18(2):37-45.
%主要函数:wavedec,detcoef,wrcoef
function y_denoised=DWTdenoising_automaticthreshold(noisydata,wavebase,nlevel,thresholdtype,threshold)
% y_denoised--去噪后信号
% noisydata--含噪信号-待去噪信号
% wavebase--母小波、小波基函数
% nlevel--分解层数
% thresholdtype--去噪方法(hard-硬阈值,soft-软阈值)
% threshold--去噪时使用的阈值策略Scale: median(C)/0.6745*sqrt(2*ln(nj)); Robust: median(C)/0.6745*sqrt(2*ln(N)); Sqtwolog: sqrt(2*ln(N))
% 读程序之前先了解[C,L]=wavedec得到的结果
N=length(noisydata); %数据长度
if size(noisydata,1)>size(noisydata,2) %处理行向量,列向量转置
noisydata=noisydata';
end
if nargin==1 %查看输入的参数个数(nargin),比如只输入了noisydata,后面的wavebase等参数均为输入wavebase='db1'; %小波基
nlevel=1; %分解层数
thresholdtype='hard'; %阈值方法
threshold='Scale';
else
if nargin==2
nlevel=1; %分解层数
thresholdtype='hard'; %阈值方法
threshold='Scale';
else
if nargin==3
thresholdtype='hard';
threshold='Scale';
else
if nargin==4
threshold='Scale';
end
end
end
end
[C,L]=wavedec(noisydata,nlevel,wavebase);
L1=fliplr(L(1:nlevel+1));
switch thresholdtype
case 'hard' %硬阈值去噪
for j=1:nlevel
CD=detcoef(C,L,j);
if strcmp(threshold,'Robust')
lambda=median(abs(CD))/0.6745*sqrt(2*log(N));
else
if strcmp(threshold,'Sqtwolog')
lambda=sqrt(2*log(N));
else
lambda=median(abs(CD))/0.6745*sqrt(2*log(L1(j))); %scale-dependent threshold end
end
for k=1:L1(j)
if abs(CD(k))<=lambda
CD(k)=0;
end
end
C(sum(L1(j+1:end))+1:sum(L1(j+1:end))+L1(j))=CD;
end
case 'soft' %软阈值去噪
for j=1:nlevel
CD=detcoef(C,L,j);
if strcmp(threshold,'Robust')
lambda=median(abs(CD))/0.6745*sqrt(2*log(N));
else
if strcmp(threshold,'Sqtwolog')
lambda=sqrt(2*log(N));
else
lambda=median(abs(CD))/0.6745*sqrt(2*log(L1(j))); %scale-dependent threshold end
end
for k=1:L1(j)
if abs(CD(k))<=lambda
CD(k)=0;
else
if CD(k)>lambda
CD(k)=CD(k)-lambda;
else
if CD(k)<-lambda
CD(k)=CD(k)+lambda;
end
end
end
end
C(sum(L1(j+1:end))+1:sum(L1(j+1:end))+L1(j))=CD;
end
otherwise
printf('Wrong Input Parameters!\n');
end
y_denoised=zeros(size(noisydata));
for j=1:nlevel
y_denoised=y_denoised+wrcoef('d',C,L,wavebase,j); %逐层恢复细节系数end
y_denoised=y_denoised+wrcoef('a',C,L,wavebase,nlevel); %恢复近似系数。